Aaloude en hedendaagsche scheeps-bouw en bestier

Architectura navalis et regimen nauticum

Zeventiende Hooftstuk.
Wiskonstige betooginge, van hoe veel water tegen de Scheeps-zyden rust.
Scheeps-meetingen.

Hoe veel water tegen't Schip rust.

HEt zal niet ongerymt, of buiten-spoorigh zyn, hier in te lasschen des waters perssing tegen stevige lichamen, en die toe te passen op de Scheeps uitterlykste deelen, om te zien wat zwaarte de zelvige drukt; 't geen (myns bedunkens) een nutte bespiegelinge tot deeze stoffe is. Hier toe is eenige toestel noodigh, welke, voleindight zynde, het gevolgh, myn begeerde, klaar betoont. De vermaarde Heer S. Stevin gaf my hier toe aanleiding, in zyne nooit volprezene Water-wigt; doch evenwel zoodanig niet, dat het myne het zyne is, maar ik volge zyne voet-stappen. Gelieft dan op de volgende Voorstellente letten.

I. Voorstel.

Dat op een bodem, die evenwydigh met het waters opper-vlak is, een gewight rust, zoo zwaar als een pylaar waters, wiens grondt is even aan de gegevene bodem, en zyne hooghte als een loot-lyn van 't opper-vlak des waters tot aan den bodem.

Laat a b c d, aan de figuren A en B, een water zyn, a b des zelfs opper-vlak, en g h een grondt, evenwydig met a b: ik zegge, op g h rust een pylaar waters e f g h. Het bewys aan d'eerste gestalte is kennelyk genoegh van zich zelven. De tweede bewyst men aldus: laat e f g h, aan de figuur B, een hardt lichaam zyn, even stof-zwaar met het water; 't is klaarblykelyk dat dit lichaam, in 't water dryvende, het water onder g h met de zwaarte des lichaams e f g h drukt: het water moet dan ook tegen g h met de zelve waarte drukken, anders zoude het lichaam niet in die plaats konnen blyven. Indien nu e f g h aan de zyde a d gehecht was, dit zoude geen verandering konnen veroorzaken: tegen de grondt g h rust dan de zwaarte van een pylaar waters, zoo groot als e f g h, 't welk te bewyzen was.

II. Voorstel.

Op een vier kante bodem, onevenwydigh met het waters opper-vlak, wiens hooghste zyde onder des zelfs opper-vlak is, rust een gewight, lichter als een pylaar waters, wiens grondt zy even aan de voorschreeve bodem, en des zelfs hooghte als een loot-lyn van 't waters opper-vlak, tot de onderste zyde des gegevene bodems; doch zwaarder als een pylaar waters van een zelve grondt, en hooghte als een loot-lyn van het waters opper-vlak, tot de bovenste zyde des gegevene bodems.

Laat e f, in de figuren C en D, de gegeven bodem zyn, e g en f h even aan e f, en even-wydig met het waters opper-vlak a b; ik zegge, op e f rust een gewight, minder als f h a i, en meerder als e g a i. Stelt of het water in e f g h geen zwaarte hadt, dit zoo zynde, laat dan dit water k gedrukt worden aan e g, met de zwaarte des pylaar waters a i g l, zoo zal, om bekende reden, het water in e f g h tegen e g met gelyke zwaarte parssen; want het onderste water houdt het bovenste met gelyke kracht tegen, als het bovenste drukt, terwyl het in standt blyft^*: doch, om het waters vloedigheits wil, zal ook gelyke drukking komen op e f en f h, en het water in e f g h, gedrukt zynde, zal ook alle zyn schutzels met gelyke kracht drukken; aangemerkt het water, behalven zyne

* Ziet Stevins Water-wight, X. Voorstel.

[p. 303]

zwaarte, welke alleen naar om laeg drukt, waar van hier niet werdt gesprooken, en 't geen ook, zonder merkelyke hinder in de practyk, of oeffening, kan werden verzuimt, vloeijendt is, welke vloeijentheit des waters, dewyl het werdt geperst naar alle kanten, met gelyke kracht tracht uit te spatten, en, by gevolgh, met gelyk geweldt tegen de vier zyden perst. Maar om dat het water in e f g h ook zwaar is, en dat deeze zwaarte tegen e f meer drukt als niet, en minder als tegen f h, zoo zal ook tegen e f meer gewight rusten als de pylaar water e g a i, en minder als het gewight des waters f h i a, 't welk ik bewyzen moest.

Anders.

Tegen de hoek e rust zoo veel als tegen eenige plaats, aan hem even, in de streep e g, om dat een punt in 't water, door des zelfs vloeijentheit, na alle zyden even veel geperst werdt^*: en tegen de hoek van ieder ondertogen paralel, of evenwydige streep, met e g, zoo veel als tegen eenige plaats in zyn streep: en om dat tegen ieder linie meer rust als tegen e g, en minder als tegen f h, zoo rust dan tegen de onder-hoeken meer als tegen de hoek e, en minder als tegen de hoek f, en, by gevolgh, tegen al de hoeken, dat is de streep e f; want alle de hoeken, of lichamelyke punten, maken de streep e f meer als tegen e g, en min als tegen f h.

* Ziet hier over Stevins Water-wight, X. Voorstel, I. Voorbeelt.

III. Voorstel.

Tegen een vierkante bodem, diens hooghste zyde in 't waters opper-vlak zy, rust een gewigt, even aan de helft van een pylaar waters, wiens grondt zy even aan de gegeven bodem, en zoo hoogh als de loot-lyn van 't waters opper-vlak, tot de onderste zyde des bodems.

Laat a b c d, aan de figuren E, een water zyn, a b des zelfs opper-vlak, en a d de gegeven bodem: ik zegge, tegen a d rust een halve pylaar waters, wiens grondt zy a d, of d e, (die ik even aan a d stel) en de hooghte a d, of ('t geen het zelve is) de driekante pylaar water a d e. Dat dit zoo zy, bewys ik aldus: deelt a d en d e ieder in even veel gelyke deelen, trekt voorts van deeze punten linien, evenwydigh met a b en a d, als hier boven: het blykt, door het voorgaande Voorstel, dat op a f meer rust als niet, en minder als de pylaar water f l; desgelyks rust op f g meer als f l of g r, en minder als g l of g m; zoo ook op g h meer als g l of h s, en minder als h l of h n; en zoo voorts op h i meer als i t, en minder als i o; op i k meer als k u, en minder als k p; en eindelyk op k d meer als d z, en minder als d q: zoo is dan de zwaarte, op a d rustende, altydt meerder als alle deeze ingeschreevene pylaren waters (die de linie a e raken) te zamen, en minder als de omschreeven pylaren; maar hoe men a d en d e in meerder deelen deelt, hoe minder haar verschil is, en hoe zy beide aan de drie-hoek a d e nader zyn. Nu dan, men kan a d en d e in zoo veel deelen verdeelen, dat eindelyk haar verschil minder is als het minste dat men kan bedenken ('t geen in de practyk zoo veel is als niet); nochtans blyft de drie-hoekige pylaar waters altydt wiskonstelyk tusschen het minste en meeste, dat is tusschen de in en om geschreevene figuur, en by gevolgh rust tegen a d een gewight zoo zwaar als de pylaar waters a d e, of een halve pylaar water, wiens grondt zy a d, en zoo hoogh als een loot-lyn van 't waters opper-vlak tot de laegste kant des bodems, 't welk ik bewyzen moest.

IV. Voorstel.

Tegen een vierkante bodem, wiens hooghste zyde onder het waters opper-vlak is, rust de zwaarte van een pylaar waters, wiens grondt even aan de bodem is, en hooghte als een loot-lyn van 't waters opper-vlak, tot het midden des gegeven bodems.

Aan de figuur F zy a b het opper-vlak des waters a b c d, d e de gegeven bodem, i het midden: ik zegge, op d e rust een gewight, zoo zwaar als een pylaar water, wiens grondt zy e d, en hooghte i k; want door 't voorgaande rust op a d de driehoekige pylaar water a d h, op a e rust a e f, en dienvolgende op e d de driehoek a d h, min de driehoekige pylaar a e f, dat is de pylaar waters e f h d: maar e f h d is even aan de pylaar, wiens grondt zy e d, en hooghte i k; want trekt l n, in 't midden van g h, evenwydigh met a d, en verlengt e f tot n, zoo zal e d l n even aan e f h d zyn; trekt dan l m rechthoekigh op a d, of zyn verlengde. Nu is e d l n een pylaar, wiens grondt zy e d, en hoogte l m: indien nu i k even aan l m is, zoo is 't voorstel bewezen; 't welk ik aldus bewyze: a e is even aan e f of d g, en a d is even aan d h, daarom is e d ook even aan g h; hare helften zyn ook even, te weten, e i is even aan g l, en dien-volgens is a i ook even aan d l; voorts zyn de hoeken l d m en k a i even, (om dat a k en d l evenwydigh zyn) en de hoek d m l is even aan de hoek a k i, als zynde beide recht; daarom zyn de driehoeken l m d en a k i gelyk, en door 't gevolg l m even aan i k, 't welk ik bewyzen moest.

[p. 304]

V. Voorstel.

Van twee vierkante bodems die even breedt zyn, maar hare lengtens ongelyk, wiens hoogste en laeghste zyden even diep onder water zyn, zullen de gewigten, tegen deeze bodems rustende, tot malkanderen zyn als hare lengtens.

Laat c e en d f, in de figuren G, de gegeven bodems zyn, a b het waters opper-vlak: ik zegge, c e is tot d f, als het gewight op c e, tot het gewigt op d f rustende; want laat g en h het midden zyn van c e en d f, g i en h k, rechthoekigh getoogen op a b, zoo zal het gewight, op c e rustende, de pylaar waters zyn, wiens grondt zy c e, en hoogte g i, en op d f de pylaar, wiens grondt zy d f, en hooghte h k, of g i (door de twee voorgaande Voor-stellen): maar deeze pylaars zyn tot malkander als c e tot d f, en daarom ook het gewight daar tegen rustende.

Merkt.

In het derde Voorstel (tot welke deeze eerste figuur, of prent, toegepast wordt) is gezeit van een halve pylaar waters, wiens grondt zy c e, of d f, en zyne hooghte de loot-lyn van 't waters opper-vlak a b, tot e o f: doch het is kennelyk dat deeze halve pylaren even zoo groot zyn als die heele, wiens grondt de zelve zy, te weten, c e, of d e, en de hooghte als de helft der zelver loot-lynen, dat is, de heele streep g i, of h k; daar om blyft ons bewys vast.

Merkt ook:

Hebbe hier voor de bodems door streepen aangeweezen, welke men nochtans verstaan moet vierkanten te zyn, van zulke breedten als men die zal willen stellen: dat zulks geen verandering by brengt, is klaar genoegh van zich zelven, en daar om onnoodigh iets meer daar af te zeggen.

VI. Voorstel.

Tegen een bodem, wiens onderste en bovenste zyden ieder in een vlak zyn, evenwydigh met het waters opper-vlak, maar beide krom (doch gelykmatigh) gebogen, zoodanig, dat alle linien van eenige punten in de bovenste zyde, tot haar lykstandige punten in de onderste zyde des bodems, alle evenwydige rechte linien zyn, rust even zoo veel gewight, als tegen een platte vierkante bodem, even lang en breedt, en even diep in 't water.

Laat a b c d, op de figuur H, een water zyn, a b het opper-vlak, e f en c d twee vlaktens, evenwydigh met de vlakte a b, en in de vlakte e f zy de opperste zyde des bodems a e g i l c, en in c d de onderste zyde b f h k m d, de twee uiterste zyn a b en c d: ik zegge, tegen deeze kromme bodem rust een gewight, als tegen een andere bodem zoude rusten, die even zoo breedt was als a b, of c d, en zoo lang als de kromme linie a e g i l c, of b f h k m d, en even diep in het water; want laat de linien a c en b d in zoo veel gelyke deelen gedeelt zyn, dat de stukken tusschen de deelingen rechte linien zyn, als in e g i l en f h k m, en e f, g h, i k, en l m, getoogen door deeze linien, dan zal de kromme bodem in vierkante bodems gedeelt zyn, als a b f e, e f k g, g h k i, i k m l, en l m d c. Desgelyks zoude men ook de gezeide platte bodem in even zoo veele en groote vierkante bodems konnen deelen, welke alle even veel zullen gedrukt werden, door het vierde Voorstel; en, by gevolg, alle de vierkanten van den krommen bodem zullen even zoo veel gedrukt werden, als alle de vier-kanten van den platten bodem, 't welk te bewyzen was.

VII. Voorstel.

Tegen een platte bodem, wiens opperste en onderste zyden evenwydigh met het waters opper-vlak zyn, en de twee andere zyden even-wydigh en gelykelyk gebogen, rust een gewight zoo zwaar als tegen een platte bodem, die even lang en breedt, en even diep in 't water is.

Laat a b, by de figuur I, de opper-vlakte des waters zyn, a b c d en e f g h de gegevene bodems, waar van a b, c d, e f, en g h gelyk zyn, en alle evenwydigh met het waters opper-vlak a b; a b en e f even diep onder water, desgelyks ook c d en g h: ik zegge, tegen a b c d, en e f g h, rust even veel water; want deelt a c en b d in eenige gelyke deelen, en trekt de evenwydige met a b, of d c, als hier boven, en aldus zal de bodem in verscheide vierkante bodems gedeelt zyn; deelt ook desgelyks e f g h: het volght, door het vierde Voorstel, dat tegen de bovenste vierkante bodem van a b c d even zoo veel rust, als tegen de bovenste van e f g h, en tegen de volgende van a b c d zoo veel, als tegen de volgende van e f g h, en zoo voort, en, by gevolgh, tegen de bodem a b c d even zoo veel, als tegen de bodem e f g h.

VIII. Voorstel.

Twee bodems, beide even diep onder het waters opper-vlak, en van gelyke breedte, van welke d' eene gebogen, en d'ander recht is, zyn gelyk langte tot langte, alzoo geprang tot geprang.

Laat a b en c d, by de figuur K, de gegeven bodems zyn, a en c even diep on-

[p. 305]

der het waters opper-vlak a b, desgelyks ook b en d: ik zegge, gelyk de langte des krommen bodems a b, tot de langte des rechten c d, alzoo is het gewigt tegen a b rustende, tot het gewigt tegen c d rustende; want laat a b en c d in verscheide vierkante bodems gedeelt werden, als in de voorgaande Voorstellen, zoo zullen in de bovenste vierkante bodems van a b en c d, te weten, a e en c f zyn, als het gewight tegen a e, tot het gewight tegen c f, door het vierde Voorstel: en in de volgende zal e g tot f h zyn, als het gewight tegen e g, tot het gewight tegen f h, en zoo voorts met de volgende: waarom alle de kleine vierkanten van de kromme te zamen, die ik in gedaghten stel, tot alle de vierkanten van de rechte te zamen, gedrukt zullen werden, of lyden, als geheele linien langte tot geheele linien langte.

Vervolgh.

Het blykt klaarlyk, dat, zoo de bodem a b noch daar benevens gebogen was als de gegeven bodems van het zeste en zevende Voorstel, dat de voorschreeven reden blyft; want deeze buiging brengt geen verandering by, gelyk klaarlyk is betoogt.

IX. Voorstel.

Tegen een driehoekige bodem, wiens onderste zyde evenwydigh met het waters opper-vlak is, rust een pylaar water, wiens grondt zy even aan de bodem, en des zelfs hooghte als de lootlyn van des waters opper-vlak, tot de diepte van het twee derde deel des gegevene bodems, van bovenen af.

Eerste Voorbeeldt,
Daar een hoek in 't waters opper-vlak is.

Laat a b c, in de figuur L, de gegeven bodem zyn, a d rechthoekigh op b c, en d e rechthoekigh getogen op b c, in een vlak, evenwydigh met het waters opper-vlak; d e zy even aan a d: voorders zy c f en b g evenwydigh getogen met d e, g e f evenwydig met b c, en eindelyk a g en a f. ⁺Dit zoo zynde, blykt, door het voorgaande Voorstel, dat tegen a b c het lichaam water b c f g a rust, te weten een pyramide, wiens grondt zy b c f g, en zyne hooghte als een loot-lyn van de onderste zyde b c tot het waters opper-vlak: en om dat een pylaar het drievoudt is van een pyramide van gelyke grondt en hooghte, zoo rust dan tegen a b c het derde deel van een pylaar water, wiens grondt zy b c f g, en zyne hoogte van b c tot het waters opper-vlak; maar b c f g is twee maal zoo groot als a b c, daarom rust tegen a b c twee derde deel van een pylaar waters, wiens grondt is a b c, of c b e, en des zelfs hooghte als een loot-lyn van het waters opper-vlak tot b c, of ('t geen het zelve is) een pylaar waters, wiens grondt zy a b c, en hooghte twee derde deel der loot-lyn van 't waters opper-vlak tot de onderste zyde b c, dat is (a d in drie gelyke deelen gedeelt zynde) tot het punt h, gelyk ik bewyzen moest.

+ Ziet Stevins Water-wigt, XX. Voorstel.

Tweede Voorbeeldt,
Daar a onder 't waters opper-vlak is.

Wederom zy a b c, aan de figuur M, de gegevene bodem, b c evenwydigh met het waters opper-vlak, a d rechthoekigh op b c, verlengt de zelve tot h in 't waters opper-vlak: voorts zy d e rechthoekigh op b c, en even aan h d; dan h e en a i even-wydigh getogen, met de doorsnydende h l, in i; eindelyk trekt i g en i f, zoo zal (door het voorgaande) tegen a b c een lichaam water rusten, even aan a b c f g i: trekt nu i k evenwydig met a b, en i l met a c, zoo is i k l f g even aan een pylaar, wiens grondt is i k l, of a b c, en zyne hooghte als twee derde der loot-lyn van b c of k l tot a i, door het eerste Voorbeeldt; en a b c l k i is een pylaar, wiens grondt zy a b c, en zyne hooghte als een loot-lyn van 't waters opper-vlak tot a i, om dat a i even is aan a h, door het werk: Nu, deeze twee pylaren, beide van even gronden, zyn t'zamen zoo groot als een pylaar, wiens grondt de zelve a b c is, en zyne hooghte als de twee loot-lynen (d'een van a tot het waters opper-vlak, en d'ander de loot-lyn, welke twee derde van een lyn is getogen uit b c recht op tot a i) te zamen in een linie, dat is, van 't waters opper-vlak tot m, de diepte van het twee derde deel des gegeven bodems, 't welk ik voor hadde te bewyzen.

X. Voorstel.

Tegen een driehoekige bodem, wiens opperste zyde evenwydigh met het waters opper-vlak is, rust de zwaarte van een pylaar water, wiens grondt even is aan de gegevene bodem, en zyne hooghte als een loot-lyn van 't waters opper-vlak tot de diepte van het derde deel des gegevene bodems, van bovenen af.

Eerste Voorbeeldt,
Daar de opperste zyde in 't waters opper-vlak is.

By de figuur N is a b c de gegeven bodem, a b is in het waters opper-vlak, c d, rechthoekigh op a b, c e rechthoekigh op een linie die evenwydig met a b is, te weten, f g, en ook evenwydigh met het wa-

[p. 306]

ters opper-vlak, en de zelve c e even aan c d, en getogen a e en b e: tegen a b c rust dan de pyramide a b c e, wiens grondt zy a b c, en des zelfs hooghte van het waters opper-vlak tot c (om dat c d even aan c e is); maar deeze pyramide is het derde deel van een pylaar van gelyke grondt en hoogte, en daarom is ook de pyramide even zoo groot als een pylaar, wiens grondt zy a b c, en zyne hooghte het derde deel der loot-lyn van 't waters opper-vlak tot het punt c, dat is (c d in drie gelyke deelen gedeelt zynde) tot het punt h.

Tweede Voorbeeldt,
Daar de opperste zyde onder 't waters opper-vlak is.

In de figuur O zy a b c, h d en c e wederom als boven, doch c e even aan de verlangde c d, tot in het waters opper-vlak k, en getogen k e en d i evenwydigh met c e, a f en b g met d i, en f i g met a b, en dan getogen f e en e g, eindelyk f l en l g, evenwydigh met a c en b c. Tegen de bodem a b c rust de zwaarte van een lichaam waters a b c e f g, dat is een pyramide f g l e, wiens grondt zy f g l, of a b c, en des zelfs hooghte als een loot-lyn van de vlakte d i, tot het punt c, of een pylaar, wiens grondt zy a b c, en zyne hooghte het derde deel der loot-lyn van d i tot h, (door het eerste Voorbeeldt) en een pylaar a b c l f g, wiens grondt zy a b c, en zyne hooghte van het waters opper-vlak tot a b (om dat d k en d i even zyn): Nu, deeze twee pylaren zyn te zamen zoo groot als een pylaar, wiens grondt zy a b c, en zyne hooghte als de twee loot-lynen t'zamen, te weten de loot-lyn van 't waters opper-vlak tot het punt h, 't welk ik bewyzen moest.

Merkt.

Het blykt, door 't zeste, zevende, en achtste Voorstel, dat, zoo de driehoekige bodems a b c, in dit, en in het naast voor-gaande Voorstel, ook geboogen waren, als in het gezeide zeste, zevende, en achtste Voorstel de vierkantige bodems gestelt zyn, tegen zulke gekromde driehoekige bodems een pylaar water rust, wiens gront zy even aan den inhoudt van de gekromde bodem, en zyne hooghte als de gezeide loot-lynen; gelyk men zulks op een zelve wyze betogen kan.

Deeze Voorstellen verstaan zynde, zal men lichtelyk konnen vinden hoe veel gewight tegen een Schip, dryvende in zee, of in eenigh ander water, komt te rusten; want men kan het zelve in vierkanten en driehoeken deelen, en vinden de zwaarten die tegen deeze drie-en vierhoe ken rusten, welke, te zamen opgetelt zynde, de begeerde zwaarte aanwyst.

Tot een voorbeeldt zullen wy ons voor-gestelt Schip weder te voorschyn brengen, in welk c d de kiel is, lang zynde 104 voeten, en e a b de vlakte des waters; ik stel c d 10 voeten onder 't waters opper-vlak; trekt nu a d alzoo, dat a b even aan c d is, te weten, de kromme a b even aan de rechte c d: dan zal men de kromme lyn f g op het midden des Schips meten, desgelyks a h en b i, en dus zal men bevinden voor

f g omtrent	18½ voeten,
voor a h omtrent	16½
en voor b i	10
	_____
komt t'zamen	45 voeten.
Het derde deel hier van voor de gemiddelde breedte des vierkants a b c d, komt	15 voeten;
deeze gemultipliceert, of vermenighvuldight, met a b, of c d,	104 voet,
	_____
komt voor den inhoudt van het vierkant a b c d	1560 voeten.
Dit wederom gemultipliceert met de loot-lyn van 't waters opper-vlak tot het midden des bodems a b c d	5 voeten,
	_____
zal komen	7800 voeten.
En zoo veel lichamelyke voeten rusten tegen 't vierkant a b c d.
Multipliceert ook a e	36 voeten,
met a h	16½
	_____
komt	594 voeten;
wiens helft	287 voeten,
voor den inhoudt van a e d.
	3½ voeten,
	_____
Dit multipliceert met zynde de loot-lyn van 't water's opper-vlak, tot op het derde deel van de diepte des bodems a e d, zal komen voor de zwaarte tegen a e d	956⅔ voeten.
Voorts multipliceert de lengte des kiels, zynde	104 voeten,
met de breedte	2
	_____
komt voor de vlakte	208 voeten.
Dit gemultipliceert met de loot-lyn	10 voeten,
	_____
komt voor de zwaarte onder de kiel	2080 voeten.

Want, volgens het eerste Voor-stel, tegen een bodem perst van onderen een pylaar water, wiens grondt zy de gestelde bodem, en zyne hooghte van de bodem tot het waters opper-vlak.

[p. 307]

Wederom gemultipliceert e d, zynde	14½ voeten,
met de breedte	1 voet,
	_______
komt voor de vlakte	14½ voeten.
Dit gemultipliceert met de helft van b i,	5 voeten,
	_______
komt het geprang tegen e d	72½ voeten.
Multipliceert ook b c	10½ voeten,
met de breedte	1 voet,
	_______
komt voor den inhoudt	10½ voeten.
Die gemultipliceert met de helft van b i	5 voeten,
	_______
komt het geprang tegen b c	52½ voeten.
Eindelyk, telt deeze zwaarten by malkanderen, te weten aldus: voor eerst, tegen a b c d rust	7800 voeten,
tegen a e d	956⅔ voeten,
komt tegen de zyde des Schips	8756⅔ voeten.
Dit twee maal genomen, komt voor het geprang tegen beide de zyden van het Schip	17513⅓ voeten.
Hier by gedaan het geprang onder de kiel,	2080 voeten,
en het geprang tegen e d	72½ voeten,
en eindelyk het geprang tegen b c	52½ voeten.
	_______
komt t'zamen	19718⅓ voeten,
voor het water dat tegen 't gantsche Schip rust.

Indien nu ieder voet water 46 pondt en 18 loot weeght, gelyk zulks aan 't water in Texel by ondervindinge werdt bevonden, zoo zal tegen zoodanigen Schip, dat 10 voet diep gaat, een zwaarte rusten van 918134 pondt en 28⅔ loot.

Desgelyks valt zeer licht te berekenen hoe veel zwaarte tegen het zelfde Schip rust, by aldien het dieper, of zoo diep niet en gaat, 't geen, kortheits halve, voorby gâ; alleen zeggende, dat, zoo het Schip 1 voet dieper gaat, dat'er dan omtrent 3559 voeten water meer tegen rust: en zoo het 1 voet lichter dryft, dat'er dan omtrent 3129 voeten water minder tegen rust.

By aldien men dan een vlietende, of ten minsten een losse stoffe, van gelyke zwaarte met het water, binnen in het Schip dede, zoo zoude het Schips hout gantsch niet te lyden hebben.

Wat voorts het diep gaan der Scheepen belangt: die van eiken-hout gebouwt zyn zinken dieper als die van vuurenhout; 't geen, na myne ondervindinge, tegen elkanderen is als 50 tot 43: zoo dat, als een eiken Schip 10 voet diep gaat, zal een vuuren Schip, van gelyke gestalte, 8⅗ voet diep gaan. Wel is waar, als het onder op 't scherpe van het Schip zoude aan komen, dat dan de ryzing zeer ongelyk zoude zyn; maar om dat dit zelden, of nooit, bloot leit, en het scherpe van 't Schip, schoon ongeballast, althans beneden het waters opper-vlak komt, zoo brengt dit geen onderscheidt by. Deeze perssing hindert een geladen Schip geenzins, maar helpt het veel eer in 't dragen van zyne last; doch een ongeladen Schip kan het perssen, als de in- en om-houten niet wel gevoeght zyn, schadelyk wezen.

Het breekt de opgegevene uitrekening eenighzins, dat een varendt Schip het water voor op stoot, en achter doet dalen; want hoe snelder voortgang, hoe hooger opsteigering: en hoe enger kolk, hoe grooter ryzing van water men voor aan het Schip zal bevinden; daar-en-tegen zal 't Schip het water achter te meer ontvaren, 't geen vermindering aan de perssing by brengt, gelyk het voor opsteigeren vermeerdering tot de zelve zwaarte veroorzaakt. Het ryzen en dalen van de baren ter zyden tegen 't Schip aan, schynt deeze rekening insgelyks te zullen verbysteren: doch alle deeze ongemakken, die dit uitrekenen schynen te ontstellen, zyn van weinigh belang; en het ryzen van 't water voor, zal met het dalen van 't zelve achter ten naasten by over een komen: gelyk als ook de diepte en hooghte der golven zoo van eene inhoudt zullen zyn, dat het verschil op een groote rekening van geene waerde is. Echter, hoe hooger het water voor tegen de boegh opryst, hoe meerder de vaert-stutting zy; en hoe dieper het Schip gaat, hoe grooter tegenstandt het voor de boegh heeft.

Een Schip dat voor stroom vaart, achte ik dat zoo veel beweeging, die des zelfs voortgang helpt, ontfangt van het omstaande water, als het lichaam waters zoude ontfangen, 't geen gelyk is aan het Schips onderwaterige deel.

Niet buitenspoorigh kan hier gevraaght worden, waar van daan het komt, als men schielyk met een groote last tegen een Schip slaat, dat het dan blyft leggen, en by aldien men met een lichte haak langzaam daar aan duuwt, dat het Schip, hoe zwaar 't ook zy, daar van bewoogen wert? Hier van schynt de reden te wezen, dat, als men langzaam duuwt, het water tydt heeft om van vooren na achteren te loopen, 't geen noodtzakelyk moet geschieden, indien het Schip bewoogen zal worden.

[p. 308]

Gevoegelyk zouden hier veele Wiskonstige en Philosophische stellingen, de Scheepen betreffende, konnen opgelost werden; als, waar om een Schip hooger schynt als het water, wanneer men op strandt staat: waar om de riemen onder water gebogen schynen, enz. doch zal dit alles, kortheits halve, verby gaan.

Het zal echter niet ondienstigh zyn, in 't kort te verklaren hoe het toestaat met des Schips zwaarheits middel-punt: Dit dan houdt zich altydt in een rechte linie met de zwaarheits middel-punt van dat lichaam waters, 't geen zoude zyn daar het Schips deel staat onder 't waters opper-vlak. Om dit nu te vertoonen, zoo beelde men zich in dat het Schip wegh genomen zy, en dat alleen over blyft dat lichaam waters 't geen even is aan het deel Schips dat onder water quam: het zwaarheits middel-punt dan van dat water zal op de zelfde plaats zyn daar het zwaarheits middel-punt was van het Schips onderwaterige deel, even groot met het zelfde water; zoo niet, moeste het zelve daar buiten zyn, en het hol waters moeste van vorm veranderen, 't geen tegen het gestelde is. Hier uit magh men dan veiligh besluiten, dat het zwaarheits middel-punt van een recht op vlottende Schip althans is in een rechte linie met het zwaarheits middel - punt van zulk een lichaam waters als zyn onderwaterigh hol beslaat, te weten, daar in, onder, of boven. Waar uit te bezeffen is, wanneer het zwaarheits middel-punt van een Schip is boven het zwaarheits middel-punt van 't genoemde deel waters, dat zulk een Schip, wanneer het niet gehouden werdt, moet omvallen, en zich in die gestalte voegen, dat zyn zwaarheits middel-punt recht onder het zwaarheits middel-punt is van dat lichaam waters 't geen het onderwaterigh Schips deel beslaat: 't welk blykt, als men merkt hoe licht een lichaam, boven zwaar zynde, uit zyn rechte linie gedreeven wordt; en dit werdt gezeit top-zwaar te wezen.

Het versterkt de Scheepen zeer, als hun zwaarheits middel-punt laegh staat. Het zyn ranke Scheepen welkers zwaarheits middel-punt boven komt, waar om de zelve licht omslaan: deeze zyn te verhelpen, met een houte huidt omlaegh daar om te leggen, zware ballast in te brengen, en anderzins.

Als de zwaarheits middel-punten der Scheepen bekent zyn, dan kan men daar uit klaarblykelyk besluiten hoe de Scheepen op het water te leggen hebben, 't zy recht op, ter zyden af, en voor of achter over.

Het geheele Schip is even zwaar aan dat deel waters 't geen zyn hol onder water beslaat; 't welk, by ondervindinge, aldus gezien kan werden: Neemt een bak waters, stelt daar een komme in, en merkt hoe hoogh het water zy; weeght daar na de komme, en doet zoo veel water in de bak, by het andere water, als de komme zwaar is, dan zult ghy bevinden dat het water van eene hoogte in de bak blyft, als het was toen de komme daar in stondt, 't welk te bewyzen was. Dit is een zaak, die by Archimedes, Stevin, Kircherus, en Gyraldus, wis-konstelyk werdt bewezen. Hier uit volght dan, hoe men de zwaarte aller Scheepen, wanneer zy vlotten, 't zy geladen of ongeladen, kan weten; by voorbeeldt.

⁺Het Schip, hier voor genoemt, en ontleedt, is lang over steven 134 voet, heeft een kiel lang 104 voet, het is wydt op de uitwatering 29 voet, laat het diep gaan 10 voet, de kiel zy diep 1 voet: om dan den inhoudt van het Schip te weten, zoo multipliceert, of vermenigvuldight, voor eerst de kiels lengte met de hooghte, of het diep gaan van 't Schip, dat hier 9 voet zy, des kiels diepte, die 1 voet is, daar af getrokken zynde, komt 936; dit dan weder met de wydte 29, komt 27144 voeten voor het binnenste lichaam, van den bodem af tot zoo verre als het Schip in 't water gaat, behalven het geene dat in 't uitschieten der stevens wordt bevat, welke beide zoo verre uitschieten als in 't water komen; laat dit, by voorbeeldt, 4 voet zyn, deeze gemultipliceert met de hoogte 9, en de wydte 27, (want stelle hier het Schip, om zyn toeloopen, 2 voet naauwer als in de midden) zoude uitmaken 972 voeten, als het een vierkant lichaam was, doch om dat het gelyk als een lyvige driehoek is, trekt de helft daar voor af, en laat voor de ware inhoudt 486 voeten: zulks dat de geheele inhoudt van dit Schips lichaam, zoo verre als het onder water steekt, zoude beloopen 27630 vierkante voeten, 't en ware het vlak op zyn hooghste 1 voet van het bovenste der kiel af oprees, waar voor af te trekken staat 1456 voeten, zoo dat noch blyft 26174 vierkante voeten voor het Schips hol: hier nu noch by gedaan het lichaam van de kiel, zynde 104 voeten vierkant, komt 26278 vierkante voeten voor den zuiveren inhoudt van het Schips onderwaterige deel. Terwyl nu een voet waters 46 pondt en 18 loot weeght, zoo zal de zwaarte des waters, 't geen even aan het Schips onderwaterig deel is, 1223569 ponden en 12 loot zyn; zegge een duizent maal duizent twee hondert drie en twintig

+ Hoe men de zwaarte van een Schip weten zal.

[p. *76]

[p. *77]

[p. 309]

duizent vyf hondert negen en zestigh ponden, en twaalf loot.

Dit zy dan alleen voorgestelt, om aan te wyzen hoe men met deeze zaak handelt: een volmaakte uitrekening, waar by op alle kleinigheden wort gelet, late voor als noch achter, dewyl zulks na deeze trant zeer lichtelyk kan geschieden. Wie dan dit uitrekenen van het gewight der Scheepen in 't werk wil stellen, die heeft naerstig te letten op de vorm der zelve.

Een nuttigh gevolgh spruit hier uit, door 't welke men altydt weten kan hoe verre een Schip in 't water zinken zal met een gegevene last, eer de zelve binnen boort is: 't geen dikmaal te laat wort gezien, als de vraght geladen is. Hier toe gebruikt men slechts den Regel van drien, en zeght: Een Schip, 't geen zoo veel weeght, zinkt zoo diep; Hoe diep zal het zelve Schip zinken, als daar noch zoo veel gewight by gedaan wert? Op deeze wyze te handelen is geoorloft, om dat het Schip buitenwaarts, boven water, alom byna van eene gestalte is, of ten minsten zoo weinig verschillende, dat het in deeze uitrekening weinigh faal aanbrengt.

Staat noch te weten, dat de Scheepen in zoet water meer zinken als in brak water, en in brak water meer als in zout water; want het zoet water is lichter, of dunder, als het zout water. Op kusten daar veele zoete vlieten zich in zee, of in des zelfs inhammen, ontlozen, gelyk in onze Zuider zee, aan de Noordtsche kust by Nova Sembla, Moscovien, en elders, vindt men het water van vermengde smaak tusschen zoet en zout.

Scheeps-meetingen.

Stelle voor eerst een vry zekere wyze van Scheepen te meeten, uitgevonden door den hoogh-geleerden achtbaren Heer Joannes Hudde, Burgermeester en Raadt der Stadt Amsterdam.

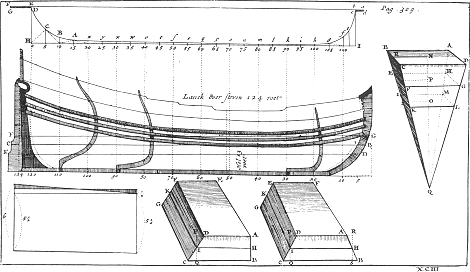
Deeze vondt, van vry kort en zeker te konnen uitvinden de zwaarte van alle last, die eenigh Schip zoude mogen in hebben, of konnen voeren, is by den onvergelykelyken Wis-konstenaar Joannes Hudde te dier geval uitgevonden, toen eenigh geschil ontstondt, tusschen zyn Koninglyke Majesteit van Denemarken, en hare Hooghmoogende, nopende het aantal der lasten, waar op de Scheepen, die na Noorwegen om hout varen, en volladen zynde, (gerekent, volgens de over-een-komste, 4000 pondt Hollandts voor een hout-last) behoorden gestelt te werden (de gedaanten van de Scheepen voornoemt zyn boven in dit Werk vertoont). En staat te weten, dat naderhandt eenige Scheepen, door gewigt van kogels, tot op een zekere diepte, geladen zynde, als ook dat Schip, 't geen na deeze wyze, eenigen tydt te vooren, en op twee verscheide malen geen half ten hondert verschillende, gemeeten was, daar mede ook zoo naauwkeurigh is bevonden over een te komen, dat men niet zeggen kon dat'er eenigh verschil tusschen beide wiert bevonden. Gelyk ook eenige Lichters, met grof geschut geladen, hier na gemeeten, uitgerekent, en de zwaarte van het zelve geschut opgenomen zynde, is de zelve zwaarte ook bevonden zoo net op een te slaan met de uitrekening, dat het zelfs de verwachting te boven ging. Twee persoonen hebben deeze meeting gedaan, en ook nooit meer als twee uuren tot ieder Schip van nooden gehadt.

Volght de gezeide meeting, met zyn betoog, my schriftelyk van den Vinder mede gedeelt, om op een bequame, gevoegelyke, en vry zekere manier te berekenen, op hoe veel lasten de lading van alle Scheepen te begrooten zy, 4000 pondt Hollandts gewight voor een last gestelt zynde.

1. Voor eerst stel ik, met de Wis-konstenaars, vast, dat alle lichaam, 't geen in 't water dryft, zoo veel zwaarte van water uit haar plaats stoot, als dat zelve lichaam zwaar is.

2. Zy nu genoomen een Schip na welgevallen, als, by voorbeeldt, dit hier nevens afgetekende, onder letter A, en gestelt dat het zelve in 't Y-water, door zyn volle lading, diep heeft gegaan tot aan de lyn G F toe, en daar na, ontladen zynde, gerezen is tot D E, zynde de hooghte van 6 Amsterdamsche voeten.

3. Zoo men nu (in gedachte) dit Schip water-pas, of evenwydigh, met het waters opper-vlak door-snydt, gaande de snydingen door D E en G F, zoo zal het stuk D E F G, tusschen beide uitgesneden, even zoo veel plaats beslaan als het water dat door deeze lading uit zyn plaats is gestooten; en derhalven (volgens het eerste) zal het gewight van zoo veel waters, als deeze plaats kan bevatten, gelyk zyn aan de zwaarte van deeze lading.

4. De grootte van deeze plaats bekent zynde in Amsterdamsche cubic - voeten, als mede de zwaarte van een Amsterdamsche cubic-voet waters in Hollandts gewight, namentlyk van Y-water, daar dit

[p. 310]

Schip ondersteldt wert te liggen, en ontladen te worden, zoo is kennelyk, by aldien men het getal dat in cubic-voeten de grootte van deeze plaats uitdrukt komt te multipliceren met het getal dat de zwaarte van deeze cubic-voet uitdrukt in Hollandtsche ponden, dat'er een uitkomst van ponden zal komen, welke, gedeelt zynde door 4000, uitleveren zal het getal der lasten daar het Schip moet op gestelt werden.

5. Hier resteert dan noch maar alleen, hoe men de grootte van deeze spatie, ofte plaats, tusschen G F en D E begreepen, meeten zal.

Om hier toe te komen, considereer ik voor eerst, dat, zoo ik dit spatium, of stuk, D E F G water-pas in 't midden door-sny, dat die sectie ons na genoegh zal representeeren de middel-grootte van alle d'andere sectien, boven en onder deeze, van 't gemelde stuk, gemerkt tusschen F E het grootste gedeelte, na 't midden van het Schip toe, byna in 't loot leit, (inzonderheit in de nieuwe Noorts-vaarders) en alleen na achteren en vooren, onder deeze middel-sectie, naauwer, en boven de zelve wel weder wyder, maar na proportie min wyder wordt; zulks dat, zoo veel deeze middel-sectie te klein is, ten opzight van de hoogere, zoo veel is die omtrent weder te groot, ten opzigt van de laegere sectien. Zoodat het dan zal aankomen op het uitvinden van de grootte der middel-sectie.

Om welkers inhoudt dan te vinden, zoo span ik een lyn, als, by voorbeeldt, B C, in 't midden tusschen D E en E F, dat is hier 3 voet boven de superficie des waters, zoodanig, dat de zelve achter en voor even verre van het midden der steven af staat, en 't Schip omtrent op het wydtste raakt.

Daar na meet ik recht-hoekigh en water-pas van deeze lyn af, hoe verre de zelve van het buitenste superficie des Schips is, gaande van 5 tot 5 voet, om dat de rondigheit van het Schip op deeze lengte van 5 voet niet merkelyk of considerabel is, maar als recht magh werden aangemerkt, en daar het zoo niet wezen magh, kan men noch een afstandt tusschen beide meeten. Concipieert nu dat dit Schip water-pas doorsneden is, gaande de sectie door deeze gespannen lyn, en dat de helft van 't plat dier doorsnyding ons wort vertoont door de figuur a d c e f g h i k l m n o p q r s t u w x y z A B C D G F a, en de gespanne lyn door de rechte I H.

Ik begin dan te meeten van achteren by het roer, uit de hoek D, de lengte D o, daar na de lengte C 5, dan B 10, en zoo voorts van 5 tot 5 voet, tot dat ik kome daar de rondte van het Schip tusschen de wydte van 5 voet eenigh aanmerkelyk onderscheidt zoude geven, indien men die zelve rondte voor een rechte lyn quame te nemen, gelyk voor aan de steven gebeurt, alwaar ik van 2 tot 2 voet heb gemeeten. Dewyl nu openbaar is, zoo men D C, C B, B A, A Z, enz. considereert als rechte lynen, dat de triangel o, C, 10, even groot is als het rectangulum C 5, 5 H; insgelyks beide de triangels C B 10, A B 10, t'zamen als het rectangulum B 10, 5 H; van gelyke de twee triangelen A 15, 10, A 15, 20, even groot als het rectangulum A 15, 5 H, om dat alle deeze perpendicularen even verre, namentlyk 5 voet, van elkander af staan, en zoo voorts met al d'andere, tot daar zy niet evenwydigh beginnen te werden: zoo is notoir dat het spatium, begrepen tusschen C H, H 110, 110 g, g h i k l m n o p q r s t u w x y z, en A B C, even groot zal zyn, als de som van al de perpendicularen daar in begrepen, namentlyk C B A, z y x w v t s r q p o n m l k i h g, gemultipliceert met 5 H, of 5 voet. Hier dan by gedaan zynde de grootte van de triangel H D C, als mede van het spatium g f e c 114, 110 g, zoo heeft men den inhoudt van de figuur, beslooten tusschen de gespannen lyn, 't Schip, en de uiterste perpendicularen; 't welk dan afgetrokken zynde van het rectangulum b E, E H, en daar by gedaan de halve sectie van de steven en 't roer, namentlyk a b c d, en E F G D, zoo krygt men de grootte van de figuur a d c e f g h i k l m n o p q r s t u w x y z A B C D G F a, welkers dubbelt den inhoudt is van de begeerde middel-sectie. Deeze grootte der middel-sectie dan in Amsterdamsche voeten gemultipliceert met de diepte die 't Schip door zyn lading was gezonken, zynde in dit exempel 6 voet, zoo kryght men een getal van cubic-voeten, welk gemultipliceert met het getal dat de zwaarte van dusdanigen cubic-voet waters uitdrukt in Hollandtsche ponden, ons een getal van ponden geven zal 't geen de zwaarte der lading komt aan te wyzen, en, by gevolg, door 4000 gedeelt zynde, het getal der lasten waar op dit Schip, na deeze ladinge, te begrooten is: 't welk het geene was dat men voorgenoomen hadde te toonen.

Maar op dat alles noch te klaarder, te eerder, en, ten aanzien van de practyk, navolgelyker magh blyken, zal ik zommige zaken, die de minst geoeffende omtrent dusdanigen stof moghten ophouden, wat zoeken te verklaren.

I. Het principium, dat een lichaam even zoo veel zwaarte van water uit zyn plaats stoot als dat lichaam zwaar is, kan niet tegen ge-

[p. 311]

sprooken worden, zoo men slechts bedenkt:

1. Dat het equilibrium zulks noodtzakelyk vereischt.

2. Dat alle Mathematici, over de konst van 't Water-wigt hebbende geschreeven, dit voor een axioma gebruiken, en, by gevolgh, dat zoo menigen experientie, als hare conclusien, daar op gevestight, confirmeeren, ook de waarheit van dit axioma bevestigen.

3. Dat de experientie met een blaas dit ook zeer krachtigh doet zien. Ik neem een opgeblazen blaas, en legh die in een bak met water; daar na vul ik de bak, tot dat die over loopt, en laat het water loopen: dat gedaan zynde, en alzoo de bak ten boorde vol gekreegen hebbende, zoo neem ik zachtjes deezen blaas daar uit, en laat al 't water dat aan den blaas mogt hangen eerst af druppen in den bak; en dan, daar aan gehangen hebbende eenige ponden gewights, (doch zoo veel niet dat de blaas gantsch onder water wordt getrokken) zoo doe ik de zelve weder zachtjes in dien bak, en vang zorghvuldig al het overloopende water, 't geen ik apart bewaar. Daar na neem ik eenigh ander lichaam, en handel daar mede t'eenemaal op de zelfde manier, eerst het zelve in dien bak leggende, daar dan water tot overloopens toe by doende, en dan weder uit gehaalt; hier na het voorgaande, of een ander even zwaar gewight daar aan gehangen, weder in de bak gedaan, en driftig bevonden werdende, gelyk noodtzakelyk alzoo moet werden geproportioneert, zoo wordt dan ook eindelyk het overloopendt water gevangen: en dit aan alle kanten perfect gedaan zynde, zal men bevinden dat het wederzydts overgeloopen water evenwigtigh is; 't geen dan de waarheit van dit principium ook zeer krachtigh bevestight.

II. Dewyl men weten moet de zwaarte van het water, waar in 't Schip leit, als het geladen of ontladen is, zoo zoude men konnen twyfelen, of men het water wel zoo naauw zoude konnen wegen, dat het verschil niet considerabel was.

Om hier af een proef te nemen, hebbe ik laten maken een cubus van kopere plaatjes, niet grooter als een halve Amsterdamsche voet van buiten, alles uitwendigh zeer accuraat, en gladt, hebbende een klein pypje in een van de hoeken, om daar door het kleinste hagel, niet grooter zynde als een spelden-hooft, in te doen, met behulp van een klein trechtertje. Ik nam hagel, om de zelve zoodanig te konnen schikken met hutzelen, dat dien hoek, daar het pypjen in was, het langste boven water dreef: hier door bevondt ik, dat met een goudt-aas het puntjen van deezen hoek, dat noch van 't gantsche lichaam boven dreef, onder raakte. Dit dan zoo verre gebraght zynde, nam ik de cubus uit het water, drooghde de zelve schoon af, en woegh hem op een schaal, die met drie goudt-azen deezen cubus, en zyn tegen-wight, daar in zynde, over sloegh, en bevondt de zelve op den 15^en Maert te wegen, doende deeze experientie in Regen-water, 5 pondt 23⅝ loot, in 't Y-water 5 pondt 24 9/16 loot, in Texel-water 5 pondt 26¼ loot, en, by gevolgh, 1 voet Regen-water te wegen 45 pondt 29 loot, Y-water 46 pondt 4½ loot, en Texel-water 46 pondt 18 loot.

Waar uit dan klaar te besluiten is, dewyl, volgens het boven staande principium, een Amsterdamsche halve voet waters, cubice genoomen, even zoo zwaar is als deezen koperen cubic van ½ voet, met al den hagel die daar in, en 't pypje dat daar aan is, gelyk men 't uit het water heeft gehaalt, dat men de zwaarte van het water zoo na kan krygen, dat het verschil geen 1/73 van een last op 200 lasten, ja noch veel minder, zoo men noch accurater schaal wilde gebruiken, zoude importeeren, en dien volgende in deeze meeting niet considerabel. Dat het verschil geen 1/73 van een last op 200 lasten zy, blykt uit de volgende rekening.

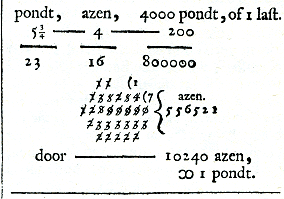
Komt zeer na 54⅓ pondt, 't geen minder is als 1/73 van een last.

De principaalste zwarigheit, en d'eenighste die'er (myns oordeels) noch maar resteert, bestaat in 't vinden der grootte van het stuk, dat door de lading in 't water komt te zinken. 1. Dewyl de lading het Schip voor en achter niet eenparigh doet zakken, en dikwils ook meer na d'een als d'ander zyde. 2. Dat de middel - sectie moogelyk al te ruwen calculatie zal geven, gemerkt de Scheepen niet eenparigh krom af loopen van boven na de kiel, noch over de lengte van 't Schip na de voor- en achter-steven, zoodanig ook, dat hier weinigh proportie schynt in te konnen gevonden werden, en alles onzeker over gelaten.

[p. 312]

Wat d'eerste zwarigheit belangt, die wordt wegh genoomen door het observeeren hoe diep dat een Schip, geladen, en ontladen, voor, achter, en wederzydts in 't midden, komt te liggen: by exempel, een Schip leit achter geladen op 12 voet, voor op 11 voet, ontladen achter op 6 voet, en voor op 5½ voet, zoo neem ik dan het midden hier uit, namentlyk 5¼, als blykt:

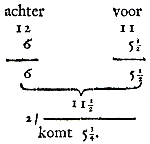
Insgelyks, een Schip, geladen zynde, by aldien ik zie dat het wat op eene zyde leit, of als men 't zeer accuraat wil weten, zoo teken ik het daar-en-boven noch wederzydts in 't midden, hoe diep het in 't water leit, en daar na, ontladen zynde, meet ik hoe hoogh het wederzydts is gerezen; het midden hier af neem ik voor de ryzing van 't Schip in de midden.

En zoo het moght gebeuren dat dit met de middel-diepte van voor en achter niet quam t'accordeeren, zoo neem ik noch eens het midden van deeze twee middens, en laat de zelve dan voor de middel-diepte over het gantsche Schip verstrekken. Dat dit nu geen considerabel verschil kan veroorzaken, wordt klaar betoont, zoo men slechts bedenkt dat de sectie wederzydts van 't Schip, eenzelvigh gaande van achteren, by exempel, op 6 voet, beginnende boven het water, en na vooren op 5½ voet eindigende, zeer weinigh kan verschillen, by die 'er geconcipieert wordt horizontaal te gaan, tegen de hooghte van 5¾ voet van achteren tot vooren toe; en dat hier door omtrent even zoo veel van achteren werdt verlooren, als van vooren aangewonnen: gelyk uit de neven-staande figuur, onder letter B, zeer gemakkelyk kan werden begrepen.

Even het zelfde geldt ook in de helling van 't Schip, die in het aangeroerde voorstel ook maar zeer weinigh kan zyn.

Wat d'andere zwarigheit belangt, namentlyk, dat de middel-sectie moogelyk al te ruwen calculatie zal geven, die neem ik voor eerst hier mede wegh, dat myn mening niet en is dat men d'aldergrootste accuraatheit zal krygen, wanneer men een Schips volle lading zal meeten, met deeze middel-sectie alleen te considereeren; maar dan mag men de zelve alleen gebruiken, wanneer de perpendiculare bogt van dit te meetene stuk zoo na over een komt met een rechte lyn, dat die als een rechte lyn, zonder merkelyk verschil, magh genoomen worden, even gelyk ik ook gezeit hebbe omtrent de boghten tusschen twee perpendicularen, in 't meeten van deeze middel-sectie.

Maar by aldien dit anders moght zyn, zoo zoude men dat stuk, ten opzight van de hoogte, in zoo veel deelen moeten deilen, dat ieder stuk deeze eigenschap hadde, en meeten dan vervolglyk ieder stuk apart: als by exempel, zynde de hooghte 6 voet, zoo zoude men dit stuk konnen verdeelen in twee stukken, ieder van 3 voeten hoog, en meeten dan ieder van deeze stukken door de middel-sectie van ieders stuk, ofte verdeelen deeze 6 voet in drie stukken, ieder van 2 voet hoogh, en meeten ieder van deeze drie als vooren.

Maar ik denk niet dat deeze accuraatheit, ten opzigt van de practyk, zeer noodig zal zyn, gelyk zoo dadelyk toonen zal. Immers altydt, zoo men de zelve begeert, kan die met weinigh meerder moeite in 't werk gestelt werden: en in allen gevalle zal daar dan geen zwarigheit over blyven, om niet te gelooven dat deeze stukken, op de gezeide wyze ieder byzonder gemeeten zynde, t'zamen na genoegh zullen uitleveren de grootte van het begeerde stuk: 't geen uit het vervolgh noch klaarder gezien zal konnen werden.

Voor het tweede zal ik dan nu gaan toonen, dat zelfs deeze middel-sectie alleen ons het begeerde na genoegh doet hebben. En om het zelve te effectueren, zal alleen noodigh zyn dat men deeze twee volgende Theoremata met aandacht nadenkt, en toepast tot de zaak.

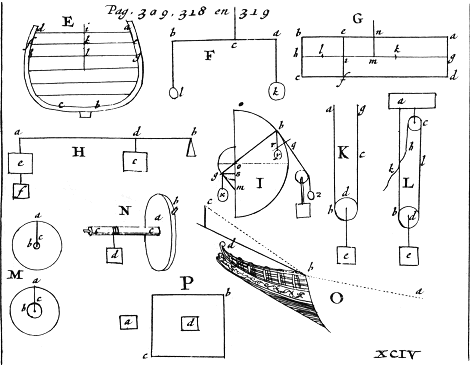
1. Dat van alle rechtlynige lichamen, als, by exempel, A E F G C B, aan de figuur C, staande het plat A D C B, als mede E F K G, perpendiculaar op de basis, en zynde D F evenwydigh met A E, en A E gesupponeert recht op A D, de lengte A E met de hooghte P Q, en de middel-breedte H I, gemultipliceert, den inhoudt van dat lichaam A E F G C B zullen geven; dewyl het triangeltje D P I even groot is als het triangeltje I Q C, en A R H als B S H, en dien volgende de geschikte vierkanten A P Q B, en R P Q S, zoo groot als de ongeschikte vierkanten A D C B, en A D C B.

2. Dat de grootte van een stuk eenes conus, waar van de basis een recht-hoek is, lang 115 voet, en breedt 28 voet, en de sectie, zynde d'andere basis van dit stuk, lang 110 voet, en breedt 26 13/23 voet, en dit stuk hoogh 6 voet, zeer na zal bekomen

[p. 313]

werden, indien men de middel-sectie van dit stuk met zyne hooghte multipliceert: ofte ook, zoo men de helft van het bovenste en onderste plat multipliceert met deeze hooghte; want men zal voor de juiste grootte van 't stuk 18492 4/23 voet krygen, voor de middel-sectie, met de hooghte gemultipliceert, 18489 3/24 voet, en voor de helft van beide de bases, met de hooghte, 18498 1/23 voet: 't geen in 't een maar 3 1/23 te weinigh, en in 't ander 6 2/23 te veel is, als blykt uit het volgende cyfer.

Uit het gestelde is
D C of A B	ɔo	115.
B C of A D	ɔo	28.
M I of L K	ɔo	110.
M L of I K	ɔo	26 18/23.
de hooghte N O	ɔo	6.
en gestelt O Q	ɔo	x.

R N		N Q		S O	O Q
of ½ A B				of ½ M I
57½	_____	6 + x	_____	55	_____x
115	_____	6 + x	_____	110	_____x
5/_____				5/_____
23				22

23 x ɔo 132 + 22 x

___________________

O Q of x ɔo 132

en N Q ɔo 138

A B	115
A D	28
	____
	920
	230
	____
de basis A B C D	3220
⅓ N Q	46
	____
	19320
	12880
	______
inhoudt van de conus A B C D Q	148120.
M I	110
M L	26 12/23
	______
	660
	220
	86 2/23
	______
de basis I K L M	2946 2/23
⅓ O Q	44
	11784
	117843 19/23
	______
inhoudt der conus M I K L Q	129627 19/23.
Dit van 148120 A B C D Q, rest 18492 4/23 voor 't stuk A B I K L D C.

Om de middel-sectie G H E F te vinden.
H E of G F	112½	is de helft van
		A B + M I.
E F	27 9/23	is de helft van
	______	B C + I K.
	784
	224
	13½
	44 1/46
	______
middel-sectie	3081 12/23
met de hooghte	6
	_______
1^o. Komt	18489 3/23
van 't middel-stuk	18492 4/23	hier boven
	_______	gevonden,
verschilt maar	3 1/23	voet, 't geen het middel-stuk grooter is.

2^o. Het bovenste plat	3220
het onderste	2946 2/23
	______
	6166 2/23
2/	_______
	3083 1/23
met de hooghte	6
	______
komt	18498 6/23,
hier van 't middel-stuk	18492 4/23,
	______
verschilt maar	6 2/23	voeten, 't geen het middel-stuk kleinder is.

Deeze vry zekere meeting dus voor af hebbende laten gaan, zal nu voorder aanraken de wyze van Scheeps-meeten, die in Hollandt gebruikelyk is geweest, en noch is, uit last van hare Hoogh-Moogende.

Alle Scheepen, of Schuiten, wierden gemeeten met Wezelsche hout-voeten; meetende de langte over de stevens, de wydte op het wydste van 't Schip, en de holte van de opper-kant der buik-denning, tot de onder-kant van 't spie-gat, 4 voet achter het mast-gebindt.

Daar na gemultipliceert, of vermenighvuldight, de langte met de wydte, de uitkomst met de holte, en gerekent 180 voet voor ieder last, te weten in Wydt-scheepen, Smal-scheepen, Dremmelaars, Damloopers, Boeijers, Beitel-aaken, en alle Rondt-scheepen.

De Rondt-schuiten wierden gerekent 194 voet voor ieder last.

Samoureuzen, Pleiten, Geubels, en Schiet-schuiten, 170 voet voor ieder last.

Alle gewegerde Kagen, 206 voet voor ieder last.

Alle ongewegerde Kagen, 240 voeten voor reder last.

De Scheepen die na Noorwegen voeren wierden gemeeten (en zulks tot voldoe-

[p. 314]

ning van de tol, in 't gebiedt van zyn Majesteit van Denemarken op de hout-lasten gestelt) van de buitenste boven-kant van d'eene steven, tot aan de uiterste kant van d'andere steven, in de langte. In de wydte wierdt gemeeten voor de groote mast, van d'eene buitenste plank, van binnen af, tot aan d'andere buitenste plank. De diepte, of het ruim van de Scheepen, wierdt gemeeten tusschen de groote en de fokkemast, daar 't op het wydtste en holste is te vinden, dicht aan 't boordt, op zyn uitwateringe, regel-recht van d'eene tot aan d'andere kant, strekkende daar na van het midden der zelve koorde af, te meeten door het zaat-hout, of kols-wyn, tot op de kiel toe.

⁺Wanneer zy dan op deeze wyze waren gemeeten, wierdt haren inhoudt gestelt volgender wyze uit te vallen.

Een Schip lang 125 voet, wydt 25 voet, hol 14 voet, met een half dek tot voorby de groote luiken, omtrent 155 lasten.

Een Schip lang 123 voet, wydt 24½ voet, hol 14 voet, met een half dek, 146 lasten.

Een Schip lang 122 voet, wydt 24½ voet, hol 13½ voet, met een half dek, 138 lasten.

Een Schip lang 120 voet, wydt 24 voet, hol 13½ voet, met een half dek, 130 lasten.

Een Schip lang 118 voet, wydt 24 voet, hol 13 voet, met een half dek, 123 lasten.

Een Schip lang 116 voet, wydt 24 voet, hol 13 voet, met een half dek, 118 lasten.

Een Schip lang 114 voet, wydt 23½ voet, hol 13 voet, met een half dek, 112 lasten.

En voorts evenmatigh met alle Scheepen van deeze gestalte.

Een Schip lang 95 voet, wydt 21½ voet, hol 12 voet, zonder half dek, 73 lasten.

Een Schip lang 90 voet, wydt 21½ voet, hol 12 voet, 68 lasten.

Een Schip lang 85 voet, wydt 21 voet, hol 11½ voet, 60 lasten. En aldus voorder evenredigh met alle Scheepen van deeze gestalte.

Een Schip lang 124 voet, wydt 25 voet, hol 13 voet, het verdek 3½ voet, 162 lasten.

Een Schip lang 122 voet, wydt 24½ voet, hol 13 voet, het verdek 3½ voet, 153 lasten.

Een Schip lang 120 voet, wydt 24½ voet, hol 13 voet, het verdek 3½ voet, 145 lasten.

Een Schip lang 118 voet, wydt 24 voet, hol 12½ voet, het verdek 3½ voet, 134 lasten.

Een Schip lang 130 voet, wydt 28 voet, hol 12 voet, met een koe-brug, of boevenet van 6 voet, groot omtrent 195 lasten.

Een Schip lang 126 voet, wydt 26 voet, hol 12 voet, daar boven 6 voet, 176 lasten.

Een Schip lang 124 voet, wydt 25 voet, hol 11½ voet, en daar boven 5½ voet, groot 166 lasten. En zoo voort met de rest.

De Scheepen welke juist van een zelfde Certer niet wierden bevonden, zoo als die in de Plakkaten uitgedrukt stonden, mat men in billigheit evenredigh na de boven staande regulen, en der Scheepen draghtigheit.

Doch dit, aldus gerekent, en begroot als vooren, slaat op tarw, of op S^t. Ubes zout-lasten. Maar vermidts de Scheepen met hout zoo diep niet als met tarw, of zout, konnen geladen werden, wegens de lichtigheit en onbuighzaamheit der houtlasten, wierdt een vyfde part van ieder Schips grootte afgekort, wanneer die met hout geladen waren.

De Scheepen, als vooren gemeeten wezende, wierden op de zydt-balken, en op de voor- en achter-steven, gebrandt.

Maar heden is hier een andere, en volmaakter, wyze van Scheeps-meeten in gebruik gekomen, by voorval van verdragh tusschen zyne Majesteit van Denemarken, en hare Hoogh-Moogende, te weten: Men vult de ledige Scheepen, van alle slag, met bekende zwaarten van kogels en geschut, tot zulk een diepte als zy gewoon zyn door zee te varen, 't geen bespeurt wordt uit de dok, of moet, en merken, die het zee- of rivier-waters opper-vlak, daar tegen kabbelende, na laat: gerekent dan 4000 pondt voor een last, dopt men de Scheepen volgens deeze ondervindinge. En om dat het meeten van alle Scheepen te lange moeite, en te groote koste zy, gist men de ongemeetene, na en in haar soort, van wat draght zy mogen zyn. Doch door dien de zee met geene water-passe linien de Scheepen snydt, als ook om dat de Scheepen niet evenredigh en wis-konstig den ander gelyken, konnen in deeze wyze van doen eenige mis-greepen voor vallen.

De meetinge, welke ten proef geschiet, wert gedaan aan Scheepen die oudt, middel-tydigh, en nieuw zyn: gelyk dit alles breedelyk in het volgende ontworpene, en daar na vastgestelde Verdragh, tusschen zyne Majesteit in Denemarken, en hare Hoogh-Moogende, in den Jare 1669. den 2^den May opgerecht, kan blyken.

WY onder geschreeven, als by zyn Koninglyke Majesteit van Denemarken, en Noorwegen, &c. ende de Ho: Moog: Heeren Staten Generaal der Vereenighde Nederlanden respectivelyk gecommitteert tot de directie, mitsgaders inspectie, meetinge, ende begrootinge der Scheepen, na Noorwegen om hout-last varende, verklaren by deezen, dat wy, in gevolge van het II. en V. artykel van het Tractaat van Elucidatie^*, van den 11 February 1666,

+ Ziet de gedrukte Contracten van Anno 1647.

* Welke hier beneden zyn ingelascht.

[p. 315]

relatif tot het Tractaat van den Jare 1647, met malkanderen iterativelyk hebben geconfereert ende gedelibereert op de uitvinding van de bequaamste, gevoegelykste en zekerste maniere van meetinge, zoo als best doenlyk zal zyn, stellende ieder houtlast, volgens het voorsz. II. en V. artykel, op 4000 ponden Hollandts gewigt, zulks dat, zoo menigh maal als een Schip zoodanige 4000 ponden zwaarte aan hout bequamelyk kan laden en voeren, het zelve voor zoo veel lasten gerekent ende getauxeert zal moeten werden; Ende dat wy daar op verscheide Scheepen met yzere kogels hebben doen af-laden, als namentlyk het Schip de Laken-kooper, Schipper Broer Hittes van Hinloopen: de drie Koningen, Schipper Doede Eelkens: het vergulde Hert, Schipper Jolle Abes: de goede Hoop, Schipper Reinke Albertsz. van Hinloopen: de Water-hondt, Schipper Nien Klaasz. van Hoorn: de Brouwer, Schipper Auke Hiddes van Hinloopen: de Jager, Schipper Hessel Pietersz. en het vergulde Hert, Schipper Agge Abes: Ende voorts geaccordeert en over een gekomen te wezen, dat drie van de voor gemelde Scheepen voor Proef-scheepen gehouden, en daar uit een generale regel geformeert zal werden, om de draghtbaarheit van de andere Scheepen, zoo geproefde als ongeproefde, daar na te calculeeren, te weten, het voorsz. Schip 't vergulde Hert, Schipper Agge Abes van Warns, zynde van de nieuwe fabryke; het Schip de Brouwer, Schipper Auke Hiddes van Hinloopen, zynde van de middelbare fabryke; en het Schip de Water-hondt, Schipper Nien Klaasz. van Hoorn, zynde van de oude fabryke; Ende dat de zelve drie Proef-scheepen, als mede alle andere Scheepen, gemeeten zullen werden op een plaats alleen in de lengte binnen stevens, lyn-recht van de eene steven tot de andere; ende in de wydte binnen de wegers op drie plaatzen, te weten, by de groote mast, onder het luik, op de helft tusschen de groote mast en de voor-steven, ende weder op de helft tusschen de groote mast en de achtersteven; ende de holte in het ruim insgelyks op de zelve drie gedetermineerde plaatzen, beginnende van de buik-denning af, naast het kols-wyn, recht opwaarts, tot aan een rechte lyn, binnen het ruim gespannen uit de hoeken daar de wegers en de onderste zolderinge t'zamen komen, daar by doende 4 duimen voor de dikte van het water-bordt; ende de holte van 't verdek van gelyken op de zelve drie plaatzen, meetende uit de hoeken binnen het verdek, daar de wagers en de onderste kant van de bovenste zoldering, of verdek, t'zamen komen, rechthoekigh nederwaarts op de onderste zoldering, daar by doende 3 duimen voor de dikte der planken van den overloop; Ende dat het een derde van 't beloop der drie voorsz. wydtens genoomen zal werden van de middelbare wydte; ende voor de middelbare holte het derde part van het beloop der drie holtens van het ruim, daar by doende drie vierde parten van de middelbare holte in de heele verdek-scheepen, twee vierde parten daar het verdek uit getimmert is tot de spaken van het braadtspit, ende in de half verdek-scheepen de helft van het half verdek: in dien verstande nochtans, dat de holte van het verdek in de Scheepen die maar half uit getimmert zyn alleen genoomen zal werden in het midden by de groote mast, ende achter tusschen de groote mast en de achter-steven op de helft; ende dat in de geschutscheepen, vermits de belemmeringe van 't geschut, geen verdek gerekent zal werden, als voor zoo veel ende naar advenant dat de zelve bevonden zullen werden het zelve verdek met hout te beladen; Ende dat men voorts de voorsz. lengte, middelbare wydte, ende middelbare holte, met malkanderen zal multipliceeren, ende het product divideeren door een zeker, vast ende onveranderlyk getal, of divizoor, uit de voorsz. drie Proef-scheepen te vinden ende te determineeren; ende dat men het quotient, of uitkomst van dien, zal houden voor het getal der lasten, waar op een Schip van zoodanigen lengte, middelbare wydte, en middelbare holte, getauxeert zal moeten werden; En dat men, om de zelve divisie te vinden, het product van de lengte, middelbare wydte, en middelbare holte, van ieder van de voorsz. drie Proef-scheepen zal divideeren door het getal der lasten, waar op ieder van de zelve, door de proef van het gewight, is bevonden; ende dat het derde part van 't beloop der drie voorsz. uitkomsten, of quotienten, gehouden zal worden voor de gerequireerde divisoor. Zynde het Proef-schip, genaamt het vergulde Hert, in voegen als vooren gemeeten, bevonden lang te zyn 120 voet, wydt by de groote mast 26 voet 5 duim, hol op dezelve plaats 12 voet, wydt in 't midden tusschen de voor-steven en de groote mast 26 voet 6 duim, hol op dezelve plaats 12 voet 7 duim, wydt in 't midden tusschen de achter-steven en de groote mast 26 voet 6 duim, hol op de zelve plaats 15 voet 3 duim, hol by de groote mast onder het verdek 4 voet 3 duim, voor 3 voet 10 duim, en achter 4 voet 10 duim; ende met kogels afgeladen wezende op de diep-

[p. 316]

te van 12 voet voor, en achter op 14¼ voet, in zwaarte ingenoomen te hebben het beloop van 227½ lasten, ieder last, als vooren, tegens 4000 pondt Hollandts gerekent. Het tweede Proef - schip, genaamt de Brouwer, lang 116 voet 6 duim, wydt in het midden 24 voet 2 duim, hol 11 voet 6 duim, voor wydt 24¼ voet, hol 11 voet 6 duim, achter wydt 24 voet 2 duim, hol 14½ voet, het verdek in 't midden 4 voet, voor 3 voet 10 duim, achter 4 voet 3 duim; ende in voegen als vooren af-geladen wezende op de diepte van 11¾ voet voor, en 13¾ voet achter, in zwaarte ingenoomen te hebben het beloop van 183½ lasten. Ende het derde Proef-schip, genaamt de Water-hondt, lang 116 voec 4 duim, wydt in 't midden 23 voet 5 duim, hol 11 voet 10 duim, voor wydt 23 voet 7 duim, hol 11 voet 3 duim, achter wydt 23 voet 5 duim, hol 15 voet, het verdek in 't midden 3 voet 10 duim, voor 3 voet 10 duim, en achter 4 voet 3 duim; ende met kogels, als vooren, af-geladen wezende op de diepte van 11⅔ voet voor, en 13⅔ voet achter, in zwaarte ingenoomen te hebben het beloop van 168⅜ lasten. Zynde mede verdragen, dat, tot vermydinge van alle gebrooken getallen, ende confusie, ofte perplexiteit, daar uit ontstaande, ende om te vinden een gelykheit in de rekening, geobserveert zal werden dat in cas een gebrooken getal in de divisoor, ofte in de uitrekening, boven het beloop van de lasten, komt over te schieten, niet importeerende ¼ van een last, daar voor niet gerekent zal werden, ende meerder importeerende als ¼, dat daar voor ½ last gerekent zal werden; als mede, in cas het gebrooken meer komt te bedragen als ½, en minder als ¾ last, dat als dan niet meer als ½ last gerekent zal werden, doch meerder bedragende als ¾, een geheel last. Ende is daar op de lengte, middelbare wydte, en de middelbare holte, van het vergulde Hert bevonden te bedragen 120 voet, 26 voet 5⅔ duim, en 16 voet 6⅓, duim: van de Brouwer 116, 6; 24, 2¼; 15, 6¼ ende van de Water-hondt 116, 4; 23, 5⅔; 15, 8½: ende der zelver respective producten 52741, 43938, en 43096: ende het beloop van de lasten, door dr proef van het gewigt, 227½, 183½, en 168⅜: ende dat de zelve producten, gedeelt door de lasten, komen te geven voor hare quotienten, of uitkomsten, 231 6/7, 239⅓ en 256: ende het ⅓ part van de zelve quotienten 242 25/63, makende het zelve gebrooken, volgens de voorgaande conventie, ½. Welk getal van 242½ voor de gemeene divisoor moet verstrekken, door welke alle de respective producten van lengte, middelbare wydte, en middelbare holte, van alle de andere geproefde en ongeproefde Scheepen gedeelt moeten werden, ende het getal der lasten, waar op ieder Schip begroot moet werden, uitgerekent. Naar het welke de Schippers hare maat-cedullen gegeven, ende de tollen, in conformiteit van het achtste artykel van het voorsz. Tractaat van elucidatie, tot nader ordre, betaalt zullen werden.

Volgen het tweede en vyfde artykel uit het Tractaat, tusschen zyne Majesteit den Heere Koning van Denemarken, Noorwegen, &c. ende hare Hoog-Moogende, gemaakt in den Hage, den elfden Februarii, 1666. over tollen, ende hout-lasten, in Noorwegen.

II.

Tot verhoeding ende correctie van alle mis-verstanden, ofte gepleeghde frauden tegens het voorschreeve Tractaat, zoo ten opzighte van de meetinge der Scheepen zelve, op Noorwegen varende, als door den aanbouw van zekere soort van Scheepen, die ten tyde van het aangaan van het voorsz. Tractaat niet bekent zyn geweest, ende ordinaris genoemt werden van de nieuwe fabrique, is toegestaan ende geaccordeert een nieuwe meetinge van Scheepen, op de bequaamste, gevoegelykste, ende zekerste maniere doenlyk zynde, in dier voegen, dat de hout-lasten van de Scheepen zullen werden uitgevonden, en begroot op vier duizent ponden gewigte; zulks dat zoo dikmaals als een Schip de zwaarte van vier duizent ponden aan hout kan inladen, het zelve voor zoo veel lasten zal werden gerekent ende getaxeert.

V.

Doch in cas over de voorschreeve beraamde meetinge verschil zoude moogen vallen, of eenige Schipper zich beklagen dat zyn Schip te hoog of te groot van lasten gestelt was, zal zoodanigen Schipper, in Noorwegen komende, ende zyn Schip, onder kennisse ende voorweten van de Koninklyke Officieren, met zoodanigh hout als ordinaris uit de Havenen van Noorwegen afgeladen werdt, wel en vol afgestut hebbende, van de gemelte Offecieren acte ende verklaringe nemen, hoe veel voeten zyn onderhebbende Schip achter en voor diep gelegen heeft van de voorzeide houtlast, betalende dien volgens ook de opgestelde tollen; doch t'zyner naaste reize zal hy zich tot Dramme in Noorwegen, ofte in eenige andere van de voornaamste Havenen in Noorwegen voorschreeven, tot

[p. 317]

de hout - ladinge bequaam, addresseeren aan de gemelde Officieren, die, t'zynen verzoeke, aanstondts ende zonder vertoeven het voorsz. Schip zullen doen laden en bezwaaren met afgewoogen yzer, ofte ander zwaar goet, tot op de zelve diepte gelyk het te vooren met hout geladen hadde gelegen, ende uit het gewigte van 't voorschreeven ingeladen yzer, ofte ander zwaar goet (te rekenen tegens vier duizent ponden Hollandts gewigte voor een last) calculeeren en begrooten het getal der hout-lasten die het zelve Schip zal konnen voerren, naar advenant van welke bevindinge den tol betaalt zal werden. Welke meetinge zal dienen voor een generale decisie: des zullen de Schippers, welkers Scheepen by zoodanige preuve bevonden werden te vooren recht en wel gemeeten te zyn, tot haren laste moeten nemen en dragen de gedane preuve, ook in toekomende meerder tollen betalen, na advenant der lasten, die hare Scheepen, in cas voorsz. bevonden werden te weinigh getaxeert te zyn geweest, zonder dat zy om 't gepasseerde gemoeit zullen werden; doch bevindende dat eenige Scheepen te hoogh op lasten gestelt ende te veel bezwaart zyn, zullen de zelvige van de betalinge der voorschreeve preuve t'eenemaal vry zyn, ende op zoodanige lasten gestelt worden als die haar bevinden, ook by zyne Koninglyke Majesteits Officieren ende Bedienden gestitueert werden 't geene dat te vooren te veel aan tol betaalt zal wezen.

Van deeze meetinge, eikkinge, en begrootinge der Scheepen, worden aan de Schippers brieven verleent, om die in Noorwegen, of elders onder 't gebiedt van zyne Majesteit van Denemarken, te vertoonen: ook werden brandt-tekens voor en achter op de stevens gezet, om tegens de eik-brieven te werden geconfereert, en vergeleken.

Eenige nieuwe aan te bouwen Scheepen, ofte andere, tot hout-ladinge te vooren niet gebruikt geweest zynde, zullen in voegen als vooren gemeeten worden, en, in cas van bezwaarnisse, een preuve onder 't gebiedt van Denemarken moogen vorderen.

Op wat wyze deeze meetinge by eenige Uitlanders geschiedt.

Zy multipliceeren de kiels langte met de breedte op het wydtste des Schips, en dit met de holte, van de kiel tot aan de verdeks-balk toe: als, by voorbeeldt, laat'er een Schip zyn, dat zy houden 100 tonnen te konnen voeren, (te rekenen twee tonnen op een last) wiens kiel zy 45 voeten, de langste verdeks balk 18 voeten, ende holte 8 voeten; deeze drie met malkander gemultipliceert, komt 6480 voeten, en zoo veel zoude den ihhoudt zyn indien het een vierkant lichaam was, zoo lang als de kiel, breedt als de wydte, en dik als de holte des Schips: maar om dat de Scheepen achter en voor smalder worden, en onder rondtachtigh zyn, zoo zien zy hoe veel de buik-stukken na achteren en na vooren korter worden als de langste, gelyk 3, 4, of 5 voeten, na dat die verre van 't midden zyn, nemende een middel-getal van deeze verkorting, als hier, by voorbeeldt, 3 voeten, welke zy met de helft van de holte, te weten 4, multipliceeren, komt 24, dit wederom met de kiels langte 45, komt 540 voeten voor het geene zy aan d'eene zyde aftrekken, en zoo veel ook aan d'andere zyde, trekkende dan twee maal 540 of 1080 voeten van 6480, blyft noch 5400 voeten voor den inhoudt van de holte des Schips onder het verdek. Deeze holte met zee-water gevult, zal dat water 396900 Fransche ponden wegen, nademaal zy rekenen de voet zee-water zwaar te zyn 73½ pondt, 'twelk het gewight is dat dit Schips hol bevatten zoude als het met water gevult was. Dan nemen zy de helft van het voorsz. gewight des waters 396900 pondt, zynde 198450 pondt, voor het gewight dat zulk een Schip voeren kan; dit gedivideert door 2000 pondt, de zwaarte van een harer tonnen, komt zeer na 100 tonnen, die dit Schip voert.

Een Schip, zeght Fournier, Fransch Schryver, draaght zoo veel als het zelve weeght.

Tweede manier.

Zy multipliceeren, als vooren, de kiels langte met de wydte, en dit met de holte, rekenende 80 voeten voor een ton.

Derde manier.

Zy addeeren tot de kiels langte de langte over steven, multipliceerende de helft van deeze somme met de wydte, en dit dan met de holte, snydende de twee achterste cyfer-letteren af, het blyvende getal wyst aan hoe veel het Schip voeren kan.

Vierde manier.

Zy multipliceeren de kiels langte met de wydte, en dit weer met de holte, het komende getal divideeren of deelen zy door de kiels langte, hier by doende de wydte van 't Schip, met de holte, dat dan t'zamen geaddeert, wyst het quotient of uitkomste aan hoe veel tonnen het Schip

[p. 318]

voert; doch als het Schip vry scherp is, nemen zy'er 10 ton af, maar zoo het buikigh en breedt is, doen zy'er 10 ton toe.

De vyfde manier, die by d'Engelschen en Franschen wel voor goedt gehouden wordt, doch myns wetens niet gebruikt, is deeze:

Men zal het Schip, als het opgemaakt is, doch noch op stapel staat, tot het verdek toe met water vullen, nemende tot dien einde een vat, waar van de zwaarte des waters, dat daar in kan, bekent is: dit dan bekent zynde, en bevonden hoe menigh maal zulk een vat vol water daar in gegooten is, als het Schip gevult is, zoo is ook bekent hoe zwaar het Schip geladen is. Indien nu dit Schip, zoo gevult, in zee was, zonder masten, touwen, of iets anders op of in te hebben boven de verdeks-balken, 't is zeker dat het dryven zoude, na dien de stoffe van 't hout lichter als het water is; want zy rekenen de voet eeken-hout 13 pondt lichter te zyn als die van 't zee-water. Maar het Schip noch belast zynde met het hout boven 't verdek, masten, touwen, menschen, en andere dingen, 't is zeker dat dit gevult Schip zinken zoude. Als men nu de zwaarte van de masten, touwen, menschen, het hout boven 't verdek, enz. half zoo zwaar rekent als het zee-water dat onder 't verdek in gegooten kan werden, ('t geen zy voor na genoegh houden) zoo zal het Schip noch konnen voeren, met zyn toetakeling, de helft van het zee-waters zwaarte, waar mede het zelve gevult was.

Om te meeten hoe veel voeten water, of andere stoffe, onder 't verdek leggen kan, zoude men deeze volgende wyze konnen gebruiken: Meet de vlakte by de twee uiterste ribben op de kiel, desgelyks de vlakte in de wydtste rib: als by voorbeeldt, dat a b c d, in de figuur E, een van deeze ribben zy, a d de onder-kant van 't verdek, met welk de streepen e f, g h, enz. evenwydigh getrokken zyn, alzoo dat de streepen a e, e g, d f, f h, enz. voor rechte linien, of streepen, konnen genoomen worden. Meet dan a d, e f, g h, en de andere evenwydige, desgelyks ook de wydte tusschen deeze evenwydige, te weten i k, k l, enz. daar na addeert a d en e f te zamen, en multipliceert de helft met i k; desgelyks addeert e f en g h te zamen, en multipliceert die met k l, en zoo voort met de andere: deeze gevonden getallen t'zamen geaddeert, komt voor de vlakte in de rib a b c d. De wydte der twee uiterste ribben dan gevonden zynde, zoo addeert de zelve te zamen: doet dan de helft deezer somme by de vlakte van de grootste rib; en eindelyk de helft van deeze somme genoomen, komt voor de gemiddelde vlakte: doet daar na by de langte over steven de langte der kiel, de helft is voor de gemiddelde langte. Multipliceert dan deeze gemiddelde langte met de gemiddelde vlakte, 't geen komt neemt voor den inhoudt van de holte.

Maar alle deeze laatste wyzen van meeting konnen weinigh dienen om de volmaakte ladinge der Scheepen te vinden; want behalven dat de holte bezwaarlyk, ja onmoogelyk door rekening volmaaktelyk kan gevonden werden, om dat de gedaanten der Scheepen zeer ongelyk, en de zelve van verscheide kring-stukken te zamen gevoegt zyn, zoo komen hier noch eenige zwarigheden by, te weten: Om dat oude Scheepen zwaarder zyn als nieuwe, voeren zy minder last; want oudt hout heeft meer ingedronken water by zich, ook maakt het meer reeten, daar het water steedts door sluipt, 't welk liet Schip bezwaart. Scheepen die van droogh hout gemaakt zyn voeren meer als die van nat hout opgetimmert zyn, om dat droogh hout lichter is als het natte. Ook dragen, na veeler gevoelen, de Scheepen des Zomers meerder als des Winters, om dat de wateren dan dikker zyn, 't geen veroorzaakt werdt door de koude. In zoet water dragen de Scheepen minder als in zout water; want zoet water is lichter als het zoute water. Licht water wederhoudt minder als zwaar water, en derhalven konnen de Scheepen in licht water beter zinken als in zwaar water; schoon Seneca van gevoelen was, dat het water niet wederhieldt, maar dat het zeker geest was, die de Scheepen op hunne kielen deede dryven.