Wisconstighe gedachtenissen. Deel 2: van de meetdaet

Tweede deel des vyfde Bovcx vande everedelicke snyding der vlacken.

DE volghende snyding der vlacken (die inde daet haer merckelick ghebruyck heeft, als onder anderen om landen in begeerde cavels of sticken te deelen) sal sijn van rechtlinighe platten, ende van t'clootvlack: De snyding der rechtlinighe platten gheschiet deur rechte linien op driederley wijse:

[p. 139]

D'eene met linien commende uyt een ghestelt punt inden omtreck: d'ander daer buyten: de derde evewijdeghe met eenighe getoonde lini, welcke verscheydenheden wy met onderscheyt beschrijven sullen, ende eerst

Vande snyding der rechtlinighe platten met een lini commende uyt een ghestelt punt inden omtreck.

5 Voorstel.

Van een ghegheven driehouck een begheert deel te snyen na een ghetoonden oirt, met een lini commende uyt een ghetoonden houck.

1 Voorbeelt.

Tghegheven. Laet A B C een drichouck sijn, ende D E een lini ghesneen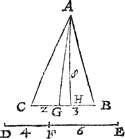



in F. Tbegheerde. Wy moeten uyt den houck A een lini trecken, die vanden driehouck een deel snye na den oirt C, in sulcken reden tottet ander deel, als D F tot F E.

Twerck.

Ick deel de sijde teghenover den houck daer de snyende lini uyt commen moet als de sijde C B in G deur het 2 voorstel van desen, sulcx dat ghelijck D F tot F E, alsoo C G tot G B: Twelck soo sijnde ick segh dat ghelijck D F tot F E, alsoo het deel A G C tottet deel A G B, waer af t'bewijs openbaer is deur het 1 voorstel des 6 boucx van Euclides.

Derghelijcke vvercking deur ghetalen.

Ick meet DF, bevinde die neem ick van 4 voeten, F E 6, B C 5, die ghedeelt in twee deelen tot malcander in sulcken reden als 4 tot 6, comt 2 en 3, daerom van C tot G ghemeten 2 voeten, ende ghetrocken A G men heeft t'begheerde. Proef. Laet de hanghende A H ghemeten sijnde, bevonden worden van 8 voeten, t'welck soo wesende de driehouck A B C doet 20, A G C 8, ende A G B 12, alwaer blijckt dat 8 en 12 de 20 maken des heelen driehoucx A B C, ende ghelijck D F 4, tot F E 6, alsoo A G C 8, tot A G B 12.

2 Voorbeelt.

Tghegheven. Laet A B C des 1 voorbeelts een driehouck sijn.

Tbegheerde. Wy moeten daer af na den oirt C een plat snyen (minder welverstaende dan t'begrijp des heelen onbekenden driehoucx) ick neem van 8 voeten, met een lini van A tot inde sijde B C.

Twerck.

Ick meet de hanghende A H die bevindende neem ick van

8.

[p. 140]

Het dobbel van t'begheerde deel is	16.
T'selve ghedeelt deur 8 eerste in d'oirden comt	2.

Daerom ghemeten van C na B 2 voeten als van C tot G, ende ghetrocken A G men heeft, t'begheerde, waer af de proef is dattet deel A G C 8 voeten doet deur het 13 voorstel des 2 boucx. Tbeslvyt. Wy hebben dan van een gegheven driehouck een begheert deel ghesneen na een ghetoonden oirt, met een lini commende uyt een ghetoonden houck, na den eysch.

6 Voorstel.

Van een ghegheven driehouck een begheert deel te snyen na een ghetoonden oirt, met een lini getrocken uyt een ghestelt punt inde sijde des driehoucx.

1 Voorbeelt.

Tghegheven. Laet A B C een driehouck sijn met een punt D inde sijde A C, ende E F sy een linighesneen in G. Tbegheerde. Wy moeten van t'punt D een lini trecken, die vanden driehouck A B C een deel snye na den oirt C, in sulcken reden tottet ander deel als E G tot G F.

Twerck.

Ick treck D H rechthouckich op C B, ende D I rechthouckich op A B, souck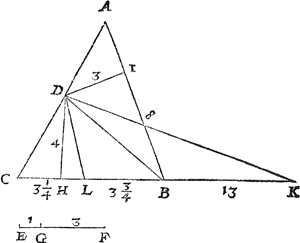



daer na deur het 2 voorstel des 4 boucx de vierde everedenige der drie D H, D I, A B, welcke sy B K: Deel daer na deur het 2 voorstel van desen C K in L, inder voughen dat ghelijck E G tot G F, alsoo C L tot L K, welcke L ick neem te vallen tusschen C B: Treck daer na D L: Dit soo sijnde ick segh dat gelijck E G tot G F alsoo het deel D L C tottet deel D L B A.

Tbereytsel. Laet getrocken worden de rechte D B en D K.

Tbewys.

Anghesien B K gront des driehoucx D B K, vierde everedenighe is der drie welcker eerste D H hooghde des driehoucx D B K, de twdede D I hooghde des drichoucx D B A, ende A B haer gront, soo is den driehouck D B K even anden driehouck D B A: Ende tot elcke vergaert den ghemeenen driehouck D L B, soo is den driehouck D L K, even anden vierhouck D L B A, daerom ghelijck den driehouck D L C, totten driehouck D L K, alsoo den selven drieouck D L C, totten vierhouck D L B A: Maer ghelijck den driehouck D L C, totten driehouck D L K, also de lini C L, tot L K, daerom ghelijck C L, tot L K,

[p. 141]

alsoo den driehouck D L C, totten vierhouck D L B A: Maer ghelijck C L, tot L K, alsoo E G, tot G F deur t'werck, daerom ghelijck den driehouck D L C, totten, vierhouck D L B A, alsoo E G tot G F.

Derghelijcke vvercking deur ghetalen.

Ick meet de nabeschreven linien met voetē, die bevindende neē ick als volght:

	D H 4, D I 3, A B 8, C B 7, E G 1, G F 3.
	Segh daer na D H 4, gheeft D I 3, wat A B 8? comt als voor B K	6.
Daer toe vergaert C B 7, comt C K		13.
De selve an tween gedeelt gelijck E G 1, tot G F 3, comt voor t'eerste deel		3¼.

Daerom soo veel voeten ghemeten van C tot L, ende ghetrocken D L men heeft t'begheerde. Proef. Doende D H 4, ende C L 3¼. soo doet den driehouck D C L 6½: T'welck soo sijnde den vierhouck D L B A sal moeten 3 mael soo veel doen, te weten 19½. daerom den selven vierhouck van soo veel bevindende, t'voornemen is beproeft: Om daer toe te commen ick seggh: C L is hier boven bevonden van 3¼. die ghetrocken van C B 7, rest 3¾ voor L B gront des driehoucx D L B, ende haer hooghde D H doet 4, daerom de driehouck D L B doet 7½. Daer toe vergaert den driehouck D A B 12 (soo veel begrijptse om dat haer gront A B 8 doet ende haer hooghde D 13) comt voor den vierhouck D L B A na t'behooren 19½.

Ander manier van vvercking deur ghetalen.

Ghenomen de maten der linien te sijn als boven soo bevinde ick den driehouck D B C van 14, D B A 12, t'samen voor den heelen driehouck A B C 26, de selve in tween ghedeelt ghelijck E G 1, tot G F 3, comt voor t'eerste deel 6½. Daerom vanden driehouck D B C 14, ghesneen 6½ na de leering des 5 voorstels van desen, men bevint dat C L lanck moet vallen 3¼ als boven, Daerom soo veel ghemeren van C na K als tot L, ende ghetrocken D L men heeft t'begheerde, waer af de proef boven ghedaen is.

Vervolgh.

By aldien den driehouck D B C te cleen waer gheweest om daer af te trecken 6½, soo soude de snyende lini ghelijck D L nootsakelick ghevallen hebben van D in A B. Daerom als sulcx ghebeurt men sal uyt het voorgestelde aldus besluyten: Anghesien datter begheert is een deel na den oirt C, in sulcken reden tottet ander deel, als E G tot G F, soo isser oock begheert een deel na den oirt A, in sulcken reden tottet ander deel, als F G tot G E: Daerom volghende daer mede de wercking als boven (die alsdan sulcx na de slinckersijde valt, als de voorgaende na de rechtersijde, soo wel inde meetconstighe wercking als in die deur getalen) men comt tottet begheerde.

Maer soo den driehouck D B C byghevalle even waer gheweest ande boveschreven 5 3/8 die van t'gheheel moeten ghesneen sijn, tis kennelick dat D B dan de begheerde snyende lini soude wesen.

2 Voorbeelt.

Tghegheven. Laet A B C des 1 voorbeelts een driehouck sijn.

Tbegheerde. Wy moeten daer af na den oirt C een deel snyen (minder welverstaende dan t'begrijp des heelen onbekenden driehoucx) ick neem van 6½ voeten, met een lini uyt D ghetrocken.

[p. 142]

Twerck.

Ick meet de hanghende D H op de sijde B C, die bevindende neem ick van	4.
Segh daer na, het dobbel des begheerden deels 6½ doet	13.
Die ghedeelt deur 4 eerste in d'oirden comt	3¼.

Daerom soo veel voeten ghemeten van C tot L, ende ghetrocken D L, men heeft t'begheerde, want alsdan doet den driehouck D L C 6½.

Vervolgh.

By aldien t'begheerde deel meerder waer gheweest dan den driehouck D B C, men soude soo veel snyen vanden driehouck D B A na den oirt B alsser ghebrake, ende t'begheerde hebben. Tbeslvyt. Wy hebben dan van een ghegheven driehouck een begheert deel ghesneen na een ghetoonden oirt met een lini ghetrocken uyt een ghestelt punt inde sijde des driehoucx na den eysch.

7 Voorstel.

Van een ghegheven rechtlinich plat een begheert deel te snyen na een begheerden oirt, met een lini ghetrocken uyt een ghegheven punt in des plats omtreck, snyende het plat in tvveen.

Merckt eer wy totte saeck commen, datter eyghentlick acht te nemen is op des voorstels laetste woorden aldus luydende: snyende het plat in tween, waer by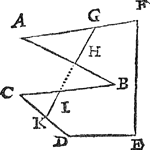



te verstaen is eyghentlick twee stucken, en niet meer, ghelijck an sommighe rechtlinighe platten gebeuren can. Laet by voorbeelt A B C D E F een rechtlinich plat sijn, met een inwendighen houck A B C, en van t'punt G inde lini A F comme een rechte lini G H I K, snyende t'ghegheven plat na eenighe begheerde rede niet in tween, maer in drien, te weten de twee verscheyden driehoucken A G H, C I K, t'samen in begheerde reden tottet derde stuck: Welcke manier van snyen inden wijsentijt bekent mach gheweest sijn, maer nu, mijns wetens niet. En mach derghelijcke oock verstaen worden op ettelicke volgende voorstellen daer sulcx ghebeuren can.

Tghegheven. Laet A B C D E F een rechtlinich plat sijn, ende G een punt inde sijde A B, ende H I een lini ghesneen in K. Tbegheerde. Wy moeten van t'punt G een lini trecken die van t'ghegeven plat na den oirt A een deel snye, in sulcken reden tottet ander deel, als H K tot K I.

Twerck.

Ick treck de vier linien G F, G E, G D, G C deelende t'ghegeven plat inde vijf driehoucken G A F, G F E, G E D, G D C, G C B, Daer na eenighe vijf linien L M, M N, N O, O P, P Q al in een rechte lini, ende tot malcander oirdentlick in sulcken reden als de boveschreven vijf driehoucken deur het 8 voorstel des 4 boucx: Deel daer na L Q in R, sulcx dat ghelijck H K tot K I, alsoo L R tot R Q, ende valt de voorschreven R neem ick tusschen O en P, welcke O P we-

[p. 143]

sende lijckstandighe



pael mettē driehouck G D C, soo deel ick de sijde D C int punt S, sulcx dat ghelijck O R tot R P, alsoo D S tot S C, ende trec G S die ick segh de begheerde te wesen, snyende den seshouck alsoo dattet deel G S D E F A, sulcken reden heeft tottet deel G S C B, als H K, tot K I, waer af t'bewijs deur t'voorgaende openbaer is.

Derghelijcke vvercking deur ghetalen.

Ick meet de voorgaende linien en driehoucken met voeten, die vindende neem ick als volght:

H K	40.
K I	10.
	_____
G A F	38.
G F E	364.
G E D	390.
G D C	666.
G B C	85.
	_____

Comt in als voor den heelen seshouck A B C D E F. 1543.

De selve 1543 ghedeelt ghelijck H K 40, tot K I 10, comt voor t'begheerde deel na A dat wy afsnyen moeten 1234 2/51 Hier toe maken de drie driehoucken G A F 38, G F E 364, G E D 390, t'samen voor den vijfhouck G D E F A 792. Maer wy moetender als gheseyt is 1234 ⅖: hebben, daer ghebreeckter dan noch 442 ⅖. die afghesneen vanden driehouck G D C na de leering des 5 voorstels van desen mette lini G S, sulcx dat den driehouck G S D begrijpe de selve 442⅖. soo sal het deel na A, als den seshouck G B D E F A doen 1234⅖. t'ander deel als den vierhouck G S C B 308⅗. welcke tot malcander openbaerlick in sulcken reden sijn als 4 tot 1. Tbeslvyt. Wy hebben dan van een ghegheven rechtlinich plat een begheert deel ghesneen na een begheerden oirt, met een lini ghetrocken uyt een ghegheven punt in des plats omtreck, na den eysch.

[p. 144]

Nv vande snyding der rechtlinighe platten
met een lini commende uyt een ghestelt punt buyten den omtreck.

DE vier voorstellen deser ghedaen te seer spitsvoudich sijnde, en merck ick niet by de Griecken bekent gheweest te hebben, dan vermoedese in eenighe overbleven schriften des wijsentijts weerom te voorschijn gherocht te wesen, uyt welcke sy ghecommen meughen sijn onder anderen ter handt van Ioannes Baptist a Benedictus (uyt wiens schriften^* vertoochse wijse ghestelt, wy de form der wercking en bewijsing deser voorstellen ghetrocken en veroirdent hebben:) Oock ter handt van Nicolas Tartaglia, die ick daer na bevonden heb dat daer af gheschreven had in Il libro della quarte parte: Mijn reden van sulck vermoeden is dusdanigh: Ymant die sich voorstelt oirdentlick te willen vervolghen de beschrijving vant snyen der platten, hem comt int ghedacht daer in te behooren de snijding deur een punt soo wel ghegheven buyten den omtreck, als daer binnen, te meer dattet in deeling van landē somwijlen dadelijck vereyscht wort: Maer sulcx soodaniger menschen ghedachten te wesen, blijckt noch deur diender veel verscheyden dit verschil malcander voorghestelt hebben, als den boveschreven Benedictus wiens schrift een brief van antwoort was op sulcken vraghe. Ten anderen Cardanus met Ludovicus Ferrarus hebben sulcx voorghehouden an Tartaglia, t'welck hy Tartaglia daer te vooren, soo hy self schrijft, in sijn^* openbaer redenstrijt voorghestelt had. My sijnder oock ander bekent die daer me, eer dese voorstellen t'haerder handt ghecommen waren, doende gheweest hebben, onder welcke ick een was.

Maer t'ghene hier af de menschen nu ter tijt ontmoet, derghelijcke ist billich toe te laten ontmoet te hebben de Vinders der seltsame wetenschappen daer af ons soo seecker teyckens ghebleven sijn, t'welck waren, soo inde bepaling van dies t'sijnder plaets verclaert is, de menschen des wijsentijts, daerom gevet groot vermoeden, datse sulcken vermaert vindlick deel der Meetconst niet onghevonden ghelaten hebben.

* Theorematicé.

* Publicâ disputatione.

8 Voorstel.

Van een ghegheven driehouck een begheert deel te snyen na een ghetoonden oirt, met een rechte lini commende uyt een punt ghegheven buyten den driehouck.

Tghegheven. Laet A B C een driehouck sijn, en een punt daer buyten D, voort sy E F een lini ghesneen in G. Tbegheerde. Wy moeten van t'punt D een rechte lini trecken snyende den driehouck in tween, soo dattet deel nae A, in sulcken reden sy tottet ander, als E G tot E G.

Twerck.

1 Lidt.

Ick treck C A of C B voorwaert: Maer om hier wat breeder verclaring te doen welcke het wesen moet, ick segh aldus: By aldienmen deur de ghelegent-

[p. 145]

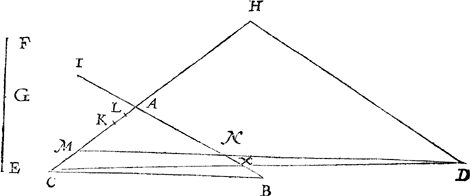heyt des gheghevens uyter ooch mercken can dat de begheerde lini diemen uyt D trecken moet, vallen sal in C A, men treckt de selve C A voorwaert, merckmense in C B te willen vallen, men treckt C B voorwaert. Maer sulcx by der oogh niet merckelick sijnde, men sal trecken een lini van D tot sulcken houck des ghegheven driehoucx A B C, daer den selven driehouck in tween deur can ghedeelt worden mette voorschreven lini of haer verlangde, welcke hier is D C, snvende A B teghenoversijde des houcx C in X. Soo nu de lini A X by ghevalle in sulcken reden bevonden wierde tot X B, ghelijck G F tot G E, t'welck deur het 2 voorstel des 4 boucx bekent wort, tis openbaer dat D C de begheerde lini soude sijn, deelende den driehouck A B C inde begheerde reden, om dat ghelijck A X tot X B, alsoo den driehouck A C X totten driehouck X C B. Maer soo de reden van A X tot X B grooter bevonden wierde dan van F G tot G E, men sal C A voorttrecken, en cleender bevonden wesende, alsdan treckmen C B voortwaert. Laet dan de selve reden grooter bevonden sijn: Dit soo ghenomen ick moet C A ghenouch voorwaert trecken, t'welck sy tot H.

2 Lidt.

Ick segh daer na E F geeft F G, wat B A? comt A I, die ick teycken inde voortghetrocken B A.

3 Lidt.

D H gheeft A I, wat C A? comt A K, die ick teycken inde lini van A na C.

4 Lidt.

Ick deel A K int middel an t'punt L.

5 Lidt.

Ick souck deur het 3 voorstel des 4 boucx de middeleveredenighe lini tusschen A L, en een lini even an A L met het dobbel van A H, welcke middeleveredenighe sy L M.

Merckt nu dat by aldien L M langer viel dan L C, of dat D M niet en gheraeckt A B, sulcx dattet afghesneen deel na A niet en waer een driehouck, soo en soudemen int 1 lidt des wercx niet C A voortghetrocken hebben, maer C B, en dan t'boveschreven werck over die sijde doen.

[p. 146]

6 Lidt.

Ick treck de rechte lini D M snyende A B in N: T'welck soo wesende ick segh den driehouck A B C in tween ghesneen te sijn mette lini D M, alsoo dattet deel A N M, in sulcken reden is tottet ander M N B C, als F G tot E G.

Tbewys.

Want dit bewijs hoe wel van een cort werck lanck sal vallen, soo sullen wijt om alles bescheydentlick te doen in 5 leden deylen, en op dattet vervolgh der selve leden en de maniere vant bewijs int gemeen opentlicker verstaen werde, soo sullen wy hier t'voornaemste inhoudt dier leden eerst int corte verhalen als volght.

Int 1 lidt sal bewesen worden dat ghelijck den rechthouck onder A C, A B, totten rechthouck onder A M, A N, Alsoo den driehouck A B C, totten driehouck A N M.

Int 2 lidt, dat ghelijck E F tot F G, alsoo den rechthouck onder A B, A C, totten rechthouck onder A C, A I.

Int 3 lidt, dat den rechthouck onder H D, A K, even is anden rechthouck onder A C, A I.

Int 4 lidt, dat den rechthouck onder M A, A K, even is anden rechthouck K A, A H.

Int 5 lidt, dat den rechthouck onder M A, A N, even is anden rechthouck onder H D, A K, en daerom oock even metten rechthouck onder A C, A I, deur het 3 lidt: Maer int 2 lidt is gheseyt dat ghelijck E F tot F G, alsoo den rechthouck onder A B, en A C, totten rechthouck onder A C en A I: En daerom gelijck E F tot F G, alsoo den rechthouck onder A B, A C, totten rechthouck onder M A, A N: Maer de twee driehoucken A B C, A N M, sijn oock inde selve reden deur het 1 lidt, daerom ghelijck E F, tot F G, alsoo den driehouck A B C, totten driehouck A N M: Ende deur ghescheyden reden, ghelijck E F min F G dats E G, tot F G, alsoo den driehouck A B C min den driehouck A N M dats den vierhouck M N B C, totten driehouck A N M, na den eysch.

Dit aldus int ghemeen gheseyt wesende, wy sullen totte eyghentlijcke beschrijving der voornoemde vijf leden commen.

1 Lidt.

Ghelijck den rechthouck onder A C, A B, totten rechthouck onder A M,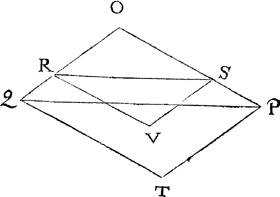



A N, alsoo den driehouck A B C, totten driehouc A N M, t'welc aldus bewesen wort: Laet om de ghegheven form deur veel linien niet te verduysteren andermael geteyckēt worden den driehouck O P Q, en gelijck metten driehouck A B C, en daer in sy ghetrocken de lini R S, even met M N, en in sulck gestalt

[p. 147]

in dees form, als M N in die, daer na sy ghetrocken Q T even en evewijdeghe met O P, en R V even en evewijdeghe met O S, daer na T P en V S: dit soo sijnde, ick segh dat ghelijck den evewijdeghen vierhouck Q O P T onder Q O, O P, tot haer heeft den driehouck O P Q, alsoo den evewijdegen vierhouck R O S V onder R O, O S, tot haer helft den driehouck O S R: Maer ghelijck den evesijdighen vierhouck onder Q O, O P, totten evesijdigen vierhouck onder R O, O S, alsoo den rechthouck onder Q O, O P, totten rechthouck onder R O, O S: Daerom ghelijck den rechthouck onder Q O, O P, totten rechthouck onder R O, O S, alsoo den driehouck O P Q, totten driehouck O S R, Maer den rechthouck onder A C, A B, is even metten rechthouck onder O Q, O P, Ende den rechthouck onder A M, A N, is even anden rechthouck onder O R, O S, en den driehouck A B C even anden driehouck O P Q, en den driehouck A N M even den driehouck O S R, daerom ghelijck den rechthouck begrepen onder A C, A B, totten rechthouck begrepen onder A M, A N, alsoo den driehouck A B C, totten driehouck A N M.

2 Lidt.

Sooder ghemaeckt waren twee rechthoucken d'een onder A B en A C, d'ander onder A I, en de selve A C tis kennelick dat die twee rechthoucken wesende van een selve hooghde, souden sijn inde reden haerder gronden B A, A I: Maer ghelijck B A tot A I, alsoo E F tot F G deur des wercx 2 lidt, daerom ghelijck den rechthouck onder A B, A C, totten rechthouck onder A I, A C, alsoo E F tot F G.

3 Lidt.

Vande drie linien H D, A I, C A, is A K de vierde everedenighe deur des wercx derde lidt, daerom den rechthouck onder d'uyterste palen H D, A K, is even anden rechthouck onder de middelste A I, C A.

4 Lidt.

Doen t'werck dus verre ghecommen was, soo moesten wy vinden een lini als A M, sulcx dat den rechthouck begrepen onder de selve A M en M K, even waer anden rechthouck begrepen onder A H, A K, de naeste wech om dat te doen die my int beschrijven van desen te vooren quam, was een^* meetconstighe wercking ghetrocken uyt een stelreghelsche wercking in deser vougen: Ick heb de ghegheven form ghetalen toegheeyghent, en ghenomen A B te doen 4, A C 3, A H 4, H D 8, E F 9, F G 4, waer me K A volghende de boveschreven wercking des 2 en 3 lidts bevonden wort van ⅔ (want segghende E F 9 gheeft F G 4 wat A B 4? comt A I 16/9 daer na H D 8 gheeft A I 16/9. wat A C 3? comt alsvooren A K ⅔) En daerom is M K van ⅔ minder dan M A. Nu dan moetende vinden de selve M A, sulcx dat den rechthouck begrepen onder haer en M K, (die als wy gheseyt hebben ⅔ minder is dan M A) even sy anden rechthouck begrepen onder A H 4, en A K ⅔. doende dien rechthouck 8/3: Soo stel ick my in ghetalen dit voor.

* Geometrica operatio sumpta ex Alpebraica operatione.

Te vindent vveeghet alen, teen 3/2 cleender als t'ander, die t'samenghemenichvuldicht uytbrenghen 8/3.

Nu dan voort onbekent begheert ghetal van M A ghestelt 1 ①, en de stelreghelsche wercking gevolght, nemende voor het tweede getal 1 ① - ⅔. haer uyt-

[p. 148]

breng doet 1 ② - ⅔ ①, die even sijn met 8/3. En tot elck deel ghedaen + ⅔ ①, comt 1 ② even met ⅔ ① + 8/3. Om nu te vinden de weerde der eerstghestelde 1 ①, dats voor M A: Ick segh 1 ②, gheeft ⅔ ① + 8/3. wat 1 ①? waer af de wercking deur het 68 probleme van ons fransche Telconst dusdanich is.

Den helft van ⅔ (der ⅔ ①) is	8/3.
Sijn viercant	1/9.
Daer toe t'ghegheven ghetal	8/3.
Gheeft somme	25/9.
Diens viercantsijde	5/3.
Daer toe vergaert ⅓ eerste in d'oirden, comt de ghesochte waerde van 1 ① dats voor A M.	2.

Want soomen neemt een tweede ghetal dat ⅔ cleender is, te weten 4/3 voor K M, en dat ghemenichvuldicht met A M 2, comt na t'behooren 8/3.

Nu soo canmen uyt dese stelreghelsche wercking, ghelijck oock uyt alle stelreghelsche werckinghen, trecken een ghemeene reghel die gheen stelreghel en is, midts in te sien de ghedaente der ghetalen vande wercking int soucken der weerde van 1 ①, t'welck is datmen neemt den helft van K A, dats L A

doende	⅓.
Diens viercant	1/9.
Daer toe ghedaen den rechthouck begrepen onder A H 4 en A K ⅔. doende	8/3.
Comt	25/9.
Daer af een viercant ghemaeckt, de sijde is van	5/3.
Daer toe vergaert A L ⅓ eerste in d'oirden, comt A M	2.
En daerom K M	4/3.

D'oirsaeck waerom wy in des wercx 5 lidt, dese stelreghelsche manier niet heel int lang en volghden, maeckende van L A een viercant, en daer toe vergarende een rechthouck even anden rechthouck onder A H, A K, en die twee t'samen in een viercant verkeerende om de sijde te vinden, en tot die sijde noch A L te vergaren, dat is om cortheyts wille gheschiet: Want anghesien de hoochde A K van t'een deser twee platten, altijt dobbel is ande hoochde A L vant ander, soo is den rechthouck onder A L en het dobbel van A H, altijt even an die twee platten t'samen, en daer toe noch vergaert het viercant van A L, soo moet dan de middeleveredenighe tusschen de twee sijden dien rechthouck begrijpende (welcker sijden een is A L, d'ander een lini even an A L mettet dobbel van A H, ghelijck int wercx 4 lidt) de selve A M voorbrengen, maer deur een corter wech: Sulcx dat ghelijck in dit 4 lidt voorghenomen was te bewijsen, den rechthouck begrepen onder M A en M K, even is andē rechthouck onder A K, A H. Nu alsoo dese stelreghelsche wercking t'sijnder plaets haer wisconstich bewijs heeft, soo is oock de voorgaende meetconstighe wercking in dit deel wisconstich deur kennis der oirsaecken.

5 Lidt.

Na dien dese twee rechthoucken onder M A, M K, en onder A K, A H even sijn, soo moeten haer sijden overhandt everedenich wesen, dat is

Ghelijck A H tot M A, alsoo M K tot A K,

En deur versaemde reden,

[p. 149]

Ghelijck A H met A M dats M H,

Tot M A,

Alsoo M K met K A dats A M,

Tot K A,

Ende want H D en A N evewijdeghe sijn inden driehouck H D M, soo segh ick:

Ghelijck M H tot M A, alsoo D H tot N A:

Maer elcke reden der twee D H, A N, en A M, K A met een selve M H everedenich sijnde, soo volght daer uyt dat

Ghelijck M A tot K A, alsoo D N tot A N,

En daerom is den rechthouck begrepen onder de buytenste palen, even anden rechthouck begrepen onder de binnenste namelick:

Den rechthouck onder M A, A N, is even anden rechthouck onder K A, D H.

Maer den rechthouck onder K A, D H, is even anden rechthouck onder A C, A I, deur het 3 lidt, Daerom den rechthouck onder M A, A N, is even anden rechthouck onder A C, A I.

Maer ghelijck E F,

Tot F G,

Alsoo den rechthouck onder A C, A B,

Totten rechthouck onder A C, A I,

Door het 2 lidt, en daerom

Ghelijck E F,

Tot F G,

Alsoo den rechthouck onder A C, A B,

Totten rechthouck onder M A, A N,

Maer ghelijck den rechthouck onder A C, A B, totten rechthouck onder M A, A N, alsoo den driehouck A B C, totten driehouck A N M deur het 1 lidt, daerom

Ghelijck E F,

Tot G F,

Alsoo den driehouck A B C,

Totten driehouck A N M.

En deur ghescheyden reden,

Ghelijck E F min G F dat E G tot F G, alsoo den driehouck A B C min den driehouck A N M dats den vierhouck M N B C, totten driehouck A N M: T'welck wy bewijsen moesten.

2 Voorbeelt deur ghetalen.

Tghegheven. Laet A B C int eerste voorbeelt andermael den ghegeven driehouck sijn, D een punt daer buyten, en de reden sy van E G tot F G, welverstaende dat A B doet 3, A C 3, E G 5, F G 4: En C A voortgetrocken wesende na H, en D H evewijdeghe met B A, ontmoetende C H in A, soo doet A H 4, en D H 6. Tbegheerde. Wy moeten vinden hoe verre van A inde linie A C sal vallen een punt als M, sulcx dat ghetrocken D M, het deel als M N B C, sy in sulcken reden tot A N M, als 5 van E F, tot 4 van F G.

Twerck.

E F 9 somme van 5 en 4, gheeft F G 4 wat B A 4 comt 16/9.

D H 8 gheeft 16/9 eerste in d'oirden, wat C A 3? comt ⅔.

[p. 150]

Diens helft	⅓.
Daer toe het dobbel van A H 4 doende	8.
Comt	8⅓.
Die ghemenich vuldicht deur ⅓ derde in d'oirden comt	25/9.
Diens viercantsijde	5/3.
Hier toe ⅓ derde in d'oirden comt	2.

Daerom segh ick, ghemeten van A na C als tót M, soo dat A M doet 2, en ghetrocken D M snyende A B in N, men heeft t'begheerde, waer af t'bewijs openbaer is deur t'bewijs vant 1 voorbeelt. Tbeslvyt. Wy hebben dan van een ghegheven driehouck een begheert deel ghesneen, na een ghetoonden oirt, met een rechte lini commende uyt een punt ghegheven buyten den driehouck na den eysch.

9 Voorstel.

Van een ghegheven driehouck een begheert deel te snyen (meughelick sijnde afghesneen te vvorden) na een ghetoonden oirt, met een lini streckende deur een punt ghegheven binnen den driehouck.

Om te verclaren d'oirsaeck waerom int voorstel geseyt wort' meughelick sijnde, soo is te weten datmen als het ghegheven punt binnen t'plat is, begheeren can een cleender of grooter deel vant plat ghesneen te worden dan meughelick is: Als by voorbeelt soo t'ghegheven plat waer een viercant, en t'ghegheven punt sijn middelpunt, en datmen daer deur begheerde een lini ghetrocken te worden dieder een derdendeel afsne, Men seght dat onmeughelick te wesen, om dat alle lini deur t'selve middelpunt ghetrocken het viercant in twee even stucken deelt: Wederom en canmen deur een driehoucx swaerheyts middelpunt gheen lini trecken daer af een cleender deel snyende dan in sulcken reden totten heelen driehouck, als van 4 tot 9, ende gheen grooter dan als van 5 tot 9, en soo voort met oneyndelicke andere: En daerom moetet begheerde meughelick sijn ghelijck t'voorstel inhout.

Tghegheven. Laet A B C een driehouck sijn, en den punt daer in D, voort sy E F een lini ghesneen in G. Tbegheerde. Wy moeten deur t'punt D een rechte lini trecken den driehouck in tween snyende, soo dattet deel na A, in sulcke reden sy tottet ander soot meughelick is, als F G tot E G.

Twerck.

Men treckt ghelijck int 8 voorstel, van D tot in C A de lini D H, evewijdich met B A, en voort en verschilt de rest de wercking vande voorgaende des 8 voorstels anders niet, dan datmen hier int vijfde lidt sal segghen min het dobbel in plaets daermen inde voorgaende wercking seght met het dobbel. Als by voorbeelt int boveschreven 5 lidt staet aldus: Ick souck de middeleveredenighe lini tusschen A L, en een lini even an A L met het dobbel van A H: Maer hier salmen aldus segghen: Ick souck de middeleveredenighe lini tusschen A L, en een lini even an A L min het dobbel van A H. D'oirsaeck daer af blijckt inde stelreghelsche wercking ghedaen na den eysch van dit voorbeelt, alwaer wy vinden 1 ② even met ①-⓪, daer wy in d'ander creghen 1 ② even met ①+⓪: Sulcx

[p. 151]

dat daer af gheen voorder verclaring des wercx, noch bewijs soo wel in ghetalen als meetconstich noodich en schijnt, te meer dat de letters der wercking inde form t'haerder plaets vervought, van sulcke beteyckeninghe sijn als int 1 voorbeelt.

Noch valter dit te bedencken:

Ten eerstē dat de langde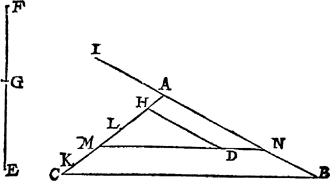



van L M die boven geteyckent is van L na C, noch boven dien mach gheteyckent worden van L na A, welcke langde in L A vallende, en dat dan de lini van dat punt ghetrocken deur D, comt te gheraecken A B, soo sijnder tottet begheerde twee besluyten: Om van t'welck by voorbeelt te spreecken, laet de volghende A B C een driehouck sijn, en t'ghegheven punt D, waer in de langde van L tot M eerst ghestelt is van L na C, daer na van L na A, vallende niet buyten L A, maer daer in tot O, sulcx dat daer na ghetrocken de rechte lini van O deur D tot P, soo wel de sijde A B gheraeckt, als d'ander lini M D N de selve A B gheraeckt. T'welck soo wesende elck afghesneen deel is een driehouck, te weten A N M, A P O, die even moeten sijn, en den driehouck O D M is oock even an N D P: Sulcx datter soo wy gheseyt hebben twee besluyten sijn, ten waermen int begheerde verclaert had welcke lini der twee datmen hebben wil, waer af d'oirsaeck openbaer is deur het dobbel besluyt dat de stelreghelsche wercking mebrengt in des bewijs 4 lidt. Ten anderen anghesien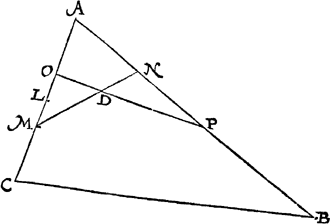



datter in A C maer twee punten en sijn als M, O, en in A B gheen ander dan N, P, deur welcke de begheerde linien ghetrocken meugen werden: Soo volght daer uyt dat de lini ghetrocken van O deur D niet gheraeckende A B, datter dan het tweede besluyt niet sijn en sal: Noch oock het eerste als t'punt N der voortghetrocken M D, niet en valt in A B: Waer uyt wijder te verstaen is, dat de wercking begost hebbende met te trecken de lini D H evewijdeghe met B A (als in des eerste voorbeelts 1 lidt, en daer uyt de punten N noch P in A B niet vallende, alsdan niet noodichte sijn sulcx andermael te versoucken met te trecken D H evewijdeghe met A C, ghelijckmen int boveschreven eerste voorbeelts 1 lidt doen mocht, want dat op d'een sijde onmeugelijck valt moet op d'ander oock onmeugelijck wesen: En de linien met meughelijck besluyt diemen op d'een sijde vindt, de selve vindtmen oock op d'ander.

Men soude hier noch meughen by voughen een voorbeelt deur ghetalen,

[p. 152]

maer anghesien t'werck gheen ander verschil en heeft dan wy gheseyt heb ben int 5 lidt te wesen, soo schijnet onnoodich, wy sullen dan totten vierhouck commen.

10 Voorstel.

Van een ghegheven vierhouck een begheert deel te snyen na een ghetoonden oirt, met een lini commende uyt of deur een punt buyten den omtreck.

1. Voorbeelt van een evevvijdeghe vierhouck vvaer af de snyende linistrecken saldeur tvvee evevvijdeghe sijden.

Tghegheven. Laet A B C D een evewijdeghe vierhouck sijn, E een punt daer buyten, voort sy F G een lini ghesneen in H. Tbegheerde. Wy moeten van t'punt E een rechte lini trecken, snyende den vierhouck in tween, soo dattet deel na B, in sulcken reden sy tottet ander, als G H tot F H.

Twerck.

Ick teycken t'punt I int middel van A D, en K int middel van B C, treck I K: Segh daer na F G gheeft G H, wat I K? Comt K L, die ick teycken in K I: Treck daer na van E deur L de lini E M L N, snyende neem ick de twee evewijdeghen A B, D C in M en N, maer soo N ghevallen hadde in B C men soude dan volghen het nabeschreven 4 voorbeelt. Dit soo sijnde, ick segh het deel, te weten den vierhouck M B C N, in sulcken reden te wesen tottet anderdeel A M N D, als G H tot F H. Tbereytsel. Laet ghetrocken werden deur L de lini O P even en evewijdeghe met B C.

Tbewys.

Anghesien I K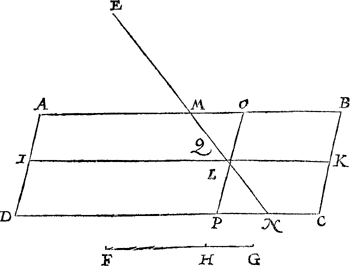



in sulcken reden is tot K L, als F G tot G H deur t'werck, soo is deur ghescheyden reden I L in sulcken redē tot L K, als F H tot G H: Ende inde selve reden moet oock sijn D P tot P C, gelijck oock moeten dier gronden vierhoucken, dats A O P D tot O B C P: Maer den driehouck L O M, is even

[p. 153]

anden driehouck L P N, daerom L O M ghetrocken van A O P D, en L P N daer toe ghedaen, soo moeter deel A M N D, even sijn mettet deel A O P D, en vervolghens A M N D is in sulcken reden totte rest M B C N, als F H tot G H, t'welck wy bewijsen moesten.

Maer soo t'ghegheven punt waer binnen den vierhouck, als ter plaets van Q hier ghestelt inde lini M N, t'werck soude sijn ghelijck t'voorgaende, want deur Q en L ghetrocken de lini M Q L N, men heeft openbaerlick t'begheerde.

2 Voorbeelt deur ghetalen.

Tghegheven. Laet A B C D andermael de ghegheven vierhouck sijn, E een punt daer buyten, voort sy F G een lini ghesneen in H, welverstaende dat A B doet 6, A D 2, F H 2, G H 1. Maer om nu de ghestalt des punts E te verclaren, ick segh dat ghetrocken wesende E I evewijdeghe met A D, en gherakende A B in I, soo doet E I 2, en I A 1. Tbegheerde. Wy moeten deur ghetalen vinden hoe verre van D inde lini DC, sal vallen een punt als K, en hoe verre van A inde lini A B, sal vallen een punt als L, sulcx dat ghetrocken de rechte lini als E L K, het deel als A L K D, sy in sulcken reden tot L B C K, als 2 van F G, tot 1 van G H.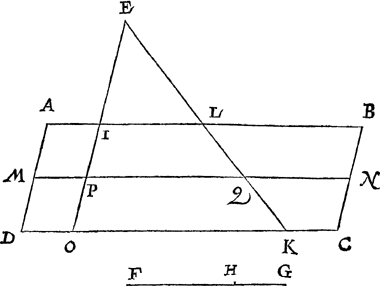

Twerck.

Ick teycken t'punt M int middel van A B, en N int middel van B C, treck M N, die ghelijck A B doen moet 6, en A M 1, als helft van A D 2, en treck E voorwaert tot O, snyende M N in P: Segh daer na F G 3, gheeft G H 1, wat M N 6?

Comt N Q	2.
Segh daer na E P 3, gheeft P Q 3, wat E O 4? comt O K	4.
Daer toe DO even an A I doende deur t' ghegheven	1.
Comt voor de begheerde langde van D K	5.

En sghelijck sal A M bevonden worden van 3, want segghende E P 3, gheeft

P Q 3, wat EI 2?
Comt I L	2.

[p. 154]

Daer toe I L	1.
Comt als gheseyt is voor de begheerde langde van A L.	4.

Waer af t'bewijs deur het 4 voorbeelt openbaer is.

En sgelijcx sal oock sijn het werck deur ghetalen als t'punt E binnen het plat ghegheven is.

3 Voorbeelt van een vierhouck soot valt, vvaer af de snyende lini strecken saldeur tvvee teghenoversijden.

Tghegheven. Laet A B C D een vierhouck sijn soot valt, E een punt daer buyten, en de reden sy van F G tot G H. Tbegheerde. Wy moeten van t'punt E een rechte lini trecken die den vierhouck in tween snijt, soo dattet deel na A, tottet ander sy inde reden van F G tot G H.

Twerck.

Ick treck twee sijden voorwaert die versamen connen, als A B, D C versamende in I: Segh daer na den vierhouck A B C D, gheeft den driehouck B C I, wat F H? comt deur het 8 voorstel des 4 boucx H K: Ick deel daer na den driehouck A D I deur het 8 voorstel van desen met een lini getrocken uyt E, soo dattet deel na I in sulcken reden sy tottet ander als K G tot G F, welcke lini sy E L M, streckende neem ick deur twee evewijdeghe sijden A B, C: Soose ghestreckt hadde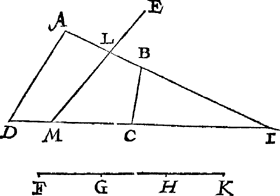



deur twee malcander raeckende sijden, men soude dan volghen het 4 voorbeelt. Dit aldus sijnde, ick segh de lini E L M soo te wesen, dattet deel A L M D, in sulcken reden is tottet deel L B C M, als F G tot G H.

Tbewys.

Anghesien A B C D in sulcken reden is tot I B C, als F H tot H K, en A L M D tot I L M, als F G tot G K deur t'werck, soo moet deur ghescheyden reden A L M D, in sulcken reden sijn tot L B C M, als F G tot G H, t'welck wy bewijsen moesten.

Merckt.

Soo t'ghegheven punt waer gheweest binnen den vierhouck A B C D, of deur het voorttrecken van twee sijden ghevallen hadde binnen den driehouck daer af veroirsaeckt, tis kennelick datmen daer af deur het 8 of 9 voorstel van desen de begheerde soude ghevonden hebben.

4 Voorbeelt van een vierhouck soot valt, vvaer af de snyende lini strecken saldeur tvvee malcander rakende sijden.

Tghegheven. Laet A B C D een vierhouck sijn soot valt, E een punt daer buyten, en de reden sy van F G tot G H. Tbegheerde. Wy moeten van t'punt E een rechte lini trecken die den driehouck in tween snijt, soo dattet deel na A, sy tottet ander inde reden van F G tot G H.

[p. 155]

Twerck.

Soomen uyter oogh conde sien, of soomen deur het 3 voorstel bevonden heeft, dat de snyende lini deur gheen twee teghenoversijden en streckt men mach aldus doen, ick treck D B, en segh, den vierhouck A B C D, geeft den driehouck A B D, wat F H? wiens vierde everedenighe pael ghevonden deur het 8 voorstel des 4 boucx is neem ick FI: Ick souck daer na een lini ghetrocken uyt E, die vande driehouck A B D een deel snye na A toe, in sulcken reden tottet ander deel des selfden driehoucx, als F G tot G I, welcke lini ghevonden deur het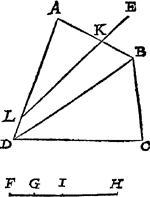



8 voorstel sy E K L snyende A B in K, en A D in L. Dit aldus sijnde ick segh de lini E K L het ghegheven plat soo te snyen, dattet deel A K L, in sulcken reden is tottet deel K B C D, als F G tot G H.

Tbewys.

Ghelijck F I tot I H, alsoo deur t'werck A B D tot B C D, voort ghelijck F G tot G I, alsoo deur t'werck A K L tot K B D L, en deur versaemde reden ghelijck F G tot G I met I H, alsoo A L K tot K B D L met B C D, dat is ghelijck F G tot G H, alsoo A K L tot K B C D L, T'welck wy bewijsen moesten.

Merckt.

Soo t'ghegheven punt had gheweest binnen den vierhouck A B C D, tis kennelick datmen daer af deur het 9 voorstel de begheerde snyende lini soude ghevonden hebben. Tbeslvyt. Wy hebben dan van een ghegheven vierhouck een begheert deel ghesneen na een ghetoonden oirt, met een lini commende uyt of deur een punt buyten den omtreck, na den eysch.

11 Voorstel.

Van een ghegheven rechtlinich plat een begheert deel te snyen na een ghetoonden oirt, met een lini commende uyt of deur een punt buyten den omtreck, snyende het plat in tvveen.

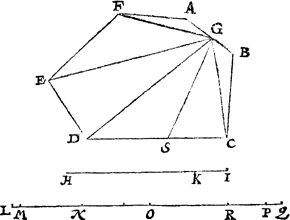
Merckt.

Eer wy totte saeck commen, soo is te ghedencken datmen met des voorstels woorden snyende het plat in t ween, sulcx verstaen sal als int merck des 7 voorstels van derghelijcke gheseyt is.

Tghegheven. Laet A B C D E F G H een rechtlinich plat sijn soot valt, I een punt daer buyten, en de reden des afghesneen deels totte rest, sy van K L tot L M. Tbegheerde. Wy moeten van t'punt I een lini trecken die den vierhouck in tween snijt, soo dattet deel na A tottet ander, sy inde reden van K L tot L M.

Twerck.

Men sal voor al mercken deur wat twee sijden sal vallen de snyende lini ghe-

[p. 156]

trocken uyt I, canment uyter oogh niet sien, men macher deur ghewisse wercking in handelen alsoo van derghelijcke int voorgaende ghenouch verclaring ghedaen is. Ghenomen dan dat ick weet de snyende lini te sullen vallen deur



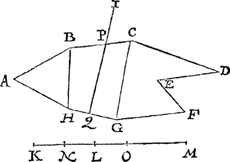B C en H G, dit soo sijnde, ick treck de twee linien B H C G, waer me t'ghegheven plat ghedeelt is in drie stucken, te weten den driehouck A B H, en den vierhouck B C G H, den vijfhouck C D E F G, En in sulcke reden als tot malcander sijn dese drie deelen des ghegheven plats, inde selve deel ick deur het 8 voorstel des 4 boucx de lini K M inde punten, N, O, te weten ghelijck tot malcander sijn A B H, B C G H, C D E F G, alsoo ordentlick vervolghende K N, N O, O M, sulcx dat N O wesende lijckstandige pael mettē vierhouck B C G H, en in haer hebbende t'ghegheven punt L, ick deel de selve B C G H deur het 10 voorstel met een lini ghetrocken uyt I, welcke sy I P Q, snyende B C in P, en H G in Q, sulcx dat ghelijck N L tot L O, alsoo B P Q H tot P C G Q: T'welck soo sijnde ick segh het deel A B P Q H, in sulcken reden te wesen tottet deel P C D E F G Q, als K L, tot L M, na den eysch, waer af t'bewijs openbaer ghenouch schijnt deur derghelijcke vant 3 voorbeelt des 10 voorstels.

Merckt.

Soo t'ghegheven punt I waer gheweest binnen het rechtlinich plat, tis kennelick datmen deur t'voorgaende daer af t'begheerde soude ghevonden hebben.

Tbeslvyt. Wy hebben dan van een ghegheven rechtlinich plat een begheert deel ghesneen na den ghetoonden oirt, met een lini commende uyt of deur een punt buyten den omtreck, snyende het plat in tween, na den eysch.

Nv vande snyding der
platten met een lini evevvijdich an een ghestelde.

12 Voorstel.

Van een ghegheven driehouck een begheert deel te snyen na een getoonden oirt, met een lini evevvijdich van een ghetoonde sijde.

1 Voorbeelt.

Tghegheven. Laet A B C een driehouck sijn, ende D E een linighesneen in F. Tbegheerde. Wy moeten vanden driehouck A B C een deel snyen na den houck A toe, in sulcken reden tottet ander deel, ghelijck D F tot F E, ende dat met een evewijdeghe lini van C B.

[p. 157]

Twerck.

Ick vinde de vierde everedenighe de drie D E, D F, A B welck sy G: Daer na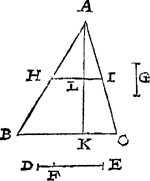



de middeleveredenighe tusschen A B en G als A H, die ick teycken in A B, ende treck H I evewijdeghe met B C: welcke H I ick segh den driehouck A B C soo te snyen, dat ghelijck D F tot F E, alsoo het deel A H I tottet deel H I C B.

Tbewys.

ANghesien G derde everedenighe is der twee A B, A H deur t'werck, soo heeft A B tot G een ghedobbelde reden van A B tot A H, daerom ghelijck A B tot G, alsoo den driehouck A B C tot haers ghelijcke driehouck A H I. Maer ghelijck A B tot G, alsoo D E tot D F deur t'werck, daerom ghelijck D E tot D F, alsoo A B C tot A H I: Ende deur verkeerde reden gelijck D F tot D E, alsoo A H I tot A B C, ende deur ghescheyden reden ghelijck D F tot D E min D F dats tot F E, alsoo A H I tot A B C min A H I dats tot H I C B.

Derghelijcke vvercking deurghetalen.

Ick meet de nabeschreven linien met voeten, die bevindende neem ick als volght: D E 4, D F 1, A B 8. Segh daer na D E 4, gheeft D F 1, wat A B 8? comt 2.

Het middeleveredenich ghetal tusschen die 2 ende A B 8 is 4.

Daerom ghemeten van A na B vier voeten als van A tot H, ende ghetrocken H I evewijdeghe met B C men heeft t'begheerde. Tbereytsel. Laet getrocken worden de hanghende van A op B C, als A K snyende H I in L, ende de selve A K sy lanck bevonden neem ick 7 voeten, ende B C 6. Proef. Angesien A K doet 7 voeten, ende B C 6 deur t'bereytsel, soo doet den driehouck A B C 21: Voort anghesien A H doet 4, H B 4, ende B C 6, soo is A L van 3½. ende H I van 3, ende vervolghens den driehouck A H I 5¼. welcke ghetrocken vande voorschreven A B C 21, blijft voor de bijl H I C B 15¾. tot welcke 5¼ in sulcken reden is, als D F 1 tot F E 3.

Ander vvercking deur ghetalen ghevonden van sijn Vorstelicke Ghenade.

De twee viercanten van A B en A H, moeten tot malcander in sulcken reden sijn als E D 4, tot F D 1: Daerom segh ick, 4 gheeft 1, wat t'viercant van A B 64? Comt 16 voor t'viercant van A H, diens sijde A H doet 4, daerom gemeten van A na B 4, die vallen neem ick in H, en ghetrocken H I evewijdeghe met B C men heeft t'begheerde.

Ander vvercking deur ghetalen ghebroken uyt^⋆ stelreghelsche vvercking.

Laet begheert sijn vanden driehouck A B C ghesneen te worden een vierendeel des selfden na A toe, welck vierendeel ick neem dat bevonden wort van 5¼.

⋆ Algebraieâ operatione.

[p. 158]

Om de selve af te snyen na den eysch, ick meet den gront B C, die bevindende neem ick van 6, en de hanghende daer op A K van 7, dese 6 en 7 stel ick als ghebroken aldus 6/7 daer deur deel ick het dobbel van t'begheerde deel 5¼. dats 10½. comt den^* mael 49/4, diens viercantsijde 3½, de selve ghemeten van A na K valt neem ick in L, daerom deur L ghetrocken H I evewijdeghe met B C men heeft t'begheerde.

Den oirspronck deses wercx is dusdanich: Ick sie dat den helft des uytbrengs der menichvulding van A L deur H I moet maken 5¼, voor t'plat des driehoucx A H I. Maer A L is tot H I, inde reden van A K tot B C, dats van 7 tot 6, daerom stel ick my selven dusdanighen werckstuck voor.

* Productus.

Vindt tvvee ghetalen tot malcander inde reden van 7 tot 6, diens uytbreng doe 10½.

En die sulcken werckstuck deur de stelreghel afveerdicht, sal daer in mercken den oirspronck deser voorgaende wercking.

1 Vervolgh.

Soo t'begheerde deel waer gheweest deur meetconstighe wercking na de sijde B C toe, als neem ick t'selve deel te moeten sijn in sulcken reden tottet ander deel na den houck A, als F E tot F D, men sal inde wercking sich voorstellen datter begheert is een deel afghesneen te moeten worden na den houck A, in sulcken reden tottet ander deel, als F D tot F E ende volghen daer mede de reghel als boven.

2 Vervolgh.

Soo t'begheerde deel waer gheweest deur telconstighe wercking na den oirt B C, men soude den heelen driehouck A B C meten, daer af treckende t'begeerde deel, doch inde wercking sich voorstellen die rest t'begheerde deel na den oirt A te wesen, ende volghen daer me de reghel als boven. By voorbeelt daer wort begheert vanden driehouck A B C ghesneen te worden 15¾ voeten: Ick meet den heelen driehouck die bevindende van 21, daer af ghetrocken 15¾. blijft 5 1/42 Daerom my selven voorstellende datter begheert is een deel afghesneen te worden van 5¼ na den oirt A, ick volgh de wercking als boven ende crijgh t'begheerde. Tbeslvyt. Wy hebben dan van een ghegheven driehouck een begheert deel ghesneen na een getoonden oirt, met een lini evewijdich van een ghetoonde sijde, na den eysch.

13 Voorstel.

Van een ghegheven bijl een begheert deel te snyen na een ghetoonden oirt, met een lini evevvijdich vande evevvijdeghe des bijls.

Tghegheven. Laet A B C D een bijl sijn, diens twee evewijdeghe A B, D C, ende E F een lini ghesneen in G. Tbegheerde. Wy moeten vanden bijl A B C D een deel snyen na A B toe, in sulcken reden tottet ander deel als E G tot G F, ende dat met een lini evewijdich van A B.

[p. 159]

Twerck.

Ick treck de onevewijdeghe D A, C B voorwaert tot datse vergaren int punt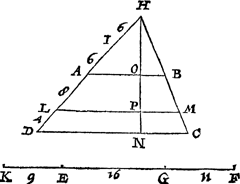



H, ende vinde de derde everedenighe der twee H D, H A, welcke sy H I geteyckent in H D: Daer na de vierde everedenighe der drie D I, IH, F E, welcke sy E K: Daer na deur het 6 voorstel deses 5 boucx vanden driehouck H D C een deel gesneen na den houck A toe, in sulcken reden tottet ander deel, ghelijck K G tot G F, ende dat met een evewijdeghe van A B, als L M, men heeft t'begheerde, te weten het deel L M B A, in sulcken reden tottet ander deel L M C D, als E G tot G F.

Tbewys.

Anghesien H I derde everedenighe is der twee H D, H A deur t'werck, soo heeft den driehouck H D C, sulcken reden tot haers ghelijcke driehouck H A B, als H D tot H I: Ende deur ghescheyden reden ghelijck H D C min H A B dats de bijl A B C D, tot H A B, alsoo H D min H I dats D I, tot H I: Maer ghelijck D I tot H I, alsoo F E tot E K deur t'werck, daerom ghelijck F E tot E K, alsoo de bijl A B C D, totten driehouck H A B: Maer ghelijck de heele lini K F ghedeelt is in G, alsoo oock den heelen driehouck H D C mette lini L M, sulcx dat ghelijck K G tot G F alsoo H L M tot L M C D deur t'werck, daerom de drie deelen des heelen driehoucx als H A B, L M B A, L M C D, sijn oirdentlick tot malcander in sulcken reden als de drie deelen der heele lini K E, E G, G F, ende vervolghens L M B A, L M C D, sijn tot malcander in sulcken reden, als haer lijckstandighe palen E G, G F.

Derghelijcke vvercking deur ghetalen.

Ick meet de nabeschreven linien met voeten die bevindende neem ick als volght.

H D	24.
H A	12.
A B	12.
E F	27.
E G	16.
G F	11.

Segh daer na H D 24, gheeft H A 12, wat H A 12? comt voor H I	6.
Die ghetrocken van H D 24, blijft D I	18.
Voort D I 18, gheeft IH 6, wat E F 27? comt voor E K	9.
Daer toe E G 16 comt voor K G	25.
Souck daer na deur het 12 voorstel van desen hoe lanck de lini H L moet sijn, om vanden driehouck H D C een deel te snyen na den houck H, in sulcken reden tottet ander deel, als K G 25, tot G F 11, ende dat met een evewijdeghe van A B als L M, ende wort bevonden voor de boveschreven H L	20.

[p. 160]

Daerom ghemeten van H tot L 20 voeten, of (om datmen sonder ghetalen den driehouck A H B niet en behouft te teyckenen) van D tot L 4 voeten, ende ghetrocken L M evewijdeghe met A B, men heeft t'begheerde. Proef. Laet ghetrocken worden H N rechthouckich op D C, ende snyende A B in O, ende L M in P, welcke H N ghemeten sijnde, wort bevonden neem ick van 18 voeten: Daerom N O doet 9, O P 6, P N 3, Want ghelijck D H 24, D A 12, A L 8, L D 4, tot malcander, alsoo oirdentlick N H 18, N O 9, O P 6, P N 3, voort doet L M 20, D C 24, want ghelijck H A 12, tot A B 12, alsoo H L 20, tot L M 20, alsoo oock H D 24, tot D C 24. T'welck soo sijnde het deel L M B A doet 96, ende L M C D 66 deur het 11 voorstel des 2 boucx, die tot malcander in sulcken reden sijn als E G 16 tot G F 11.

Ander vvercking deur ghetalen.

Ick meet de volghende linien met voeten, die bevindende neem ick als volght A B 12, D C 24, O N 9: Daerom doet den ghegeven bijl deur het 11 voorstel des 2 boucx	162.
De selve ghedeelt ghelijck E G 16 tot G F 11, comt voor t'bovenste deel dat wy af moeten snyen	96.
Daer toe vergaert des bijls vervullende drichouck H A B, welcke deur het 3 vervolgh vant 6 voorstel des 2 boucx (alwaer t'vinden der hanghende H O gheleert wort) sijn sal van	54.
Maken t'samen	150.
Daerom soo veel ghesneen vanden driehouck H D C na de leering des 12 voorstels van desen, men bevint dat H P lanck moet sijn	15.

Sulcx dat deur t'punt P ghetrocken L M evewijdege met A B, men heeft t'begheerde. Proef. Van H N 18 ghetrocken H P 15, blijft voor P N 3, die getrocken van N O 9, blijft voor O P 6: T'welck soo sijnde, L M B A doet 96, L M C D 66, die tot malcander in sulcken reden sijn als E G 16, tot G F 11.

1 Vervolgh.

Soo t'begheerde deel waer gheweest na de sijde D C toe, als neem ick t'selve deel te moeten sijn in sulcken reden tottet ander deel na A B, als E G tot G F. Men sal inde wercking sich voorstellen datter begheert is een deel afghesneen te moeten worden na den houck A, in sulcken reden tottet ander deel, als F G tot G E, ende volghen daer me de reghel als boven.

2 Vervolgh.

Sooder begheert waer vanden bijlgesneen te worden een menichte van voeten (doch minder dan t'begrijp des ghegeven bijls) men sal den heelen bijl meten, ende daer af treckende t'begheerde deel, soo heeft het selve begheerde deel tot die rest de behoirlicke reden daer de bijl in moet ghedeelt sijn, daerom volghende mette selve de voorgaende wercking men comttottet begheerde.

Tbeslvyt. Wy hebben dan van een ghegheven bijl een begheert deel ghesneen na een ghetoonden oirt, met een lini evewijdich vande evewijdeghe des bijls na den eysch.

[p. 161]

14 Voorstel.

Van een ghegheven rechtlinich plat een begheert deel te snyen na een ghetoonden oirt, met een lini evevvijdich van een ghestelde lini.

Tghegheven. Laet den seshouck A B C D E F een rechtlinich plat sijn, G H een ghestelde lini ende I K een lini ghesneen in L.

Tbegheerde. Wy moeten vanden seshouck een deel snyen na F toe, in sulcken reden tottet ander deel, als I L, tot L K, ende dat met een lini evewijdich van G H.

Twerck.

Ick treck snyende linien uyt al de houcken daer snyende linien ende evewijdeghe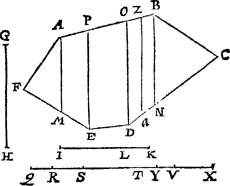



met G H uyt vallen connen, als uyt de houcken, A, B, D, E, ghelijck de linien A M, B N, D O, E P, Vyt welcke snydinghen de deelen des ghegheven seshoucx, vallen connen driehoucken, bijlen, of evewijdeghe vierhoucken, ende gheen ander. Vinde daer na deur het 8 voorstel des 4 boucx eenighe vijf linien Q R, R S, S T, T V, V X tot malcander in sulcken reden als oirdentlick de vijf platten A F M, A M E P, PEDO, O D N B, B N C: Snije daer na Q X in Y, sulcx dat ghelijck I L tot L K, alsoo Q Y tot Y X, ende valt de selve Y neem ick tusschen T en V, welcke T V lijckstandighe pael sijnde mette bijl O D N B, ick deel de selve bijl deur het 13 voorstel van desen mette lini Z a evewijdeghe van G H, in twee deelen, tot malcander in sulcken reden als T Y tot Y V: T'welck soo sijnde, ick segh dat gchjck I L tot L K, alsoo het deel Z a D E F A tottet deel Z a C B, waer af t'bewijs deur t'werck openbaer is.

Angaende wercking deur ghetalen, ghemerckt datse deur t'voorgaende kennelick ghenouch schijnt en sullen die hier niet stellen.

Vervolgh.

Deur dese deyling des landts A B C D E F mette lini Z a, is kennelick ghenouch alle deeling des selven lants in verscheyden begeerde cavels, of evegroot, of van verscheyden grootheden, want ghelijck t'punt Y hier viel tusschen T en V, alsoo sal t'punt van een ander deel vallen tot een ander plaets der linien, en daerom haer lijckstandighe pael der platten inde selve reden ghedeelt, men heeft overal t'begheerde. Tbeslvyt. Wy hebben dan van een gegeven rechtlinich plat een begheert deel ghesneen na een getoonden oirt met een lini evewijdich van een ghestelde lini na den eysch.

[p. 162]

15 Voorstel.

Van een ghegheven clootvlack een begheert deel te snyen, met een plat na een ghetoonden oirt.

Tghegheven. Laet A B C D een clootvlack sijn, diens as A C, ende E F een lini ghesneen in G. Tbegheerde. Wy moeten van t'selve clootvlack een deel snyen met een plat na den oirt C, in sulcken reden tottet ander deel, ghelijck E G tot G F.

Twerck.

Ick deel A C in H deur het 2 voorstel van desen sulck dat ghelijck E G tot G F,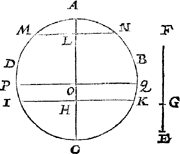



alsoo C H tot H A, treck voort deur t'punt H het plat I K rechthouckich op den as A C: T'welck soo sijnde ick seg dattet deel des clootvlacx I C K na den oirt C, in sulcken reden is tottet ander deel I A K, als E G tot G F.

Tbewys.

De bultighe clootvlacken der coordsneen eens selfden cloots sijn inde reden van haer assen als ghetrocken wort uyt het bouck des cloots en seuls van Archimedes.

Daerom ghelijck C H tot H A, alsoo het bultich clootvlack I C K tottet bultich clootvlack I A K: Maer gelijck C H tot H A, alsoo E G tot G F deur t'werck, daerom ghelijck E G tot G F, alsoo t'bultichvlack I C K tottet bultich vlack I A K.

Derghelijcke vvercking deur ghetalen.

Ick meet den as A C, die bevindende neem ick van 12 voeten, E G van 2, G F van 4, inder voughen dattet een afghesneen deel sulcken reden moet hebben tottet ander als 2 tot 4.

Om hier toe te commen ick deel A C 12 in twee sticken, tot malcander in sulcke reden ghelijck E G 2, tot G F 4, comt voor t'eerste deel 4: Daerom ghemeten van C na A 4 voeten, welcke commen neem ick tot H, ende deur t'punt H een plat ghetrocken rechthouckich op den as A C, soo is t'bultich vlack I C K t'begheerde Proef. Het heel clootvlack doet 452 4/7 deur het 18 voorstel des 2 boucx: Ende het clootvlack I C K 150 6/7, t'selve getrocken vant heel clootvlack 452 4/7, rest voor het clootvlack I A K 301 5/7, tottet welck I C K 150 6/7 sulcken reden heeft als E G 2, tot G F 4.

Vervolgh.

Sooder begheert waer een deel des bultich clootvlacx van een coordsne, die is deur t'voorgaende bekent: Als by voorbeelt om te hebben het vijfdendeel des clootvlacx I A K, men vindt het vijfdendeel vanden as A H daer in bestaende, welck vijfdendeel sy A L, want deur t'punt L ghetrocken t'plat M N rechthouckich op den as, soo is t'bultich clootvlack M A N t'begheerde.

[p. 163]

Andersins mochtmen het vijfdendeel van A H oock meten van H tot O, treckende deur t'punt O t'plat P Q rechthouckich op den as, want den bultighen^* riem begrepen tusschen P Q K I is openbaerlick het begheerde.

Tbeslvyt. Wy hebben dan van een ghegheven clootvlack een begeert deel ghesneen, met een plat na een ghetoonden oirt, na den eysch.

* Zona.

Merckt.

Sooder begheert waer een seker deel van een ongheschickt bultich vlack, ghelijck ghemeenelick sijn de vlacken van berghachtighe landen, daer in en can gheen lini ghetrocken worden evewijdich met een ghegheven rechte lini, ghemerckt de linien in sulcke vlacken crom sijn: Doch wy sullen hier wat segghen van t'ghene in sulcke bedeeling der landen dadelick ghebruyckt wort, te weten datmen in stevan een rechte lini, neemt de ghemeene sne des bultich vlacx en eens plats rechthouckich op den sichteinder, welcke ghemeene sne opt landt gevonden wort met te steken verscheyden baecken in een selve sichtstrael, en daer na van baeck tot baeck te kielspitten, of ander teyckens te stellen. Laet tot voorbeelt A B C D sulckē berchachtich lant sijn, waeraf na den oirt A, ghesneen moet worden een vierendeel des selfden, met een plat rechthouckich op den sichteinder, en evewijdich vande lini E: Om nu tottet werck te commen, men meet het heel landt in sijn verscheyden stucken na de manier vant 3 voorbeelt des 11 voorstels vant 2 bouck, wort bevondē neem ick van 100 morghen, waer af het begheert vierendeel doet 25 morghen, die afghesneen moeten sijn na den oirt A. Om daer toe te commen, ick vergaer soo veel der voorschreven ghemeten stucken na den oirt A, alsser ten naesten by tot die begheerde



25 morghen behouven, teyckenende met baken een lini als neem ick B D, die ten naesten by de selve 25 morgen na A schijnt te sullen afsnyen: Daer na het vlack B D A hermeten sijnde, ist datment van 25 morghen bevint men heeft t'begheerde: Dies niet maer datter te luttel of te veel is, ick neem te luttel een morghen, soo moeter nevens B D een ander lini ghetrocken worden als F G mette selve B D evewijdich: Of anders gheseyt alsoo dattet plat deur F G rechthouckich op den sichteinder, evewijdich sy mettet plat deur B D oock rechthouckich op den sichteinder: Voort dattet vlack of den riem F G D B doe een morghen. Om nu te weten hoe breet den selven riem daer toe sal moeten wesen, Ick meet haer langde B D die bevindende neem ick van 300 roē, daer deur ghedeelt de 600 roen van een morghen, comt 2 roen voor de breede, waer me den riem F G D B na ghenouch een morghen sal meughen doen, en

[p. 164]

F G A het begheert deel sijn van 25 morghen: Doch soo de saeck noch nauwer rekening vereyschte, men mocht die morghen hermeten en soo veel daer af of toe doen deur een ander ghetrocken lini dan F G, als de saeck vereyschte.

Maer sooder begeert waer een seker deel afghesneen met een plat rechthouckich op den sichteinder en deur een ghegheven punt inden omtreck, als neem ick andermael een vierendeel des vlacx A B C D, met een plat afghesneen deur t'punt F, men soude deur F ten naesten by t'selve vierendeel afsnyen alsvooren, met een verdochte lini van F tot neem ick D, welck vlack hermeten sijnde en te cleen bevonden van neem ick ½ morghen, men sal een ander lini trecken als F G soo dat den driehouck F D G de selve halve morghen begrijp: Om die te vinden men deelt het dobbel van ½ morghen dats 1 morghen of 600 roen, deur F D 300 roen, en t'ghene daer uyt comt is voor de verheyt tusschen de linien van D totte begheerde F G.