Beghinselen der weeghconst
(1586)–Simon Stevin–XI. Vertooch. XIX. Voorstel.Wesende een driehouc wiens Ga naar margenoot* plat rechthouckich op den Ga naar margenoot* sichteinder is, met sijn grondt daer af euewidich, ende op elck der ander sijden een rollende cloot met malcanderen euewichtich: | |||||||
[pagina 41]
| |||||||
Ghelijck des driehoucx rechter sijde tot de slincker, also t'staltwicht des cloots op de slincker sijde, tottet staltwicht des cloots op de rechter sijde.
Tghegheven. Laet A B C een driehouck wesen diens plat sy rechthouckich op den sichteinder, ende den grondt A C euewydich vanden sichteinder, ende op de sijde A B, die dobbel sy an B C, ligghe een cloot D, ende op de sijde B C een cloot E, euewichtich ende euegroot met den cloot D. T'begheerde. Wy moeten bewysen dat ghelijck de sijde A B 2, tot B C 1, alsoo t'staltwicht des cloots E, tottet staltwicht des cloots D. 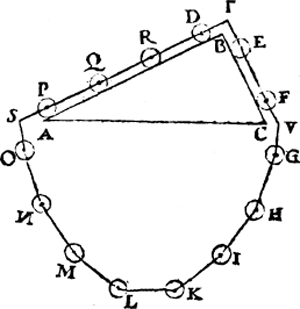 T'bereytsel. Laet ons maecken rondtom den driehouck A B C eenen crans van veerthien clooten, euegroot, euewichtich, ende euewijt van malcanderen, als E, F, G, H, I, K, L, M, N, O, P, Q, R, D, al ghesnoert an een lini, streckende door haer Ga naar margenoot* middelpunten, also dat sy op die middelpunten drayen meughen; Datter oock twee clooten passen op de sijde B C, ende vier op B A, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, ouer welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die bouen den driehouck staen, Ga naar margenoot* euewydich sijn vande sijden A B, B C; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien A B, B C. Tbewys. Soo t'staltwicht der vier clooten D, R, Q, P, niet euen en waer met het staltwicht der twee clooten E, F, t'een of t'ander sal swaerder sijn, latet wesen (soot meughelick waer) der vier D, R, Q, P; Maer de vier clooten O, N, M, L, sijn euewichtich met de vier clooten G, H, I, K, de sijde dan der acht clooten D, R, Q, P, O, N, M, L, is swaerder na de ghestalt dan de sijde der ses clooten, E, F, G, H, I, K: maer want het swaerste altijt het lichtste overweeght, de acht clooten sullen neerwaert rollen, ende d'ander ses rijsen: Latet soo wesen, ende D | |||||||
[pagina 42]
| |||||||
sy gheuallen daer nu O is, ende E, F, G, H, sullen sijn daer nu P, Q, R, D, ende I, K, daer nu E, F, sijn. Maer dit soo wesende, den crans der clooten sal alsulcken gestalt hebben als sy te vooren dede, ende sullen om de selue redenen de acht clooten ter slincker sijde wederom staltwichtigher sijn dan de ses clooten ter rechter, waer duer de acht clooten wederom neer sullen rollen, ende d'ander ses rijsen, welcke valling ter eender, ende rijsing ter ander, om dat de reden altijt de selue is, altijt ghedueren sal, ende de clooten sullen uyt haer seluen een eeuwich roersel maken, t'welck valsch is. Het deel dan des crans D, R, Q, P, O, N, M, L, is euestaltwichtich met het deel E, F, G, H, I, K: Maer van sulcke euewichtighe ghetrocken euewichtighe, de resten sijn euewichtich, laet ons dan van dat deel trecken de vier clooten O, N, M, L, ende van dit de vier clooten G, H, I, K, (welcke euen sijn ande voornoemde O, N, M, L,) de resten D, R, Q, P, ende E, F, sullen euestaltwichtich sijn, Maer wesende dese twee euestaltwichtich met die vier, E sal tweemael staltswaerder sijn als D. Ghelijck dan de lini B A 2, tot de lini B C 1, also t'staltwicht des cloots E, tottet staltwicht des cloots D. Tbeslvyt. Wesende dan een driehouck wiens plat, &c. | |||||||
I. Vervolgh.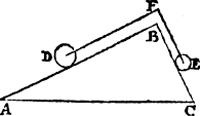 Laet A B C een driehouck sijn als vooren, wiens sijde A B dobbel sy an B C, ende laet op A B ligghen een cloot D, ende op de sijde B C een cloot E euewichtich anden helft van D, ende an F sy een vastpunt daer over de lini D F E (te weten uyt het Ga naar margenoot* middelpunt des cloots D ouer F tot int middelpunt des cloots E) slieren mach, alsoo dat D F euewijdich blijue van A B, ende F E van B C. Dit also sijnde, anghesien de vier clooten P, Q, R, D, hier vooren, euestaltwichtich waren met de twee clooten E, F, soo sal desen cloot D, euestaltwichtich sijn teghen den cloot E: want ghelijck die P, Q, R, D, tot E, F, also dese D tot E: Daerom ghelijck de lini A B, tot B C, alsoo den cloot D tot den cloot E. | |||||||
II Vervolgh.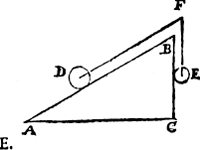 Laet ons nu d'een sijde des driehouckx als B C (ande welcke A B dobbel is) rechthouckich stellen op A C als hier neuen; Ende den cloot D die dobbel is an E, sal noch met E euestaltwichtich sijn, want ghelijck A B tot B C, also den cloot D tot den cloot E. | |||||||
[pagina 43]
| |||||||
III. Vervolgh.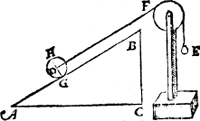 Laet ons nu inde plaets van t'punt F, stellen een caterol als hier neuen, also dat de scheefheflini van D naer F euewydich blijue van A B, ende inde plaets vanden cloot E sy eenich wicht van form soot valt, maer euewichtich anden cloot E: t'selue is noch euestaltwichtich met D, Daerom ghelijck A B tot B C, alsoo noch den cloot D tottet ghewicht E. | |||||||
IIII Vervolgh.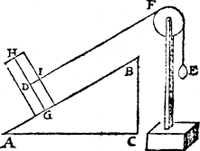 Anghesien den cloot des 3e veruolgs naect de lini A B, in t'punt G, als vastpunt, soo sal den as G H rechthouckich sijn opGa naar margenoot+ A B; Daerom laet ons weren den cloot, ende stellen in die plaets den pilaer D euewichtich met den cloot, alsoo dat den as G H (diens vastpunt G) rechthouckich sy op A B, ende de scheefheflini tusschen D F noch euewijdich van A B, ende sniende de sijde des pilaers in I, Als hier neuens. Ende is openbaer dat ghelijck A B tot B C, (dat is dobbel als vooren) also den pilaer D tottet t'ghewicht E. | |||||||
V. Vervolgh.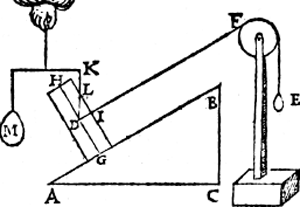 Laet ons trecken de hanghende lini uyt het Ga naar margenoot* middelpunt des pilaers D als D K, sniende de sijde des pilaers in L, t'welck soo sijnde, den driehouck L D I is ghelijck an den driehouck A B C, want de houcken A C B ende L I D sijn recht, ende L D is euewydich van B C ende D I van A B: Daerom ghelijck A B tot B C, alsoo | |||||||
[pagina 44]
| |||||||
L D tot D I; Maer ghelijck A B tot B C, alsoo den Pilaer tot t'ghewicht E door het 4e veruolg, daerom ghelijck L D tot D I, also den pilaer tot E. Laet ons nu ande lini K D voughen trechthefwicht M met den pilaer euestaltwichtich, t'selue ghewicht M sal met den pilaer euewichtich sijn door het 14e voorstel: Daerom ghelijck L D tot D I, also M tot E. | |||||||
VI. Vervolgh.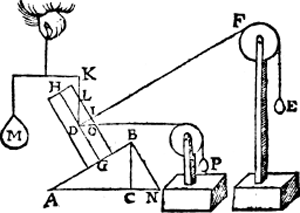 Laet ons trecken B N, sniende de voortghetrocken A C in N: Insghelijcx D O, sniende de voortghetrocken L I dat is de sijde des pilaers in O, ende also dat den houck I D O, euen sy an den houck C B N. Laet ons oock voughen an D O t'scheefhefwicht P, dat den pilaer (de ghewichten M, E gheweert sijnde) in die standthaude. Nu anghesien D L, des driehouckx D L I, Ga naar margenoot* lijckstandighe is met B A des driehouckx B A C, ende D I met B C, men besluyt daer uyt aldus: Ghelijck B A tot B C, alsoo t'staltwicht van B A tottet staltwicht van B C (door het 2e vervolg) Ende oock ghelijck D L tot D I, also t'staltwicht van D L tot t'staltwicht van D I, dat is alsoo M tot E. Maer de lijckstandighe linien van dese ghelijcke driehoucken A B N, L D O, sijn B A met D L, ende B N met D O, Daerom segghen wy als vooren, Ghelijck B A tot B N, alsoo het staltwicht van B A tot het staltwicht van B N (door het 1e vervolgh) Ende oock ghelijck D L tot D O, also het staltwicht van D L tot het staltwicht van D O, dat is also M tot P. Maer by aldien de lini B N, ghetrocken waer van B af ouer d'ander sijde van B C, so soude de lini D O, dan oock vallen van D ouer d'ander sijde van D I, dat is, daer D O nu valt onder D I, sy souder dan bouen vallen, ende t'voorgaende bewijs soude oock dienen tot sulcke gestalt, te weten, dat wy noch segghen souden, ghelijck B A tot B N, alsoo t'staltwicht van B A, tottet staltwicht van B N; Ende ghelijck D L tot D O, alsoo t'staltwicht van D L, tottet staltwicht van D O, dat is, also M tot P. Inder voughen dat dese Ga naar margenoot* eueredenheydt niet alleen en bestaet inde voorbeelden, alwaer de heflini als D I rechthouckich is op den as, maer op allen houcken.
T'voorgaende mach oock verstaen worden van een cloot ligghende op een lini A B als hier neuens, alwaer wy segghen als vooren, gelijck L D tot D O, alsoo M tot P (welverstaende dat C L | |||||||
[pagina 45]
| |||||||
rechthoukich ghetrocken is op A B, dat is euewydich met den as G H des cloots D) maer t'ghewicht M is euen an den cloot D, daerom segghen wy gelijck L D tot D O, also t'ghewicht des cloots, tot P. 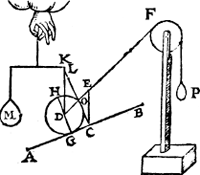 Maer want L D ende D O binnen t'lichaem des cloots metter daet niet bequamelick en connen beschreuen worden, so laet ons trecken de hanghende C E, ende sullen dan hebben buyten t'lichaem een driehouck C E O, ghelijck anden driehouck L D O, welcker Ga naar margenoot* lijckstandighe sijden sijn L D met C E, ende D O met E O, daerom ghelijck L D tot D O, alsoo C E tot E O, ende veruolghens ghelijck C E tot E O, alsoo t'ghewicht des cloots, tot P.
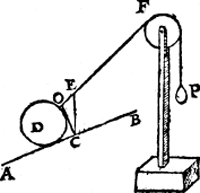 Laet ons nu tot meerder claerheyt dit alleen stellen sonder d'ander linien als hier neuen, alwaer wy segghen ghelijck C E tot E O, also t'ghewicht des cloots D tot P.
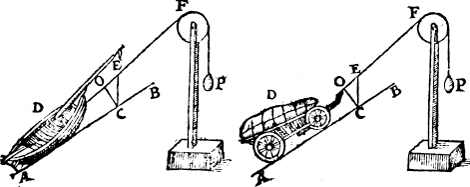 Ende dit niet alleen van clooten maer van ander lichamen slierende, ofte rollende, op punten ofte linien als hier onder, (daer wy eygentlicker af handelen sullen inde Weeghdaet) alwaer wy noch segghen ghelijck C E tot E O, also t'ghewicht des lichaems D tottet ghewicht P. | |||||||
[pagina 46]
| |||||||
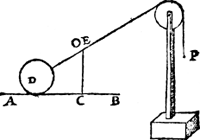 Waer uyt oock blijct, dat wesende de lini A B euewydich vanden Ga naar margenoot* sichteinder als hier neuens, dat C E ende C O dan in een selfde lini sullen vallen, waer duer tusschen E en O gheen langde en sal sijn, ende vervolghens C E en sal tot E O gheen reden hebben, daermen by verstaen sal dat een swaerheydt inde plaets van P hoe cleen sy mocht wesen, en sal niet euestaltwichtich connen sijn teghen t'lichaem D, maer salt (Ga naar margenoot* Wisconstelick verstaende) voorttrecken hoe swaer het sy: Waer uyt volght, dat alle swaerheden voortghetrocken langs den sichteinder, als schepen int water, waghens langs t'platte landt, &c. en behouuen gheen vlieghesterctens macht tot haer verroersel, meer dan de omstaende verhindernissen en veroirsaecken, als Water, Locht, Naecsel der assen, teghen de bussen, naecsel der rayers teghen de straet, ende dierghelijcke.
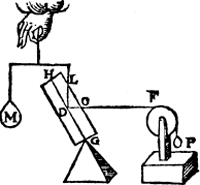 Maer anghesien den driehouck A B N int 6e veruolg, tot dese Ga naar margenoot* eueredenheyt niet en gheeft noch en neemt, laet ons hem weeren, ansiende G voor vastpunt des pilaers rustende op een pin als hier neuen, ende sullen noch segghen ghelijck L D tot D O, also M tot P. | |||||||
VII. Vervolgh.Maer op dat nu blijcke dese Ga naar margenoot* eueredenheydt niet alleen also te bestaen inde pilaren alwaer de rechtheflini als D L, comt uyt t'middelpunt des pilaers, ende diens vastpunt is des assens uyterste, als hier vooren G int 6e vervolg; Soo laet A B C een driehouck sijn, wiens sijde A B dobbel is an B C, ende B C sy Ga naar margenoot* hanghende op A C: Ende laet D E een pilaer sijn diens as F G rechthouckich op A B, ende sniende A B in t'punt H, ende I sy eenich ander punt in den selven as; | |||||||
[pagina 47]
| |||||||
Laet oock K L een ander pilaer sijn, euen ende ghelijck anden pilaer D E, wiens as M N, ende O een punt des as naeckende B C, ende van ghelijcke gestalt in sijn pilaer, als H inden pilaer D E; Laet oock P een ander punt sijn van sulcker ghestalt inden pilaer K L, als I inden pilaer D E; Ende laet Q een vastpunt sijn daer ouer de lini I Q P slieren mach, alsoo dat de lini I Q Ga naar margenoot* euewydich sy van A B, ende Q P euewydich van B C. 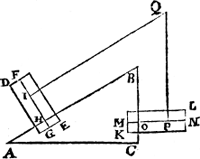 Ende om de redenen die int 19e voorstel vande 14 clooten verclaert sijn (t'welck wy hier deur soodanighe veel slierende pilaren oock souden connen bewysen, maer want sulcx uyt t'voorgaende kennelick is, wy slaent ouer) het staltwicht des pilaers K L, sal dobbel sijn an t'staltwicht des pilaers D E. | |||||||
VIII. Vervolgh.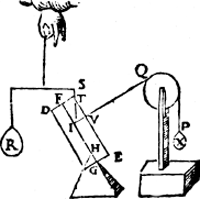 Laet ons nu an I des 7e veruolgs voughen trechthefwicht R euestaltwichtich met den pilaer, diens rechtheflini sy I S, sniende de sijde des pilaers in T, ende I Q snie de sijde des pilaers in V, ende laet an de lini P Q hanghen een ghewicht X, inde plaets vanden pilaer K L, t'welck euen sy anden helft van t'staltwicht des selfden pilaers K L, Laet ons oock weeren den driehouck A B C, ende den pilaer D E doen rusten op t'punt H als hier neuen. Ende om de redenen als vooren, ghelijck T I tot I V, alsoo R tot X. Ende dit niet alleen als I V rechthouckich is op den as F G, maer cromhouckich soot valt, waerafmen besonder bethooch soude mueghen doen, maer tis openbaer ghenouch door het 6e vervolgh. | |||||||
IX. Vervolgh.Wy hebben int 8e vervolgh dese Ga naar margenoot* eueredenheyt verclaert, alwaer t'roerende punt I, hooger was dan t'vastpunt H, ende alwaer de scheefheflini I V helde naer de sijde des vastpunts H; Wy moeten nu | |||||||
[pagina 48]
| |||||||
bethooghen de selue eueredenheyt oock so te bestaen in d'ander ghestalten, ende eerst alwaer troerende punt leegher sy dan t'vastpunt, ende alwaer de scheefheflini afwyct vande sijde des vastpunts in deser voughen. 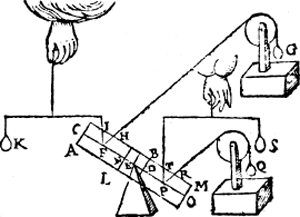 Laet A B een pilaer sijn, diens as C D, ende vastpunt E, ende t'verroerlick punt F, ende t'scheefhefwicht dat hem in die gestalt houdt sy G, diens scheefheflini F H, ende F I sy rechtheflini, diens rechthefwicht K. Laet L M oock een pilaer sijn, euen ende ghelijck an den pilaer A B, wiens as sy N O, ende vastpunt E, ende verroerlick punt P, also dat E N euen sy an E D, ende E F an E P, ende t'scheefhefwicht Q sy euen an G, ende sijn scheefheflini sy P R, Ga naar margenoot* euewydich van F H, ende trechthefwicht S sy euen an K, ende sijn rechtheflini sy P T. Dit soo sijnde laet ons vergaren de twee pilaren A B ende L M, ansiende A M voor een heel pilaer, wiens Ga naar margenoot* swaerheyts middelpunt ende vastpunt sal E sijn door t'ghestelde. Laet ons nu weeren de ghewichten K, G, S, Q, ende den pilaer A M sal op E alle ghestalt houden diemen hem gheeft door het 7e voorstel, hy sal dan soo blijuen, ende den pilaer A B sal alsoo euewichtich blijuen teghen den pilaer L M. Laet ons nu de ghewichten Q G weder andoen, hanghende euewichtighe van ghelijcke ghestalt, an euewichtighe, ende door het 13e voorstel, Q sal anden pilaer A M euen sulcken macht doen als G: Ende veruolghens Q doet sulcken macht an huer pilaer L M, als G an huer pilaer A B; maer de macht van G is A B in die ghestalt te houden door het 6 vervolg, de macht dan van Q is oock L M in die ghestalt te houden. Insghelijcx soo is oock de macht van K, den pilaer A B in die ghestalt te houden, daerom oock is de macht van S den pilaer L M in die ghestalt te houden; Nu ghelijck I F tot F H, also K tot G door het 8e vervolg, Maer T P, is euen an I F, ende P R an F H, ende S an K, ende Q an G, ghelijck dan T P tot P R, alsoo S tot Q. Dese eueredenheydt dan, als wy gheseyt hebben, is so wel inde voorbeelden alwaer t'roerende punt P leegher is dan t'vastpunt E, ende alwaer de scheefheflini P R afwyct vande sijde des vastpunts E, als daert hoogher is, ende daer de scheefheflini helde naer t'vastpunt. | |||||||
[pagina 49]
| |||||||
X. Vervolgh.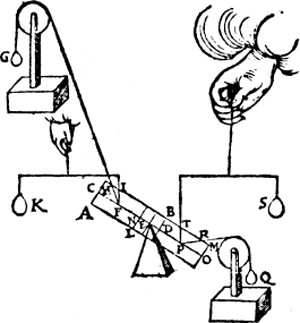 Laet ons stellen een form ghelijck an die des 9 veruolghs, alleen daer in verschillende dat dese F H wyct ouer d'ander sijde van F I, ende dat den houck H F C, euen sy anden houck R P O, waer duer G anden pilaer A M euen soo grooten ghewelt doet als Q, ende om de redenen des 9 veruolgs (die wy om cortheyt ouerslaen) G doet euen sulcken ghewelt anden pilaer A B, als Q anden pilaer L M; Nu ghelijck T P, tot P R, alsoo S tot Q door het 9e veruolgh, maer I F is euen an T P, ende F H an P R, ende K an S, ende G an Q, daerom ghelijck I F tot F H, also K tot G. | |||||||
XI Vervolgh.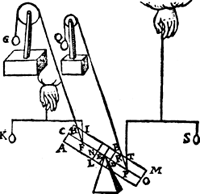 Laet ons stellen een form ghelijck an die des 10 veruolgs, alleen daer in verschillende dat dese P R wyckt ouer d'ander sijde van P T, ende dat P R euewydich sy met F H, waer deur Q an den pilaer A M, euen soo grooten ghewelt doet als G, ende om de redenen des 9e veruolghs, Q doet euen sulcken gheweldt anden pilaer L M, als G anden pilaer A B, Nu ghelijck I F tot F H, also K tot G door het 6 veruolgh: Maer T P is euen an I F, ende P R an F H, ende S an K, ende Q an G, daerom ghelijck T P tot P R, also S tot Q. Ende inder seluer voughen salmen van den anderen ghestalten door haer contrarien altijt dese eueredenheyt bewysen. | |||||||
[pagina 50]
| |||||||
XII. Vervolgh.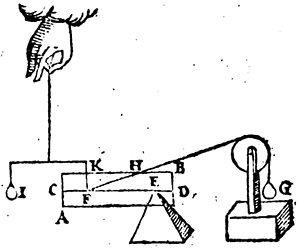 Maer dat dese Ga naar margenoot* eueredenheydt oock bestaet inde ghestalt daer den as euewydich is vanden Ga naar margenoot* sichteinder, wort aldus bethoont: Laet A B een pilaer sijn, diens as C D Ga naar margenoot* euewijdich sy vanden sichteinder, ende t'vastpunt daer in E, ende t'roerlick punt F, ende G t'scheefhefwicht dat den pilaer in die ghestalt houdt, wiens scheefheflini F H, ende I trechthefwicht dat den pilaer oock in die ghestalt houdt, wiens rechtheflini F K; T'welck soo sijnde, Laet K F tot F H een ander reden hebben (soot mueghelick waer) dan I tot G, By voorbeelt K F sy tot F H, als 1 tot 2, maer I tot G, als 3 tot 7. Dit so ghenomen, laet ons den pilaer der eerste form neerduwen, ofte der tweeder form oplichten tot dat K F sulcken reden hebbe tot F H, als 3 tot 7, ende alsdan sal G oock euestaltwichtich sijn teghen den pilaer door de voorgaende vervolghen; Inder voughen dat den pilaer hoogher ende leegher verheuen, sal teghen G euestaltwichtich blijven, t'welck openbaer onmueghelick is, als oock Ga naar margenoot* wisconstlick sal blijcken door t'volghende 22 voorstel. K F dan en heeft tot F H gheen ander reden dan I tot G. 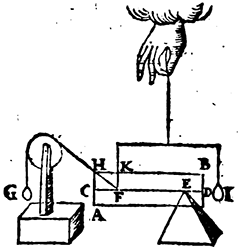 Uyt dese voorgaende bescrijuen wy een vertooch soodanich. | |||||||
XII. Vertooch. XX. Voorstel.Wesende inden as des pilaers een vastpunt, ende een roerlick, daer an hy door een rechthefwicht ende scheefhefwicht in seker standt gehouden wort: Ghelijck rechtheflini tot scheefheflini, also rechthefwicht tot scheefhefwicht. Tghegheven. Laet A B een pilaer sijn diens as C D, ende t'vast- | |||||||
[pagina 51]
| |||||||
punt E, ende roerlick punt F, daeran den pilaer door t'rechthefwicht G in die ghestalt ghehouden wort, daer an oock den pilaer door t'scheefhefwicht H (welverstaende G gheweert sijnde) in die ghestalt ghehouden wort, ende de rechtheflini snie de sijde des pilaers in I, maer de scheefheflini snie de selue sijde in K: Ick seg dat ghelijck de rechtheflini I F, tot de scheefheflini F K, alsoo trechthefwicht G, tot het scheefhefwicht H. waer af t'bewys uyt de voorgaende openbaer is. 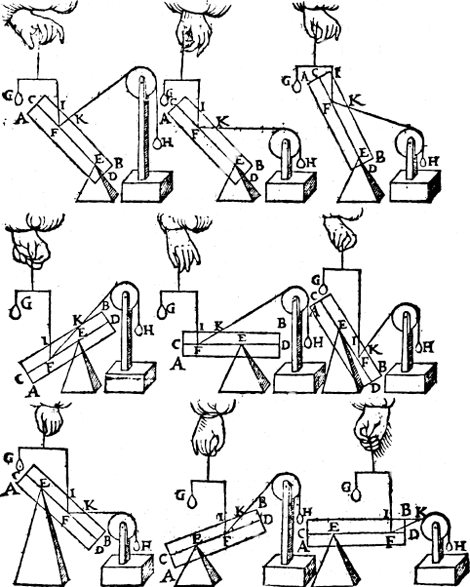 | |||||||
[pagina 52]
| |||||||
T'beslvyt. Wesende dan inden as des pilaers een vastpunt, &c. Merckt. Soo eenighe der linien als I F, F K, de sijde des pilaers niet en sneen, men sal die sijde voorder trecken tot dat sy ghesneen wort, als inde voorgaende laetste form. | |||||||
XIII. Vertooch. XXI. Voorstel.Wesende inden as des pilaers een vastpunt, ende een roerlick, daer an hy door een rechtdaelwicht ende scheefdaelwicht in seker stant gehouden wort: Ghelijck rechtdaellini tot scheefdaellini, also rechtdaelwicht tot scheefdaelwicht.
T'ghegheven. Laet A B een pilaer sijn, diens as C D, ende vastpunt E, ende roerlick punt F, daer an den pilaer door trechtdaelwicht G in die ghestalt ghehouden wort, daer an oock den pilaer door t'scheefdaelwicht H (welverstaende G gheweert sijnde) in die ghestalt ghehouden wordt, ende de rechtdaellini snie de sijde des pilaers in I, maer de scheefdaellini snie de selue sijde in K. Tbegheerde. Wy moeten bewysen dat ghelijck de rechtdaellini I F tot de scheefdaellini F K, alsoo t'rechtdaelwicht G tot het scheefdaelwicht H. Tbereytsel. Laet ons teeckenen t'punt L, alsoo dat E L euen sy an E F, ende voughen an t'punt L t'rechthefwicht M, dat den pilaer in die ghestalt can houden, diens rechtheflini L N: Insghelijcx t'scheefhefwicht O, dat den pilaer oock in die ghestalt can houden, wiens scheefheflini L P euewydich sy met F K. 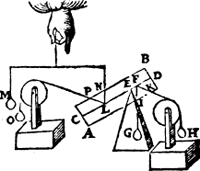 Tbewys. Ghelijck N L tot L P, alsoo M tot O, duer het 20e voorstel, maer de macht van G is anden pilaer euen met de macht van M, ende de macht van H met die van O duer het 13e voorstel, ende I F is euen an L N, ende F K, an L P; Daerom ghelijck de rechtdaellini I F tot de scheefdaellini F K, alsoo t'rechtdaelwicht G tottet scheefdaelwicht H, Sghelijcx sal oock t'bewys sijn van alle d'ander ghestalten als inde formen hier na volghende. | |||||||
[pagina 53]
| |||||||
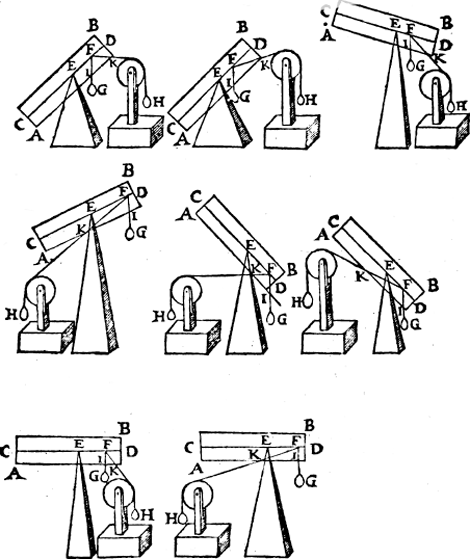 T'beslvyt. Wesende dan inden as des pilaers een vastpunt ende een roerlick, &c. | |||||||
IX. Eysch. XXII. Voorstel.Wesende ghegheuen een bekenden pilaer, met een vastpunt inden as, ende een roerlick punt, an t'welck eenich onbekent treckghewicht den pilaer in ghegheuen ghestalt houdt: Dat treckwicht bekent te maken. | |||||||
[pagina 54]
| |||||||
T'ghegheven. Laet A B C D een pilaer sijn wegende 6 ℔, ende ghedeelt als int 1e voorstel, ende t'vastpunt sy X, ende het roerende punt S, an t'welck gheuoecht sy een onbekent scheefhefwicht Y, met den pilaer euestaltwichtich, ende sijn scheefheflini snie de sijde des pilaers A B in OE. T'begheerde. Wy moeten dat onbekende scheefhefwicht Y bekent maken. 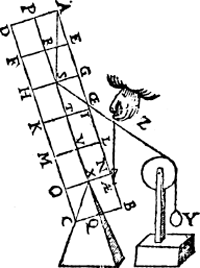 Twerck. Men sal sien wat rechthefwicht an S den pilaer in die ghestalt soude houden, wort beuonden door 14e voorstel, van 4 ℔, daer naer salmen ondersoucken wat reden eenighe Ga naar margenoot* hanghende lini als Z AE, heeft tot Z OE, ick neme als van 2 tot 1, daer uyt seg ick 2 gheeft 1, wat t'rechthefwicht van 4 ℔? comt voor Y 2 ℔, t'welck ick seg sijn waer ghewicht te sijne. T'bereytsel. Laet ons trecken de hanghende door S welcke sy A S. T'bewys. Ghelijck A S tot S OE, also t'rechthefwicht tottet scheefhefwicht Y door het 20e voorstel, maer den driehouck OE Z B, is ghelijck anden driehouck OE S A, welcker Ga naar margenoot* lijckstandige linien sijn OE Z met OE S, ende Z AE met S A: Daerom ghelijck A S tot S OE, alsoo AE Z tot Z OE, ende vervolghens ghelijck AE Z 2, tot Z OE 1, also t'rechthefwicht 4 ℔ tot Y, daerom Y weghende 2 ℔ is bekent ghemaect, t'welck wy bewysen moesten. Ende sghelijcx sal den voortganck sijn in allen anderen voorbeelden. T'beslvyt. Wesende dan ghegheuen een bekenden pilaer met een vastpunt inden as, &c. | |||||||
Ie Merck.Wy souden inde wercking hebben mueghen segghen, A S 2, gheeft S OE 1, wat t'rechthefwicht 4 ℔? comt voor Y 2 ℔, maer op dat sy lijckformigher souden siin an t'ghene inde daet gheschiet (want men can binnen int lichaem qualick de linien A S, S OE trecken) wy hebben de hanghende lini Z AE int voorbeelt uytwendich genomen. | |||||||
IIe Merck.Tis openbaer door de Ga naar margenoot* verkeerde ende oueranderde Eueredenheydt, hoe dat elck van d'ander onbekende Ga naar margenoot* palen als Rechthefwycht, Rechtheflini, Scheefheflini, Pilaer, door drie bekende palen altijt bekent sullen worden, welcker bescriuing wy om de cortheyt achterlaten. | |||||||
[pagina 55]
| |||||||
XIIII. Vertooch. XXIII. Voorstel.Even ghewichten der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as euen houcken makende; doen anden pilaer euen ghewelden.
Tghegheven. Laet A B een pilaer sijn diens as C D, ende vastpunt daer in E, ende t'roerlick punt F, an t'welck een scheefhefwicht G sy, dat den pilaer in die ghestalt houde, ende diens scheefheflini F H. Laet oock an t'selue punt F gheuoucht wesen een scheefhefwicht I, ouer d'ander sijde, ende met G euewichtich, ende diens scheefheflini F K, den houck K F D euen make anden houck H F C. 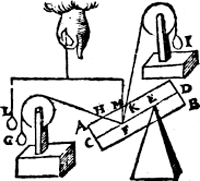 T'begheerde. Wy moeten bewysen dat I anden pilaer euen sulcken ghewelt doet als G, te weten dat I (G gheweert sijnde) den pilaer oock in die gestalt sal houden. T'bereytsel. Laet an t'punt F gheuoucht worden t'rechthefwicht L dat den pilaer oock in die ghestalt can houden, ende sijn rechtheflini sy F M. T'bewys. Want de linien F H, F K, sijn tusschen de Ga naar margenoot* euewydighe H K, C D, ende dat den houck H F C, euen is (door t'ghegheuen) an den houck K F D, so sijn F H ende F K euen, waer uyt volght dat ghelijck M F tot F H, alsoo M F tot F K, Maer ghelijck M F tot F H, alsoo L tot G, daerom oock ghelijck M F tot F K, also L tot G; maer I is euen an G door t'ghestelde, ghelijck dan M F tot F K, alsoo L tot I. T'welck so sijnde, I houdt den pilaer in die ghestalt door het 20 voorstel. Sghelijcx sal oock t'bewijs sijn in alle ander voorbeelden. T'beslvyt. Euen ghewichten dan der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as euen houcken makende; doen anden pilaer even ghewelden, t'welck wy bewysen moesten. | |||||||
XV. Vertooch. XXIIII. Voorstel.Als des ghewichts trecklini rechthouckich op den as is; Soo doedet anden pilaer ghegeuener ghestalt de grootste ghewelt. | |||||||
[pagina 56]
| |||||||
T'ghegheven. Laet A B een pilaer sijn diens as C D, ende vastpunt E, ende roerlick punt F, waer an gheuoucht is t'scheefhefwicht G, dat den pilaer in die ghestalt houdt, ende also dat sijn scheefheflini H F rechthouckich op den as C D is, Laet oock an F gheuoucht worden t'scheefhefwicht I, euen an G, ende sijn scheefheflini sy K F. T'begeerde. Wy moeten bewysen dat G meerder ghewelt doet anden pilaer, dan I, oock gheen meerder ghewelt daer an doen en can. T'bereytsel. Laet ons an F voughen t'rechthefwicht L dat den pilaer in die ghestalt houden can, diens rechtheflini F M. T'bewys.
Des Ga naar margenoot* bewysredens tweede voorstel wort aldus bethoont, T'ghewicht G (t'welck den pilaer in die ghestalt houdt) heeft sulcken reden tot L, als H F tot F M, maer I is euen an G, ende K F is meerder dan F H,Ga naar margenoot+ daerom I heeft minder reden tot L, dan K F tot F M, waer duer soo wy bouen gheseyt hebben, t'gewicht I is te licht om den pilaer in die ghestalt te houden; maer G cander hem in houden, G dan doet anden pilaer meerder ghewelt dan I. Maer dat G daer an gheen meerder doen en can, is daer uyt openbaer, dat van F op de sijde des pilaers gheen corter lini en can ghetrocken worden dan F H, anghesien sy daer op rechthouckich is. 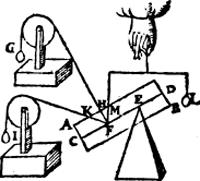 T'beslvyt. Als dan des ghewichts trecklini rechthouckich op den as is, soo doedet an den pilaer ghegheuener ghestalt de grootste ghewelt, t'welck wy bewysen moesten. | |||||||
Vervolgh.Het blijft dat hoe de houcken der trecklinien vande ghewichten, op den as den rechthouck naerder sijn, hoe de ghewichten meerder ghewelt doen; Ende ter contrarie hoe sy vanden rechthouck meer verschillen, hoe de ghewichten minder ghewelt doen. | |||||||
[pagina 57]
| |||||||
XVI. Vertooch. XXV. Voorstel.Twee oneuewydighe linien daer een pilaer an hangt beyde oneindelick voortghetrocken, snien malcanderen inde swaerheydts middellini des pilaers. | |||||||
Ie Voorbeelt.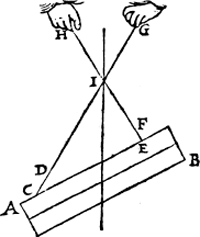 T'ghegheven. Laet A B een pilaer sijn hanghende ande twee oneuewydige linien C D, E F, welcke voortghetrocken sijn tot G, H, sniende malcander in I. T'begeerde. Wy moeten bewysen dattet punt I inde swaerheyts middellini is des pilaers A B. Tbewys. Den houck F E C, ofte I E C, ofte H E C, is al een selfden houck, also oock is D C E, ofte I C E, ofte G C E, daerom wat punten wy inde linien H E, ende C G voor uytersten nemen, den pilaer houdt daer an sijn ghegheuen standt. Laet ons nemen I, ghemeen uyterste punt van d'een ende d'ander lini, den pilaer dan houdt daer an sijn ghegeuen standt. Maer hanghende den pilaer an t'punt I, so is de Ga naar margenoot* hanghende door I des pilaers swaerheydts middellini inde welcke I is. | |||||||
IIe Voorbeelt.T'ghegheven. Laet A B een pilaer sijn hanghende ande oneuewydighe linien C D, E F, welcke voortghetrocken sijn tot G, H, sniende malcander in I. T'begheerde. Wy moeten bewijsen dattet punt I, inde swaerheydts middellini is des pilaers A B. Tbewys. Laet ons D G ende F H ansien voor stylen ofte stiue linien daer den pilaer op rust, welcke door de 2e begheerte niet en breken noch en buygen; der seluer ghewelt is euen ande ghewelt der linien C D, E F, want ghelijck dese den pilaer in sijn ghegheuen standt houden alsoo oock die. Ende wat punten wy inde linien D G, F H voor uytersten nemen, den pilaer | |||||||
[pagina 58]
| |||||||
houdt daer op sijn ghegheuen standt. Laet ons nemen I, ghemeen uyterste punt van d'een en d'ander lini; den pilaer dan houdt daer op (Ga naar margenoot* Wisconstlick verstaende) sijn ghegheuen standt, maer rustende den pilaer op t'punt I, soo is de hanghende door I des pilaers swaerheydts middellini, inde welcke I is. 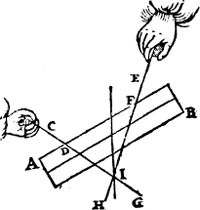 | |||||||
III. Voorbeelt.T'ghegheven. Laet A B een pilaer sijn welcke in die standt ghehouden wort door de scheefdaellini C D, ende scheefheflini E F, de selue sijn voortghetrocken tot G, H, sniende malcanderen in I. 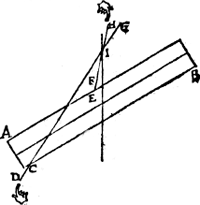 T'begheerde. Wy moeten bewysen dat I inde swaerheydts middellini is des pilaers A B. T'bewys. Laet ons G C ansien voor styl, ofte stijue lini ende nemen dat de macht die an D int neertrecken was, nu neersteeckende sy in yder punt tusschen C en G daermen haer stelt, ende den pilaer A B, sal alsoo op allen punten diemen tusschen C, G ende E, H voor uytersten neemt, sijn ghegheuen standt houden. Laet ons nemen I ghemeen uyterste van d'een en d'ander lini, den pilaer dan houdt daer an sijn ghegheuuen standt; maer hanghende den pilaer an t'punt I, de hanghende door I is des pilaers swaerheyts middellini, inde welcke I is. | |||||||
IIII. Voorbeelt.T'ghegheven. Laet A B een pilaer sijn, welcke in die standt ghehouden wort door de scheefdaellini C D, ende de scheefheflini E F, de selue sijn voortghetrocken tot G H, sniende malcanderen in I. T'begheerde. Wy moeten bewysen dat I inde swaerheyts mid- | |||||||
[pagina 59]
| |||||||
dellini is des pilaers A B. T'bewys. Laet ons H E ansien voor stijl, ofte stiue lini, ende nemen dat de macht die an E int opheffen was, nu opstekende sy in yder punt tusschen E en H, daermen haer stelt, ende den pilaer A B sal also op allen punten diemen tusschen C G ende E H voor uytersten neemt, sijn ghegheuen standt houden. Laet ons nu nemen I ghemeen uyterste punt van d'een en dander lini, den pilaer dan houdt daer op sijn ghegheuen standt, maer rustende den pilaer op t'punt I, soo is de hanghende door I des pilaers swaerheydts middellini, inde welcke I is. 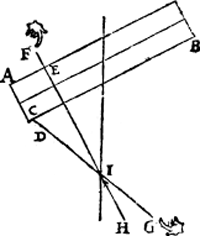 T'beslvyt. Twee oneuewydighe linien dan, daer een pilaer an hangt beyde oneyndelick voortghetrocken, snien malcanderen inde swaerheydts middellini des pilaers, t'welck wy bewysen moesten. | |||||||
XVII. Vertooch. XXVI. Voorstel.Soo d'eene der twee linien daer een pilaer an hangt rechthouckich op den Ga naar margenoot* sichteinder is, d'ander salder oock rechthouckich op sijn: Ende sooder d'een scheefhouckich op is, dander salder oock scheefhouckich op wesen: Ende soo dese naer die neigt, die sal naer dese neighen: Maer so dese van die wyckt, die sal oock van dese wycken.
T'ghegheven. Laet A B een pilaer sijn hanghende an twee linien, d'een C D rechthouckich op den sichteinder, d'ander E F (soot mueghelick waer) scheefhouckich, ende G H sy des pilaers swaerheydts middellini. T'begheerde. Wy moeten bewysen t'hinhoudt des voorstels. T'bereytsel. Laet C D ende E F voortghetrocken worden, sniende malcander in I. T'bewys. Soo den pilaer in die ghestalt blijft hanghende ande linien C D, E F, sy sal op alle vastpunten in die voortghetrocken linien de selue ghestalt houden, ouermidts de houcken I C E, ende I E C, niet en veranderen: Daerom ghenomen I | |||||||
[pagina 60]
| |||||||
ghemeen vastpunt dier twee linien, den pilaer sal daer an in sijn ghegheuen standt blijuen hanghende, ende I C sal swaerheydts middellini sijn: maer dat is onmueghelick, wanttet G H haer euewydeghe is. T'selue sal oock alsoo bethoont worden als de lini E F ouer dander sijde neigt. Wesende dan I C rechthouckich op den sichteinder, d'ander lini als E F en cander niet scheefhouckich op sijn; nootsaecklick dan rechthouckich: Ende veruolghens sooder E F scheefhouckich op is, dander moeter oock scheefhouckich op sijn. 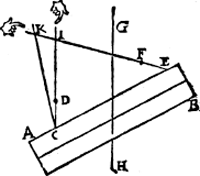 Voorder, anghesien E F neigt naer de sijde van A, soo sal de lini die den pilaer in die ghestalt houdt moeten neighen naer E F. Want laetse (soot mueghelick waer) daer van wycken, als C K, sniende de voortghetrocken E I in K, inder voughen dat de hanghende lini door K, sal om de redenen als bouen swaerheydts middellini wesen des pilaers, t'welck noch ongheschicter is dan doen wy die seyden door I te vallen: D'ander lini dan die den pilaer in de ghestalt can houden, en wyckt van E F niet, sy en is met haer oock gheen euewydighe als bouen bethoont is, ende ter sijden uyt te wijcken is openbaer onmueghelick, sy neigt dan nootsaecklick naer E F. Ende soo E F over d'ander sijde neigde, men sal insghelijcx bethoonen dat d'ander lini van haer wycken sal. T'beslvyt. Soo d'eene dan der twee linien, &c. | |||||||
XVIII. Vertooch. XXVII. Voorstel.Hanghende een pilaer euestaltwichtich teghen twee scheefhefwichten: Ghelijck scheefheflini tot rechtheflini, alsoo elck scheefhefwicht tot sijn rechthefwicht.
T'ghegheven. Laet A B een pilaer sijn wiens as C D, ende twee punten daer in E, F, welcker scheefhefwichten die hem in die standt houden sijn G, H, ende rechthefwichten I, K, ende scheefheflinien E L, F M, ende rechtheflinien E N, F O. T'begheerde. Wy moeten bewysen dat gelijck L E tot E N, alsoo G tot I, ende ghelijck M F tot F O, alsoo H tot K. T'bewys. Laet ons F ansien voor vastpunt, ende E voor t'roerlick, daerom (door het 20e voorstel) ghelijck L E | |||||||
[pagina 61]
| |||||||
tot E N, alsoo G tot I. Laet ons ten tweeden E ansien voor vastpunt, ende F voor t'roerlick; Daerom (door t'voornoemde 20e voorstel) ghelijck M F tot F O, alsoo H tot K. 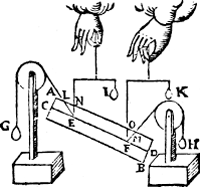 T'beslvyt. Hanghende dan een pilaer euestaltwichtich teghen twee scheefhefwichten: Gelijc scheefheflini tot rechtheflini, alsoo elck scheefhefwicht tot sijn rechthefwicht, t'welck wy bewysen moesten. | |||||||
Vervolgh.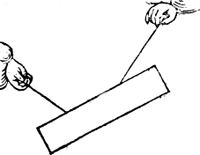 Hanghende een bekende pilaer an twee oneuewydige linien als hier neuen; T'blyckt dat bekent sal worden hoe veel ghewichts an yder lini hangt, ofte hoe veel ghewelts yder lini doet. 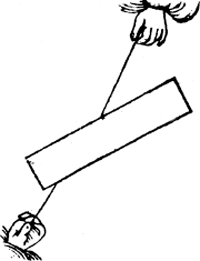 | |||||||
Merckt.Wy hebben tot veel voorbeelden der voorstellen deses boucx, genomen den pilaer, als bequaemste form tot de verclaring des voornemens, oock vastpunt ende roerlickpunt ghestelt inden as. Wy sullen nu door dit laetste voorstel, bethoonen de reghelen van dien gemeen te wesen over alle formen der lichamen hoedanich sy siin met vastpunt ende roerlickpunt daert valt. | |||||||
[pagina 62]
| |||||||
XIX. Vertooch. XXVIII. Voorstel.Alle de Ga naar margenoot* eueredenheden, welcke hier vooren beschreuen sijn vanden pilaer tot de ghewichten an hem hanghende, ende dier ghewichten linien: De selue te wesen van yder lichaem tot de ghewichten an hem alsoo hanghende, ende dier ghewichten linien.
T'ghegheven. Laet ons t'voorbeelt nemen der eueredenheydt des 20e voorstels aldus: Het sy een pilaer A B, diens as C D, ende swaerheyts middelpunt E, ende vastpunt daer in F, ende roerlick punt G, an t'welc gheuoucht sy een scheefhefwicht H, dat den pilaer in die ghestalt houde, diens scheefheflini G I. Daer naer trechthefwicht K, dat den pilaer oock in die ghestalt houde, diens rechtheflini G L, alwaer wy segghen, ghelijck I G tot G L, also H tot K. 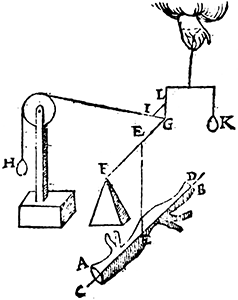 T'begheerde.Wy moeten bewysen dat dese eueredenheydt niet alleenlick also en bestaet in t'lichaem A B een pilaer sijnde, maer van sulcke form alst valt. 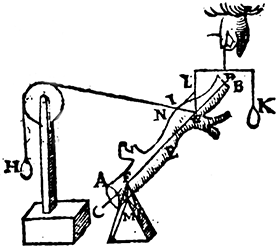 Tbewys. Laet ons den pilaer A B (blijuende de linien F G ende I L op haer plaetsen) neertrecken, alsoo dat hy bliue hanghende an sijn Ga naar margenoot* swaerheyts middelpunt E, wiens ghestalt dan sy als hier neuens. Ende door de 3e begheerte den pilaer en veroirsaect op de punten F, G, gheen ander swaerheydt dan d'eerste; ende alles blijft noch euestaltwichtich, ende ghelijck I G tot G L, alsoo noch H tot K. | |||||||
[pagina 63]
| |||||||
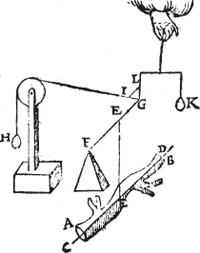 Laet nu de form des pilaers (al de stoff bliuende) verandert worden in eenighe ander ongheschickte form, als A B hier neuens, diens swaerheytds middelpunt E sy, ende een rechte lini daer deur C D (welcke vinding des swaerheyts middelpunts ende rechter linien inde Weeghdaet verclaert sal worden, Ga naar margenoot* werckelick, niet Wisconstelick) ende alles blijft noch euestaltwichtich, ende ghelijck I G tot G L, alsoo noch H tot K.
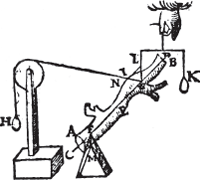 Laet nu t'lichaem A B opghetrocken worden, tot dat F G is inde lini C D, wiens ghestalt dan sy als hier neuens, ende alles blijft noch euestaltwichtich: want het lichaem A B hoogher ofte leegher hanghende, blijft van een selfde ghewicht door de 3e begheerte, ende veruolghens ghelijck I G tot G L, alsoo noch H tot K. De eueredenheydt dan des 20e voorstels en is niet alleenelick alsoo met den pilaer, maer met yder lichaem: Ende der ghelijcke salmen oock alsoo bethoonen van al t'ghene hier vooren in alle d'ander voorstellen vanden pilaer gheseyt is. Tbeslvyt. Alle de eueredenheden dan, welcke hier vooren bescreuen sijn vanden pilaer tot de ghewichten an hem hanghende, ende dier ghewichten linien; de selue sijn van yder lichaem tot de ghewichten an hem alsoo hanghende, ende dier ghewichten linien, t'welck wy bewysen moesten. | |||||||
[pagina 64]
| |||||||
Vervolgh.Tis oock openbaer dat de ghegheuen punten als F, G, niet nootsaeckelick en moeten inde lini C D sijn, maer daert valt. by voorbeelt ande uytersten des lichaems M, N, Want voortghetrocken de lini I N tot inde rechte C D, t'welck ick neem te vallen in G; sghelijcx ghetrocken door M de Ga naar margenoot* hanghende tot inde lini C D, welcke ick neem te vallen in F, de voornoemde eueredenheyt, te weten ghelijck I G tot G L, alsoo H tot K, blijft noch staende.
Einde des eersten bovcx. |
|

