Beghinselen der weeghconst

[p. 11]

Het andere deel vande voorstellen.

I. Vertooch.⁺       I. Voorstel.⁺

Wesende twee euestaltwichrighe swaerheden, de swaerste heeft sulcken reden tot de lichtste, als den langsten erm tot den cortsten.

+ Theorema.

+ Propositio.

1e Voorbeelt.

⁺Tghegheven Laet A B C D een pilaer sijn weghende 6 ℔. welcke ghedeelt sy in 6 euen deelen, door ^* platen euewydich van sijn grondt A D, als E F, G H, l K, L М, N О, sniende den as P Q in R, S, T, V, X: Laet ons nu nemen L M D A voor de swaerste swaerheydt, wiens swaerheyts middelpunt is S, ende L М СВ voor de lichtste swaerheydt, wiens swaerheyts middelpunt is Х, ende S X is dier deelen balck door de 7^e bepaling, ende Tis t'swaerheyts middelpunt des heelen pilaers, ende T I d'hanthaef, waer an L M D A ende L M C B evestaltswichtich hangen, ende T X is den langsten erm, ende T S den cortsten door de 8^e bepaling.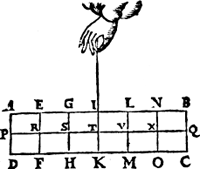

tbegheerde. wy moeten bewysen .dat ghelijck de swaerste swaerheydt L М D A, tot de lichste L M C B, alfo den langsten erm T X, tot den cortsten T S. tbewis.⁺ De swaerste swaerheydt L M D A weeght 4 ℔, ende de lichtste L M C B 2 ℔, ende den langsten erm T X heeft sulcken reden tot de cortste Т S, ghelijck 2 tot 1 door t'ghegheven: Maer ghelijck 4 tot 2, аlsoo 2 tot 1, ghelijck dan de swaerste swaerheyt L M D A, tot de lichtste L M C B, аlso den langsten erm T Х, tot den cortsten T S.

Maer op datmen niet en dencke dit daer alfo by gheualle ghesciedt te sijne, wy sullender ^* Wisconstich bewys afdoen aldus:

+ Datum.

* Plana parallela.

+ Demonstratio.

* Mathematicam demonstrationem.

IIe Voorbeelt

Tghegheven. Laet A B C D wederom een pilaer sijn, ghedeelt

[p. 12]

met een plat euewijdich van A D, als E F, sniende den as G H, waert sy in I, ende het swaerheyts middelpunt van het deel E F D A sy K, int middel van G I, ende van het deel E F C B, sy L int middel van I H, ende des heels A B C D sy M int middel van G H, ende M N sal der deelen E F D A ende E F C B handthaef sijn, daer an sy euestaltwichtich hanghen.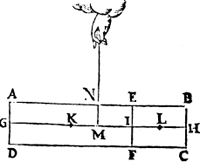

⁺Tbegheerde. Wy moeten bewysen dat ghelijck het lichaem ofte de swaerheydt (twelck hier een selfde is om ^* haer eueredenheydt, want ghelijck tlichaem E F D A, tot tlichaem E F C B, alsoo diens swaerheydt tot desens, ouermidts den pilaer door tghestelde oueral eenuaerdiger swaerheydt is) van E F D A, tot E F C B, also den langsten erm M L, tot den cortsten M K. Tbewys, I^e Lidt. M H is euen an M G door tghegheven, laet tot elck doen K M, soo sal dan K H euen sijn an M G met K M; daer naer van d'eene ghetrocken G K, ende van d'ander K I (welcke G K ende K I euen sijn door tghegheven) soo sal K M met K M euven blijven an I H; Ende haer helften als K M ende I L sullen oock euen sijn. II^e Lidt. Laet tot elck (te weten K M ende I L) doen M I, Ende M L sal euen sijn an I K. III^e Lidt. Ghelijck G I tot haer helft K I, also I H tot haer helft I L, ende door ^* oueranderde eueredenheyt ghelijck G I tot I H, also K I tot I L, maer K I is euen an M L door het 2^e lidt, ende I L an M K door het 1^e lidt, daerom ghelijck G I tot I H, alsoo M L tot M K; Maer ghelijck G I tot I H, also het lichaem ofte de swaerheyt E F D A, tot E F C B. Ghelijck dan de swaertste swaerheyt E F D A, tot de lichtste E F C B, also den langsten erm M L, tot den cortsten M K.

NV mocht yemant segghen, ghy hebt dat voorstel wel bewesen in deelen die tsamen een heel pilaer maken eenvaerdigher swaerheyt, maer wie weet of dat also plaets sal houden in allen anderen verscheyden deelen van ongeschicter form, ende oneueswaerder stof, daerom sullen wy de ghemeenheydt des voorstels aldus bethoonen: Laet ons achten dat den balck K L der 1^e ghestalt hier boven, in haer plaets blijue, ende dat het stick E F D A neerghetrocken wordt, ende dat het blijue hangende met een lini uyt sijn swaerheyts middelpunt an tpunt K, ende dat insghelijcx oock neerghetrocken sy het ander stick E F C B, ende dat het blijue hanghende by sijn swaerheydts middelpunt an

+ 1. Ghestalt.

* Proportionen.

* Alternam proportionem

[p. 13]

tpunt L, ende dat E F C B niet ⁺ en ghenake an E F D A, ende haer ghestalt sy dan soo dees form uytwijst. Nu doen het lichaem in d'eerste ghestalt hinck ande hanthaef M N, alsdoen was E F D A euestaltwichtich met E F C B; Maer t'ghewicht E F DA in dees tweede ghestalt neerghetrocken synde, en brengt an K L gheen meerder noch minder swaerheyt dan in d'eerste ghestalt door de 3^e begheerte.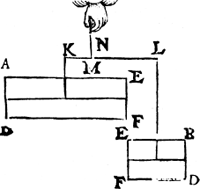

Sghelijcx en brengt tghewicht E F C B der tweede ghestalt, an L K gheen meerder swaerheyt dan in d'eerste ghestalt, daerom de ghewichten der tweede ghestalt sijn an K L de selfde die sy in d'eerste waren, daerom oock de balck K L blijft noch inde selue eerste ghestalt, waer duer E F D A noch euestaltwichtich blijft met E F C B. De sticken dan des pilaers blijven soo wel euestaltwichtich verscheyden, als doen sy an malcanderen waren, ende de ermen oock inde selve reden.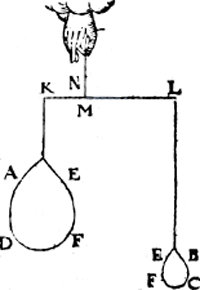

Dit so synde, laet ons de lichamen E F D A ende E F C B der tweede ghestalt ander formen gheven,⁺ die alsoo duwende (neemt dat de stof sy van was, cleye, ofte yet soodanich t'welck sulcx lijde) dat E F D A der tweede ghestalt, sy E F D A deser derde ghestalt, ende dat E F C B der tweede ghestalt, sy E F C B deser derde ghestalt; Ende is openbaer dat K L noch in haer selue ghestalt sal blyuen, ende de ermen M L, M K, inde selue reden, ende veruolgens E F D A noch euestaltwichtich met E F C B, want dees verandering der form (al de stofbliuende) en veroirsaect gheen verandering des ghewichts.

Laet ons ten laetsten weeren E F D A der derde ghestalt ende hanghen in diens plaets een lichaem van loot des selfden ghewichts, ende inde plaets van E F C B een hauten lichaem des seluen ghe-

+ 2. Ghestalt.

+ 3 Ghestalt.

[p. 14]

wichts, wiens vierde ghestalt alsdan sy ⁺ als hier nevens. Ende is kennelick dat K L noch inde selue gestalt sal blijven, ende vervolgens E F D A noch euestaltwichtich met E F C B, ende de ermen noch inde selue reden.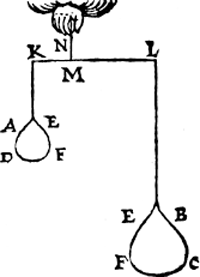

+ 4 Ghestalt.

III. Voorbeelt.

Men can tvoorgaende oock bethoonen, blyuende de twee swaerheden hanghende an eenen lichamelicken balck, in deser voughen: Laet den pilaer A B C D ghesneen sijn in twee deelen, met een plat door den as E F, ende den as des ondersten deels E C sy G H, ende E C sy doorsneen met een plat I K euewijdich vanden gront E D, sniende den as G H in L, ende het swaerheydts middelpunt van het deel I K D E sy M int middel van G L, ende van het deel I K C F sy N int middel van L H, ende des heels A B C D sy O in middel van E F, ende O P sy swaerheydts middellini des heels A B C D, ende M Q van I K D E, ende N R van I K C F. Dit soo sijnde tis kennelick dat des heels pilaers rechter sijde, euewichtich is teghen haer slincker.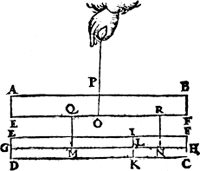

Laet ons nu het onderste deel E F C D neertrecken, also dat het blyue hanghende ande linien M L ende N R, als hier neuens. Ende is openbaer dat den lichamelicken balc A B F E noch in haer eerste ghestalt sal blijven. Laet ons nu achten dat het deel I K D E, ghesneen sy van I K C F, ende dat elck deel vallen mach daert wil, maer sy hanghen an haer swaerheyts

[p. 15]

middelpunten M, N, sy houden dan haer eerste ghegheuen ghestalt door de 4^e bepaling, daerom A B F E blijft oock noch in sijn eerste gedaente. Maer I K D E, sulcken reden te hebben tot I K C F, als den erm O R, tot den erm O Q, is vooren beprouft; Inder voughen dat tghene eerst betoocht was anden weegconstighen balck (dat is een lini) sulcx hebben wy hier verclaert an een lichamelicken. Tbeslvyt. We-⁺sende dan twee euestaltwichtige swaerheden, de swaerste heeft sulcken reden tot de lichtste (van wat stof ofte form oock de lichamen sijn) als den langsten erm tot den cortsten, twelck wy bewysen moesten.

+ Conclusio.

Vervolg

Vyt het verkeerde des voorgaenden voorstels volght, dat hebbende de swaerste swaerheydt sulcken reden tot de lichtste, als den langsten erm tot den cortsten, dat die twee swaerheden euestaltwichtich sijn.

I. Eysch.       II. Voorstel.⁺

Wesende ghegheven bekende swaerheden, haer hanthaef te vinden.

+ Problema.

Ie Voorbeelt.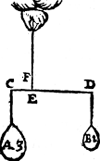

Tghegheven. Laet d'een swaerheyt A sijn weghende 3 ℔, hanghende an C, d'ander B van 1 ℔ hanghende an D, ende C D sy balck.

Tbegheerde Wy moeten haer hanthaef vinden. Twerck. Men sal C D also deelen, dat haer meeste stick naest de swaerheydts middellini van de minste swaerheydt, sulcken reden hebbe tot het minste stick, ghelijck de meeste swaerheyt tot de minste, twelck sy in E, te weten dat E D sulcken reden hebbe tot E C, als 3 ℔ van A, tot 1 ℔ van B. Ick seg dat de hangende door E, als E F, d'hanthaef is.

II Voorbeelt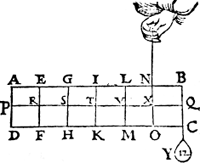

Tghegheven. Laet d'een swaerheydt sijn den pilaer A B C D weghende 6 ℔, ghedeelt als den pilaer int beghin des eersten voorstels; Ende an Q hanghe een ghewicht Y van 12 ℔. Tbegheerde. Wy moeten d'handthaef vinden. Twerck. De swaerheydts middellini des pilaers is I T, ende van tgewicht Y is B Q, ende T Q is balck,

[p. 16]

de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 12 ℔ van Y, tot 6 ℔ vanden pilaer, weluerstaende tcortste stick naer de swaerheydts middellini vande swaerste swaerheydt Y, twelck vallen sal in X, inder voughen dat N X de begheerde hanthaef is.

III. Voorbeelt.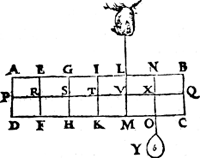

Tghegheven. Laet A B C D wederom den pilaer sijn, gedeelt als vooren, hanghende nu Y 6 ℔ an X. Tbegheerde. Wy moeten d'handthaef vinden. Twerck. De swaerheydts middellini des pilaers is I T, ende van Y is N X, ende T X is balck: de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 6 ℔ van Y, tot 6 ℔ des pilaers, twelck vallen sal in V, indervoughen dat V L de begheerde handthaef sijn sal.

Tvoornoemde werck op een ander manier.

D E swaerheydts middellini van M L B C Y, is N X, ende van M L A D is S G, ende S X is balck, de selue salmen in tween deelen, also dat de stucken de reden hebben als 8 ℔ van M L B C Y, tot 4 ℔ van M L A D: welverstaende tcortste stick naer de swaerheyts middellini van tswaerste deel, twelck vallen sal in V, inder voughen dat V L wederom de begheerde handhaef sijn sal als vooren.

IIII. Voorbeelt.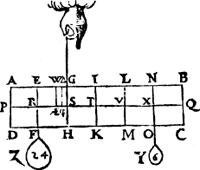

Tghegheven. Laet A B C D wederom den pilaer sijn, ghedeelt als vooren, hanghende Y 6 ℔ an X, ende Z 24 ℔ an R. Tbegheerde. Wymoeten d'hanthaef vinden. Twerck. De

[p. 17]

swaerheydts middellini van A B C D Y, is L V door het 3^e voorbeelt, ende van Z is R E, daerom is R V balck; de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 12 ℔ van A B C D Y, tot 24 ℔ van Z: welverstaende tcortste stic naer de swaerheyts middellini van tswaerste deel, twelck vallen sal in S, inder voughen dat S G de begheerde handthaef sijn sal.

Tvoornoemde werck op een ander manier.

DE swaerheydts middellini van A B C D Z is AE W door het 3^e voorbeelt, alsoo dat S AE doet ⅖ van S R, ende de swaerheydts middellini van Y is X N, ende AE X is balck, de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 30 ℔ van A B C D Z, tot 6 ℔ van Y: welverstaende tcortste stick naer de swaerheydts middellini van tswaerste deel, twelck vallen sal in S, inder voughen dat S G wederom de begheerde handthaef is als vooren.

Tvoornoemde werck op een ander manier.

DD swaerheydts middellini van Y Z, is (door het eerste voorbeelt) Φ Δ, alsoo dat S Φ doet ⅕ van S R, ende de swaerheyts middellini vande pilaer T I, ende T Φ is balck: de selue salmen in tween deelen, also dat de sticken de reden hebben als 30 ℔ van Y met Z, tot 6 ℔ vande pilaer, te weten tcortste stick naer de swaerheydts middellini van tswaerste deel, twelck vallen sal in S, inder voughen dat S G wederom de begheerde handthaef is als vooren.

Ve Voorbeelt.

Tghegheven. Laet A B C D wederom den pilaer sijn ghedeelt als vooren, hanghende Y 6 ℔ an X, ende Z 24 ℔ an R, ende AE 12 ℔ an Q. Tbegheerde. Wy moeten d'handthaef vinden. Twerck. De swaerheydts middellini van A B C D Y Z is S G door het 4^e voorbeelt, ende van AE is Q B, ende S Q is balck:de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 36 ℔ vanden pilaer met Y

[p. 18]

ende Z, tot 12 ℔ van AE, te weten tcortste stick naer de swaerheydts middellini van tswaerste deel, twelck vallen sal in T, inder voughen dat T I de begheerde handthaef sal sijn.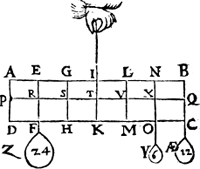

Ende soomen noch hinghe an P 24 ℔, d'handthaef soude S G sijn, ende so voorts met allen anderen swaerheden diemen anden pilaer soude meughen hanghen. Tbewys. De swaerste swaerheydt A int eerste voorbeelt, heeft sulcken reden tot de lichtste B, als den langsten erm E D, tot den cortsten E C, daerom E F door de 9^e bepaling is d'hanthaef. Sghelijcx sal oock tbewijs sijn van al dander voorbeelden, twelck wy om de cortheyt achterlaten.

Tbeslvyt. Wesende dan ghegheven bekende swaerheden, wy hebben haer handthaef gheuonden naer den eysch.

Merckt.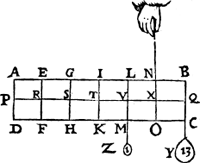

Soomen tghewicht Y des 2^en voorbeelts verswaerde van 1 ℔, ende datmen an V hinge 1 ℔, inder vougen dat haer ghestalt dan waer als hier onder, Tis kennelick uyt het voorgaende dat X N noch handthaef blijft, ende alles an haer euest altwichtich hangt. Tselve sal X N oock blijven, soomen Z 1 ℔ hangt an T, ende dat Y doe 14 ℔, ofte Z 1 ℔ an S, ende dat Y doe 15 ℔, ofte Z 1 ℔ an R, ende dat Y doe 16 ℔, ofte Z 1 ℔ an P, ende dat Y doe 17 ℔, ende soo oirdentlick voort by aldien den pilaer langher waer; te weten, verswarende Y altijt van 1 ℔, voor elcke langde als X V, daermen Z voorder an verschuyft. Waer uyt de ^* Ghedaenten des Onsels bekent sijn, als inde Weeghdaet breeder daer af sal ghehandelt worden.

* Qualitates.

II. Eysch.       III. Voorstel

Wesende ghegeven twee euestaltwichtighe swaerheden, d'een bekent dander onbekent, ende d'hanthaef: Die onbekende bekent te maken.

[p. 19]

I. Voorbeelt.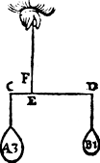

Tghegheven. Laet A ende B twee euestaltwichtighe swaerheden sijn, welcker A hanghende an C weeght 3 ℔, maer B hangende an D is onbekent, ende E F sy d'handthaef.Tbegheerde. Wy moeten tghewicht van B bekent maken. Twerck. Men sal ondersoecken wat reden den erm E D heeft, tot den erm E C, wort beuonden, neem ick, als van 3 tot 1, daer om segh ick, E D 3, gheeft E C 1, wat A 3 ℔? comt voor B 1 ℔.

II. Voorbeelt.

Tghegheven. Laet inde form des 2^en voorbeelts van het 2^e voorstel den pilaer A B C D voor d'een swaerheyt weghen 6 ℔, ende dander onbekende swaerheyt sy tghewicht daer an hanghende Y, ende d'hanthaef sy X N. Tbegheerde. Wy moeten tghewicht van Y bekent maken. Twerck. Anghesien T I swaerheyds middellini is des pilaers, ende Q B, van Y, soo sal T Q balck sijn, diens cortsten erm X Q, ende langsten X T; Daerom salmen ondersoucken wat reden den erm X Q, heeft tot X T, wort beuonden neem ick, als van 1 tot 2. Ick seg dan, X Q 1, geeft X T 2, wat den pilaer 6 ℔? comt voor Y 12 ℔. Der ghelijcke voorbeelden mochten wy hier stellen op dander formen der voorbeelden des 2^en voorstels, ten waer die door de voorgaende kennelick ghenouch sijn. Tbewys. Laet B int eerste voorbeelt, soot meughelick waer, swaerder sijn dan 1 ℔, de swaerste swaerheydt dan en sal niet sulcken reden hebben tot de lichtste, als den langsten erm tot den cortsten; twelck teghen het 1^e voorstel is; B dan en is niet swaerder dan 1 ℔. Sghelijcx salmen oock bethoonen dat sy niet lichter en is, sy weeght dan effen 1 ℔, twelck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven twee euestaltwichtige swaerheden, d'een bekent dander onbekent, ende d'hanthaef: Wy hebben die onbekende bekent ghemaect, naer den eysch.

III. Eysch.       IIII. Voorstel.

Wesende ghegeuen twee bekende euestaltwichtighe swaerheden met de langde van d'eenen erm: de langde des anderen erms te vinden.

Tghegheven. Laet A ende B twee euestaltwichtighe swaerheden sijn, welcker A hanghende an C weeght 3 ℔, ende B hanghende an D 1 ℔, ende de langde des erms D E sy 6 voeten. Tbegheerde.

[p. 20]

Wy moeten de langde des anderen erms vinden. Twerck. Men sal segghen A 3 ℔, gheeft B 1 ℔, wat D E 6 voeten? comt voor E C 2 voeten. Ende der ghelijcke voorbeelden mochten wy stellen op de formen der voorbeelden des 2^e voorstels, ten waer die door tvoorgaende kennelick ghenouch sijn.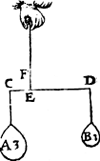

Tbewys. Laet E C, soot meughelick waer, langher sijn dan 2 voeten; den langsten erm sal dan minder reden hebben tot den cortsten, dan de swaerste swaerheyt tot de lichtste, twelck tegen het eerste voorstel is, E C dan en is niet langher dan 2 voeten; Sghelijcx salmense oock bewysen niet corter te sijn, sy is dan effen van twee voeten, twelck wy bewijsen moesten.

Tbesluyt. Wesende dan ghegheven twee euestaltwichtighe swaerheden met de langde van d'eenen erm, wy hebben de langde des anderen erms ghevonden, naer den eysch.

IIII. Eysch.       V. Voorstel.

Wesende ghegheven een pilaer: te vinden een gewicht in ghestelde reden tot des pilaers ghevvicht.

Tghegheven. Laet A B C D een pilaer wesen, diens as E F, ende haer ^* middelpunt G, ende de ghestelde reden sy van 2 tot 3.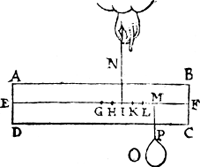

Tbegheerde. Wy moeten een ghewicht vinden in sulcken reden tot den pilaer, als van 2 tot 3, dat is euen an sijn ⅔. Merckt. Ghelijck de ^* Meetconstighe ende Telconstighe voorstellen verscheyden werckinghen hebben, alsoo oock de Weegconst, want men soude vanden pilaer een stuck connen snien in sulcken reden tot den heelen pilaer, als van 2 tot 3, Oft andersins om den pilaer heel te laten, men mocht hem teghen ander stof weghen, daer af nemende de ⅔, maer wy willent Weegconstlicker doen in deser voughen. Twerck. Men sal van tmiddelpunt G af, naer F, teeckenen eenighe vijf punten (te weten 5 voor de somme der

* Centrum.

* Geometricae & Arithmeticae propositiones.

[p. 21]

ghegheuen palen 2. 3) als H, I, K, L, M, van malcanderen euewijt; Ende van het tweede punt I (van het tweede om dat 2 het ander der ghegeuen ghetalen is) salmen den pilaer ophanghen byde swaerheyts, middellini I N; Daer naer salmen an tvijfde punt M een ghewicht hanghen als O, euen so swaer dat alles in euestaltwichticheyt sy, twelck soo wesende, ick seg dat tghewicht van O, in sulcken reden is tot tghewicht des pilaers, als 2 tot 3, ofte dat O euen is ande ⅔ des pilaers.

Tbewys. G is ^* swaerheydts middelpunt des pilaers A B C D, ende M P swaerheyts middellini van O, daerom ghelijck den erm I G tot den erm I M, alsoo O tot den pilaer door het 1^e voorstel, maer I G heeft sulcken reden tot I M, als 2 tot 3, daerom O heeft sulcken reden tot den pilaer, als 2 tot 3, twelck wy bewysen moesten, Tbeslvyt. Wesende dan ghegheuen een pilaer, wy hebben gheuonden een ghewicht in ghestelde reden tot des pilaers ghewicht, naer den eysch. Merckt. Wy souden oock meughen voorbeelden stellen met Redenen van ^* onmetelicke palen, maer sulcx is openbaer ghenouch door tvoorgaende, metsgaders tghene wy vande onmetelicke grootheden elders gheschreuen hebben.

* Centrum gravitatis.

* Incommensurabilium terminorum.

II Vertooch.       VI Voorstel.

Wesende een hanghende pilaer ghesneen door sijn swaerheydts middelpunt, met een plat euewijdich van den gront, ende wesende tvastpunt in dat plat bouen het swaerheyts middelpunt: Den as des pilaers blijft euewijdich vanden ^* sichteinder.

Tghegheven. Laet A B C D een pilaer sijn, ghesneen door sijn swaerheydts middelpunt met een plat F G, euewijdich vanden grondt A D, ende laet H vastpunt inde swaerheydts middellini I G wesen, bouen het swaerheyts middelpunt E, ende K L sy as, ende M N sichteinder.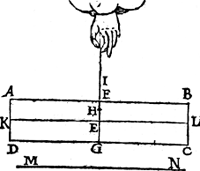

Tbegheerde. Wy moeten bewysen dat den as K L euewijdich blijft vanden sichteinder M N.

Tbewys. Laet K L soot meughelick waer, oneuewijdich sijn vanden sichteinder M N, als in

* Horizon.

[p. 22]

dees tweede form, ende laet I H voortghetrocken worden tot in O, sniende A B in P, ende laet het stuck des pilaers P O C B alsoo euewichtich blijuen hanghen teghen P O D A, maer dat is grooter ende swaerder dan dit (want F G D A, is euen an F G C B, ende minder is den driehouck F H I ghesneen van F G C B, dan de driehouck O H G gesneen van F G D A, daerom, &c.) het swaerder dan sal euewichtich sijn an een lichter t'welck ongeschickt is, K L dan blijft euewijdich vanden sichteinder M N, als in d'eerste form.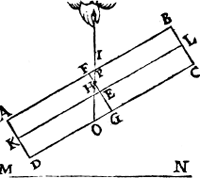

Tis oock te anmercken als voor ghemeenen Weegconstighen Reghel, dat

Alle swaerheyts middelpunt eens hangenden lichaems is in siin swaerheydts middellini.

Maer tswaerheydts middelpunt hier bouen E en is inde tweede form niet in sijn swaerheydts middellini I O, tis dan een onmeughelicke ghestalt. Tbeslvyt. Wesende dan een pilaer ghesneen, &c.

III Vertooch.       VII Voorstel.

Wesende tvastpunt het swaerheydts middelpunt des hanghenden pilaers, hy houdt alle ghestalt diemen hem gheeft.

Tghegheven. Laet A B C D een pilaer wesen, diens swaerheydts middelpunt E vast sy, daer by hanghende ande lini E F, ende den as G H sy euewijdich vanden sichteinder I K.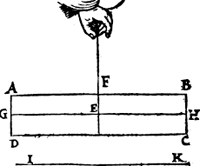

Tbegheerde. Wy moeten bewysen dat den pilaer A B C D alle ghestalt houdt diemen hem gheeft.

Tbewys. Laet ons den ghegheuen pilaer (tpunt E vast blijuende) een ander ghestalt gheuen dan d'eerste, als in dees tweede form,

[p. 23]

ende laet F E voortghetrocken worden tot in L, sniende A B in M, ende en laet den pilaer soot meughelick waer niet in die ghestalt blijuen, dan het stick M L D A, ofte M L C B neervallen; Maer dees twee deelen sijn ghelijck euegroot, ende daerom oock eueswaer, het eene dan van euewichtighe sal swaerder sijn dan t'ander, twelc ongeschickt is: Den pilaer dan blijft in die ghestalt, ende sgelijcx in allen anderen diemen hem soude meughen gheven.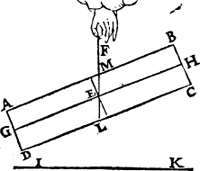

Tbeslvyt. Wesende dan tvastpunt het swaerheydts middelpunt des pilaers, hy houdt alle ghestalt diemen hem gheeft, twelck wy bewysen moesten.

IIII Vertooch.       VIII Voorstel.

Wesende den pilaer ghesneen door sijn svvaerheyts middelpunt, met een plat euewydich vanden gront, ende wesende tvastpunt in dat plat beneden het swaerheydts middelpunt: Den pilaer (natuerlick verstaen) keert om tot dat sijn swaerheydts middelpunt is in sijn swaerheydts middellini.

Tghegheven. Laet A B C D een pilaer wesen, ghesneen door sijn swaerheyts middelpunt E, met een ^* plat F G euewydich vanden grondt A D, ende laet G vastpunt sijn, beneden tswaerheydts middelpunt E, met welck punt G den pilaer ligt ofte rust op tpunt des pins H, ende I K sy as, euewydich vanden ^* sichteinder L M.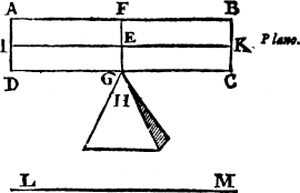

Tbegheerde. Wy moeten bewysen dat den pilaer omkeeren sal, tot dat sijn swaerheydts middelpunt is in sijn swaerheyts middellini.

* Plano.

* Horizonte.

[p. 24]

maer dit natuerlick verstaen, want ^* Wisconstelick ghenomen soo can sy daer op rusten.

* Mathematice.

Tbewys.

A.	Al dat ligt moet grondt hebben daert opt rust,
E.	Dees pilaer en heeft gheen grondt daer hy op rust,
E.	Dees pilaer dan en can soo niet ligghen.

Des ^* Bewijsredens tweede voorstel is daer uyt openbaer, dat het punt gheen grootheyt en is, ende veruolghens gheen grondt: wel is waer dat wy dickmael nemen door tghestelde een lichaem alsoo te rusten, maer metter daet en connen wy dat niet te weeg brenghen. Inder voughen dat hoewel den as I K euewydich ghestelt is vanden sichteinder L M, soo sal nochtans den pilaer (tpunt G vast blyuende) omkeeren ouer die sijde daer hy eerst begint. Maer dat hy so lang keeren sal tot dat sijn swaerheydts middelpunt inde swaerheydts middellini is, is door het 6^e voorstel openbaer. Tbeslvyt. Wesende dan den pilaer ghesneen, &c.

* Syllogismi

Ie Merck.

Yemant mocht hier noch de verclaring begheeren des verschils tusschen hanghen en ligghen, waer op d'antwoort is dat wy een lichaem voor hanghende houden, als siin swaerheyts middelpunt is onder, oft in tghenaecksel daert opt rust; Maer tswaerheyts middelpunt daer bouen siinde, alsdan houden wijt voor ligghen, staen, oft sitten; Ligghen, als de langste siide des lichaems haer streckt langs den sichteinder: Staen, als sy daer op rechthoukich is; daerom ist oock dat wy den teerlinck (ouermidts siin siiden al euen lanck siin) soo eyghentlick segghen te staen als te ligghen, ende te liggen als te staen. Sitten is wat tusschen ligghen en staen.

IIe Merck.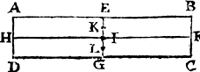

Soo yemant thinhout der voorgaende drie voorstellen door eenighe ervaring wilde sien, hy mocht nemen een reghel van houdt ofte ander stof eenvaerdigher dickte ende swaerheyt, als A B C D, teeckenende de punten E, F, G, H, inde middelen der linien A B, B C, C D, D A, treckende E G, ende H F, malcander sniende in I, maeckende daer naer een seer cleen gaetken an I, ende daer boven een gaetken als K, ende onder I een gaetken als L. Ende stekende een naelde door tgatken K, die vrielick daer in drayen mach, d'eruaringh sal bethoonen dat H F altijt euewydich sal blijven vanden sichteinder. Maer de naelde in I stekende, de reghel sal daerop alle ghestalt houden diemen haer gheeft. Ende de naelde in L ghesteken, alles sal omkeeren ouer

[p. 25]

die syde daert eerst beghint, tot dat I is in haer swaerheyts middellini, waer af d'oirsaeck inde voornoemde 6^e, 7^e, 8^e, voorstellen ^* Wisconstlick blijckt.

* Mathematicè.

V. Vertooch.       IX. Voorstel.

D'hanthaef oneindelick voortghetrocken, deelt alle balcken tweer swaerheden in haer ermen.

Tghegheven. Laet A B twee swaerheden sijn ende haer middellinien C D, E F, ende haer balck C E, ende d'hanthaef G H, inder voughen dat C G is tot G E, als de swaerheydt B tot A, Laet I K noch een balck wesen, oneuewydich van C E, ende laet G H oneindelick voortghetrocken worden naer L, sniende den balck I K in M.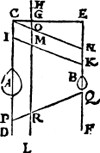

Tbegheerde. Wy moeten bewysen dat I M, ende M K, oock de ermen sijn der swaerheden A B; dat is ghelijck B tot A, alsoo M I tot M K. Tbereytsel. Laet ghetrocken ⁺ worden C N, euewydich van I K, sniende H L in O.Tbewys. Ghelijck C G tot G E, also C O tot O N, Maer C O is euen an I M, ende O N an M K, daerom ghelijck C G tot G E, alsoo I M tot M K, maer ghelijck B tot A, also C G tot G E, door tghegheuen, daerom ghelijck B tot A, also M I tot M K, tselfde sal also bewesen worden van allen balcken tusschen C D ende E F, als P Q, doorsneen in R, ende allen anderen diemen soude meughen trecken.

Tbeslvyt. D'hanthaef dan oneindelick voortghetrocken, deelt alle balcken tweer swaerheden in haer ermen, twelck wy bewysen moesten.

+ 2. v. 6. B. E. 34. v.1 B. E.

I. Vervolgh.

Hier uyt blijct datmen om te vinden de swaerheydts middellini tweer swaerheden, niet nootsaeckelick en moet nemen een ^* euewydige vanden ^* sichteinder, maer alsulcke alsmen wil, ende als best te pas comt.

* Parallela

* Horizonte.

II Vervolgh.

Anghesien alle swaerheydts middelpunt inde hanghende swaerheyts middellini is, soo volght dat alle rechte lini begrepen tusschen twee swaerheydts middelpunten, oock dier swaerheden balck is, ende het onderscheydt der ermen diens balcx, oock het swaerheydts middelpunt te wesen der twee swaerheden.

[p. 26]

5. Eysch.       10. Voorstel.

Wesende ghegeuen een vastpunt des bekenden pilaers, ende bekende euestaltwichtige swaerheden an hem hanghende: Te vinden of den as euewydich sal blijven vanden ^* sichteinder, ofte alle ghestalt houden diemen hem gheeft, ofte omkeeren tot dat sijn swaerheydts middelpunt is in sijn swaerheyts middellini.

Tghegheven. Laet A B C D een pilaer sijn weghende 4 ℔, ende ghesneen door sijn swaerheydts middelpunt E, met een plat F G euewydich vanden grondt A D, ende laet H vastpunt wesen beneden tmiddelpunt E int middel van E G; Ende anden pilaer twee ghewichten hanghen als I, K, elck wegende 4 ℔, welcker middellinien vastpunten sijn D, C, ende laet L M den as, ende N O sichteinder wesen.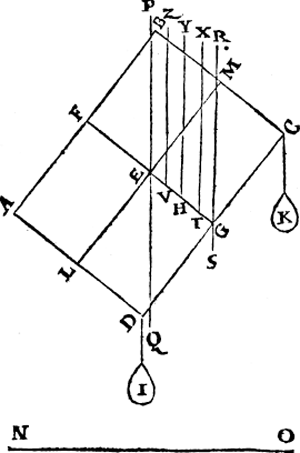

Tbegheerde. Wy moeten vinden of den as L M euewydich sal connen blijven vanden sichteinder N O; ofte alle ghestalt houden diemen haer gheeft; Ofte ommekeeren tot dat haer swaerheydts middelpunt E is inde swaerheyts middellini door H, welcke verscheydenheden vallen connen naer de reden der swaerheyt des pilaers, tot de ghewichten dieder anhanghen.

Twerck. Men sal trecken door E de hanghende swaerheyts middellini P Q des pylaers, daer naer door

* Horizonte.

[p. 27]

G de swaerheyts middellini R S der ghewichten I, K, ende E G sal balck sijn, daer naer salmen sien door het 2^e voorstel waer tvastpunt der hanthaef valt: want commet onder H, soo keert L M tot sy euewydich blijft vanden sichteinder N O; Maer commet in H, sy houdt alle ghestalt die men haer gheeft; Commet bouen H, alles keert om. Maer den pilaer weeght 4 ℔, ende I, K, elck 4 ℔ tsamen 8 ℔ door tghegheuen, daerom ghedeelt E G in T, alsoo dat E T, sulcken reden heb tot T G, als 8 tot 4: Ick seg dat L M keeren sal (ouermidts T onder H comt) tot sy euewydich is vanden sichteinder. Laet nu den pilaer weghen 4 ℔, ende I en K elck 2 ℔, tsamen 4 ℔, daerom ghedeelt E G in H (welcke H tmiddel van E G is door tghegheuen) alsoo dat E H sulcken reden heb tot H G, als 4 tot 4: Ick seg dat L M (ouermits het in H viel) alle ghestalt sal houden diemen haer gheeft. Laet nu den pilaer weghen 4 ℔, ende I, K, elck 1 ℔, tsamen 2 ℔, daerom ghedeelt E G in V, also dat E V sulcken reden hebbe tot V G, als 2 tot 4, Ick seg dat den pilaer met al de rest omkeeren sal (ouermitds V boven H comt) tot dat H is in haer swaerheydts middellini. Tbewys. Ten eersten I en K elck 4 ℔ weghende, dat dan L M keert tot sy euewydich is vanden sichteinder, blijct aldus: De hanghende door T ghelijck T X, is swaerheyts middellini des heels, daerom die latende, ende hanghende tgheheel ande ^* hanghende door H, als H Y (welcke H ons ghegheuen vastpunt is) so sal de sijde naer B C K, swaerder sijn dan naer A D I, daerom oock sal de sijde B C K neerdalen, tot dat H inde swaerheydts middellini is des heels, ende dan sal L M euenwydich sijn vanden sichteinder N O.

Ten tweeden I, K, elck 2 ℔ weghende, dat dan L M alle ghestalt houdt, wort aldus bethoont: Laet ons achten dat I ende K opgeschorst sijn, alsoo dat D tswaerheydts middelpunt sy van I, ende C van K, ende door de 3^e begheerte sy en sullen anden pilaer gheen oirsaeck van verandering der swaerheydt wesen; Twelck soo sijnde, H is tswaerheyts middelpunt van soodanighen lichaem vergaert uyt den pilaer ende de twee ghewichten I K, ende door de 4 bepaling tsal daer op alle ghestalt houden diemen hem gheeft, tselfde sal also bewesen worden in alle ghestalten daermen L M in soudc connen stellen.

Ten laetsten I, K, elck 1 ℔ weghende, dat dan alles omkeert, wort aldus bethoont: De hanghende door V ghelijck V Z, is swaerheyts middellini des heels, daerom die latende, ende hanghende tgheheel ande hanghende H Y door H ghegheuen vastpunt, so sal de sijde naer A D I, swaerder sijn dan naer B C K, daerom oock sal de sijde A D I neerdalen, tot dat H inde swaerheyts middellini is des heels, ende ofmen schoon L M (alles op tvastpunt H draeyende) euewydich stelde vanden sichteinder N O, sy en can so niet blyuen door het 8 voorstel, maer alles sal omkeeren, t'welck wy bewysen moesten.

* Perpendicularem.

[p. 28]

Tbeslvyt. Wesende dan ghegheuen een vastpunt des bekenden pilaers, &c.

Uyt het voorgaende is ghenouch blijckelick den ghemeenen voortganck in allen anderen, als van pilaren welcker vastpunt is buyten de lini als F G, ende der ghewichten vastpunten op ander plaetsen dan D C; Maer ouermits wy hier voornamelick trachten de oirsaecken vande ghedaenten des waeghs grondelick te openbaren (daer af inde Weeghdaet breeder sal gheseyt worden) so en geven wy van sulcke ongheschicte ghestaltheden gheen besonder voorbeelden.

6. Eysch.       II. Voorstel.

Wesende ghegheuen een bekende pilaer, ende bekende swaerheden daer an hanghende: Te vinden het vastpunt daer op hy alle ghestalt houdt diemen hem gheeft.

Ie Merck.

Soo tweer euewychten als A, B, vast punten C, D, waren in des pilaers as, euewyt van t'middelpunt E, als in dees form, tis kennelick door het tweede deel des bewys van het 10^e voorstel, dat E tbegheerde punt soude sijn, maer wy sullen tvoorbeelt van ongheschicter ghestalt gheuen.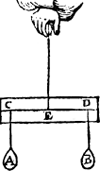

IIe Merck.

Tis openbaer dat wesende de twee vastpunten der ghewichten als C D, ende tvastpunt des hanthaefs als E, alle drie in een rechte lini als hier bouen, ende an C D euen ghewichten ghehanghen, soo groot ofte cleen alst valt: E sal altijt tvastpunt blijuen, daer sy alle ghestalt op houden diemen haer geeft. Maer soo die drie punten als C E D in een rechte lini wesende C ende D niet euewyt en waren van E, ende datmen an haer ghewichten hinghe ^* euerednich met de ermen, dat E noch altijt tvastpunt sal blijven daer sy alle ghestalt op houden diemen haer geeft.

Tghegheven. Laet A B C D een pilaer sijn weghende 10 ℔, diens swaerheydts middelpunt E, ende laet de ghewichten daer an hanghende wesen F 1 ℔, diens vastpunt G, ende H 4 ℔, wiens vastpunt I. Tbegheerde. Wy moeten het vastpunt vinden daerop sy alle ghestalt houden diemen haer gheeft. Twerck. Men sal

* Proportionales.

[p. 29]

trecken G I balck der gewichten F H, daer naer salmen vinden haer ermen door het 2^e voorstel, dat is ghelijck F 1 ℔, tot H 4 ℔, also den erm K I, tot K G, daer naer salmen trecken E K balck des pilaers ter eender, ende der ghewichten F H ter ander sijden, de selve E K ghedeelt in L, alsoo dat den erm E L sulcken reden hebbe tot L K, als 5 ℔ van F H, tot 10 ℔ des pilaers, L sal tbegheerde punt sijn op twelck sy alle ghestalt sullen houden diemen haer gheeft, waer af tbewijs openbaer is door het 7^e voorstel.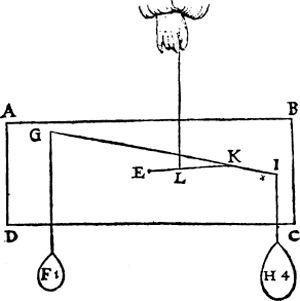

VII. Eysch.       XII. Voorstel.

Wesende ghegheuen een bekende pilaer, met sijn vastpunt ende bekende ghewichten daer an hanghende die den as euewydich houden vanden ^* sichteinder: Te vinden een ghewicht hanghende ter begheerder plaets des pilaers, dat den as in ghegheuen ghestalt houde.

* Horizonte.

I. Voorbeelt.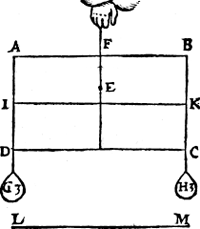

Tghegheven. Laet A B C D een pilaer sijn weghende 6 ℔, diens vastpunt E, ende hanthaef E F, ende twee ghewichten G, H, elck 3 ℔ weghende, welcker vastpunten C, D; ende I K, sy as, euewydich vanden sichteinder L M, ende D sy tpunt voor de begheer-

[p. 30]

de plaets. Daer naer wort den as I K (alles draeyende op E) verheuen als inde tweede form. Tbegheerde. Wy moeten een ghewicht an D vinden, dat den as I K in die gestalt houde. Twerck. Men sal vinden door het II^e voorstel, tvastpunt daer op den as alle ghestalt houde diemen haer gheeft twelck N sy: Daer naer salmen trecken D N, ende de ^* hanghende E O, sniende N D in O, daer naer salmen sien wat reden N O heeft tot O D, ick neme als van 1 tot 2, daerom hanghe ick an D een ghewicht P van 6 ℔, te weten in sulcken reden tot den pilaer met de twee ghewichten G, H, al tsamen 12 ℔, als van 1 tot 2; Ick seg P 6 ℔, te wesen het begheerde ghewicht.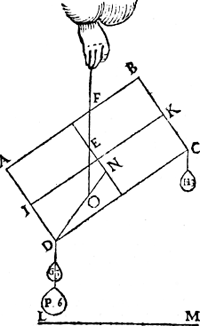

Tbewys. Tswaerste ghewicht 12 ℔ des erms O N, heeft sulcken reden tot het lichtste 6 ℔ des erms O D, ghelijck den langsten erm O D, tot den cortsten O N; Daerom hanghet al euestaltwichtich ande handthaef E F door het 1^e voorstel. Ende veruolghens den as I K blijft in haer ghegeuen ghestalt.

* Perpendicularem.

II. Voorbeelt.

Laet A B C D een pilaer sijn weghende 6 ℔, diens vastpunt E, ende hanthaef E F, ende G een ghewicht van 2 ℔, diens vastpunt H, ende I een gewicht van 1 ℔, diens vastpunt K, ende den as L M sy euewijdich vanden ^* sichteinder N O, ende P sy een punt inden pilaer voor de begheerde plaets. Daer naer werdt den as L N (alles draeyende op E) verheuen, als inde tweede form.

* Horizonte.

Tbegeerde.

Wy moeten een ghewicht an P vinden, dat den as L M in die ghestalt houde.

[p. 31]

Twerck.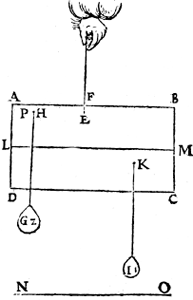

Men sal vinden door het II^e voorstel tvastpunt daerop tghegheuen alle gestalt houdt diemen hem gheeft, twelck Q sy, daer naer salmen trecken P Q, ende de ^* hanghende E R, sniende P Q in R: siende daer naer wat reden R Q heeft tot R P, ick neem als van 1 tot 2, so hang ick an P een gewicht S van 4½ ℔ te weten in sulcken reden tot den pilaer met de twee ghewichten G, I, al tsamen 9 ℔, als van 1 tot 2; Ick segh S 4½ ℔ te wesen het begheerde ghewicht.

* Perpendicularem.

Tbewys.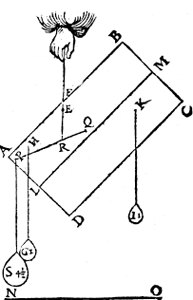

Tswaerste ghewicht 9 ℔ des erms R Q, heeft sulcken reden tot het lichtste gewicht 4½ ℔ des erms R P, gelijck den langsten erm R P, tot den cortsten R Q, daerom hanghet al euestaltwichtich ande handthaef E F door het 1^e voorstel, ende veruolghens den as L M blijft in haer ghegheuen ghestalt, twelck wy bewysen moesten.

Tbeslvyt.

Wesende dan ghegheuen een bekenden pilaer met sijn vastpunt, &c.

[p. 32]

VI. Vertooch.       XIII. Voorstel.

Een daelwicht ende een hefwicht an hem euen, doen met euen houcken an euen ermen even ghewelden.

1e Voorbeelt met rechtwichten.

Tghegheven. Laet A des balcx B C vastpunt, ende A B met A C twee euen ermen sijn, ende an B hanghe het rechtdaelwicht D, ende an C sy het rechthefwicht E, euewichtich an D, ende sijn balck sy F G, diens vastpunt H, ende euen ermen H F, H G, ende den houck A B I, sy euen anden houck A C F. Tbegheerde. Wy moeten bewysen dat het rechtdaelwicht D, ende trechthefwicht E, ande euen ermen A B, A C, euen ghewelden doen. Tbereytsel. Laet an C een ghewicht K hanghen, euen an D.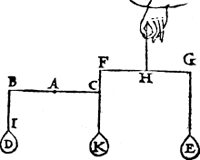

Tbewys. Laet ons weeren E, ende is blijckelijck dat de macht van D is de ermen A B, A C, in die ghegheuen ghestalt te houden, want D is euen an K, ende A B an A C. Laet nu D weeren, ende E wederom anhanghen, ende de macht van E is oock de ermen A B, A C, in die ghegheuen ghestalt te houden, want K is euen an E, ende H F an H G, daerom E ende D, doen an euen ermen A B, A C, euen ghewelden.

IIe Voorbeelt met scheefwichten.

Tghegheven. Laet A des handthaefs vastpunt, ende A B met A C twee euen ermen sijn, ende an B hanghe tscheefdaelwicht D, diens scheefdaellini B E, ende an C sy tscheefhefwicht F, euen an D, ende sijn scheefheflini sy C G, ende den houck A B E, sy euen anden houck A C G.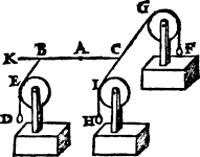

Tbegheerde. Wy moeten bewysen dat het scheefdaelwicht D, ende tscheefhefwicht F, ande euen ermen A B, A C, euen gewelden doen. Tbereytsel. Laet an C een scheefdaelwicht H

[p. 33]

hanghen euen an D, diens scheefheflini C I, ^* euewydich sy van B E, ende C B sy wat voortghetrocken tot in K. Tbewys. Laet ons weeren F, ende is kennelick dat de macht van D teghen H, is de ermen A B, A C, in die ghegheuen ghestalt te houden, want D is euen an H, ende den erm A B, an A C, ende den houck A C I, anden houck K B E. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen A B, A C, in die ghegheuen ghestalt te houden, ouermidts H euen is an F.

* Parallela.

III Voorbeelt.

Tghegheven. Laet A des handthaefs vastpunt, ende A B met A C twee euen ermen sijn, ende an B hanghe het scheefdaelwicht D, diens scheefdaellini B E, ende an C sy het scheefhefwicht F, euen an D, diens scheefheflini sy C G, ende den houck K C G, sy euen anden houck K B E. Tbegheerde. Wy moeten bewysen dat het scheefdaelwicht D, ende het scheefhefwicht F, ande euen ermen A B, A C, euen ghewelden doen. Tbereytsel. Laet an C een scheefdaelwicht H hanghen euen an D, diens scheefdaellini C I, also dat den houck A C I, euen sy anden houck A B E. Tbewys. Laet ons weeren F, ende is kennelick dat de macht van D is de ermen A B, A C, in die ghegheuen ghestalt te houden, want D is euen an H, ende den erm A B an A C, ende den houck A C I, anden houck A B E. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen A B, A C, in die ghegheuen ghestalt te houden, ouermits H euen is an F.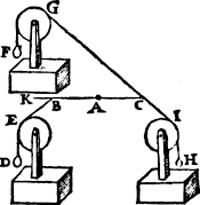

Tbeslvyt. Een daelwicht dan ende een hefwicht an hem euen, doen met euen houcken an euen ermen euen ghewelden, twelck wy bewysen moesten.

VIII. Eysch.       XIIII. Voorstel.

Wesende ghegheuen een pilaer, ende twee punten inden as, t'een vast t'ander int langste deel verroerlick: Te vinden een rechthefwicht an tverroerlick, dat den pilaer in sijn ghegheuen standt houde.

Tghegheven. Laet A B C D een pilaer sijn, weghende 6 ℔,

[p. 34]

ende die ghedeelt als int beghin des 1^e voorstels, ende vastpunt sy R, ende roerlick V, int langste deel des as R Q, want int cortste R P ist onmueghelick dat eenich rechthefwicht den as in haer ghegheven stant houde. Tbegheerde. Wy moeten een rechthefwicht an V vinden, dat den pilaer in die stant houde. Twerck. Men sal de lini Q R voorttrecken tot in Y, also dat R Y euen sy an R V: Daer naer salmen vinden tghewicht Z an Y, eustaltwichtich met den pilaer, tselve (gedenckende dat R vastpunt is) sal van 4 ℔ wesen door het 3^e voorstel; Ick seg daerom dat het begheerde rechthefwicht twelck AE sy, van 4 ℔ sal wesen.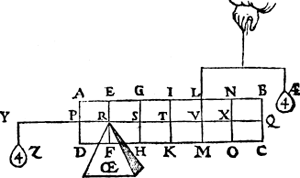

Tbewys. Ouermidts den erm R V des rechthefwichts AE, euen is anden erm R Y des ghewichts Z, ende AE euen an Z, soo is de ghewelt AE euen an de ghewelt van Z door het 13^e voorstel. Maer de ghewelt van Z is (AE gheweert sijnde) den pilaer in die standt te houden, die ghewelt dan van AE (Z gheweert sijnde) is oock den pilaer in die standt te houden, twelck wy bewysen moesten. Tbeslvyt. Wesende dan ghegheuen een pilaer, ende twee punten inden as, t'een vast, t'ander int langste deel verroerlick: Wy hebben gheuonden een rechthefwicht an tverroerlick, dat den pilaer in sijn ghegheuen standt houdt naer den eysch.

Merckt.

Men soude oock mueghen segghen metten cortsten V R 3, gheeft R T 2, wat den pilaer 6 ℔? comt voor AE 4. ℔ als vooren, waer af de reden int volghende 15 voorstel blijcken. sal.

1e Vervolch.

Anghesien den heelen pilaer door tghestelde 6 ℔ weeght, waer af AE de 4 ℔ verheft, so volght nootsaeckelick datter opt punt R, dat is op tsop des keghels OE, 2 ℔ rusten.

[p. 35]

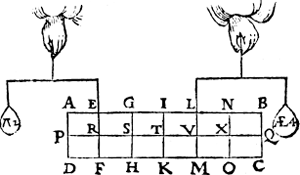Ofte soomen an R een rechthefwicht II voughde, inde plaets des keghels OE, als hier neuen, dat II sal weghen 2 ℔.

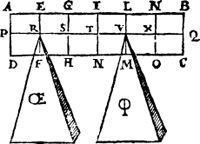Ofte somen an V een keghel Ф voughde, inde plaets des rechthefwichts AE, als hier neuen, dat op den keghel OE rusten sal 2 ℔, ende op den keghel Ф 4 ℔.

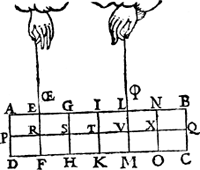Ofte soomen den pilaerophinghe an twee ^* euewidige linien OE R, ende Ф V, als hier neuen, dat ande lini OE R hanghen sal 2 ℔, ende ande lini Ф 4 ℔.

* Parallelas.

[p. 36]

II Vervolg.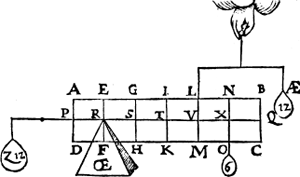

SO anden pilaer (tpunt R vast sijnde als vooren) eenich ghewicht ofte gewichten hinghen, trechthefwicht sal oock bekent worden. Laet by voorbeelt an X hanghen 6 ℔, soo sal Z moeten weghen 12 ℔ door het 3^e voorstel, ende vervolghens AE 12 ℔.

VII Vertooch.       XV Voorstel.

Wesende twee punten inden as des pilaers, t'een vast t'ander verroerlick: Trechthefwicht an tverroerlick met den pilaer euestaltwichtich, heeft sulcken reden tot den pilaer als het asstick tusschen het swaerheyts middelpunt des pilaers, ende het vastpunt, tot het asstick tusschen tvastpunt ende t'verroerlick punt.

Verclaring.

Laet ons nemen de formen des 14 voorstels, al waer blijct dat ghelijck AE 4 ℔, tot tghewicht des pilaers 6 ℔, alsoo T R tot R V. Maer om d'oirsaeck hier af ^* Wisconstelick te verclaren, soo is te weten dat ghelijck t'ghewicht Z, tottet ghewicht des pilaers, alsoo R T tot R Y door het 1^e voorstel; Maer AE is euen an Z, ende R V is even an R Y door tghegeuen, ghelijck dan AE tot den pilaer, alsoo T R tot R V. Tbeslvyt. Wesende dan twee punten inden as des pilaers t'een vast tander verroerlick, &c.

* Mathematicè.

VIII Vertooch.       XVI Voorstel.

Wesende twee punten inden as des pilaers t'een vast t'ander verroerlick: Trechthefwicht an tverroerlick dat den pilaer in een ghestalt houdt, sal hem in alle gestalten houden.

[p. 37]

Tghegheven. Laet ons den pilaer met sijn ghewichten des 14^e voorstels wat verkeeren op tvastpunt R, ende dat AE 4 ℔ noch sy rechthefwicht, alsoo dat dan alles van gestalt sy als hier neuen.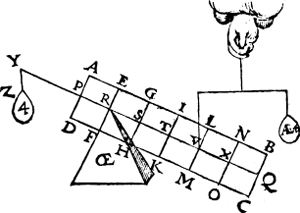

Tbegheerde. Wy moeten bewysen dattet rechthefwicht AE den pilaer oock in die ghegheuen ghestalt houdt.

Tbewys. Laet ons weeren AE ende anhanghen Z 4 ℔, ende door het 10^e voorstel den pilaer sal in die ghestalt bliuen: Maer AE doet by V soo grooten ghewelt anden pilaer als Z by Y door het 13^e voorstel, daerom gheweert Z, ende AE anghehangen, soo sal AE den pilaer oock in die ghestalt houden. Tbeslvyt. Wesende dan twee punten in den as des pilaers t'een vast tander verroerlick, trechthefwicht an tverroerlick, dat den pilaer in een ghestalt houdt, sal hem in alle ghestalten houden, twelck wy bewysen moesten.

IX Vertooch.        XVII Voorstel.

Rvstende een pilaer op twee punten in den as: Ghelijck het asstick tusschen t'swaerheyts middelpunt ende tslinckerpunt, tottet asstick tusschen tswaerheytds middelpunt ende trechterpunt, alsoo tghewicht des pilaers rustende op trechterpunt, tottet ghewicht rustende op tslinckerpunt.

Tghegheven. Laet A B C D een pilaer sijn wegende 6 ℔, ghedeelt als int 1^e voorstel, rustende met de twee punten R, V, op de punten van OE, AE. Tbegheerde. Wy moeten bewysen dat ghelijck het asstick T R, tottet asstick T V, also tghewicht rustende mettet punt V op tpunt van AE, tottet tghewicht rustende mettet tpunt R op tpunt van OE. Tbewys. T R is dobbel an T V door tghestelde,

[p. 38]

ende opt tpunt van AE rust 4 ℔, ende van OE 2 ℔ door 1^e veruolg des 14^en voorstels, maer 4 ℔ is tot 2 ℔ oock dobbel, ghelijck dan T R tot T V, alsoo tghewicht rustende op tpunt van AE, tot tghewicht rustende op tpunt van OE.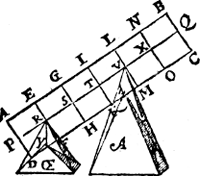

Maer om tghemeen nootsaeckelick veruolgh in allen te bewysen, laet ons voorttrecken V R tot in Z, also dat R Z euen sy an R V; aensiende daer naer R voor tvastpunt, so sal an Z moeten hanghen Π 4 ℔, om de pilaer in die ghestalt te houden door het 3^e voorstel. Maer tghene an V den pilaer in die ghestalt houdt als AE, doet daer an alsulcken ghewelt als Π, door het 13 voorstel; An AE dan rust een ghewicht even an Π.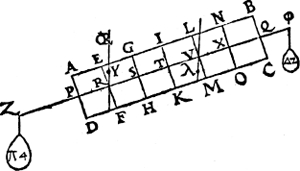

Laet ons insghelicx voorttrecken, R V tot in Φ, also dat V Φ even sy an V R, ansiende daer naer V voor vastpunt, soo sal an Φ moeten hanghen Δ 2 ℔, om den pilaer in die ghestalt te houden door het 3^e voorstel, maer tghene an R den pilaer in die ghestalt houdt als OE, doet daeran alsulcke gewelt als Δ door het 13 voorstel, An OE dan rust een ghewicht euen an Δ. Nu anghesien Π euestaltwichtich is teghen den pilaer op tghemeen vastpunt R, so heeft den erm T R, sulcken reden tot den erm R Z, als Π tot den pilaer door 1^e voorstel. Insghelijcx nemende V voor tvastpunt, soo heeft den erm T V sulcken reden tot den erm V Φ, als Δ tot den pilaer, maer R Z is altijt euen an V Φ: Wy hebben hier dan twee ^* eueredenheden elck van vier ^* palen, welcker tweede palen an malcanderen euen sijn, ende welcker laetste palen an malcanderen oock euen sijn. Maer alle twee eueredenheden elck van vier palen, welcker tweede palen an mal-

* Proportiones.

* Terminis.

[p. 39]

cander euen sijn, ende welcker laetste palen an malcander oock euen sijn, die hebben dander palen oock euerednich, daerom ghelijck T R tot T V, alsoo Π tot Δ; maer Π is even an tghewicht des pilaers rustende met tpunt V op tpunt van AE, ende tghewicht Δ is euen an t'ghewicht des pilaers rustende met tpunt R op tpunt van OE, daerom ghelijck T R tot T V, also tghewicht rustende mettet tpunt V op tpunt van AE, tottet ghewicht rustende mettet punt R op tpunt van OE. Tbeslvyt. Rustende dan een pilaer op twee punten inden as, &c.

Vervolgh.

Soo de twee punten daer den pilaer op rust, waren inde ^* hanghende linien door R en V, de selue ghewichten die hier vooren op elck rustende punt waren, soudender nu oock op sijn. Laet by voorbeelt door de punten R, V, hanghende linien ghetrocken worden, ende punten inde selue ghestelt als Y λ, Ghenomen nu dat Y ende λ de punten sijn daer den pilaer op rust, tis kennelick dat op Y rusten sal 2 ℔, ende op λ 4 ℔, waer uyt alsulcken vertooch openbaer is.

* Perpendicularibus.

10. Vertooch.        XVIII. Voorstel.

Rvstende een pilaer op eenighe twee punten, ghelijck het asstick tusschen tswaerheyts middelpunt ende de hanghende door t'slinckerpunt, tottet asstick tusschen t'swaerheydts middelpunt ende de hangende door trechterpunt, also tghewicht des pilaers rustende op trechterpunt, tottet ghewicht rustende op t'slinckerpunt.

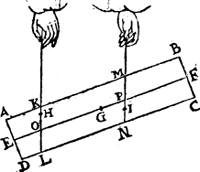Tghegheven. Laet A B C D een pilaer wesen, diens as E F, ende swaerheydts middelpunt G, ende de twee punten daer d'een pilaer op rust H I, waer duerghetrocken sijn de hangende linien K L, M N, sniende den as in O, P; Ick seg dat ghelijck G O tot G P, alsoo de swaerheydt rustende op tpunt I, tot de swaerheydt rustende op H, waer af tbewijs openbaer is door tvervolgh des voorgaenden 17^en voorstels,

[p. 40]

nochtans om alhier wat breeder vande nootsakelickheyt te segghen, so laet ons achten al of H ter plaets van O waer, twelck soo ghenomen tghewicht alsdan op H rustende, heeft sulcken reden tottet ghewicht op P rustende, ghelijck G P, tot G O, duer het 17^e voorstel; Laet ons voort nemen dattet punt H vast blijuende, den pilaer in haer ghegheuen ghestalt neerghetrocken worde, soo verre als van H tot O, ende duer de 3^e begheerte, de swaerheydt an H rustende blijft de selue. Sghelijcx salmen bethoonen de swaerheyt dieder op P rust, oock te rusten op I, daerom ghelijck G O tot G P, also de swaerheyt rustende op I, tot de swaerheyt rustende op H.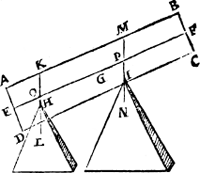

Tbeslvyt. Rustende dan een pilaer op eenighe twee punten, &c.

Vervolgh.

Tbliict uyt het voorgaende dat soomen begheerde te weten de reden van tghewicht rustende op I, tottet tghewicht rustende op H, datmen trecken soude de hanghende linien K L, M N, sniende den as E F in O, P, ende de reden van G O tot G P soude de begheerde sijn, waer uyt oock openbaer is, dat des pilaers swaerheyt bekent wesende, soo is oock tghewicht bekent rustende op yder punt als H ende I.