Zur Begriffsgeschichte des 'Paradoxon'
(1933)–K. Schilder–Mit besonderer Berücksichtigung Calvins und des nach-kierkegaardschen ‘Paradoxon’
[pagina 87]
| |||||||
Kapitel II
| |||||||
[pagina 89]
| |||||||
§ 1. Die Kierkegaardsche Wendung.Wenn wir oben die Auffassung von De Morgan und Andreas Duhm, nach der sich im 18. Jahrhundert eine Wendung in der Geschichte des Begriffes ‘Paradox’ anbahnte, zurückgewiesen haben, so besteht doch aller Grund, eine solche Wendung im 19. Jahrhundert zu konstatieren. Denn sie nimmt unstreitig ihren Anfang bei dem Dänen Sören Kierkegaard, geb. am 5. Mai 1813. Wir haben dies nicht so zu verstehen, als ob diese akute Aenderung in der Verwendungsart des Wortes ‘Paradox’ sofort einschneidende Folgen hatte oder Nachahmung fand; denn das ernsthafte Kierkegaardstudium fällt erst in spätere Zeit. Als Kierkegaards Tätigkeit als Schriftsteller schon einen Höhepunkt erreicht hatte, teilte er übrigens mit, ‘nicht einmal einen Verleger’ zu haben.Ga naar voetnoot1) Aber weil später vieler Anknüpfung an Kierkegaard um so bewusster und stärker ist, darum ist Kierkegaards Verwendung des Wortes doch in der Tat von grösster Bedeutung. Die allgemein-übliche Bedeutung des Begriffes, der uns hier beschäftigt, behält | |||||||
[pagina 90]
| |||||||
wohl zu Kierkegaards Zeiten und auch nachher, bis in unsere Zeit hinein, ihre Geltung, wie wir sahen, aber daneben und - wie wir sehen werden - demgegenüber stellt Kierkegaard einen ganz anderen Paradoxbegriff.Ga naar voetnoot1) Dies erhellt schon aus einem einfachen Studium seiner Schriften. Nur ganz selten trifft man die ursprüngliche Bedeutung des Paradoxen als das ohne weiteres Unerwartete bei ihm an, und dann auch noch nur indirekt.Ga naar voetnoot2) Aber es fällt sofort auf, dass bei Kierkegaard ein ‘paradoxer’ Gedankeninhalt dem, der das Paradoxe in ein Gedankensystem zu inkorporieren versucht, nicht nur (wie früher) Mühe verursacht, sondern - und das ist das tatsächlich Neue - dass zwischen dem wesentlich Paradoxen und dem wesentlich Systematischen ein (unversöhnlicher) Gegensatz behauptet wird. Denn das Paradox geht über jedes System hinaus; ‘es gibt eine Anschauung der Welt, wo das Paradox höher als jedes System steht’.Ga naar voetnoot3) Und weil es hier geht um den Gegensatz zwischen dem Relativen und dem Absoluten (denn: das Relative findet seinen Niederschlag im System, das Absolute im Paradox), darum bedeutet die Erhebung des Paradoxes über das System unmittelbar, dass das wesentliche Paradox dem System gegenüber gestellt wird. ‘Dass relative Gegensätze mediiert (vermittelt) werden können, dazu brauchen wir wahrlich nicht Hegel, weil es in dem bekannten Satze liegt, dass die unterschieden werden können; dass absolute Gegensätze mediiert werden könnten, dagegen wird Persönlichkeit in alle Ewigkeit protestie- | |||||||
[pagina 91]
| |||||||
ren, und dieser Protest ist inkommensurabel für das Assertum der Mediation’.Ga naar voetnoot1) Es ist selbstverständlich hier der Ort noch nicht, um den Gedankengang, aus dem dies alles bei Kierkegaard hervorkommt, nachzugehen. An dieser Stelle unserer Untersuchung wollen wir nur allein dem Worte Paradox nachgehen. Der Inhalt, den es bei Kierkegaard hat, wird schon einigermassen deutlich aus den folgenden Ueberlegungen. a) Das Kierkegaardsche Paradox ist im Grunde nicht deswegen eine crux für das Denken, weil der Mensch sich selbst im Wege steht, oder weil ein Gedanke von ihm einen anderen Gedanken, auch von ihm, ein Ding von unten ein anderes Ding von unten zu bekämpfen scheint, sondern es findet seinen tiefsten Grund darin, dass Gott dem Menschen, die Ewigkeit der Zeit, das Absolute dem Relativen, die Offenbarung dem Menschenleben mit seinen Gegebenheiten begegnet. ‘Gott ist als Lehrer aufgetreten.... er hat Knechtsgestalt angenommen; einen anderen an seiner Statt, eine hohe Vertrauensperson für sich zu senden, konnte ihm nicht genügen.... Zwischen Mensch und Mensch ist ja das sokratische Verhältnis’ (bei dem der Lehrer und der Lernende für einander eine ‘Veranlassung’ sind, um sich selber zu verstehen, bei dem die beiden einander also nötig haben, und der Lehrer also niemals in absoluter Weise Lehrer sein, sondern nur als ‘Hebamme’ fungieren kann), ‘das Höchste, das Wahrste’. ‘Von Sokrates aus gesehen.... ist ja der Lernende selbst die Wahrheit’ .... Aber Sokrates ‘wollen wir verlassen’. Käme Gott (also) nicht selbst, so bliebe alles sokratisch; wir.... verlören das Paradox.Ga naar voetnoot2) Gottes Auftreten bringt nun mit sich, dass der Mensch ‘als der Einzelne sich in ein absolutes Verhältnis zu dem Absoluten setzt’, ‘das ist das Paradox’.Ga naar voetnoot3) Beispiel ist Abraham, | |||||||
[pagina 92]
| |||||||
der Isaak opfert, gegenüber Agamemnon: Agamemnon ‘gibt Iphigenie auf und hat dadurch Ruhe gefunden in dem Allgemeinen...., der tragische Held ist bald fertig und hat bald ausgestritten; er vollzieht die unendliche Bewegung und ist nun beruhigt in dem Allgemeinen. Dem Ritter des Glaubens kommt kein Schlaf in die Augen. Denn er wird beständig geprüft.... in Spannung gehalten’.Ga naar voetnoot1) b) Darum ist das Paradox ein Entweder-Oder nicht von leichtem Leben und mühevollem Leben, sondern von Tod und Leben; tertium non datur, da das Absolute die Existenz überwältigt. Kierkegaard erinnert an die Erzählung von Sara, der Tochter Raguels und Hannas: ‘niemand ist unglücklicher als sie; denn sie weiss, dass der böse Dämon, der sie liebt, den Bräutigam in der Hochzeitsnacht töten wird.... Dies unergründliche Leid, das keine Zeit heben, keine Zeit heilen kann: zu wissen, dass es nichts helfen würde, wenn auch das Dasein alles für einen täte!...Sara war (unglücklich in der Liebe), ehe sie es wurde.’Ga naar voetnoot2) Auch zergliedert er die ‘Sage von Agnete und dem Nixen’; dieser letztere ist der Verführer, der jedoch Agnetes Unschuld machtlos gegenüber steht. Was soll der Nix tun? ‘Die Reue kann.... entarten in ein dämonisches Verlangen, sich selbst zu quälen.... Mit Hilfe des Dämonischen würde also der Nix der Einzelne sein, der als der Einzelne über dem Allgemeinen stünde. Wie zu dem Göttlichen kann der Einzelne zu dem Dämonischen in ein absolutes Verhältnis treten. Das ist das Gegenstück zu dem Paradox, von dem wir sprechen’Ga naar voetnoot3). Das ‘Gegenparadox’ würde dann hier sein, ‘dass die Gottheit Agnete retten wird (so würde wohl das Mittelalter die Bewegung vollziehen)’Ga naar voetnoot4). Es gibt Naturen, die ‘man nicht dadurch retten (kann), dass man sie in eine Idee der Gesellschaft hineinmediiert.... Naturen von der Art stehen von Grund aus im Paradox...., | |||||||
[pagina 93]
| |||||||
entweder (gehen sie) verloren in dem dämonischen Paradox oder (werden) erlöst in dem göttlichen Paradox’.Ga naar voetnoot1) So ist also die Berührung mit dem Absoluten immer Ursache des Paradoxes. Wir kehren zu Abraham zurück: ‘entweder gibt es also ein Paradox: dass der Einzelne als der Einzelne in einem absoluten Verhältnis steht zu dem Absoluten; oder Abraham ist verloren’.Ga naar voetnoot2) c) Nur dort ist also das Wesen der wahren Paradoxie, des ‘paradoxon sensu eminentiore’, wo das Absolute darin auftritt; das relative Paradox verdient diesen Namen eigentlich nicht. ‘Das Paradoxreligiöse stellt den Gegensatz der Existenz und des Ewigen als absolut hin’.Ga naar voetnoot3) Wieder wird auf Abraham verwiesen: ‘die Liebe zu Isaak ist es,.... die durch ihren paradoxen Gegensatz mit seiner Liebe zu Gott seine Tat zu einem Opfer macht.... Erst in dem Augenblick, da seine Tat in absolutem Widerspruch mit seinem Gefühle steht, erst da opfert er Isaak’.Ga naar voetnoot4) Deutlich ist hier Kierkegaards Ausspruch, dass das Christentum die Behauptung handhabt ‘dass sich das Paradoxe, von dem es redet, nicht denken lasse, verschieden also von einem relativen Paradox, das sich höchstens schwer denken lässt.’Ga naar voetnoot5) d) Deswegen heisst dieses Paradox denn auch selbst absolut oder ‘das Paradox sensu strictissimo’. Im Glauben ist ein ‘Verhältnis zum absoluten Paradox’; die Leidenschaft des Glaubens ‘ergriff’ es ‘als das absolute Paradox (nicht als das relative)’.Ga naar voetnoot6) Als solches hat es seine eigene ‘qualitative Dialektik’Ga naar voetnoot7) und wird besonders besprochen unter dem vielsagenden Titel ‘eine metaphysische Grille’.Ga naar voetnoot8) | |||||||
[pagina 94]
| |||||||
e) Demgemäss ist das Paradox nicht durch das Denken, sogar des martyr nicht, ‘erzeugt’, es ist nicht ‘durch ein Verstandes-Quantitieren des immer Schwierigeren zu erreichen’, sondern es tritt ihm von aussen her entgegen, überwältigt, beherrscht ihn als eine objektiv bestehende Wirklichkeit. Wo das Paradox so auftritt, da hat das ‘Innere’ des Menschen keine Identität ‘mit Stimmung, Gefühl usf.’Ga naar voetnoot1) Hat der Verstand das Paradox entdeckt? Nein, ‘da im Gegenteil das Paradox es ist, welches dies (d.h. das quia absurdum K.S.) entdeckte’.... ‘Das Paradox sagt selbst: Komödien, Romane und Lügen müssen wahrscheinlich sein, wie sollte aber ich wahrscheinlich sein? Das Aergernis bleibt ausserhalb des Paradoxes; was Wunder, da das Paradox das Wunder ist? Das hat der Verstand nicht entdeckt; im Gegenteil, es war das Paradox, das dem Verstande seinen Platz auf dem Verwunderungsstuhl anwies.... Wenn der Verstand sich mit seiner Herrlichkeit im Vergleich zum Paradox brüstet, da dies so ganz elend und verachtet sich darstellt, so hat der Verstand das nicht erfunden, sondern das Paradox ist selbst der Erfinder; es überlässt dem Verstande all das Splendide, auch die splendiden Sünden (vitia splendida).... Wenn der Verstand das Paradox nicht in seinen Kopf hineinbringen kann, so hat nicht der Verstand das erfunden, sondern das Paradox selbst’.Ga naar voetnoot2) Die Objektivität des Paradoxes führt Kierkegaard sogar zu der Stilfigur, dass er ‘dem Paradox’ bestimmte ‘Aeusserungen.... in den Mund’ legt.Ga naar voetnoot3) f) Wie beim Göttlichen und dem Dämonischen, wie beim Absoluten und dem Entscheidenden, so ist auch hier beim Paradox jede ‘Mediation’ vollständig ausgeschlossen; sie ist hier eine Torheit. ‘Dieses Paradox lässt sich nicht mediieren’Ga naar voetnoot4); dieser Ausdruck ist nach Geismar konstant | |||||||
[pagina 95]
| |||||||
in Kierkegaards Dänisch für das deutsche ‘vermitteln’.Ga naar voetnoot1) Auch ‘der Standpunkt’ also, auf dem der Einzelne in seinem paradoxen ‘Verhältnis zum Absoluten steht’, ‘lässt sich nicht mediieren’.Ga naar voetnoot2) Wenn Abraham versuchen würde zu ‘mediieren’, ‘muss er zugestehen, dass er in einer Anfechtung war; und wenn dies der Fall ist, kommt er nie dazu, Isaak zu opfern, oder muss er, wenn er Isaak geopfert hat, reuevoll zu dem Allgemeinen zurückkehren’; aber dies würde bedeuten - siehe oben - ein Herausfallen aus dem Paradox.Ga naar voetnoot3) ‘In der Zeit vor dem Ausgang war Abraham entweder in jeder Minute ein Mörder, oder wir stehen vor dem Paradox, das höher ist als alle Mediation’.Ga naar voetnoot4) Wo das Paradoxe sich mediieren lässt, ist es ‘nicht wesentlich paradox’.Ga naar voetnoot5) Es ist wahr, dass ‘das Paradox für den Einzelnen leicht mit einer Anfechtung verwechselt werden kann’,Ga naar voetnoot6) und die Anfechtung - siehe oben - ist ‘das Allgemeine’, in dem der Einzelne also aus dem absoluten Paradox herausfällt; und - ‘das Allgemeine ist.... eben die Mediation’.Ga naar voetnoot7) Aber dies alles ‘ist kein Grund, es (das Paradox, K.S.) zu vertuschen’.Ga naar voetnoot8) Darum darf die Kirche auch von ihren Mitgliedern keine Mediation verlangen; denn damit wird der Ritter des Glaubens zu einen ‘tragischen Helden’ degradiert; ‘die Idee der Kirche ist.... qualitativ nicht verschieden von der des Staates, wenn der Einzelne durch eine einfache Mediation Mitglied der Kirche werden kann’.Ga naar voetnoot9) g) Weil ‘die Mediation’ unter allen Umständen durchaus verfehlt heisst, kann dem Inhalt des Paradoxes kein Platz im Denken eingeräumt werden. Das Paradox lässt sich nicht | |||||||
[pagina 96]
| |||||||
denken, überhaupt nicht. Wir hörten ‘das Paradox’ schon fragen: ‘wie sollte.... ich wahrscheinlich sein?’Ga naar voetnoot1) ‘Das Paradox ist das Wunder’Ga naar voetnoot2), - und Kierkegaard pflegt dies Wort nicht zu ‘mediieren’ ...., es würde ihm ja auch nicht möglich sein; denn durch die enge Verknüpfung von Paradoxon und Glauben würde er seine These nicht verändern können, ohne zugleich den Glauben seines Charakters eines ‘Wunders’ zu berauben; auch der Glaube heisst ‘Wunder’.Ga naar voetnoot3) In seiner Unterscheidung zwischen der Religiosität A und der Religiosität B (wobei dann A die allgemein-menschliche, B die christliche ‘Religiosität’ andeuten soll), weist er darauf hin, ‘dass in der Religiosität B das Erbauliche ein ausserhalb des Individuums befindliches Etwas (ist)’; und hiermit korrespondiert dann ‘das Paradox-Erbauliche’, das ‘entspricht der Bestimmung: Gott in der Zeit als einzelner Mensch; denn wenn es so ist, verhält sich das Individuum zu etwas, was sich ausserhalb seiner befindet. Dass sich dies nicht denken lässt, ist ja eben das Paradox.’ Hiermit steht oder fällt das Christentum; denn es behauptet, ‘dass sich das Paradoxe, von dem es redet, nicht denken lasse, verschieden also von einem relativen Paradox, das sich höchstens schwer denken lässt.’Ga naar voetnoot4) Hiermit steht oder fällt natürlich auch die Religiosität B; denn man erkennt hier sofort die Konsequenz, dass mit ‘der Unverständlichkeit des Paradoxes’ korrespondieren muss die Behauptung, ‘dass es zum Paradox-Religiösen keine Analogien gibt.’Ga naar voetnoot5) Wo das grosse Paradoxon des ‘Gottmenschen’ auftritt, ‘ist es ganz sicher, dass dem Menschen darüber der Verstand stillstehen muss’.Ga naar voetnoot6) ‘Das absolute Paradox’ ‘verbittet sich alle Erklärung’.Ga naar voetnoot7) Gerade weil ‘das | |||||||
[pagina 97]
| |||||||
Paradox das Historische ewig und das Ewige historisch (macht)’, muss es ausserhalb der Diskussion gestellt werden: ‘wer das Paradox anders versteht, erwirbt sich die Ehre, dasselbe erklärt zu haben, und diese Ehre gewann er dadurch, dass er sich nicht damit begnügte, es zu verstehen’.Ga naar voetnoot1) ‘Das Paradox (war) paradox genug, sich nicht zu entblöden und den Verstand für einen Tölpel und Holzklotz zu erklären, der höchstens zu demselben Ja und Nein sagen kann, was nicht gerade eine gute Theologie abgibt’.Ga naar voetnoot2) h) Weil nun Gott und Mensch, Ewigkeit und Zeit, Religiosität A und Religiosität B, das Allgemeine und das absolut Paradoxe Gegensätze sind, genügt eine blosse Katargese des Verstandes nicht; die Logik in Kierkegaards Beweisführung zwingt zu der Lehre vom Widerspruch gegen den Verstand, zu der These, dass das Paradoxe auch das Absurde ist. So taucht das Skandalon auf und das sacrificium intellectus. ‘Das Paradox und der Verstand’ müssen ‘zusammenstossen’Ga naar voetnoot3), das eine hat sein ‘Elend’, das andere seine ‘Herrlichkeit’Ga naar voetnoot4), wenigstens - in der Darstellung, der Empfindung. Wenn in der alten, oben besprochenen allgemeinen Bedeutung des Wortes das ‘Paradox’ immer als ‘Anfechtung’ für den Verstand gegolten hat, so weist Kierkegaard dieses Wort als viel zu schwach, ja, als fundamentale Haeresie zurück, um das auf seinem Standpunkt in der Tat allein noch übrigbleibende Wort ‘Aergernis’, Skandalon, zu wählen. Und während früher ‘paradox’ und ‘absurd’ von einander unterschieden wurden, da werden sie hier notwendigerweise synonym. ‘Das Absurde gehört nicht zu den Differenzen, die im eignen Umkreis des Verstandes liegen. Es ist nicht identisch mit dem Unwahrscheinlichen, dem Unerwarteten, dem Unvermuteten’ (wir können hinzufügen: dem Paradoxen, aufgefasst in der früher allgemein mit diesem Worte verbundenen Bedeu- | |||||||
[pagina 98]
| |||||||
tung).Ga naar voetnoot1) Indem nun der ‘Ritter des Glaubens’ das absolute Paradox ergreift, ergreift er das Absurde; in der Zergliederung von Abrahams Opfer wechseln übrigens die Qualifikationen ‘paradox’ und ‘absurd’ einander ab;Ga naar voetnoot2) der reiche Jüngling jedoch aus Christi bekannter Parabel, der zum Opfer nicht fähig war, ist gerade daran gescheitert, dass er dem Absurden nicht zugelassen hat, sich in seinem Leben zu verwirklichen.Ga naar voetnoot3) ‘Das Paradox ist ja das Paradox, quia absurdum’.Ga naar voetnoot4) Der Verstand ‘ist abgedankt’;Ga naar voetnoot5) ‘dem Paradox und dem Absurden’ müssen wir ‘alle gleich nahestehen’.Ga naar voetnoot6) Nicht nur über oder ausserhalb, sondern ‘gegen’ den Verstand ist das Paradoxreligiöse.Ga naar voetnoot7) Und weil das Paradox ‘Glauben gegen den Verstand fordert’ ‘bringt (es) sogleich das Aergernis an den Tag’.Ga naar voetnoot8) Ja, es ist wohl ‘schwer’,Ga naar voetnoot9) ‘seinen Verstand und sein Denken aufzugeben und seine Seele auf dem Absurden zu halten’, und ‘dass das Paradox für den Einzelnen leicht mit einer Anfechtung verwechselt werden kann, ist wohl wahr’, wie es auch wahr ist, ‘dass mancher seiner ganzen geistigen Konstitution nach durch das Paradox abgestossen wird’. Aber - das alles ‘ist kein Grund, es zu vertuschen’, man muss das Paradox ‘von einer Anfechtung unterscheiden’;Ga naar voetnoot10) denn die Anfechtung gehört wieder zum ‘Allgemeinen’; mit ihr hat man auch zu kämpfen bei der ‘Mediation’, und sie gibt wieder das Bild des nur ‘tragischen Helden’, und dessen Niveau ist von dem des Ritters des Glaubens ja wesentlich unterschieden.Ga naar voetnoot11) Darum haben wir eine andere, ‘eine neue Kategorie’ nötig,Ga naar voetnoot12) um | |||||||
[pagina 99]
| |||||||
Abraham und sein Paradox zu verstehen; wir begegnen da nicht der Anfechtung, sondern - viel schlimmer - dem Aergernis, dem Skandalon. Kierkegaard spricht hierüber besonders unter dem Titel ‘Das Aergernis am Paradox (eine akustische Täuschung)’.Ga naar voetnoot1) ‘Wenn das Paradox und der Verstand in dem gemeinsamen Verständnis ihrer Verschiedenheit zusammenstossen’, gibt es zwei Möglichkeiten: ‘der Zusammenstoss ist glücklich’, oder er ist ‘unglücklich’, nämlich, wenn ‘der Zusammenstoss nicht im Verständnis eingetreten ist’; diese unglückliche Liebe des Verstandes hat ‘ihren Grund in missverstandener Selbstliebe’ und heisst nun ‘das Aergernis’.Ga naar voetnoot2) Das Aergernis kann ‘als eine indirekte Probe für die Richtigkeit des Paradoxons angesehen werden’.Ga naar voetnoot3) Der Held, der ‘sich als ein Paradox nicht verständlich machen kann’, ist damit ‘seiner Zeitgenossen σϰάνδαλον geworden’.Ga naar voetnoot4) Das Paradox, ‘elend’ und von allem, was ‘splendide’ ist, beraubtGa naar voetnoot5), findet keine Anerkennung in der ‘Spekulation’; deshalb muss diese sich ‘ärgern’. So muss der ‘Gegenstand des Glaubens’, eben weil er Paradox ist, darin auch ‘Zeichen des Aergernisses’Ga naar voetnoot6) sein. Das Paradox ist zugleich ‘Widerspruch’;Ga naar voetnoot7) und Christus, der Paradox und Zeichen des Aergernisses genannt wird, ist denn auch zugleich Zeichen des Widerspruchs.Ga naar voetnoot8) Und so wird von selbst die alte Auffassung des Paradoxons als incitamentum intellectus aufgegeben: hier ist es sacrificium intellectus geworden, sein Kreuz; eine Qualifikation, die von jeglicher Rhetorik frei ist.Ga naar voetnoot9) i) Wer das sacrificium intellectus bringen muss und ans | |||||||
[pagina 100]
| |||||||
‘Kreuz’ geschlagen wird, der hat natürlich sein Gefühl der ‘Not’. Kierkegaard wird übrigens nicht müde, dies zu versichern. Wiederholt häufen sich die Ausdrücke: ‘die Not, die Angst, das Paradox’.Ga naar voetnoot1) Die Not des Ritters des Glaubens, der als der Einzelne das Paradox ist, heisst sogar ‘entsetzlich’.Ga naar voetnoot2) Und wenn jemand bemerken möchte, dass jedes Paradox, auch das Paradox in seiner früheren Bedeutung, ein Gefühl der ‘Not’ mit sich bringt, dann weisen wir doch wieder auf einen wesentlichen Unterschied. Zum Teil ist dieser schon in allen vorhergehenden Abschnitten (a-h) aufgezeigt, aber wir können dem Gesagten noch dies hinzufügen: erstens: bei dem Paradox in seiner früheren Bedeutung war die ‘Not’, in die der Denker sich gestellt sah, eigentlich immer eine kollektive, ja, ohne den Gedanken der Kollektivität war sie aufgehoben (denn die allgemeingültigen Denkgesetze liessen sich nicht, wie es schien, versöhnen mit der als paradox empfundenen Wirklichkeit oder Meinung; und eben dieselben allgemeinen Denkgesetze wurden auch sofort zu Hilfe gerufen, um das Paradox zu überwinden, zu beseitigen; und wenn der Denker glauben konnte, dass in der Tat er allein in den paradoxen Netzen verwirrt war, dann war zu gleicher Zeit der scheinbare Widerspruch zu den allgemeinen Gesetzen des Denkens und des Lebens aus seinem Gesichtsfeld verschwunden, die Not war also eigentlich aufgehoben); aber bei dem Kierkegaardschen Paradox ist die ‘Not’ gerade umgekehrt daraus entstanden, dass man als der Einzelne aus dem Allgemeinen vollkommen losgelöst ist. Und zweitens: bei der früheren paradoxen Verwirrung gibt es immer die (wohltuende, da eine Lösung bringende) Arbeit zur Ueberwindung des Paradoxes, während hier bei Kierkegaard eine Ueberwindung des Paradoxes nichts anderes bedeuten würde als den Untergang; wenn Abraham das Paradox ‘überwindet’, ist Abraham verloren: die Not ist eine bleibende, sie ist ein | |||||||
[pagina 101]
| |||||||
articulus stantis aut cadentis fidei. Wir wollen diese beiden Punkte einzeln besprechen. j) Was das erste betrifft: in dieser ‘Not’ ist der Einzelne ganz isoliert. Er ist der Einsame. ‘Das ist die Not und Angst im Paradox, dass er, menschlich geredet, sich schlechterdings nicht verständlich machen kann’.Ga naar voetnoot1) ‘Der Ritter des Glaubens ist als das Paradox der Einzelne, absolut nur der Einzelne.’Ga naar voetnoot2) ‘Der Wille des Himmels’ - gesetzt den Fall, dass das Paradox wirklich, und dann absolut, besteht - ist dem Träger der Religiosität B ‘nicht durch einen Augur verkündigt, sondern auf durchaus privatem Wege zur Kenntnis gekommen’; der Himmel hat ‘sich in ein ganz privates Verhältnis zu ihm gesetzt’.Ga naar voetnoot3) Darum kann er ‘nicht reden, ob er auch noch so gern wollte’.Ga naar voetnoot4) Der tragische Held (auch der des alten Paradoxes) ‘ist offenbar, und in diesem Offenbarsein der Ethik lieber Sohn. Das passt nicht auf Abraham; er tut nichts für das Allgemeine, und er ist verborgen’.Ga naar voetnoot5) Alle Nothilfe in diesem paradoxen Leiden, sowohl die erwiesene als die erfahrene, ist hier aus dem Gesichtskreis gebannt. ‘Der wahre Glaubensritter ist immer die absolute Isolation, der unechte ist sektiererisch.’Ga naar voetnoot6) ‘Naturen’, die ‘von Grund aus im Paradox stehen’, haben nichts an der Spekulation und nichts an der Ethik: ‘die Ethik hält sie eigentlich nur zum Narren.’Ga naar voetnoot7) ‘In dem Paradox des Glaubens fällt das Allgemeine als Mittelbestimmung aus.’Ga naar voetnoot8) k) Deshalb - und es wird deutlich werden, dass Kierkegaards Lehre vom ‘Augenblick’ keineswegs dagegen streitet - ist die Not, die paradoxe Not, auch beständig. ‘Der Ritter des Glaubens wird beständig in Spannung | |||||||
[pagina 102]
| |||||||
gehalten’ (darin unterscheidet er sich von dem nur tragischen Helden).Ga naar voetnoot1) Er unterscheidet sich auch von dem ‘sektiererischen’ Menschen, der versucht, ‘von dem engen Pfade des Paradoxes abzubiegen’.Ga naar voetnoot2) Die ‘Reue’, die fortwährend wieder ‘unter der Dialektik stehen wird, ob sie nun tief genug ist usw.’, reicht denn auch gerade deswegen nicht zu der einsamen Höhe des Paradoxes: ‘wo sie aufhört, fängt das Paradox an’;Ga naar voetnoot3) der Glaube an die Versöhnung bleibt, aber ist denn auch beständig paradox. ‘Es will dem Glaubenden auch nicht einmal das Paradoxe sein und ihm dann unter der Hand nach und nach, das Verständnis verschaffen; denn das Martyrium des Glaubens (seinen Verstand zu kreuzigen) ist nicht das Martyrium eines Augenblickes, sondern gerade der Fortdauer.’Ga naar voetnoot4) ‘Das Christentum ist eine Existenzmitteilung, die das Existieren paradox macht, weshalb es, solange existiert wird, das Paradox bleibt.’Ga naar voetnoot5) Der Christ hat nicht nur einmal das Kreuz des Paradoxes tragen müssen, ist auch nicht nur je und dann darunter zusammengebrochen, nein: er ist ‘ans Paradox genagelt’.Ga naar voetnoot6) l) Scheinbar streitet gegen den Ausspruch, dass wir es nicht mit einem ‘Martyrium eines Augenblickes’ zu tun haben, der immer wieder hervortretende Gedanke, dass das Paradox und ‘der Augenblick’ zusammen gehören. Aber mit diesem ‘Augenblick’ wird etwas ganz anderes gemeint, als in dem Gegensatz: Augenblick-Fortdauer, siehe oben! ‘Das Paradox ist der Augenblick.’ ‘Mit dem Paradox tritt das Aergernis ins Dasein; tritt es aber erst ins Dasein, so haben wir wieder den Augenblick..... Wenn wir den Augenblick nicht annehmen, so wenden wir uns wieder zu Sokrates zurück, und ihn wollten wir ja eben | |||||||
[pagina 103]
| |||||||
verlassen.... Wird der Augenblick statuiert, so ist das Paradox da; denn das Paradox in unendlicher Abbreviatur kann man den Augenblick nennen; mit dem Augenblick wird der Lernende die Unwahrheit’ (anders also als bei Sokrates).Ga naar voetnoot1) Deutlich spricht hier dieser Passus: ‘Darin liegt ja eben das Sokratische, dass der Lernende den Lehrer von sich stossen kann, weil er selbst die Wahrheit ist und die Bedingung hat; ja, darin lag eben die sokratische Kunst, der sokratische Heroismus, dass er den Menschen dazu verhalf, dass sie dies tun konnten’. Aber der Glaube ist anders: ‘Der Glaube muss den Lehrer beständig festhalten. Damit aber der Lehrer die Bedingung geben kann, muss er Gott sein; damit er den Lernenden in den Besitz derselben bringen kann, muss er Mensch sein. Dieser Widerspruch ist wieder Gegenstand des Glaubens und ist das Paradox, der Augenblick.’Ga naar voetnoot2).... ‘Der genannte Widerspruch besagt, dass der Mensch im Augenblick die Bedingung erhalte, welche als Bedingung für das Verständnis der ewigen Wahrheit eo ipso die ewige Bedingung ist. Verhält es sich anders, so stehen wir wieder bei der sokratischen Erinnerung’.Ga naar voetnoot3) Aber ‘der sokratische Satz: alle Erkenntnis ist Erinnerung, gehört der Spekulation an und Erinnerung ist Immanenz, und vom spekulativen und ewigen Gesichtspunkte aus gibt es kein Paradox’.Ga naar voetnoot4) Wir müssen uns also vom Sokratischen abwenden, auch noch aus einem anderen Grunde. Denn das sokratische Verhältnis kennt nur Lehrer und Schüler in derselben Dimension, sie stehen auf derselben Ebene. Darum kann hier der Lehrer den Schüler auch nicht auf das Kierkegaardsche Paradox stossen lassen. Das ist ja ein Moment von jener anderen Relation zwischen Lehrer (Gott) und Lernendem (dem Gläubigen), die beide aus zwei ganz anderen ‘Welten’ sind: aus der Ewigkeit der Lehrer, | |||||||
[pagina 104]
| |||||||
in der menschlich-zeitlichen Existenz der Lernende. So wird die Parallelie zwischen ‘Paradoxon’ und ‘Augenblick’ bei Kierkegaard durchsichtig: auch ‘der Augenblick ist der Einschlag der Ewigkeit’.Ga naar voetnoot1) Die wesentlichen Grundbestimmungen von Kierkegaards Paradoxon kehren also alle wieder in seiner Struktur des Augenblicks. Dieser ist nicht ‘der archimedische Punkt’, den man auf dem Papiere so leicht und billig konstruieren kann, indem man ‘zuerst Endlichkeit, dann Unendlichkeit’ setzt und dann sagt, auch auf dem Papier: ‘es muss vermittelt werden’; denn ‘nicht auf dem Papiere, sondern in der Existenz’ ereignet sich ‘die Szene’.Ga naar voetnoot2) Und dort ist ‘der Augenblick der Resignation’, in dem ‘nicht vermittelt, sondern gewählt’ wirdGa naar voetnoot3); und dort ist ‘die Aufgabe’, ‘sich die Geschicklichkeit einer Wiederholung der leidenschaftlichen Wahl zu erwerben und das existierend auszudrücken’.Ga naar voetnoot4) Denn das absolute τέλος darf nicht in ein relatives ‘herabgesetzt werden’;Ga naar voetnoot5) darum ist die Mediation eine Todsünde in jedem wahrhaft paradoxen Verfahren und tritt ‘der Augenblick’ in die Existenz hinein. Die Parallelie zwischen Paradoxon und Augenblick kann verdeutlicht werden an der von Geismar gegebenen Zeichnung:Ga naar voetnoot6)  Die obere Linie, sagt Geismar, ‘soll.... das Ewige, das Gute, das ewig sich selbst gleicht’, die untere ‘die Zeitmomente, die ohne inneren Zusammenhang aufeinander folgen’, bezeichnen. ‘Die Aufgabe ist nun: mit dem Auge auf das Zukünftige gerichtet (rechts) das Ewige in das | |||||||
[pagina 105]
| |||||||
Zukünftige zu führen. Im Punkte ×), das den “Augenblick” im eigentlich Kierkegaardischen Sinne bezeichnet, wird das Ewige in das Zeitliche hineingeführt. In diesem Punkte ist das Ewige augenscheinlich das Zukünftige....’ (existenzielle Einstellung). Dagegen ‘ist die Aufmerksamkeit des Spekulierenden rückwärts gerichtet auf das Ewige in dessen ewigen Sein’ (spekulierende Einstellung).Ga naar voetnoot1) m) Es erregt einige Verwunderung, dass, nachdem so viele Male Sokrates und ‘das sokratische Verhältnis’, als etwas, das überwunden werden musste, hingestellt wurden, das Paradox doch auch wieder ‘sokratisch’ genannt wird. Aber dennoch geschieht dies. So heisst z.B. ‘die Sündenvergebung sokratisch paradox, insofern als sich die ewige Wahrheit zu einem Existierenden verhält, sensu strictiore’.Ga naar voetnoot2) Hermann Diem will sogar einen Unterschied annehmen zwischen ‘dem sokratischen Paradox’ und ‘dem christlichen Paradox’.Ga naar voetnoot3) Demgegenüber konstruieren andere, z.B. Martin Thust und Torsten Bohlin, das sokratische ‘Prinzip’ oder Element in Kierkegaards (Paradox-)Lehre so, dass kein Grund besteht, sokratisches und christliches Paradox einander in dieser Weise gegenüberzustellen.Ga naar voetnoot4) Wir schliessen uns unsererseits aus verschiedenen GründenGa naar voetnoot5) dieser | |||||||
[pagina 106]
| |||||||
letzteren Auffassung an und glauben, dass Kierkegaard selbst sie legitimiert: Sokrates kann ja von verschiedenen Gesichtspunkten aus betrachtet werden. Als er oben unter a) und l) zur Sprache kam, wurde er betrachtet in seinem Verhältnis als Lehrer zum Lernenden, zum Schüler. Zwischen Lehrer und Lernendem ist ein Wechselverhältnis, sagt Kierkegaard;Ga naar voetnoot1) denn der Lehrer sucht ebenso gut wie der Schüler;Ga naar voetnoot2) und was Sokrates betrifft: er weiss, dass ‘alles Lernen und Suchen nur Erinnerung ist, so dass der Unwissende nur eines Hinweises bedürfe, um durch sich selbst sich auf das zu besinnen, was er weiss; die Wahrheit wird also nicht in ihn hineingebracht; sie war schon in ihm’.Ga naar voetnoot3) Darum kann Sokrates niemals in eigentlichem Sinne für den Schüler ein ‘Vater’ sein; er bringt es nicht weiter als bis zur ‘Hebamme’, sei es denn auch ‘eine von Gott selbst examinierte Hebamme’.Ga naar voetnoot4) Für die ‘sokratische Betrachtung’ ist ‘jeder Mensch sich selbst | |||||||
[pagina 107]
| |||||||
das Zentrale’.Ga naar voetnoot1) Zwischen Schüler und Lehrer besteht ein Verhältnis, das dadurch bestimmt wird, dass beide in derselben ‘Dimension’ leben; der eine hat den anderen nötig, wenn es auch nur wäre, um sich selbst zu verstehen.Ga naar voetnoot2) Legt man also auf dieses Verhältnis vom Lehrer zum Schüler, von Hebamme zum Kind den Nachdruck, dann tritt in der Tat ein scharfer Gegensatz zwischen dem sokratischen und dem absolut Paradoxen - Begegnung von zwei ganz ‘anderen’ Dimensionen - ins hellste Licht. Das absolute Paradox kommt von Gott, der in die Zeit hineintritt; und Gott steht zum Schüler in einem ganz anderen Verhältnis, kommt zu ihm aus einer total anderen ‘Dimension’, greift von dort aus ein in des Menschen Existenz. Gott hat dabei den Schüler absolut nicht nötig.Ga naar voetnoot3) Er steht denn auch zu ihm am allerwenigsten in einem Wechselverhältnis gegenseitiger Abhängigkeit; denn Gott, anders als Sokrates, ist jetzt der absolute Lehrer.Ga naar voetnoot4) Er kommt nicht wie Sokrates zum Schüler in einem ‘zufälligen, verschwindenden’ Ausgangspunkt in der Zeit,Ga naar voetnoot5) sondern er überwältigt ihn in einem Augenblick, der, gerade weil Gott hier auftritt, ‘eigener Natur’ ist, ein Augenblick, der ‘erfüllt vom Ewigen’ ist, und der darum heissen muss: ‘die Fülle der Zeit’.Ga naar voetnoot6) Auch ist Gott bei der Unterweisung nicht angewiesen auf die ‘Erinnerung’, auf das also, was schon im Schüler vorhanden ist, sondern vielmehr tut Gott etwas, was ein menschlicher Lehrer nie tun kann; ‘nicht bloss die Wahrheit gibt (er), sondern auch die Bedingung (ihres Verständnisses) verschafft (er)’.Ga naar voetnoot7) Gerade dies Letzte, nämlich dass auch die Bedingung des Verständnisses ‘verschafft’ werden muss, macht Sokrates machtlos und hindert ihn in alle Ewigkeit daran, absoluter Lehrer zu werden, paradox | |||||||
[pagina 108]
| |||||||
zu sein im absoluten Sinne des Wortes, paradox gegenüber dem Lernenden. Denn ‘alle Unterweisung beruht darauf, dass die Bedingung in letzter Instanz doch vorhanden ist; fehlt sie, so vermag ein Lehrer nichts. Denn in diesem Falle muss er ja den Lernenden nicht umbilden, sondern umschaffen, bevor er beginnt, ihn zu lehren. Aber dies vermag kein Mensch; soll es geschehen, so muss es durch Gott selbst geschehen.’Ga naar voetnoot1) Obgleich also aller Grund vorhanden ist, das sokratische Verhältnis mit Bezug auf die Relation: Schüler - Lehrer ärmlich, unparadox, ja, sogar unfähig zum Durchbruch des Paradoxes in absolutem Sinne zu nennen, so kann man ‘Sokrates’ doch noch auf andere Weise sehen. Man kann ihn nämlich sehen in seinem eigenen Verhältnis zu Gott, zur Wahrheit, zum Absoluten. Wir hörten schon, wie nach Kierkegaards Meinung Sokrates, obgleich nur Hebamme, doch eine von Gott examinierte Hebamme war. Hebamme - das ist das Verhältnis zum Kind, dem Objekt der ‘Paedagogie’, dem νήπιος. Aber ‘von Gott examiniert’ - das ist die persönliche Haltung gegenüber der Wahrheit, Sokrates' eigener Umgang mit der absoluten Wahrheit oder seine Verlegenheit ihr gegenüber. Und es ist offenbar dieses letztere Verhältnis von Sokrates gegenüber der Wahrheit, das Kierkegaard dazu veranlasst, dem erst unsokratischen Paradox doch das Epitheton ‘sokratisch’ zu geben. Denn Sokrates hatte ein grosses Verdienst: die Betonung der Existenz. ‘Der Spekulierende (ist) ein Existierender, den Ansprüchen der Existenz unterworfen. Dies zu vergessen, ist kein Verdienst, aber wohl es festzuhalten, ein grosses Verdienst, und das tat eben Sokrates.’Ga naar voetnoot2) ‘Vergessen wir nie, dass Sokrates' Verdienst darin bestand, den Erkennenden als Existierenden hinzustellen’.Ga naar voetnoot3) Sokrates ‘begriff...., wie misslich es war, sich spekulierend aus der Existenz in die Ewigkeit zurückzunehmen, da doch der Existierende keine | |||||||
[pagina 109]
| |||||||
Misslichkeit an sich hatte, ausser der, dass er existierte.’Ga naar voetnoot1) Hierin unterscheidet Sokrates als Typ sich denn auch in günstiger Weise von Plato. Wohl stellen beide den sokratischen Satz auf: alles Erkennen ist ein Sicherinnern.Ga naar voetnoot2) ‘Dieser Satz deutet den Anfang der Spekulation an, aber Sokrates verfolgte ihn daher auch nicht, sondern er blieb wesentlich platonisch. Hier biegt der Weg ab: Sokrates betont wesentlich das Existieren, während sich Plato, dies vergessend, in Spekulation verliert. Sokrates hat gerade das unendliche Verdienst, kein Spekulant, der das Existieren vergisst, sondern ein existierender Denker zu sein.’Ga naar voetnoot3) ‘Die Betonung der Existenz und damit der Innerlichkeit ist das Sokratische, der Erinnerung und Immanenz nachzugehen das Platonische’.Ga naar voetnoot4) Es ist Sokrates' Verdienst, dass man ihn nicht halten kann ‘auf der Höhe des Satzes, dass alle Erkenntnis Erinnerung sei’. Wenn das möglich gewesen wäre, dann wäre er ein spekulativer Philosoph geblieben; aber nun ist er ein existierender Denker.Ga naar voetnoot5) Er begriff, dass ‘für einen Existierenden das Wesentliche das Existieren ist’.Ga naar voetnoot6) Und so ist Sokrates wegen seiner ‘Unwissenheit’ zu loben. ‘Die sokratische Unwissenheit ist der Ausdruck für die objektive Ungewissheit, des Existierenden Innerlichkeit ist die Wahrheit.’Ga naar voetnoot7) Denn Sokrates war ‘in seiner Unwissenheit innerhalb des Heidentums im höchsten Mass in der Wahrheit’.Ga naar voetnoot8) Und ‘die sokratische Unwissenheit war so der mit der ganzen Leidenschaft der Innerlichkeit festgehaltene Ausdruck dafür, dass sich die ewige Wahrheit zu einem Existierenden verhält und ihm deshalb, so lange er existiert, ein Paradox bleiben muss’.Ga naar voetnoot9) So wird die Brücke von | |||||||
[pagina 110]
| |||||||
‘Sokrates’ zum Kierkegaardschen Paradox geschlagen. ‘Das Paradox ist die objektive Ungewissheit, welche die Leidenschaft der Innerlichkeit ausdrückt, in welcher eben die Wahrheit besteht. So das Sokratische. Die ewige, wesentliche Wahrheit, d.h. die, welche sich wesentlich zu einem Existierenden verhält, indem sie wesentlich das Existieren betrifft...., ist das Paradox,’ sagt Kierkegaard.Ga naar voetnoot1) Und nun kann er - vgl. S. 105, Note 5) - wiewohl er einen ‘gleichwohl unendlichen Unterschied zwischen ‘dem Sokratischen’ einerseits und dem ‘über das Sokratische Hinausgehenden’ andererseits poniert, doch eine Analogie zwischen beiden sehen. ‘Die Wahrheit als Paradox wird eine Analogie zum Paradox sensu eminentiore, die Leidenschaft der Innerlichkeit im Existieren wird eine Analogie zum Glauben sensu eminentiore.... Jetzt.... steht nichts im Wege, in Bezug auf Sokrates und Glauben vom Paradox zu reden, was ganz richtig ist, wenn man's bloss richtig versteht’; es liessen sich denn auch, sagt Kierkegaard, ‘belehrende Vergleiche’ zwischen der griechischen πίστις einerseits und seinem ‘Glauben sensu eminentiore’ andererseits ‘anstellen’.Ga naar voetnoot2) ‘Die sokratische Innerlichkeit im Existieren ist eine Analogon zum Glauben, nur dass dessen Innerlichkeit, die nicht dem Abstoss der Unwissenheit, sondern des Absurden entspricht, unendlich tiefer ist’.Ga naar voetnoot3) n) Deswegen ist das Paradox, jetzt wieder in eigentlichem, eminentem Sinne verstanden, denn auch stets Objekt des Glaubens, ja, das Paradoxon macht den Glauben selbst paradox. Denn weil der Glaube ‘das Absurde’ annimmt (eine Benennung, die, wie wir sahen, das Paradoxe bezeichnet) wird der Glaube selbst ‘das Paradox des Daseins.’Ga naar voetnoot4) ‘So ist ja der Glaube ebenso paradox wie das Paradox? Ganz richtig! wie sollte er denn sonst im Paradox seinen Gegenstand haben und in seinem Verhältnis zu diesem | |||||||
[pagina 111]
| |||||||
glücklich sein?’Ga naar voetnoot1) Und so heisst auch die Religiosität B kurzweg: die paradoxe Religiosität.Ga naar voetnoot2) Ihr Glaube hat einen Mut, der ‘paradox und demütig’ ist.Ga naar voetnoot3) Von Angst, Not und Paradox hörten wir in einem Atem reden, aber der Glaube lässt hier doch keine aporetische Haltung zu: wenn man das Paradox nicht als Objekt des Begreifens, sondern des Glaubens annimmt, versteht man zugleich: ‘wenn man bloss alle Versuche zu begreifen als sich selbst widersprechend aufzeigen kann, so bekommt die Sache ihre rechte Stellung.’Ga naar voetnoot4) o) Wenn eine aporetische Haltung hier auch ausgeschlossen ist, so ist doch ebensosehr die des bourgeois satisfait eine Unmöglichkeit; denn nur in der grossen Leidenschaft ist man Glaubensritter und Schüler des Paradoxons. ‘Der Glaube ist die höchste Leidenschaft in einem Menschen.’Ga naar voetnoot5) Dieser Gedanke wird bei Kierkegaard ganz besonders konkret, weil er eine Parallele zieht zu ‘dem Paradox der Liebe’.Ga naar voetnoot6) ‘Das Paradox ist des Denkers Leidenschaft, und der Denker ohne Paradox ist wie der Liebende ohne Leidenschaft: ein mittelmässiger Patron’.Ga naar voetnoot7) Wie jedoch jede Leidenschaft ihren eigenen Untergang will, so sucht der Verstand in seiner höchsten Leidenschaft den Anstoss, ‘obgleich der Anstoss auf die eine oder andere Weise sein Untergang werden muss.’Ga naar voetnoot8) ‘In seiner Paradoxie’ kann ‘der Verstand’ ‘es nicht lassen, immer wieder zu ihm (d.h. dem Unbekannten) zu kommen’; ‘die paradoxe Leidenschaft des Verstandes stösst.... beständig gegen dieses Unbekannte an’.Ga naar voetnoot9) Und darin findet der Glaube ein inniges Glück. ‘Wenn das Paradox und der | |||||||
[pagina 112]
| |||||||
Verstand in dem gemeinsamen Verständnis ihrer Verschiedenheit zusammenstossen, so ist der Zusammenstoss glücklich wie das Verständnis der Liebe, glücklich in der Leidenschaft’, die später Glaube genannt wird;Ga naar voetnoot1) denn dort geschieht das Liebeswunder, dass ‘der Verstand sich selbst beiseite schafft und das Paradox sich selbst hingibt.’Ga naar voetnoot2) Der Gegensatz zu diesem glücklichen Zusammenstoss ist: das Aergernis; hierbei ist ‘der Zusammenstoss nicht im Verständnis eingetreten’; darum ist jetzt ‘das Verhältnis unglücklich’; der Verstand hat hier seine ‘unglückliche Liebe’.Ga naar voetnoot3) Daher kommt es denn auch, dass bei der glücklichen Liebe das Pathos unaufhörlich erneuert wird; das Paradoxe ist ‘zu neuem Pathos abstossend’; kein Wunder, da ‘der Verstand sich selbst aufgab und das Paradox sich hingab (halb zog sie ihn, halb sank er hin)’.Ga naar voetnoot4) p) Indem so das Element der Liebe (in den Glauben) hineingetragen wird, werden alle vorhergehenden Bestimmungen des Paradoxes noch ausserordentlich verschärft. Nicht tragisch, wortlos, keine Lehre, keine Anfechtung, Schweigen - all diese Umschreibungen werden jetzt noch deutlicher. Denn Liebe, Leidenschaft, Pathos verhindern den tragischen Ablauf, solange sie kräftig sind, sie vermeiden das Wort, rufen den Lehrer nicht, sind strikt persönlich und konkret (der Einzelne). Das Tragische liegt ‘zwischen’Ga naar voetnoot5) den Polen, zwischen denen der paradoxe Glaubensritter sich bewegt, ist ‘billig’,Ga naar voetnoot6) allgemein, erreicht also nicht das Paradox. Und das Wort findet die paradoxe Leidenschaft auch nicht: Abraham kann ‘nicht reden’; ‘sobald ich rede, drücke ich das Allgemeine aus; wenn ich das nicht tue, versteht mich niemand.’Ga naar voetnoot7) Weil der paradoxe Mensch der Einzelne ist, dessen ‘augenblickliche’ Position in der | |||||||
[pagina 113]
| |||||||
existenziellen Einstellung, gerade weil sie ihn (nach einer ‘eschatologischen’ Terminologie) setzt in ‘die Fülle der Zeit’, ihn eigentlich positionslos macht auf der Ebene der Zeit und von allem, was sich horizontal auf dieser Ebene bewegt, darum kann er sich ‘schlechterdings keinem anderen verständlich machen’; ‘der eine Ritter des Glaubens kann dem anderen Ritter des Glaubens nicht helfen’; ‘Kompanie ist in diesen Regionen ganz undenkbar’.Ga naar voetnoot1) ‘Menschlich geredet ist er von Sinnen’, das ‘ist noch der mildeste Ausdruck für ihn’.Ga naar voetnoot2) Auf die Frage, ob der paradoxe ‘Ausspruch’, der zu ihm kam, publici iuris oder ‘ein privatissimum’ ist, ist die Antwort eine unzweideutige Wahl des letzteren Wortes.Ga naar voetnoot3) Sein ‘Inneres’ ist ‘in einem Aeusseren nicht auszudrücken.Ga naar voetnoot4) Ausser der ‘Ethik’ hält auch jede gegebene oder denkbare ‘Dogmatik’ ihn ‘zum Narren’; ein Lehrer kann ihm nichts geben; er kann selber auch kein Lehrer werden; er ist ‘stets Zeuge, niemals Lehrer’.Ga naar voetnoot5) Der menschliche Lehrer ist höchstens ‘Anlass’, ‘ein verschwindender Durchgang’; denn das Verhältnis zwischen Lehrer-Schüler ist Relativität; aber hier ist der gläubige Schüler Gottes also nichts Geringeres als ‘eine neue Kreatur’, aber das dann wieder - ‘im Augenblick’. ‘Wenn daher ein Christ (der paradox ein Schüler des Gottes, das heisst eine neue Kreatur ist) innerhalb des Christentums wieder ein Schüler von dem und dem wird, so erweckt dies einen indirekten Verdacht, sein ganzes Christentum sei wohl etwas ästhetischer Galimathias’; denn: ‘in ästhetischer Auffassung ist der eine Lehrer, der andere lernt, dann er wieder Lehrer u.s.w.’Ga naar voetnoot6) Auch Kierkegaard selber ist kein Lehrer; diese Konsequenz wird nicht übersehen; sein Buch ‘ist also überflüssig, | |||||||
[pagina 114]
| |||||||
darum bemühe sich keiner damit, sich auf das Buch zu berufen; denn wer sich darauf beruft, hat es eo ipso missverstanden’.... und den Verfasser ‘in die Bürgerliste eingeführt’.Ga naar voetnoot1) Wehe denen, die sein Paradox jemals zu einem ἔνδοξον machen würden!Ga naar voetnoot2) Und was Christus betrifft: ‘Christus ist das Paradox, das die Geschichte nie verdauen, noch in einen allgemeinen Syllogismus umsetzen kann’.Ga naar voetnoot3) Hier geht der Logos von Joh. I, der Gott, der Fleisch ward, in ‘Sigê’ unter: der tragische Held möge ‘all sein Tun’ liegen sehen ‘in dem Gebiete des Offenbaren’, aber wer ‘gegen das Paradox anstösst’, erfährt es: sowohl ‘das göttliche’ als auch ‘das dämonische’ sind ‘beide’ ‘Schweigen’.Ga naar voetnoot4) Und ‘auch die Not und Angst des Paradoxes’ liegt ‘gerade in dem Schweigen’. Wer ‘fordern’ würde, dass Abraham paradoxus ‘reden soll’, der würde ihn gerade ‘wieder aus dem Paradox herausheben, ihn in dem entscheidenden Augenblick das Paradox suspendieren lassen wollen’.Ga naar voetnoot5) q) So muss wohl alles auslaufen auf ein Anwenden, hier, der ‘letzten’ Worte, die Theologie und Philosophie ersinnen können. Was die Theologie auf Gott und Gottes Wort angewandt hat, das wird hier vom Paradox ausgesagt: Es ist index et iudex sui et falsi.Ga naar voetnoot6) Und das ‘teure’ Wort der Philosophie ist hier nicht zu kostbar: ‘wir brauchen eine neue Kategorie, um Abraham zu verstehen.’Ga naar voetnoot7) ‘Das Paradox ist eine Kategorie. Darum dreht sich eigentlich alles.... Das Paradox ist nicht eine Konzession, sondern eine Kategorie, eine ontologische Bestimmung, die das Verhältnis ausdrückt zwischen einem existierenden Geist und der ewigen Wahrheit’.Ga naar voetnoot8) | |||||||
[pagina 115]
| |||||||
§ 2. Radikalismus der Kierkegaardschen Wendung.Auch ohne dass schon die Frage nach dem theologisch-philosophischen Hintergrund des Kierkegaardschen Paradoxes erörtert wurde, kann aus den Zitaten, die gegeben wurden, doch wohl sofort ersehen werden, wie radikal Kierkegaard das Wort ‘Paradox’ losgelöst hat von der Bedeutung, die es jahrhundertelang gehabt hat. Wir wollen versuchen, durch einen Vergleich des früheren Paradoxes mit dem Kierkegaardschen die wichtigsten Unterschiede hervorzuheben. Wir nennen dabei das Paradox in seiner früheren allgemeinen Bedeutung A, das Kierkegaardsche B. Bei A ist das Paradox immer etwas, das überwunden werden soll; bei B ist sein Ueberwundenwerden eine Unmöglichkeit, Sündenfall, Niederlage. - Paradox A ist incitamentum intellectus, B ist sacrificium intellectus. - Das Martyrium des Paradoxes A kann nur bei den Entarteten Platz machen für ein Wonnegefühl, (Sophisten), das des Paradoxes B ist (in der Leidenschaft der Liebe) selbst eine Wonne geworden. - Im Falle des Paradoxes A ist das Genie, als von Anfang an nicht orientiert am Allgemeinen, in der günstigsten Lage, um vom Paradox loszukommen, im Falle B ist das Genie, als ‘von Anfang an desorientiert im Verhältnis zu dem Allgemeinen’, in der günstigsten Lage, um zum Paradox zu kommen.Ga naar voetnoot1) - Paradox A ist ein Zusammenstoss von Meinungen, die korrespondieren oder nicht korrespondieren mit Wirklichkeiten, die beide auf derselben Ebene liegen; daher verursacht es eine ‘tragische’ Lage, sucht | |||||||
[pagina 116]
| |||||||
man nach einem ‘Ausgang’, nicht so wie man (ästhetisch) ‘gespannt ist auf den Ausgang wie auf den Ausgang eines Romans’, sondern weil im Denken und also im Sein, im Leben, Not ist. Aber Paradox B ist ein Zusammenstoss von Wort Gottes und menschlicher Existenz, von Ewigkeit und Zeit, also von dem, das nicht auf derselben Ebene liegt; daher geht es über jede tragische Lage hinaus und ist das Suchen nach einem Ausgang, das Gespanntsein auf den Ausgang, gerade ein Beweis, dass man ‘von dem Paradox nichts wissen will’. -Ga naar voetnoot1) Paradox A bedeutet eine πτῶσις, seine Ueberwindung eine ἀνάστασις, beide auf derselben Ebene. Paradox B ist ἀνάστασις, aber dann auf keiner einzigen ‘Ebene’. - A ist Inzident, B Kategorie. - A ist Anfechtung, B niemals. - Zu A kommt ‘Sokrates’ nur auf dem Weg seines Wissens, und er fühlt sich dann gedrückt in einer relativen Unwissenheit; zu B kommt Sokrates nur durch Unwissenheit, die ihn zum Befreier machen könnte, wenn das einem Menschen gegeben wäre. - Die paradoxe Not A suspendiert jede ‘Hebamme’ von ihrem Dienst; die paradoxe Not B setzt die ‘Hebamme’ gerade in ihren Dienst ein. - Paradox A ist immer eine Sache des Allgemeinen, kann nur auftauchen, wo allgemeine Gesetze des Denkens und Handelns sind; Paradox B ist ein dem Allgemeinen den Rücken Zukehren, ein Isoliertsein als Einzelner. - Paradox A setzt voraus die ‘Kompanie’, deren ‘Meinung’ widersprochen worden ist, und seine Lösung ist immer aus den Denkgesetzen der ‘Gemeinschaft’ gefunden oder kehrt aus dem ‘privatissimum’, wo sie gefunden ward, segnend zu der Gemeinschaft zurück. Aber Paradox B setzt gerade die Loslösung aus der ‘Kompanie’ voraus, bleibt auf das privatissimum beschränkt, kann nicht segnend (kritiklos) auf die Gemeinschaft einwirken. - Paradox A muss eine Brücke schlagen zum ἔνδοξον; Paradox B ruft das Wehe über jeden Brückenbauer aus. - Wenn A auftaucht, dann ist die Aporie da, wer B gekannt hat, | |||||||
[pagina 117]
| |||||||
ist über die Aporie erhaben - sofern er B begegnet, und so oft er das tut. - A ist der Schrecken des intellektuellen Lebens, B ist sein Pathos, das eigentliche Pathos.Ga naar voetnoot1) - A kommt in der Relation Lehrer-Lernender vor; B quält und segnet sie beide, aber dann privatim, und wischt ihre Relation, ihre Unterscheidungsnamen aus. - A ist gegen die herrschende, B gegen alle Meinung. - Im Moment A kommt man sicher zur Ungewissheit, im Moment der Ungewissheit kommt man vielleicht zu B. - Leidenschaft will A niederschlagen, Leidenschaft will sich mit B vereinigen, aber in Liebe. - A tritt dem praktisch Denkenden in den Weg, B ist eine erkenntnistheoretische Gegebenheit; A ist eine Crux bei der Vollendung eines Lehrbuches, B ist das erste. Kapitel in den Prolegomena eines Zeugnisses. - A ist nicht absurd; denn es will gerade davon wegfliehen, B ist selbst absurd. - A ist nur möglich, wenn die Denkgesetze Geltung haben, B nur, wenn dieser Geltung fundamental widersprochen ist. - A sucht Aufhebung, B Aufbewahrung des Widerspruches. - A ist eine Sache von Schwäche oder Kraft, B von Tod oder Leben. - A kann es geben in der Religiosität A, B nur bei der Religiosität B. - ‘Wenn das Schiff ein Leck bekommen hat, dann das Schiff’ verzweifelt ‘durch Pumpen zu halten und’ ‘den Hafen aufzusuchen’: das ist Paradox A. ‘Wenn das Schiff ein Leck bekommen hat, dann das Schiff begeistert durch Pumpen zu halten und doch den Hafen nicht aufzusuchen’: das ist Paradox B.Ga naar voetnoot2) - ‘Wenn der Spekulant das Paradox so erklärt, dass er es aufhebt, und nun wissentlich weiss, dass es aufgehoben ist, dass das Paradox also nicht das wesentliche Verhältnis der ewigen, wesentlichen Wahrheit zu einem ist, der im stärksten Grade existiert, sondern nur ein zufälliges Relations-verhältnis zu beschränkten Köpfen, so herrscht ein wesentlicher Unterschied zwischen dem Spekulanten und dem | |||||||
[pagina 118]
| |||||||
Einfältigen’;Ga naar voetnoot1) der erstere steht an der Spitze der Gemeinschaft (‘Kommunie’) aller Grübler über Paradox A und beschwört, dass er wenigstens nie wieder zu rufen brauche, so wie seine Nachhut es im selben Moment noch tut: hier stehe ich, ich kann nicht anders, Gott helfe mir, amen!, denn was ihn, den Spekulanten, betrifft: er hat sich selber geholfen. Und der andere, der Einfältige: er beugt sich ganz allein als neue Kreatur im Lehrzimmer des Paradoxes B und ruft, noch immer als der Einzelne, nur Gott vernehmbar: hier liege ich, ich will nicht anders, Gott hat mir geholfen, amen. ‘Geholfen’, - das bedeutet hier: ‘besiegt’. | |||||||
[pagina 119]
| |||||||
§ 3. Die Wendung auf mathematischem Gebiet.Zwischen Kierkegaards Philosophie und der Mathematik scheint ein grosser Abstand zu liegen; so gross, dass der Uebergang von Kierkegaard zur Mathematik, auch insoweit es sich um die Begriffsgeschichte des Paradoxons handelt, eigentlich etwas Ueberraschendes hat. Dennoch gibt es - wie wir sehen werden - verborgene Verbindungsdrähte zwischen einer Philosophie der Antithese ‘absolut-existentiell’ und der Mathematik mit ihrem Unendlich-Endlich-Problem. Auf mathematischem Gebiet hat sich nämlich viel geändert. ‘Calculum vera dicere, & eorum rationes, quae ad repraesentandum proponuntur, ita reddere, ut sunt, nemo est qui dubitet’; dieser uns schon bekannte AusspruchGa naar voetnoot1) eines Jesuiten (1773) würde in unserer Zeit nicht mehr gehandhabt werden können. Auf der Prager Tagung der Deutschen Mathematiker-Vereinigung (1929) wurde offen durch Heinrich Behmann erklärt, dass ein solches Fortschreiten der Mathematik auf dem Wege logischer Folgerichtigkeit nur noch von dem Nichteingeweihten behauptet werden könne.Ga naar voetnoot2) Wenn es auch nur die Als-Ob-Philosophie wäre, die hier Zweifel erweckt, ja leugnet ‘calculum vera dicere’, so bleibt es doch eine Tatsache, dass dieser Zweifel besteht. Und wie wir sehen werden, hat die Als-Ob-Philosophie | |||||||
[pagina 120]
| |||||||
auch auf mathematischem Gebiet ihre Anhänger gefunden. Aus dieser blossen Andeutung wird schon deutlich, dass dann auch auf dem Gebiet der Mathematik (und verwandter Wissenschaften) die Verwendungsgeschichte des Wortes ‘Paradox’ uns vor Schwierigkeiten stellen muss. Denn das Wort war, auch als terminus technicus, schon lange in der Mathematik bekannt; von ihren Paradoxen und Paradoxien nannten wir schon viele Beispiele. Wir bemerkten zugleich, dass dabei stets nach paradoxfreien Lösungen der Schwierigkeiten gesucht wurde, d.h. die herrschende Strömung in der Mathematik ging auch weiterhin von dem Gedanken aus, der sich uns bis auf Kierkegaard als den herrschenden zeigte, dass das Paradox, genau genommen, galt als ein Ding, das überwunden werden musste. Die herrschende Strömung, sagten wir; denn wohl behauptete u.a. L.E.J. Brouwer im Jahre 1908 die Unzuverlässigkeit der logischen Prinzipia auf dem Gebiete der Mathematik, aber noch 1919 erklärte er selber, dass diese Auffassung damals noch wenige Anhänger gefunden hatte.Ga naar voetnoot1) In dieses Suchen nach einer widerspruchslosen Mathematik hatte auch Kants Auftreten so gut wie keinen Umschwung gebracht, nicht einmal mit Bezug auf die Nomenclatur: Kants Ausdruck ‘Antinomie’ konnte das schon eingebürgerte Wort Paradoxon nicht verdrängen. Aber doch hat die Tatsache, dass Kant von ‘Antinomien’ sprach, hier grosse Bedeutung. Denn hinter den verschiedenen mathematischen Paradoxa, wie sie von alters her bekannt waren, lagen schliesslich verschiedene Probleme der Logik und Metaphysik, insonderheit die Frage nach Inhalt und Brauchbarkeit des Begriffes des ‘Unendlichen’. Nun hatte Kant in seiner ‘Transzendentale(n) Elementarlehre’ seine bekannten Antinomien der reinen Vernunft aufgestellt; und in der ersten und zweiten Antinomie hatte er die für die Mathematik ganz besonders kardinalen Probleme: u.a. | |||||||
[pagina 121]
| |||||||
‘ein unbestimmtes Quantum als ein Ganzes’, ‘das Unendliche’, ‘die Unendlichkeit einer Reihe’, ‘die Menge’ und ‘die Zahl’, ‘Teil und Ganzes’ usw. auf die Tagesordnung gebracht, und zwar gerade unter der Ueberschrift: Von den Antinomien.Ga naar voetnoot1) Kants scharfe Problemstellung zwang also die Mathematik, ihre Paradoxe immer wieder aufs neue zu untersuchen, auch in philosophischem Denken, und, besonders in der Infinitesimalrechnung und in den vor- und nach-Cantor'schen Paradoxien des Unendlichen, sich die Frage zu stellen, ob das Denken hier vor eine echte, unlösliche Antinomie gestellt war oder nicht. Von ‘Durchbrechung von Axiomen und algebraïschen Gesetzen’ musste wohl geredet werden,Ga naar voetnoot2) aber wurden die Denkgesetze durchbrochen? Die Frage wurde so dringend, dass Cantor eintrat für eine ‘freie Mathematik’, ‘deren Maszstab lediglich die immanente gedankliche Folgerichtigkeit und nicht die Darstellung und Bewährung in irgendeiner transienten objektiven Realität ist’;Ga naar voetnoot3) hier drohte also schon, erst eine Scheidung, bald ein Streit zwischen Logik und Ontologie. Andere zogen sich mit ihren mathematischen Paradoxa hinter die Verschanzung einer ‘formalen Logik’ zurück und behaupteten, dass ferner die ‘eidetische Logik’ mit der Mengenlehre, in der die Paradoxa gerade so quälend wurden, nichts zu schaffen habe.Ga naar voetnoot4) Bei einem solchen Stand der Dinge war die Frage eigentlich schon berechtigt, ob das doch schon ziemlich ungeschützte Wort ‘Paradoxon’ nicht auch noch seinen letzten Schutz verlor, ob es nicht immer mehr seiner alten Bedeutung (nach der eine logische Absurdität für den Begriff ‘Paradoxon’ absolut nicht konstituierend war) beraubt und tatsächlich für vogelfrei erklärt wurde. Und als bald bei diesem Stand des Problems die Als-Ob-Philosophie innerhalb des Gebietes der Mathematik selbst von dem ‘Widerspruch im Richtigen’ | |||||||
[pagina 122]
| |||||||
zu reden anfing,Ga naar voetnoot1) um zu versichern, dass nicht nur die bis dahin bekannten Paradoxa, sondern eigentlich alle mathematischen Grundbegriffe bei näherer Untersuchung ‘innere Widersprüche’ enthielten und dass sie ‘der geltenden Logik ins Gesicht’ schlügen, da war der terminus technicus Paradoxon in der Tat ins Chaos geworfen. Stand man vor einem unentrinnbaren Konflikt mit den allgemeinen Denkgesetzen oder nicht? Wenn ja, war das Paradoxon dann Ausnahme oder Regel? War die Mathematik ‘frei’ von einer bestimmten Logik, oder sogar frei zu einer eigenen Logik? Waren die Paradoxa hier verwandt mit wesentlichen, strengen Antinomien,Ga naar voetnoot2) oder ist es ein ganz normales, unumgängliches Werk, zu operieren mit Begriffen, die nicht widerspruchsfrei sind?Ga naar voetnoot3) Die ‘neue Grundlagenkrise der Mathematik’Ga naar voetnoot4), von der H. Weyl spricht, gab auch auf dem Gebiet der Mathematik den Begriff ‘Paradoxon’ einer allgemeinen Verwirrung preis. Es ist hierbei jedoch deutlich, dass auf dem Gebiet der Mathematik keine Rede sein konnte von einer so scharf gezeichneten, so akuten Umkehr in der Verwendungsart | |||||||
[pagina 123]
| |||||||
des Begriffes Paradoxon, wie sie sich, wie wir sahen, auf dem Gebiet der Theologie und der Philosophie durch das geniale Auftreten Kierkegaards vollzogen hatte. Das spricht für sich. Wir nennen nur zwei Umstände zur Erklärung, ausser der schon genannten Unsicherheit, die eigentlich selbst schon alles sagt. An erster Stelle ist es bemerkenswert, dass geraume Zeit bestimmte, unter diesem Namen bekannte Paradoxa, als scharf gestellte Fragepunkte und cruces für das Denken, eigentlich am kräftigsten in der Mathematik c.s. lebten. Gewiss hatte und gebrauchte die Logik in ihrer Propaedeusis noch immer ihr doch wohl sehr altes Erbe von den Sophisten; man denke nur an die klassischen Zeno'schen ‘Beweise’: ein Bewegtes kann nie eine beliebige Strecke durchlaufen; Achilles kann die Schildkröte nicht einholen; der fliegende Pfeil ruht in jedem Augenblick, also verändert er seine Lage nicht. Und so gab es Paradoxe mehr, an denen sich die Technik des ‘formal’-logischen Denkens übte, wir nennen nur das Lügner-Paradoxon,Ga naar voetnoot1) das Sophisma des EvathlusGa naar voetnoot2) und das Krokodilsdilemma.Ga naar voetnoot3) Aber ausser solchen sehr alten Erbstücken kannte weder Theologie noch Philosophie bestimmte, mit scharfer Problemstellung als cruces intellectus unter eine Formel gebrachte Paradoxa. Ganz anders verhielt es sich dagegen mit der Mathematik. Sie hatte dieselben Paradoxa, die wir soeben nannten, an denen die Schulpropaedeusis der Logik sich nach oben arbeitete, selbständig als Fragen behandelt und schon von alters her begriffen, | |||||||
[pagina 124]
| |||||||
dass metaphysische und theologische Fragen über die Unendlichkeit und das Kontinuum dahinter lagen. Wir erinnern nur daran, dass z.B. in der Korrespondenz zwischen F.G. le Baron de Nulandt und Chr. Huygens das Paradoxon Galileis mit direkt theologischen Fragen verknüpft wurdeGa naar voetnoot1) oder dass M. Bettinus in seinem schon erwähnten Apiarium (wenngleich bei ihm die Grenze zwischen dem genus der iucunda und der nicht-iucunda schwer zu ziehen ist) doch die Denkkraft ans Werk gesetzt hat, indem er mit seinen Paradoxa circa aequalitatem et inaequalitatem figurarum ein corollarium verband über die.... paradoxica de Angeli extensione à coelis ad usque terras, und zwar im Zusammenhang mit Scotus. Auch für rein mathematische Forschung hatte die Mathematik schon etliche bestimmte Paradoxa unter einem festen Namen registriert (I, § 3). Ja, sie machte aus den klassischen Paradoxa auch in der jüngsten Zeit, besonders nach Cantor und Russell, rein mathematische Paradoxa. So werden, z.B. durch Eugen Böckli, Russell und viele andere, die Zeno'schen ‘Beweise’ oder Paradoxa gerade als Paradoxien der Zeit aus der isolierten Sphäre der formalen Logik herausgezogen und hinübergetragen in die mathematisch-philosophische Sphäre, wo dann jeder für sich eine Lösung dafür sucht, Böckli durch den kritischen Idealismus, Russell durch seine Typentheorie, u.s.w. Das Registrieren von festen, auf eine Formel gebrachten Paradoxa wird dann auch noch immer fortgesetzt; man kommt sogar zu neuen Unterscheidungen. So wird z.B. das klassische Lügner-Paradoxon ebenso wie das ganz neue Paradoxon von Richard, über das wir noch sprechen werden, unter die nicht rein-formallogischen bezw. rein-mathematischen Widersprüche gerechnet, die dann mit dem Namen semantisch bezeichnet werden.Ga naar voetnoot2) | |||||||
[pagina 125]
| |||||||
Soweit nun die festen, auf eine Formel gebrachten, von alters her bekannten Paradoxa einmal ihren historischen Namen empfangen haben, sind sie auch unter diesem Namen bekannt geblieben, ungeachtet der Frage, ob diejenigen, die sich dieses Namens bedienten, Paradoxa in weiterem oder in engerem, praegnantem Sinn darin glaubten erkennen zu müssen. Dies Verschleiertlassen des Begriffes Paradoxon hatte dann natürlich auch wieder Einfluss auf die Neubildung von Paradoxa; auch dabei konnte jeder die crux für das Denken auf seine eigene Weise auslegen. An zweiter Stelle wurde eine scharfe und acute Veränderung in der Verwendung des Wortes und Begriffes ‘Paradoxon’ (wie wir ihr bei Kierkegaard begegneten) auch durch den schon erwähnten Umstand verhindert, dass weitaus die meisten Mathematiker auch weiterhin jeden ‘Widerspruch im Richtigen’ verneinten und ihre Wissenschaft von logischen Absurditäten in striktem Sinne frei nannten. Wohl zeigt Ph. Kohnstamm, dass er die Situation nicht richtig sieht, wenn er schreibt: ‘Die neuere Mathematik hat, namentlich in den Spuren Dedekinds, die Methoden des Definierens und Argumentierens zu so grossem Scharfsinn emporgehoben, dass man nicht nur die Zeno'schen Schwierigkeiten als überwunden betrachten darf, sondern zugleich sagen kann, dass auf diesem Gebiet - im Gegensatz zu dem, was seinerzeit Hegel noch meinen konnte - gewiss nicht mehr gesprochen zu werden braucht von einer coincidentia oppositorum’.Ga naar voetnoot1) Aber doch besteht das Streben, soweit zu kommen. Auf obenerwähnter Prager Tagung klagte H. Behmann nicht über ein zuwenig, sondern über ein zuviel an Lösungen der Paradoxa. Wiesehr man denn auch noch immer in den breiten Schichten der Mathematiker sich bemüht, einer solchen coincidentia oppositorum zu entkommen, zeigt wohl die Diskussion über das sogenannte Russellsche Paradoxon. | |||||||
[pagina 126]
| |||||||
Es handelt von der ‘Klasse aller sich nicht selbst enthaltenden Klassen’ oder, wie Bertrand Russell es selber ausdrückt, von ‘predicates not predicable of themselves’. Es gibt, wie Russell das Problem stellt,Ga naar voetnoot1) class-concepts (Schönflies substituiert hier: Mengen, Benno Urbach: Begriffe) which can be asserted of itself. Was das Wort ‘class-concept’ betrifft, verweisen wir auf seinen Ausspruch, dass man ‘class’ und ‘class-concept’ klar unterscheiden muss; ‘the class must be distinguished from the class-concept or predicate by which it is to be defined: thus men are a class, while man is a class-concept’ (p. 19). Ueber diese class-concepts bemerkt nun Russell, dass es solche gibt, die ein Glied (term) sind ihres eigenen Umfanges und andere, die es nicht sind. Der Begriff nicht-rot z.B. is selber nicht rot, der Begriff der Begriffe ist selber jedoch auch ein Begriff. Demgegenüber steht dann wieder, dass der Begriff ‘Mensch’ selber kein Mensch ist und der Begriff ‘rot’ selber nicht rot. Nehmen wir nun einen Begriff, der das Gemeinsame aller Begriffe der letztgenannten Art zusammenfasst, und nennen wir den z.B. Z, dann ist Z der Be- | |||||||
[pagina 127]
| |||||||
griff der Begriffe, die nicht ein Glied (term, member) ihres eigenen Umfanges sind. Es wird nun die Frage gestellt, ob auch Z ein Glied seines eigenen Umfanges ist oder nicht. Nennen wir nun die Begriffe, die nicht ein Glied ihres eigenen Umfanges sind a. Z ist dann der Begriff aller a. Nimmt man an, dass Z wohl ein Glied seines eigenen Umfanges ist, dann ist Z also (weil in diesem Umfang alle a begriffen sind) ein a. Aber.... wenn Z ein a ist, dann ist Z doch kein a; denn es war vorausgesetzt, dass a heissen sollten alle Begriffe, die kein Glied ihres eigenen Umfanges sind. Nimmt man an, dass Z nicht ein Glied seines eigenen Umfanges ist, dann ist Z kein a (nach der Voraussetzung). Aber wenn Z nicht ein Begriff ist, der nicht ein Glied seines eigenen Umfanges ist (so hiess a), dann ist Z wohl ein Glied seines eigenen Umfanges, und das Entgegengesetzte war gerade vorausgesetzt. Wiewohl Russell selbst sofort versuchte, dies Problem ‘to solve’ - er selber bezeichnete es als the contradiction with regard to predicates not predicable of themselves - so quälte doch dieses bestimmte Paradox die Geister auch weiterhin. Es hat ‘eine förmliche Bestürzung im Lager der modernen Mathematik hervorgerufen’,Ga naar voetnoot1) und veranlasste sogar einige zu der Klage, dass ‘der ganze wissenschaftliche Aufbau’ dadurch ‘in Frage gestellt’ sei.Ga naar voetnoot2) Schon daraus erhellt, dass die Lösung, die Russell selber davon gab, im selben Werk, in dem er auch das Problem stellte (später auch noch in den mit A.N. Whitehead herausgegebenen Principia Mathematica, vol. I, 2e Aufl., 1925, p. 1, 60 ff.), nicht allgemein angenommen wurde. Aber die Versuche, zu einer Lösung zu kommen, wurden nicht aufgegeben. Sie kehren immer wieder, so z.B. | |||||||
[pagina 128]
| |||||||
bei Benno UrbachGa naar voetnoot1) oder, wieder auf eine andere Weise, bei Otto Samuel, der übrigens im Titel seines diesbezüglichen Aufsatzes nicht von Paradoxa, sondern von ‘diskursiven Sophismen’ spricht.Ga naar voetnoot2) Wieder auf andere Weise sucht Schönflies ‘die Quelle des Russellschen Paradoxons aufzudecken’Ga naar voetnoot3) oder Hugo Dingler, Joseph Petzoldt, Julius König, Hans Lipps u.s.w.Ga naar voetnoot4) Dieselbe Tendenz, zu einer paradoxfreien BetrachtungGa naar voetnoot5) zu kommen, finden wir in den mannigfachen Konstruktionen einer Mengenlehre und, im Zusammenhang damit, in den verschiedenen Versuchen, die gemacht werden, um zwischen ‘endlich’ und ‘unendlich’ jedem Schein einer antinomischen Relation zu entgehen, m.a.W.: um das Wort ‘Paradoxon’, auch, ja besonders, wo es in der Mengenlehre infolge der Relation: endlich-unendlich vorkommt, von jedem Verdacht der logischen Absurdität zu befreien. Auch in dieser Hinsicht hat Bertrand Russell in seinen ‘Principles of Mathematics’ § 337-350 (vgl Principia I, 60-65) in einem Kapitel über ‘the philosophy of the infinite’ (infinity and continuity) sich bemüht, sowohl Probleme zu stellen als auch zu lösen, die mit dem Unendlichkeitsbegriff zusammenhingen. Er gibt sogar in seinen ‘Principles’ (p. 358) eine Analogie zu dem Zeno'schen Paradoxon von Achilles und der Schildkröte, nämlich im Paradoxon von Tristam Shandy. Dieser verwendete 2 Jahre auf die Beschreibung der 2 ersten Tage seines Lebens, konnte | |||||||
[pagina 129]
| |||||||
also niemals fertig werden, aber, sagt Russell, ‘if he had lived for ever and not wearied of his task, then, even if his life had continued as eventfully as it began, no part of his biography would have remained unwritten’, § 340. Beweis: a) T.S. writes in a year the events of a day; b) the series of days and years has no last term; c) the events of the nth day are written in the nth year; d) any assigned day is the nth, for a suitable value of n; e) hence any assigned day will be written about; f) hence no part of the biography will remain unwritten; g) since there is a one-one correlation between the times of happening and the times of writing, and the former are part of the latter, the whole and the part have the same number of terms. Dieses Paradoxon, sagt Russell, deduces that whole and part may be similar.Ga naar voetnoot1) Auch hier stehen wir wieder vor derselben Tatsache wie soeben; die Lösung, die Russell selber gab, befriedigte viele nicht. Aber das Problem blieb in der Mengenlehre auf der Tagesordnung; die Versuche von einigen, die Mengenlehre (Mannigfaltigkeitslehre), wie auch die Zahlenlehre, soviel wie möglich ‘von der Mathematik abgerückt’ zu halten,Ga naar voetnoot2) fanden ungenügende Unterstützung. Es wurden gerade umgekehrt andere Paradoxa aufgestellt, die man, was die Problemstellung betrifft, kaum von den klassischen, rein formal-logischen unterscheiden kann. So z.B. das Paradoxon von Richard, das durch L.E.J. Brouwer in vereinfachter Form so wiedergeben wird: Gibt es eine kleinste ganze Zahl, die nicht durch einen Satz von höchstens zwanzig Worten definiert werden kann? Einerseits ja; denn die Anzahl Sätze von höchstens zwanzig Worten ist natürlich endlich. Aber andererseits nein; denn wenn sie bestünde, würde sie durch den hier oben als Frage gestellten Satz von 18 Worten definiert sein.Ga naar voetnoot3) Oder das von | |||||||
[pagina 130]
| |||||||
Russell und Jörgen Jörgensen (A Treatise of formal Logic, Copenh., London, 1931, III, 165) erwähnte Paradox von Berry: 111777, ‘the lowest integer not nameable in fewer than 19 syllables (one-hun-dred-and-el-ev-en-thou-sand-sev-en-hun-dred-and-sev-en-ty-sev-en) is found to be nameable in 18 syllables (the-least-in-te-ger-not-name-a-ble-in-few-er-than-nine-teen-syl-la-bles)’. Oder das Paradoxon von Burali-Forti: wenn eine, was ihre Reihenfolge betrifft, wohlgeordneteGa naar voetnoot1) Reihe von Ordnungszahlen alle Ordnungszahlen enthält, dann muss diese Reihe selbst eine neue Ordnungszahl definieren, die nicht in ihr selbst enthalten ist. Der Begriff der Menge aller Ordnungszahlen muss also widerspruchsvoll sein; die im Problem gestellte Annahme muss also falsch sein, m.a.W. keine Menge von Ordnungszahlen enthält jemals alle Ordnungszahlen.Ga naar voetnoot2) Es hat für unseren Zweck jetzt keinen Sinn, auf diese Dinge weiter einzugehen. Wohl interessiert uns in diesem Stadium unserer Untersuchung die Frage, welchen Inhalt der Begriff ‘des Unendlichen’ in diesen Paradoxien der Mengenlehre hat. Denn in § 1 und § 2 dieses Kapitels zeigte sich uns bei der Besprechung von Kierkegaard, dass auch bei ihm die Lehre der Paradoxie eigentlich ihren Anfang nimmt mit dem Begriff des Unendlichen. Auch in den mathematischen Paradoxien tritt dieser Begriff auf, und sofort wird unter seinem Einfluss die Zahl der Paradoxa grösser. Liegt hier eine Uebereinstimmung vor? Um diese Frage zu beantworten, achte man wohl darauf, dass die Behandlung der Mengenlehre, namentlich was den Begriff des Unendlichen betrifft, eigentlich in der Mathematik sich aufs neue nicht so sehr an Kant oder Leibniz geknüpft hat, wenn diese auch hier und dort in der Diskussion als Urheber des Problems in den Vorder- | |||||||
[pagina 131]
| |||||||
grund gestellt werden,Ga naar voetnoot1) als vielmehr an Bernard Bolzano in seinem bekannten Werk ‘Paradoxien der Unendlichkeit’.Ga naar voetnoot2) Dies hat nun für uns insoweit Bedeutung, als auf den ersten Blick die Problemstellung von Bolzano der Kierkegaards ähnlich zu sein scheint. Und zwar nicht so sehr, weil auch Bolzano an Hegel Kritik übt,Ga naar voetnoot3) sondern vor allem, weil auch seine Problemstellung, wie die Kierkegaards, eigentlich ihren Ausgangspunkt im ‘Unendlichen’ nimmt. ‘Nicht zwar, wie Kästner sagt, alle, aber gewiss die meisten paradoxen Behauptungen, denen wir auf dem Gebiete der Mathematik begegnen, sind Sätze, die den Begriff des Unendlichen entweder unmittelbar enthalten, oder doch bei ihrer versuchten Beweisführung in irgendeiner Weise sich auf ihn stützen’, sagt er.Ga naar voetnoot4) ‘Eine Vielheit, die so beschaffen ist, dass jede endliche Menge nur einen Teil von ihr darstellt’ nennt er nun ‘eine unendliche Vielheit’;Ga naar voetnoot5) und von hier aus sucht er dann zu kommen zu einer Bestimmung ‘eines Unendlichen überhaupt’.Ga naar voetnoot6) So gelangt Bolzano zu dem Begriff ‘unendlich gross’: ‘eine Grösse, grösser als jede Anzahl der zur Einheit angenommenen’, und zu dem Begriff ‘unendlich klein’: ‘eine Grösse.... so klein, dass jedes Vielfache derselben kleiner ist als die Einheit’.Ga naar voetnoot7) Die scheinbar hier vorhandene Analogie mit Kierkegaards Problemstellung nun kann man nicht ohne weiteres abtun mit der Bemerkung, dass wir uns bei Bolzano und bei Kierkegaard doch auf jedesmal ganz anderen Denkgebieten befinden; denn wenn wir auch sogleich diesem Bedenken volles Recht widerfahren lassen werden, so bleibt es doch | |||||||
[pagina 132]
| |||||||
eine Tatsache, dass Bolzano selbst (der in derselben Zeit wie Kierkegaard schrieb) im voraus jeder radikalen Loslösung der seiner Ansicht nach unverkennbaren und unvermeidlichen gedanklichen Zusammenhänge zwischen seinem Begriff des ‘Unendlichen’ einerseits, und dem der Philosophie im allgemeinen andererseits, widersprochen hat. Es sei ihm, sagt er, bekannt, dass ‘einige Philosophen, zumal der neueren Zeit, wie Hegel und seine Anhänger’, das ‘Unendliche’, wie die Mathematiker es kennen, ‘verächtlich das schlechte Unendliche nennen’, und dass sie ‘ein viel höheres, das wahre, das qualitative Unendliche kennen wollen, welches sie namentlich in Gott und überhaupt im Absoluten nur finden’. Bolzano weiss, welches Argument diese Philosophen dafür anführen, sie denken sich das mathematisch-Unendliche ‘nur als eine Grösse, welche veränderlich ist und in ihrem Wachstume keine Grenze hat’. Nun ist Bolzano selber bereit, anzuerkennen nicht nur, dass diese von philosophischer Seite gegebene Umschreibung des mathematisch-Unendlichen in der Tat auf Aeusserungen vieler Mathematiker selbst sich berufen kann, sondern auch, dass die ablehnende Kritik von Hegel c.s. an einem solchen Begriff ‘einer in das Unendliche nur wachsenden, nie es erreichenden Grösse’ richtig ist und von ihm geteilt wird. Aber er bemerkt weiter: ‘was ich nur nicht zugestehe, ist bloss, dass der Philosoph einen Gegenstand kenne, dem er das Prädikat der Unendlichkeit beizulegen berechtigt ist, ohne in diesem Gegenstande in irgendeiner Beziehung erst eine unendliche Grösse oder doch die Vielheit nachgewiesen zu haben’. Bolzano glaubt, dass die Philosophie zu ihrem Begriff ‘Gott’, ‘das Absolute’ oder ‘das All’ also letztlich auch nur kommen kann allein über die Brücke des ‘unendlich Vielen’.Ga naar voetnoot1) Nicht so sehr in metaphysischem, als in erkenntnistheoretischem Gedankengang will also Bolzano seinen Platz neben Hegel und - so könnten wir mit Bezug auf die Paradoxien hinzufügen - neben Kierkegaard, auf dem- | |||||||
[pagina 133]
| |||||||
selben Niveau anerkannt sehen. Man kann also die von uns wenigstens auf den ersten Blick behauptete Analogie zwischen Bolzanos und Kierkegaards Ausgangspunkt auf dem Weg zur Konstruktion des Paradoxons nicht so ohne weiteres bestreiten mit der Behauptung, dass das Unendliche des einen in einer anderen ‘Dimension’ liege als das des anderen. Bolzano bestreitet gerade die erkenntnistheoretische Legitimierbarkeit dieser beide Denker gegeneinander abgrenzenden Behauptung. Man muss anerkennen, dass, auch in Anbetracht der allgemeinen Verwirrung in der Verwendung des Prädikats ‘unendlich’, auch wo es auf Gott oder das Absolute angewandt wurde,Ga naar voetnoot1) die Problemstellung von Bolzano der Kierkegaardschen wenigstens ähnlich sah. Und doch ist diese Analogie nicht mehr als Schein. Sie liegt nur im Klang des Wortes ‘unendlich’. Denn gerade durch seine scharfe Abgrenzung von ‘Glauben’ und ‘Denken’ (Spekulation) kann Kierkegaard zu einem Gegensatz zwischen unendlich und endlich, Gott und Menschen kommen, während Bolzano bei der Verteidigung seines Unendlichkeitsbegriffes gegen den ‘Tadel’ von Hegel c.s. sich gerade auf beider Einheit beruft und die Spekulation, sowohl die Hegels als auch seine eigene, ihre Autarkie behalten lässt. Man hat Bolzano und Lotze die ersten Intuitionisten genannt, die nach Kant für die Mathematik von Bedeutung waren, und Bolzano in metaphysicis zur monadologischen Schule gerechnet und zur normativen in logicis.Ga naar voetnoot2) Und hieraus erhellt, dass die Paradoxie bei Bolzano, obgleich sie ihre Probleme bei ‘dem Unendlichen’ ansetzt, schon gleich durch eine tiefe Kluft von Kierkegaards Gedankengang radikal getrennt ist. Bei Kierkegaard kommt ‘das’ (der) Unendliche aus sich selbst heraus zum Menschen und dessen Existenz (Gott | |||||||
[pagina 134]
| |||||||
ward Mensch); bei Bolzano kommt der Mensch zum Unendlichen (über das ‘unendlich Viele’ kommt der Philosoph zum qualitativen Unendlichen, Absoluten, Gott). Kierkegaard kennt ‘den’ Unendlichen, Bolzano nur ‘das’ Unendliche. Kierkegaard lässt den nexus cosmicus von Gott aus durchbrechen; sein Paradoxon ist gerade immer wieder, und zwar jedesmal im ‘Augenblick’, niemals in ‘Stetigkeit’, Folge eines unmittelbaren Einwirkens Gottes; aber bei Bolzano bleibt die Paradoxienlehre immer mit dem ‘Gesetz der Stetigkeit’ verbunden, setzt sie dieses Gesetz voraus wie auch den nexus cosmicus, und muss sie gerade in ihrer Konstruktion also absichtlich absehen ‘von einem unmittelbaren Einwirken Gottes’.Ga naar voetnoot1) Kierkegaards Unendliches kommt aus einer für uns ganz anderen ‘Dimension’, das des Bolzano nicht; das ‘Unendliche’ ist bei ihm denn auch nicht wie bei Kierkegaard zu ersetzen durch ‘das Ewige’. Dies alles nun ist zugleich charakteristisch für die ganze Art und Weise, wie in der Mathematik überhaupt das Unendliche aufzutreten pflegt. Im allgemeinen ist in der Mathematik das Unendliche eine Art werdender Unendlichkeit, ‘die man besser Endlosigkeit nennt’Ga naar voetnoot2) (Zahlenreihe, Unbegrenztheit des Raumes). Daneben tritt das Unendliche auf in dem Kontinuum (Raum, Zeit, Bewegung). ‘If a class u has terms, but not any finite number of terms, then it has an infinite number. This is the positive theory of infinity’.Ga naar voetnoot3) Die für die Kierkegaardsche Problemstellung so kennzeichnende Skizzierung einer ‘vertikalen’ Begegnung mit der horizontalen Welt und einer Schneidung von ihr ‘im Augenblick’ ist also für die Mathematik völlig unbrauchbar; endlich und unendlich liegen hier beide auf derselben ‘horizontalen’ Ebene. Das mathematisch-Unendliche ist, wie Eisler in seinem Wörterbuch bemerkt, kein ‘Gegebenes...., sondern es wird nur in grenzenlosem Fort- | |||||||
[pagina 135]
| |||||||
gang (Prozess, Regress) des Denkens, in unvollendbarer Synthese, gesetzt, postuliert, zur Aufgabe gemacht’. Dies auf die ‘Unendlichkeit’ der Kierkegaardschen Dialektik zu übertragen, würde bei ihm Blasphemie bedeuten. Kierkegaard weigert sich, das Unendliche je bildlich zu fassen; aber die Mathematik, z.B., wenn sie spricht von einem ‘unendlich kleinen’, das von Null unterschieden werden muss, A, kann, auch wenn A transsubjectiv gemacht wird, wenigstens von ihrem eigenen Standpunkt aus dem Gedanken nicht entkommen, dass sie hier ‘unendlich’ in einer bildlichen Bedeutung gebraucht.Ga naar voetnoot1) Während bei Kierkegaard das Paradox dadurch entsteht, dass der Absolute oder das Unendliche als der (das) Eine transzendent in unsere Existenz eintritt, so ist in der Mengenlehre mit ihren vielen Paradoxien nach vieler Meinung, auch nach H. Poincaré und B. Russell, ‘das gemeinsame störende Moment aller bisherigen Paradoxien der Mengenlehre aufzudecken in dem Hinweise auf das dabei offen oder versteckt gebrauchte Wort “alle”’.Ga naar voetnoot2) Endlich, während Kierkegaards Konstruktion des Paradoxons steht oder fällt mit der Annahme einer ‘Todeslinie’ zwischen endlich und unendlich, gibt es ‘für die Mengenlehre.... zwischen dem Endlichen und dem Unendlichen keine grundsätzliche Schranke; ja das Unendliche erscheint ihr sogar als das Einfachere’, wie Hermann Weyl im Anschluss an Descartes, Galilei, Leibniz zeigen will.Ga naar voetnoot3) Gerade der mathematische Unendlichkeitsbegriff muss deshalb - anders als der Kierkegaardsche - wohl auch weiter darnach streben, seine Paradoxa von inneren Widersprüchen frei zu halten. Hierin sind Weyl, Lipps, Zermelo, | |||||||
[pagina 136]
| |||||||
Cantor, Bolzano, Poincaré, Russell, Schönflies, Hessenberg, Dedekind, Julius König, Isenkrahe, Urbach, Dingler, Samuel, J.K. KreibigGa naar voetnoot1), BergmannGa naar voetnoot2) u.s.w. sich schliesslich einig. Und wenn auch in der letzten Zeit, namentlich infolge des Auftretens von L.E.J. Brouwer, die Frage nach der Exaktheit der Mathematik wieder mit Nachdruck in den Vordergrund getreten ist, und wenn auch zwischen der intuitionistischen und der formalistischen Richtung in der Mathematik eine Meinungsverschiedenheit herrscht über die Frage, of die mathematische Exaktheit im menschlichen Intellekt liege (die intuitionistische Auffassung) oder ‘auf dem Papier’ (die formalistische), so hält doch das Problem der Widerspruchlosigkeit beide fest.Ga naar voetnoot3) Brouwer, selber Intuitionist, schreibt wohl einen Aufsatz unter der Ueberschrift: ‘De onbetrouwbaarheid der logische principes’, aber stellt doch fest, dass die Paradoxa von Burali-Forti, Russell, Richard ihren Ursprung in einem Irrtum finden;Ga naar voetnoot4) er erkennt die Zuverlässigkeit der Prinzipien des Syllogismus und der Kontradiktion anGa naar voetnoot5) und verneint wohl die Zuverlässigkeit des principium tertii exclusi in der Mathematik, aber kommt schliesslich nur zu dem Schluss, dass über die Frage nach der unbegrenzten Geltung dieses Prinzips in der Mathematik nicht mit Sicherheit entschieden werden kann. Die in der Mathematik gewöhnlich als bewiesen geltenden Beweise muss man seiner Ansicht nach unter- | |||||||
[pagina 137]
| |||||||
scheiden in richtige und nicht-kontradiktorische.Ga naar voetnoot1) Auch die Formalisten ihrerseits, sagt Brouwer, wenden das principium contradictionis an; daher kommt es denn auch, dass sie, wenn sie auf ein peinliches Paradox stossen (z.B. von Burali-Forti) dies gerne in eine mildere Form redigieren.Ga naar voetnoot2) Zum Schluss: die symbolische Mathematik (Hilbert) möge für sich davon abgesehen haben, die Wahrheit der Mathematik sicherzustellen, doch will sie in jedem Fall die Widerspruchslosigkeit der alten Analyse sicherstellen.Ga naar voetnoot3) Um diese Widerspruchslosigkeit geht es also immer wieder, nicht nur bei der axiomatischen Methode.Ga naar voetnoot4) Eine eigentlich bestimmte Entscheidung in entgegengesetztem Sinne, also eine volkommene Preisgabe jeden Suchens nach Widerspruchslosigkeit, muss jedoch, wie gesagt wurde, aufgewiesen werden bei einem Anhänger von Vaihingers Als-Ob-Philosophie. Hier muss besonders das schon erwähnte Buch von W. Dieck genannt werden. Die darin vertretenen Gedanken hatte er schon vorher ausgesprochen in einem Aufsatz: Die Paradoxien der Mengenlehre (Annalen d. Philosophie, Jahrg. V, Heft 2, 6. Juli 1925). Schon hier hatte Dieck die Auffassung verteidigt, dass in den Paradoxien der Mengenlehre die ‘Geburtsfehler’ des menschlichen Denkens überhaupt zutage treten. In der Mengenlehre nämlich wird s.E. mit innerlich widerspruchsvollen Begriffen gearbeitet; sie sind ihm ‘die tiefste und letzte Quelle’ ihrer Paradoxien. Und hier schliesst er sich an Vaihinger an, und versucht den fiktiven Charakter des Mengenbegriffs (wenn etwas ‘Vieles’ ist, kann es nicht zugleich ‘Eines’ sein) aufzudecken. Es wundert ihn, dass die Mathematiker Herrn | |||||||
[pagina 138]
| |||||||
Vaihinger in der Entdeckung des Fiktionsbegriffs nicht zuvorgekommen sindGa naar voetnoot1), und er nennt es geradezu unverständlich, wenn die Mathematiker die durch den Fiktionsbegriff umschriebene Eigentümlichkeit unseres Denkens in Abrede stellen wollen. Denn die angeführten Widersprüche des Mengenbegriffs sind ‘ein notwendiges Uebel’. Nicht nur mit Rücksicht auf rein mathematische Fragen, sondern auch in anderer Hinsicht, z.B. in der Ausarbeitung des Aetherbegriffes,Ga naar voetnoot2) schliesst er sich an Vaihingers Fiktionslehre an, ‘dass unser Denken sich innerlich widerspruchsvoller Begriffsbildungen mit Erfolg zu bedienen vermag’.Ga naar voetnoot3) Vaihinger hatte sich übrigens selbst - teils mit Unrecht - für seine Theorie über den Nutzen und das Recht fiktiver (und dabei widerspruchsvoller) Begriffe ín der Mathematik auf Poincaré, Couturat, Russell u.a. berufen.Ga naar voetnoot4) Von der ‘Fiktion’, wie Vaihinger sie aufstellt, gibt Dieck folgende Umschreibung: ‘..... in sich widerspruchsvolle Begriffe, die doch zur Beherrschung der Wirklichkeit notwendig oder nützlich sind’, eine Umschreibung, die, wie Dieck gegenüber Hankel, Hölder und anderen Mathematikern, auch im Zusammenhang mit dem Unendlichkeitsbegriff, bemerkt, für die Mathematik schon gleich die Konsequenz nach sich zieht, ‘dass innerer Widerspruch von Begriffen mit ihrer praktischen oder theoretischen Brauchbarkeit sehr wohl Hand in Hand gehen kann’.Ga naar voetnoot5) Uebrigens gilt auch die Sprache für Dieck als ‘Bewahrerin,.... Erzeugerin,.... Ernährerin jener in sich widerspruchsvollen Begriffe’.Ga naar voetnoot6) Die Anknüpfungspunkte für diese Darlegung können bei Vaihinger selbst leicht gefunden werden. Vaihinger hatte in seiner Fiktionslehre einen Unterschied gemacht zwischen Fiktionen und Semifiktionen. Die letzteren widersprechen | |||||||
[pagina 139]
| |||||||
wohl der gegebenen Wirklichkeit, aber sind noch nicht in sich selbst widerspruchsvoll; die ersteren sind jedoch auch in sich selbst widerspruchsvoll.Ga naar voetnoot1) Hierzu gehören u.a. der Begriff des Atoms, des Dinges an sich. Die Fiktionen gehen denn auch über in Antinomien;Ga naar voetnoot2) das logische Gesetz des Widerspruchs wird vergewaltigt.Ga naar voetnoot3) Namentlich die Infinitesimalrechnung wird ausführlich erörtert, wobei er sich auf Leibniz beruft.Ga naar voetnoot4) Die Mathematik, so wird festgestellt, beruht auf einer vollständig imaginativen Grundlage, sogar auf Widersprüchen;Ga naar voetnoot5) Fläche, Linie, Punkt u.s.w., das Unendliche: es sind alles widerspruchsvolle Fiktionen.Ga naar voetnoot6) Von hier aus zieht Dieck die Linien nun weiter. Ebenso wie Vaihinger den Punkt, die Linie, die Fläche, die Null, die Zahl ∞, das Differenzial, den Differenzialquotient, das Integral u.s.w. als Fiktionen betrachtet, so nennt auch Dieck (der offenbar eigene Wege einschlägt, wenn er von Paradoxen spricht) es nacheinander eine ‘paradoxe Erscheinung’, dass die Einheit ‘der natürliche Anfang aller Zahlen’, logisch genommen, selbst nicht als Zahl angesehen werden kann,Ga naar voetnoot7) so glaubt er, dass die Einheit nicht widerspruchsfrei mit der Vielheit verbunden ist,Ga naar voetnoot8) und sieht er innere Widersprüche in der Null (jener ‘Ziffer, die das Fehlen einer Ziffer an bestimmten Stellen einer Zahl zum Ausdruck bringt’)Ga naar voetnoot9), so nennt er die Null ‘zugleich ein Etwas und ein Nicht-Etwas’,Ga naar voetnoot10) eine Auffassung, die sogar durch Hinweis auf das Nirwana(!) unterstützt werden muss,Ga naar voetnoot11) und ver- | |||||||
[pagina 140]
| |||||||
mehrt er die Anzahl innerer Widersprüche in der Null noch durch einen, indem er der Null zugleich den Charakter einer ‘kleinsten Zahl’ zuschreibt, obwohl es eine ‘kleinste Zahl’ in Wirklichkeit nicht gibt.Ga naar voetnoot1) Eine gleiche Erörterung folgt dann über die Zahl ∞ (nach ihm: ‘jenseits jeder gegebenen Grösse’ S. 27); ‘mit dieser Zahl ∞ rechnen wir ähnlich wie mit jeder anderen endlichen Zahl. Ist das nicht Gebrauch einer unendlichen Grösse als einer vollendeten?’ Also auch hier wieder ‘innere Widersprüche’.Ga naar voetnoot2) Weiter kommt er zu den negativen Zahlen; schon 10 - 10 heisst ‘widersinnig’; denn die Fiktion der Menge 0 muss helfen zur Lösung der Aufgabe 10 - 10. Wieviel mehr werden dann die negativen Zahlen selbst innere Widersprüche in sich enthalten?Ga naar voetnoot3) Michael Stifel - sagt Dieck - nannte sie schon ‘absurd’, um ihren widerspruchsvollen Charakter anzudeuten.Ga naar voetnoot4) Ferner heisst auch innerlich widerspruchsvoll die Erweiterung der Mengenzahl zur BeziehungszahlGa naar voetnoot5) (zu Beziehungs- oder Rechenzahlen rechnet Dieck zu allererst die negativen Zahlen)Ga naar voetnoot6); man kommt auf diese Weise ‘zu neuen Zahlbegriffen, die von den Ausgangszahlen wesentlich verschieden, mit ihnen geradezu unvereinbar sind’.Ga naar voetnoot7) Es hat für unseren Zweck keinen Sinn, weiter auf Diecks viele andere Beispiele einzugehen, umso mehr nicht, weil offenbar in dem letzten Beispiel die ‘inneren Widersprüche’ mehr oder weniger verblassen; denn es handelt sich hier um ein Weiterbauen auf ein schon gelegtes Fundament; eine Ueberwucherung des Zweckes | |||||||
[pagina 141]
| |||||||
durch das Mittel, wie Vaihinger sagt.Ga naar voetnoot1) Für unseren Zweck hat es jetzt nur noch Bedeutung zu untersuchen, wie bei dieser Auffassung das Wort ‘paradox’ noch gebraucht werden kann. Wir weisen auf einige bestimmte Paradoxa:
| |||||||
[pagina 142]
| |||||||
Es ist also nicht zufällig, sondern konsequente Auswirkung von Diecks Grundgedanken, wenn gerade er sich weigert, an den obenerwähnten vielen Versuchen, die mathematischen Paradoxa, auch die von B. Russell, zu lösen, sich zu beteiligen. ‘In der Menge M aller Mengen, die sich selbst nicht als Moment enthalten, haben wir mit einem Begriffe zu tun, der seinen inneren Widerspruch deutlich an den Tag legt. Gegen die Folgerichtigkeit der Mengenlehre beweist er nach dem hier vertretenen Standpunkte nichts; vielmehr ist er lediglich ein Kronzeuge dafür, dass unser Denken gesetzmässige Widersprüche in sich schliesst.... ein philosophisches Argument gegen die alte Erkenntnislehre, dass das richtige Denken von jeglicher Art inneren Widerspruches frei sei’.Ga naar voetnoot2) Und wenn Hausdorff (cf. Russell) sagt: ‘wir müssen das geheiligte Axiom totum parte maius verletzen’, so bemerkt Dieck dazu in seinem vorher erwähnten Aufsatz: ‘Die Mathematiker haben recht daran getan, trotz der augenscheinlichen Widersprüche ihrer Begriffsbildungen diese nicht preiszugeben.... Zwar irrten sie bisher in ihrer Rechtfertigung, denn die Widersprüche des Unendlichen sind nicht bloss scheinbar, sondern wirklich. Aber sie sind zugleich notwendig und gesetzmässig’ | |||||||
[pagina 143]
| |||||||
(S. 51). Vaihinger hat die Mathematiker befreit von der ‘Seelenqual’, ‘an den Widersprüchen des Begriffssystems ernsten Anstoss nehmen’ zu müssen (53). Und diese Auffassung wird nach Dieck nicht nur von der Mengenlehre, sondern auch von den übrigen Zweigen der Mathematik ‘geschützt’ (die inzidentell unter Formel gebrachten Paradoxa sind daher keine anomalen cruces, sondern paradigmata des normalen mathematischen Verfahrens geworden). Diecks obige Aussagen sind wohl sehr bemerkenswert. Sie beweisen zugleich, dass das Wort ‘Paradox’ durch Dieck sich noch weiter von seiner ursprünglichen Bedeutung entfernte, als sich uns früher schon zeigte. (§ 1 u. 2.) Nicht weil er es gebraucht, sondern weil er es nicht verwirft, es nicht durch andere, neue Ausdrücke ersetzt. Für Russell war ein innerer Widerspruch eine crux und Ausnahme; die Russellsche ‘contradiction’, über die wir sprachen, konnte ‘only be solved by abandoning some common-sense assumption’ (deswegen war sie crux), und, ‘no other similar difficulty, so far as I know, occurs in any other portion of the Principles of Mathematics’ (hier zeigt sie sich also als Ausnahme).Ga naar voetnoot1) Aber für Dieck ist der innere Widerspruch keine crux, sondern zweckmässig; denn der Widerspruch baut den Begriff auf, kann nicht entbehrt werden, ist Widerspruch im Richtigen. Auch ist er keine Ausnahme, sondern Regel. Obgleich also Dieck das Wort ‘Paradox’ weiter für bestimmte Paradoxa reserviert, so ist doch unbemerkt ‘das’ Paradox zur Regel geworden, zur ‘Kategorie’; denn was in jenen namentlich genannten Paradoxa andere zu dieser Namengebung veranlasste, ist nach Dieck und der Vaihingerschen Philosophie überall zu finden. Wir stehen hier also vor einer neuen Wendung in der Verwendungs- und Begriffsgeschichte des Wortes ‘Paradox’. Sie bedeutet für den wissenschaftlichen Verkehr ein neues Hindernis, wenngleich anerkannt werden muss, dass | |||||||
[pagina 144]
| |||||||
diese nicht so radikal ist wie die Kierkegaardsche. Denn was dies letztere betrifft, so macht die Vaihinger-Diecksche Auffassung das Paradox zu einer allgemeinen und regelmässigen Erscheinung im Denken, die man nicht überwinden, sondern als zweckmässiges Hilfsmittel erkennen muss, aber andererseits unterscheidet sie sich doch von Kierkegaards Umwälzung in der Begriffsgeschichte des Wortes ‘Paradox’ darin, dass, was in dem Vaihinger-Dieckschen Paradoxon ein konstitutives Element ist, keineswegs (wie bei Kierkegaard) vertikal das horizontale Denken sprengt, ja, nicht einmal überall die (mathematische!) Unendlichkeit auf die Endlichkeit stossen lässt, sondern in der horizontalen Denkebene selbst ganz und gar eingeschlossen bleibt. In diesem Punkt behält also der antike und bis auf Kierkegaard nachgewiesene ‘Paradoxbegriff’ seine Geltung hier auch weiter. Aber in diesem horizontalen Denkprozess wird sodann, wie bei Kierkegaard, das Paradox zu einer normalen Erscheinung, zu einem Element ‘im Richtigen’. Wenn wir alle Variationen des ‘Paradoxes’ in seinem alten (vor-Kierkegaardschen) Typus zu einem Grundtypus zusammenfassen, dann begegnen wir also an dieser Stelle unserer Untersuchung einem prinzipiell 3. Typus: der erste (vor Kierkegaard) liegt in der horizontalen Welt, als Hindernis für das Denken; der zweite (Kierkegaard) liegt dort, wo die horizontale und die vertikale Welt (Ewigkeit, Zeit, u.s.w.) sich schneiden und ist Beiseitsetzung des (‘spekulierenden’) Denkens; der dritte (hier) liegt wieder in der horizontalen Welt, aber ist konstruktives Element im Denken. In Typus I ist in dem Kontinuum Relativität gegen Relativität gestellt; in II ist in dem Diskontinuum Absolutheit gegen Relativität gestellt; in III ist in dem Kontinuum Endlichkeit mit Endlichkeit, Relativität mit Relativität schöpferisch verbunden zu gedanklichem Aufbau, zu höherem Bau. I ist für die ‘Spekulation’ obstruktiv, II destruktiv, III konstruktiv. So haben Dieck-Vaihinger dazu beigetragen, das doch schon so schwerbelastete Wort Paradox zu einem dritten | |||||||
[pagina 145]
| |||||||
Grundtyp zu bringen; es ist hier noch ungeeigneter geworden für wissenschaftlichen Gebrauch als es schon war. Bei einem solchen Stand der Dinge braucht nur einer zu kommen, der die Gabe der Popularisierung hat, und die Sprachenverwirrung der Gelehrten wird auf das Volk übergehen und den paradoxen Rausch ebenso ‘herrlich’ machen wie die ‘Not’ früher peinlich war dort, wo das Paradox auftrat. Wenn man bedenkt, dass später von seiten der in Kierkegaards Kielwasser fahrenden dialektischen Theologie (Haitjema) behauptet wurde, dass Vaihingers Lehre vom Paradox (nämlich in der Fiktion) nur einen Schlag umgedreht zu werden braucht, um vollkommen richtig zu seinGa naar voetnoot1) und dass z.B. durch Gustav Spengler, über ‘das Verhältnis der Philosophie des Als-Ob H. Vaihingers zu Meinongs “Annahmen”’ (welches Werk man auch wiederholt zitiert findet im Zusammenhang mit den mathematischen Paradoxien) ausführlich geschrieben ist,Ga naar voetnoot2) dann erhellt, dass doch wohl Verbindungsfäden laufen zwischen dem einen und dem anderen Denkgebiet, und dann bekommt Vaihingers Fiktionenlehren auch für die praktische Ueberbelastung des Begriffes ‘Paradox’ reelle Bedeutung. Man spricht in der Mathematik also noch wohl von mathematischen Paradoxen, aber Inhalt und Rechtmässigkeit dieses Namens werden schon auf mathematischem Gebiet verschieden aufgefasst. Mit auch für den allgemeinen Sprachgebrauch fatalen Folgen wird die Verwirrung dann noch grösser, wenn in der mathematischen Literatur immermehr die Neigung aufkommt, für bestimmte Paradoxa diesen Namen mit ‘Antinomien’ abwechseln zu lassen. Es hat eine Zeit gegeben, in der das Wort ‘Antinomie’ ungefähr | |||||||
[pagina 146]
| |||||||
gleichen Inhalt haben konnte wie das alte Wort ‘Paradox’, z.B. (nach Eisler): Widerstreit zweier Urteile oder Schlüsse, welche (anscheinend) von gleicher Ueberzeugungskraft und Geltung sind, wiewohl sie einander widersprechen.Ga naar voetnoot1) Aber schon die Ableitung von ‘nomos’ statt von ‘doxa’ (Meinung) gibt dem Worte ‘Antinomie’ einen enger begrenzten Inhalt, und besonders die Weise, in der Kant das Wort gebraucht hat, so nämlich, dass sowohl Thesis wie Antithesis als falsch galten, hat das Wort ‘Antinomie’ noch weiter von ‘Paradox’ entfernt, als es ursprünglich in dem doppelten Gegensatz von anti-para einerseits, und nomos-doxa andererseits, der Fall war. Dass also namentlich in der Mathematik die Neigung aufkommt, ‘Antinomie’ und ‘Paradox’ als Synonyme zu gebrauchen, kann die babylonische Sprachenverwirrung nur verschlimmern. Im J. 1887 schrieb Frédéric Loliée, den wir schon erwähnten, über ‘un pays sans limites, le plus curieux du monde à parcourir, qui se nomme Paradoxe, où chacun a planté son pavillon un peu au hasard, mais dont nul voyageur encore n'a embrassé complètement l'étendue’.Ga naar voetnoot2) In den Jahren nach 1887 sollte noch mehr Ursache zum Klagen über dies ‘planter au hasard’ gegeben werden. Und dass auch die Mathematik dazu beitragen würde, wiewohl gerade sie als die Wissenschaft galt, die jeden Schritt auf ihrem Weg legitimieren konnte, charakterisiert wohl sehr scharf die veränderte Lage. Es bleibt bedauernswert, dass, obwohl mit klarem Bewusstsein durch Russell (und Russell-Whitehead) selbst mathematische und logische Paradoxa aufs engste verbunden wurden, sie nichtsdestoweniger allerlei termini systemlos durcheinander gebraucht haben. Paradox, contradiction, sie werden umschichtig (z.B. auf einer Seite, 63, mit Bezug auf das Paradox von Burali-Forti) gebraucht; wir sprachen schon darüber, dass daneben auch noch der Ausdruck ‘Antinomie’ auftrat. | |||||||
[pagina 147]
| |||||||
Dass diese fortschreitende Unbrauchbarwerdung des Wortes ‘Paradox’ als terminus technicus zu bedauern ist, bedarf keines längeren Beweises, auch nicht hinsichtlich der Mathematik. Weyl hat mit Recht darauf hingewiesenGa naar voetnoot1), dass die heutige Mathematik mit den allgemeinen Grundfragen der Erkenntnistheorie aufs engste verknüpft ist, dass es hier geht um die alten Gegensätze: Realismus und Idealismus, Sein und Werden. Dass bei einer solchen Debatte das Wort ‘Paradox’ unaufhörlich vorkommt und doch eigentlich in alle Richtungen zeigt, das ist schon an und für sich eine Erschwerung der bereits ‘verzweifelten Lage’. Eine ‘verzweifelte Lage’, - denn wiewohl Ph.E.B. Jourdain in einer satirischen Schrift im Hinblick auf die Paradoxa von Russell (Thristam Shandy) und auf die ‘paradoxes of logic’ der Mathematiker überhaupt spottend über die ‘hierarchy of jokes’ gesprochen hat, darf man ihn doch daran erinnern, dass auch für diese ‘hierarchy’ das Wort würde gelten müssen, das er jetzt nur für seinen eigenen ‘joke’ scheint zitieren zu wollen; ‘even a joke should have some meaning’.Ga naar voetnoot2) | |||||||
[pagina 148]
| |||||||
§ 4. Anhaltende Unsicherheit auf mathematischem Gebiet.K. Grelling hat in der Geschichte der Mengenlehre zwei Perioden unterschieden: a) die klassische (nach Cantor), die zugleich die ‘naive’ war, in Bezug auf die Grundlagen; b) die ‘kritische’, die ‘hauptsächlich die Bereinigung der Grundlagen zum Ziel hatte’, und konstatierte im Jahre 1924, dass diese zweite Periode sich ihrem Ende näherte.Ga naar voetnoot1) Aber diese Vorhersage hat sich nicht erfüllt: die Diskussion ist noch in vollem Gang, und es wird immer schwerer ihr zu folgen. Schon aus dieser einen Tatsache wird deutlich, dass die Unsicherheit, die auf mathematischem Gebiet in Bezug auf die Paradoxien herrscht, und die bedauernswerte Verwirrung, die in Bezug auf den Inhalt des ‘Paradoxons’ auf mathematisch-philosophischem Gebiet herrscht, noch wohl geraume Zeit anhalten werden. Es gibt jedoch noch verschiedene andere Faktoren, die hier in Betracht kommen und die die soeben ausgesprochene Erwartung rechtfertigen. Wir nennen einige davon. 1. Die Parodoxa der Mathematik lassen sich, wie uns deutlich wurde, immer weniger von rein logischen Paradoxa unterscheiden. Immer schwerer wird der Mathematiker mit cruces belastet, die früher nur den Logiker angingen und umgekehrt. In unserem vorhergehenden Paragraphen gaben wir schon einige Beispiele, die die Probleme der Mathematik immer deutlicher als direkte Probleme auch der Logik, der Theologie und der Philosophie zeigten. Dieser Prozess nun steht nicht still und wird un- | |||||||
[pagina 149]
| |||||||
umwundenanerkannt. So rechnet Hasso HärlenGa naar voetnoot1) ‘l'Antinomie Richard’ zu ‘les paradoxes de détermination verbale’ und glaubt, dass diese ‘dépendent essentiellement des singularités de la langue’. Daneben kennt er für ‘tous les autres - c'est à dire ceux de Russell, de Burali-Forti et leurs variantes -’ eine zweite Kategorie, die schliesslich alle dieselbe ‘contradiction’ enthalten, die er dann als ‘paradoxie logique’ bezeichnet. In die durch Russell eröffnete Reihe von Paradoxa, in der als erstes seine ‘Paradoxie des Prädikates imprädikabel’Ga naar voetnoot2) auftritt, werden noch immerfort neue, zum Teil Varianten davon, gestellt, z.B. das Paradoxon des Wortes ‘heterologisch’. ‘Autologisch’ nennt Grelling, der dieses Paradox als erster im Jahre 1908 veröffentlichte, Wörter, welche selber ‘unter den Begriff fallen, den sie bezeichnen’ (dreisilbig, kurz, deutsch), ‘heterologisch’ dagegen sind nicht-autologische Wörter (z.B. einsilbig, lang, französisch). Nun kann man wieder Russells Linie folgen: das Wort ‘heterologisch’ fällt, wenn es autologisch ist, unter den Begriff, den es bezeichnet, ist also heterologisch; ist es jedoch heterologisch, dann fällt es unter seinen eigenen Begriff, ist also autologisch.Ga naar voetnoot3) Man kann natürlich immer weiter gehen; so hat, um den Typus der Russell'schen paradoxen Begriffsbildungen zu typieren, Leonard Nelson nicht nur auf Fichtes ‘reines Ich’ hingewiesen, sondern auch auf den nach ihm damit ‘identischen’ Begriff des ‘erkenntnistheoretischen Subjekts, das alle Subjekte erkennt, die sich nicht selbst erkennen. Angenommen also, es erkennt sich selbst: dann gehört es.... zu den Subjekten, die sich | |||||||
[pagina 150]
| |||||||
nicht selbst erkennen.... Angenommen aber, es erkennt sich nicht selbst: dann gehört es.... zu den Subjekten, die es erkennt.’Ga naar voetnoot1) 2. Die durch Russell begonnene Erlösung der mathematischen Paradoxa aus ihrer wissenschaftlichen Isolation stellte natürlich das schon von Kant, und nachher von J.F. Fries (System der Logik) neu untersuchte, aber später vernachlässigte Problem des Verhältnisses der Mathematik und der Logik mit umso grösserer Schärfe in den Vordergrund, aber die Meinungen gehen in diesem Kardinalpunkt schon gleich sehr weit auseinander. Der scharfen Abgrenzung beider Wissenschaften, wie z.B. H. Rickert sie gewollt hat, der die Logik der Mathematik nicht anders gegenüberstehen sah als den anderen Spezialwissenschaften und der der Logik in diesem Zusammenhang nur die Aufgabe zuwies, ‘den Begriff der ZahlGa naar voetnoot2) überhaupt auf seine logischen, wie seine alogischen Bestandteile hin’ zu untersuchen,Ga naar voetnoot3) stehen auf Seiten der praktizierenden Mathematiker die weitest auseinanderlaufenden, an dieser Problemstellung nahezu immer vorübergehenden Meinungen gegenüber. | |||||||
[pagina 151]
| |||||||
In ganz besonderem Sinn ist in dieses Problem verwickelt ein erst in den letzten Jahrzehnten entwickeltes System der Logik, das unter dem Namen Logistik oder symbolische Logik bekannt ist (Peano, Hilbert, J. Venn, Frege, Russell-Whitehead, Schröder u.a.). Hier werden, im Unterschied von der aristotelisch-scholastischen Logik, die Begriffe und Aussagen nicht durch Wörter, sondern durch Zeichen und Formeln wiedergegeben, und weil diese anfänglich im Anschluss an die schon gebräuchlichen mathematischen Zeichen gewählt wurden, kam auch der Name Algebra der Logik auf. So wird z.B. der Modus Barbara, bekannt aus der scholastischen Logik, folgendermassen wiedergegeben: (x). φx) χx: (x). χx) ψx:). (x). φx) ψx (d.h. ist alles, was φ ist, χ und alles, was χ ist, ψ, so ist alles, was φ ist, ψ). Das Zeichensystem wird noch stets verbessert; so ist z.B. diese Symbolisierung des Modus Barbara schon durch eine neuere überholt.Ga naar voetnoot1) Ueber das Verhältnis der Mathematik und Log(ist)ik wird nun hier durchweg mit grossem Selbstbewusstsein gesprochen. Indem der Repräsentant der Logistik Rudolf Carnap von vorneherein feststellt, dass die alte Logik ‘ihren Todesstoss bekam’, gerade durch die Entdeckung der Paradoxien der Mengenlehre, tritt er mit der Prätention auf, dass ‘erst die Logistik’ imstande war, die logischen Antinomien der Mengenlehre zu überwinden, und erklärt nun die ganze Mathematik, die Geometrie, die Arithmetik, zu ‘Zweigen der Logistik’.Ga naar voetnoot2) In gleichem Sinn weist Hasso HärlenGa naar voetnoot3) hin auf die Versuche von Chwistek, Lésniewski u.a., um Logik und Mathematik symbolisch-semantisch zu begründen, und glaubt, dass diese Bestrebungen schon ihre ‘schöne Rechtfertigung’ erlangt haben. In diesem Zusammenhang verdient David Hilbert besondere Erwähnung. Dieser will ‘wegen der engen Ver- | |||||||
[pagina 152]
| |||||||
knüpfung und Untrennbarkeit arithmetischer und logischer Wahrheiten’ von Grund auf beginnen und Logik und Mathematik sich zu gleicher Zeit nebeneinander entwickeln lassen, sie ‘zusammen’ ‘formalisieren’.Ga naar voetnoot1) Er will ‘nichts Geringeres, als die allgemeinen Zweifel an der Sicherheit des mathematischen Schliessens definitiv aus der Welt.... schaffen’.Ga naar voetnoot2) Um das zu erreichen, führt er seine bekannten ‘logischen Zeichen’ ein; so bedeutet z.B. ⟶ ‘folgt’ (also ist a ⟶ b eine Verneinung, dass a richtig und zugleich b falsch ist, m.a.W.: aus a folgt b); für ‘nicht’ wird wieder ein anderes Zeichen (‾) eingeführt u.s.w.Ga naar voetnoot3) Zu der eigentlichen so formalisierten Mathematik kommt dann jedoch die sogenannte Metamathematik; diese ist notwendig zur Sicherung der erstgenannten. Im Gegensatz zu den ‘rein formalen Schlussweisen der eigentlichen Mathematik’ will ja diese Metamathematik ‘das inhaltliche Schliessen zur Anwendung’ kommen lassen ‘aber lediglich zum Nachweis der Widerspruchslosigkeit der Axiome’.Ga naar voetnoot4) Hilbert umschreibt diese Metamathematik als ‘die inhaltliche Theorie der formalisierten Beweise.’Ga naar voetnoot5) ‘Die Axiome und beweisbaren Sätze.... sind die Abbilder der Gedanken, die das übliche Verfahren der bisherigen Mathematik ausmachen, aber sie sind nicht selbst die Wahrheiten im absoluten Sinne. Als die absoluten Wahrheiten’, sagt Hilbert, ‘sind vielmehr die Einsichten anzusehen, die durch meine Beweistheorie hinsichtlich der Beweisbarkeit und der Widerspruchsfreiheit jener Formelsysteme geliefert werden’. (Axiome und beweisbare Sätze sind die Formeln, die entstehen durch Gewinnung neuer | |||||||
[pagina 153]
| |||||||
beweisbaren Formeln aus den Axiomen mittelst formalen Schliessens und andererseits durch Hinzufügung neuer Axiome nebst dem Nachweis der Widerspruchsfreiheit mittelst inhaltlichen Schliessens). So kommt HilbertGa naar voetnoot1) zu u.a. folgenden ‘Axiomen der Negation’: A ⟶ (Ā ⟶ B) (Satz vom Widerspruch). (A ⟶ B) ⟶ {(Ā ⟶ B) ⟶ B} (Prinzip des tertium non datur). {A ⟶ (B &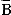 )} ⟶ Ā (Satz vom Widerspruch). )} ⟶ Ā (Satz vom Widerspruch).
Es ist deutlich, dass hier die logischen Prinzipia zugleich mit den mathematischen, und zwar nach der Methode der Algebra der Logik, auf eine Formel gebracht werden und, statt Ausgangspunkt und Grundlage der Beweisführung zu sein, zum Objekt mathematischer Beweisführung gemacht werden. Dieser symbolischen Formalisierung der Mathematik steht jedoch die intuitionistische Auffassung von anderen (Brouwer, Weyl) gegenüber. Grenzt Rickert die Logik gegen die Mathematik ab, will Hilbert sie beide zugleich formalisieren, so kommt Brouwer dagegen immer wieder darauf zurück, dass nicht, wie man früher meinte, die Mathematik die Logik voraussetzt (hierin, im Negativen, stimmt er also überein mit Hilbert, der ja auch die Widerspruchsfreiheit seiner Axiome ohne jegliche mathematische Intuition darlegen will), sondern dass umgekehrt die Logik die Mathematik voraussetzt (hierin, im Positiven, weicht er also prinzipiell von Hilbert ab). Diese im Jahre 1919 und später noch ausdrücklich vertreteneGa naar voetnoot2) Meinung war schon 1907 in seinem ‘Over de grondslagen der Wiskunde’ verteidigt worden.Ga naar voetnoot3) Die Mathematik heisst dort unabhängig von logischen Gesetzen; praktische Logik und theoretische Logik sind gerade umgekehrt Anwendungen von verschiede- | |||||||
[pagina 154]
| |||||||
nen Teilen der Mathematik;Ga naar voetnoot1) weshalb denn auch nach Brouwers Meinung dem klassischen Syllogismus (alle Menschen sind sterblich, Sokrates ist ein Mensch, ergo: Sokrates ist sterblich) eine Projektierung in die Anschauungswelt eines mathematischen Systems zugrunde liegt.Ga naar voetnoot2) Einen logischen Aufbau der Mathematik, unabhängig von der mathematischen Intuition, hält Brouwer für unmöglich.Ga naar voetnoot3) So kommt Brouwer dazu, wie übrigens schon eben berührt wurde, die Unzuverlässigkeit der logischen Prinzipia zu proklamieren.Ga naar voetnoot4) Namentlich das principium exclusi tertii kommt hier in Betracht, und der oben aufgewiesene prinzipielle Unterschied zwischen Hilbert und Brouwer wird wohl darin deutlich, dass Hilbert, überzeugt, dass ‘die Anwendung der transfiniten Schlussweisen, so wie sie in der Analysis und in der Mengenlehre geschieht, doch stets richtige Resultate liefert’, glaubt, ‘auf dem Boden des Finiten’ (‘auf rein anschauliche und finite Weise’) ‘die freie Handhabung und volle Beherrschung des Transfiniten’ erreichen zu können,Ga naar voetnoot5) während dagegen Brouwer zwischen beiden Gebieten eine scharfe Trennung macht, wenn er ausspricht, dass das principium tertii exclusi eine zuverlässige Schlussweise ist, solange es sich nur um bestimmte, endliche, diskrete Systeme handelt, aber dass in unendlichen Systemen dieses Prinzip vorläufig nicht zuverlässig ist.Ga naar voetnoot6) Darum hat denn auch Brouwer ausdrücklich, gegenüber den Versuchen von Dedekind, Mannoury, die die Arithmetik der ganzen Zahlen logisch aus den allerprimitivsten Begriffen beweisen wollen, als seine Ueberzeugung ausgesprochenGa naar voetnoot7) und bestätigtGa naar voetnoot8), dass solche rein | |||||||
[pagina 155]
| |||||||
formalen Beweise der Widerspruchsfreiheit unmöglich sind; selber hat er sowohl die MengenlehreGa naar voetnoot1) als die FunktionenlehreGa naar voetnoot2) unabhängig vom logischen Satz des ausgeschlossenen Dritten begründet. So entfernt sich Brouwer immer weiter von Hilbert, der Intuitionist von dem Formalisten. Hilbert sichert erst das ‘tertium non datur’ selbst und darnach auch dessen Anwendung für dasselbe Gebiet (transfinit), wo Brouwer es unzuverlässig werden sieht.Ga naar voetnoot3) Es bedarf keines näheren Beweises, dass diese Meinungsverschiedenheiten tief einschneiden und natürlich nicht isoliert bleiben können. Auch die anderen logischen Prinzipia werden hier zur Debatte gestellt: so wird auch Schönflies' Versuch, die schon durch EuklidGa naar voetnoot4) befolgte Methode des indirekten Beweises ausschliesslich vom Principium contradictionis abhängig zu machen, von Brouwer für unrechtmässig gehalten.Ga naar voetnoot5) Und dass die Debatte für das ganze Gebiet, auch für das der verwandten Wissenschaften, einschneidende Bedeutung hat, kann z.B. demonstriert werden an Erik Franks Behauptung, dass die konkrete Wirklichkeit sich keineswegs nach dem Satz des Widerspruchs richtet; so sind z.B. in jedem bewegten Körper kontradiktorisch entgegengesetzte Prädikate verbunden, nach seiner Meinung.Ga naar voetnoot6) ‘Das Wesen der Bewegung besteht nun einmal darin, an einem Orte zu sein und zugleich auch nicht zu sein’, also: ‘sowohl noch nicht, als nicht mehr.’Ga naar voetnoot7) Wir nennen Erik Frank gerade an dieser Stelle, weil so an diesem Punkt unsere Uebersicht zurückgreift sowohl auf Kant, den Frank | |||||||
[pagina 156]
| |||||||
bestreitet,Ga naar voetnoot1) als auf Zeno, dessen Formel, τὸ ϰινούμενον οὔτ᾽ ἐν ᾧ ἐστι τόπῳ ϰινεῖται οὔτ᾽ ἐν ᾧ μὴ ἔστι, von Frank übernommen wird.Ga naar voetnoot2) So bringt die Kontroverse über das Verhältnis der Mathematik und der Logik und im Zusammenhang damit über Stellung und Wert der logischen Prinzipia, uns von selbst zurück zu den Paradoxien der Zeit, von denen wir ausgegangen sind. Aber die Paradoxa verbergen sich immer mehr hinter dem Paradoxon, und jede Vertiefung der Diskussion wirkt in diese Richtung weiter. 3. Bis dahin wird die mathematische Problemstellung in der Tat - auch hinsichtlich der Probleme des Paradoxons - aus ihrer Isolation erlöst. Bei Russell wurde sie urgent (mehr als bei Bolzano, Leibniz, Kant, weil er mehr das Ohr der Mathematiker hatte), und in der Vertiefung der Debatte über einzelne Paradoxa zu einem Streit über die Grundfrage des Paradoxons wirkte sich die Aufhebung der Isolation der mathematischen Paradoxa noch weiter aus; denn die Kierkegaardsche Wendung in der Geschichte des Paradoxons bedeutete gerade eine Zurückführung der multa zum multum in der paradoxen ‘Not’, und Kierkegaards Problemstellung hat, weil sie dialektisch ist, die spätere Entwicklung der Theologie und Philosophie beherrscht Aber nachdem wir an diesen Punkt gekommen sind, stossen wir jetzt auf eine merkwürdige Abbiegung der Linie der mathematischen Kontroversen. Die Isolation, die erst aufgehoben wurde, kehrt in den inter-mathematischen Debatten nun doch praktisch wieder. Sobald doch von inzidentell gefundenen Paradoxa die Aufmerksamkeit abgelenkt wird, um sich zu stellen vor das Problem ‘des’ Paradoxons überhaupt, vor das Problem der Widerspruchsfreiheit, ja oder nein, vor die Frage der Aufhebung der logischen Grundsätze, ob oder nicht, drängt sich unmittelbar die Frage nach vorne, inwieweit in der modernen Mathematik das Paradox, die Antinomie, der Widerspruch etwas zu schaffen hat mit irgend- | |||||||
[pagina 157]
| |||||||
einer Wirklichkeit und mit ihrer ‘Not’. In diesem Punkt nun wird der anfänglich gewonneneGa naar voetnoot1) Kontakt zwischen der Mathematik und den anderen Denkgebieten, namentlich der Logik, der allgemeinen Philosophie und - was hier von selbst spricht - auch der Theologie,Ga naar voetnoot2) mehr oder weniger aufgehoben. Denn schon als wir uns mit Kierkegaard beschäftigten, zeigte sich uns, dass bei ihm das Paradox dort auftritt, wo der wirkliche Gott mit seiner wirklichen Ewigkeit auftritt in der wirklichen Existenz des wirklichen Menschen, der wirklichen Zeit. Dies Hineintragen des Paradoxons in eine wirklich ‘kritische Lage’, dies Hervorrufen einer wirklichen ‘Not’ bei einem inhaltlichen Denker ist seit Kierkegaard in Philosophie und Theologie immer schärfer in den Vordergrund getreten. Das erhellt schon aus den dort gebräuchlichen Schlagworten: Kairos, Krisis, Skandalon, Deus loquens, Existenz, Ich-Du-Verhältnis u.s.w. ‘Die neuere Mathematik - oder sagen wir einfach: Herr Hilbert’Ga naar voetnoot3) - dagegen verliert in ihrer Problemstellung hinsichtlich der Paradoxie und in ihren Versuchen zur Beseitigung der Paradoxie und zur Sicherstellung der Widerspruchslosigkeit gerade immer mehr den Boden der Wirklichkeit und sogar das Interesse für sie und erklärt dies auch ausdrücklich. So werden z.B. die vielbesprochenen ‘Klassen’ definiert als logische Fiktionen oder als Quasigegenstände oder als ‘die Extension einer Eigenschaft’.Ga naar voetnoot4) Wenn Hilbert sich anschickt, die ‘Notlage’, in die die Paradoxien der Mengenlehre und der Infinitesimalrechnung die Mathematik gebracht hatten, zu überwinden,Ga naar voetnoot5) beginnt er selbst mit der Erklärung, dass die Sätze, mit denen er operiert, zu bedeutungslosen, aus Zeichen aufgebauten Fi- | |||||||
[pagina 158]
| |||||||
guren werden; die Mathematik wird bei ihm in ihrem ersten Anlauf keine Erkenntnis mehr, sondern ein Formenspiel.Ga naar voetnoot1) Erst in der sogenannten Metamathematik kommt man zur Erkenntnis, aber diese hat dann gerade dies Spiel zu ihrem Gegenstand; das Schachspiel wird hier immer wieder als Beispiel und Analogie genannt.Ga naar voetnoot2) ‘Ganz entsprechend wie beim Uebergang von der inhaltlichen Zahlenlehre zur formalen Algebra betrachten wir die Zeichen und Operationssymbole des Logikkalkuls losgelöst von ihrer inhaltlichen Bedeutung. Dadurch erhalten wir schliesslich an Stelle der inhaltlichen mathematischen Wissenschaft.... nunmehr einen Bestand von Formeln mit mathematischen und logischen Zeichen, welche sich nach bestimmten Regeln aneinander reihen.’Ga naar voetnoot3) Nicht nur wird der Abstand zwischen Mathematik und Wirklichkeit hier also noch grösser gemacht als er schon ist, was natürlich unmittelbar seine Rückwirkung in der Naturwissenschaft findet (EinsteinGa naar voetnoot4) z.B. gibt davon Rechenschaft), sondern man entfernt sich auch immer weiter von dem Kern der Debatten, die in der Philosophie und der Theologie über den Widerspruch, das Paradoxon u.s.w. an der Tagesordnung sind: für letztgenannte ist gerade hinsichtlich des ‘inhaltlichen Schliessens’ die paradoxe Not das grosse Problem; für Hilbert mit seinem Logikkalkul und seiner Zeichensprache dagegen, ist ‘das inhaltliche Schliessen durch ein äusseres Handeln nach Regeln ersetzt’, und dies muss dann dazu dienen, die | |||||||
[pagina 159]
| |||||||
Paradoxie zu überwinden und das Problem zu stellen.Ga naar voetnoot1) Solange nun über diese Meinungen der Streit, z.B. zwischen Frege und Hilbert (Korselt), geführt wird, kann Hilbert nicht viel einwenden gegen Freges Klage, dass Hilberts Unabhängigkeitsbeweise ‘die eigentlichen Axiome, die Axiome im Euklidischen Sinne, gar nicht betreffen; denn diese sind doch wohl Gedanken’, während Hilberts ‘(Pseudo)axiome keinen Gedankeninhalt haben’.Ga naar voetnoot2) Und zugleich fällt hier ins Auge die Illusorität von Hilberts Behauptung, dass mit seiner Beweistheorie ‘die Mathematik sich gewissermassen erweitert zu einem Schiedsgericht, einem Tribunal höchster Instanz, um prinzipielle Fragen zum Austrag zu bringen - auf einer konkreten Basis, auf der sich alle müssen einigen können und jede Behauptung kontrolliert werden kann’.Ga naar voetnoot3) Schon die an diese Worte sich unmittelbar anschliessende Behauptung, a) dass ‘es keinen Weg gibt’, ‘auf dem jedes mathematische Problem sich lösen lässt’, und b) dass nichtsdestoweniger ‘der Nachweis, dass die Annahme der Lösbarkeit eines jeden mathematischen Problems widerspruchsfrei ist’, in den Bereich seiner Theorie fällt,Ga naar voetnoot4) wird beinahe alle, die auf nicht-mathematischem Gebiet sich in das Problem des Paradoxons hineindenken, ein auf diese Weise angekündigtes Schiedsgericht, wenigstens hinsichtlich ihrer Probleme, für inkompetent erklären lassen. Es ist also nicht zu erwarten, | |||||||
[pagina 160]
| |||||||
dass die mathematischen Debatten selber binnen absehbarer Zeit führen werden zu einer scharfen, beherrschenden Problemstellung, sowohl hinsichtlich bestimmter Paradoxa als auch hinsichtlich des Paradoxons überhaupt, ‘der Paradoxie’; dazu ist, wie Hugo Dingler, L. Chwistek u.a. bemerkt haben,Ga naar voetnoot1) die Logistik (die, wie bei Hilbert, die logischen Probleme in symbolischen Zeichen wiedergibt und bearbeitet) selber ohne Hilfe von aussen nicht imstande. Als zweiter Faktor, der die allgemeine Sprachen- und Problemverwirrung vergrössern hilft, kommt der Umstand hinzu, dass die Mathematik in demselben Zeitraum, in welchem sie sich an alle Wissenschaften richtet, um teilzunehmen an dem Stellen und Lösen der Fragen, doch tatsächlich sich von diesen anderen entfernt und zwar gerade dann, wenn es um die Grundprobleme des Paradoxons geht. Dies stellte sich schon anfänglich heraus, als wir den Anfang der heutigen mathematischen Forschung bei Bolzano sich abzeichnen sahen (das Unendliche); jetzt, wo wir am Ende desselben Weges Hilbert begegnen, kehrt diese Erscheinung in verschärfter Form zurück. 4. Die ungewollte Isolation, in welcher die Mathematik gerade hinsichtlich des Paradoxons trotz allem sich schliesslich festgefahren hat, bringt sie in eine nichts weniger als beneidenswerte Lage. Die am meisten entgegengesetzten Meinungen kreuzen sich. Der eine hofft, in der logischen Symbolik, wofern das Denken sich darin ‘von den Fesseln und Verführungen der gewöhnlichen Sprachen so weit wie möglich frei machen’ will, eine Exaktheit zu erlangen, die ‘den für das Zustandekommen der in Rede stehenden Widersprüche verantwortlichen Fehler aufzudecken und zu vermeiden’ vermag;Ga naar voetnoot2) der andere weist jedoch darauf hin, dass auch die Logistik ihre Kontradiktionen, ihre Antino- | |||||||
[pagina 161]
| |||||||
mien hatGa naar voetnoot1) und dass diese für die Intuitionisten ein Problem, aber für die Symbolisten ein testimonium paupertatis sind,Ga naar voetnoot2) oder nennt Hilberts Geometrie kurzweg ‘pseudogéometrie’.Ga naar voetnoot3) Der eine betrachtet die Algebra der Logik als Prärequisit der klassischen Logik, der andere, neuerdings z.B. J. Jörgensen in seinem schon erwähnten Buch (II, 133), meint, dass die Algebra der Logik die klassische Logik voraussetzen muss. Der eine sieht in Cantors Mengenlehre einen genialen Griff, durch welchen es ihm gelungen ist, ‘auch die unendlichen Mengen unter die Herrschaft der mathematischen Formeln und Gesetze zu zwingen’,Ga naar voetnoot4) der andere beschuldigt Cantor, dass er auch wie Hilbert und die Logistik den mathematischen Boden eigentlich verlassen habe.Ga naar voetnoot5) Auf der einen Seite suchen die Mathematiker ihre ‘Algebra der Logik’ bis zum Aeussersten zu verfeinern; als rezentes Beispiel könnten wir auf David Yule hinweisen, der im Anschluss an Ernst Schröder folgende Zeichen gebraucht für die Relation der ‘Klassen’:
und der dann an der Hand des folgenden bekannten | |||||||
[pagina 162]
| |||||||
SchemasGa naar voetnoot1) aus dem auf  gebauten Postulatensystem ein gebauten Postulatensystem ein 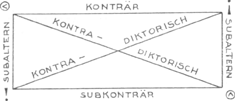 zweites ableitet und von der ‘herkömmlichen Lehre der Subalternation, wonach das subalternierende Urteil das subalternierte einschliesst’, eine ‘Berichtigung’ gibt. Oder auch, man sieht sie im Zusammenhang mit Schriftzeichen, Schriftnamen und Schriftsprache neue Paradoxa aufstellen und behandeln (z.B. die Antinomie von Dixon).Ga naar voetnoot2) Aber auf der anderen Seite steht die Meinung derer, die diesem ganzen Klassenkalkul jeden Wert absprechen und die Formalisierung der Logik wie auch die Aufstellung der logischen Paradoxe für sinnlos halten.Ga naar voetnoot3) Und während sich die Lösungen der Paradoxien des Unendlichen vervielfältigen, und sogar zu den Haupttypen der Lösungsversuche (intuitionistisch, axiomatisch, logistisch) noch Einzelversuche (wie von T. Brodén, s.J. Jörgensen, III, 162) hinzutreten, wird noch immer, auch von solchen, die halbwegs einverstanden sind, an der Grundlage dieses ganzen Gedanken- und Sprachgebäudes fundamentale Kritik geübt, z.B. von Natorp und der Marburger Schule, die unter Berufung auf Veronese behaupten, dass der Unterschied zwischen dem Endlichen und dem Unendlichen sich relativieren mussGa naar voetnoot4), oder auch von Skolem- | |||||||
[pagina 163]
| |||||||
Löwenheim, wenn sie, um mit FraenkelGa naar voetnoot1) zu reden, in ihrer ‘Paradoxie’ ‘einen neuen, beunruhigend wirkenden Angriff auf die axiomatische Begründung der Mengenlehre und Analysis’ wagen und darlegen, ‘dass jeder Zahlausdruck entweder widerspruchsvoll ist oder schon innerhalb eines abzählbar unendlichen Denkbereichs erfüllbar ist’.Ga naar voetnoot2) Diesen auf logistischem Weg bewiesenen Satz muss die heutige Wissenschaft sich noch überlegen, sagt Fraenkel.Ga naar voetnoot3) Die Berliner Akademie hat im Jahre 1784 eine Preisaufgabe ausgeschrieben: wie man so viele wahre Sätze aus einer widerspruchsvollen Voraussetzung habe ziehen könnenGa naar voetnoot4) und hatte dabei ein Auge auf Begriffe wie ‘unendlich kleine Grössen’ u.s.w. (dies im Zusammenhang mit Eulers Auseinandersetzungen). Jetzt, anderthalb Jahrhunderte später, stellen manche das Problem noch so, aber trennen sich dann in verschiedene Gruppen, von denen die eine die Antwort für möglich, die andere für unmöglich hält. Noch wieder andere halten die Problemstellung selber für falsch, aber auch diese gehen wieder in verschiedene Richtungen. Da die Diskussion über die mathematischen Paradoxien so verläuft, ist der Schluss berechtigt, dass zwar insoweit die Mathematik hinsichtlich des Problems des Paradoxons parallel läuft zu den Untersuchungen in der allgemeinen Philosophie und Theologie, als von inzidentell entdeckten Paradoxa die Aufmerksamkeit sich verschiebt nach dem Kern des Problems der Paradoxalität der Erkenntnis überhaupt, aber dass übrigens die | |||||||
[pagina 164]
| |||||||
mathematische Diskussion die Neigung zeigt, mit ihren Paradoxen und deren Problemen sich doch - wenigstens praktisch - wieder zu isolieren, trotz der Tatsache, dass Russell die mathematischen Paradoxa aus ihrer vormaligen Isolation befreit hatte, und auch trotz Versuchen einer ‘Zeitschrift für die Zusammenarbeit von Philosophie und Einzelwissenschaft’Ga naar voetnoot1) wo z.B. Robert Heiss den Begriff ‘heterologisch’ widerspruchsvoll zu einem Grundgesetz der Begriffe genannt hat, und ‘geradezu seinsmässig’, weil s.E. das Problem ‘seinen eigentlichen Ort hat in einer Problematik des Seins’, in ‘Seinswidersprüchen, - sei es auch nur innerhalb der Aussagesphäre’.Ga naar voetnoot2) Dass, wie Heiss meint, im Paradoxon des ‘heterologisch’ ‘der Logos als benennendes Sein seinem Benannten, als ausdrückendes Sein seinem Ausgedrückten widerspricht’,Ga naar voetnoot3) das ist eine Behauptung, und das zeigt eine Problemstellung, welche die mathematische Diskussion im allgemeinen noch nicht zu fesseln vermögen. Weil ausserdem ihre Schwierigkeiten sich nur knüpfen an die oben gekennzeichneten Paradoxen-Typen I und III (weil ihr Unendlichkeitsbegriff sich völlig von dem Kierkegaardschen, als Typus genommen, unterscheidet), bleibt sie auch ausserhalb der Dialektik, wie diese sonst für die Problemstellung des Paradoxons kennzeichnend ist. Ihre eigene Unsicherheit ist dann der letzte Faktor, der sie daran hindert, in der allgemeinen Debatte über das Paradoxon einen eigenen Ton hören zu lassen. Obwohl das Unendlichkeitsproblem, das, wie G. RitterGa naar voetnoot4) zeigte, schon die Spätscholastik (Cusanus!) beschäftigte, noch immer die mathematische Diskussion schwierig macht, so ist es doch unrichtig, mit Erh. Schmidt die Uneinhelligkeit | |||||||
[pagina 165]
| |||||||
der Mathematiker auf der Verschiedenheit ihrer Stellungnahme zum Begriff des Unendlichen beruhen zu lassen.Ga naar voetnoot1) Diese Verschiedenheit ist nur eine Ursache unter vielen anderen, woraus sich die ‘verzweifelte Lage’ erklären lässt.Ga naar voetnoot2) |
|


 b: die Klasse a ist völlig in der Klasse b eingeschlossen;
b: die Klasse a ist völlig in der Klasse b eingeschlossen; b: die Klasse a ist teilweise aus der Klasse b ausgeschlossen;
b: die Klasse a ist teilweise aus der Klasse b ausgeschlossen;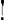 b: die Klasse a ist teilweise in der Klasse b eingeschlossen;
b: die Klasse a ist teilweise in der Klasse b eingeschlossen; b: die Klasse a ist völlig aus der Klasse b ausgeschlossen; -,
b: die Klasse a ist völlig aus der Klasse b ausgeschlossen; -,