Die conste vanden getale
(1999)–Marjolein Kool–Een studie over Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw, met een glossarium van rekenkundige termen
[pagina 56]
| ||||||||||||||||||||||||||||||||||||||||||||||
Hoofdstuk 3
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 57]
| ||||||||||||||||||||||||||||||||||||||||||||||
3.1 ProloogVrijwel alle rekenboeken beginnen met een voorrede waarin het belang van die edel conste arithmeticaGa naar voetnoot4 breed wordt uitgemeten. Van der Gucht schrijft bijvoorbeeld in zijn woord vooraf: Arithmetica, ... twelcke is Vertalingen of parafrases van klassieke citaten moeten de lofprijzing kracht bijzetten. Erg populair zijn een citaat van Augustinus: Niemant en can hemelsche noch en een van Aristoteles: Die niet rasch en sijn inder PetriGa naar voetnoot8 gebruikt een citaat van Isidorus: Neempt dat ghetal van den Van der Schuere schrijft een uitvoerige berijmde Ode op het tal-constboeck.Ga naar voetnoot10 In de gedrukte rekenboeken volgt na de lofprijzing van de rekenkunde vaak nog | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 58]
| ||||||||||||||||||||||||||||||||||||||||||||||
een eerbiedige opdracht aan een of meer belangrijke personen. Van der Gucht begint zijn zend-brief met: De edele, wijse ende zeer Wentsel richt zich tot de notabelen van de wel-vermaerde coop-stadt MiddelburgGa naar voetnoot12 Van der Schuere richt zijn opdracht in het Frans aan Govaert Willemsz. marchant en la tres-renommee ville d'Amsterdam.Ga naar voetnoot13 Van den Dijcke schrijft Aen de achtbare eersame discrete ende seer voorsienighe ... cooplieden van Antwerpen myne goetgunstighe heeren ende vrienden.Ga naar voetnoot14 De opdracht is mogelijk bedoeld om het aanzien van het werk te verhogen en het is niet uitgesloten dat degenen aan wie de opdracht gericht is, de publicatie van het boek financieel ondersteund hebben.Ga naar voetnoot15 Soms is een rekenboek uit vriendschap of bewondering aan iemand opgedragen. Van den Hoecke draagt in een Latijnse passage zijn werk op aan Guilhelmus Rhetius of Willem van Rethy, een premonstratenzer, die van ±1535 tot 1540 prior van de St. Michielsabdij te Antwerpen is. Van den Hoecke prijst Rhetius om zijn grote wiskundige kennis en schrijft dat hij een aantal keren wiskundige vraagstukken met hem besproken heeft. Drie jaar later, draagt ook Gemma Frisius zijn rekenboek aan Rhetius op.Ga naar voetnoot16 Het werk van Van den Hoecke is het enige Nederlandstalige rekenboek dat aan een ‘geleerde’ wordt opgedragen. In de andere rekenboeken is, als er al van een opdracht sprake is, deze gericht aan kooplieden en notabelen. Dit komt overeen met de doelstelling van de boeken: men wil praktische rekenkunde voor koop- en ambachtslieden beschrijven en men heeft niet de pretentie een wiskundige verhandeling voor ‘geleerden’ te schrijven.Ga naar voetnoot17 De meeste auteurs dekken zich in hun inleiding bij voorbaat in tegen eventuele kritiek op hun werk. Van Varenbraken: Ende [ic] bidde een | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 59]
| ||||||||||||||||||||||||||||||||||||||||||||||
al waert dat sij vondenGa naar margenoot+ Van Halle verdedigt zich op rijm: Ick bidts u al hebdyGa naar margenoot+ Niet alle fouten die in een rekenboek voorkomen zijn de schuld van de auteur. Soms heeft de drukker zijn werk niet goed gedaan. Petri: Dat aen sommighe plaetzen Stockmans richt zich in zijn inleiding tot den schimpers met: Laet blijven u schimpighe Wentsel vaart aan het eind van zijn rekenboek woedend uit naar zijn collega's Ludolf van Ceulen en Felix van Sambeke die beweerd zouden hebben, dat hij een be- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 60]
| ||||||||||||||||||||||||||||||||||||||||||||||
paald interestvraagstuk in zijn boek met interesttabellenGa naar voetnoot22 verkeerd zou hebben opgelost.Ga naar voetnoot23 Wentsel heeft het vraagstuk inderdaad niet goed opgelost, maar hij wil zijn ongelijk niet bekennen en berispt ook zijn vriend Anthony Smyters, omdat deze hem niet steunt in de kwestie. Meskens merkt op dat dergelijke twisten de rekenmeesters stimuleren om hun argumenten zoveel mogelijk te verduidelijken en in die zin zijn ze een eerste aanzet tot een soort van bewijsvoering.Ga naar voetnoot24 Dit is mogelijk, maar in de Nederlandse rekenboeken worden verder geen sporen van twisten, debatten of discussies aangetroffen. Argumenten en bewijzen spelen in de rekenboeken geen enkele rol. | ||||||||||||||||||||||||||||||||||||||||||||||
3.2 ‘Gehele’ getallenIn het eerste gedeelte van de rekenboeken worden de hoofdbewerkingen voor de ‘gehele’ getallen behandeld.Ga naar voetnoot25 Ook het rekenen met munten, maten en gewichten wordt in dit gedeelte uitgelegd. Het rekenen met breuken volgt later.Ga naar voetnoot26 Het aantal behandelde hoofdbewerkingen varieert per rekenboek.Ga naar voetnoot27 Enkele auteurs onderscheiden zeven hoofdbewerkingen: numeratie, optellen, aftrekken, halveren, verdubbelen, vermenigvuldigen en delen.Ga naar voetnoot28 In de meeste rekenboeken worden halveren en verdubbelen niet uitgelegd; er komen dan dus in het totaal vijf hoofdbewerkingen voor. HelmduynGa naar voetnoot29 merkt op: Dit alsdan wetende, salmenGa naar margenoot+ Enkele auteurs tellen in hun rekenboeken slechts vier hoofdbewerkingen. Zij zonderen namelijk numeratie uit. Van Halle: Int sypher syn 4 specien...Ga naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 61]
| ||||||||||||||||||||||||||||||||||||||||||||||
3.2.1 NumeratieIn het hoofdstuk numeratie wordt uitgelegd hoe men de Hindoe-Arabische cijfers moet lezen en schrijven. Pijck:Ga naar voetnoot32 Numeratio, het beghinsel vanGa naar margenoot+ In Latijnse rekenboeken vindt men in het hoofdstuk numeratie herhaaldelijk stukjes getallenleer. Bijvoorbeeld een definitie van getal en een bespreking van de vraag of nul en een al dan niet getallen zijn. Ook worden er getallen in allerlei groepen ingedeeld.Ga naar voetnoot34 In de Nederlandstalige rekenboeken is dit niet gebruikelijk. Slechts Van der Schuere gaat kort op dit onderwerp in. Getallen definieert hij als volgt: Ghetallen zijn daer door de Over het getal nul schrijft Van der Schuere: O die men ‘nullo’ - dat is Bij Van der Schuere is er echter geen sprake van een apart hoofdstuk over getal- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 62]
| ||||||||||||||||||||||||||||||||||||||||||||||
lenleer. De enige Nederlandstalige auteur die dit onderwerp wel uitgebreid, in een apart hoofdstuk, aan de orde stelt, is Van Halle.Ga naar voetnoot37 In de overige rekenboeken houdt numeratie uitsluitend het leren lezen en schrijven van Hindoe-Arabische getallen in. De enige indeling van getallen die in vrijwel alle rekenboeken wordt gemaakt is die in eenheden, tientallen en samengestelde getallen, respectievelijk digiten, articulen en compositen genoemd. Deze traditionele indeling speelt in de rest van de behandelde rekenkunde geen rol meer.Ga naar voetnoot38 De nul krijgt relatief veel aandacht, waarschijnlijk omdat het voor leerlingen die uitsluitend de Romeinse cijfers kennen een nieuw fenomeen is. Bij het traditionele rekenen met penningen en in het Romeinse cijfersysteem komt voor nul geen symbool voor. Bij het rekenen met Hindoe-Arabische getallen, waar de waarde van de cijfers door hun plaats bepaald wordt, wordt voor nul een symbool ingevoerd dat bovendien een dubbele betekenis heeft. Enerzijds betekent het niets, anderzijds kan de nul de waarde van een getal veranderen als deze daaraan toegevoegd wordt. In het voorgaande citaat van Van der Schuere is die dubbelfunctie vermeld. Van Varenbraken schrijft over de nul: Ende tot desen dygyten oftGa naar margenoot+ Door de nul in de articulen te vervangen door een van de digiten ontstaan de compositen: Ende van dese digyten endeGa naar margenoot+ Als het principe van het Hindoe-Arabische getalsysteem is uitgelegd, wordt het onmiddellijk toegepast op zeer grote getallen. Van Varenbraken legt bijvoorbeeld uit hoe een getal van 18 cijfers gelezen moet worden.Ga naar voetnoot41 Zie figuur 3.1. Van der Gucht behandelt zelfs een getal van 30 cijfers.Ga naar voetnoot42 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 63]
| ||||||||||||||||||||||||||||||||||||||||||||||
Verschillende auteurs gebruiken de term duusentduust voor miljoen.Ga naar voetnoot43 Dat maakt het uitspreken van grote getallen nogal onoverzichtelijk, zoals bijvoorbeeld blijkt uit het volgende citaat van Van den Hoecke: 9876543210, segghet: neghenGa naar margenoot+  Figuur 3.1. Schema met de plaatswaarden van de cijfers in een getal.Ga naar voetnoot45
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 64]
| ||||||||||||||||||||||||||||||||||||||||||||||
Struik onderzocht de wijze waarop het woord millioen in de Nederlandse taal is ingeburgerd.Ga naar voetnoot46 Volgens hem komt het pas in 1589 voor de eerste keer in een Nederlandstalig rekenboek voor. Dat zou in het rekenboek van Stockmans zijn, aangenomen dat de editie van 1589 met die van 1609 overeenstemt.Ga naar voetnoot47 Deze bewering is niet juist. Het woord millioen komt namelijk al in 1510 voor in het hoofdstuk over penningrekenen in D-Man-1510 en eveneens in de rekenboeken H-GeU-1532, H-BKB-1568, D-Guc-1569 en H-TSB-1578. Volgens Struik blijven de geleerden zich langer tegen de term verzetten dan de rekenmeesters. In het Latijnse rekenboek van Gemma Frisius komt de term inderdaad niet voor. Mogelijk beschouwde hij, net als zijn collega's, het woord als een onwetenschappelijke volksterm. Cardanus schrijft in zijn Practica Arithmetica van 1537: Milliaria millium quae vulgo Cardanus woonde in Italië, waar de term al halverwege de veertiende eeuw in de volkstaal voorkwam. Van Varenbraken verwerpt in zijn rekenboek het woord millioen om didactische redenen; duusentduust vindt hij duidelijker: Nu tellen sommighe aldus ende De auteurs die wel kiezen voor het woord millioen, hebben ook niet veel moeite met ‘nieuwe’ benamingen voor nog grotere getallen, zoals blijkt uit het volgende overzicht: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 65]
| ||||||||||||||||||||||||||||||||||||||||||||||
Pijck en Van Halle tekenen in grote getallen na elke 3 cijfers een verticaal streepje, om de leesbaarheid van het getal te vergroten.Ga naar voetnoot50 Van Halle schrijft hier over: Aldus machmen voorts van alle In verschillende rekenboeken komen naast Hindoe-Arabische cijfers ook incidenteel Romeinse cijfers voor. In D-Man-1508 zijn de getallen van 1 tot en met 38 in Romeinse en Hindoe-Arabische cijfers genoteerd.Ga naar voetnoot52 Heyns gebruikt in zijn rekenboek op de linkerpagina Romeinse cijfers en rechts Hindoe-Arabische, vermoedelijk om zijn leerlingen met beide systemen vertrouwd te maken.Ga naar voetnoot53 Heyns, Van Halle, Van den Dijcke en Stockmans gebruiken in een schema een bijzondere mengvorm van de traditionele Romeinse cijfers met het ‘moderne’ plaatswaarde-systeem.Ga naar voetnoot54 Zie figuur 3.2. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 66]
| ||||||||||||||||||||||||||||||||||||||||||||||
 Figuur 3.2. Het gebruik van Romeinse cijfers om de uitspraak van Hindoe-Arabisch getallen uit te leggen.Ga naar voetnoot55
Van der Gucht combineert telwoorden met Romeinse cijfers om de plaatswaarden van 1 tot en met 1030 uit te spreken. Zo geeft hij bijvoorbeeld 1030 weer met C.M. miliote miliote.Ga naar voetnoot56 Van den Hoecke gebruikt Romeinse cijfers uitsluitend in het colofon om het jaartal weer te geven.Ga naar voetnoot57 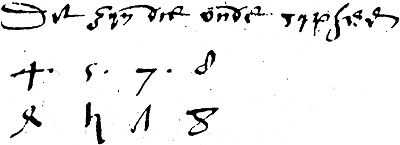 Figuur 3.3. De oude cijfervormen.Ga naar voetnoot58
Van Halle, Van der Gucht en Pijck geven voor de cijfers 4, 5, 7 en 8 nog een alternatieve schrijfwijze.Ga naar voetnoot59 Zie figuur 3.3. Het zijn de oudere cijfervormen, die aanvankelijk in West-Europa in gebruik waren. De cijfers 4, 5 en 7 kregen in de veertiende eeuw in Italië hun moderne vorm. Deze vorm heeft zich in de loop van de vijftiende eeuw mede door de boekdrukkunst in de overige landen van Europa verspreid.Ga naar voetnoot60 In het rekenboek van Van der Gucht verschijnen de oude vormen zelfs in | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 67]
| ||||||||||||||||||||||||||||||||||||||||||||||
druk. Alle drie de auteurs laten de oude vormen zien, maar gebruiken ze verder niet. | ||||||||||||||||||||||||||||||||||||||||||||||
3.2.2 OptellenVrijwel elke hoofdbewerking wordt ingeleid door een soort definitie. Van Varenbraken begint zijn uitleg over optellen als volgt: Additio es... om te adderen,Ga naar margenoot+ De zestiende-eeuwse methode van optellen komt overeen met de huidige manier van cijferend optellen. De getallen worden onder elkaar geplaatst en kolomsgewijs opgeteld. Sommige auteurs tellen van boven naar beneden, anderen van beneden naar boven, zoals bijvoorbeeld Van der Gucht: ... beghinnende ter Stockmans telt ook van beneden naar boven, maar bij het controleren van zijn berekeningen werkt hij in omgekeerde richting.Ga naar voetnoot63 De meeste auteurs beginnen hun uitleg met een eenvoudige optelling waarbij nog niet onthouden hoeft te worden. Daarna volgt een moeilijker voorbeeld. Petri behandelt de navolgende optelling waarin wel onthouden moet worden: Omme te addeeren 457 met 683,Ga naar margenoot+ 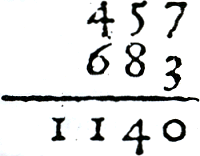 Figuur 3.4. Optelling.
De som van de cijferkolommen overschrijdt de 9 en er moet dus een getal naar de volgende kolom getransporteerd worden. De voorbeelden worden geleidelijk aan moeilijker, dat wil zeggen dat er meer en grotere getallen opgeteld worden. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 68]
| ||||||||||||||||||||||||||||||||||||||||||||||
Als het optellen met ‘kale’, dat wil zeggen onbenoemde getallen genoeg geoefend is, volgen de berekeningen met munten, maten en gewichten. Deze berekeningen kunnen door het ontbreken van decimale munten en maten soms behoorlijk ingewikkeld zijn. Van Varenbraken telt bijvoorbeeld vier geldbedragen op die Jan, Pieter, Willem en Wouter schuldig zijn.Ga naar voetnoot65 Zie figuur 3.5. 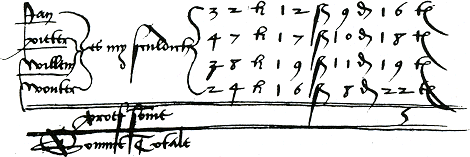 Figuur 3.5. Optelling van vier geldbedragen.
Op de eerste regel staat: Jan es my sculdich 32 ponden 12 schellingen 9 penningen 16 miten. Om deze optelling uit te kunnen voeren, worden eerst alle muntsoorten afzonderlijk opgeteld. Dat levert de proefsomme op van 131 ponden 64 schellingen 38 penningen en 75 miten. Deze proefsomme wordt eerst gecontroleerd op rekenfouten en daarna gereduceerd, dat wil zeggen dat de verschillende muntsoorten in grotere eenheden omgerekend worden. Daarvoor gebruikt men de volgende gegevens: 1 penning = 24 miten, 1 schelling = 12 penningen, 1 pond = 12 schellingen. Uiteindelijk blijkt na reductie van de proefsomme dat de totaalsomme in deze optelling gelijk is aan: 134 ponden, 7 schellingen, 5 penningen en 3 miten. De meeste auteurs maken geen gebruik van proefsommen. Nadat een kolom is opgeteld, wordt er meteen overgedragen naar de volgende kolom. Het optellen met munten, maten en gewichten wordt in de meeste rekenboeken intensief geoefend. Stockmans geeft bij zijn uitleg over optellen acht vraagstukken met verschillende muntsoorten, zes vraagstukken met verschillende inhoudsmaten en zestien vraagstukken met verschillende gewichten.Ga naar voetnoot66 Van der Schuere geeft zelfs een voorbeeld waarin tijd wordt opgeteld.Ga naar voetnoot67 Zie figuur 3.6. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 69]
| ||||||||||||||||||||||||||||||||||||||||||||||
 Figuur 3.6. Optelling van tijden.Ga naar voetnoot68
Van den Hoecke behandelt het optellen en aftrekken van munten, maten en gewichten in een apart hoofdstuk. Hij begint daarmee als de hoofdbewerkingen voor de gehele getallen alle vier behandeld zijn.Ga naar voetnoot69 Pijck is de enige auteur die optellingen behandelt waarbij de som gegeven is en een van de termen gevraagd wordt:Ga naar voetnoot70 Vindt mij een getal alsmen Enkele auteurs behandelen voor elke hoofdbewerking de manier waarop die hoofdbewerking tijdens het rekenen benoemd wordt.Ga naar voetnoot72 Van den Hoecke schrijft over het taalgebruik bij optellen: Die maniere van te Spreken:Ga naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
3.2.3 AftrekkenVan Halle begint zijn uitleg als volgt: Substractio oft aftreckingheGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 70]
| ||||||||||||||||||||||||||||||||||||||||||||||
Evenals het optellen wordt ook het aftrekken op dezelfde wijze uitgevoerd als thans gebruikelijk is. De aftrekker wordt onder het aftrektal geplaatst en kolomsgewijs van rechts naar links afgetrokken. Van Varenbraken schrijft: Set die betalinghe recht metGa naar margenoot+ Het aftrekken wordt in de meeste rekenboeken geoefend met vraagstukken waarin van het aflossen van schuld sprake is. Van Varenbraken behandelt bijvoorbeeld het volgende vraagstuk: Jan Niemant es my sculdich Na het eenvoudige aftrekken volgen aftrekkingen waarin geleend moet worden. Raets berekent 5428 - 436. Zie figuur 3.7. Om te substraheren 436 vanGa naar margenoot+  Figuur 3.7. Aftrekking.
6 van 8 ende daer sullen | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 71]
| ||||||||||||||||||||||||||||||||||||||||||||||
ghetal 4 een, soo doen die 2 In de meeste rekenboeken gebeurt het lenen door in de naaste kolom het aftrektal met 1 te verminderen, zoals in het voorgaande citaat. In andere rekenboeken gebeurt het ook wel door in de naaste kolom de aftrekker met 1 te vermeerderen.Ga naar voetnoot78 Van der Gucht en Pijck behandelen beide methodes.Ga naar voetnoot79 Van der Gucht: Maer alzo dicwils als dat Bij Van den Hoecke wordt het complement van de aftrekker bij het aftrektal opgeteld en 1 bij de aftrekker in de volgende kolom. Bijvoorbeeld bij de berekening van 9721 - 6892: Nu trect 2 van 1. Dat en mach | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 72]
| ||||||||||||||||||||||||||||||||||||||||||||||
Tevens behandelt Van den Hoecke nog een voorbeeld waarin het aftrektal van links naar rechts wordt afgetrokken. Het aftrekken van munten, maten en gewichten krijgt in de meeste rekenboeken uitgebreid aandacht. Het lenen is bij dit soort vraagstukken gecompliceerder omdat het afhangt van de waarde van de munt, de maat of het gewicht hoeveel er geleend wordt. Van Varenbraken trekt bijvoorbeeld twee geldbedragen van elkaar af, die elk uit vier verschillende muntsoorten bestaan:Ga naar voetnoot82 Schult 334 ponden 13 schellingen 9 penningen 13 miten Voordat de aftrekking kan plaatsvinden, moet er eerst geleend worden. 1 pond = 20 schellingen, 1 schelling = 12 penningen, 1 penning = 24 miten. Vervolgens wordt dan de aftrekking aldus: Schult 333 ponden 32 schellingen 20 penningen 37 miten Uit figuur 3.8 blijkt dat Van Varenbraken in zijn berekening een fout heeft gemaakt. Hij houdt 11 penningen in de Reste over, terwijl het er 10 moeten zijn. 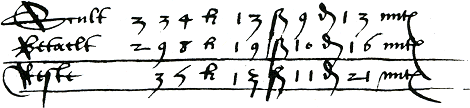 Figuur 3.8. Aftrekking van geldbedragen.
Het taalgebruik bij aftrekken is als volgt. Pijck: Ende dit es spreeckwoort van Negatieve getallen spelen in de rekenboeken geen rol. Van den Hoecke vermeldt bij het aftrekken: Het onderste getal en sal | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 73]
| ||||||||||||||||||||||||||||||||||||||||||||||
Van der Gucht adviseert om in het geval dat het bovenste getal kleiner is dan het onderste, de zaak om te keren en het bovenste getal van het onderste af te trekken, zodat men kan zien - indien er sprake is van het aflossen van een schuld - hoe groot het bedrag is dat te veel is betaald: Ware zy minder, zoo zoude zyGa naar margenoot+ Zie bijvoorbeeld figuur 3.9.Ga naar voetnoot86  Figuur 3.9. Aftrekking waarbij een ‘negatieve’ uitkomst ontstaat.Ga naar voetnoot87
Pijck behandelt ook bij het aftrekken weer een aantal vraagstukken die in geen enkel ander rekenboek zijn aangetroffen: Vindt mij een getal dwelck | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 74]
| ||||||||||||||||||||||||||||||||||||||||||||||
3.2.4 Halveren en verdubbelenDe hoofdbewerkingen halveren en verdubbelen komen slechts in enkele rekenboeken voor. Van Varenbraken en Van der Gucht behandelen eerst halveren en daarna verdubbelen.Ga naar voetnoot90 Anderen beginnen met verdubbelen. CreszfeltGa naar voetnoot91 ziet niet in waarom hij halveren en verdubbelen als aparte hoofdbewerkingen zou behandelen, omdat... ...dubelyren niet anders isGa naar margenoot+ Van Halle sluit zich hier bij aan: Waert dat saeke dat duplatio Desondanks behandelt hij een aantal verdubbelingsvraagstukken. Ook Van der Gucht onderkent de overeenkomst met vermenigvuldigen en delen, maar vindt het blijkbaar toch belangrijk om apart aandacht te besteden aan halveren en verdubbelen: De vierde specie es ghenaemtGa naar margenoot+ Wentsel behandelt het halveren en verdubbelen niet: Wanttet onder de handt,Ga naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 75]
| ||||||||||||||||||||||||||||||||||||||||||||||
Situaties waarin halveren of verdubbelen nootsakelicken voorvalt liggen in de rekenboeken niet voor het oprapen.Ga naar voetnoot96 Het behandelen van halveren en verdubbelen als aparte hoofdbewerkingen is mogelijk een kwestie van traditie.Ga naar voetnoot97 Van Varenbraken begint zijn uitleg over halveren als volgt: Mediatie en es anders niet,Ga naar margenoot+ En bij verdubbelen schrijft hij: Duplicatio... en es anders Halveren gebeurt van links naar rechts. Bij deze bewerking speelt het onderscheid tussen even en oneven getallen een rol. Van Varenbraken gaat ervan uit dat zijn leerlingen dit onderscheid wel kennen. In D-Man-1508 wordt het uitgelegd: Oft dye somme ghescreven es Als er een oneven cijfer in het getal voorkomt, wordt de ongedeelde 1 als 10 bij het volgende cijfer opgeteld. Van Varenbraken: Jan ende Pieter moeten elck | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 76]
| ||||||||||||||||||||||||||||||||||||||||||||||
moeten hebben voor sijnGa naar margenoot+ Als een oneven getal gehalveerd wordt, ontstaat er een breuk. In het rekenboek van Van Varenbraken is dat geen probleem, daar zijn namelijk al eerder breuken aan de orde geweest, maar in verschillende rekenboeken komen bij halveren breuken voor, voordat ze ‘officieel’ behandeld zijn. Soms kan dit voortijdig rekenen met breuken al tamelijk ingewikkeld zijn, bijvoorbeeld in vraagstukken waarin sprake is van herhaald halveren.
Herhaald halveren en herhaald verdubbelen worden vaak aan het eind van de uitleg van halveren en verdubbelen behandeld. Als de som van een reeks halveringen of verdubbelingen moet worden bepaald, wordt er eigenlijk al vooruit gelopen op het hoofdstuk over reeksen, Progressio. Pijck berekent bijvoorbeeld de som van een reeks verdubbelingen met een regel die in moderne notatie uitgedrukt kan worden door: n Additie van dobbeleringenGa naar margenoot+ Herhaald halveren en herhaald verdubbelen worden vaak toegepast in vraagstukken die qua inkleding nogal gekunsteld aandoen. Zoals bijvoorbeeld dit vraagstuk uit het rekenboek van Van der Gucht: Een man vraechde eenen | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 77]
| ||||||||||||||||||||||||||||||||||||||||||||||
32 reysen toe ende datter danGa naar margenoot+ Het volgende voorbeeld is afkomstig uit het rekenboek van Van Halle: Daer is een joncker die Van Varenbraken behandelt het volgende vraagstuk: Een man heeft ghecocht een | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 78]
| ||||||||||||||||||||||||||||||||||||||||||||||
datter daer en tenden bleve,Ga naar margenoot+ 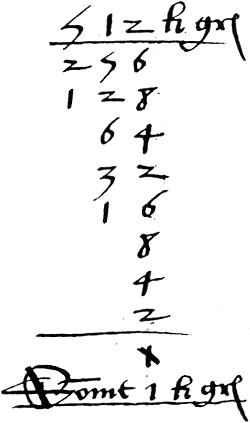 Figuur 3.10. Een bedrag wordt negen keer gehalveerd.Ga naar voetnoot106
Vraagstukken over herhaald verdubbelen en halveren met een meer realistische context komen in de rekenboeken niet voor. | ||||||||||||||||||||||||||||||||||||||||||||||
3.2.5 VermenigvuldigenVan den Hoecke beschrijft vermenigvuldigen als volgt: Multiplicatie is deen ghetalGa naar margenoot+ Voorafgaand aan de uitleg van vermenigvuldigen worden de tafels van vermenigvuldiging gegeven. In de meeste rekenboeken worden de tafels in een vierkant schema weergegeven. De afmetingen variëren van 10 × 10 tot 13 × 13.Ga naar voetnoot108 Het ge- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 79]
| ||||||||||||||||||||||||||||||||||||||||||||||
bruikelijkst is het schema waarin de tafels tot 12 × 12 zijn opgenomen zoals bij Van Varenbraken.Ga naar voetnoot109 Zie figuur 3.11.  Figuur 3.11. Tafels van vermenigvuldiging.Ga naar voetnoot110
In H-GeU-1592 komt een rechthoekig schema voor van wel zeer bijzondere afmetingen. Het bevat de tafels tot 17 × 27 en ook hier krijgt de lezer het advies deze tafels uit het hoofd te leren.Ga naar voetnoot111 Van der Gucht en Pijck geven vier verschillende vierkante schema's.Ga naar voetnoot112 Het eerste is het bekende met de tafels tot 12 × 12. Het laatste bevat de tafels van 13 tot en met 20. Tamelijk overbodig lijken de middelste twee schema's. In het ene staan de tafels van 10, 20, 30, ...., 90. In het andere de producten van 10 × 10, 10 × 20, 10 × 30, ..., 90 × 90, in sommige rekenboeken komen de tafels van vermenigvuldiging in kolomvorm voor.Ga naar voetnoot113 Zie figuur 3.12. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 80]
| ||||||||||||||||||||||||||||||||||||||||||||||
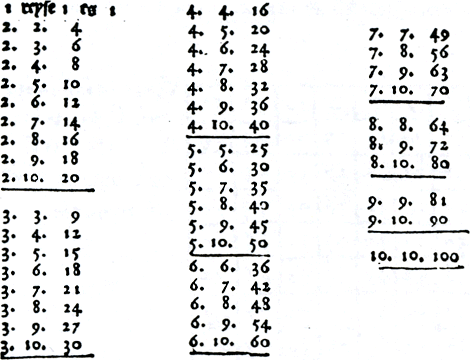 Figuur 3.12. Tafels van vermenigvuldiging in kolomvorm.Ga naar voetnoot114
Van Halle geeft ook nog een driehoekige tabel.Ga naar voetnoot115 Zie figuur 3.13. Het vermenigvuldigen gebeurt in de meeste rekenboeken cijferend onder elkaar op de manier zoals dat thans nog steeds gebruikelijk is. Het enige verschil is dat rechts van de tussenproducten in de berekening geen nullen genoteerd worden, maar plaatsen opengelaten worden, wat in principe op hetzelfde neerkomt. 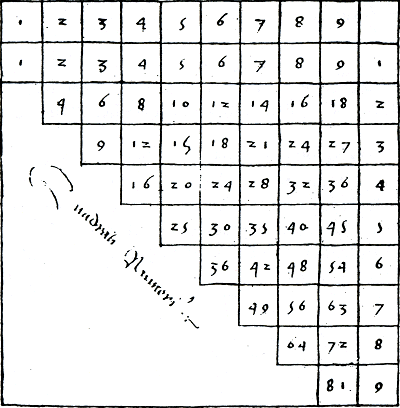 Figuur 3.13. Tafels van vermenigvuldiging in een driehoekig schema.Ga naar voetnoot116
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 81]
| ||||||||||||||||||||||||||||||||||||||||||||||
Van der Schuere vermenigvuldigt bijvoorbeeld als volgt: Multiplicatio met tweeGa naar margenoot+ Zie figuur 3.14. 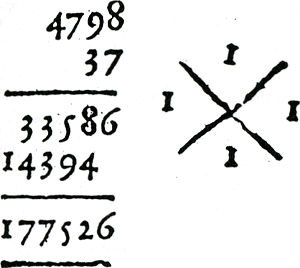 Figuur 3.14. Vermenigvuldiging met ‘proef’.
Berekeningen met munten, maten en gewichten die in het hoofdstuk over vermenigvuldigen voorkomen, zijn er alle op gericht om grotere eenheden om te rekenen in kleinere. Van der Schuere:Ga naar voetnoot118 345 ponden 13 schellingen 6 penningen. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 82]
| ||||||||||||||||||||||||||||||||||||||||||||||
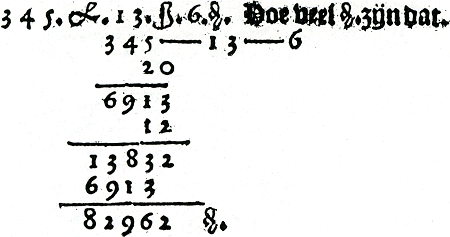 Figuur 3.15. Een geldbedrag omrekenen in een kleinere munteenheid.Ga naar voetnoot119
In sommige rekenboeken wordt het complementaire vermenigvuldigen uitgelegd. Het voordeel van deze methode is dat men slechts de tafels tot en met 5 × 5 uit het hoofd hoeft te kennen. De methode van Van der Gucht zou men met de volgende regel kunnen weergeven: ab = 10(a + b - 10) + (10 - a)(10 - b). Hij berekent 7 × 7 aldus: Om dit te doene, zo stelt | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 83]
| ||||||||||||||||||||||||||||||||||||||||||||||
buten of datze ghij bij uGa naar margenoot+ In figuur 3.16 is te zien hoe de berekening eruitziet. 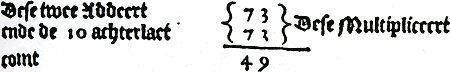 Figuur 3.16. Complementair vermenigvuldigen van 7 × 7.Ga naar voetnoot121
Van Halle schrijft dat deze methode geschikt is voor factoren die groter dan of gelijk aan 5 zijn: Men moet weeten dat die Ondanks deze waarschuwing berekent hij toch 5 × 4.Ga naar voetnoot123 Zie figuur 3.17. 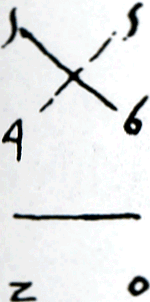 Figuur 3.17. Complementair vermenigvuldigen van 5 × 4.
Wellicht heeft hij de regel aangepast. In moderne notatie: ab = 10(a + b) + (10 - a)(10 - b) - 100. Maar dan zou de vermenigvuldiging 2 × 3 ook complementair mogelijk moeten zijn. Van Halle schrijft echter: Twee mael drye... ten duech Het voordeel dat de tafels boven 5 × 5 niet gekend hoeven worden, valt weg als men, zoals Van Halle, het complementair vermenigvuldigen gaat toepassen als beide factoren 5 of minder zijn, of als dat geldt voor een van de factoren. Van der GuchtGa naar voetnoot125 behandelt nog vijf andere vermenigvuldigmethoden, die alle op hetzelfde basisprincipe neerkomen. Het onderscheid zit hem in de notatie. In de eerste variant zijn de cijfers van de vermenigvuldiger van links naar rechts ge- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 84]
| ||||||||||||||||||||||||||||||||||||||||||||||
bruikt zodat het grootste tussenproduct bovenaan staat. Van den HoeckeGa naar voetnoot126 behandelt deze variant ook. In de tweede en de derde variant zijn de tussenproducten diagonaal genoteerd. Ten slotte zijn in de rechthoekige schema's van de vierde en vijfde variant alle tussenproducten volledig genoteerd zodat er tussentijds geen cijfers onthouden hoeven worden, zoals te zien is in figuur 3.18.Ga naar voetnoot127 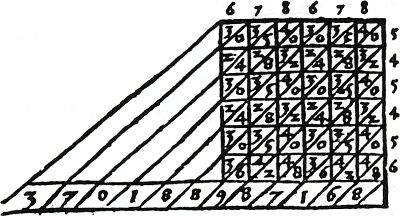 Figuur 3.18. Vermenigvuldiging: 678678 × 545456 = 370188987168. Elk tussenproduct wordt in het schema genoteerd.
Deze manier van vermenigvuldigen komt ook in H-TSB-1578 voor. Het is daar de enige methode die geleerd wordt. Wentsel behandelt naast de gebruikelijke vermenigvuldigmethode nog een andere, waarbij de tussenproducten voluit boven de factoren worden opgeschreven en men dus eveneens niets hoeft te onthouden.Ga naar voetnoot128 Zie figuur 3.19.  Figuur 3.19. Vermenigvuldiging 72 × 264 = 19008. Elk tussenproduct wordt boven de factoren genoteerd.
Als er in de vermenigvuldiger een nul voorkomt, noteert Van Halle als tussenproduct een rijtje nullen. Bijvoorbeeld als hij 402 guldens in stuivers wil omrekenen.Ga naar voetnoot129 Zie figuur 3.20. 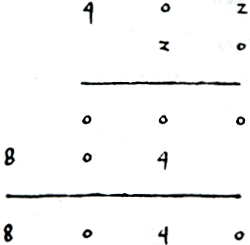 Figuur 3.20. Vermenigvuldiging: 402 × 20. In de vermenigvuldiger komt een nul voor.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 85]
| ||||||||||||||||||||||||||||||||||||||||||||||
Later bij multipliceren int corte slaat hij de nul in de vermenigvuldiger over: Alser inde middele van datGa naar margenoot+ Jaartallen spelen in het hoofdstuk over vermenigvuldigen vaak een rol. Het rekenboek van Van Varenbraken is volgens een mededeling op fol. 185r in 1532 voltooid.Ga naar voetnoot131 Bij de uitleg van vermenigvuldigen komt het volgende vraagstuk voor: Men mocht vraghen hoe Vraagstukken met een vergelijkbare context zijn ook in andere rekenboeken te vinden. Zo vraagt bijvoorbeeld Van Halle in zijn rekenboek van 1568: Aldus maectmen hoeveeleGa naar margenoot+ Pijck geeft in H-BSA-1584 een vergelijkbaar vraagstuk met het jaartal 1585. Wentsel gaat in D-Wen-1599 uit van het jaartal 1598. Van den Dijcke vraagt in zijn rekenboek van 1591 hoeveel dagen, uren en minuten er zijn in 1591 jaren. In de herdruk van 1600 is het aantal jaren in dit vraagstuk veranderd in 1600. Van Maanen suggereert dat het jaartal in dit type vraagstukken soms een aanknopingspunt kan bieden voor het dateren van ongedateerde rekenboeken.Ga naar voetnoot134 Uit voorgaande voorbeelden blijkt dat de jaartallen die in vraagstukken voorkomen inderdaad herhaaldelijk overeenkomen met de datering van het rekenboek waaruit ze afkomstig zijn, maar bij het trekken van conclusies op basis van dit gegeven blijft uiteraard voorzichtigheid geboden.Ga naar voetnoot135
Enkele auteurs behandelen het taalgebruik bij vermenigvuldigen. Van der Gucht: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 86]
| ||||||||||||||||||||||||||||||||||||||||||||||
Zegghende: 6 reysen 7 es 42,Ga naar margenoot+ Van Halle: Een maniere om te wetene | ||||||||||||||||||||||||||||||||||||||||||||||
3.2.6 DelenVan Varenbraken begint zijn uitleg over delen als volgt: Divisio, die sevenste specie,Ga naar margenoot+ Van den Hoecke begint met: Divisio oft deelinghe gheeftGa naar margenoot+ Van der Gucht is de enige auteur die erop wijst dat het ook voor delen van belang is de tafels van vermenigvuldiging uit het hoofd te kennen: Hier toe dient oock wel van De deelmethode die in de meeste rekenboeken wordt aangetroffen heeft veel overeenkomsten met de staartdeling die tegenwoordig gebruikt wordt,Ga naar voetnoot141 maar | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 87]
| ||||||||||||||||||||||||||||||||||||||||||||||
wijkt er op bepaalde punten van af. De deler wordt links onder het deeltal geplaatst en bij iedere stap in de berekening doorgestreept en opnieuw, een plaats verder naar rechts genoteerd. Het quotiënt verschijnt rechts van het deeltal en de resultaten van de tussenstappen worden boven het deeltal geschreven. Petri behandelt het volgende voorbeeld: Omme te deelen 27648 doer 36
De deler 36 wordt weer een plaats verder naar rechts opgeschreven. Het laatste cijfer van het quotiënt is 8: 8 × 3 = 24, 28 - 24 = 4, noteer 4 boven de 8 van 28. 8 × 6 = 48, 48 - 48 = 0. Voor de uiteindelijke berekening zie figuur 3.21.Ga naar voetnoot143 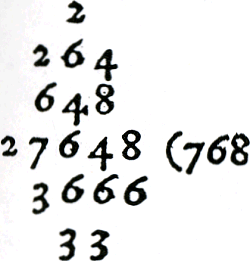 Figuur 3.21. Deling: 27648:36 = 768.Ga naar voetnoot144
Bij grotere delingen kan men in de vorm van de berekening een zeilschip herkennen. Zie figuur 3.22.Ga naar voetnoot145 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 88]
| ||||||||||||||||||||||||||||||||||||||||||||||
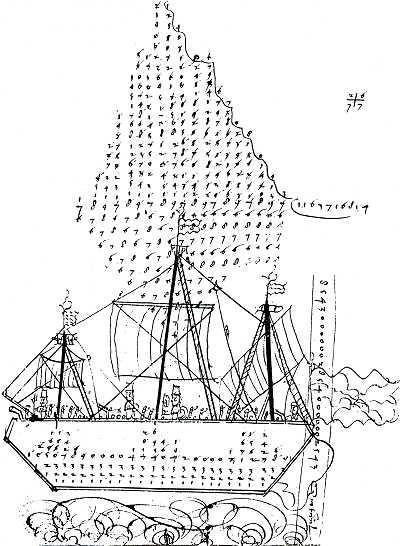 Figuur 3.22. Delingen in de vorm van een zeilschip.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 89]
| ||||||||||||||||||||||||||||||||||||||||||||||
Luca Pacioli noemt deze manier van delen galea vel batello.Ga naar voetnoot146 In H-GeU-1584 staat bij een deling dat deze galeye wordt genoemd.Ga naar voetnoot147 Zie figuur 3.23.  Figuur 3.23. Deling in de vorm van een zeilschip.Ga naar voetnoot148
Verschillende auteurs noteren het quotiënt niet rechts van het deeltal, maar tussen twee horizontale lijnen onder het deeltal.Ga naar voetnoot149 Van Halle hanteert een manier van delen waarbij onder de steeds voortschuivende deler de tussenproducten worden genoteerd die van het deeltal worden afgetrokken: Daer leet een in sijnenGa naar margenoot+ 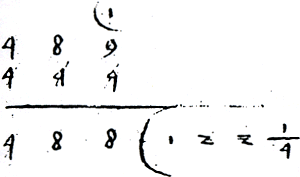 Figuur 3.24. Deling: 489:4 = 122¼.
Een staartdeling met de ‘staart’ naar beneden komt uitsluitend voor in het rekenboek van Wentsel:Ga naar voetnoot151 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 90]
| ||||||||||||||||||||||||||||||||||||||||||||||
Andere maniere van Zie figuur 3.25. 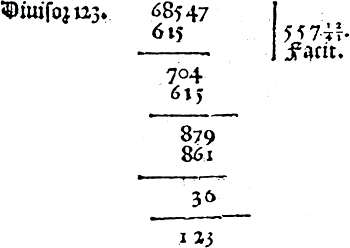 Figuur 3.25. Staartdeling.Ga naar voetnoot152
Na de delingen met ‘kale’ getallen komen ook in dit hoofdstuk de berekeningen met munten, maten en gewichten aan de orde. Het zijn berekeningen waarin kleinere eenheden omgerekend worden in grotere. Van der Schuere: Om te maken van penningen Hij berekent bijvoorbeeld hoeveel guldens er zijn in 394880 penningen. 394880:16 = 1234 guldens.Ga naar voetnoot154 Als er bij delen een rest overblijft, wordt die als breuk geschreven, dat wil zeggen de rest is de teller en het deeltal is de noemer.Ga naar voetnoot155 Van den Hoecke: 3726303 ghedeylt doer 4826 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 91]
| ||||||||||||||||||||||||||||||||||||||||||||||
rest 631. Dit stelt op hem Is er in de deling sprake van een geldbedrag, dan verloopt de behandeling van de rest anders. Van der Gucht behandelt het volgende vraagstuk: Het zijn 5 persoonen, de 4395⅗ ponden: 5 = 879 ponden rest ⅗ ⅗ pond wordt omgerekend naar een kleiner muntsoort en dan alsnog door 5 gedeeld. ⅗ pond = 12 schellingen, 12:5 = 2 schellingen rest 2 De ongedeelde rest van 2 schellingen wordt omgerekend naar penningen: 2 schellingen = 24 penningen, 24:5 = 4 penningen rest 4 4 penningen = 96 miten, 96:5 = 19 miten rest 1 Kortom: 4395⅗ ponden: 5 = 879 ponden 2 schellingen 4 penningen 19⅕ miten
Wat betreft het taalgebruik bij delen schrijft Pijck: De maniere van Spreken in Van Halle: Alser in eenighe somme coemptGa naar margenoot+ ‘hoe dicwils’ oft ‘hoe | ||||||||||||||||||||||||||||||||||||||||||||||
3.3 De proevenBij elke hoofdbewerking wordt uitgelegd hoe de berekening gecontroleerd kan worden. Dit gebeurt met de proeven. De oorsprong van de proeven ligt in het feit dat men aanvankelijk gewend was tijdens berekeningen de cijfers die voortkwamen uit de tussenstappen uit te wissen of door te strepen. Dat laatste komt ook | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 92]
| ||||||||||||||||||||||||||||||||||||||||||||||
nog in verschillende rekenboeken voor.Ga naar voetnoot160 Narekenen van de berekening is dan vrijwel onmogelijk. Bij penningrekenen worden de penningen steeds verlegd zodat het ook daar onmogelijk is om na afloop de gemaakte berekening na te lopen op zoek naar eventueel gemaakte fouten. Een proef is dan de enige controlemogelijkheid. In de meeste rekenboeken worden berekeningen gecontroleerd met de negenproef. Ook het uitvoeren van de inverse bewerking is gebruikelijk. Soms wordt de zevenproefGa naar voetnoot161 gehanteerd. Een enkele keer wordt er gecontroleerd met de preuve bij 3.Ga naar voetnoot162 Bij het penningrekenen wordt alleen met de inverse bewerkingen gecontroleerd. De negen-, zeven- en drieproef kunnen niet worden uitgevoerd omdat bij het penningrekenen zelfs de begingetallen, termen en factoren, verdwenen zijn aan het eind van de berekening. De negenproef bij de controle van een optelling is gebaseerd op de gelijkheid (a + b) mod 9 = (a mod 9 + b mod 9) mod 9. Van der Schuere beschrijft de methode als volgt: Proeve: Werpt alle de negenen In figuur 3.26 staat een voorbeeld van een optelling met een controle door de negenproef uit het werk van Van der Schuere.Ga naar voetnoot164 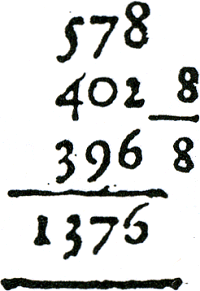 Figuur 3.26. Optelling met ‘proef’.
Eerst worden de negens uit de termen weggeworpen: 5 + 7 + 8 rest 2, 4 + 0 + 2 rest 6, 3 + 9 + 6 rest 0. De gezamenlijke rest is 8. Deze 8 wordt rechts van de optelling | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 93]
| ||||||||||||||||||||||||||||||||||||||||||||||
boven het streepje genoteerd. Dan worden de negens uit de som weggeworpen: 1 + 3 + 7 + 6 rest 8. Deze 8 wordt onder het streepje genoteerd. Zowel boven als onder het streepje staat 8 en daaruit blijkt dat de optelling waarschijnlijk correct is uitgevoerd. In de meeste rekenboeken wordt niet uitgelegd hoe dat uytwerpen van alle de negenen, ofwel dat uitzoeken van wat u over de neghenen blijft, in zijn werk gaat. Slechts een enkele auteur maakt duidelijk dat de termen uit de optelling niet gewoon door 9 gedeeld worden, maar dat de losse cijfers van elke term worden opgeteld en dat 9 steeds wordt afgetrokken zodra dat mogelijk is.Ga naar voetnoot165 Van Varenbraken legt uit: Nu trect alle die 9en uut die Bij vermenigvuldigen is de controle van de negenproef gebaseerd op de gelijkheid: (ab) mod 9 = ((a mod 9)(b mod 9)) mod 9. Van der Schuere: Proeve. Daer ghy medeGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 94]
| ||||||||||||||||||||||||||||||||||||||||||||||
In figuur 3.27 staat een vermenigvuldiging uit het werk van Van der Schuere met rechts daarvan in het kruis een controle met de negenproef.Ga naar voetnoot168 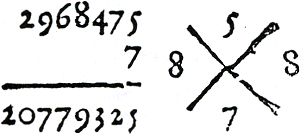 Figuur 3.27. Vermenigvuldiging met ‘proef’.
Onderin het kruis: de vermenigvuldiger 7 rest 7. Boven in het kruis: het vermenigvuldigtal 2 + 9 + 6 + 8 + 4 + 7 + 5 rest 5. Rechts in het kruis: het product van wat boven en onder in het kruis staat 5 × 7 rest 8. Links in het kruis: het product van de vermenigvuldiging 2 + 0 + 7 + 7 + 9 + 3 + 2 + 5 rest 8. Zowel links als rechts in het kruis staat 8. De vermenigvuldiging is dus waarschijnlijk correct uitgevoerd. Van Varenbraken controleert ook een deling met de negenproef. Dat wil zeggen, hij controleert eigenlijk de inverse berekening. Hij heeft berekend 301:20 = 15 rest 1 en hij controleert met de negenproef de berekening 20 × 15 + 1 = 301.Ga naar voetnoot169 De negenproef is niet waterdicht. Fouten die een veelvoud van 9 zijn, nullen te veel of te weinig en fouten in de volgorde van de cijfers worden er niet mee ontdekt. Sommige auteurs zijn zich dat bewust.Ga naar voetnoot170 Van der Gucht noteert: Het mach oock wesen, dat uGa naar margenoot+ Het controleren met behulp van de inverse bewerking is zekerder. Van der Gucht merkt op: De warachtichste, zekerste Sommige andere auteurs verkiezen de negenproef boven de inverse bewerking omdat de eerste eenvoudiger zou zijn. Stockmans schrijft: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 95]
| ||||||||||||||||||||||||||||||||||||||||||||||
Daer sijn menigherley ende Een andere reden om de negenproef te gebruiken ligt in het feit dat men een berekening nog niet kan controleren met de inverse bewerking zolang die inverse bewerking nog niet geleerd is. Bovendien wordt het controleren van een optelling door middel van de inverse bewerking aftrekken ingewikkeld, wanneer de optelling uit meer dan twee termen bestaat.
Van Halle behandelt voor elke bewerking drie verschillende controlemogelijkheden: de inverse bewerking, de zeven- en de negenproef.Ga naar voetnoot174 Van Varenbraken controleert de hoofdbewerkingen als volgt:Ga naar voetnoot175
Van der Schuere en Pijck controleren ook het worteltrekken.Ga naar voetnoot176 Pijck doet dat met de negenproef en de inverse bewerking: Multipliceert den gevonden | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 96]
| ||||||||||||||||||||||||||||||||||||||||||||||
Bij het rekenen met breuken komen minder regelmatig proeven voor dan bij de gehele getallen. Als er wordt gecontroleerd, gebeurt dat door middel van de inverse bewerkingen. Berekeningen die met de regel van drieën zijn uitgevoerd, worden gecontroleerd met de omgekeerde regel van drieën.Ga naar voetnoot178 Petri controleert geen enkele berekening.Ga naar voetnoot179
Opvallend is dat de auteurs die de zevenproef gebruiken dit doen voordat de bewerking ‘delen’ is uitgelegd, terwijl delen door 7 een belangrijke handeling in deze proef is. Van Halle is de enige auteur die zich dit blijkbaar realiseert. Hij begint de zevenproef met de tafel van 7, daarna volgen tabellen waarin de rest na deling door 7 is af te lezen. Zie figuur 3.28.Ga naar voetnoot180 | ||||||||||||||||||||||||||||||||||||||||||||||
3.4 BreukenVan Halle begint met een rijmpje: Breect uwe geheelen inGa naar margenoot+ Van Varenbraken introduceert het begrip ‘breuk’ als volgt: Soe moety weten dat den De breukstreep was niet algemeen verplicht. In D-Man-1508 staat: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 97]
| ||||||||||||||||||||||||||||||||||||||||||||||
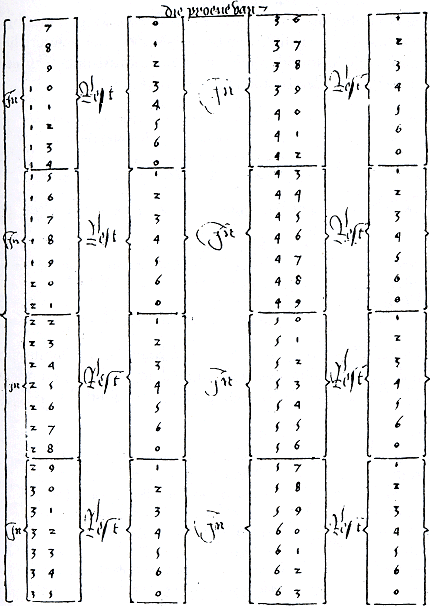 Figuur 3.28. Overzicht van resten die ontstaan na deling door 7.Ga naar voetnoot183
enz. Ende men mach tusschen beydenGa naar margenoot+ In D-Man-1508 komt de breukstreep overal voor, in de herdruk van 1510 geen enkele keer. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 98]
| ||||||||||||||||||||||||||||||||||||||||||||||
3.4.1 BasisvaardighedenVoordat de leerling toe is aan het uitvoeren van de hoofdbewerkingen met breuken, moet hij eerst een aantal basisvaardigheden beheersen. Van der Schuere heeft die het overzichtelijkst en volledigst ondergebracht in de hoofdstukjes abbreviatio en reductio. In abbreviatio worden breuken vereenvoudigd: Abbreviatio, vercortinghe,Ga naar margenoot+ Om een breuk te vereenvoudigen worden teller en noemer door hetzelfde getal gedeeld: Wat is t'minste ghetal vanGa naar margenoot+ Enkele auteurs behandelen bij het vereenvoudigen van breuken het delingsalgoritme van Euclides om de grootste gemeenschappelijke deler van teller en noemer te vinden.Ga naar voetnoot187 Zo gebruikt Van der Gucht het delingsalgoritme om de breuk 1573/1859 te vereenvoudigen: Neemt den nominatuer oft Reductio is bij Van der Schuere de verzamelnaam voor vijf verschillende basishandelingen met breuken.Ga naar voetnoot189 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 99]
| ||||||||||||||||||||||||||||||||||||||||||||||
Twee procedures zijn algemeen:
Drie procedures hebben betrekking op het rekenen met munten, maten en gewichten:
Bij het gelijknamig maken van twee of meer breuken wordt een gemeenschappelijk veelvoud van de noemers gezocht. Slechts zelden is dat het kleinste gemeenschappelijke veelvoud. Petri beschrijft het gelijknamig maken als volgt: Omme te reduieren veel Slechts in een enkel rekenboek wordt getoond dat men soms ook een kleiner gemeenschappelijk veelvoud kan vinden.Ga naar voetnoot191 Pijck schrijft bijvoorbeeld: Oft canmen een getal gevindenGa naar margenoot+ Het kunnen bepalen welke van twee breuken de grootste is, heeft later voordelen bij de bewerking aftrekken. Daar moet steeds de kleinste breuk van de grootste worden afgetrokken om een negatieve uitkomst te voorkomen. Het is dus nodig | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 100]
| ||||||||||||||||||||||||||||||||||||||||||||||
dat de leerling te weten kan komen welke breuk de grootste is. Petri behandelt het als volgt: Omme te erkennen welckeGa naar margenoot+  Figuur 3.29. ⅘ is groter dan ¾.
Om te laten zien hoe men kleinere munten kan omrekenen in grotere, rekent Van der Schuere 16 stuivers om in ⅘ gulden: Om cleene gelden, maten ende 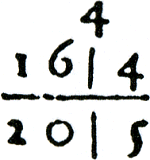 Figuur 3.30. Zestien stuivers = ⅘ gulden.
De weg terug, een gedeelte van een grote eenheid omrekenen naar een kleinere eenheid, wordt door Van der Schuere genoemd: Deelen van ghewichten, geldenGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 101]
| ||||||||||||||||||||||||||||||||||||||||||||||
Stockmans geeft onder andere het volgende voorbeeld: ¾ van eenen gulden, hoe veelGa naar margenoot+ Als een van de weinigen behandelt Van der Schuere ook nog: Wetende de weerdije des deels, Van der Schuere berekent: 16 × 5/4 = 20 stuivers. Hoewel Van der Schuere een groot aantal vaardigheden behandelt als voorbereiding op het rekenen met breuken, ontbreekt bij hem een onderwerp: het berekenen van een breuk van een breuk. Dat onderwerp komt bij de meeste van zijn collega's uitvoerig aan de orde. Wildy weten wat ghebroken van Rekenkundig gezien is hier sprake van een vermenigvuldiging maar de meeste auteurs maken toch onderscheid tussen het berekenen van een breuk van een breuk en het vermenigvuldigen van breuken. Ze behandelen het als een apart onderwerp, voorafgaand aan de hoofdbewerkingen. Van der Gucht: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 102]
| ||||||||||||||||||||||||||||||||||||||||||||||
Om te reduceren een ghebrokenGa naar margenoot+ Bij het berekenen van een breuk van een breuk doen veel auteurs een poging om enig rekenkundig begrip bij te brengen. Dat komt elders in de rekenboeken vrijwel niet voor. Slockmans: Om te verstaen wat dat het isGa naar margenoot+ Pijck vertelt een vergelijkbaar verhaal over een man die 5 kinderen heeft en ¼ huis. Bovendien schrijft hij: Gebroken van gebroken en is Het nut van het begrip breuk van een breuk blijkt als er binnen een vraagstuk verschillende hoofdbewerkingen voorkomen. Geen van de auteurs bespreekt de volgorde waarin dan de hoofdbewerkingen uitgevoerd moeten worden. Nergens wordt expliciet meegedeeld dat vermenigvuldigen voor optellen en aftrekken gaat. Breuk van een breuk beschouwt men echter als één getal. Bij vraagstukken waarin naast vermenigvuldigen nog andere bewerkingen voorkomen, zijn er dankzij dit uitgangspunt geen problemen in de volgorde: Alser ghebroeken der | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 103]
| ||||||||||||||||||||||||||||||||||||||||||||||
questie, soe moetmet dat Van der Gucht behandelt het volgende vraagstuk: Addeert ⅔ van ¼ tot ¾ van ⅓.Ga naar margenoot+Ga naar voetnoot203 Hij berekent: (⅔ × ¼) + (¾ × ⅓) | ||||||||||||||||||||||||||||||||||||||||||||||
3.4.2 Breuken optellen en aftrekkenBij het optellen en aftrekken van breuken behandelen de meeste auteurs eerst een voorbeeld met gelijknamige breuken. Gebruikelijk is om bij aftrekken de aftrekker na het aftrektal te noteren. Sommige auteurs doen het andersom.Ga naar voetnoot204 Bijvoorbeeld Petri: ⅔ van ¾ blijft 1/12.Ga naar margenoot+Ga naar voetnoot205 Na de gelijknamige breuken volgen de ongelijknamige. Gebruikelijk is de methode van het kruiselings vermenigvuldigen. Stockmans legt het als volgt uit: Om te adderen gebroken die Veel auteurs onderscheiden bij de hoofdbewerkingen allerlei afzonderlijke situaties voor breuken, ‘breuken van breuken’ en gemengde getallen. Bij iedere situatie wordt een voorbeeld uitgewerkt. Stockmans onderscheidt bij optellen:Ga naar voetnoot207 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 104]
| ||||||||||||||||||||||||||||||||||||||||||||||
Ook Van den Hoecke, Van der Gucht en Pijck onderscheiden allerlei afzonderlijke situaties bij optellen en aftrekken, maar bij de bewerkingen vermenigvuldigen en delen behandelen ze al de situaties in één keer met een algemene regel.Ga naar voetnoot208 Slechts zelden wordt meer dan één oplosmanieren voor een vraagstuk behandeld. Uitzondering op de regel is Van den Hoecke die 2⅔ + ⅘ op twee manieren berekent:Ga naar voetnoot209 So reduceert 2⅔, coemt 8/3. DitGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
3.4.3 Breuken halveren en verdubbelenHet halveren en verdubbelen van breuken wordt alleen bij Van Varenbraken, Creszfelt en Pijck behandeld.Ga naar voetnoot211 Van Varenbraken: Die wil leeren medierenGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 105]
| ||||||||||||||||||||||||||||||||||||||||||||||
Pijck geeft aan dat een breuk ook gehalveerd kan worden door de teller door 2 te delen. Ook voor het verdubbelen van een breuk geeft hij verschillende mogelijkheden: Om te doubleren ⅜, sooGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
3.4.4 Breuken vermenigvuldigenHet vermenigvuldigen van breuken gebeurt door de tellers met elkaar te vermenigvuldigen en het product van de noemers daar onder te schrijven. Van den Hoecke: Wildy multipliceren ghebrokenGa naar margenoot+ 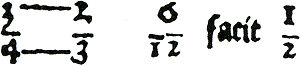 Figuur 3.31. ¾ × ⅔ = 6/12 = ½.
Vervolgens worden ook voor vermenigvuldigen, net als bij de andere hoofdbewerkingen, allerlei afzonderlijke vermenigvuldigsituaties met breuken, breuken van breuken, ‘gehele’ en gemengde getallen behandeld. Van Varenbraken legt het vermenigvuldigen van een ‘geheel’ getal met een breuk als volgt uit: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 106]
| ||||||||||||||||||||||||||||||||||||||||||||||
Wildy ghebroken met heele Van Varenbraken is de enige auteur die ook een nul voorstelt als mogelijke noemer van het ‘gehele’ getal. Bij optellen merkt hij terecht op: De nul is een ghetal... dat niet en gheeft ofte en neempt,Ga naar voetnoot216 maar uit voorgaand citaat blijkt dat hij zich niet realiseert dat deze opmerking bij vermenigvuldigen niet opgaat. Tot slot van zijn uitleg over het vermenigvuldigen van breuken behandelt Van Varenbraken het vermenigvuldigen van een breuk met een gemengd getal: Wildy heele ende ghebroken Pas als het gemengde getal herschreven is tot een breuk kan de gebruikelijke procedure van teller maal teller en noemer maal noemer plaatsvinden. Van den Hoecke en Wentsel zijn de enige twee auteurs die opmerken dat het product van twee breuken kleiner kan zijn dan de factoren zelf.Ga naar voetnoot218 Wentsel: Men en moet niet verwondert | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 107]
| ||||||||||||||||||||||||||||||||||||||||||||||
Bij delen door een breuk die kleiner dan 1 is, is het quotiënt groter dan het deeltal. Daar maakt alleen Wentsel een opmerking over. | ||||||||||||||||||||||||||||||||||||||||||||||
3.4.5 Breuken delenIn de rekenboeken komen twee manieren voor om breuken te delen:
De eerste werkwijze komt in H-TSB-1578 en in de rekenboeken van Raets en Van der Schuere voor.Ga naar voetnoot220 Van der Schuere: Zijn de noemers ghelijck, soo Bij Van Varenbraken, Van den Hoecke, Petri, Van Halle, Van der Gucht en Pijck wordt het delen van breuken uitgevoerd door middel van kruiselings vermenigvuldigen.Ga naar voetnoot222 Van Halle: Hier naer volcht die vierde Wentsel plaatst de deler links van het deeltal: In de divisie in 't ghebrokenGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 108]
| ||||||||||||||||||||||||||||||||||||||||||||||
het dividendum aen deGa naar margenoot+ De omgekeerde volgorde is echter gebruikelijker. Pijck: Tgetal datmen divideren wiltGa naar margenoot+ Pijck is de enige auteur die bij het delen van breuken teller en noemer tegen elkaar wegdeelt als dat kan. Hij behandelt twee voorbeelden. Zijn werkwijze luidt, in moderne notatie weergegeven:Ga naar voetnoot226 ⅗:12/13 = ⅗ × 13/12 = ⅕ × 13/4 = 13/20 Bij het rekenen met breuken worden maar enkele berekeningen gecontroleerd. Slechts aan het eind van hun hoofdstuk over het rekenen met breuken maken sommige auteurs een algemene opmerking over het controleren met behulp van de inverse bewerking. Stockmans meldt bijvoorbeeld: De multiplicatie is de preuveGa naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
3.4.6 Decimale breukenIn 1585 verschijnt l'Arithmétique van Simon Stevin waarin zich La Disme bevindt, een verhandeling over het rekenen met decimale breuken. Een vertaling | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 109]
| ||||||||||||||||||||||||||||||||||||||||||||||
hiervan in het Nederlands verschijnt in datzelfde jaar onder de titel De Thiende.Ga naar voetnoot228 Stevin is niet de eerste die gebruik maakt van decimale breuken. Ze komen ook al voor in het Chinese werk van Yang Hui (dertiende eeuw) en in het werk van de Arabische wiskundige al-Kashi (eerste helft vijftiende eeuw).Ga naar voetnoot229 Stevin is wel de eerste die het rekenen met decimale breuken systematisch onderwijst. Hij legt om te beginnen zijn notatiesysteem uit. 3 (1) 7 (2) 5 (3) 9 (4) betekent 3759/10.000.Ga naar voetnoot230 Dan volgen de vier hoofdbewerkingen. Bij het vermenigvuldigen behandelt hij het voorbeeld: 32 (0) 5 (1) 7 (2) vermenigvuldigd met 89 (0) 4 (1) 6 (2). Daartoe wordt 3257 vermenigvuldigd met 8946. Het product hiervan is 29137122. Om het product van de oorspronkelijke vermenigvuldiging te vinden, - tegenwoordig zou men zeggen: om de komma te plaatsen - kijkt men naar het laatste tekenGa naar voetnoot231 van de twee factoren. Dat is in beide gevallen een 2. Het laatste teken van het product wordt de som van de twee ‘factortekens’ en dat is in dit geval dus 4. De uitkomst van de vermenigvuldiging is 2913 (0) 7 (1) 1 (2) 2 (3) 2 (4). Om het quotiënt van een deling te vinden, moet het teken van de deler afgetrokken worden van dat van het deeltal. Bij de deling 7 (2) gedeeld door 4 (5) berekent Stevin 7000: 4. Bij het worteltrekken deelt hij het laatste teken door 2. De wortel van 529 is 23 en de wortel van 5 (2) 2 (3) 9 (4) is 2 (1) 3 (2). Als het laatste teken oneven is, wordt er een nul aan de decimalen ‘achter de komma’ toegevoegd. In de overige Nederlandse rekenboeken worden de decimale breuken niet behandeld. | ||||||||||||||||||||||||||||||||||||||||||||||
3.5 SymbolenIn de rekenboeken wordt over het algemeen de uitleg in volzinnen gegeven. Dat levert vaak grote stukken tekst op waarin de leerling het overzicht makkelijk kwijtraakt. In hoofdstuk 5 is beschreven welke middelen men op den duur gaat gebruiken om oplosmethodes korter en overzichtelijker weer te geven.Ga naar voetnoot232 De moderne rekenkundige symbolen spelen daarbij nauwelijks een rol. De symbolen + en - komen wel een hoogst enkele keer in de rekenboeken voor, maar ze hebben dan een andere functie.Ga naar voetnoot233 In het rekenboek van Wentsel worden ze bijvoorbeeld gebruikt om over- en ondergewicht aan te duiden: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 110]
| ||||||||||||||||||||||||||||||||||||||||||||||
9 pijpen olie van oliven,Ga naar margenoot+  Figuur 3.32. Overzicht van de gewichten van negen vaten olijfolie.
Van den Hoecke gebruikt de symbolen + en - als een soort toestandstekens bij de regel van ‘valse positie’ om aan te geven hoeveel de berekening met de veronderstelde waarde afwijkt van de gewenste uitkomst.Ga naar voetnoot235 Ook Van der Schuere gebruikt twee symbolen om ‘meer’ en ‘minder’ uit te drukken. Hij doet dat in zijn Rekeninghe van Plus ende Minus.Ga naar voetnoot236 ‘Meer’ duidt hij aan met + en voor ‘minder’ gebruikt hij een minteken met puntjes. Zie figuur 3.33.Ga naar voetnoot237  Figuur 3.33. Voorbeeld van Rekeninghe van Plus ende Minus.
Van den Hoecke, Petri en Van Halle gebruiken de symbolen + en - voor optellen en aftrekken van wortels en algebraïsche vormen.Ga naar voetnoot238 Zie bijvoorbeeld figuur 3.34.Ga naar voetnoot239 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 111]
| ||||||||||||||||||||||||||||||||||||||||||||||
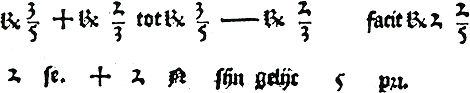 Figuur 3.34. Het gebruik van de symbolen + en -.Ga naar voetnoot240
Het rekenen met wortel- en algebraïsche vormen behoort niet tot de standaardstof van de rekenboeken. Het zijn onderwerpen die de auteurs naar eigen zeggen soms toevoegen voor de ‘geleerden’. Kennelijk zijn de symbolen + en - voor optellen en aftrekken, aanvankelijk alleen gebruikt in de ‘hogere rekenkunde’. In de praktische rekenkunde komen ze in de zestiende eeuw niet voor. Overigens is in de voorgaande afbeelding te zien, dat er een soort hoofdletter R wordt gebruikt om worteltrekken aan te duiden. Het hedendaagse wortelteken √ komt voor bij Petri en Van der Schuere.Ga naar voetnoot241 Symbolen voor vermenigvuldigen en delen en is-gelijk-tekens komen in de rekenboeken niet voor. | ||||||||||||||||||||||||||||||||||||||||||||||
3.6 Munten, maten en gewichten | ||||||||||||||||||||||||||||||||||||||||||||||
3.6.1 Overzichten van munten, maten en gewichten met hun waardeIn de zestiende eeuw zijn er zeer veel verschillende munten, maten en gewichten in gebruik. De rekenboeken sluiten daarbij aan. Stockmans begint bijvoorbeeld zijn werk met een overzicht van de afkortingen die hij gebruikt voor de munten: De plincipaelste characteren in | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 112]
| ||||||||||||||||||||||||||||||||||||||||||||||
gewichte ende heeft 16 oncen. Er werden niet alleen zeer veel verschillende munten, maten en gewichten gebruikt, bovendien kon de waarde die men eraan toekende per stad of streek verschillen. In veel rekenboeken zijn tabellen te vinden waarin de koersen in de verschillende steden zijn opgenomen. Stockmans behandelt bijvoorbeeld de korenmaten. Hij kondigt zijn overzicht als volgt aan: Een kort verhael van deGa naar margenoot+ In figuur 3.35 staat een klein stukje uit dat overzicht.Ga naar voetnoot244  Figuur 3.35. Fragment uit een overzicht van korenmaten.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 113]
| ||||||||||||||||||||||||||||||||||||||||||||||
Van der Gucht behandelt deze materie nog uitvoeriger. Hij geeft tabellen waarin munten, gewichten, graan-, wijn-, land- en houtmaten, maten van honing, zout, hop, sme-colenGa naar voetnoot245 en tijd vergeleken worden. Daarnaast geeft hij nog een opsomming van: Diveersche stoffe ende waere Van den Hoecke behandelt de munten maten en gewichten van Antwerpen, Wenen, Neurenberg, Hongarije, Frankfurt, Lyon, Venetië en Florence. | ||||||||||||||||||||||||||||||||||||||||||||||
3.6.2 Rekenen met munten, maten en gewichtenHet rekenen met munten, maten en gewichten wordt tegelijk uitgelegd met de hoofdbewerkingen voor ‘gehele’ getallen. Bij optellen en aftrekken worden geldbedragen en gewichten opgeteld en afgetrokken. Bij vermenigvuldigen worden grotere eenheden in kleinere omgerekend en bij delen gebeurt dat andersom. Alleen Van den HoeckeGa naar voetnoot247 behandelt het optellen en aftrekken met munten, maten en gewichten in een apart hoofdstuk. Vervolgens wordt in een aantal rekenboeken in het gedeelte over het rekenen met breuken nog aandacht besteed aan enkele soorten berekeningen met munten, maten en gewichten. In reductie leert de leerling een gebroken eenheid omrekenen naar een kleinere, bijvoorbeeld ⅕ pond = 4 stuivers en omgekeerd. Sommige auteurs leggen ook nog uit hoe men de waarde van een gehele munt of maat, of een geheel gewicht kan berekenen als de waarde van een gedeelte is gegeven.Ga naar voetnoot248 Als de basis voor het rekenen met munten, maten en gewichten gelegd is, is de leerling toe aan het oplossen van vraagstukken waarin munt-, lengte- en gewichtseenheden een rol spelen. Deze vraagstukken worden met de regel van drieën opgelost, die, als het gaat om het wisselen van geld, vaak wisselregel wordt genoemd.Ga naar voetnoot249 In de meeste rekenboeken is veel oefenmateriaal over dit onderwerp te vinden. Bijvoorbeeld bij Van der Schuere: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 114]
| ||||||||||||||||||||||||||||||||||||||||||||||
Yemant verwisselt 3213Ga naar margenoot+ Ervaren rekenaars kenden allerlei handige rekenstrategieën en muntomrekeningen om het rekenwerk in dit soort vraagstukken te vereenvoudigen en te versnellen.Ga naar voetnoot251 | ||||||||||||||||||||||||||||||||||||||||||||||
3.6.3 OmrekentabellenAls het rekenen met munten, maten en gewichten te ingewikkeld werd, kon men terugvallen op speciale omrekentabellen, waarin men de uitkomst van bepaalde berekeningen kon vinden zonder dat er gerekend hoefde te worden. Van Halle bijvoorbeeld heeft zijn penningtafelen, waarin postulaten van Hoorn, Carolus-guldens, Andriesguldens en Angelotten omgerekend zijn naar Vlaemsch geldt.Ga naar voetnoot252 In een oogopslag is af te lezen dat 7 Carolusguldens = 1 pond 3 schellingen en 4 groten. Niet alle aantallen zijn meteen af te lezen. Voor bijvoorbeeld 540 postulaten moet de waarde van 500 postulaten bij die van 40 postulaten opgeteld worden. In de tafelen der comanscapen valt de prijs van goederen af te lezen.Ga naar voetnoot253 Bijvoorbeeld: hoeveel kosten 20 ellen als 1 el 11 penningen kost? Zoek 20 in de linkermarge van de tabel en trek van daaruit een horizontale lijn naar rechts. Zoek 11 in de bovenrand en trek van daaruit een verticale lijn omlaag. Daar waar beide lijnen elkaar snijden staat het antwoord: 1 schelling, 6 groten, 4 penningen. Deze tabellen zijn waarschijnlijk in de eerste plaats bedoeld voor gebruikers die wel konden lezen, maar niet konden rekenen. Van der Gucht: Hier naer volghen de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 115]
| ||||||||||||||||||||||||||||||||||||||||||||||
lakenen, lijnwaet, ende ander Maar ook degenen die zelf wel konden rekenen, maakten er graag gebruik van. Met behulp van deze tabellen konden ze immers snel, zonder veel rekenwerk, de uitkomst van een omrekening vinden of controleren.Ga naar voetnoot255 Er bestonden in de zestiende eeuw boekjes die uitsluitend gevuld waren met omrekentabellen.Ga naar voetnoot256 In de rekenboeken van Van den Hoecke, Raets en Pijck ontbreken ze.Ga naar voetnoot257 Hun leerlingen moeten al het omrekenwerk zelf verrichten of hun informatie uit een tabellenboek halen. | ||||||||||||||||||||||||||||||||||||||||||||||
3.7 WorteltrekkenHet worteltrekken wordt in verschillende rekenboeken behandeld, maar het wordt nergens tot de hoofdbewerkingen gerekend. De meeste auteurs stellen het onderwerp pas na de regel van drieën aan de orde. Van Varenbraken en RaetsGa naar voetnoot258 beperken hun uitleg tot het trekken van de tweedemachtswortel. Van den Hoecke, Van Halle, Van der Gucht en PijckGa naar voetnoot259 behandelen ook het trekken van de derdemachtswortel. Slechts Van der SchuereGa naar voetnoot260 geeft uitleg over het trekken van nog hogere wortels. Van Halle legt uit wat een kwadraat en wat een wortel is: In arithmetica ofte int | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 116]
| ||||||||||||||||||||||||||||||||||||||||||||||
Zie figuur 3.36. Van deese exempelen ende  Figuur 3.36. Kwadraatgetallen.
| ||||||||||||||||||||||||||||||||||||||||||||||
3.7.1 Het trekken van de tweedemachtswortelRaets geeft de eerste negen kwadraatgetallen met het advies die uit het hoofd te leren.Ga naar voetnoot262 Pijck doet dat ook en voegt er meteen de eerste negen derdemachtsgetallen aan toe.Ga naar voetnoot263 De methode van tweedemachtsworteltrekken begint met het van rechts naar links groeperen in tweetallen van de cijfers van het getal waaruit de wortel getrokken moet worden. Er wordt een verticale streep na of een punt boven elk tweede cijfer gezet. De cijfers die op deze manier aan de linkerkant overblijven, vormen het getal waar om te beginnen de wortel uit getrokken moet worden. Dit kan soms ook één cijfer zijn. Tevens komt het aantal puntjes of streepjes overeen met het aantal cijfers van de wortel. Van Halle: Deese punctkens, boovendien Dus als bijvoorbeeld Van der Gucht de wortel uit 481636 wil trekken,Ga naar voetnoot265 verdeelt hij het getal als volgt, gaande van rechts naar links, in groepjes: 48 | 16 | 36. Hij weet nu dat de gevraagde wortel uit drie cijfers bestaat en dat hij de worteltrekprocedure met het getal 48 moet beginnen.Ga naar voetnoot266 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 117]
| ||||||||||||||||||||||||||||||||||||||||||||||
Het getal waaruit de wortel getrokken wordt staat in het midden van de berekening, de getallen die voor de tussenstappen nodig zijn, worden hieronder genoteerd en de resten die uit de tussentijdse aftrekkingen overblijven worden erboven geschreven. De gevraagde wortel schrijft men soms rechts van het getal waaruit men de wortel wil trekken en soms daar direct onder. Zie bijvoorbeeld figuur 3.37. Hier is de gevonden wortel 694 direct onder het begingetal 481636 geschreven. Cijfers die niet meer nodig zijn in de berekening worden doorgestreept. De auteurs van de rekenboeken leggen de procedure uit door middel van een stap-voor-stap uitgerekend voorbeeld. In algemene bewoordingen komt hun methode hier op neer: stel dat de wortel getrokken wordt uit een getal dat bestaat uit de cijfers mp | qr | st.Ga naar voetnoot267 Kies a, het eerste cijfer van de gevraagde wortel, zodanig dat het kwadraat van a zo groot mogelijk is, maar kleiner dan het getal mp. Bereken mp - a2 = uv (u en uv kunnen gelijk aan nul zijn) en schrijf dit verschil uv boven mp. Schrijf 2⋅a onder het begingetal. Zie afbeelding 1a, waar de wortel uit 481636 wordt getrokken. De cijfers uv vormen samen met de cijfers qr van het tweede groepje het volgende getal - uvqr - dat aan de orde komt (wanneer u of uv gelijk aan nul zijn, bestaat dit getal uit slechts 3 of 2 cijfers). Kies b, het tweede cijfer van de gevraagde wortel, zodanig dat het verschil: uvqr - 2⋅a⋅b⋅10 - b2 = wx zo klein mogelijk is. Zie afbeelding 1b. De cijfers wx vormen samen met de cijfers st van het derde groepje, het volgende getal - wxst - dat aan de orde komt. Kies c, het derde cijfer van de gevraagde wortel, zodanig dat het verschil: wxst - 2⋅(10⋅a + b)⋅c⋅10 - c2 = yz zo klein mogelijk is. Als yz = 0 dan is er geen rest en dan is het kwadraat van de gevonden wortel gelijk aan het begingetal. Zie afbeelding 1c. Van der Gucht berekent de wortel uit 481636 als volgt:Ga naar voetnoot268 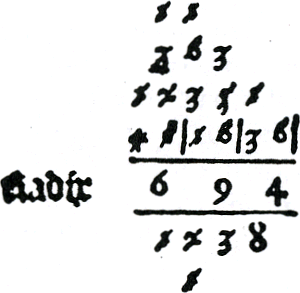 Figuur 3.37. De wortel uit 481636 is 694.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 118]
| ||||||||||||||||||||||||||||||||||||||||||||||
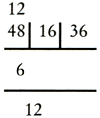 Afb. 1
a. Het eerste cijfer van de gevraagde wortel is 6. Schrijf dat tussen de horizontale lijnen: 48 - 62 = 12 Noteer 2⋅6 = 12 onder de horizontale lijnen. 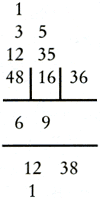 b.
Het tweede cijfer van de gevraagde wortel is 9. Schrijf dat tussen de horizontale lijnen: 1216 - 2⋅6⋅9⋅10 - 92 = 55 Van der Gucht voert deze berekening in twee stappen uit, namelijk: 121 - 12⋅9 = 121 - 108 = 13 136 - 92 = 136 - 81 = 55 Noteer 2⋅69 = 138 onder de horizontale lijnen. 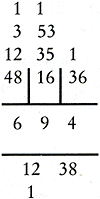 c.
Het derde cijfer van de gevraagde wortel is 4. Schrijf dat tussen de horizontale lijnen: 5536 - 2⋅69⋅4⋅10 - 42 = 0 Van der Gucht voert deze berekening in twee stappen uit, namelijk: 553 - 138⋅4 = 553 - 552 = 1 16 - 42 = 0 Dus de wortel uit 481636 is 694.
De voorgaande worteltrekprocedure zou men als volgt kunnen samenvatten:Ga naar voetnoot269 als R het gegeven getal is waaruit de wortel getrokken moet worden en als 100⋅a + 10⋅b + c de gevraagde wortel is, dan worden de cijfers a, b en c zodanig gekozen dat R - a2⋅1002 - (2⋅a⋅b⋅10 + b2)⋅102 - (2⋅(10⋅a + b)⋅c⋅10 + c2) = 0 Dat is gelijkwaardig met R - (100⋅a + 10⋅b + c)2 = 0 Deze procedure is op vergelijkbare wijze uit te breiden of in te korten voor getallen waarvan de wortel respectievelijk uit meer of minder dan drie cijfers bestaat.Ga naar voetnoot270 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 119]
| ||||||||||||||||||||||||||||||||||||||||||||||
3.7.2 De restVan den Hoecke trekt de wortel uit een getal van maar liefst 10 cijfers. In figuur 3.38 is te zien hoe de berekening er na afloop uitziet.Ga naar voetnoot271  Figuur 3.38. De wortel uit 9421807355 is 97065 rest 193130.
De rest is 193130, dat zijn de cijfers die in de berekening rechtsboven aan de schuine zijde overblijven.Ga naar voetnoot272 Met deze rest wordt de wortel verder benaderd. De benadering die Van den Hoecke en Pijck geven van √(a2 + b) is in moderne notatie:Ga naar voetnoot273 a + b/2a + 1. Van den Hoecke: Dobbeleert den radix 97065,Ga naar margenoot+ De benadering van de wortel is nu 97065 193130/194131
Van Halle behandelt deze benaderingsmethode eveneens en heeft een vergelijkbare methode voor derdemachtswortels: als n de gevonden wortel is, dan wordt de noemer van de rest 3n2 + 3n + 1.Ga naar voetnoot275 Van den Hoecke en Van der Schuere behande- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 120]
| ||||||||||||||||||||||||||||||||||||||||||||||
len een andere benaderingsmethode voor wortels. Ze voegen nullen toe om nog een aantal decimalen te kunnen berekenen. Van der Schuere: Om radix te trecken uyt Om de wortel uit 31 te berekenen voegt Van der Schuere acht nullen toe en snijt hij na afloop vier cijfers van de wortel af. √3100000000 = 55677 dus √31 = 5 5677/10000 | ||||||||||||||||||||||||||||||||||||||||||||||
3.7.3 Het trekken van de derdemachtswortelDe methode om de derdemachtswortel te trekken begint met het groeperen van de cijfers van het getal waaruit de wortel getrokken wordt, gaande van rechts naar links, in groepjes van drie cijfers. Het aantal groepjes komt overeen met het aantal cijfers van de gevraagde wortel. Dus als bijvoorbeeld Van der Gucht de derdemachtswortel uit 16389610 wil trekken,Ga naar voetnoot277 verdeelt hij dat getal, gaande van rechts naar links, als volgt in groepjes: 16 | 389 | 610. Hij weet nu dat de gevraagde wortel uit drie cijfers bestaat en dat hij de worteltrekprocedure met het getal 16 moet beginnen.Ga naar voetnoot278 Net als bij het trekken van de tweedemachtswortel staat het getal waaruit de wortel getrokken wordt in het midden van de berekening, de getallen die voor de tussenstappen nodig zijn, worden hieronder genoteerd en de resten die uit de tussentijdse aftrekkingen overblijven worden hierboven geschreven. De gezochte wortel schrijft men soms rechts van het getal waaruit men de wortel wil trekken, soms daar direct onder. Zie bijvoorbeeld figuur 3.39. Hier is de gevonden wortel 254 direct onder het begingetal 16389610 genoteerd. Ook de procedure voor het trekken van derdemachtswortels behandelen de auteurs - net als die voor tweedemachtswortels - uitsluitend aan de hand van uitgewerkte voorbeelden. In algemene bewoordingen komt hun methode hier op neer: stel dat de derdemachtswortel getrokken wordt uit een getal dat bestaat uit de cijfers efg | hjk | lmp.Ga naar voetnoot279 Kies a, het eerste cijfer van de wortel, zodanig dat de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 121]
| ||||||||||||||||||||||||||||||||||||||||||||||
derdemacht van a zo groot mogelijk is, maar kleiner dan efg. Bereken efg - a3 = qrs (q, qr en qrs kunnen gelijk aan nul zijn) en schrijf dit verschil qrs boven efg. Schrijf het drievoud van a onder de horizontale lijnen. Zie afbeelding 2a. De cijfers qrs vormen, samen met de cijfers hjk van het tweede groepje, het volgende getal - qrshjk - dat aan de orde komt (wanneer q, qr en qrs gelijk aan nul zijn, bestaat het getal uit 5, 4 of 3 cijfers). Kies b - het tweede cijfer van de gevraagde wortel - zodanig dat het verschil: qrshjk - 3⋅a⋅b(10⋅a + b)⋅10 - b3 = tuv zo klein mogelijk is. Schrijf het drievoud van 10⋅a + b onder de horizontale lijnen. Zie afbeelding 2b. De cijfers tuv vormen, samen met de cijfers lmp van het derde groepje, het volgende getal - tuvlmp - dat aan de orde komt. Kies c - het derde cijfer van de gevraagde wortel - zodanig dat het verschil: tuvlmp - 3⋅(10⋅a + b)⋅c⋅(100⋅a + 10⋅b + c)⋅10 - c3 = wxy zo klein mogelijk is. Zie afbeelding 2c. Als wxy = 0, is er geen rest en dan is de derdemacht van de gevonden wortel abc gelijk aan het begingetal. Van der Gucht berekent de derdemachtswortel uit 16389610 als volgt:Ga naar voetnoot280
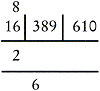 Afb. 2
a. Het eerste cijfer van de gevraagde wortel is 2. Schrijf dat tussen de horizontale lijnen: 16 - 23 = 16 - 8 = 8 Noteer 3⋅2 = 6 onder de horizontale lijnen. 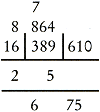 b.
Het tweede cijfer van de gevraagde wortel is 5. Schrijf dat tussen de horizontale lijnen: 8389 - 3⋅2⋅5⋅25⋅10 - 125 = 764 Van der Gucht voert deze berekening in twee stappen uit, namelijk: 838 - 5⋅25⋅6 = 838 - 750 = 88. 889 - 53 = 889 - 125 = 764 Noteer 3⋅25 = 75 onder de horizontale lijnen. 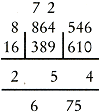 c.
Het derde cijfer van de gevraagde wortel is 4. Schrijf dat tussen de horizontale lijnen: 764610 - 3⋅25⋅4⋅254⋅10 - 64 = 2546 Van der Gucht voert deze berekening in twee stappen uit, namelijk: 76461 - 4⋅254⋅75 = 76461 - 76200 = 261 2610 - 43 = 2610 - 64 = 2546 Dus de derdemachtswortel uit 16389610 is 254 rest 2546. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 122]
| ||||||||||||||||||||||||||||||||||||||||||||||
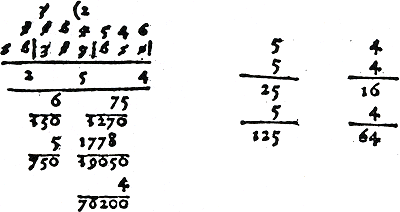 Figuur 3.39. De derdemachtswortel uit 16389610 is 254 rest 2546.
De voorgaande procedure voor het trekken van derdemachtswortels zou men als volgt kunnen samenvatten:Ga naar voetnoot281 als R het gegeven getal is waaruit de derdemachtswortel getrokken moet worden en als 100⋅a + 10⋅b + c de gevraagde wortel is, worden de cijfers a, b en c zodanig gekozen dat R - a3⋅1003 - (3⋅a⋅b⋅(10⋅a + b)⋅10 + b3)⋅103 - (3⋅(10⋅a + b)⋅c⋅(100⋅a + 10⋅b + c)⋅10 + c3) = 0 Dat is gelijkwaardig met R - (100⋅a + 10⋅b + c)3 = 0 Deze procedure is op vergelijkbare wijze uit te breiden of in te korten voor getallen waarvan de wortel respectievelijk uit meer of minder dan drie cijfers bestaat.Ga naar voetnoot282
Van der Schuere behandelt naast de gebruikelijke manier van worteltrekken nog een andere methode waarbij hij binomiaalcoëfficiënten hanteert, de zogeheten genituren. Om te beginnen legt hij uitvoerig uit hoe die genituren in een driehoekig schema geplaatst moeten worden. Zie figuur 3.40.  Figuur 3.40. Schema met binomiaalcoëfficiënten, de zogeheten genituren.Ga naar voetnoot283
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 123]
| ||||||||||||||||||||||||||||||||||||||||||||||
Om dan te nemen d'eyghen Vervolgens geeft hij een tabel met de tweede tot en met de negende macht van de getallen van 1 tot en met 9. Op fol. 197v trekt Van der Schuere de derdemachtswortel uit 1488936 met behulp van genituren. Eerst wordt het getal gaande van rechts naar links in groepjes van drie cijfers verdeeld: 14 | 886 | 936. Dan moet om te beginnen uit 14 de derdemachtswortel getrokken worden. 2 is het eerste cijfer van de gezochte wortel: 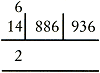 Met behulp van de gevonden 2 en de genituren 1, 3, 3, 1, die horen bij de derdemachtswortel, wordt het volgende cijfer x van de wortel berekend. In moderne notatie: zoek de grootste gehele waarde voor x zodat 22 ⋅ 3 ⋅ 102 ⋅ x + 2 ⋅ 3 ⋅ 10 ⋅ x2 + x3 nog van 6886 kan worden afgetrokken. x = 4 voldoet hieraan. Van der Schuere noteert: 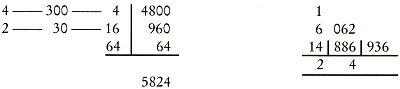 De rest die overblijft is 1062 De procedure wordt herhaald met 24: zoek de grootste gehele waarde voor x zodat 242 ⋅ 3 ⋅ 102 ⋅ x + 24 ⋅ 3 ⋅ 10 ⋅ x2 + x3 nog van 1062936 kan worden afgetrokken. x = 6. De rest is 0. Zo wordt gevonden 3√1062936 = 246.Ga naar voetnoot285 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 124]
| ||||||||||||||||||||||||||||||||||||||||||||||
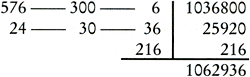 Van der Schuere trekt ook wortels met een macht groter dan 3. Bijvoorbeeld de negendemachtswortel uit 38443359375. De wortel is 15.Ga naar voetnoot286 Van der Schuere legt uit dat men in plaats van de negendemachtswortel ook de derdemachtswortel uit de derdemachtswortel kan trekken. In de rekenboeken waarin het worteltrekken wordt behandeld, komt meestal ook het worteltrekken uit breuken voor. Van der Gucht legt uit dat men dan de wortel uit de teller en de wortel uit de noemer moet trekken. Om den wortel te trecken int Van Halle voegt nullen toe als dit niet zo mooi uitkomt: Stelt voir den teller endeGa naar margenoot+ Van Halle behandelt een aantal vraagstukken waarin het worteltrekken wordt toegepast. De meeste zijn geometrisch van aard. Bijvoorbeeld het volgende, waarin de stelling van Pythagoras gebruikt wordt: Daer es eenen toren 200 | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 125]
| ||||||||||||||||||||||||||||||||||||||||||||||
 Figuur 3.41. De lengte van een ladder wordt berekend met de stelling van Pythagoras.Ga naar voetnoot290
| ||||||||||||||||||||||||||||||||||||||||||||||
3.7.4 Rekenen met wortelvormenVan Halle en Van den Hoecke noteren wortelvormen met een soort hoofdletter R en een exponent.Ga naar voetnoot291 Van Halle noteert bijvoorbeeld: R9a 512 en is niet meerder 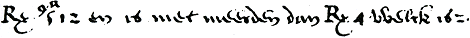 Figuur 3.42. 9√512 = √4 = 2.Ga naar voetnoot293
Van den Hoecke begint het rekenen met wortelvormen met drie basisregels: - Om te bringhen twee onghelike | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 126]
| ||||||||||||||||||||||||||||||||||||||||||||||
Met ‘gelijke wortels’ wordt hier bedoeld wortels met dezelfde wortelindex. De methode die Van den Hoecke gebruikt om wortels tot ‘gelijke wortels’ te herleiden, kan in moderne notatie worden weergegeven door: n√a = np√ap bijv. R2a 6 en R3a 10 worden herleid tot R6a 216 en R6a 100 - Om te reduceren radix van De regel die Van den Hoecke gebruikt om de wortel van een wortel te berekenen kan men weergeven door: n√(p√a) = np√a bijv. R2a van R4a coemt R8a - Abbreviacie ofte minderinge Om een wortel te herleiden tot een wortel met een lagere wortelindex gebruikt Van den Hoecke een regel die men kan weergeven door: np√amp = n√am bijv. R6a 64 is gelijk aan R3a 8 Van den Hoecke onderscheidt drie soorten wortelvormen: - Rationael oft nutte.Ga naar margenoot+Ga naar voetnoot297 Bijv. de tweedemachtswortel uit een kwadraat of de derdemachtswortel uit een kubiek getal. Modern: n√an - Communicanten. Dat sijn | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 127]
| ||||||||||||||||||||||||||||||||||||||||||||||
Uit voorbeelden die Van den Hoecke geeft, blijkt dat communicanten getallen zijn die te schrijven zijn als product van een rationaal en een irrationaal getal. Bijv. √8 = 2√2 en √18 = 3√2 - Irrationalen, de welcke Voor het optellen van wortels gebruikt Van den Hoecke een regel die modern kan worden weergegeven door: √a + √b = √(a + b + 2√(ab)) bijv. √8 + √18 = √(8 + 18 + 2√(18 × 8)) = √50 Irrationale getallen worden opgeteld door er een + teken tussen te schrijven:Ga naar voetnoot300 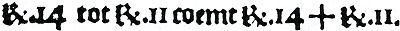 Figuur 3.43. Optelling van irrationale getallen.
Het aftrekken van wortels gebeurt volgens hetzelfde principe als het optellen. Vermenigvuldigen en delen gaat alleen met gelijksoortige wortels.
Modern: n√a × n√b = n√(ab) en n√a : n√b = n√(a : b)
Zijn de wortels niet gelijksoortig, dan moeten ze dat eerst gemaakt worden. Van den Hoecke licht dat toe met de vermenigvuldiging van wortel 9 en 4: Wildi multipliceren R 9 met 4, Modern: √9 × 4 = √9 × √16 = √144 = 12
Ten slotte behandelt Van den Hoecke ook nog het rekenen in binomio, dat wil zeggen met vormen als a ± √b en √a ± √b. Daarvoor is het van belang de tekenregels goed te kennen. Voor vermenigvuldigen luiden ze als volgt: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 128]
| ||||||||||||||||||||||||||||||||||||||||||||||
Als ghi multipliceert + metGa naar margenoot+ Een voorbeeld van vermenigvuldigen in binomio: Wildy multipliceren R 7 - 2Ga naar margenoot+ | ||||||||||||||||||||||||||||||||||||||||||||||
3.8 PenningrekenenHet rekenen met penningen is van oudsher de gebruikelijke manier van rekenen geweest. In hoofdstuk 2 is beschreven hoe deze rekenmethode zich nog lange tijd heeft kunnen handhaven naast het ‘moderne’ rekenen met Hindoe-Arabische cijfers. In verschillende rekenboeken worden beide rekenmethodes uitgelegd. Bij Petri gaat het penningrekenen aan het rekenen met Hindoe-Arabische getallen voorafGa naar voetnoot304, maar in de meeste rekenboeken is de volgorde andersom.Ga naar voetnoot305 | ||||||||||||||||||||||||||||||||||||||||||||||
3.8.1 NumeratieDe getallen worden voorgesteld door penningen op horizontale lijnen te leggen. Een penning op de eerste (onderste) lijn is 1 waard, op de tweede lijn 10, op de derde lijn 100, op de vierde lijn 1000, enz. Een penning tussen twee lijnen is 5x zoveel waard als de penningen op de lijn eronder en heeft de helft van de waarde van de penningen op de lijn erboven. Een penning die tussen de lijn van 10 en de lijn van 100 ligt, is dus bijvoorbeeld 50 waard. In de rekenboeken van Van Varenbraken, Van Halle en Van der Gucht worden geen lijnen gebruikt, maar liggers. Dat zijn penningen in een verticale lijn die tijdens de berekeningen blijven liggen.Ga naar voetnoot306 Deze liggers hebben dezelfde functie als de lijnen in het penningrekenen met lijnen. Een penning die naast de eerste (onderste) ligger gelegd wordt, is 1 waard, naast de tweede 10, naast de derde 100, enz. Het is ook mogelijk penningen tussen twee liggers te leggen die dan respectievelijk de waarde 5, 50, 500, enz. krijgen. De linkerafbeelding in figuur 3.44 is afkomstig uit het rekenboek van Van den Hoecke.Ga naar voetnoot307 Het getal 76 is uitgebeeld op lijnen. De rechterafbeelding is uit het rekenboek van Van Varenbraken.Ga naar voetnoot308 Het ge- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 129]
| ||||||||||||||||||||||||||||||||||||||||||||||
tal 786 is uitgebeeld met penningen. De auteur heeft, waarschijnlijk ter verduidelijking, waardegetallen op de penningen geschreven. In werkelijkheid kwam op rekenpenningen geen waardegetal voor. 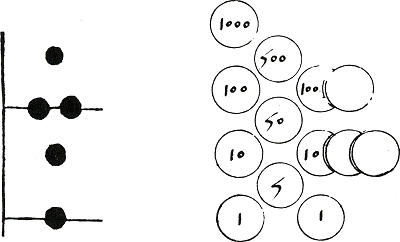 Figuur 3.44. Links: 76 uitgebeeld op lijnen. Rechts: 786 uitgebeeld met behulp van liggers.
| ||||||||||||||||||||||||||||||||||||||||||||||
3.8.2 De hoofdbewerkingenNadat het principe van het voorstellen van getallen door middel van penningen is uitgelegd, volgen de hoofdbewerkingen. Meestal zijn dat optellen, aftrekken, vermenigvuldigen en delen. Van Varenbraken behandelt ook halveren en verdubbelen.Ga naar voetnoot309 Van der Gucht gebruikt geen afbeeldingen, waardoor zijn uitleg tamelijk duister wordt. Hij behandelt bij het penningrekenen uitsluitend vermenigvuldigen en delen.Ga naar voetnoot310 Ook Van Halle beperkt zich hiertoe: Te addeeren ende subtraheeren Optellen gebeurt door de eerste term met penningen uit te beelden en daar de volgende aan toe te voegen. De som van de optelling is niet altijd meteen af te lezen. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 130]
| ||||||||||||||||||||||||||||||||||||||||||||||
Men moet eerst resolveren, dat wil zeggen: twee penningen in het gebied tussen twee lijnen vervangen door één penning op de lijn erboven en 5 penningen op één lijn vervangen door één penning in de daaropvolgende ruimte tussen twee lijnen. Als er bij een aftrekking ‘geleend’ moet worden, komt de omgekeerde handeling voor: één penning vervangen door meer penningen in een lagere tussenruimte of op een lagere lijn. Het is gebruikelijk om bij penningrekenen het begingetal neer te leggen en daar de rekenhandeling mee uit te voeren. Van Varenbraken behandelt echter bij vermenigvuldigen twee manieren. Bij de tweede manier legt hij beide factoren neer: Maer ic, meester Christiaen, Gebruikelijker is de manier waarop Van der Gucht de vermenigvuldiging 360 × 20 uitvoert. Nadat hij 360 met penningen heeft voorgesteld, worden deze penningen opgeraapt en stuk voor stuk vervangen door 20 op de overeenkomstige hoogte aan de andere kant van de liggers: Voor elcken pennijnck die ick Als de berekening klaar is, is het product zichtbaar en zijn de factoren verdwenen. Controleren met de negenproef is niet mogelijk. Dat gebeurt met de inverse bewerking. Delen wordt uitgevoerd door de deler herhaald van het aftrektal af te trekken. Van Varenbraken rekent 79992 miten om in Brabantse stuivers. Dat is de deling 79992:72. Iedere keer als er 72 penningen van het aftrektal opgeraapt zijn, wordt er 1 penning aan de linkerkant van de liggers neergelegd: | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 131]
| ||||||||||||||||||||||||||||||||||||||||||||||
Ghy moet ... legghen voor elc Om het herhaald aftrekken mogelijk te maken, moet er tijdens de deling voortdurend geresolveerd worden, dat wil zeggen penningen van een hogere waardeplaats moeten vervangen worden door meer penningen op een lagere plaats. Dit maakt delen met penningen een tamelijk gecompliceerde bewerking. De meeste auteurs behandelen de hoofdbewerkingen met penningen in dezelfde volgorde als bij het rekenen met Hindoe-Arabische cijfers. Van den Hoecke wijkt hiervan af. Hij behandelt bij het penningrekenen eerst het optellen en vermenigvuldigen en daarna pas het aftrekken en delen. Deze volgorde ligt meer voor de hand want ze klimt op van makkelijk naar moeilijk. Bij optellen en vermenigvuldigen hoeft immers pas op het eind van de berekening geresolveerd te worden en niet tijdens de berekening zoals bij aftrekken en delen.Ga naar voetnoot315 | ||||||||||||||||||||||||||||||||||||||||||||||
Ten slotteTot zover de basis van de rekenkunde, dat wil zeggen het leren lezen en schrijven van Hindoe-Arabische getallen en het leren rekenen met deze getallen. Wat betreft deze basis vertonen de rekenboeken grote onderlinge overeenkomsten: dezelfde onderwerpen worden in dezelfde volgorde behandeld. Het gaat in elk rekenboek om optellen, aftrekken, vermenigvuldigen en delen met ‘gehele’ getallen en breuken, toegelicht aan de hand van vele voorbeeldberekeningen. Onderwerpen die bij vele, doch niet bij alle auteurs voorkomen zijn: halveren en verdubbelen, het controleren van berekeningen, overzichten van en het rekenen met munten, maten en gewichten, worteltrekken en penningrekenen. Enigszins afwijkend zijn de rekenboeken H-GKB-1564 en D-Hey-1561, omdat hierin uitsluitend het rekenen met penningen wordt uitgelegd, en De Thiende van Stevin, omdat het daarin gaat om het rekenen met decimale breuken. Toch zijn deze werken bij het onderzoek betrokken, omdat ook hier de hoofdbewerkingen, dat wil zeggen de basisprincipes van het rekenen, worden uitgelegd. In het eerste deel van de rekenboeken komen al eenvoudige, praktische toepassingen van de rekenkunde voor, maar de meeste en moeilijkere toepassingen volgen pas in het tweede gedeelte van de rekenboeken. Daar worden allerlei rekenregels gepresenteerd en legt de auteur uit hoe men die kan gebruiken om vraagstukken op te lossen. Een beschrijving van deze toegepaste rekenkunde is te vinden in het volgende hoofdstuk. |
|


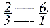 . Ende
. Ende