Die conste vanden getale

Een studie over Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw, met een glossarium van rekenkundige termen

[p. 19]

Hoofdstuk 1
De verbreiding van de Hindoe-Arabische cijfers en de bijbehorende rekenmethode in Europa

Vanaf de vroege Middeleeuwen is in Europa het rekenen met penningen op een rekenbord de gebruikelijke rekenmethode. In de twaalfde eeuw komt daar een nieuwe rekenmethode bij, die gebruik maakt van tien cijfers en een decimaal plaatswaardesysteem. Dit rekenen met Hindoe-Arabische cijfers dankt zijn naam aan de vermoedelijke oorsprong in India¹ en de transmissie naar het Westen door de Arabieren. In Europa blijft gedurende lange tijd zowel de oude als de nieuwe rekenmethode in gebruik, maar op den duur verdwijnt het traditionele rekenen met penningen en blijft het moderne rekenen met de pen alleen over. Op vergelijkbare wijze raken de Romeinse cijfers langzamerhand steeds meer in onbruik, tot na verloop van tijd in geschreven documenten uitsluitend Hindoe-Arabische cijfers voorkomen.

Dit leidt tot de volgende vragen:

-	Hoe zijn de Hindoe-Arabische cijfers en de bijbehorende rekenmethode alom in gebruik geraakt in Europa?
-	Welke factoren hebben ertoe bijgedragen dat het traditionele penningrekenen uiteindelijk volledig verdwijnt?
-	Hoe komt het dat er voor de Romeinse cijfers ten slotte slechts een marginale rol overblijft?

Deze vragen zullen in dit hoofdstuk aan de orde komen.

1 Er wordt ook wel verondersteld dat de cijfers meer naar het Oosten - in China - hun oorsprong hebben. Zie Wang Ling 1954.

1.1 Het traditionele penningrekenen

Vijfhonderd jaar voor Christus maken de Grieken hun berekeningen met behulp van schijfjes van glas, been of ivoor op een rekenbord met verticale lijnen. Dit rekenen met schijfjes is vermoedelijk overgenomen uit Azië, Mesopotamië of India² en het bereikt via de Romeinen ten slotte West-Europa, waar het gedurende de Middeleeuwen steeds meer in gebruik raakt. Het bord waarop men de berekening uitvoert, wordt abacus genoemd.

De methode ondergaat in de loop der tijden wel enige wijzigingen. De schijfjes worden van metaal gemaakt en de verschillende volkstalen ontwikkelen er hun

2 Pullan 1970, p. X.

[p. 20]

eigen benamingen voor: jeton, counter, Rechenpfennig, reken- of legpenning. Bovendien wordt het bord een kwartslag gedraaid zodat de lijnen horizontaal lopen.³ Een penning op de onderste lijn is 1 waard, een penning op de tweede lijn is 10 waard, op de derde lijn 100, enz. Een penning tussen twee lijnen krijgt de helft van de waarde van de lijn waar hij onder ligt. Dat houdt dus in dat de velden tussen de lijnen op het rekenbord respectievelijk 5, 50, 500, enz. waard zijn. Zie bijvoorbeeld figuur 1.1 waar de rekenaar in de linkerkolom van zijn lijnenschema (voor de kijker rechts) het getal 26 heeft neergelegd.

Figuur 1.1. Rekenen met penningen. Afbeelding van de titelpagina van Köbel 1514.

3 Menninger 1969, p. 340.

[p. 21]

Hoe men precies met penningen heeft gerekend, wordt uitgelegd in hoofdstuk 3.⁴ Maar hier is het van belang om alvast op te merken, dat men voor het penningrekenen geen pen en papier nodig heeft. Men hoeft dus niet te kunnen lezen en schrijven. Het penningrekenen past daarom uitstekend in de vroeg-Middeleeuwse samenleving, waarin de meeste mensen niet geletterd zijn. Als het noodzakelijk is om een rekenresultaat, een paginanummer of een datum schriftelijk vast te leggen, gebruikt men Romeinse cijfers, die voor dit doel toereikend zijn. Met Romeinse cijfers worden geen berekeningen gemaakt, alleen maar rekenresultaten genoteerd.

De rekenpenningen worden door geestelijken en kloosterlingen gebruikt bij het maken van computusberekeningen. Dat zijn berekeningen waarmee men de datum van het paasfeest kan vaststellen. Deze berekeningen zijn tamelijk gecompliceerd en kunnen niet uit het hoofd gemaakt worden.⁵ Ook kooplieden gebruiken rekenpenningen voor berekeningen die niet uit het hoofd uitgevoerd kunnen worden.

In de twaalfde eeuw verschijnt naast de traditionele rekenmethode met penningen een nieuwe rekenmethode die met de pen moest worden uitgevoerd. Deze methode doet langs twee wegen haar intrede.

4 Zie paragraaf 3.8.

5 Zie p. 41.

1.2 De nieuwe rekenmethode met Hindoe-Arabische cijfers: een tweetakkig begin

In 1202 schrijft de Italiaan Leonardo van Pisa (ook Fibonacci genoemd, ca. 1170-1240) zijn Liber abaci.⁶ Hoewel de titel anders doet vermoeden, heeft dit werk niets met de traditionele abacus of het penningrekenen te maken. Het woord abacus betekent in het dertiende-eeuwse Italië ‘de kunst van het rekenen’. Leonardo van Pisa behandelt in zijn uitvoerige werk van 400 pagina's onder andere het rekenen met Hindoe-Arabische cijfers. De tekst is in het Latijn geschreven en bevat zeer veel voorbeelden en vraagstukken, ook op het gebied van de algebra, die overigens vrijwel allemaal ook in Arabische werken te vinden zijn.

Leonardo van Pisa schrijft in zijn werk dat hij de nieuwe rekenmethode geleerd heeft in Noord-Afrika, waar hij zijn jeugd heeft doorgebracht. Later maakte hij als koopman reizen door de Arabische wereld, waar hij wederom met deze rekenmethode in aanraking kwam.

Latere auteurs hebben het Liber abaci veelvuldig gebruikt. De moeilijkere passages, met name die over algebra, nemen ze niet over, maar vooral de eerste zeven hoofdstukken worden al snel in het Italiaans vertaald en als bron gebruikt voor nieuwe boeken over het rekenen met Hindoe-Arabische cijfers. In deze abacus-boeken zijn de wiskundige bewijzen die Leonardo van Pisa van zijn oplosmetho-

6 Uitgegeven in Boncompagni 1857.

[p. 22]

des gaf, achterwege gelaten, maar de vele vraagstukken zijn gretig overgenomen en aangevuld met andere.⁷

Opvallend in de abacusboeken zijn de vele commerciële vraagstukken, die zich moeten hebben voorgedaan in het dagelijkse leven van de dertiende-eeuwse Italiaanse koopman, die juist in deze tijd, waarin de handel een enorme bloei doormaakt, behoefte krijgt aan een goed rekensysteem. Er zijn nog enkele honderden Italiaanse abacusboeken uit de veertiende tot en met de zestiende eeuw overgeleverd.⁸ Het werkelijke aantal abacusboeken dat in die tijd geproduceerd is, moet bijzonder groot zijn geweest.

De abacusboeken worden onder andere gebruikt op de scuole of botteghe d'abaco. Op deze speciale rekenscholen onderwijzen de maestri d'abaco de nieuwe rekenmethode met name aan koopmanszonen. Voorzover bekend is de eerste rekenschool in 1284 in Verona gesticht, later ontstonden ze ook in grote handelssteden als Venetië, Milaan, Pisa, Siena en Lucca. In Florence zijn in 1343 zes van dergelijke scholen.⁹

Via handelsbetrekkingen verspreidt de rekenmethode met Hindoe-Arabische cijfers en zijn vele praktische toepassingen zich vanuit Italië over de rest van Europa. In de veertiende eeuw worden Duitse koopmanszonen naar Italië gestuurd om daar de nieuwe rekenkunde te leren. Ze bezoeken onder andere rekenscholen in Venetië.¹⁰

Later worden in Duitse handelssteden als Hamburg, Lübeck en Neurenberg rekenscholen naar Italiaans voorbeeld opgericht. In 1457 zijn er in Neurenberg al drie van dergelijke scholen. Dat aantal groeit uit tot 48 rekenscholen in 1613. Dan wordt er een gilde van rekenmeesters opgericht en wordt het aantal scholen tot 28 teruggebracht.¹¹

De praktische, Italiaanse abacusboeken, die hun oorsprong hebben in het Liber abaci van Leonardo van Pisa, vormen niet de enige weg waarlangs de Hindoe-Arabische cijfers in Europa doordringen. Het Westen heeft op veel meer manieren in contact gestaan met het Oosten en Noord-Afrika.¹² In de twaalfde eeuw zijn enige Arabische rekentractaten via handelsroutes door het Middellandse-zeegebied in Europa, met name in Spanje en Sicilië terechtgekomen. Daar worden ze in het Latijn vertaald.¹³ Het bekendste Arabische werk over rekenkunde dat deze weg heeft afgelegd is het negende-eeuwse rekentractaat van al-Khwarizmi (ca. 780-850). Deze geleerde was verbonden aan het hof van al-Mansur in Bagdad. Het is niet zeker wie zijn rekentractaat in het Latijn vertaald heeft. Mogelijk was dat Adelard van Bath (1116-1142) of Robert van Chester (twaalfde eeuw).¹⁴ Het ori-

7 Het Liber abaci lag weliswaar ten grondslag aan deze abacusboeken, maar omdat het veel wiskundiger is en in het Latijn geschreven is, wordt het zelf niet tot de abacusboeken gerekend.

8 Egmond 1980, p. 15.

9 Villani 1969, deel III, p. 324.

10 Swetz 1987, p. 10.

11 Vogel 1950, p. 240.

12 Gibson 1995, p. 316.

13 De Hindoe-Arabische cijfers komen al eerder in het Westen voor, namelijk in het werk van Gerbert van Aurillac en in Spanje in twee tiende-eeuwse Latijnse manuscripten. In deze werken wordt echter niet met de Hindoe-Arabische cijfers gerekend. Zie p. 35.

14 Folkerts 1997, p. 159.

[p. 23]

ginele werk en zijn vertaling zijn verloren gegaan, maar er is wel een twaalfde-eeuwse bewerking van de Arabische rekentekst overgeleverd, die begint met de woorden Dixit algorizmi...¹⁵ Sinds die tijd wordt de term algorismus eeuwenlang gebruikt om de nieuwe rekenmethode aan te duiden. Ook de thans nog gebruikelijke term algoritme vindt hier zijn oorsprong.

Van het rekenboek van al-Khwarizmi zijn verschillende latere bewerkingen gemaakt. Deze rekenteksten hebben op hun beurt dertiende-eeuwse geleerden geïnspireerd tot het schrijven van eigen werken over de nieuwe rekenkunde. Rond 1230 schrijft Johannes van Sacrobosco (Sacro Busto, Holywood of Halifax)¹⁶ zijn Algorismus vulgaris. Het werk van deze Engelsman, die van 1231 tot aan zijn dood aan de universiteit van Parijs wiskunde doceert, is in een groot aantal manuscripten overgeleverd en veel gebruikt aan universiteiten in Frankrijk, Engeland, Duitsland en Italië. De docent dicteerde tijdens zijn college steeds een paar zinnen uit het algorismustractaat en voorzag deze vervolgens van commentaar en voorbeelden. Er zijn veel afschriften en bewerkingen van Sacrobosco's werk overgeleverd. Het bekendste is het commentaar van Petrus de Dacia (eind dertiende eeuw), dat vier keer zo omvangrijk is als het originele werk van Sacrobosco.

Het Carmen de algorismo van de Fransman Alexander de Villa Dei (Alexandre de Villedieu, eerste helft dertiende eeuw) heeft een vergelijkbare rol gespeeld. Het werk is geheel in hexameters geschreven, vermoedelijk om mnemotechnische redenen. De Hindoe-Arabische cijfers komen alleen aan het begin van het werk voor. Daarna worden de getallen in woorden gegeven. Hoewel de tekst op sommige plaatsen moeilijk te doorgronden is, is hij veel gebruikt en net als het werk van Sacrobosco in enkele honderden manuscripten overgeleverd.

Een vergelijking van de dertiende-eeuwse algorismustractaten en de Italiaanse abacustractaten uit dezelfde tijd levert meer verschillen dan overeenkomsten op. Beide tekstsoorten behandelen de basisprincipes van het rekenen met Hindoe-Arabische cijfers. Beide hebben een belangrijke rol gespeeld in de verbreiding van de nieuwe rekenmethode in Europa. Maar de auteurs hebben twee totaal verschillende doelgroepen op het oog waardoor vorm en inhoud van beide tekstsoorten sterk verschillen.

De abacustractaten zijn geschreven in de volkstaal en bevatten tientallen rekenregels waarmee vooral praktische vraagstukken opgelost worden. De meeste abacustractaten zijn zeer uitgebreid. Honderden pagina's met vraagstukken en hun oplossing zijn eerder regel dan uitzondering. De boeken worden gebruikt op rekenscholen om kinderen, met name koopmanszonen, de nieuwe rekenmethode met haar praktische toepassingen te onderwijzen.

De algorismustractaten zijn in het Latijn geschreven en veel theoretischer van

15 Deze bewerking is in twee dertiende-eeuwse manuscripten overgeleverd: een fragment in Cambridge (University Library, Ii. 6.5, fol. 104r-111v) en de volledige tekst in New York (Hispanic Society of America, HC 397/726, fol. 17r-24v). Folkerts verzorgde een editie van beide teksten, zie Folkerts 1997.

16 Sacrobosco is waarschijnlijk rond 1200 in Halifax geboren. Hij is gestorven in Parijs. Het jaar van zijn dood kan zowel 1244 als 1256 zijn; een vers op zijn grafsteen geeft geen zekerheid: M Christi bis C quarto deno quater anno: 1000 + 200 + 4 + (10 × 4) = 1244 of 1000 + 200 + (4 + 10) × 4 = 1256. Gumbert-Hepp 1987, p. 16.

[p. 24]

aard. Dat wil zeggen dat de auteurs wél de rekenkundige bewerkingen met Hindoe-Arabische cijfers behandelen, maar die slechts met een enkel voorbeeld toelichten. Die voorbeelden gaan niet uit van een toepassingssituatie, laat staan dat er sprake is van een realistische handelscontext. Omdat rekenregels en praktische toepassingen van de rekenkunde ontbreken, zijn de algorismusmanuscripten over het algemeen niet langer dan ongeveer tien bladzijden. Ze worden aan de universiteit gebruikt. In de loop van de zestiende eeuw verdwijnt de algorismus-traditie. Slechts enkele algorismusboeken worden gedrukt of in de volkstaal vertaald.¹⁷

De abacusboeken verschijnen daarentegen steeds vaker in druk. Het begin daarvan ligt ergens tussen 1471 en 1482. In deze tijd wordt in Bamberg een blokboek in de Duitse taal gedrukt over de nieuwe rekenmethode met haar praktische toepassingen. De pagina's van dit rekenboek zijn in hun geheel uit een blok hout gesneden.¹⁸ In Treviso wordt in 1478 voor het eerst een rekenboek met losse letters gedrukt. Dit boek is in de Italiaanse taal geschreven.¹⁹ In 1482 drukt men in Bamberg met losse letters het Duitse rekenboek van Ulrich Wagner.²⁰

In de loop van de zestiende eeuw worden ook in de andere Europese landen steeds meer rekenboeken gedrukt. Deze boeken bevatten naar Italiaans voorbeeld veel vraagstukken en toepassingen van de rekenkunde. Naarmate het papier goedkoper wordt en de boekdrukkunst zich verder ontwikkelt, neemt het aantal vraagstukken, en daarmee de omvang van de boeken, toe. Ze zijn geschreven in de verschillende volkstalen. Alleen al in de Nederlandse taal zijn er van vóór 1601 maar liefst 24 gedrukte boeken over de nieuwe rekenmethode overgeleverd. De eerste gedrukte tekst in de Nederlandse taal over dit onderwerp verschijnt in 1508 te Brussel bij Thomas van der Noot.²¹

De boekdrukkunst draagt ertoe bij dat veel vraagstukken uit de abacustraditie wijd verbreid worden en soms zelfs nog in de hedendaagse reken- en wiskunde-boeken voorkomen. Dat geldt bijvoorbeeld voor het vraagstuk over de tijd waarin een badkuip gevuld kan worden met behulp van twee verschillende waterpijpen. Dit probleem, dat al in negende-eeuwse bronnen uit India voorkomt,²² wordt eveneens aangetroffen in het rekenboek van Filippo Calandri uit 1491, maar ook, in iets gemoderniseerde vorm, in een hedendaags wiskundeboek.²³ Leerlingen van tegenwoordig weten vaak niet dat ze soms vraagstukken oplossen die al minstens 1000 jaar als opgave in omloop zijn.²⁴

17 Egmond 1976, p. 317. Het Nederlandse rekenboek H-BaU-1445 past qua vorm en inhoud in de traditie van de algorismustractaten. Het is het enige overgeleverde algorismustractaat in de Nederlandse taal.

18 Schröder 1996, p. 31.

19 Swetz verzorgde een Engelse vertaling van deze zogeheten Treviso-arithmetica, zie Swetz 1987.

20 Er is slechts een fragment van dit boek overgeleverd, bestaande uit 26 vraagstukken. Een jaar later verschijnt bij dezelfde drukker in Bamberg nog een Duits rekenboek. Vermoedelijk is ook dit boek door Ulrich Wagner geschreven. In dit rekenboek wordt de nieuwe rekenmethode uitvoerig uitgelegd en toegepast. Zie Schröder 1996, p. 29.

21 D-Man-1508. Zie p. 247.

22 Tropfke 1980, p. 578.

23 Calandri 1491, k3v en Abels 1988, p. 151.

24 Over de rol die vraagstukken uit de abacustraditie kunnen spelen in het hedendaagse wiskundeonderwijs, zie Kool 1992a, 1993, 1994a, 1994b en 1995.

[p. 25]

Terug nu naar de Middeleeuwen. Dankzij de algorismustractaten dringt de nieuwe rekenmethode in kringen van geleerden door, terwijl de abacustraditie de rekenkunde in bredere lagen van de bevolking verbreidt. In het voorgaande zijn de verschillen tussen beide tekstsoorten behandeld. Deze hangen samen met de verschillende doelgroepen die men op het oog heeft. In het verlengde hiervan zou men verwachten dat ook de auteurs zeer verschillend waren: in het Latijn schrijvende universitaire geleerden voor de theoretische algorismustractaten en in de volkstaal schrijvende rekenmeesters voor de praktische abacusboeken, met wellicht een diepe kloof tussen beiden. Snelders gaat hier inderdaad vanuit, maar in werkelijkheid blijkt er nauwelijks van een kloof sprake te zijn geweest.²⁵ Wel zijn er vele auteurs die uitsluitend in de volkstaal over toegepaste rekenkunde schrijven. Zij hebben geen universitaire opleiding genoten en richten zich tot een eenvoudig, dat wil zeggen niet-geleerd publiek. Auteurs als Adriaen van der Gucht,²⁶ Bernaert Stockmans,²⁷ Willem Raets²⁸ en anderen behoren hier toe.

Stockmans schrijft in de voorrede van zijn rekenboek:

Dit en is den gheleerden
niet gheschreven,
maer den eenvuldighen⁺
alleen ghegheven.²⁹

Naast niet-geleerde auteurs zijn er echter ook auteurs die wel aan de universiteit gestudeerd hebben of daar zelfs doceren, en die zich in hun rekenboeken niet uitsluitend tot geleerden richten, maar ook rekening houden met een eenvuldig publiek, of zelfs speciaal voor deze doelgroep boeken in de volkstaal over toegepaste rekenkunde schrijven.

Eén van hen is Luca Pacioli (ca. 1445-1514). Hij doceert wiskunde aan verschillende Italiaanse universiteiten en kent dus ongetwijfeld de algorismustractaten. Maar in zijn Italiaanse Summa³⁰ besteedt hij ook veel aandacht aan de praktische

25 Snelders 1983, p. 214.

26 Adriaen van der Gucht schrijft in 1569 een Nederlands rekenboek, D-Guc-1569, dat in 1594 herdrukt wordt. Uit de titel van het rekenboek blijkt dat hij schoolmeester in Brugge is. Daar is hij waarschijnlijk de rest van zijn leven blijven wonen. Zie Smeur 1960, p. 42.

27 Het Nederlandse rekenboek van Bernaert Stockmans dat is overgeleverd, is uit 1595, D-Sto-1595, maar de voorrede wordt afgesloten met de datum 20 juli 1589. Mogelijk stamt de eerste uitgave van het boek uit 1589. Het werk is in de zeventiende eeuw herhaaldelijk herdrukt. Stockmans werd in 1572 opgenomen in het gilde van schoolmeesters van Antwerpen. Hij vertrok waarschijnlijk in 1575 naar Noord-Nederland waar hij in 1591 schoolmeester te Dordrecht was. In de voorrede van zijn rekenboek noemt hij zichzelf francoysche meester. In 1593 keert hij weer terug naar Antwerpen, waar hij brouwer wordt. Zie Groote 1967, p. 305.

28 Van Willem Raets (gest. tussen 1566 en 1576) is een Nederlands rekenboek uit 1580 overgeleverd, D-Rae-1580. Dit boek is een door Michiel Coignet verzorgde heruitgave van een rekenboek uit 1566 dat niet meer is teruggevonden. Volgens Bierens De Haan 1887, XXIII, p. 146-147 is Willem Raets wijnroeier te Maastricht. (Een wijnroeier bepaalt met behulp van een wijnroede, dat is een stok voorzien van een specifieke maatverdeling, de diepte van een ton. Op basis van dat gegeven berekent hij de inhoud van de ton.) Aan het rekenboek van Raets is inderdaad een tractaat over wijnroeien toegevoegd, maar uit het stadsarchief van Antwerpen blijkt dat Raets twee maal heeft deelgenomen aan een ‘examen’ voor officieel wijnroeier, maar nooit geschikt werd bevonden (SAA Pk 1409, fol. 15r-17v). Het tractaat over de wijnroede is mogelijk door Coignet toegevoegd. Raets is koopman en drijft handel samen met zijn vrouw (SAA Pk 639-640, fol. 97r-v en 99r). Zie Meskens 1993, p. 26. (SAA = Stadsarchief Antwerpen).

+ eenvuldighen: eenvoudigen.

29 D-Sto-1595, inleiding.

30 Pacioli 1491.

[p. 26]

rekenkunde.³¹ In Duitsland zijn er in de vijftiende en zestiende eeuw verschillende auteurs die aan de universiteit doceren en toch ook Duitse rekenboeken in de stijl van de rekenmeesters publiceren. Het zijn Johannes Widman (1489), Heinrich Schreyber (1518) en Peter Apian (1527).³² Ook Gielis van den Hoecke, auteur van een Nederlands rekenboek, heeft een universitaire opleiding genoten.³³ Hij begint zijn werk met een Latijnse opdracht aan de wiskundige Guilhelmus Rhetius. Stevin heeft aan de universiteit van Leiden gestudeerd en richt zich in De Thiende tot koop- en ambachtslieden.³⁴

Voorgaande voorbeelden tonen aan dat zestiende-eeuwse geleerden niet uitsluitend theoretische werken voor publiek uit eigen kring schrijven, maar ook toegepaste rekenkunde voor een niet-geleerd publiek behandelen. Bovendien blijken geleerden op den duur zelf steeds meer belangstelling te krijgen voor de toepassingen van de rekenkunde. Johan Scheubel (1494-1570) is verbonden aan de universiteit van Tübingen. Hij schrijft in 1545 een uitvoerig rekenboek van 255 folia in het Latijn. Aan de titel voegt hij toe:

Non solum ad usum quendam
vulgarem, sed etiam
cognitionem et scientiam
exquisitiorem arithmeticae
accomodatum.⁺³⁵

Scheubel is er kennelijk van overtuigd dat toepassingen van de rekenkunde kunnen leiden tot meer kennis en wetenschap van dat vak. Hij draagt zijn werk op aan de Doktoren und Magistern des Senats der Universität Tübingen.³⁶

Ook Johannes Noviomagus, Gemma Frisius en Petrus Beausardus publiceren Latijnse rekenboeken³⁷ waarin het rekenen met Hindoe-Arabische cijfers wordt behandeld, gevolgd door toepassingen van de rekenkunde in de vorm van rekenregels en vraagstukken. Men vermoedt dat het werk van Gemma Frisius, dat zeer vaak herdrukt is, aan de universiteiten gebruikt werd.³⁸ Daar zijn geen bewijzen van, maar het is duidelijk dat werken als die van Gemma Frisius en zijn collega's de toegepaste rekenkunde in geleerde kringen verbreiden.

Ten slotte blijkt dat sommige auteurs ertoe overgaan om in Nederlandstalige re-

31 Cifoletti 1992, p. 10.

32 Reich 1996, p. 187.

33 Gielis van den Hoecke (ca. 1505-...) noemt zichzelf in zijn voorrede Aegidius Hoecke. Hij wordt in 1521 ingeschreven aan de universiteit van Leuven. In 1535 woont hij in Gent, waar hij een kantoor heeft, almanakken verkoopt en misschien les geeft aan de school van zijn oom Eligius Houcarius. In 1537 schrijft hij een Nederlands rekenboek, D-Hoe-1537, dat in 1545 herdrukt wordt. Zie Bockstaele 1985, p. 5-9.

34 D-Ste-1585, p. 3. Simon Stevin (1548?-1620) wordt in Brugge geboren. Vermoedelijk maakt hij reizen door Polen, Pruisen en Noorwegen voordat hij zich in 1581 in Leiden vestigt, waar hij zich in 1583 inschrijft aan de universiteit. Hij schrijft onder andere over wiskunde, natuurkunde, astronomie, boekhouden, vestingbouw en rechtsgeleerdheid. In 1585 verschijnt De Thiende, D-Ste-1585, een boekje over het rekenen met decimale breuken. Stevin heeft een goede relatie met Prins Maurits. In 1600 krijgt hij de opdracht om een instructie samen te stellen voor een aan de Leidse universiteit te verbinden ingenieursschool. Zie Smeur 1965, p. 12-13.

+ Non...accomodatum: Niet alleen voor een of ander eenvoudig gebruik, maar ook geschikt om meer uitgelezen kennis en wetenschap van de rekenkunde te verwerven.

35 Scheubel 1545, titelpagina.

36 Reich 1996, p. 187.

37 Noviomagus 1539, Frisius 1540 en Beausardus 1573.

38 Smeur 1960, p. 21.

[p. 27]

kenboeken Latijnse passages op te nemen³⁹ of enkele onderwerpen te behandelen die speciaal voor geleerden bestemd zijn, zoals algebra, getallenleer en het trekken van wortels van een hogere macht dan drie. De verschillen tussen praktische rekenboeken in de volkstaal en theoretische rekenboeken in het Latijn zijn in sommige gevallen erg klein.

39 Dat doet bijvoorbeeld Christianus van Varenbraken in H-GeU-1532, fol. 157r-v en 160r-v. Van Christianus van Varenbraken is niet meer bekend dan wat hij over zichzelf schrijft in handschrift 2141 van de universiteitsbibliotheek van Gent. Hij schrijft dat hij meester in de zeven vrije kunsten is en verschillende ongeletterden heeft leren lezen en spellen. In het handschrift in Gent bevindt zich een rekentractaat van zijn hand, H-GeU-1532, maar daarnaast ook een tractaat over geometrie, een muziektractaat (zie Braekman 1981) en twee spellingtractaten (zie Braekman 1978). Het is niet bekend of Van Varenbraken auteur of scribent van deze tractaten is.

1.3 Rekenen met de pen of rekenen met penningen?

In de vorige paragraaf is beschreven hoe naast de traditionele rekenmethode van het rekenen met penningen, het rekenen met de pen in gebruik komt. Deze nieuwe rekenmethode wordt in de loop van de zestiende eeuw weliswaar door steeds meer mensen geleerd, maar dat betekent niet dat de traditionele rekenmethode snel in onbruik raakt. Het betekent evenmin dat buiten de rekenboeken in officiële documenten, kasboeken, rekeningen en dergelijke de Romeinse cijfers al snel door de Hindoe-Arabische worden vervangen. Daar gaan meer dan vijf eeuwen overheen.

Al in de twaalfde eeuw wordt het werk van al-Khwarizmi in het Latijn vertaald. Al in 1202 schrijft Leonardo van Pisa zijn Liber abaci, maar in 1698 worden in de Zuidelijke Nederlanden nog rekenpenningen geslagen⁴⁰ en in 1707 behandelt Leonhard Sturm in zijn Kurtzer Begriff der gesamten Mathesis nog steeds het penningrekenen.

Eeuwenlang zijn het rekenen met de pen en het penningrekenen naast elkaar in gebruik geweest en de vraag doet zich voor hoe de verstandhouding was tussen de beoefenaars van de traditionele rekenmethode en de nieuwlichters. In de literatuur wordt het nogal eens voorgesteld alsof ze als concurrenten tegenover elkaar stonden. Swetz schrijft: ‘In the late Middle Ages and early Renaissance, a bitter controversy raged between the advocates of the Hindu-Arabic system - the algorists - and the abacists.’⁴¹ Volgens Boyer stelt de afbeelding op de titelpagina van het rekenboek van Adam Ries (1492-1559) een wedstrijd voor tussen de oude en de nieuwe rekenmethode.⁴² Zie figuur 1.2.

Ries rept in zijn boek met geen woord over een wedstrijd. Hij behandelt beide rekenmethodes en schrijft dat het penningrekenen een goede voorbereiding op de nieuwe rekenmethode vormt. Mensen die eerst met penningen hebben leren reke-

40 Barnard 1916, p. 90.

41 Swetz 1987, p. 30.

42 Boyer 1968, p. 309.

[p. 28]

Figuur 1.2. Rekenaars met de pen (in dit geval krijt of houtskool) en rekenaars met de penningen gebroederlijk aan één tafel. Afbeelding van de titelpagina van Ries 1533.

nen mügen alsdann mit geringer Mühe auff den Ziffern ihre Rechnung vollbringen.⁴³ Peeter Heyns gebruikt in zijn rekenboek op elke linkerpagina Romeinse cijfers en op elke rechterpagina Hindoe-Arabische cijfers.⁴⁴ Waarschijnlijk wil hij zijn leerlingen beide getalsystemen leren. Overigens vermeldt Heyns op de titelpagina van zijn rekenboek dat hij zijn werk schrijft...

43 Menninger 1969, p. 431.

44 Peeter Heyns (1537-1598) is in 1574-1575, 1579-1580 en 1584-1585 deken van het gilde van schoolmeesters in Antwerpen. Tevens is hij van 1579 tot 1585 wijkmeester in deze stad. Dat houdt in dat hij het contact tussen het stadsbestuur en de bevolking moet onderhouden en allerlei administratieve taken moet verrichten, met name het aanleggen van een wijkregister, de inning van de honderdste en vijfde penning, zorgen voor inkwartiering van troepen, uitvoeren van volks- en andere tellingen, enz. Zie Meskens 1994, p. 33. Heyns bestuurt lange tijd samen met zijn vrouw Anna Smits een school in Antwerpen. Na de val van de stad in 1585 komt hij via Frankfurt en Stade (Duitsland) rond 1595 in Haarlem terecht, waar hij samen met zijn schoonzoon Offermans een school houdt. Zie Smeur 1960, p. 34. In 1561 schrijft Heyns een Nederlandstalig rekenboek, D-Hey-1561, en in 1584 een Franstalig rekenboek (Heyns 1584). Bovendien publiceert hij nog een schoolboek over schoonschrijven (Heyns 1568) en een aardrijkskundeboek (Heyns 1577). Zie Resoort 1989, p. 79.

[p. 29]

Tot profyte van die willen
leeren lustich rekenen met
penninghen oft penne.⁴⁵

Dit suggereert dat hij zowel het penningrekenen als het schriftelijk rekenen behandelt. Dat blijkt niet zo te zijn. In zijn rekenboek gebruikt hij weliswaar de Hindoe-Arabische cijfers, maar hij rekent er niet mee. Het penningrekenen is de enige methode die Heyns aan de orde stelt. Maar het ziet er niet naar uit dat hij deze keuze gemaakt heeft om zich tegen de nieuwe rekenmethode af te zetten.

Ook uit andere voorbeelden blijkt dat conservatieven en nieuwlichters niet tegenover elkaar staan. Integendeel. Verschillende mensen in de zestiende eeuw kennen en gebruiken beide rekenmethodes. Dat geldt bijvoorbeeld voor Petrus Ramus (1515-1572) die in zijn Arithmetica libri tres (1555) het rekenen met Hindoe-Arabische cijfers behandelt, maar voor zijn persoonlijke rekenwerk het rekenbord trouw blijft.⁴⁶

Er zijn ook verschillende rekenboekauteurs - zoals de hiervoor genoemde Adam Ries - die in hun werk beide methodes behandelen. Vaak blijkt dat al uit de titel. Zo schrijft bijvoorbeeld Christoff Rudolff in 1526 Künstliche rechnung mit der Ziffer vnd mit den zal pfenningen sampt der wellischen Practica. In 1510 verschijnt een uitgebreide herdruk van het eerste gedrukte rekenboek in de Nederlandse taal uit 1508. Aan de uitleg van het rekenen met Hindoe-Arabische cijfers is een instructie over penningrekenen toegevoegd: Die maniere om te leeren cijfferen ende rekenen metter pennen ende metten penningen Na die gherechte conste Algorismi. Int gheheele ende int ghebroken.⁴⁷ Verschillende Nederlandse rekenboeken volgen, waarin beide rekenmethodes worden uitgelegd.⁴⁸ De oude rekenmethode wordt daarin minder uitvoerig behandeld dan de nieuwe, maar afgezien daarvan worden beide methodes als gelijkwaardige alternatieven gepresenteerd.

Wat is er de oorzaak van dat het zo lang duurt voordat het rekenen met de pen de oude rekenmethode volledig heeft vervangen? Er zijn verschillende oorzaken aan te wijzen, maar de belangrijkste heeft te maken met het alfabetiseringsproces dat zich gedurende de Middeleeuwen in de Nederlanden heeft voltrokken. Zolang men niet kan schrijven, is het natuurlijk uitgesloten dat men leert rekenen met de pen.

In de vroege Middeleeuwen kunnen de meeste mensen niet lezen en schrijven, maar over het algemeen ervaren ze hun ongeletterdheid niet als problematisch. Geschreven teksten spelen in hun leven nauwelijks een rol. Aanvankelijk komt geletterdheid voornamelijk voor bij geestelijken en monniken. Zij lezen religieuze geschriften en geven de inhoud daarvan mondeling door aan de ongeletterden. Daarnaast moeten landheren steeds vaker officiële documenten, brieven en kronieken kunnen lezen. Langzaam maar zeker neemt de behoefte om te leren lezen

45 D-Hey-1561, titelpagina.

46 Verdonk 1966, p. 129.

47 D-Man-1510.

48 H-GeU-1532, D-Hoe-1537, D-Pet-1567, H-BKB-1568 en D-Guc-1569.

[p. 30]

toe. De concilies van 1179 en 1215 stimuleren de oprichting van parochiescholen en inderdaad komen die al spoedig in groten getale voor. Maar op deze scholen ligt de nadruk op het memoriseren van de teksten die veelvuldig gebruikt worden tijdens de kerkdiensten. De jonge leken worden opgevoed tot devote gelovigen en trouwe kerkgangers en slechts enkele leerlingen leren echt goed lezen.⁴⁹

Met het ontstaan en de ontwikkeling van steden krijgt men steeds meer te maken met ambtelijke voorschriften en wettelijke regels waarvan men kennis moet nemen. Natuurlijk kan men zich laten voorlezen, maar op den duur gaat het steeds meer voordelen bieden als men zelf kan lezen. Tegelijkertijd ondergaan de geschreven teksten enkele veranderingen. Aan zakelijke documenten stelt men andere eisen dan aan religieuze geschriften. Ze moeten sneller en goedkoper gemaakt worden en dus gaat men kleinere stukken perkament beschrijven, zonder illustraties en in een sneller - cursief - handschrift.⁵⁰ Gaandeweg ontdekt men de kracht en het gemak van het geschreven woord boven het gesproken woord en het geheugen.

Vooral kooplieden gaan bij de toenemende handel in de vijftiende en zestiende eeuw de voordelen van geschreven documenten ervaren. Ze bemerken vooral het nut van lees- en schrijfvaardigheid op het moment dat ze niet langer meer zelf met hun handelswaar op reis gaan, maar in plaats daarvan met partners gaan werken en commissionairs op pad sturen, voorzien van handels- en wisselbrieven. Hun gecompliceerde handelstransacties kunnen ze schriftelijk vastleggen en als ze eenmaal kunnen schrijven is de stap naar de nieuwe rekenmethode met de pen niet meer zo groot.

Rond 1600 kan in de Nederlanden 40% van de vrouwen en 60% van de mannen haar of zijn handtekening zetten. Dit wordt wel als een indicatie voor de mate van geletterdheid van de Nederlandse bevolking gehanteerd,⁵¹ maar iemand die zijn handtekening kan zetten, hoeft nog niet per definitie te kunnen lezen en schrijven. En als hij of zij misschien wel de techniek van het lezen heeft geleerd, is dat nog geen waarborg voor geletterdheid, die immers tevens het begrip van de gelezen tekst impliceert. Aan het eind van de zestiende eeuw lag het functionele alfabetisme ongetwijfeld veel lager dan de bovenvermelde percentages wellicht suggereren. Daar komt nog bij dat in het zestiende-eeuwse onderwijs het leren lezen aan het leren schrijven vooraf ging en dat voor schrijfonderwijs meer schoolgeld betaald moest worden. Veel ouders namen hun kinderen van school af tegen de tijd dat ze aan schrijven toe waren.⁵²

Voor mensen die niet kunnen schrijven, maar wel willen leren rekenen blijft er maar een mogelijkheid over: het traditionele penningrekenen. Van Varenbraken geeft in zijn rekenboek expliciet aan dat hij het penningrekenen uitlegt voor degenen die niet kunnen schrijven:

49 Dodde 1997, p. 13. Zie p. 43.

50 Clanchy 1979, p. 100.

51 Dodde 1997, p. 9.

52 Booy 1977, p. 55. De Booy onderzocht het plattelandsonderwijs in de provincie Utrecht. Mogelijk kwamen stadskinderen vaker aan het schrijfonderwijs toe, maar in de zestiende eeuw waren er desondanks veel mensen die niet konden schrijven.

[p. 31]

Om dies wille dat veel⁺
persoonen niet scriven
en connen dien nochtans de
conste der rekeninghe wel
van noode es te weten, so
sal ic de selve conste hier
naer bescriven... hoemen
die metten penninghen ende⁺
legghelde orboren sal.⁺⁵³

Wie wel kan schrijven, kan leren rekenen met de pen, maar ook onder geletterden zijn er velen die de traditionele rekenmethode met penningen blijven hanteren, zoals bijvoorbeeld de eerder genoemde Petrus Ramus.⁵⁴

Sommige rekenboekauteurs laten de keuze voor een van beide rekenmethodes afhangen van de omstandigheden. Van Halle⁵⁵ geeft aan dat het penningrekenen voordelen heeft bij het toepassen van de Welsche of Italiaanse praktijk:⁵⁶

Dese rekeninghe is seer
licht metter pennen, maer⁺
noch veel lichter metten
legpenninghen.⁺⁵⁷

Hij licht deze uitspraak niet nader toe. Van der Gucht beweert dat het penningrekenen handig kan zijn als je geen pen op zak hebt:

Ghelijckt dicwils ghebuert,⁺
dat de coop-lieden wel wat
paeyements ofte ghelts over⁺
hemlieden hebben ende⁺
juuste gheen penne en hint⁺
ofte greffie-boucxken, zo⁺
volght hier naer van dien⁺
een corte instructie.⁵⁸

Het penningrekenen blijft nog lange tijd een goed alternatief, omdat het nu eenmaal bepaalde voordelen heeft ten opzichte van het rekenen met de pen. Zo kunnen getallen met behulp van penningen aanschouwelijk voorgesteld worden. Het getal vier bijvoorbeeld wordt door vier penningen weergegeven en niet door een abstract symbool. Bij de bewerking ‘optellen’ worden echt penningen toegevoegd en bij ‘aftrekken’ worden ze weggehaald. Dat is concreter dan wat cijfertjes onder elkaar plaatsen.

+ Om dies wille dat: omdat.

+ penninghen ende legghelde: rekenpenningen.

+ orboren: beoefenen.

53 H-GeU-1532, fol. 185r.

54 Zie p. 29.

55 Over Peter van Halle (1550-...) is weinig bekend. Er is een Nederlands rekenboek van hem overgeleverd, H-BKB-1568. Uit een inleidend gedicht in dit boek blijkt dat hij het in 1568 op achttienjarige leeftijd in Mechelen heeft geschreven.

56 Een toelichting op de Welsche of Italiaanse praktijk is te vinden in paragraaf 4.3.

+ licht: gemakkelijk.

+ legpenninghen: rekenpenningen.

57 H-BKB-1568, fol. 251v.

+ Ghelijckt: omdat het.

+ wat paeyements: wat aan betaalmiddel [bedoeld wordt: muntgeld].

+ over hemlieden: bij zich.

+ hint: inkt.

+ greffie-boucxken: notitieboekje.

+ dien: [verwijst hier naar penningrekenen].

58 D-Guc-1569, fol. 112r.

[p. 32]

Een ander voordeel van het penningrekenen is, dat er geen nul nodig is. Bij het cijferrekenen is de nul onmisbaar. De dubbele betekenis van dit symbool wordt lange tijd als moeilijk ervaren. Nul betekent ‘niets’, maar tegelijkertijd kan dit cijfer de waarde van een getal veranderen als het daaraan toegevoegd wordt. 31 betekent bijvoorbeeld iets heel anders dan 310 of 301. In de rekenboeken waarin de nieuwe rekenmethode wordt uitgelegd, besteedt men uitvoerig aandacht aan dit nieuwe cijfersymbool.⁵⁹ Desondanks treden er nog herhaaldelijk fouten op in het noteren van de nieuwe getallen. Zo worden bijvoorbeeld sommige manuscripten foutief gefolieerd: 98, 99, 100, 1001, 1002,...⁶⁰

Penningrekenen is goedkoop. Officieel gebeurt het met penningen op een rekenbord, maar niet iedereen bezit zo'n bord of heeft zulke penningen. Men kan ook steentjes gebruiken. Uit het voorgaande citaat van Van der Gucht blijkt dat men zich met wat paeyements (munten) kan redden. Een rekenbord met lijnen is niet per se noodzakelijk. Een paar met krijt of houtskool getrokken lijnen op een tafelblad voldoen ook.⁶¹ In de rekenboeken van Van Varenbraken, Van Halle en Van der Gucht worden tijdens het penningrekenen geen lijnen gebruikt, maar liggers:⁶² penningen in een verticale rij, die tijdens de berekeningen blijven liggen en die een rekenbord met lijnen overbodig maken.⁶³ Deze manier van penningrekenen zonder lijnen komt ook in verschillende Franse rekenboeken voor.

Overigens hoeft ook het rekenen met Hindoe-Arabische cijfers niet duur te zijn. Papier is weliswaar kostbaar, maar het gebruik van een lei heft dit bezwaar op. Prosdocimo de Beldomandi (ca. 1375-1428) schrijft in zijn Algorismus (1483) dat een rekenaar een lei bij zich moet hebben om makkelijk uit te kunnen wissen wat hij geschreven heeft. Op illustraties in zestiende-eeuwse rekenboeken komt vaak een lei of een schoolbord voor of rekent men op het tafelblad.⁶⁴ Hoewel het papier geleidelijk aan goedkoper wordt, blijft de lei tot in de twintigste eeuw op school in gebruik.⁶⁵

Ten slotte noemt Swetz nog een argument voor het rekenen met penningen. Hij schrijft dat aan het gebruik van een rekenbord een zekere sociale status en prestige zijn verbonden. Hij leidt dat af uit het feit dat Shakespeare in zijn werk regelmatig het rekenen met penningen (counters) vermeldt. Het bezit van een rekenbord of rekentafel zou alleen voor een selecte groep zijn weggelegd.⁶⁶

Afgezien van de vraag of het terecht is om een dergelijke conclusie uitsluitend op basis van het werk van Shakspeare te trekken, is het inderdaad niet uitgesloten dat men aan het bezit van een rekenbord of rekentafel een zekere status kon ontlenen, maar dat betekent niet dat het penningrekenen zelf een elitaire aangelegen-

59 Zie p. 62.

60 King 1995, p. 183.

61 Zie figuur 1.2 op p. 28.

62 H-GeU-1532, H-BKB-1568 en D-Guc-1569.

63 Een munt rechts van de eerste ligger is 1 waard, rechts van de tweede ligger 10, rechts van de derde ligger 100, enz. Voor verdere uitleg zie p. 128.

64 Zie figuur 1.2 op p. 28.

65 Thijssen 1926, p. 22.

66 Swetz 1987, p. 181-182.

[p. 33]

Figuur 1.3. Penningrekenen zonder lijnen. Afbeelding uit Livre 1501.

[p. 34]

heid was. Hiervoor is al beschreven dat het ook met beperkte middelen uitvoerbaar was. Uit de rekenboeken blijkt nergens dat penningrekenen uitsluitend voor de happy few was weggelegd en cijferrekenen minder aanzien genoot.

Het penningrekenen heeft zoals gezien voordelen ten opzichte van het rekenen met Hindoe-Arabische cijfers, maar het omgekeerde geldt net zo goed. Delen, worteltrekken en rekenen met breuken is met Hindoe-Arabische cijfers veel gemakkelijker.

Ook op andere gebieden van de wiskunde gaat men op den duur de voordelen van de Hindoe-Arabische cijfers ontdekken. In de vijftiende eeuw verschijnen de nieuwe cijfers in astronomische tabellen en kalenders.⁶⁷ Ook voor het noteren en oplossen van tweede- en derdegraadsvergelijkingen in de algebra is een handig getalsysteem onmisbaar.

Voor de traditionele rekenmethode zijn eigenlijk twee systemen nodig; de penningen voor het rekenwerk en de pen om in Romeinse cijfers de uitkomst te noteren, maar bij het rekenen met Hindoe-Arabische cijfers kan men zowel voor het uitvoeren van de berekening als voor het noteren van de uitkomst hetzelfde systeem en hetzelfde materiaal gebruiken.

Nog een voordeel van het rekenen met de pen is de mogelijkheid om de gemaakte berekening na te lopen om eventuele fouten op te sporen. In de praktijk viel dat niet mee omdat men de gewoonte had tijdens de berekening cijfers door te strepen die niet meer nodig waren. In de latere rekenboeken verdwijnt die gewoonte. Bij penningrekenen is het in ieder geval uitgesloten om na afloop de berekening na te lezen omdat de begingetallen tijdens het rekenproces van het rekenbord verdwijnen.

Een ander bezwaar van het rekenbord, dat het schriftelijk rekenen niet kent, schuilt in het gebruik van de losse rekenobjecten. Een stoot tegen het rekenbord of een zwaai met een wijde mouw over de berekening en alle zorgvuldig neergelegde penningen schuiven van hun lijn. Uiteraard kent het schriftelijke rekenen een vergelijkbaar bezwaar. Als de inkt nog niet droog is, kan een wijde mouw ook in een zorgvuldig genoteerde berekening schade aanrichten.

Uit het voorgaande blijkt dat zowel de oude als de nieuwe rekenmethode voor- en nadelen kent en het is begrijpelijk dat zelfs met een groeiende alfabetisering er nog veel tijd verstrijkt voordat het rekenen met Hindoe-Arabische cijfers het penningrekenen volledig heeft verdrongen.

67 In de veertiende en vijftiende eeuw werken de astronomen van het Merton College in Oxford aan de Alphonsinische tabellen. Deze tabellen waren voltooid in 1272 in opdracht van koning Alphonso X van Castilië. De astronomen uit Oxford passen de tabellen aan, aan de meridiaan van Oxford. Hun gebruik van Hindoe-Arabische cijfers heeft waarschijnlijk een positieve uitwerking gehad op de verspreiding van de nieuwe getalsymbolen in Engeland. William Rede (1325-1385) was een van deze astronomen. Zie Yeldham 1926, hoofdstuk IX.

[p. 35]

1.4 Het gebruik van Hindoe-Arabische cijfers buiten de rekenboeken

Veel zestiende-eeuwse kooplieden die kunnen rekenen met Hindoe-Arabische cijfers gebruiken in hun kasboeken toch nog de Romeinse cijfers om de uitkomsten van hun berekeningen te noteren. Omgekeerd zijn er kasboeken waarin de totaalbedragen in Hindoe-Arabische cijfers zijn weergegeven terwijl er aanwijzingen zijn dat de optellingen met penningen zijn gemaakt. Kortom, de verbreiding van de rekenmethode met Hindoe-Arabische cijfers gaat niet gelijk op met de toepassing van die cijfers in geschreven documenten.

In de tiende eeuw komen de Hindoe-Arabische cijfers al voor in twee Latijnse manuscripten die in Spanje zijn ontstaan. Het zijn Codex Vigilanus uit het klooster Albelda (976) en Codex Emilianus uit San Millán de la Cogolla bij Burgos (992).⁶⁸ Deze teksten gaan niet over reken- of wiskunde.

Gerbert van Aurillac (ca. 940-1003), die in 999 Paus Sylvester II wordt, schrijft een werk over de abacus.⁶⁹ Zijn rekenpenningen zijn voorzien van Hindoe-Arabische cijfers. Dat is opmerkelijk, want rekenpenningen zijn doorgaans niet van cijfers voorzien en in die tijd zeker niet van Hindoe-Arabische. Gerbert verblijft rond 968 in Catalonië en kan daar met deze cijfers in aanraking zijn gekomen.⁷⁰

De Hindoe-Arabische cijfers doen uiterst langzaam hun intrede in geschreven documenten. In de dertiende eeuw worden ze hooguit een enkele keer gebruikt voor de paginanummering van manuscripten.⁷¹ In de statuten van de Arte del Cambio in Florence, dat is het gilde van de geldwisselaars, worden in 1299 de nieuwe cijfers verboden in de kasboeken.⁷² Een dergelijk verbod kan alleen maar betekenen dat de nieuwe cijfers al bij een tamelijk grote groep bekend zijn, maar kennelijk nog steeds weerstand oproepen. Men vreest dat er met de Hindoe-Arabische cijfers makkelijker gefraudeerd kan worden dan met de Romeinse cijfers. In getallen die met Romeinse cijfers zijn geschreven wordt de laatste eenheid vaak als j en niet als i geschreven. Dit wordt waarschijnlijk gedaan om fraude tegen te gaan. Aan het eind van het getal kan dan in ieder geval niets meer toegevoegd worden.⁷³

De weerstand in Italië tegen een algemeen gebruik van de nieuwe cijfers als notatiemiddel is opvallend, want afgaande op het grote aantal Italiaanse abacustractaten dat is overgeleverd, wordt de rekenmethode met Hindoe-Arabische cijfers in dit land al vrij snel op grote schaal geleerd. Toch komen in de officiële documenten en kasboeken van de Italiaanse kooplieden de nieuwe cijfers weinig voor. Vermoedelijk rekende men op de moderne manier, maar werd het eindresultaat met traditionele Romeinse cijfers in het kasboek genoteerd.

Zo gebruiken bijvoorbeeld twee vooraanstaande bankiersfamilies in het veer-

68 Folkerts 1997, p. 7.

69 Gerbert ca. 980.

70 Struik 1994, p. 127.

71 Pullan 1970, p. 36.

72 Dit verbod wordt herhaald in de statuten van 1300, 1313, 1314, 1316, 1320, 1347 en 1384. Nagl 1889, p. 162.

73 Meskens 1994, p. 55.

[p. 36]

tiende-eeuwse Florence, Peruzzi en del Giudice, in hun boekhouding geen Hindoe-Arabische cijfers.⁷⁴ Een enkele keer worden bedragen in een combinatie van woorden en Romeinse cijfers geschreven. In de koopmansboeken van de Medici komen zowel Hindoe-Arabische als Romeinse cijfers voor. Pas na 1494 worden in hun boeken de Romeinse cijfers niet meer gebruikt. In 1348 eist de universiteit van Padua dat men in de boekenlijsten de prijzen in Romeinse cijfers vermeldt:

Non per cifras, sed per⁺
literas claras.⁷⁵

Ook in de kasboeken uit de andere Europese landen komen nog lange tijd Romeinse cijfers voor. Meskens onderzocht bijvoorbeeld de boekhouding van Frans de Pape, een zestiende-eeuwse wijnaccijnsmeester en lakenkoopman uit Antwerpen. De Pape gebruikt nog lange tijd Romeinse cijfers in zijn kasboeken. Pas rond 1560 is hij volledig op Hindoe-Arabische cijfers overgeschakeld. In de gildeboeken van het Antwerpse schoolmeestersgilde komen pas na 1580 geen Romeinse cijfers meer voor.⁷⁶

Het langdurige gebruik van Romeinse cijfers in de landen boven de Alpen hoeft ook daar niet te betekenen dat al die tijd het rekenwerk met penningen wordt gedaan. Volgens Meskens bestaan er rekeningen van gilden waarin in het officiële gedeelte Romeinse cijfers zijn gebruikt terwijl in de marges berekeningen met Hindoe-Arabische cijfers staan.⁷⁷ Omgekeerd bestaan er kasboeken waarin Hindoe-Arabische cijfers voorkomen terwijl een puntendiagram in de marge aantoont dat het rekenwerk met penningen is uitgevoerd. Zie figuur 1.4.

Figuur 1.4. Fragment uit een Engels kasboek uit 1600.⁷⁸

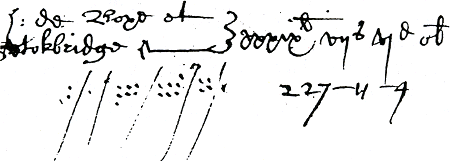
Uit voorgaande voorbeelden blijkt dat de getalsymbolen die in officiële documenten en boekhoudingen worden gebruikt, - Romeinse of Hindoe-Arabische - weinig zeggen over de rekenmethode die door de schrijver gehanteerd is - penningen of de pen -.

Op den duur onderkent men ook buiten de rekenboeken de voordelen van de

74 Nagl 1889, p. 163-164.

+ Non...claras: niet door middel van cijfers, maar door middel van duidelijke letters.

75 Met letters kan men in dit verband zowel Romeinse cijfers als ook in woorden geschreven bedragen bedoelen. Swetz 1987, p. 182.

76 Meskens 1994, p. 55.

77 Meskens 1996, p. 155.

78 De bedragen zijn in Romeinse cijfers genoteerd. Het puntendiagram wijst erop dat ze met behulp van rekenpenningen zijn opgeteld, waarna het totaal in Hindoe-Arabische cijfers is weergegeven.

[p. 37]

Hindoe-Arabische cijfers. Die blijken vooral bij het noteren en lezen van grote getallen, want daar bieden ze veel meer overzicht dan de Romeinse cijfers. Bovendien is het systeem van de Hindoe-Arabische cijfers onbeperkt uitbreidbaar zonder dat er nieuwe symbolen nodig zijn. De auteurs van de zestiende-eeuwse rekenboeken demonstreren deze eigenschap graag met een overtuigend voorbeeld. Van Varenbraken legt bijvoorbeeld uit hoe men een getal van 18 cijfers moet lezen.⁷⁹

Soms stuit men op een soort compromis tussen de oude en de nieuwe notatie-wijze. Op de graftombe van een vrouwe van IJsselstein vindt men het jaartal 1471 aangeduid door XIIII^cLXXI.⁸⁰ Deze mengvorm van de oude Romeinse cijfers met het moderne plaatswaardesysteem komt ook in enkele zestiende-eeuwse rekenboeken voor.⁸¹ Een andere combinatie van oud en nieuw is te vinden in het rekenboek van Christianus van Varenbraken uit 1532. Bij zijn uitleg van het penningrekenen gebruikt hij Hindoe-Arabische cijfers.⁸² Omgekeerd wordt in sommige rekenboeken in het hoofdstuk numeratie, over het lezen en schrijven van Hindoe-Arabische getallen, de plaatswaarde in deze getallen aangeduid met Romeinse cijfers.⁸³

79 H-GeU-1532, fol. 129v. Zie figuur 3.1 op p. 63.

80 Struik 1994, p. 111.

81 D-Hey-1561, H-BKB-1568, D-Dij-1591, D-Sto-1595. Zie hoofdstuk 3, p. 65-66.

82 H-GeU-1532, fol. 185r-191r.

83 D-Guc-1569, fol. 13r en H-BSA-1584, fol. 1r.

Ten slotte

De Nederlandse rekenboeken uit de vijftiende en zestiende eeuw hebben een belangrijke rol gespeeld in de verbreiding van het rekenen met Hindoe-Arabische cijfers. Ze passen alle op één na in de traditie van de Italiaanse abacusboeken.⁸⁴ Ze zijn geschreven in de volkstaal en bevatten veel voorbeelden en vraagstukken die voor het grootste deel uit het dagelijks leven van de koopman afkomstig zijn. In een aantal Nederlandse boeken speelt naast de nieuwe rekenmethode ook het traditionele penningrekenen een rol.⁸⁵ In de zestiende-eeuwse Nederlanden zijn de oude en de nieuwe rekenmethode allebei in gebruik, als gelijkwaardige alternatieven en niet als elkaar beconcurrerende tegenstellingen, zoals soms ten onrechte wordt verondersteld. De nieuwe rekenmethode wordt wel steeds bekender - mede dankzij de Nederlandse rekenboeken - maar dat betekent niet dat de oude methode vrij snel naar de achtergrond wordt geschoven. Het houdt evenmin in dat in kasboeken en officiële documenten de Romeinse cijfers niet meer gebruikt worden om getallen te noteren. De Hindoe-Arabische cijfers en de bijbehorende rekenmethode weten de Romeinse cijfers en het penningrekenen pas volledig te verdringen aan het eind van een eeuwenlang, complex proces dat beïnvloed wordt

84 H-BaU-1445 behoort, hoewel in de volkstaal geschreven, tot de traditie van de algorismustractaten.

85 D-Man-1510, H-GeU-1532, D-Hoe-1537, D-Pet-1567, H-BKB-1568, D-Guc-1569. In D-Hey-1561 en in H-GKB-1564 komt uitsluitend het penningrekenen aan de orde.

[p. 38]

door de toenemende alfabetisering, de ontwikkeling van de papierprijzen, de handel, de boekdrukkunst, de wiskunde en niet te vergeten het onderwijs.

In het volgende hoofdstuk zal duidelijk worden welke rol het onderwijs in dit proces gespeeld heeft. Uit het beeld dat geschetst zal worden van het zestiende-eeuwse onderwijs, met name van het rekenonderwijs, zal blijken in welke scholen de Nederlandse rekenboeken worden gebruikt.