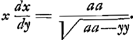Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 264]
| |
No 2742.
| |
[pagina 265]
| |
mam potestatem ascendere, certum est, si omnes aequationes inter (ψ), et (y) usque ad vigesimam potestatem examinentur eo modo, et in eum finem, qui pag. 9 praescriptus estGa naar voetnoot2), quod infallibiliter pervenietur ad aequationem, in qua invenietur x ∞ √2ay-yy, quod probabit in illa aequatione inter (ψ) et (y) segmentum semicirculare, cujus basis est (y), aequale esse (aψ). Sed quis mihi spondere posset (y) et (ψ) in circulo non ascendere ultra centesimam, vel etiam superiorem potestatem? quare etiam credo, quod e re mea non est quadraturam circuli, aut hyperbolae eo modo solus quaerere, circa quam secundum omnem apparentiam frustra me fatigarem. non opus erat circa subnormalem pag. 12 ad septimam potestatem literae (y) ascendere, sed rem eo modo, quo inveneram, sed est per varios circuitus proposui. Haec verba (an vero subnormalis ad nullam curvam pertineat) non satis intelligo, nam si concedas mihi liberè meam opinionem dicere, implicare contradictorium mihi videtur, quod subnormalis illa ad nullam curvam pertineret. nullo modo ego ex subnormali ad curvam, ad quam illa pertinet, pervenire possum, si data sit aequatio inter subnormalem, et perpendicularem (x) vel inter subnormalem, perpendicularem (x) et basim (y). magno teneor desiderio videndi talem methodum, qua a priori in duobus illis casibus, in quibus subnormales sunt ∞ aay-2yyx/3aa-2xy 2y+y3/xx perveniatur ad curvas, ad quas illae pertinent, nec non cognoscere causam, quare illa methodus a priori aliis casibus applicari non possit: in illis vero casibus, in quibus data est proportio inter subnormalem, et basim (y), invenio, aut curvam, ad quam illa subnormalis pertinet, aut figuram curvilineam, a cujus quadratura illa curva dependeat, ex. gr. si subnormalis data sit aa/√aa-yy invenio curvam dependere a quadratura circuliGa naar voetnoot3) quod cum jungatur cum iis, quae a te circa illam subnormalem inventa suntGa naar voetnoot4), proportionem circuli ad hyperbolam cognitam reddet. | |
[pagina 266]
| |
Rudis artis pingendi ego in plano delineare non possum corpora, quae mihi necessaria sunt ad demonstrandum, quomodo ex quadraturis pag. 8 eliciam aequationes pag. 9 nec non quomodo pag. 10 solutionem secundae propositionis meae cum quadratura per (x) detur, ad quadraturam hyperbolae, et circuli deducam, sed non semper eo devenio, nam plerumque invenio curvilineam figuram, cujus quadratura cognita est, ut in proposito tuo exemplo y4 ∞ ddyy-ccxx vel, quod idem est 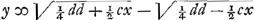 . .
Quis, et ex qua Huygheniorum familia sim, rogas, tui sum, Vir nobilissime, observantissimus, ne vero videantur facta mea cum verbis non convenire, ad singula haec respondebo, pater meus, qui urbis Verensis, cujus ego nunc scabinus, olim concionator fuit, patrem habuit urbis Tholonae consulem, cujus avus inter brabantinae provintiae nobiles numeratus, peregrinando fere peregrinus in patria sua factus, filium reliquit, qui nostrae familiae primus provinciae Zelandiae incola fuit. quare nomina nostra conveniant, cum diversa armorum insignia non eandem nobis esse familiam ostendant, rationem nullam ego reddere possum. propediem mihi iter est in Hollandiam, permissionem te salutandi rogabo, et inter fortunae beneficia numerabo, si praesens tibi, quod jam hisce literis facio, dicere possim, quantopere me tibi devinctum agnosco, quod Vir tanti nominis, et eruditionis ad me scribere dignatus sis. Vale.
Dabam Verae 3 Martii 1692.
Appendicula tua, postquam has literas scripieram reddita mihi est, mutatio in illa nullam causam aliquid mutandi literis meis praebet, nisi in iis, quae scripsi de invenienda proportione inter circulum et hyperbolam, quae pro non scriptis haberi peto. |
|


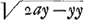 , supponamus (ψ); nec (y) ultra vigesi-
, supponamus (ψ); nec (y) ultra vigesi-