Oeuvres complètes. Tome VIII. Correspondance 1676-1684
(1899)–Christiaan Huygens–
[pagina 443]
| |||||||||
No 2317.
| |||||||||
[pagina 444]
| |||||||||
quam erit, ut de Dioptricâ tamquam infallibili et certissimâ scientiâ multum gloriemur. Verum an haec hactenus per authores praestita sint, penes te esto judicium. Examinentur omnes quot umquam de Dioptricâ scripserunt, ne unus ferè, quod credo, curioso veritatis veneratori satisfaciet. Keplerus, alias optimus Author, in suis DioptricisGa naar voetnoot2) necessarias ex praemissis conclusiones non deducit; sed conjecturis potius, quam certâ et infallibili mathematicâ demonstratione, inventa sua colorare annititur. Exemplo sit nobis unica, loco omnium Propositio 86Ga naar voetnoot3), ubi per duo vitra convexa objecta exhibere conatur distincta &c. 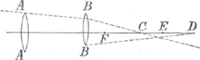 Posito C. foco vitri objectivi D. foculo ocularis, itemque oculo in E. ita ut per objectivum AA solum confusè videat propter nimiam divergentiamGa naar voetnoot4). Verum per solum oculare BB, itidem confusè propter radiorum convergentiam. Scilicet causam priori contrariam. Sic nimiae priori divergentiae mederi putat, et distinctam oculo praestari visionem. Quod equidem, quamvis certum est, necessariam tamen non invenit consequentiam. Si dixisset Keplerus, ex oculo E confuse admodum propter nimiam divergentiam vel vicinitatem, punctum C apprehendi, quod tamen in F collocatum distinctissime cerneretur, et probasset deinceps radium AC vel BC per vitrum BB inflexum iri in F, nonne sanè ad oculum demonstrasset, rem ad libitum peractam? Multa et egregia quidem meo judicio docet Keplerus, quae an veritati consentiant satis, nondum disquisivi, displicent nihilominus demonstrationes. Nobilissimus Cartesius ut ut naturam refractionum solidè explicet, non tamen etiam satis definivit nobis, ampliationis objectorum per Telescopia proportionem, adeo ut quae Cap. VII § 14. et 15 Dioptricae perferuntur, minus sufficere videantur, clarè et distinctè apparentis imaginis perceptioni; Totus enim in eo est ut vitrorum Hyperbolicorum beneficio cuncta exequatur, unde cum nullus hac usque inveniatur Artifex, qui Hyperbolicas vitro figuras inducere, aut dextre polire novit, non tantus forsan ex ipsius Dioptricâ fructus sentitur, quam si vitris circularibus inventa applicasset; quod tamen fieri potest; et si siat, apparebit statim, quantum inter hyperbolica intersit et circularia. Quantum autem intersit adhibere in Telescopiis hyperbolica, experiremur sufficienter, si praxis Theoriae satis conveniret, nam cum praecipua lentium hyperbolicarum virtus sit, perfectum constituere focum, atque hinc hyperbolicae, ocularis etiam minimae patientes fiant, proportio certe amplicationis objectorum impensé, et in infinitum augeretur, si in locum circularium Hyperbolicae substituantur; | |||||||||
[pagina 445]
| |||||||||
quod quidem ego per calculum exponere satis possem, verum ad opportunius potius tempus nunc differo. Honoratus FaberGa naar voetnoot5) ut in multis fere conjecturas potius, multa etiam falsissima nullis innixa demonstrationibus obtrudat nobis, ita profecto miserrimè se torquet in demonstrando Telescopio vulgari, quod instructum ordinariè vitro objectivo convexo, et oculari cavo. Inspiciatur si placet, Prop. 44 § 1. Dioptr. Ubi supponit Author, punctum G esse centrum vel focum utriusque
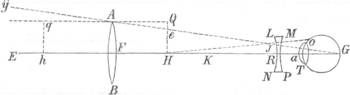 lentis, quo posito, EA, qui propter puncti E. maximam a lente distantiam axi parallelus supponendus, refringatur in AG, qui in NL incidens, flectatur denuo in IO, tamquam si IO radius e puncto H procederet (ubi hallucinatur author cum IO parallelus esse debeat axi RG) sic objecti longinqui punctum E, ab oculo apprehendi putat, tamquam si conspiceretur in H, loco multum propriore. Ut cum lineae YE, AF, duabus EG, YG interceptae aequales videantur, visae scilicet sub eodem Angulo AGF. Hinc concluderetur necessario, Objectum hoc longinquum YE, vel potius AF, (cum YE representetur per AF) per Telescopium cerni in H sub mole QH 2|2 AFGa naar voetnoot6). Ergo sub angulo QGH multo 3|2 AGF. adeo ut sit QGH ad AGF, id est diameter objecti per Telescopium apparens, ad diametrum nudo oculo visam, ita GF ad GH, vel potius, ut sit QRH, ARF ∷ RF, RH. Haec summa est demonstrationis Fabri. Verum quis umquam tam demens est, ut angulum visorium in G vel R putet constitui, et perinde esse, ubinam constituatur; velut credat, objectum in H cerni sub specie et mole QH 2|2 AF. Falsissima haec sunt, et non nisi conjecturis innituntur. Nec video quid mihi responsurus sit author, si in casu (ubi IO fuerit parallelus Axi FG, ergo radii ex E puncto longinquo venientes oculum intrent tamquam si venirent ex h, verbi gratiâ, puncto, non multò minus, remoto) si inquam juxta Fabri regulam, cum sit, q RH, ARF ∷ RF, Rh, inde colligam, hoc casu objectum per Telescopium multò minus cerni, quam nudo oculo; cum tamen ex- | |||||||||
[pagina 446]
| |||||||||
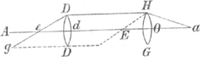
perientiâ teste contrarium verum sit, ut quidem multò etiam quam in priori casu majus appareat. Miserius adhuc procedit Prop. 50 § 1 et seqq. in demonstrando Microscopio duabus instructo lentibus, cujus proprietatem, ut rotundè loquar, non modo non intelligit, multo minus aliis perfectae cognitioni viam sternit. Et quidem in Telescopio, quod componitur e duobus convexis, Prop. 45. § 3. ut probet Diametrum objecti libero oculo spectati esse ad diametrum ejusdem spectati cum geminâ lente, ita semidiametrum lentis ocularis ad semidiametrum objectivae, ut hoc probet inquam, tot verborum circuitibus demonstrationes suas involvit et
 implicat, ut fere mens ejus assequi non possit. Si dixisset breviter: esse et HaB, Bed∷Be, HaGa naar voetnoot7), utique scopum satis attigisset. Et non paulum gloriatur is de inventa an proportione quadam, an verò demonstratione, cum addit haec formalia: Quod nescio an ullus hactenus demonstraverit. Interim tamen me legisse memini in Systemate Tuo SaturnioGa naar voetnoot8) longè ante ipsum hoc a Te inventum fuisse, et demonstratum in tuis Dioptricis, etiamsi hactenus videre eadem non licuit. Quorum tum desiderio sic teneor, ut si talis aspiret aura quo tuas in Dioptricis speculationes perlegere mihi contingat, omne id, quod in Dioptricis desidero, repletum iri certo certius persuasum habeam, ut potè a tanto ingenio profectum, quod in omnibus tuis scriptis non elucet modò, sed et orbis totus admiratur: Verum non licet nobis esse tam beatis hactenus, Ergo itaque multa in praefatis Authoribus mihi relicta esse dubia perpendens, nec certi quid in re incertâ colligere ausus, propriis etiam viribus aliquid conatus sum. Et quidem suppositâ primò proportione refractionis ex aere in vitrum fractae, adhibitisque ut in Algebrâ litterarum Alphabeti speciebus, radiorum in quasvis superficies planas sive sphericas incidentium ad refractos proportionem designare valui, neque sic eorum cursus ubique etiam ne per lentes quidem, me latere potuit. Unde certus de Radiorum cursu, et directâ ad eorum normam visione, qualem qualem me Telescopiorum vel Microscopiorum theoriam puto assecutus sum, sufficientem fere, quae multis me dubiis quibus eram antea implicitus, nunc extricet. Sic enim processi. 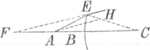 Sit radius ex aere in vitrum incidens AE 2 | 2 v. Superficiei circularis convexae EB semidiameter EC 2|2 y. Sit etiam proportio refractionis AE, AH∷r, i. Invenitur refractus, EF id est x 2|2 ivy/ry+rv-iv vel facto | |||||||||
[pagina 447]
| |||||||||
a 2|2 iv/rGa naar voetnoot9) erit x 2|2 ay/y+v-a. Vel etiam facto f 2|2 r×y+v/iGa naar voetnoot10), Erit x 2|2 vy/f-v. Et inventa erit proportio radii incidentis AE, ad refractum EF∷f-v,y. Ubi tamen noto propter paruitatem arcùs BE, nullam me sensibilem inter AE et ADGa naar voetnoot11), item inter FE et FB differentiam ponere, sed alterum pro altero adhibere, etiamsi reverà et Geometrice differant. Sic etiam in aliis. Quibus sic jactis fundamentis, incidi tandem in Lectiones Opticas D. Barrow AngliGa naar voetnoot12), quem eâdem mecum methodo usum statim cognovi, ut Lectionem XIV, ubi in specie agit de lentibus, ne hilum quidem a me discrepet, et eo modo convenire videatur, ac si conjunctâ operâ radiorum cursus per lentes objectorumque picturas definire, propositum nobis fuisset. Verum ille solum manet intra limites lentis unius convexo planae &c. nec ulterius procedit. Nihil agit de combinatione lentium, nec etiam de visorii anguli ampliatione per quascunque lentes. Totus autem ille est in designandà perfectâ imagine, id est, loco vel puncti objecti apparente situ quem quidem in radiis ad oculum divergentibus vel parallelis describit satis; sed in convergentibus demonstrare nescit quem etiam nodum, pagina
Ultimà Lectionum Opticarum Utinam feliciore conatu (sunt ejus verba), resolvendum aliis committit. Quod unice me torquet etiam et fateri cogit, nondum apparentis distantiae rationem a me satis esse exploratam. Nam etiamsi putem satis feliciter me posse designare anguli visorii quantitatem, vel objecti per lentes spectati proportionem ad objectum libero oculo visum, etiamsi etiam objecti campus mihi satis sit perspectus, vel certus sim de distinctâ vel confusâ visione, vel de erecto vel everso objecti situ, numquam tamen de loco, ubinam aestimari debeat, quid certi pronuntiare audeo ne in divergentibus quidem ad oculum radiis, quod et mirum Tibi videri posset. Observanti
 enim mihi per lentem B, cujus radius BC 2|2 100 part: punctum D, quod distabat a lente partibus 69 2|2 BD. imago puncti D apparuit in E, fuitque BE mensurata in iisdem partibus 2|2 194, Leges tamen Dioptricae eandem multo majorem faciebant, aequalem scilicet 222 part: eximiâ 28 partium differentiâ. Latitat forsitan in oculo involutum quod, et non nisi per plurimas ad id institutas observationes investigabile, a quibus tamen abstinere cogor, ne officiam visui. Quid autem hâc in re molitus sim paucis exponam. Experienti mihi pate- | |||||||||
[pagina 448]
| |||||||||
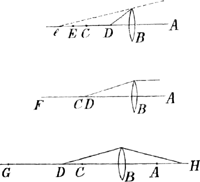 bat manente eadem oculi a lente distantia AB quo magis objectum removeretur a lente, eo magis apparentem ejus imaginem a lente etiam recedere. Adeoque puncti D intra centrum C positi imaginem minus in E; in centro vero collocati, magis in F; maxime verò extra centrum posili imaginem removeri in G; ut sic BG esset 3|2 BF et haec major BE. Unde cum in primo casu radii ad oculum essent divergentes, in secundo paralleli, in tertio convergentes imagines judicabam a radiis divergentibus oculo impressas, ut in primo casu, minus; a parallelis autem ut in secundo casu, magis; et a convergentibus ut in tertio, maximè removeri. Quibus sic positis, ut explicarem horum trium casuum et praecipue tertii Phaenomena vel dictorum punctorum determinarem apparentia E, F et G loca, non male me facturum credebam, si supponerem, cujusvis puncti distantiam non certò posse dignosci, nisi adhibitis duobus oculis (qua etiam praecipua Cartesio Cap. VI § 13 distantiae percipiendae via est) sicque mentem Geometricâ quâdam ratiocinatione tamquam è duobus angulis et interjacente latere distantias colligere. Deinde cum in modo dictâ observatione punctum E secundum Dioptricae leges debuisset abesse 222 partibus, quod tamen observatum fuerat, non nisi 194 partibus remotum, putabam aliquatenus mihi causam creatam suspicandi, oculos insitâ naturae vi disponi ut eorum acies tenderet magis ad propinqua quam remota. Quid ergo, si hinc concluserim, In radiis  ad oculum divergentibus ut in primo casu, etsi per Dioptricae leges imago aestimaretur ultra E eandem tamen ab oculis a et b, naturaliter ad propinqua inclinatis, in propiore E puncto apprehendi. Et in radiis parallelis, imaginem puncti D, quae alias duplex videretur, puta, ab 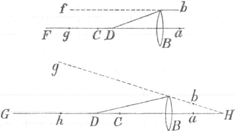 oculo a in g, et ab oculo b in f; nihilominus tamen unicam apparere in F, coalitis scilicet per oculorum aciem ad propinquiora inclinatam punctis f et g in unicum F. Tandemque in convergentibus ad oculum radiis, eandem imaginem, quae procul omni dubio ab oculis a et b dupla appareret, scilicet in h et g, tamen oculorum acie, ab insitâ naturae vi, ad propriora tendente, non duplam, sed simplicem videri, et collocatam in G, tota intercapedine gh prorsus evanescente; Praeterea rationem et naturam ipsam dictare, majorem intercapedinem gh, quo coaliscat in unicum punctum G. majorem etiam distantiam requirere quam minus interstitium fg. Quid inquam, si talia con- | |||||||||
[pagina 449]
| |||||||||
cluserim, Amplitudo tua judicabit, num istorum Phaenomenῶν causam attigisse me putabit nec ne? Ut ut sit, apparet nihilominus rationibus meis experientiam omnino suffragari. Etiamsi dictarum imaginum E, F et G distantias in terminis definire nondum audeam; quas non nisi e crebris ad id institutis observationibus colligi posse arbitror, quibus vel naturae oculorum, eorumque sitûs, vel vitrorum, vel etiam situum objectorum rationes penitius inspiciantur. Verum ingens hic occurrit mihi dubium, nam si eo, quo dictum modo aestimatio loci vel distantiae fieret, sequeretur distantiam etiam objecti necessariò eo majorem futuram quo magis oculi a Lente removerentur, repugnante nihilominus experientiâ; Exempli
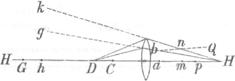 gratia, si propterea punctum G, magis quam F dissitum videretur, quod intervallum gh 3|2 sit fg intervallo, Ergo cum translatis a et b oculis ad m et n, intercapedo kh adhuc fiat major quam gh, utique ad tollendam eam, majorem etiám distantiam quam G requiri necesse esset, ut sic objectum, hanc ob causam ulterius adhuc cerneretur, ultra scilicet G in H, quod tum, ut dictum, ipsi experientiae repugnaret; Eà enim teste, quo magis oculi a lente recedunt, eo minus objectum a lente videbitur distare, ut observatum a D. Barrow, citato loco. Hic haereo, quid respondere nescius, nisi quod fallacia sit, scilicet, quod propter communem regulam: Quo majora apparent objecta eo propriora videri, idem objectum ab oculis m et n multo majus quam in a et b, spectatum, maximeque sic auctum apparens, putetur tantò propius accessisse, quanto majus objectum sese praesentaverit; praesertim ubi, propter lentis parvitatem admoto tantum unico oculo, non is de distantiâ satis agnoscere valeat; sed ea apparente objecti magnitudine eandem aestimet. Et praeterea, etiamsi ex supradictâ visionis lege propter maximam intercapedinem kh, multo longius in H aestimandum esset objectum, non tamen id putetur magis abesse quam G, cum puncti G remotissima ab oculis distantia et locus sit, ad quem oculorum interstitium sensibilem habere proportionem possit, nec ulterior etiam ultra G locus magis apprehendatur. Caeterum inquirens in aliorum scripta, ultro se obtulit Collegium curiosum SturmiiGa naar voetnoot13) nuperrime editum, cujus mihi copiam fecit Nobilissimus et Amplissimus Vir P.E. Vegelin a ClaerbergeGa naar voetnoot14), Amicus et Summus Fautor meus, | |||||||||
[pagina 450]
| |||||||||
et ut vidi praedictum Sturmium plurimas curiosas observationes instituisse, et in earum causas sedulò inquisivisse, quoad Dioptrica tamen, scilicet Telescopia et Microscopia, paulum ab ipso solidè tractatum repperi. Exemplo sit nobis vulgare
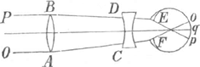 Telescopium ab ipso, ut putat, demonstratum. Sicut ex ipsius Schemate colligo, Imaginem op pingi putat a radiis parallelis PB et OA; quod quam absurdum sit, sic ostendo: PB et OA iisque intercepti omnes, cum paralleli sint, ergo procedunt ab unico objecti remoti puncto; Unicum vero objecti remoti punctum in retinam depingere imaginem sive spatium op. non autem punctum, pugnat sane contra omnes visionis distinctae leges, quae requirunt, ut radii ab uno objecti puncto venientes in unum retinae punctum coeant, ibidemque imaginem effingunt, Cartes: Dioptr: Cap: V § 6 et alibi passim. Igitur imago quae a Radiis PB, et OA imprimitur retinae non erit spatium op, sed non nisi unicum punctum q, scilicet. Sic in Microscopio unius lentis, ampliationem objecti aestimat, non consideratâ ab oculo distantiâ et loco; Positâ scilicet crassitie vitri ab 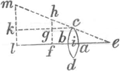 2|2 8. plium. Diametro cd. 2|2 17, et invento foco 3|2 10. dicit objecti magnitudinem apparentem ad veram se habere ut 14 ad 1. Certissime Cartesius docet Cap: VI. §. 16. Dioptricae a Te etiam approbatae in Systemate tuo Saturnio pag. 5. aestimationem magnitudinis non posse institui, nisi collatâ vel cognitâ ejus distantiâ. Falsissimam ergo Sturmii experientiam dico, si putet objectum gf videri ex e, tamquam collocatum in f, sub mole hf, ita ut hf esset ad gf∷ 14, 1. Sic enim hf non esset multo major 2gf, cum sit ef non multo major 2if. Verum si videatur objectum gf per lentem tamquam in justâ ab oculo distantiâ (justâ inquam quae requiritur ordinarie ad minima quaecumque libero oculo videnda) remotum puta in l, ita ut exempli gratiâ, ea, el∷1, 14, poterit adhuc Sturmii experientia sustineri cum objectum eo modo appareat sub mole m l, ut sit m l, k l∷14, 1. Sic etiam alia majora Microscopia ex pluribus constantia lentibus, cum hoc simplice conferens, exempli gratiâ tertium, in quo EB 2|2 8, AC 2|2 37. BL 2|2 500. LG 2|2 10, MN 2|2 90. GR 2|2 114. RO 2|2 20. PQ 2|2 80. dicit per tertium hoc, objectum 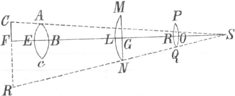 apparere duplo adhuc majus, quam per modo dictum simplex, adeo ut per hoc, objecti magnitudo apparens nunc sit ad veram ∷ 28, 1. Quod tamen ex hac vitrorum combinatione nequaquam colligere possum meae enim Dioptricae insistens, invenio radios a quolibet objecti puncto ad oculum parallelos fore, quoties FE distantia scilicet objecti a lente facta fuerit 2|2 47½: Sed existente FE 3|2 47½, radios ad oculum fieri convergentes, Divergentes vero, si FE 2|2 47½. Deinde primi casus Telescopium (quod radios ad oculum mittens parallelos, distinctam procul dubio visionem praestat) sub calculum trahens, inveni in distantiâ 140 | |||||||||
[pagina 451]
| |||||||||
partium, proportionem FC, FL ∷ 1, 12⅓ fere cum in priore simplice eadem proportio reperiretur ∷ 1, 14 ut dictum. Cederet ergo juxta Dioptricae leges hoc maximum minori simplici, contra experientiam Sturmii cui tamen non multum tribuo, cum is in aestimandâ objecti apparente magnitudine, nullâ habitâ ratione distantiae nihil certi definire potuerit. Infinita talia possem producere, sed et tibi hoc taediosum foret, nec tanti etiam momenti essent, quod te a melioribus speculationibus abstinerent. Hoc tamen addo, nullum memoratorum Authorum mihi videri perfecte scopum attigisse, vel talia tradidisse quae Dioptrices perfectionem omnino evincant, ut potius credam, talem in Dioptricâ adhuc reperiri defectum, qui nisi optimâ ejus culturâ suppleri, vel aboleri nequit. Nullus enim praefatorum, in terminis nobis definivit anguli visorii quantitatem, nullus determinavit nobis certissime objectorum per lentes apparentiarum magnitudinem, locum, situm, figuram et campum et similia. Solus Barrow, majori quam respectu lentium et Telescopiorum requiritur scrupulositate objectorum imagines definit quidem, in quibuscumque superficiebus vitrorum, sed non nisi in unicâ superficie, non in lente, multò minus in lentibus pluribus combinatis, id est Telescopiis vel Microscopiis: Sed et tanta in lentibus scrupulositas nihil proderit, cum destituti hyperbolicis vitris, in sphaericis minima vix attendere valeamus; sicut ex foci constitutione apparet, qui in sphaericis, non nisi praeter propter definiri potest. Desisto ergo a pluribus recensendis, parcens tempori, prolixitatisque meae veniam petens. Vale diu feliciterque Reipublicae litterariae et publico bono, et amicâ me responsione dignare
Illustr: nominis tui Cultor et officiosissimus Bernh: Fullenius.
Franekera d iv. Id Aug: |
|

