Oeuvres complètes. Tome VIII. Correspondance 1676-1684

N^o 2216.
Christiaan Huygens à J.P. De la Roque.
février 1680.

La pièce a été publiée dans le Journal des Sçavans¹⁾.
Elle fait suite à la pièce No. 2212.

Demonstration de la justesse du Niveau dont il a esté parlé dans le II. Journal.

Le premier point de la Rectification étoit de faire en sorte que le centre de gravité de la croix suspenduë²⁾ fût dans la ligne droite qui joint les points où les

1) Du Lundy 26. Fevrier m. dc. lxxx.

2) Voir la figure 2 de la pièce N^o. 2212.

[p. 274]

filets sont attachez aux deux branches. Afin que l'on comprenne la necessité de cette preparation, il faut sçavoir qu'il ne suffit pas que la Lunette suspenduë par l'une & l'autre des branches consecutivement vise à un mesme point de l'object; parce que cela peut arriver, & que pourtant ce point de l'object soit beaucoup



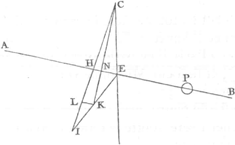au-dessus ou au-dessous du plan Horizontal. Car soit AB l'axe du cylindre de la Lunette: CI la ligne des suspensions ou attaches des filets, desquels on ne considere icy aucune longueur, parce qu'il est constant que quelque grande ou petite qu'elle soit, cela ne fait rien à la situation du corps suspendu: Et que AB, CI, se couppent à angles parfaitement droits au point H. Soit de plus supposé le centre de gravité de la croix en E, dans l'axe AB, mais plus vers B que n'est le point H. La croix étant donc suspenduë par C, la ligne de direction, qui de C tend au centre de la Terre, sera CE, de sorte que AB, baissera au-dessous du Plan Horizontal, auquel CE est perpendiculaire, d'un angle égal à HCE. Et si le rayon visuel AB, passant par le fil Horizontal & par le centre du verre objectif B, continuë d'aller en ligne droite jusqu'au point de l'object, il est evident que ce point sera donc au dessous du plan Horizontal. Cependant en renversant la lunette et la suspendant par I, mais en sorte que le bout B demeure du côté où il étoit, il est aisé de voir qu'elle doit prendre la même situation qu'elle avoit estant suspenduë par C, parce que la ligne de direction passera derechef par le point E. Donc le fil Horizontal visera comme devant au même point de l'object, & le niveau ne laissera pas d'être faux.

Or par la premiere partie de la rectisication, l'on découvre ce défaut & on le corrige. Car premierement si le centre de gravité de la croix est en H, la ligne de direction sera CI, & il est certain qu'en attachant du poids en I, cela ne doit point changer la situation de la croix, & partant la Lunette visera au mesme point qu'auparavant. Mais le centre de gravité de la croix estant en E, si l'on attache un poids en I, le bout B doit s'élever, & par consequent la Lunette doit viser plus haut qu'elle ne faisoit. Ce qui se voit en tirant la ligne IE, & la divisant en K, en sorte que la partie IK soit à KE comme la pesanteur de la croix est au poids attaché en I, car le centre de gravité commun sera K, & CK la ligne de direction: Et l'angle KCE sera égal à celuy dont s'élevera l'axe AB; puisque la ligne CE est élevée sur CK de cet angle, & que AB fait toûjours les mesmes angles qu'auparavant avec CE.

Et afin qu'on ne doute point qu'en mettant le poids en I, l'on découvre assez quand le centre de gravité de la croix est hors de la ligne des suspen-

[p. 275]

sions, je dis que si ce poids est égal à celuy de la croix, l'angle KCE sera sensiblement égal aux ⅔ de l'angle ICE, qui est celuy dont l'axe AB, & partant aussi le rayon visuel, baissoit plus du côte B, qu'il n'auroit fait si le centre de gravité de la croix eût esté en H. Car en menant KL parallele à EH, elle divisera IH par le milieu, & HN fera ⅔ de LK; mais LK est la moitié de HE. Donc HN fera ⅓ de HE, & NE par cons. ⅔ de HE. Mais comme EN est a EH, ainsi sensiblement l'angle ECN est à ECH, à cause de leur petitesse, c'est à dire ECK à ECI.

Comme donc l'angle ECK est celuy dont la lunette à haussé en adjoûtant du poids en I, il faut en reculant le petit poids P vers H, la faire hausser encore la moitié autant puis que l'angle KCI est la moitié de KCE, & alors la ligne de direction sera CI, dans laquelle sera necessairement le centre de gravité de la croix, puisque le centre de gravité du poids en I s'y trouve, & aussi le centre de gravité du composé de ce poids & de la croix, dont on entend que le petit poids P fait partie. Si la Lunette baissoit en mettant le poids en I, il faudroit la faire baisser encore de la moitié autant; dont la demonstration est la mesme. Cette connoissance de la quantité des angles peut servir à rendre la premiere preparation du Niveau plus aisée.

Quant à l'autre point de la verification, il est évident par les choses cy-devant expliquées, que quand le centre de gravité de la croix est dans la droite des suspensions CI, cette ligne sera perpendiculaire à l'Horizon, soit que l'on suspende la croix par C ou par I, & soit qu'on y attache du poids par en bas, ou qu'on y laisse pendre la croix seule. De plus il est certain, supposé la longueur égale de ses branches & des filets, que le centre du cylindre de la Lunette, qui soit au point H, sera à la même hauteur dans les deux suspensions. Soient donc DHM, EHP, les axes du cylindre dans l'une & l'autre suspension, supposant premierement qu'ils ayent des positions differentes. Soit O le point de l'objet où vise le fil Horizontal: Et OM, OP, les rayons de lumiere qui du point O tendent au centre de l'ouverture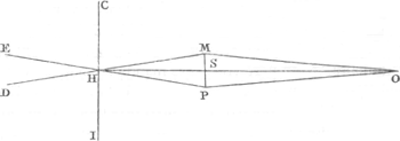



du verre objectif, & qui de là, de même que tous les autres rayons qui du point O tombent sur le verre objectif, vont rencontrer le fil Horizontal; soit que ce fil passe dans l'axe de la Lunette on non. Car cela s'ensuit par les loix de la Dioptrique, puisque le sil paroît couvrir le point O, & que l'un et l'autre sont vûs distinctement.

Ayant mené les droites HO, MP; cette derniere sera parallele à CI, puisque HM, HP sont égales & également inclinées sur CI. Les angles M, P, du triangle MHP, sont donc égaux. Mais il est constant que les angles HMO, HPO sont aussi

[p. 276]

égaux, sans qu'il soit besoin d'avoir égard à ce qui arrive aux rayons OM, OP au dedans de la lunette, ny si le verre objectif est bien centré, c'est à dire s'il a sa plus grande epaisseur au centre. Donc les angles M, P, du triangle MOP sont égaux de même, & ce triangle est Isoscele, comme MHP. Partant la droite HO coupera MP à angles droits. Mais MP éstoit parallele à CI: donc OH est perpendiculaire à CI; & partant le point O dans le plan Horizontal du centre de la Lunette H. Ce qui étoit à prouver.

Que si les centres du verre objectif M & P, sont coïncidents dans un même point, comme en S; la droite HS sera perpendiculaire à CI, puisque les angles CHS, IHS sont alors égaux, attendu le renversement de la Lunette. Mais puisque SO tend au même point O dans les deux suspensions, elle sera necessairement en ligne droite avec HS, parce que si elle faisoit angle, cet angle seroit vers le haut en l'une des suspensions, & vers le bas en l'autre, & ainsi le fil viseroit à deux points differens, contre ce que l'on suppose. Donc toute la ligne OSH est perpendiculaire à CI, & partant le point O est dans le plan Horizontal du centre H.