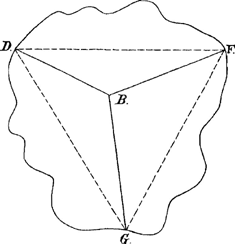
hoek haar Complement tot 180 Graden genomen, zoo zullen dese Complementen zyn de hoeken GBF, GBD, DBF, in voegen dat de kleynste hoek tegen over het swaarste gewigt gevalt, waar door dan het punt B ligtelyk gevonden wort, als men maar alleenlyk op 2 zyden des driehoeks DBG Cirkelbogen beschryft, die de gevonden hoeken tot de zyden behoorende begrypen, want de doorsnyding van sulke twee bogen is het punt B; den Triangel DFG gelykzydig zynde, zoo moet het getal van 't swaarste gewigt gequadrateert zynde niet grooter zyn als de 2 quadraaten van de kleynder
gewigten met te zamen het product van haar multiplicatie.
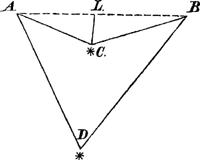
My is in dese selve materie dit VraagstukGa naar voetnoot5) in den sin gekomen, zynde niet swaarder als het voorgaande en wenste wel te zien hoe UE. het zelve ontbinden zoude. ACBD is een doorgaande touw, glyende over de schyven A, B in midden van welke hangt het gewigt C, en regt daar onder het swaarder gewigt D; als nu CL, dat is van de knop C tot de regte AB, is 1, en LD 7, BC of AC 4, de vrage is wat rede de swaarte D heeft tegen die van C. Hier op by gelegenheyd een letter tot antwoord verwagtende, blyf ik
UE. Dienstwillige en toegenegen Vriend Christiaan Huygens van Zuylichem.
's Gravenhage den 9 April 1659. |
-
voetnoot1)
- Ce recueil
Mathematische Liefhebberije met het Nieuws der Fransche en Duytsche Scholen in Nederland. te Purmerende, Bij P. Jordaan, Boekverkooper. in-8o.
a été publié par J. Oostwoud en XI volumes, de 1754 à 1765. Il a été continué par L. Schut jusqu'en 1769, volumes XII-XVII.
-
voetnoot2)
- Ce problème est énoncé comme il suit (voir la figure première de la page 570):
Met haer drien hebbense een meyr bedijckt, als DFG, daer aen dat D tot onkosten ghedaen heeft 1050, F 1000, en G 650 rijcxdaelders, Om dit bedijckte Meyr hebbense elck een Huys ghebouwt, alsoo dat haer huysen (of de schoorsteenen van haer huysen) een gelijck zijdighen driehoeck maecken, dat is van D tot F, en van F tot G, en van G tot D, elck 1200 roeden: zijn voort van voornemen om een Kerck te maecken ontrent het midden in B, doch die het meeste gelt aen onkosten ghemaeckt heeft, die begheert de Kerck naest te hebben: waer in dat zij over een dragen, dat elck zijn Rijckxdaelders, die hij tot onkosten ghemaeckt heeft (of het gewicht daer van) sal hanghen in zijn schoorsteen, en dat met een sijne draedt over gladde schijven ontrent het midden in B vast gemaeckt, ende waer dan dit vast gemaeckte punt B getrocken wordt daer sal de Kerck staen. De vrage is hoe veel Roeden dat elck de Kerck van zijn huys hebben sal, dat zijn de lenghten BD, BF en BG.
-
voetnoot3)
- Consultez l'ouvrage:
Mathematische calculatie, Dat is, Wiskonstige Rekening: leerende het vinden van verscheyden Hemelloopsche Voorstellen, en dat door de Tafelen Sinus, Tangents of Logarithmus wiskonstelick uyt te rekenen: Als oock tuyghwercklick op een liniael uyt te passen. Als mede 't beschrijven en uytrekenen der Zonwysers: zijnde alles seer vermakelick voor de Liefhebbers dezer Konst, ende niet min gedienstigh voor Schippers en Stuerlieden. Noch is hier by gevoeght de Wis-konstige Musyka, waer in getoont wort de oorsake van 't geluyt, de redens der Zangh-toonen, en verscheyden dingen tot de Zangh-en Speel-konst behoorende, Door Dirck Rembrandtsz. van Nierop, Liefhebber der Mathematische Konsten. t'Amsteldam, By Gerrit van Goedesbergen, Boeckverkooper op 't Water, in de Delssche Bybel. Anno 1659. in-8o.
-
voetnoot4)
- Tade Philips, arpenteur à Schagen, était autodidacte.
-
voetnoot5)
- Consultez, sur la solution de ce problème, la pièce No. 612.
|



