Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 4]

N^o 951.
[P. de Fermat] à [P. de Carcavy].
[décembre 1661].
Appendice III au No. 948.¹⁾

La copie se trouve à Leiden, coll. Huygens^a).

Esto yssois EAPS in semicirculo LVABE, cujus centrum H, diameter LE. Perpendiculus ad diametrum radius HA, Asymptotos infinita yssoidis recta LR ad diametrum perpendicularis. Ajo spatium contentum sub EL, yssoide infinitâ EAPS, et asympto²⁾ infinita LR, esse triplum semicirculi LAE; ideoque si alterâ semicirculi parte eadem fiat constructio ambo spatia culminantia in puncto E esse tripla totius circuli.

Demonstratio non est operosa, imo satis elegans. Sumantur duo puncta I et G in

1) Cette copie est de la main de de Carcavy.

a) De Monsieur de Carcavy qui l'avoit de Monsieur de Fermat. J'ay demonstrè cette Proposition 4⁶⁾ auparavant [Chr. Huygens].

6) Huygens vent dire: 4 ans auparavant. Consultez les Lettres Nos. 475 et 479 et la pièce No. 483.

2) Lisez: asymptota.

[p. 5]

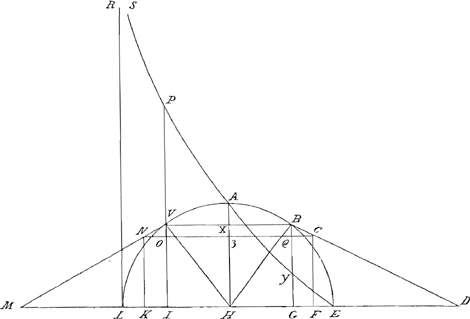
diametro utcumque aequaliter à centro distantia, ita ut rectae HI, HG sint aequales, ideoque rectae LI, GE. A punctis I et G excitentur perpendiculares occurrentes yssoidi in punctis P, Y, et circulo in punctis V et B. Jungantur radij HV, HB, et a punctis V et B ducantur tangentes VM, BD, occurentes diametro in punctis M et D. Sumatur minima quaeuis ultra punctum I, recta IK, et ultra punctum G, recta GF, ipsi IK aequalis, et a punctis K et F excitentur perpendiculares ad diametrum rectae KN, FC, occurentes tangentibus in punctis N et C, à quibus demittantur perpendiculares NO, CQ, in recta³⁾ VI, BG. His ita constitutis patet spatium yssoidale aequari omnibus rectangulis sub PI, IK, et sub YG, GF, utcumque ubilibet sumptis, bases ipsis KI, GF aequales habentibus et altitudines singulis rectis ad yssoidem similiter applicatis. Est autem de natura yssoidis ut VI ad IE ita IE ad IP. Sed IE est aequalis rectis IH, et HE sive HV. Ergo est ut IV ad summam rectarum HI, HV, ita IE ad IP. Sed propter similitudinem triangulorum HVI, VMI, VNO, est ut IV ad summam rectarum HI, HV, ita recta NO ad summam rectarum NV, VO⁴⁾. Ergo ut NO, siue KI est ad NV plus VO, ita est recta IE. ad rectam IP. rectangulum igitur sub IP, IK, aequatur rectangulo sub IE in NV plus rectangulo sub IE in VO. Ex aliâ autem parte est ex natura yssoidis, ut BG ad GE ita GE ad GY. Sed GE est aequalis rectae HE, siue HB minus HG. Ergo est ut BG ad BH minus HG. ita GE ad GY, ut autem BG ad BH minus HG ita propter similitudinem triangulorum & jam demonstratis⁵⁾ recta QC siue GF est ad BC minus BQ, ideoque rectangulum sub YG in GF aequabitur rectangulo sub GE in BC, minus recangulo sub GE in BQ. Ex constructione autem cum rectae HI, HG, sint aequales, item rectae KI, GF, patet reliquas aequari, nempe VN, ipsi BC, VO ipsi BQ. Unde patet duo recttangula correlatiua sub PI in IK, et sub YG in GF, siue in eandem IK, aequalia esse rectangulis sub IE in NV plus GE in BC, siue LI in NV, plus IE in VO, minus GE in BQ, siue in VO. Rectangula autem duo sub IE in NV et sub LI in NV, aequantur unico rectangulo sub diametro LE in NV. Rectangulum vero IE in VO minus GE in VO aequatur rectangulo sub IG in VO siue rectangulo sub IH siue VX in VO bis. Ergo summam rectangulorum sub PI in IK et sub GY in eandem IK aequatur rectangulo sub diametro EL in VN, et rectangulo sub VX in VO bis. Rectangula autem omnia sub diametro et portionibus tangentium VN in quadrante circuli LVA ductarum repraesentant rectangulum sub diametro in quadrantem LVA. Hoc est duplum semicirculi LAE. Rectangula autem omnia sub VX in VO bis sive ductâ O3Q parallelâ diametro, rectangula omnia sub VX in X3 bis repraesentant totum semicirculum LAE. Ergo spatium yssoidale quod aequatur duobus illis rectangulorum seriebus, aequatur triplo semicirculi, ut patet.

3) Lisez: rectas.

4) Nous avons quelque fois dû corriger NO en VO.

5) Lisez: demonstrata.

6) Huygens vent dire: 4 ans auparavant. Consultez les Lettres Nos. 475 et 479 et la pièce No. 483.