Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 479.
Christiaan Huygens à R.F. de Sluse.
5 avril 1658.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 476. R.F. de Sluse y répondit par le No. 481.

5 Apr. 1658.

Slusio.

Nobilissime Domine

Quod scribis de dimensione solidi Hyperbolici ex conversione circa ordinatim applicatam per centrum sectionis, pridem adverteram, quum manifestè sequatur ex aequiponderatione portionis hyperbolae et trianguli oppositi ab asymptotis comprehensi quae ut scis quadraturae meae extitit fundamentum. de altero autem solido tuo quod sit conversione circa ipsum asymptoton nunquam equidem cogitaveram sed video ex eadem illa aequali gravitatione portionis et trianguli deduci posse. Vel ex illa quoque Hyperbolae proprietate, qua parallelogramma inter asymptotos et sectionem inter se aequalia habentur. E qua et Toricellius

[p. 164]

infiniti solidi mensuram olim invenit. Et ego primam connexionem gravitatis centri cum quadratura, licet diversam ejus demonstrationem tradiderim. Fusum autem Hyperbolicum quod dicis si cylindro aequare possemus quadratura haud dubiè reperta esset. Sed hoc ego inter ἀδύνατα habui jam diu.

Venio ad Cissoidis proprietatem plane insignem, quam quidem eo libentius tecum communico quod nisi prior hanc Lineam in medium produxisses, nunquam fortasse examinandam sumsissem.

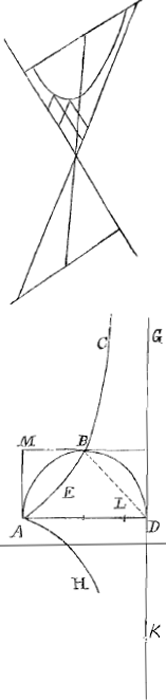
Esto Cissoides AEBC. Circulus à quo genita ABD. Asymptotos DG. Dico spatium infinitum inter hanc et Cissoidem lineamque AD interjectum, triplum esse semicirculi ABD. Cui simile quid in nullis adhuc alijs curvis reperi. Nam spatium inter hyperbolam et asymptoton, uti extensione ita magnitudine quoque infinitum est, uti et in Conchoide, licet solida utra que certam magnitudinem non excedant. Jam si ab altera parte lineae AD replicetur eadem Cissoides spatij infiniti utrimque centrum gravitatis erit L ita dividens AD ut pars AL sit quintupla LD. quod ex conjunctis tuo meoque inventis innotescit. Ergo et revolvendo Cissoidem et asymptoton circa huic parallelum axem AM, orietur solidum infinitum à spatio ABCGD, quintuplum semispirae à semicirculo ABD. Quae quidem omnia liquidè perspicis.

Adjungo ἀπαγογὴν ad circuli quadraturam, quales non multae obtingunt. Nempe si spatio AEBM a Cissoide Dioclis (nam productam Slusianam appellare debemus) et rectis AM, MB contentum, quarum haec tangit semicirculum in vertice; huic inquam spatio si quadratum vel circulum aequalem exhibere possimus, de Circuli Quadratura confectum negotium erit.

Plura addere propter temporis angustiam non licet. Nisi id unum me esse

Tui observantissimum