Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 700.
P. de Fermat à P. de Carcavy.
1659.
Appendice II au No. 698.

La copie se trouve à Leiden, coll. Huygens.¹⁾
Elle a été publiée par Ch. Henry dans le Bull. di Bibliogr. T. 17.

2^e lettre. J'enuoyay l'annee passee à Monsieur Frenicle la demonstration par la quelle ie prouuois qu'il n'y a aucun nombre que le seul 7. qui estant le double d'un quarré - 1. ayt²⁾ la racine d'un quarré de la mesme nature, car 49. est le double d'un quarré 25. - 1.^a)

Je veux mesme que Monsieur de Zulichem voye que cette comparaison des lignes spirales et paraboliques se peut rendre plus generale, et peut estre serat il surpris de lire la proposition suiuante, Dont je luy garentis la verité.

En la figure 38.³⁾ de Monsieur Destonuille on peut considerer les spirales quarrees, cubiques, quarrequarrees &c. tout de mesme que les paraboles cubiques, quarre-quarrees &c.

Si la spirale ordinaire, en la quelle comme toute la circonference a la portion E8B, ainsi la droicte BA, à la droite AC, se compare auec la parabole ordinaire en laquelle comme la droitte RA, a la droitte 6A, ainsi le quarré de la droitte RP, est au quarrè de la droitte 5Q, Et le Rapport est tel, Si AR est faicte esgale à ½ de la circonference totale, et l'appliquee RP, au rayon AB, la ligne parabolique PQA, sera esgale à la spirale BCDA, comme demonstre Monsieur Destonuille.

Mais en prenant la spirale quarree, qui est celle du second genre, en la quelle comme toute la circonference est à la portion E8B, ainsi le quarré du rayon AB,

1) Elle est écrite de la main de P. de Carcavy.

2) Lisez: soit.

a) Je n'ay pas veu cette demonstration, Je tascheray à la recouurer pour vous l'enuoyer. [de Carcavy.]

3) Consultez la reproduction ci-contre de la figure 38 de la planche IIII de son ouvrage ‘Lettres de A. Dettonville’. Voir la Lettre N^o. 560, note 32.

[p. *9]

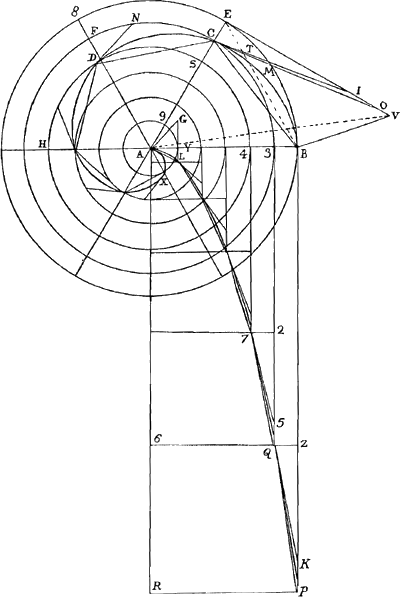Planche III. Figure 38, des LETTRES DE A. DETTONVILLE, 1659, in-4^o.

[p. 539]

est au quarré du rayon AC, on peut la comparer auec la parabole cubique, qui est la parabole du second genre. Soit fait en la parabole cubique l'axe AR, esgal aux ⅔ de la circonference totale, et l'appliquee RP, aussy esgale au rayon AB, la parabolique AP, du second genre sera esgale à la spirale du second genre BCDA.

Si la spirale est cubique il la faudra comparer auec la parabole quarréquarree et faire les ¾ de la circonference totale esgaux à l'axe AR, de la parabole quarréquarree, et l'appliquee RP, touiours esgale au rayon AB, la parabole quarréquarree PQA du 3^e genre, sera esgale à la spirale cubique, du 3^e genre, en laquelle comme toute la circonference à la portion E8B, ainsi le cube du rayon AB, au cube de la droitte AC, Et à l'infini en augmentant touiours chaque numerateur et denominateur de la fraction, de l'unité.

L'axe de la parabole ordinaire estant ½ de la circonference.

L'axe de la parabole cubique ⅔ de la mesme circonference.

L'axe de la parabole quarré quarree ¾.

L'axe de la parabole cubique^4) ⅘ puis ⅚. &c.

D'ou il est aisé de conclure qu'il y a des spirales dans cette progression qui sont plus grandes que la circonference du cercle qui les produit mais qu'elles sont touiours moindres que la somme de ladite circonference et du rayon. Voyla un paradoxe geometrique sur le quel peut estre Monsieur Destonuille et Monsieur de Zulychem n'ont pas encore resué, En tout cas ie les supplie de croire que ie ne l'ay point de personne, et que ma methode dont uous aues le chiffre long tems auant que le liure⁵⁾ de Monsieur Destonuille parut est la source de beaucoup d'autres belles descouuertes sur le suiet des lignes courbes comparees ou auec des droictes, ou auec d'autres lignes courbes de diuerse nature. Je vous en diray peut estre un iour qui uous surprendront.

Monsieur de Zulychem desire encore scauoir si ma methode s'estend a trouuer la dimension des surfaces courbes des conoides et des spheroides, vous pouuez l'assurer que vouy⁶⁾, et qu'elle ua encore bien plus loin, Il m'entendra asses lors que ie luy assureray, premierement, que ie n'ay point veu aucune de ses propositions sur ce suiet.

4) Il s'agit ici de la parabole du cinquième degré.

5) Les ‘Lettres de A. Dettonville’. Voir la Lettre N^o. 560, note 32.

6) Lisez: ouy.

[p. 540]

2^e que la surface du conoide parabolique au tour de l'axe, se trouue par la reigle et le compas et est un probleme plan, que les surfaces des conoides hyperboliques et spheroides supposent la quadrature de l'hyperbole, et quelque fois de l'Ellipse, Et qu'enfin le conoide parabolique au tour de l'appliquee fait une surface courbe qui suppose pour estre exactement mesuree la quadrature de l'hyperbole. Je puis mesme donner une ligne droicte esgale a toute portion de parabole donnee, en supposant la quadrature de l'hyperbole, c'est a dire de l'espace hyperbolique, J'aiousterois toutes les constructions de mes propositions, mais le loisir me manque,