Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 533]

N^o 365.
Christiaan Huygens à [Cl. Mylon.]¹⁾
[1656].

La minute se trouve à Leiden, coll. Huygens.

1) Dans la Lettre N^o. 297 Huygens écrivit à de Carcavy au sujet de cette construction. Il n'est donc pas improbable que la pièce, que nous donnons ici, soit une copie de la construction que Huygens envoya à de Carcavy. Dans ce cas la date serait antérieure au 1^er juin 1656 et même au 31 mai, date d'une lettre perdue de Mylon. (Voir la Lettre N^o. 296, note 1.)

Problema.

Parabola data et puncto ducere ab eo rectam quae parabolae ad rectos angulos occurrat.

Sit data parabola BA²⁾ et punctum C, sit autem non in axe datum, nam in eo si fuerit satis nota est constructio. Ducatur ex C in axem parabolae BG perpendicularis CF, et à vertice B sumatur BH dimidio recti lateris aequalis, et dividatur HF bifariam in K, sitque KL ad axem BK perpendicularis et aequalis quartae parti CF. tum centro L circumferentia describatur quae transeat per verticem parabolae B, ea parabolam secabit. secet igitur in A, et jungatur CA. dico hanc parabolae occurrere ad angulos rectos. Sit intersectio rectae CA et axis parabolae in puncto G, et ducatur AE quae sit dicto axi ad angulos rectos. Ostendendum est igitur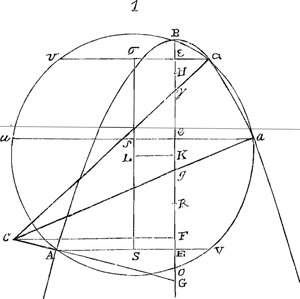



interceptam EG dimidio lateris recti aequalem esse: Hinc enim facile colligitur rectam per A ductam, quae cum CA rectos faciat angulos, parabolam contingere. Ducatur LS ipsi AE perpendicularis, occurrat autem eadem AE circumferentiae circuli in V; axis verò parabolae dictam circumferentiam secet in O. Constat igitur et AV bifariam dividi in S, et BO in K. Sed et KF ipsi KH aequalis est ex constructione. ergo et FO ipsi HB, quae dimidium est lateris recti. Quamobrem sumptâ FR aequali FO, erit

2) Voir aussi les figures de la page suivante.

[p. 534]

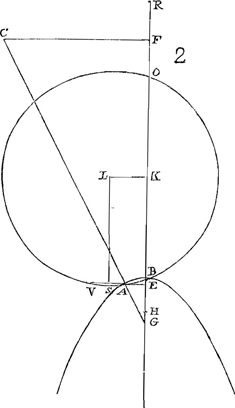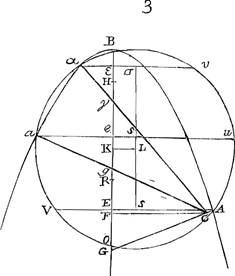tota OR aequalis recto lateri. Quia autem ex circuli proprietate rectangulum BEO aequale est rectangulo AEV, erit sicut BE ad EA ita VE ad EO, sed ut BE ad EA ita est EA ad latus rectum. Ergo ut EA ad latus rectum, hoc est, ad OR, ita VE ad EO; et permutando ut AE ad EV ita RO ad OE. Unde sicut OR ad RE ita AE ad duplam ES; apparet enim duplam ES prout requiritur aequari differentiae duarum AE, EV vel earundem summae. Ergo sumptis consequentium duplis, sicut AE ad quadruplam ES, sive quadruplam KL, hoc est, ad FC, ita OR ad duplam RE, hoc est FR ad RE. Est autem ut AE ad FC, sic GE ad GF. Ergo GE ad GF ut RF ad RE. Ac proinde GE ad EF ut RF ad FE. Itaque GE ipsi FR aequalis est. Haec autem aequalis est dimidiae OR, hoc est, dimidio lateri recto. Ergo et GE dimidio lateri recto aequalis erit. Quod erat ostendendum.