Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–
[pagina 442]
| |
No 308.
| |
[pagina 443]
| |
le dè la premiere fois; et puis B deux fois de suite et puis A deux fois de suite, et ainsi jusques à ce que l'un ou l'autre ait gagnè. Pour faire les partis je nommeray d ce qui est mis au jeu; Et je mettray x pour la part qui en appartient au joueur A. Or il est evident que quand A aura fait le premier coup, et B ses deux coups de suite; et encore A l'un de ses deux coups, sans que ny l'un n'y l'autre ait rencontrè, que alors A aura derechef la mesme apparence pour gaigner qu'il avoit des le commencement, et que par consequent il luy appartiendra derechef la mesme part de ce qui est mis au jeu, c'est a dire x. Partant lors que A vient a faire le premier de ses deux coups de suite il aura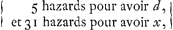 , car de 36 divers coups que produisent 2 dez, il y en a 5 de 6 points, c'est a dire qui luy donnent d, ou ce qui est mis au jeu: et 31 qui luy font manquer les 6 points, et ainsi luy donnent x, le mettant en estat d'avoir encore un coup a faire devant que le tour de B soit venu. Mais , car de 36 divers coups que produisent 2 dez, il y en a 5 de 6 points, c'est a dire qui luy donnent d, ou ce qui est mis au jeu: et 31 qui luy font manquer les 6 points, et ainsi luy donnent x, le mettant en estat d'avoir encore un coup a faire devant que le tour de B soit venu. Mais 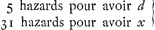 valent autant par le theoreme precedent que valent autant par le theoreme precedent que 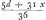 Cecy est donc la part de A lors que A fait le premier de ses deux coups de suite.
Le coup d'auparavant c'est quand B fait le dernier de ses deux coups, et parce qu'il gaigne en amenant 7 points les quels se rencontrent en 6 façons differentes, et qu'alors A perd. donques à ce coup A aura Cecy est donc la part de A lors que A fait le premier de ses deux coups de suite.
Le coup d'auparavant c'est quand B fait le dernier de ses deux coups, et parce qu'il gaigne en amenant 7 points les quels se rencontrent en 6 façons differentes, et qu'alors A perd. donques à ce coup A aura
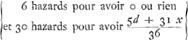 car son tour sera venu de faire deux coups de suite, les quels hazards par le precedent Theoreme valent 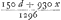 . Cecy est donc la part de A, lors que B fait le dernier de ses 2 coups de suite. quand donc B fait le premier de fes 2 coups, A aura . Cecy est donc la part de A, lors que B fait le dernier de ses 2 coups de suite. quand donc B fait le premier de fes 2 coups, A aura 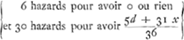 ce qui vaut ce qui vaut 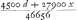 . Quand donc A fait le premijer coup de tous, A aura . Quand donc A fait le premijer coup de tous, A aura 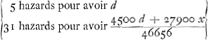 ce qui vaut ce qui vaut 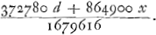 . cecy est donc egal à x. Et partant x egal à 10355/22631. Le parti du joueur A est donc 10355/22631 de ce qui est mis au jeu. Et le reste 12276/22631 est le party de B. Et l'un est à . cecy est donc egal à x. Et partant x egal à 10355/22631. Le parti du joueur A est donc 10355/22631 de ce qui est mis au jeu. Et le reste 12276/22631 est le party de B. Et l'un est à
| |
[pagina 444]
| |
l'autre comme 10355 à 12276, qui sont les mesmes nombres de Monsieur de Fermat. Dans la 2de question ou il suppose que le joueur A joue premierement 2 fois, et puis le joueur B 3 fois, et en suite le joueur A trois fois: la methode est tout a fait semblable, et j'y trouve aussi les mesme nombres que Monsieur de Fermat, mais qu'il les faut transposer. C'est a dire que le party de A est à celuy de B, comme 87451 à 72360. au lieu qu'il a mis 72360 à 87451. La 3me est, quand trois joueurs A, B et C parient avec toutes les 52 cartes que celuy qui aura plustost un coeur gaignera, et que l'on suppose que A prend la 1re carte, B la 2de C la 3me et ainsi consecutivement jusques à ce que l'un ait gagnè. Il y a 13 coeurs parmy ces 52 cartes, c'est pourquoy s'il arrivoit que toutes les autres 39 fussent prises selon le dit ordre sans que personne eust rencontrè un coeur, alors ce seroit le tour du joueur A de prendre, et il auroit gagnè asseurement. Quand donc C prend la 39me carte, au cas que jusques la personne n'ait rencontrè, il est certain que A aura 13 hazards pour avoir perdu et 1 hazard pour avoir tout ce qui est mis au jeu, que j'appelleray d comme devant. Or d'avoir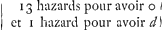 cela vaut 1d/14 par nostre theoreme, d'icy je cognois que quand B prend la 38me carte, A aura cela vaut 1d/14 par nostre theoreme, d'icy je cognois que quand B prend la 38me carte, A aura 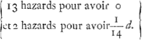 (C'est quand B manque de rencontrer un coeur, car alors c'est à C de prendre la 39me.) lesquels hazards valent 1/105 d.
Quand A prend la 37me. A aura donc (C'est quand B manque de rencontrer un coeur, car alors c'est à C de prendre la 39me.) lesquels hazards valent 1/105 d.
Quand A prend la 37me. A aura donc 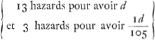 ce qui vaut 1368/1680 d. Ainsi en reculant tousjours d'une carte l'on scaura à la fin la part de A, lors qu'il prend la premiere de toutes. ce qui vaut 1368/1680 d. Ainsi en reculant tousjours d'une carte l'on scaura à la fin la part de A, lors qu'il prend la premiere de toutes.
Et de la mesme maniere se trouvera le party de B, et le reste sera celuy de C. La 4me est, quand deux joueurs jouent a la prime avec 40 cartes et que le joueur A entreprend de ramener prime, et B parie que A ne reussira pas dans les quatre premieres cartes. l'on m'a dit que d'avoir prime c'est avoir 4 cartes differentes, à scavoir une de chasque sorte. Je trouve donc que le party de A est à celuy de B comme 1000 à 8139, de sorte que l'on peut bien parier 8 contre 1, que quelqu'un n'amesnera pas prime. La 5me et derniere question est, quand deux joueurs jouent au piquet, et que le premier entreprend d'avoir 3 as dans ses douze premieres cartes, et l'autre parie qu'il ne les aura pas. Pour resoudre cellecy, je supposeray, qu'il prend ses 12 cartes une a une, car il n'importe aucunement. S'il arrive donc que celuy qui l'entre- | |
[pagina 445]
| |
prend ayant pris 11 cartes, ait desia rencontrè 2 as: il y aura parmy les 25 cartes qui restent encore 2 as. Et partant il aura en ce cas 2 hazards pour avoir gaignè, c'est pour avoir d et 23 hazards pour avoir o. c'est à dire pour perdre. Ce qui vaut 2/25 d. Quand il a pris 10 cartes, s'il a rencontrè 2 as, il aura donc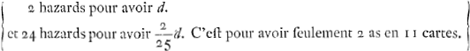 les quels hazards valent 49/325 d. Mais quand il a pris 10 cartes s'il n'a encore que 1 as, Il y aura parmy les 26 restantes 3 as. c'est pourquoy alors il aura 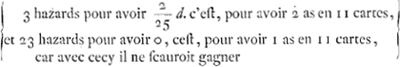 les quels hazard valent 3/325 d. Quand il a pris 9 cartes, s'il a 2 as, il aura  les quels hazards valent 1875/8775 d.
Mais ayant pris 9 cartes s'il n'a encore qu' 1 as, il aura les quels hazards valent 1875/8775 d.
Mais ayant pris 9 cartes s'il n'a encore qu' 1 as, il aura 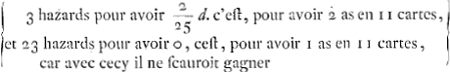 ce qui vaut 219/8775 d. Et en fin si parmy ses 9 cartes il n'a encore aucun as, il aura  les quels hazards valent 12/8775 d. Ainsi par cette methode en reculant tousjours d'une carte je scauray à la fin la part du joueur A, lors qu'il n'a encore pris aucune carte, et que par consequent il n'a pas encore un as. laquelle ayant ostée de d le reste sera la part du joueur B. Ce qu'il falloit trouver. Si j'estois bien informè de l'estat de la question au jeu de la chance que Mon- | |
[pagina 446]
| |
sieur de Fermat dit estre la plus malaisée j'essayerois aussi de la resoudre. Pour celles que je viens de traiter, je vous prie Monsieur de me faire la faveur de les communiquer à Monsieur Milon. Et que je puisse scavoir si ce que Messieurs de Fermat et Pascal en auront trouvè sera conforme a ce que j'en explique. Je desire aussi fort de scavoir s'ils ne se servent pas du mesme theoreme que moy. J'ay appris par vostre lettre ce que Monsieur Pascal entend par les asymptotes de l'ellipse et du cercle, et il est vray qu'elles ont quelques unes des proprietez, qu'ont les vraijes asymptotes de l'Hyperbole, mais il y en a bien aussi qu'elles n'ont pas. Vous verrez dans mon traitè de la quadrature de l'Hyperbole ces mesmes lignes, ou elles font les costez des triangles aequiponderants au sections de l'ellipse et du cercle. et c'est en quoy il y a une fort notable ressemblance de proprietez entre elles et les asymptotes de l'Hyperbole. J'espere que vous aurez receu ces livres, parce qu'on m'asseure qu'ils sont arrivè a Paris. C'est chez Monsieur HenryGa naar voetnoot1) advocat au Parlement qu'on les a adressez, ce que j'escris aussi à Monsieur Milon et en quel lieu il demeure. Je suis
Monsieur
Vostre treshumble et tresobeissant serviteur Chr. Huygens de Zuylichem. |
|

