Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 24]

N^o 14.
Christiaan Huygens à M. Mersenne.
[28 octobre 1646.]

La minute se trouve à Leiden, coll. Huygens.
Mersenne y répondit par le No. 17.
Elle a été publiée par M. Henry, d'après une copie de la Bibliothèque Nationale à Paris, qui diffère de la minute.¹⁾

Monsieur,

I'admire le bonheur, qui a faict tomber encore entre vos mains, le papier, qui n'estoit destiné qu' a la veüe de mon Pere a tout le plus; et d'avantage vostre benignité qui m'avez estimé digne d'une lettre²⁾ si courtoise et pleine de bonne affection, envers moij.^a) Mais voicij ce que je responds à vos objections. Vous dites en premier lieu que tout grave n'est pas capable de recevoir un mouvement si viste que soit celuij du corps qui auroit descendu d'une ou plusieurs lieues de haut. Ie ne puis pas consentir a cela, et m'en rapporte a la Philosophie de Monsr. des Cartes, qui entre autres loix de la nature a remarqué cellecy, à scavoir que toute chose continue son mouvement de la mesme vistesse que luy a esté donnée unefois, si quelque autre chose ne l'empesche; si donc la ou il n'y avoit point d'air nij autre empeschement



nous supposions quelqun qui avecq un arc tiroit deux flesches a la fois, l'une de bois pesant et l'autre de paille ou chose semblable, il est manifeste qu'elles iroient de vistesse esgale, a scavoir de celle qu'avoit la chorde de l'arc en retournant en sa premiere posture, et ne cesseroyent jamais, car il n'y a cause imaginable qui les arresteroit; Ie dis donques que tout corps est capable de quelconque vistesse, et que ce que la paille et la laine tirees hors d'un Canon tombent tout court, ne procede d'autre chose que de l'empeschement de l'air.

1) On a changé dans le texte, donné par M. Henry, l'orthographe de quelques mots qu'on ne trouve jamais écrit de cette manière chez Chr. Huygens; par ex. ‘tumber’ en ‘tomber’, ‘Huggens’ en ‘Huygens’. Aussi nous semble-t-il que la lettre, que M. Henry a fait imprimer, n'est qu'une copie.

2) La lettre ne se trouve pas dans notre collection.

a) L'édition de M. Henry a: ‘en recognoissance de quoy ie tascheray de vous rendre tout service et satisfaction que je pourray; Premierement donc ie respondray a vos obiections.’

[p. 25]

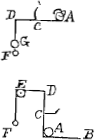
La seconde objection estoit, que pour garder in vacuo les proportions des nombres 1, 3, 5, 7, il estoit necessaire que le grave tombast par tous les degrez de tardité et que cela n'estoit point, à cause que la pierre avoit au commencement de sa cheute desja une certaine vistesse. Ie dis que sans doute elle passe par tous les degrez de tardite, et qu'elle a eu moindre vistesse que quelconque vistesse donnee. Car soit donnee la balle de plomb A qui roule sur le plan horizontal AB de B vers A avecq fort peu de vistesse contre le bras de la balance DCA, dont C est le poinct fixe, il est evident que le poids F. lié de la corde FED qui passe par dessus la poulie, peut estre si peu pesant que la balle A^b) le pourra leuer quelque peu.

Or tel est le principe sur lequel est fondee ma raison, que si la gravite P en commencant sa cheute passe en certain temps par l'espace PS, et au temps suivant par l'espace SR; et que la mesme en un autre temps du commencement de sa cheute passe par l'espace PV, et au temps suivant par l'espace VM; et que le temps de la cheute par l'espace PS soit au temps

b) M. Henry ajoute: ‘en poussant contre le bras de la balance ACD, le pourra faire sauter quelque peu haut: prenons derechef la mesme balance comme en la seconde figure, et soit pendu d'un costé la poids R³⁾ de mesme gravité que la boule A, et d'autre costé, la boule A mise dessus l'autre bras de la balance, cecy donc sera en equilibre: or il est possible de lever si peu en haut la boule A, qu'en tombant derechef sur la place elle pourra a grand peine faire sauter le poids R avec le poids F adiouxté. Il est donc aussy manifeste qu'en tombant d'une petite hauteur elle peut avoir esgale ou moindre vistesse qu'en roulant de la vistesse donnee sur le plan AB; car en l'un et l'autre cas c'estoit la force du mouvemant de la boule qui faisoit sauter le poids F, et la force esgale ne peut estre causée que d'une esgale vistesse. Mais ce qui fait sembler le contraire, a scavoir que la boule aurait une certaine vistesse en commençant sa cheute, c'est qu'on ne voit jamais que fort peu de la tardité avec laquelle elle commence sa cheute; car quand on ne voit aussy qu'un peu sur la fin la course de la boule roulante contre le bras de la balance, il semble qu'elle va fort viste.
Or tel est le principe quj m'a fait trouver la proportion des nombres impairs 1, 3, 5, 7 etc. Que sj quelque gravite au premier minute de la cheute passe l'espace d'un pied, et qu'au minute suyvant elle passe quelque autre nombre de pieds, prenons 5 pieds; et que la mesme gravité du commencement de la cheute passe par exemple aux 4 premiers minutes 10 pieds: qu'aussy aux 4 suyvants minutes elle en passera 50, parce que 1 est à 5, comme 10 à 50.

3) C'est le point indiqué par G dans la première figure de notre texte.

[p. 26]

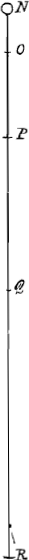par SR comme le temps par PV au temps par VM; que alors l'espace PS est a SR comme PV à VM. Comme par exemple, si une pierre en tombant passe au premier minute de sa cheute un pied de mesure, et au second minute 5 pieds; que la mesme pierre parce qu'aux deux premiers minutes elle a donc passe 6 pieds, aussi aux deux suivants minutes elle en passera 30; car 1 est a 5 comme 6 à 30.^c)

Cecy estant concedé, soient passé en egals temps les espaces AB, BC, CD, etc. il est donc manifeste que comme l'espace AB à BC, ainsi est l'espace AC à CE, et AD à DG. Car comme le temps par AB a esté egal au temps par BC ainsi le temps par AD a esté egal au temps par DG.

Voions a cest heure s'il ij a quelque progression Geometrique, que puissent avoir les espaces AB, BC, CD etc, passez en temps esgaux. Soit donc l'espace AB ∞ a^d) BC ∞ b; si c'est donc une progression Geometrique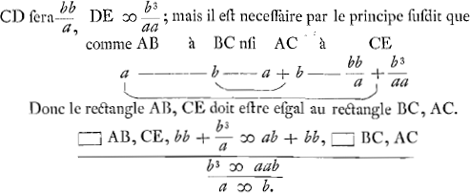

De cette Analyse s'ensuit que les dits espaces ne peuvent estre en aucune progression Geometrique que de l'esgalité. Lopinion doncque de ceux qui disent, qu'ils sont en la progression 1, 2, 4, 8 est fort ridicule. Car par exemple, posons que le poids N passe au premier temps par l'espace NO, 1, au second OP 2, au 3^me PQ 4, au 4^me QR 8: Et prenons a cest heure le[s] deux premiers temps auxquels il a passe par l'espace NP, pour le premier; ayant doncque passé au premier temps par l'espace NP 3 (car NO 1, et OP 2, sont 3) il passera au second temps a scavoir au 3^me et 4^me, selon leur progression 6,

c) Au verso de la minute l'auteur a écrit ces mots, que l'on retrouve en partie dans l'édition de M. Henry (voir Note b): Que si la gravite P au premier minute de sa cheute passe l'espace d'un pied, et qu'au minute suivant elle passe quelque autre nombre de pieds, prenons 5 pieds. et que la mesme gravite du commencement de sa cheute passe par exemple aux 4 premiers minutes 10 pieds; qu'aussi au 4 suivants minutes elle en passera 20 pieds parce que 1 est à 5 comme 4 à 20.

d) Dans l'édition de M. Henry on trouve le signe ∙∥∙, que Huygens n'emploie jamais: il se sert toujours du signe ∞.

[p. 27]

mais au 3^me et 4^me il a passé par l'espace PR 12 (car PQ 4 et QR 8 sont 12), il faudroit donc que 6 fust esgal a 12, ce qu'est absurde.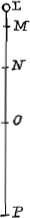

Voions donc s'il y a quelque progression Arithmetique en la quelle les espaces puissent estre. Que le poids L donc aye passé au premier temps par l'espace LM ∞ a, au second MN a + x, au troisieme NO a + 2x, au 4^me OP a + 3x. il faut donc selon mon principe que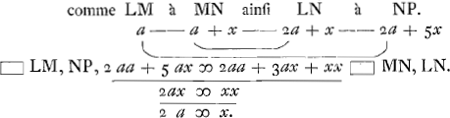



Nous avons doncq trouvé la progression arithmetique en laquelle sont les dits espaces, car x estant trouvé esgal à 2a l'espace MN a + x sera 3a, NO a + 2x sera 5a, OP a + 3x sera 7a. Et de cette Analyse est manifeste



qu'il n'y a point d'autre progression Arithmetique en la quelle puissent estre les dits espaces, et par consequent que l'opinion de ceux qui disent qu'ils sont 1, 2, 3, 4, etc. est absurde.^e) Car posons que le poids E passe en esgaux temps les espaces EF, 1, FG 2, GH 3, HI 4; prenons puis les deux premier temps au quels il passe EG, pour le premier; passant doncq au premier temps par EG 3 il passera selon leur progression au temps egal suivant, (qui est esgal au 3^me et 4^me,) 6; il faudroit donc que l'espace GI fust 6, mais il est 7, estant composé de GH 3 et HI 4; 6 donc devroit estre 7 ce qu' est absurde. Mais si on examine de la mesme façon la progression trouvée 1, 3, 5, 7, 9, 11, on ne trouvera rien d'absurd car 1 est à 3 comme 1 et 3, c'est 4, à 5 et 7, c'est 12; et comme 1, 3, 5, c'est 9 à 7, 9, 11, c'est 27, etc.

Et ie ne trouve point d'autres progressions qui ayent quelque regularité, et la proprieté requise que cellecy. Et pour cela je croij qu' il n'y a point d'ordre du tout, ou que c'est celuy de ces nombres impairs.

Tout cecy doit estre considere comme en une place ou il n'y a point d'empeschement d'air ny d'autre chose mais seulement une uniforme attraction d'en bas, soit grande ou petite.

Touchant la parabole, que font les missiles cela ne peut pas manquer, car in vacuo le mouvement^f) donné au missile qui le fait aller de costé de vistesse egale, ne cessera jamais si quelque chose ne l'empesche; Or l' attraction d'en bas ne luy resiste point du tout, estant supposé qu'elle est à angles droicts au mouvement horizontale. Le reste depend de la proprieté de la parabole qui est assez connüe.

e) L'édition de M. Henry a: ‘absurde et contradictoire à soy mesme.’

f) L'édition de M. Henry a ‘le mouvement horizontal.’

[p. 28]

Ie fineray icij de peur de ne vous detenir pas trop longtemps, et vous envoyeray par une autre lettre la demonstration de ce qu' une corde ou chaine pendue ne faict point une parabole, et quelle doit estre la pression sur une corde matematique ou sans gravité pour en faire une; d'ont j'ay aussi trouve la demonstration, il n'y a pas longtemps.

Et en attendant avecq grand desir quelque particularitez des centres de percussion^g) je demeureray

Monsieur

Vostre treshumble. Christien Huygens.^h)

g) L'édition de M. Henry a encore: ‘car c'est icy une matiere jncogneue.’

h) L'édition de M. Henry a la date: ‘A leyden le 28^e d' octobre 1646.’

3) C'est le point indiqué par G dans la première figure de notre texte.