Geschiedenis van de wetenschappen in België. 1815-2000

[p. 99]

5 De wiskunde
Jean Mawhin

Jean-Guillaume Garnier: door Hess, Brussel, Koninklijke Bibliotheek Albert I. Prentenkabinet ▪

▪ De analyse en de mechanica

Aan het begin van de 19de eeuw ontwaakte de Belgische wiskunde uit een diepe slaap van meer dan honderd jaar. De differentiaal- en integraalrekening, die in België beroemde wegbereiders had zoals Gregorius a Sancto Vincentio (1584-1667) en René-François de Sluse (1622-1685), en waarvan de ontwikkeling en toepassingen de hele 18de-eeuwse wiskunde inspireerden, werd in onze universiteiten niet onderwezen vóór 1817. Commandant Charles-François Le Prud'homme d'Hailly (1746-1827), burggraaf van Nieuwpoort en een voormalig genieofficier publiceerde, naast filosofisch werk, wel enkele verhandelingen over differentiaal- en integraalrekening en de integratie van de partiële differentiaalvergelijkingen. Hoewel hij hiermee lid werd van de Académie royale de Belgique en van het Institut de France, zijn deze werken, en ook die over de stabiliteit van gewelven, heden ten dage al lang vergeten.

Een tekort aan bekwame wiskundigen uit eigen land dwong de rijksuniversiteiten van Luik, Leuven en Gent (1817), om aanvankelijk een beroep te doen op buitenlandse geleerden om hun studenten differentiaal- en integraalrekening aan te leren. Zo werd te Gent deze taak toevertrouwd aan de Fransman Jean-Guillaume Garnier (1766-1840), auteur van meerdere gerespecteerde handboeken en te Leuven aan de Sardiniër Gaspard-Michel Pagani (1796-1855). In Luik werd daarentegen wel Jan-Michiel Vanderheyden (1768-1836), oud-hoogleraar van de Oude Leuvense Universiteit, benoemd. Na de onafhankelijkheid was dit tekort grotendeels weggewerkt en werden vooral Belgische wiskundigen aan de Belgische universiteiten benoemd.

Hoewel de wiskundigen van het latere België geen essentiële bijdrage leverden tot de ontwikkeling van de wiskundige analyse tijdens de 18de en de eerste helft van de 19de eeuw, namen ze toch actief deel aan de felle discussies over de grondslagen van deze discipline. Zoals overal elders verzetten de aanhangers van het gebruik van het ‘oneindig kleine’ zich tegen de adepten van de ‘methode der limieten’; daarnaast waren er wiskundigen die de infinitesimaalanalyse zuiver algebraïsche fundamenten wilden geven. Deze belangstelling voor de fundamenten blijkt uit de eerste uitgegeven universiteitscursussen differentiaal- en integraalrekening.

In 1854 liet Jean-Alexis Timmermans (1801-1864) de lessen die hij sinds 1835 gaf aan de universiteit van Gent uitgeven. Dit is waarschijnlijk de eerste Belgische cursus wiskundige analyse. In de inleiding wordt de keuze van de gebruikte methode

[p. 100]

Jean-Alexis Timmermans, door F. Demeersman. Brussel, Koninklijke Bibliotheek Albert I, Prentenkabinet ▪

toegelicht: ‘De manier waarop de infinitesimaalrekening hier wordt uiteengezet, is die welke is voorgesteld door Landen en Dalembert [sic] en veronderstelt de aanvaarding van limieten. Deze methode heeft tegenover haar concurrent, de methode van het oneindig kleine, het enorme voordeel dat ze uiterst nauwkeurig en juist is. Immers, ze past de regels van de aritmetica en algebra slechts toe op eindige, en bijgevolg voor de geest begrijpbare kwantiteiten, terwijl de andere methode zonder meer aanneemt dat diezelfde regels nog gelden wanneer men kwantiteiten neemt van een niet te omschrijven grootte en bijgevolg niet bevattelijk voor onze zintuigen en ons verstand. Er is dus getracht om uitsluitend uit het principe der limieten op een planmatige en uniforme wijze alle fundamentele stellingen van de differentiaalrekening af te leiden; maar de oude methode van Leibnitz [sic] biedt te grote voordelen wat betreft bondigheid en eenvoud om er zomaar aan voorbij te gaan; daarom zijn er meestal twee bewijzen: het ene bewijs bedoeld om de geest te overtuigen, het andere om hem te ontlasten en beter te doen onthouden’. Het is duidelijk: de uitdrukking ‘Belgisch compromis’ bestaat al veel langer dan vandaag. Uit dit citaat mogen we echter niet zonder meer afleiden dat de cursus een voorloper is van de moderne uiteenzettingen over de differentiaalrekening. Het fundamenteel begrip limiet wordt nergens gedefinieerd en twee ‘bewijzen’, een meetkundig en een analytisch, moeten de lezer ervan overtuigen dat elke willekeurige functie een afgeleide heeft! De van Luxemburg afkomstige Antoine Meyer (1803-1857) was eerst hoogleraar aan de Koninklijke Militaire School en aan de Université libre de Bruxelles en daarna aan de universiteit van Luik. In 1855 publiceerde hij de cursus differentiaalrekening die hij sinds 1849 in laatstgenoemde instelling doceerde. Het Avant-propos bevat een korte, kritische analyse van de verschillende voorgestelde methoden om de ‘afgeleide’ f′_x = dy/dx van een functie y = f(x) te definiëren. Kort samengevat: ‘men merkt dus dat deze methoden te herleiden zijn tot twee hoofdconcepten: de definitie van Euler, name-

Antoine Meyer. Lithografie door E. Meyer. Brussel, Koninklijke Bibliotheek Albert I. Prentenkabinet ▪

[p. 101]

lijk dy = 0, dx = 0, en de methode van het oneindig kleine, die in haar deducties een absurd principe hanteert’. Dan beschrijft hij de methode van Ernest Lamarle (1806-1875), hoogleraar burgerlijke bouwkunde aan de universiteit van Gent: ‘volgens deze methode valt de verhouding 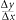uiteen in twee delen: het eerste deel, onafhankelijk van Δx, aangeduid met f′_x; het tweede, variërend met Δx, voorgesteld door η. Men heeft dus: 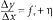. Lamarle definieert vervolgens de differentiaal dy met de vergelijking dy = f′_x∙Δx. Deze definitie is exact en de auteur moet worden gezien als de eerste die de ware betekenis van de differentiaal heeft gegeven’. Meyer begint zijn Préface dan ook als volgt: ‘Ik heb getracht deze elementen onafhankelijk te maken van de methode van fluxies, van het oneindig kleine, van het uiterst kleine, van de afgeleiden en van de limieten. Het is bekend dat geen van deze methoden de geest totaal bevredigt: de ene geven tegenstrijdige resultaten, de andere missen nauwkeurigheid of berusten op vage redeneringen en leiden tot lange, omslachtige berekeningen. De methode die ik gebruik en als de enige juiste beschouw, heeft als dubbel voordeel dat ze de differentiaalrekening de duidelijkheid geeft van de algebra én dat ze tot resultaten komt langs de gemakkelijkste, eenvoudigste en kortste weg’. Een lezing van het werk toont aan dat Meyer onterecht optimistisch is. In feite berust zijn benadering op een ‘theorema’ dat stelt dat voor elke functie y = f(x), f(x+Δx) steeds kan geschreven worden onder de vorm f(x)+f′_x∙Δx+η(x,Δx)∙(Δx)². Het ging hier duidelijk om een herhaling van de mislukte poging van Lagrange om de differentiaalrekening een zuiver algebraïsche basis te geven.

Meyers opvolger Mathias Schaar (1817-1867) was ook van Luxemburgse afkomst en werd bekend met werk over hogere aritmetica en Euleriaanse functies. In 1862 publiceerde Schaar zijn cursus infinitesimaalanalyse, een werk dat hij ook aan de universiteit van Gent gebruikte nadat hij in 1864 Timmermans was opgevolgd. Dit boek, dat door de overeenkomst met de aan de Ecole polytechnique gebruikte Cours d'analyse van Sturm op plagiaat lijkt, voldeed uiteraard aan de strenge maatstaven die in die tijd in Frankrijk werden gehanteerd. Schaar was ook verantwoordelijk voor de introductie van de studie van ‘functies van een complexe veranderlijke’ in de cursussen van de tweede cyclus.

De discussies over de fundamenten van de analyse beperkten zich niet tot de inleidingen van de universiteitscursussen infinitesimaalrekening. Meerdere werken werden geheel aan het onderwerp gewijd. Zo is Lagranges algebraïsche benadering te vinden in een door F. Haeck enthousiast verdedigde verhandeling uit 1845 van François-Joseph Gilain (1823-1858). In dezelfde periode steunde Jean-Nicolas Noël (1783-1867), hoogleraar aan de universiteit van Luik, de infinitesimaalmethode in het eerste werk uit de reeks Mémoires de la Société royale des Sciences de Liège, waarin staat te lezen: ‘Iedere kwantiteit is te verwaarlozen en is te zien

Mathias Schaar. Lithografie door J. Schubert. Brussel, Koninklijke Bibliotheek Albert I. Prentenkabinet ▪

[p. 102]

als absoluut nul ten opzichte van een andere die haar oneindig maal bevat: het is een nul in relatie tot deze laatste, hoewel deze nul een waarde heeft en niet de absolute nul is of het niets, duidend op de afwezigheid van iedere grootheid’. In dezelfde reeks verscheen in 1868 het postume Exposition nouvelle des principes du calcul différentiel et intégral van de meetkundige Jean-Baptiste Brasseur (1802-1868), uitgegeven door zijn opvolger François Folie. De Luxemburger Brasseur had sinds 1829 aan het boek gewerkt. Als we Folie mogen geloven dan is de auteur ‘erin geslaagd de Langrange-methode, die enkel de eindige analyse gebruikt, even gemakkelijk hanteerbaar en even nauwkeurig te maken als de methode van de limieten of die van de fluxies’. Het werk van Cauchy maakte evenwel de publicatie van dit werk in 1829 bijna overbodig.

Louis-Philippe Gilbert. Lithografie door J. Schubert. Brussel, Koninklijke Bibliotheek Albert I. Prentenkabinet ▪

De bijdragen van de eerder vermelde Ernest Lamarle hebben meer weerklank gekregen. Bij zijn mislukte poging om aan te tonen dat iedere continue functie afleidbaar is, tenzij op uitzonderlijke punten, introduceerde Lamarle impliciet de ‘getallen van lagere en hogere afgeleiden van een functie’, heden bekend onder de naam ‘Dini-afgeleiden’ en fundamenteel voor de ontwikkeling van de moderne theorie van de functies van reële veranderlijken. Een latere poging van dezelfde auteur om de infinitesimaalrekening een geometrische en kinematische basis te geven, bleek niet zo succesvol.

De polemiek over de fundamenten van de infinitesimaalrekening bereikte ook het middelbaar onderwijs toen werd besloten tot de invoering van elementaire begrippen uit de differentiaal- en integraalrekening. De ‘infinifuges’ (voorstanders van de limietentheorie) verzetten zich hardnekkig tegen de ‘infinicoles’ (voorstanders van het gebruik van het oneindig kleine), op een manier die vergelijkbaar is met de strijd rond de ‘moderne wiskunde’ een eeuw nadien.

Pagani's opvolger te Leuven was Louis-Philippe Gilbert (1832-1892). Hoewel Gilbert was geboren in België (waar hij bleef wonen) uit een Franse vader en een Belgische moeder, behield hij de Franse nationaliteit. Deze encyclopedische geest en polemist schreef een cursus analyse waarvan de tweede editie (1878), samen met een beroemd traktaat van de Italiaan Ulisse Dini (1845-1918), het eerste leerboek was waarin een voorbeeld stond van een overal continue en nergens afleidbare functie. De grafiek van zo'n functie is in huidige termen een ‘fractaal’, een wiskundige constructie die het midden houdt tussen een kromme en een vlak en waaraan men een dimensie toekent tussen één en twee. Gilberts cursus bevatte ook, lang voor de Franse equivalenten, recente verbeteringen gerealiseerd in Frankrijk, Duitsland en Italië op het vlak van de rigoureuze presentatie van de fundamenten van de analyse.

In Luik werkte Gilberts ‘alter ego’, Eugène Catalan (1814-1894), eveneens een in onze streken geboren Fransman. Deze oud-leerling van de Ecole polytechnique was even vrijzinnig en republikeins als Gilbert katholiek en behoudsgezind was, en hij liet

[p. 103]

dit graag merken tijdens de revolutiedagen van 1830, 1848 en 1851 te Parijs. Dit was erg nadelig voor de toekomstkansen van zijn academische loopbaan in Frankrijk, waar hij ondanks een rijk en gevarieerd wiskundig oeuvre nooit een post van hoogleraar aan een universiteit of een belangrijke school kreeg toegewezen. Gelukkig bood de Belgische regering hem in 1865 de leerstoel analyse van de universiteit van Luik aan. Catalan kweet zich toegewijd van zijn taak tot aan zijn emeritaat in 1884.

Catalan was een bijzonder inventief wiskundige. In de algebra heeft hij het belangrijke begrip ‘circulerende determinant’ ontdekt. In de hogere aritmetica introduceerde hij getallen gedefinieerd door de formule: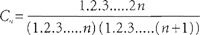



Men noemt ze ook de ‘getallen van Catalan’ en ze komen voor in talrijke ‘combinatorische vraagstukken’. De zogenaamde ‘constante van Catalan’ C is gelijk aan de som van de oneindige reeks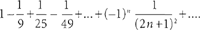

Ze bedraagt bij benadering 0,915965... en het is nog steeds onbekend of C rationaal of irrationaal is. Het ‘theorema van Catalan’, dat eerder de ‘hypothese van Catalan’ zou moeten worden genoemd aangezien het nog altijd niet is bewezen, stelt dat de diofantische vergelijking (d.w.z. waarvan enkel de oplossingen in gehele getallen worden weerhouden)

x^y - z^t = 1,

geen andere oplossing heeft dan x =3, y =2, z =2, t=3, op voorwaarde dat x,y,z,t > 1.

Catalan publiceerde ook een wat ongeordende maar van intelligente commentaar voorziene cursus analyse. Die inspireerde de cursus van zijn opvolger Joseph Neuberg (1840-1926), een Luxemburgse specialist van de ‘géometrie du triangle’, die, tot de hervorming van de moderne wiskunde, generaties adolescenten tot verrukking dan wel tot wanhoop heeft gedreven.

Tot slot kan men niet voorbijgaan aan de cursus analyse van Paul Mansion (1844-1919), hoogleraar aan de universiteit van Gent en een onvermoeibaar

Emile Delpérée, Portret van Eugène Catalan, 1884. Luik, Université de Liège, Collections artistiques ▪

gangmaker van de wiskunde in België. Net zoals dat van Gilbert, was het boek van Mansion een grote stap voorwaarts in het strenge exposé van de infinitesimaalanalyse. Bovendien was er op toegezien dat het aanleren van deze moeilijke discipline gebeurde vanuit een historisch perspectief.

In 1874 startten Catalan en Mansion met Nouvelle correspondance mathématique, een wiskundig tijdschrift dat de opvolger was van het beroemde

[p. 104]

Correspondance mathématique et physique van Adolphe Quetelet. In 1880 werd het vervangen door Mathesis, een tijdschrift over elementaire wiskunde, geleid door Mansion en Neuberg, dat snel tot buiten de grenzen befaamd zou worden.

Alles was klaar voor een rijke oogst. De loopbaan van Belgiës beroemdste analist ving aan met een meesterlijk bewijs dat een korte toelichting verdient. Het is bekend dat een geheel getal groter dan één een priemgetal wordt genoemd als het alleen deelbaar is door zichzelf en door één. Zo zijn 2, 3, 5, 7, 11, 13, 17 en 19 de priemgetallen kleiner dan 20. Euclides had al aangetoond dat er priemgetallen bestaan die zo groot zijn als men maar wenst, doch de verdeling der priemgetallen over de gehele getallen leek elke wet te tarten. De grote Duitse wiskundige, astronoom en fysicus Carl Friedrich Gauss (1777-1855) veronderstelde echter in 1798, bij het bestuderen van de tafels der priemgetallen, dat het getal π(n) van de priemgetallen kleiner dan of gelijk aan n, bij benadering gelijk is aan n/log n, waarbij log n de neperiaanse logaritme van n aanduidt. De benadering wordt steeds beter als n groter wordt. Meer exact geformuleerd, neigt de relatieve fout tussen de twee uitdrukkingen naar 0 wanneer n oneindig groot wordt. Die verrassende hypothese bracht twee schijnbaar ver van elkaar gelegen domeinen samen: de getallentheorie, rijk van het discrete, en de infinitesimaalrekening, paradijs van het continue. De grootste wiskundigen van de 19de eeuw probeerden dit resultaat tevergeefs te bewijzen. Pas in 1896 zouden twee wiskundigen onafhankelijk van elkaar maar op basis van gelijkaardige technieken, ontsproten uit de theorie van de functies van een complexe veranderlijke, de hypothese omzetten in het ‘theorema der priemgetallen’: de Fransman Jacques Hadamard (1865-1963) en de Belg Charles-Jean de La Vallée Poussin (1866-1962), die hoogleraar was aan de Katholieke Universiteit van Leuven publiceerde in de Annales de la Société scientifique de Bruxelles. De familie van Charles de La Vallée Poussin telde meerdere eminente universiteitsprofessoren, onder wie zijn neef en leermeester Louis-Philippe Gilbert.

In zijn Journal d'un bourgeois de Paris geeft Eugène Catalan een kritische visie op zijn tijd. Luik, Université de Liège. CICB, Ms. 1.308 ▪

[p. 105]

Wiskundig model, door Eugène Catalan gebruikt tijdens zijn cursussen. Luik, Centre d'Histoire des Sciences et des Techniques ▪

De La Vallée Poussin volgde Gilbert op na diens vroege overlijden in 1892. De jonge docent was nog maar 26 jaar, maar hij had al wel gestudeerd in Parijs bij Camille Jordan (1838-1922), Charles Hermite (1822-1901), Gaston Darboux (1842-1917) en Henri Poincaré (1854-1912). Zijn eerste publicaties hadden reeds de aandacht getrokken van de Belgische wiskundige wereld, in het bijzonder van Paul Mansion. Het succes van 1896 gaf hem internationale bekendheid, nadien bevestigd met belangrijke werken over de integratietheorie van Riemann en Lebesgue (‘integreerbaarheidstest van de La Vallée Poussin’), de benadering van functies (‘kern van de La Vallée Poussin’), de harmonische analyse (‘convergentietest en sommatiemethode van de La Vallée Poussin’), de conforme afbeelding en de potentiaaltheorie. Daarnaast schreef hij talloze notities over niet-euclidische meetkunde, waarschijnlijkheidsrekening, de beperkte relativiteit, de beweging van een lichaam en over wat later lineaire programmering werd genoemd. De La Vallée Poussin redigeerde en publiceerde zijn cursus analyse volgens de traditie van Gilbert. De cursus kende tussen 1903 en 1959 twaalf uitgaven, werd vertaald in het Russisch en heruitgegeven bij Dover in de Verenigde staten. Talrijke Europese en Amerikaanse wiskundigen erkennen de analyse te hebben geleerd via het boek van de La Vallée Poussin. De tweede uitgave, uit 1909, was trouwens het allereerste werk over elementaire analyse dat de ‘integraal van Lebesgue’ verklaarde, terwijl de derde editie, uit 1914, reeds het belangrijke begrip ‘totale differentiaal’ van een functie van meerdere veranderlijken uiteenzette.

Tijdens de Eerste Wereldoorlog werd de La Vallée Poussin uitgenodigd om les te geven aan de universiteit van Harvard, het Collège de France, de Sorbonne en de universiteit van Genève. Hieruit

Charles-Jean de la Vallée Poussin, Leuven. Archief KULeuven ▪

[p. 106]

Cours d'analyse infinitësimale (1903) van Charles-Jean de La Vallée Poussin. Louvainla-Neuve, Bibliothèque des Sciences exactes ▪

volgden klassiek geworden monografieën over de integratie en de benadering van functies. Toen op het einde van de oorlog de International Mathematical Union werd opgericht, werd de La Vallée Poussin de eerste voorzitter. Hij was doctor honoris causa van verschillende buitenlandse universiteiten en lid van meerdere academiën. Toen de Katholieke Universiteit van Leuven voor haar eminente analist in 1928 een jubileumviering organiseerde, was het erecomité een echte ‘who is who’ van de wiskunde uit die tijd. Kort daarna verleende Koning Albert I de titel van baron aan deze onbetwistbare leider van de Belgische wiskunde.

De La Vallée Poussin overleed op 96-jarige leeftijd jaar. Hij had 60 jaar lesgegeven aan de Leuvense universiteit, was 64 jaar lid geweest van de Académie royale de Belgique en had driekwart eeuw de wiskunde beoefend! Over de wiskunde zei hij: ‘van zodra ze mij is geopenbaard, heb ik mezelf onvoorwaardelijk overgeleverd. Ik heb haar veel gevraagd en hoewel ze me had kunnen afwijzen, heeft ze me onafgebroken plezier bezorgd. Ze is voor mij een altijd mooie, altijd verscheiden, altijd nieuwe wereld geweest, zoals dat hoort tussen geliefden’. En voorts: ‘De wiskundige wetenschap is een kunst, en een kunst laat een belangrijke plaats aan het gevoel en aan de individuele esthetiek. Wiskundige theorieën zijn constructies waarvan de opbouw minstens voor een deel vrij blijft, en de artiest die ze ontwerpt, legt er een deel van zichzelf in. Hij laat zich leiden door een bepaald gevoel voor schoonheid, iets dat men smaak noemt en het product is van de opvoeding, het milieu, een of ander verafgelegen onderbewustzijn, dat voortkomt uit het diepere vernuft van het ras, maar dat zich onttrekt aan de analyse, wat dan weer bewijst dat zelfs in meetkunde het hart soms zo zijn redenen heeft die de rede niet begrijpt’. Ook al was de La Vallée Poussin een estheet, een aristocraat van het intellect, een befaamd professor, bevriend met alle grote wiskundigen van zijn tijd, toch werkte hij aan de wiskunde als een eenzame smid. Nergens, ook niet aan de Leuvense universiteit, creëerde hij een school, en de weinige leerlingen die hij had, beschikten niet over de kracht noch over het nodige talent om de fakkel door te geven.

Hetzelfde kan niet worden gezegd van Théophile De Donder (1872-1957), hoogleraar aan de Université libre de Bruxelles. Aan hem dankt deze instelling een traditie van kwalitatief onderzoek in de wiskunde, de wiskundige natuurkunde en de theoretische scheikunde. Beïnvloed door het onderricht van Poincaré te Parijs, ontwikkelde De Donder de theorie van de ‘integraalinvarianten’ en verrichtte hij pionierswerk in wat later de theorie van de ‘buitenste differentiaalvormen’ zou worden genoemd, een machtig hulpmiddel dat vandaag onmisbaar is in de wiskunde en de theoretische fysica.

De Donder gebruikte reeds in 1904 werk van Elvin Christoffel (1829-1900), Gregorio Ricci (1853-1925) en Tullio Levi-Civita (1873-1941) over ‘absolute differentiaalrekening’. Het is dan ook niet verwonderlijk dat hij onmiddellijk het belang heeft ingezien van Einsteins eerste werken over ‘algemene relativiteit’, en er de technieken van zijn eigen ‘variatierekening’ op heeft toegepast. Een interessante briefwisseling met de grote Duitse geleerde

[p. 107]

uit de periode 1916-1923 biedt een bijzonder levendige en leerrijke kijk op dit onderzoek. De Donders wiskundig standpunt verschilde soms totaal van Einsteins natuurkundig standpunt. Later zullen we dieper ingaan op een gelijkaardig meningsverschil tussen Einstein en Georges Lemaître (1894-1966), die door De Donder als een van zijn leerlingen werd beschouwd.

In de thermodynamica introduceerde De Donder een nieuwe formulering van de tweede wet, gebaseerd op het belangrijke concept ‘affiniteit’. Dat heeft geleid tot de ontwikkeling van de thermodynamica van onomkeerbare processen en van de beroemde School van Brussel. Terloops merken we op dat deze productieve auteur (meer dan tweehonderd artikels en mededelingen, een tiental boeken, en een uitgebreide briefwisseling met de Broglie, Eddington, Lorentz. Volterra en Einstein) ook een begaafd muzikant was en meerdere stukken voor piano componeerde. Het mag dan ook niet verbazen dat De Donder in 1911, ter gelegenheid van zijn eerste les wiskundige natuurkunde aan de universiteit van Brussel, zijn lievelingsdiscipline zo definieert: ‘De wiskundige natuurkunde omsluit het zuiverste beeld dat het aanschouwen van de Natuur in een mens kan oproepen; dit beeld heeft alle kenmerken van een kunstwerk: het heeft eenheid, het is echt en subliem; dit beeld is voor de fysische natuur wat de Muziek is voor de duizenden geluiden die de lucht vullen, en aldus is de wiskundige Natuurkunde een onuitputtelijke bron van hogere geneugten, laat ze ons van de Natuur houden en geeft ze aan de ziel een verrijking die charmeert en verheft’.

Niettegenstaande zijn belangrijkste bijdragen tot de experimentele fysica behoren, heeft Joseph Plateau (1801-1884), hoogleraar aan de universiteit van Gent, zijn naam gegeven aan een van de moeilijkste problemen in de variatierekening: het ‘probleem van Plateau’. Dit is het bepalen van het vlak (of vlakken) met het kleinste oppervlak dat steunt op een ruimtekromme. Plateau wist deze oppervlakken experimenteel te demonstreren en te onderzoeken met een zeepfilm steunend op gebogen ijzerdraad. Talrijke 19de-eeuwse wiskundigen, onder wie Lamarle en Catalan, berekenden bijzondere oplossingen van de corresponderende partiële differentiaalvergelijking, in 1760 reeds geformuleerd door Joseph-Louis Lagrange (1726-1813). Pas in 1931 zouden Jesse Douglas (1897-1965) en Tibor Radó (1895-1965) het eerste bewijs leveren van het bestaan van een oplossing in algemene omstandigheden. Een precieze beschrijving van het geheel van oplossingen is heden nog altijd veraf.

Pierre-François Verhulst (1804-1849), een tijdgenoot van Plateau, gaf een blijvende bijdrage aan wat nu de ‘wiskundige populatietheorie’ heet. Nadat hij uit Italië, waar hij verbleef voor zijn gezondheid, was verbannen omdat hij de paus had willen overtuigen de Pauselijke Staten een grondwet te verlenen, werd Verhulst in 1834 hoogleraar aan de Koninklijke Militaire School. Tussen 1835

Pierre-François Verhulst. In: Annuaire de l'Académie royale des Sciences. des Lettres et des Beaux-Arts de Belgique, 1850. Brussel, Académie royale de Belgique ▪

[p. 108]

en 1840 gaf hij ook les aan de Université libre de Bruxelles. Onder impuls van Quetelet, die nochtans niet dezelfde conclusies wilde trekken als zijn leerling, stelde Verhulst in 1847 een differentiaalvergelijking op die de bekende ‘vergelijking van Malthus’

dn/dt = an,

die de evenredigheid uitdrukt tussen het groeipercentage van een populatie en de populatie zelf, modificeert door de invoering van een term van weerstand tegen de exponentiële toename van de populatie:

dn/dt = an - bn².

Bijna een eeuw later werd Verhulsts werk door de Amerikaanse onderzoeker Raymond Pearl (1879-1940) weer opgenomen. Sedertdien werd de ‘vergelijking van Verhulst’ met succes toegepast op diverse populaties, van drosophilae tot schapen, en zelfs op enkele menselijke populaties. De oplossingen zijn functies waarvan de grafiek een S-vormige kromme is, een zgn. ‘logistische kromme’. De oplossingen van de corresponderende differentievergelijking

n_k+1 = An_k - Bn²_k, k = 0, 1, ...,

hebben een veel gecompliceerder gedrag, en die maken haar momenteel tot één van de paradigma's van de ‘chaostheorie’.

De toegepaste analyse is ook verduidelijkt door Junius Massau (1852-1909), hoogleraar analytische mechanica en grafostatica te Gent. We danken aan hem de creatie van de ‘grafische integratie’, waarvan de toepassing zich uitstrekt tot de partiële differentiaalvergelijkingen. Hij was tevens een van de grondleggers van de ‘theorie der rekentafels’ of de ‘nomografie’, die tot doel heeft de numerieke berekeningen te vervangen door grafische tafels die in een oogopslag de resultaten geven. Massau's werken kregen een voorname plaats in de Cours de géométrie de l'Ecole polytechnique van Maurice d'Ocagne (1862-1938); Junius Massau is een van de meest geciteerde auteurs in het beroemde traktaat over praktische analyse van Friedrich Adolf Willers (1893-1959).

De buste van Junius Massau in de Aula van de Universiteit Gent ▪

▪ De meetkunde

De heropleving van de studie van de meetkunde in België in de eerste helft van de 19de eeuw was ondenkbaar zonder de bijdragen van Adolphe Quetelet (1796-1874) en Germinal Dandelin (1794-1847), beiden geboren uit een Franse vader en een uit onze streken afkomstige moeder. De militaire loopbaan van Dandelin, oud-leerling van de Ecole polytechnique, bracht hem tot de graad van kolonel. Quetelet was niet alleen statisticus, maar ook beurtelings dichter, literator, wiskundige, socioloog, historicus, fysicus, meteoroloog en astronoom. Hij exploreerde de grotten van Han in 1822 en stichtte in 1826 de Sterrenwacht van Brussel, die hij veertig jaar leidde. Als klasgenoten in het Lyceum van Gent startten beide meetkundigen hun samenwerking met het schrijven van een opera in één bedrijf op muziek van Charles Ots (1776-1845), getiteld Jean Second ou Charles-Quint dans les murs de Gand. De wiskundigen kunnen, achteraf gezien, alleen maar blij zijn dat deze poging zonder succes is gebleven.

In die tijd kon men nog denken dat de theorie der kegelsneden voltooid was. Toch werd ze tussen 1820 en 1822 vernieuwd door twee verhandelingen van Quetelet en Dandelin waarin met name werd gesteld dat de brandpunten van een snede van een rechte kegel door een vlak de contactpunten zijn

[p. 109]

van dat vlak en van de twee sferen ingeschreven in de kegel en rakend aan het vlak. Het theorema behoort tot een geheel van resultaten dat door de Franse wiskundige Théodore Olivier (1793-1853) in 1847 de ‘Belgische theorema's’ werd genoemd, een ‘nationalistische’ benaming - zeldzaam in de wiskunde - die nog steeds wordt gebruikt. Volgens Michel Chasles (1793-1880) was dit theorema de eerste constructie ooit van de brandpunten van de kegelsneden in de kegel. Henri Lebesgue (1875-1941) beaamde dit honderd jaar later: ‘de theorema's - naar mijn weten de enige genoemd naar een Natie - hebben gezorgd voor een nieuw wiskundig feit: de bepaling van de brandpunten en richtlijnen van het snijvlak van een omwentelingskegel; tegelijk hebben ze de middelen gegeven om het elementair onderwijs van de theorie der kegelsneden te vernieuwen, te vereenvoudigen, te verkorten en te verstevigen’.

Tussen 1823 en 1825 bestudeerde Quetelet de ‘brandvlakken’, omhulde krommen van lichtstralen uitgezonden vanuit een gegeven lichtbron en

Bernard Gaillot, Le géomètre. Brussel. Koninklijke Bibliotheek Albert I, Prentenkabinet ▪

Mémoire sur une nouvelle théorie des sections coniques dans le solide. Handschrift van Adolphe Quetelet over de kegelsneden. Brussel, Acadeémie royale de Belgique ▪

weerkaatst door een kromme. Dit verschijnsel kan men waarnemen in een kop koffie die voldoende wordt belicht. De krommen spelen een belangrijke rol in talrijke moderne wiskundige theorieën.

Samen met Garnier lanceerde Quetelet in 1824 Correspondance mathématique et physique, het eerste Belgisch tijdschrift dat volledig aan wis- en natuurkunde was gewijd. Als vast secretaris van de Académie royale de Belgique van 1835 tot 1874 introduceerde hij in 1833 het Bulletin de l'Académie royale de Belgique, dat model zou staan voor de bekende Comptes Rendus de l'Académie des Sciences de Paris.

Hoewel hij vooral bekendheid genoot als meetkundige, heeft Dandelin in 1826 een opmerkelijk

[p. 110]

werk gepubliceerd over de benadering van de oplossingen van numerieke vergelijkingen, waarin hij een in 1834 door de Rus Nicolas Lobatchewsky (1792-1856) en in 1837 door de Zwitser Carl Gräffe (1799-1873) opnieuw ontdekte methode ontwikkelde die nog steeds bekend is als de ‘methode van Dandelin-Gräffe’.

De technieken van Quetelet en Dandelin waren ingenieus maar elementair. Ze deden geen beroep op de analytische meetkunde, noch op de analyse. Hun manifest was ongetwijfeld de eerder vermelde verhandeling van Chasles, een antwoord op een vraag van de Académie royale de Belgique uit 1830. Het doel van deze verhandeling, zo schreef Chasles, was ‘aantonen dat de Meetkunde, die zelf al meer dan een eeuw lang vond dat ze machteloos was en afhing van de hulpmiddelen en verwezen-

Buste van Pierre-Germinal Dandelin, door Charles Van Oemberg. Brussel, Paleis der Academiën ▪

lijkingen van de algebraïsche Analyse, integendeel vatbaar was voor algemene principes en creatieve methodes zoals die van de Analyse’. Deze principes waren een handleiding voor de Belgische meetkundigen Jean-Baptiste Brasseur (1802-1868), François Folie (1833-1905), Constantin Le Paige (1852-1929) en François Deruyts (1864-1902).

Ons land bleef niet onaangeroerd door de debatten over de niet-euclidische meetkundes. Lange tijd had men geprobeerd het beroemde vijfde postulaat van Euclides (door een punt buiten een rechte gaat hoogstens één rechte evenwijdig aan de gegeven rechte) te bewijzen, totdat enkele geleerden het originele idee opvatten zich toe te leggen op de logische opbouw van een meetkunde die was gebaseerd op de negatie van dit postulaat. De publicaties van János Bolyai (1802-1860) en Nicolas Lobatchewsky in die richting verschenen net vóór de Belgische onafhankelijkheid.

De belangrijkste Belgische bijdragen in dit domein staan op naam van Joseph-Marie De Tilly (1837-1907), luitenant-generaal in de artillerie en commandant-directeur van de Koninklijke Militaire School. Ze dateren uit een periode waarin onderzoek naar niet-euclidische meetkunde nog gelijk stond met ketterij. De Tilly liet ze zelfs onvermeld in een uitgebreid rapport over de mathematische bijdragen dat hij opstelde naar aanleiding van het honderdjarig bestaan van de Académie royale de Belgique. De generaal-meetkundige deed elders het relaas over de totstandkoming van zijn ontdekkingen: ‘Ik had alle fundamentele formules van de nieuwe meetkunde gevonden zonder de naam van die Russische meetkundige te kennen en zonder te weten dat tot dan toe geen enkele meetkundige aan het postulaat had getwijfeld; maar ik moet toegeven dat ik er toen niet eens zelf aan twijfelde, en ik hoopte nog een contradictie in mijn formules te vinden. Lobatchewsky's werken bevestigden enkel dat het ijdele hoop was, maar ze leerden me niets nieuws inzake de belangrijkste formules’.

In 1878 nam De Tilly de notie afstand als eerste niet herleidbaar begrip en bewees hij dat de drie soorten meetkunde, de ‘riemannse’ (door een punt buiten een rechte gaat geen enkele rechte

[p. 111]

parallel met de gegeven rechte), de ‘euclidische’ en de ‘lobatchewskische’ (door een punt buiten een rechte gaan oneindig veel rechten parallel met de gegeven rechte) er uit kunnen worden afgeleid. Hij trachtte ook, zonder succes, te bewijzen dat er geen andere meetkundige systemen bestaan. De Tilly was ook een pionier in de ontwikkeling van een niet-euclidische mechanica. Zijn werk was een inspiratiebron voor Massau, Mansion, De Donder en de La Vallée Poussin. Deze laatste toonde aan dat de kinematische beschouwingen die De Tilly gebruikte om te bewijzen dat er slechts drie soorten meetkunde kunnen bestaan die met het gewone systeem de begrippen rechte en vlak gemeen hebben, kunnen worden vervangen door zuiver meetkundige axioma's.

De eerste bijdragen van Belgische mathematici tot de ‘infinitesimaalmeetkunde’ (vandaag spreekt men van differentiaalmeetkunde) waren bescheiden en beperkt in omvang. We onthouden echter dat Pagani in 1832 in de studie van ruimtekrommen zorgde voor de introductie van de triëder, gevormd door de tangens, de hoofdnormaal en de binormaal in een punt. Veel later zouden de Franse meetkundigen Jean Frenet (1847) en Joseph Serret (1851) hetzelfde doen. Men kan het betreuren dat de gekende triëder nog steeds universeel bekend staat onder de naam ‘triëder van Serret-Frenet’.

Alphonse Demoulin (1869-1947), hoogleraar te Gent, heeft zijn hele loopbaan gewijd aan de infinitesimaalmeetkunde. Hij volgde te Parijs les bij Gaston Darboux, bekend van Leçons sur la théorie des surfaces, en te Leipzig bij Marius Sophus Lie (1842-1899), de ontwerper van de theorie der continue groepen. Na eerdere pogingen van Ribaucourt, had Darboux de ‘methode van de mobiele triëder’ met succes ingevoerd en toegepast. Elie Cartan (1869-1951) heeft ze omgevormd tot een bruikbaar en heden onmisbaar werkinstrument voor de ijktheorieën in de fysica. De ‘mobiele triëder’ is een ingenieuze aanpassing van de coördinaatassen; in plaats van ze onbeweeglijk te houden, zoals in de analytische meetkunde, verbindt men aan ieder punt op de bestudeerde kromme of het bestudeerde vlak een passend assenstel, en bestudeert men achtereenvolgens de eigenschappen van

Joseph Marie De Tilly. Gravure door Georges Montenez, Brussel, Koninklijke Bibliotheek Albert I, Prentenkabinet ▪

de geometrische objecten tegenover deze mobiele assen en de verplaatsing van deze assen. Kort na de eeuwwisseling introduceerde Demoulin een pentasfeer met mobiele referentie (figuur gevormd door vijf, twee aan twee orthogonale sferen), en creëerde hij de ‘anallagmatische meetkunde’, waarin de conforme groep de voornaamste is. Demoulin toonde ook aan hoe men de methode van de mobiele triëder origineel kan gebruiken in een aan Arthur Cayley (1821-1895) ontleende versie van de euclidische meetkunde en in de projectieve meetkunde. Voor zijn werken over tripelorthogonale systemen kreeg hij in 1911 de Prix Bordin van het Institut de France, en in 1919 de tienjaarlijkse prijs voor zuivere wiskunde van de Belgische regering.

Elie Cartan, die niet veel citeerde, liet niet na Demoulin te vermelden in zijn beroemd werk over de mobiele triëder. De andere geciteerde auteurs zijn Darboux, Lie, Maurer, Vivanti, Cotton, Bianchi,

[p. 112]

Lucien Godeaux. Burijngravure door Jos. Bonvoisin, 1947. Brussel, Koninklijke Bibliotheek Albert I, Prentenkabinet ▪

Fubini, Cech, Eisenhart en Ado. In zijn Notice erkende de grote Franse meetkundige dat hij veel belang hechtte aan Demoulins werk: ‘Men weet wat een voordeel Darboux heeft gehaald uit het gebruik van de mobiele tripelorthogonale triëder in de studie van krommen en vlakken. Demoulin heeft Darboux' methode veralgemeend door in de conforme en de projectieve ruimte mobiele referentiesystemen te gebruiken. E. Cotton ... heeft een veel ruimere veralgemening aangewezen... Ik verbind mijn theorie van de structuur van de continue groepen aan een veralgemening van de theorie van de mobiele triëder, analoog aan die van E. Cotton’. Het bekend boek over projectieve differentiaalmeetkunde van Guido Fubini (1874-1943) en Eduard Cech (1893-1960) had een noot moeten bevatten met een samenvatting van Demoulins werken, maar de Belgische meetkundige had helaas geen tijd om ze te redigeren. Het boek bevat nochtans meerdere verwijzingen naar de werken van onze landgenoot. Alphonse Demoulin, die te Gent differentiaal- en integraalrekening, hogere analyse en hogere meetkunde onderwees, moest omwille van de volledige vernederlandsing van de universiteit in 1936 stoppen met lesgeven; in 1939 werd hij in de grootste stilte toegelaten tot het emeritaat.

Een andere grote Belgische meetkundige was Lucien Godeaux (1887-1975), wiens lange carrière de hier behandelde periode overstijgt. Hij ontdekte de ‘algebraïsche meetkunde’, die zijn voorkeur genoot, in een verhandeling van Federigo Enriques (1871-1946), waarna hij naar Bologna trok om les te volgen bij de meester zelf. Hij definieerde de discipline als volgt: ‘De projectieve meetkunde is vatbaar voor een heel verschillende extensie, verkregen door uitbreiding van het concept homografie. Veronderstellen we voor meer eenvoud de gewone ruimte S₃. Als twee punten x en x' homoloog zijn in een homografie, dan zijn de coördinaten van het ene punt evenredig aan de eerstegraadspolynomen met betrekking op de coördinaten van het andere. Kan men de voorwaarde dat het polynomen van de eerste graad moeten zijn, laten vallen en toch overeenkomsten bekomen die het algebraïsche en een-eenduidige karakter van de homografieën behouden?’ De ‘birationale transformaties’ of ‘transformaties van Cremona’ (een eenvoudig voorbeeld in het vlak is de inversie tegenover een cirkel) geven een bevestigend antwoord op deze vraag.

Het is erg moeilijk om Godeaux' bijdrage tot de algebraïsche meetkunde en de projectieve differentiaalmeetkunde kort te bespreken; ze is door hemzelf uitstekend geanalyseerd in een Notice. Godeaux was de initiator en belangrijkste ontwerper van de theorie van de involuties op algebraïsche oppervlakken. De omvang van zijn wetenschappelijk oeuvre is vrijwel uniek in de geschiedenis van de wiskunde: circa 1.200 titels - notities en bijdragen in binnen- en buitenlandse wetenschappelijke tijdschriften, monografieën, didactische, vulgariserende en wetenschapshistorische werken. Elk deel van het Bulletin de la Classe des Sciences de l'Aca-

[p. 113]

démie royale de Belgique tussen 1921 en 1975 bevat minstens één bijdrage van Godeaux, en van de eerste 44 delen van het Bulletin de la Société royale des Sciences de Liège, bevatten alleen de delen 23, 29 en 36 geen tekst van Godeaux, wat ruimschoots wordt gecompenseerd door de gemiddeld vijf à zes artikels in de andere delen.

Ook al heeft de vooruitgang van de abstracte algebra, de topologie en de theorie van de functies van meerdere complexe veranderlijken het aanzien van de algebraïsche meetkunde sterk gewijzigd in vergelijking met de Italiaanse traditie waardoor Godeaux werd beïnvloed, toch worden de werken van onze landgenoot nog altijd geciteerd in recente publicaties, en staan de ‘oppervlakken van Godeaux’ nog steeds centraal in het hedendaags onderzoek.

Een bespreking van de werken van Lucien Godeaux mag niet voorbijgaan aan twee vulgariserende boekjes over meetkunde. Het woord vooraf van het tweede begint met de woorden: ‘We hebben getracht het boek te schrijven dat we zelf hadden willen lezen toen we twintig waren. Moge het van enig nut zijn!’ De wens van de auteur is ongetwijfeld uitgekomen; zijn werk lag aan de basis van meer dan één wiskundige roeping. Lucien Godeaux heeft veel artikels geredigeerd over wetenschapsgeschiedenis, dikwijls in het kader van zijn activiteiten voor de Classe des Sciences van de Academie royale de Belgique, waarvan hij 45 jaar lid was. Een dun boekje, gepubliceerd tijdens de Tweede Wereldoorlog, is het eerste en enige overzichtswerk over de geschiedenis van de wiskunde in België sinds Quetelet - een reeks korte essays, geschreven naar aanleiding van één of andere viering van de onafhankelijkheid of van een instelling buiten beschouwing gelaten.

Naast zijn imposant oeuvre als onderzoeker staat een rijke onderwijscarrière, eerst aan de Koninklijke Militaire School, vervolgens aan de universiteit van Luik. Lucien Godeaux onderwees er wiskundige analyse en algebra, alsook analytische, projectieve, infinitesimaal- en hogere meetkunde. Hij heeft ook nog tijd en energie gevonden om in 1921 samen met De Donder en Alfred Errera (1886-1960), hoogleraar aan de Université libre de Bruxelles en een eclectisch wiskundige, het Belgisch Wiskundig Genootschap te stichten, in 1948 gevolgd door het Belgisch Centrum voor Wiskundig Onderzoek, dat hij leidde tot in 1966. Het BCWO organiseerde tussen het einde van de jaren '40 en het begin van de jaren '70 internationale congressen van hoog niveau, wat de ontwikkeling van de wiskunde in ons land heeft gestimuleerd. Godeaux, een ambassadeur van de Belgische wiskunde, was doctor honoris causa van meerdere buitenlandse universiteiten. Hij kreeg in 1940 de Prix Poncelet van de Académie des Sciences de Paris en in 1950 de tienjaarlijkse prijs voor zuivere wiskunde.

Lucien Godeaux. La Géométrie, Luik, 1931 Luik, Centre d'Histoire des Sciences et des Techniques ▪

[p. 114]

▪ De waarschijnlijkheidsrekening en de statistiek

Het belang van Quetelet voor de ontwikkeling van de toepassingen van de statistiek op de sociale wetenschappen wordt algemeen erkend, alsook zijn rol in het onderwijs en de vulgarisering van deze discipline. Maar men moet toegeven dat deze Belgische geleerde niet op een betekenisvolle wijze heeft bijgedragen tot de ‘wiskundige statistiek’. Het volgende citaat verwoordt de mening van Gnedenko en Sheinin: ‘Het is onmogelijk zich een beeld te vormen van de ontwikkeling van de bevolkingsstatistiek in de 19de eeuw zonder de werken te bestuderen van de meetkundige, astronoom en meteoroloog Lambert-Adolphe-Jacques Quetelet (1796-1874). Deze waren ingegeven door de ideeën van Laplace, Poisson en andere geleerden, zoals J.B. Fourier, die een statistische beschrijving gaf van Parijs en van het Departement van de Seine (1821-1829). Ofschoon hij op het gebied van de wetenschap zelf niets duurzaams naliet, was Quetelet een talentvol vulgarisator van de statistiek die de belangstelling van het Europese publiek wist te vatten. Quetelet was voorzitter van de Belgische Centrale Commissie voor Statistiek en organisator van het eerste internationaal congres voor statistiek’.

Ook Karl Marx (1818-1883) had zo zijn eigen idee over het statistisch oeuvre van Quetelet: ‘In het verleden is hij erg nuttig geweest; hij bewees dat alle ogenschijnlijk wisselvallige gebeurtenissen uit het sociale leven een intrinsieke noodzakelijkheid bezitten, te wijten aan hun periodieke recurrentie en hun periodiek gemiddelde. Nochtans is hij er nooit in geslaagd deze noodzakelijkheid te interpreteren. Hij boekte geen enkele vooruitgang; hij stelde zich tevreden met het uitbreiden van zijn waarnemingen en berekeningen’.

De Franse wiskundige Joseph Bertrand (1822-1900) trok Quetelets concept van de ‘gemiddelde mens’ in het belachelijke: ‘In het lichaam van de gemiddelde mens plaatst de Belgische auteur een gemiddelde ziel. Men moet, om de morele kwaliteiten samen te vatten, 20.000 karakters samensmeden tot één enkel. De type-mens kent dus hartstocht noch ondeugd, is dwaas noch moedig, is onwetend noch geleerd, is meestal ingedommeld tussen slaap en waakzaamheid, twijfelt steeds tussen ja en nee; kortom hij is middelmatig in alles. Na 38 jaar het gemiddelde rantsoen te hebben gegeten van een gezonde soldaat, zou hij sterven, niet van ouderdom, maar van een gemiddelde ziekte die de statistiek bij hem zou vaststellen’. In 1949 zou een andere Franse wiskundige, Maurice Fréchet (1878-1973), de mogelijkheden van de moderne statistiek gebruiken om het concept van Quetelet te herwaarderen.

Quetelet schreef ook vulgarisatiewerken over de waarschijnlijkheidstheorie. Het is niet verwonderlijk dat de waarschijnlijkheidsrekening en de theorie van de waarnemingsfouten een belangrijke plaats hebben gekregen in het Belgisch hoger

Adolphe Quetelet, Congrès international de statistique, 1873, frontispice. Brussel, Koninklijke Sterrenwacht van België ▪

[p. 115]

onderwijs. Hoewel onze geleerden in de hier behandelde periode geen fundamentele bijdragen hebben geleverd, zijn toch enkele geïsoleerde notities (De Tilly, Liagre, Catalan, Mansion, de La Vallée Poussin) en verhandelingen gerealiseerd. De vroegste uitgave was ongetwijfeld die van Jean-Baptiste Liagre (1815-1891), bestemd voor de leerlingen van de Koninklijke Militaire School. Vooral het praktische deel is interessant. Antoine Meyers cursus aan de universiteit van Luik werd na zijn dood gepubliceerd door zijn opvolger François Folie, en vertaald in het Duits. Ook Paul Mansion, die te Gent Emmanuel-Joseph Boudin (1820-1893) opvolgde in de leerstoel waarschijnlijkheidsrekening, publiceerde de cursus van zijn voorganger. Edouard Goedseels (1857-1928), administrateur-inspecteur van de Sterrenwacht en hoogleraar te Leuven, verwerkte zijn persoonlijke ideeën over de theorie van de waarnemingsfouten en de methode van de kleinste kwadraten in meerdere werken.