Geschiedenis van de wetenschappen in België. 1815-2000

[p. 90]

Lambert-Adolphe-Jacques Quetelet, door Jean-Baptiste Madou, lithografie van P. Dagobert, 1839, Brussel. Koninklijke Bibliotheek Albert I, Prentenkabinet ▪

[p. 91]

4 Adolphe Quetelet, een boegbeeld van de wiskunde
Theodore M. Porter

Lambert-Adolphe-Jacques Quetelet (1796-1874) was de leider van de 19de-eeuwse beweging die ijverde voor het kwantificeren van de wetenschappen. Hij was toonaangevend in de statistiek, een nieuwe sociale wetenschap waarvan hij zelfs de stichter kan worden genoemd. Hij droeg tevens bij tot de herleving van de Brusselse Academie, waar het onderzoek het accent van zijn eigen belangstelling kreeg.

Quetelet werd geboren in Gent en groeide op onder Frans bewind als leerling aan een Frans lyceum. Later schreef hij met waardering over de waardigheid en het respect die de wetenschappen onder Napoleon te beurt vielen, maar als jongeman was hij eerder een romanticus, meer verknocht aan poëzie en kunst dan aan wetenschap. Kort na de Franse nederlaag aanvaardde hij een opdracht als wiskundeleraar in een college opgericht door de regering van de nieuwe Verenigde Nederlanden. Daarna studeerde hij wiskunde aan de Gentse universiteit onder de wiskundige Jean-Guillaume Garnier (1760-1840). Hij was een van de eerste wetenschappers die onder het nieuwe politieke bewind maturiteit verwierf, en hij was zeker een van de meest ambitieuze. Hij geloofde dat de wetenschappen in de Belgische provincies konden tot bloei gebracht worden met de hulp van de overheid. In het begin van de jaren 1820 had hij een gunstig antwoord gekregen op zijn verzoek te Brussel een sterrenwacht te bouwen. Zelf was hij de meest geschikte kandidaat om dit observatorium te leiden. In 1823 mocht hij naar Parijs gaan om er te leren hoe dit moest worden verwezenlijkt.

Later vertelde hij hoe hij, in Parijs aangekomen zonder ook maar een aanbevelingsbrief, niettemin hartelijk werd onthaald door de astronoom Alexis Bouvard (1767-1843). Al gauw werd hij voorgesteld aan de grote figuren van de Franse wetenschap, onder wie Pierre-Simon Laplace (1749-1827) en Joseph Fourier (1768-1830). Bouvard leerde hem omgaan met wetenschappelijke instrumenten en de kunst van het observeren. Laplace en Fourier hadden voor hem een meer diepgaande en algemene betekenis. Zij toonden de weg naar de kwantificering van de wetenschappen door toepassing van de waarschijnlijkheidsrekening. Overtuigd dat de waarschijnlijkheidsrekening een hulpmiddel kon zijn voor de wetenschappen - zowel voor de studie van de natuur als voor de studie van de samenleving - keerde de jonge wiskundige naar Brussel terug.

Het proefschrift van Adolphe Quetelet. Dissertatio mathematica inauguralis de quibusdam locis geometricis, nec non de curva focali. Gent, 1819. Brussel, Koninklijke Sterrenwacht van België ▪

[p. 92]

Zelfs vóór zijn reis naar Parijs had hij reeds betoogd dat vooruitgang in de wetenschap kon worden bereikt via een collectieve onderneming. Er zijn veel fenomenen, zo argumenteerde hij, die door hun variatie en complexiteit ongeschikt zijn om door individuele onderzoekers te worden bestudeerd. Hij wilde vooral de kwantitatieve studie van de natuurlijke historie bevorderen. Hij trachtte niet zozeer de wereld door middel van laboratorium-proeven te begrijpen, maar wel door rechtstreeks metingen en observaties te doen op de natuurlijke

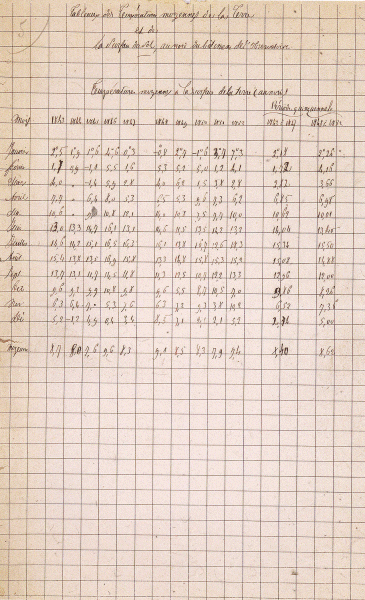
Tabel met de gemiddelde temperaturen van de bodem aan de noordkant van het gebouw van de Sterrenwacht handschrift van A. Quetelet. Brussel, Académie royale de Belgique ▪

wereld, door waar het mogelijk was te meten en te tellen, en met behulp van de wiskunde te zoeken naar patronen in de getallenreeksen. Dit soort onderzoek was van de jaren 1820 tot de jaren 1850 wijdverspreid. De wetenschapshistorica Susan Faye Cannon noemde dit type wetenschapsbeoefening ‘humboldtiaans’ naar de Duitse geleerde Alexander von Humboldt (1769-1859), maar niemand was er meer in bedreven of meer aan verknocht dan Quetelet.

Zijn eigen belangstelling ging vooral naar periodieke verschijnselen: de getijden, het weer, de bloeitijd van planten. Deze aanpak zette hem ook aan te zoeken naar periodiciteit waar het minder voor de hand lag, zoals in het aardmagnetisme, en ook in menselijke aangelegenheden. Hij werd ook toonaangevend in kwantitatieve studies waarin periodiciteit geen rol speelde, zoals in de voorbereiding van sterrenkaarten. Quetelet was een leider in de internationale organisatie van dergelijke metingen. Hierin stond hij dichter bij de Britten, inzonderheid zijn vriend John Herschel (1792-1871), en de Duitsers, dan bij de Fransen, die minder enthousiast waren over dergelijke internationale samenwerking.

Na de Belgische onafhankelijkheid in 1830 werd het kwantitatief meten op grote schaal een centraal onderdeel van wat we een nationale wetenschapsstijl kunnen noemen, hoewel het uiteraard geenszins een uniek Belgisch gegeven was. Quetelet betrok zijn collega's en zijn eigen studenten bij dit werk. Hierin ligt misschien een verklaring voor het feit dat slechts weinigen van hen een onafhankelijke reputatie verwierven, en dat België in de 19de eeuw niet als leidinggevende wetenschapsnatie naam heeft gemaakt. Toch bekeek Quetelet de verwezenlijkingen van de Academie met fierheid. Hij bracht ze meermaals in herinnering in de ‘éloges’ die hij schreef als vaste secretaris van de Académie royale de Belgique, en in twee historische werken, gedeeltelijk op deze ‘éloges’ gebaseerd en laat in zijn leven gepubliceerd. Deze boeken, Histoire des sciences mathématiques chez les Belges en Sciences physiques et mathématiques chez les Belges au commencement du XIX^e siècle, vormen samen als het ware een collectieve autobiografie, hoewel geschreven - en dat is veelbetekenend - door een enkele auteur.

[p. 93]

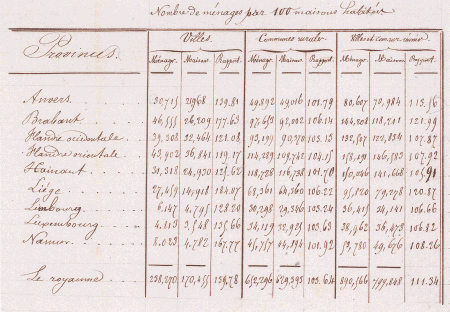
Tabel met het aantal huishoudens per honderd bewoonde woningen, handschrift van A. Quetelet. Brussel, Académie royale de Belgique ▪

Achteraf gezien hadden Quetelets wetenschappelijke verwezenlijkingen niet zozeer betrekking op de natuurwetenschappen, dan wel op de humane en de sociale wetenschappen. Op basis van zijn wetenschappelijke productie en het groot enthousiasme waarvan hij in zijn geschriften blijk gaf, mag men de wetenschap van de samenleving redelijkerwijs als zijn belangrijkste interessegebied aanduiden. Misschien omdat de term ‘statistiek’ niet langer wordt gebruikt in de betekenis van een maatschappijwetenschap, wordt hij veel minder dan Auguste Comte (1798-1857) beschouwd als de grondlegger van de sociologie, hoewel de statistiek minstens tot in de jaren 1880 in grotere kring als maatschappijwetenschap bij uitstek werd erkend, meer dan de toenmalige sociologie of de antropologie. Uiteraard heeft Quetelet niet op zijn eentje de statistiek als menswetenschap uitgevonden. Hij kon terugvallen op het werk van mensen als Condorcet (1743-1794), die pleitte voor de wiskundige waarschijnlijkheidsrekening als basis van een wetenschap van verkiezingen en jury's in de late 18de eeuw, en op Laplace, wiens Essai philosophique sur les probabilités aanspoorde tot het gebruik van kwantitatieve berekeningen in de studie van maatschappelijke verschijnselen, zoals dat reeds zijn nut had bewezen in de fysica.

Comte en de volgelingen van Saint-Simon, door wie hij zich liet inspireren, namen het voortouw van een beweging die in een uitermate troebele periode van de Europese geschiedenis een maatschappijwetenschap wilde construeren. Quetelet keek ook vol bewondering naar Thomas Robert Malthus (1766-1843), auteur van een controversiële studie over het bevolkingsvraagstuk, waarvan de latere edities uitgebreide statistische gegevens bevatten. Meer algemeen was de 19de eeuw een periode waarin cijfers over de politieke en sociale toestand voor het eerst overvloedig, betrouwbaar en publiek beschikbaar werden. Quetelet zelf had een prominent aandeel in de organisatie van de officiële statistiek in België. De Belgische administratieve vorm van een centrale statistische commissie werd overal bewonderd en in enkele gevallen door andere Europese staten geïmiteerd. Zijn invloedrijk werk over misdaad, bevolkingstoename, prijzen, en over geboorten, overlijdens en huwelijken, zou niet mogelijk zijn geweest zonder de

[p. 94]

beschikbaarheid van documenten zoals de Franse compilaties van criminele en militaire statistieken die vanaf de jaren 1820 werden gepubliceerd, en de bevolkingstellingen, door de belangrijkste landen van Europa en Noord-Amerika ingevoerd tussen ca. 1790 en 1830.

De plotselinge toename van het tellen en meten in het humane veld in Quetelets tijd kan niet enkel aan zijn invloed worden toegeschreven. Hij onderscheidde zich eerder als meest invloedrijk woordvoerder van de statistiek als ‘wetenschap’, uitgebreid steunend op de wiskunde en gemodelleerd naar de hemelmechanica. Hij bedacht enkele ambitieuze namen voor deze wetenschap: eerst, in 1831, ‘sociale mechanica’, en dan, als ondertitel van zijn succesrijk boek uit 1835, ‘sociale fysica’. Geen van deze labels kende veel bijval. De naam van deze maatschappijwetenschap bleef ‘statistiek’, een studierichting die meer werd geassocieerd met administratie en hervorming dan met fysica en biologie. Hijzelf was zich terdege bewust van de noodzakelijkheid van een bureaucratische statistiek, en hij maakte er zelfs propaganda voor, maar tegelijk was hij er ontevreden mee. Statistiek, zo betoogde hij, moest een zaak zijn van geleerden, van getrainde mathematici zoals hijzelf. Zij moesten de waarschijnlijkheidsrekening toepassen op hun cijfers. Dit zou hen helpen vreemde fouten en beschamende blunders te vermijden, die volgens hem al te vaak opdoken in de eigentijdse literatuur over sociale cijfers. Zijn kritiek was niet helemaal overtuigend, want zelf gebruikte hij de waarschijnlijkheidsrekening slechts zelden in zijn statistische geschriften over misdaad, zelfmoord, huwelijken en mortaliteit. Niettemin was zijn geloof in een statistische wetenschap oprecht, wanneer zij werd beoefend door wetenschappers die konden opereren buiten en boven de beperkingen van de politieke belangen en de bureaucratische beslommeringen.

Quetelets statistische geschriften weerspiegelden de typische bezorgdheid over misdaad en sociale instabiliteit die de basis vormde van vele liberale pogingen om de patronen of wetmatigheden van de samenleving op het spoor te komen. Waarschijnlijk is het niet toevallig dat zijn statistische ambities vooral gestalte kregen in de onmiddellijke

Oproep voor een volkstelling in Brussel, 1842. Brussel, Académie royale de Belgique ▪

nasleep van de revolutie van 1830. In een ander revolutiejaar, 1848, publiceerde hij uittreksels van een kort essay over de analogieën tussen fysische en morele wetten dat hij, naar eigen zeggen, had opgesteld in een vorige periode waarin de politieke gemoederen waren opgelaaid. Het volledige handschrift bevindt zich nu in het Queteletfonds. Hierin betoogde hij dat aangezien de fysische wereld geregeerd wordt door zo'n bewonderenswaardige wetten, er ook behoudswetten moeten zijn die de morele wereld besturen. Het jaar daarop, tenminste als dit manuscript inderdaad werd geschreven in 1830, begon hij een ‘sociale mechanica’ te bepleiten, waarin hij tal van analogieën uit de fysica, zoals kracht, evenwicht, afwijking en fout verwerkte.

Wetenschappelijke wetmatigheden waren inderdaad een van zijn grootste bekommernissen. In 1829 drukte hij zijn verbazing uit over de nieuwe Franse misdaadstatistiek, die scheen aan te geven dat sommige misdaden elk jaar in gelijke aantallen worden begaan. Hij vroeg zich af of het menselijk gedrag werd gedreven door een of andere mysterieuze voorbeschikking. Rond 1830 waren dit soort regelmatigheden het fundament van zijn sociale wetenschap geworden.

[p. 95]

Er bleef iets paradoxaals aan het bepalen van ‘misdaadwetten’. Letterlijk genomen is misdaad uiteraard juist een overtreding van de wet. Ook op moreel vlak schijnen moorden en zelfmoorden eerder het resultaat van onbeheerste passies, die het halen op de gangbare rationaliteit. En wie kan ooit hopen de drijfveren te doorgronden die een getormenteerde ziel ertoe kunnen aanzetten zijn eigen leven of dat van een ander te beëindigen? Op het niveau van het individu is misdaad een thema voor romanschrijvers, detectives en priesters, wier kennis onvolledig blijft, zelfs wanneer zij een groot gevoel voor intuïtie hebben. Op het niveau van de samenleving worden deze onzekerheden daarentegen op een of andere manier omgezet in een onveranderlijke regelmaat, die wetenschappelijk kan bestudeerd worden. Quetelet noemde ze, met enige overdrijving, sociale wetten, volstrekt vergelijkbaar met de mechanische wetten die gelden voor de bewegingen van hemellichamen. Hij vroeg zich zelfs af of dit soort orde in de menselijke aangelegenheden verenigbaar kan zijn met de traditionele doctrines van de menselijke wil.

Hij besloot dat er uiteindelijk geen tegenstrijdigheid was en dat individuen een beperkte mate van vrijheid behielden, die slechts verloren leek te gaan in de grote massa. Maar deze nieuwe benadering dreigde de aandacht af te wenden van het individu. Bij statistiek kwam het erop neer afstand te nemen, te kijken naar de oceaan en niet naar de golven. Quetelet vroeg zich af of het zin had individuen verantwoordelijk te stellen voor de criminaliteit in de samenleving. Want, wat ook van de vrijheid van een individu mag worden gezegd, het misdaadniveau in een samenleving kan niet worden begrepen in termen van vrije acties van autonome personen. Het is eerder een sociaal fenomeen, dat een verklaring vraagt in collectieve eerder dan in persoonlijke termen. Elke samenleving heeft andere misdaadpatronen. De misdaadfrequentie varieert naargelang de dag, het seizoen, het klimaat. Zij is ook beïnvloed door wettelijke en juridische structuren, door onderwijsvoorzieningen en door godsdienst. Quetelet zei niet dat de staten hun gevangenissen moesten sluiten, maar hij betwijfelde of de verantwoordelijkheid voor de criminaliteit in de eerste plaats kon worden gelegd bij individuele misdadigers. Niet strengere straffen maar sociale hervormingen leken hem de meest redelijke strategie om de misdaad te bestrijden.

Zijn intellectuele stellingname had dus een morele inslag. Hij hielp mee een statistische wereld te scheppen van massafenomenen, misdaadcijfers en alfabetiseringsgraden. Consequent beschouwde hij het collectieve als iets dat in zekere zin meer reëel, of ten minste meer vatbaar was voor wetenschappelijk begrip dan het individu. Zijn publicaties

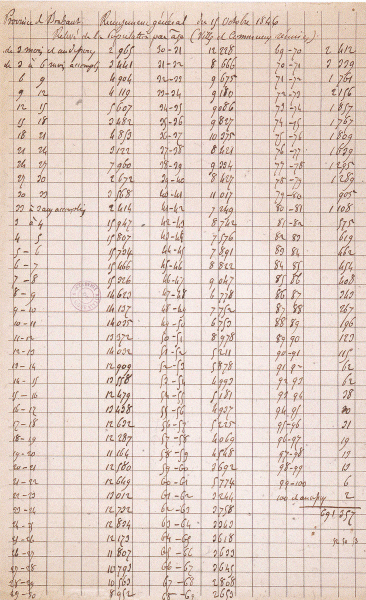
Tabel over de volkstelling van 1846. De bevolking per leeftijd voor alle steden en gemeenten in de provincie Brabant handschrift van A Quetelet. Brussel, Académie royale de Belgique ▪

[p. 96]

stonden niet bol van mannen en vrouwen van vlees en bloed, maar van groepen en abstracte concepten. Aan een ervan dankt hij zijn grote bekendheid: de gemiddelde man. Dit wezen, zo argumenteerde hij, is het eigenlijke studieobject van de sociale wetenschap. De gemiddelde man is een eenvoudige constructie van metingen, gaande van lichamelijke afmetingen tot zedelijke en immorele daden. De grootte van de gemiddelde man is bijvoorbeeld gelijk aan de gemiddelde grootte van alle mannen in de samenleving. (Vrouwen, voor wie hij weinig aandacht had in zijn statistische geschriften, werden gekarakteriseerd door andere gemiddelde waarden). Het morele karakter van de gemiddelde man was misschien een wat moeilijker te vatten begrip. Quetelet gebruikte hier de ‘gemiddelde neigingen’ als kenmerk; als één individu op honderd een diefstal beging in een bepaald jaar, dan zou de gemiddelde man een neiging tot misdaad hebben gelijk aan één op honderd. Dat maakte van de gemiddelde man een eerder oppervlakkig en onopvallend persoon, en sommige critici verwierpen hem als de verpersoonlijking van de middelmatigheid. Quetelet evenwel prees de gemiddelde man als vertegenwoordiger van de samenleving, het

Le vrai statisticien, voorgedragen tijdens een banket van de Commission centrale de Statistique, 13 maart 1865. Brussel, Académie royale de Belgique ▪

model van het ware, het mooie en het goede. In de gemiddelde man smolten alle uitersten weg, en wat overbleef waren de kenmerken van een hele samenleving. De gemiddelde man is het deugdelijke midden tussen twee ondeugdelijke extremen. Hij incorporeert een regelmaat en stabiliteit die gewone individuen missen.

De doctrine van de gemiddelde man was kenmerkend voor Quetelets sociale wetenschap in zijn meest abstracte en metaforische vorm. Zij werd ruim bekritiseerd door zijn opvolgers, zelfs door diegenen die aan hem het meest schatplichtig waren. Hij werd er, enigszins terecht, van beschuldigd de samenleving enkel te zien als een geheel, een verzameling van individuen die allen fundamenteel gelijk zijn. Hij kreeg ook het verwijt, ditmaal tegen alle bewijzen in, dat hij een sociaal determinisme bepleitte dat hervormingen onmogelijk maakte. Kritieken als deze waren vooral te horen in Duitsland, waar het project om de statistiek om te vormen tot een universitaire en academische wetenschap de meeste successen boekte. Quetelets sociale fysica, gemodelleerd naar de hemelmechanica en gebaseerd op analogieën met fysische wetten en concepten, kon zich niet doorzetten in de sociale wetenschappen. Niettemin werd de kwantitatieve analyse van sociale fenomenen met de bedoeling regelmatigheden te vinden en te verklaren zeer snel een belangrijke vorm van sociaal onderzoek, en dat is zo gebleven. Quetelet droeg bij tot deze zeer praktische activiteit, niet alleen door zijn voorbeeld, maar ook door zijn inspanningen als organisator. Vanaf 1853 organiseerde hij een reeks statistische congressen - het eerste kwam samen in Brussel - om te beraadslagen over de problemen van de officiële statistiek, en om te trachten de kwantitatieve gegevens zo nuttig mogelijk te maken voor het onderzoek van de oorzaken. Het meest kenmerkende streven van de statistische congressen was wellicht de harmonisering van statistische categorieën, zodat dezelfde cijfers hetzelfde zouden betekenen in de rapporten van verschillende naties. Deze uniformiteit bleek echter moeilijk te verwezenlijken. De afgezanten kwamen snel tot de vaststelling dat bijvoorbeeld misdaadcijfers niet echt vergelijkbaar konden zijn tenzij de ver-

[p. 97]

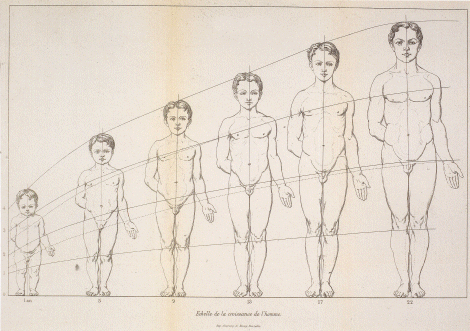
Groeischaal van de man. In: A. Quetelet, Anthropométrie ou mesure des différentes facultés de l'homme. Brussel-Leipzig-Gent, 1871. Brussel, Koninklijke Sterrenwacht van België ▪

schillende landen ook dezelfde wetten aannamen. Toch droegen deze administratieve activiteiten bij tot de ontwikkeling van de vergelijkende statistiek, en daarbij waren Quetelets inspanningen van zeer grote invloed.

Quetelet speelde ook een belangrijke rol in de ontwikkeling van een wiskundige statistiek. Als wiskundige was Quetelet niet erg origineel. De formules in zijn populaire werken over waarschijnlijkheidsleer waren meestal ontleend aan werken van vooraanstaande mathematici zoals Laplace en Poisson. De meeste van zijn ideeën over de toepassing van de waarschijnlijkheidsrekening hadden hun wortels in de praktijk van de foutentheorie, die sinds het begin van de 19de eeuw meer en meer gebruikelijk was geworden in de astronomie, de geodesie en andere domeinen waarin metingen centraal stonden. De belangrijkste nieuwigheid die Quetelet introduceerde was deze methode uit te breiden tot een geheel ander domein. De foutentheorie was tot dan toe heel specifiek geassocieerd met metingen en foutbeheersing. Astronomen namen redelijkerwijs aan dat de planeten of asteroïden die zij bestudeerden een reële positie innamen en in een reële baan bewogen. Als hun metingen min of meer afwijkingen vertoonden, wat altijd wel het geval was, dan moest dit te wijten zijn aan meetfouten in de waarnemingen. De numerieke analyse had tot doel de positie of de baan te bepalen die het best verenigbaar was met de observaties.

[p. 98]

In 1805 vond Adrien-Marie Legendre (1752-1833) een oplossing, de zogenaamde ‘methode van de kleinste kwadraten’. Men berekende het punt of de lijn waarbij de som van de kwadraten van de afwijkingen van de meetwaarden t.o.v. deze lijn minimaal was. In het meest eenvoudige geval, wanneer de astronoom de waarnemingen voor een enkel punt wilde corrigeren, was deze methode van de kleinste kwadraten niets anders dan het berekenen van de gemiddelde waarde.

Quetelet zag de sociale statistiek altijd als een analogie met hemelse data. De relatie tussen de gemiddelde man en de diversiteit van reële mannen in een bepaalde regio, was, volgens hem, zoals die tussen de reële positie van een ster en een cluster min of meer afwijkende meetwaarden. Op basis van deze analogie, en gesteund door enkele antropometrische gegevens, concludeerde hij in 1844 dat de ‘foutencurve’ toegepast door Laplace en door Carl Friedrich Gauss (1777-1855) op astronomische kwantiteiten ook gold voor de variaties van reële mensen rond de gemiddelde waarde. Op die manier droeg hij ertoe bij om de techniek van de foutencurve om te zetten in de zogenaamde ‘Gaussof normaalverdeling’. Waarschijnlijkheid werd zo van een maat die de grenzen van de menselijke kennis aangaf, een instrument voor het onderzoek van variabiliteit in de natuurlijke en sociale wereld. Quetelets ideeën vormden het startpunt voor de Engelse biometrische school, opgezet door Francis Galton (1822-1911) en Karl Pearson (1857-1936), die de wiskundige statistiek ontwikkelden tot een geheel van instrumenten voor de analyse van gegevens in tal van domeinen.

Quetelet zelf claimde nooit enige filosofische originaliteit voor dit werk, voor een deel omdat hij het als een natuurlijk uitvloeisel zag van de theorie van de ‘kleinste kwadraten’. Zijn hardnekkigheid in het beschouwen van variatie als een equivalent voor fout was gedeeltelijk verantwoordelijk voor de latere kritiek van Duitse statistici en Franse mathematici, die hem volstrekt onfilosofisch vonden. Zijn visie was inderdaad vooral praktisch, een programma voor georganiseerde waarnemingen dat zou toelaten het complexe statistische domein begrijpelijk te maken in dezelfde termen die Laplace en Newton hadden toegepast op de hemelmechanica. Min of meer buiten zijn bedoelingen om hielp hij mee aan de creatie van een nieuw soort wetenschap, gebaseerd op sleutelbegrippen als kans en variatie, en zoekend naar collectieve verbanden die, althans in praktijk, niet konden worden herleid tot wetmatige relaties tussen individuen.