Het denken van den schaker

D. Het Bewijsschema in een Objectief Oplosbare Stelling: zet W₁ is de beste.

§ 9. De tweedeelige structuur van het bewijsschema.

Voor het gemak neem ik aan, dat wit aan zet is en dat er maar één oplossing is, n.l. W₁; dus niet twee of meer aantoonbaar gelijkwaardige voortzettingen. Dan moet dus worden aangetoond, dat wit d.m.v. 1.W₁ tegen elk tegenspel van zwart betere resultaten kan bereiken dan met behulp van andere eerste zetten W₂, W₃, .... W _n bij juiste beantwoording door zwart mogelijk is.

Met behulp van de in § 8 ingevoerde ‘cijfers’ kan nu gemakkelijk worden

[p. 23]

aangetoond, dat een volledig bewijs uit twee deelen moet bestaan. Immers, te bewijzen is:

1)	Door 1.W1 te spelen bereikt wit tegen elk tegenspel van zwart minstens een zeker minimum resultaat, b.v. ‘8’.
2)	Na alle andere zetten: 1.W2, 1.W3, .... 1.W n kan zwart, tegen elk tegenspel van wit, bewerkstelligen, dat wit met minder genoegen moet nemen: wit bereikt b.v. maximaal ‘6’.

Het eerste deel, betreffende het gunstige minimum-resultaat van den zet W₁ zal ik het positieve deel van het bewijs noemen; het tweede deel, betreffende het minder gunstige maximum-resultaat van de andere eerste zetten is dan het negatieve deel.

In het positieve deel moet op iederen zet van zwart door wit één afdoend antwoord kunnen worden gegeven, terwijl omgekeerd in het negatieve deel bij iederen zet van wit telkens één repliek van zwart behoort. Meer dan één afdoende repliek is voor het bewijs overbodig, m.a.w. in het positieve deel kunnen we alleen vertakkingen verwachten wanneer zwart moet spelen, in het negatieve deel alleen als wit aan zet is.

Het positieve deel - ‘na 1. W₁ bereikt wit minstens “8”’ - verloopt dus als volgt:

Na den zet 1. W₁ heeft wit op alle antwoorden van zwart (1...., Z₁₁, 1...., Z₁₂, 1...., Z₁₃ enz.) telkens de bijbehoorende replieken 2. W₁₁, 2. W₁₂, 2. W₁₃ gereed; heeft zwart dan b.v. na 2. W₁₂ weer de antwoorden: 2...., Z₁₂₁ en 2...., Z ₁₂₂, enz. ter beschikking, dan volgen daarop resp. de replieken 3. W₁₂₁ en 3. W₁₂₂ enz. Tenslotte komt aan alle vertakkingen op een zeker punt een eind, op het punt namelijk, waarop een stelling ontstaan is, die zich leent tot een ondubbelzinnige, objectieve beoordeeling. Het einde van iedere variant is zoo a.h.w. een cijfer, en wel een cijfer grooter dan of gelijk aan 8.

Nu zal bij het negatieve deel van het bewijs geen eindcijfer hooger dan ‘6’ mogen voorkomen. Met loopende indices kunnen we dit negatieve deel dan als volgt beschrijven:

Op alle zetten 1. Wi (i = 2, 3, 4, ....n) heeft zwart antwoorden 1. ...., Zi ter beschikking, zoodanig dat iedere tweede zet van wit 2. Wik (k = 1, 2, 3 ....ni, waarbij i = 2, 3, 4, ....n) beantwoord wordt door een bijbehoorende repliek 2...., Zik, iedere derde zet 3. Wikl (l = 1, 2, ....nik; k = 1, 2, ....ni; i = 2, 3, 4 ....n) door een bijbehoorende repliek 3 ...., Zikl enz. enz.; zoodanig dat tenslotte de eindresultaten in cijfers van het standpunt van wit uitgedrukt de waarde 6 niet overschrijden. Slaagt men erin voor het positieve deel de zetten Wi, Wik, Wikl enz., voor het negatieve deel de zetten Zi, Zik, Zikl enz. zoo te bepalen, als zij voor het bewijs vereischt worden, dan is daarmee ook werkelijk bewezen, dat 1. W₁ de sterkste zet is.

Als illustratie een bijzonder geval, het geval namelijk waarin wit zijn tegenpartij kan mat zetten, zeggen we in drie zetten. Het bewijs is hier aan-

[p. 24]

zienlijk eenvoudiger, in de eerste plaats omdat de taxatie aan het einde van een variant en de vergelijking der resultaten achterwege kan blijven, in de tweede plaats omdat de lengte van geen enkele variant hier de drie zetten overschrijdt. Te bewijzen is:

1)	na 1. W1 volgt bij ieder tegenspel van zwart mat in ten hoogste drie zetten.
2)	Na andere zetten 1. W2, ...., 1. Wn kan zwart mat in drie zetten verhinderen, tegen elk tegenspel van wit.

De eenige complicatie, die zich kan voordoen, ligt besloten in het ‘ten hoogste 3 zetten’ bij het positieve deel: het kan zijn, dat wit na sommige antwoorden op 1. W₁ reeds op den tweeden zet mat geeft. Als we voor de aantallen vertakkingen ter vereenvoudiging kleine getallen aannemen - vier zetten voor zwart na 1. W₁, waarvan twee onmiddellijk tot mat leiden; twee mogelijke zetten voor wit naast 1. W₁, e. dgl. - dan kunnen we een schematische voorstelling van de twee deelen maken als hieronder is weergegeven:

Positief deel:

Negatief deel: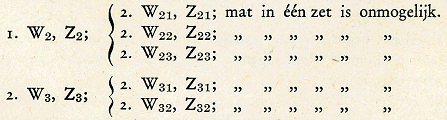

Hierin zijn de Z-vertakkingen in het positieve, en de W-vertakkingen in het negatieve deel duidelijk te zien. Het is intusschen niet noodzakelijk dat twee met verschillende indices aangeduide zetten ook werkelijk verschillend zijn; soms volgt b.v. op verschillend verweer van zwart dezelfde matzetting.

Het schema, althans het positieve deel ervan, doet denken aan de oplossing van een schaakprobleem: mat in 3 zetten, zooals die in een schaakrubriek wel eens gepubliceerd wordt. Met het negatieve deel van het bewijs heeft de oplosser van het probleem, die alleen den ‘sleutelzet’ W₁, en het juiste vervolg voor wit, dus de verdere W-zetten moet vinden, weinig te maken; de componist echter des te meer! Eén van zijn groote zorgen bij de

[p. 25]

compositie is immers het vermijden van ‘nevenoplossingen’. Hij moet werkelijk het bewijs kunnen leveren, dat 1. W₁ de beste zet is, dus dat geen enkele andere zet tot het gewenschte mat in 3 zetten leidt.

In de partijpractijk is dit natuurlijk anders: wanneer een speler werkelijk kans ziet het mat af te dwingen, dan zal hij dat in het algemeen gauw uitvoeren, zonder zich al te druk te maken over ‘nevenoplossingen’, of zelfs over kortere wegen naar het doel. Maar een dergelijke onverschilligheid t.a.v. het negatieve gedeelte van het bewijs bestaat alleen in geval van aperte succesmogelijkheden, zooals direct winnende combinaties, niet pareerbare dreigingen enz., waarbij een vergelijken met andere zetten overbodig is. Meestal heeft echter ook het negatieve deel wel zijn beteekenis.

§ 10. De beteekenis van het schema voor het denkproces.

Er is natuurlijk geen sprake van dat iedere schaker dit bewijsschema voortdurend ter beschikking heeft, laat staan in de hier gegeven wiskundige inkleeding. Zelfs in een werkelijke schriftelijk uitgewerkte analyse is deze grondvorm niet altijd gemakkelijk te ontdekken als gevolg van het feit, dat groepen varianten worden samengevat, of gedeelten van het bewijs worden weggelaten. Als de tegenpartij in de stelling van uitgang een ernstige ‘dreiging’ heeft, dan kunnen bij het negatieve bewijs alle zetten, die die dreiging niet pareeren, worden weggelaten. Kan er in een materieel en positioneel schijnbaar hopelooze situatie een zoogenaamde patcombinatie worden uitgevoerd, waardoor de partij reglementair remisie wordt, dan heeft het weinig zin, nog te vragen naar het negatieve bewijs, dat andere zetten geen remise opleveren. Heeft wit de keuze tusschen het uitvoeren van een dwingende gewelddadige combinatie en een aantal rustige zetten, die het stellingsbeeld niet wezenlijk veranderen, dan kunnen deze laatste bij de analyse gezamenlijk worden behandeld en met een enkel woord worden afgedaan. Zoo zijn er meer vereenvoudigende samenvattingen mogelijk.

Nog veel minder verloopt het gewone denkproces volgens de lijnen van een dergelijk bewijs. Door den beperkten denktijd en de noodzaak om alles uit het hoofd te berekenen kan de speler voor het bord ook daar vaak geen bewijs leveren, waar de analyse het wel kan; bovendien is er in een schaakstelling niet zooals bij een wiskundevraagstuk bij gegeven wàt er bewezen kan en moet worden. De speler moet dit zelf ontdekken: het denkproces is zoeken en beredeneeren tegelijk. Tot een bewijs komt het daarom maar betrekkelijk zelden. De gevallen, waarin het spelen van een zet nièt gepaard gaat met de volkomen zekerheid, dat het werkelijk de beste zet is, zijn in de meerderheid.

Maar tóch, het is tenslotte een gemotiveerde keuze en het denkproces moge dan geen bewijs bevatten, een beredeneering van den gekozen zet moet er toch in besloten liggen. Bij mijn onderzoek bleek het dan ook inderdaad mogelijk te zijn uit den tekst van het protocol een beredeneering van den

[p. 26]

gekozen zet af te leiden, die vaak zeer wel vergelijkbaar was met het boven gegeven bewijsschema. Zoo was het dikwijls mogelijk een positief en een negatief deel van de uiteindelijke redeneering te onderscheiden, ook al kwam deze heelemaal niet langs den logischen weg tot stand. Zoo vormden soms alle mislukkingen van in het begin met positieve bedoelingen geprobeerde voortzettingen later, na het vinden van een betere methode, tezamen het negatieve deel van de beredeneering. Daarbij werden dan alle oorspronkelijk beschouwde nevenvarianten van tegenspel nu in het negatieve bewijs ‘doode takken’. Bijvoorbeeld: het subject heeft de keuze tusschen den actieven combinatoiren zet 1. W₁ en de rustige voortzetting 1. W₂. Hij wil W₁ spelen en berekent daartoe de gevolgen van vier mogelijke methoden van tegenspel van zwart, Z₁₁, Z₁₂, Z₁₃ en Z₁₄. Bij de eerste drie ‘slaat de aanval door’, maar het antwoord 1....Z₁₄ weerlegt den zet W₁, zoodat hij tot 1. W₂ besluit. Het negatieve deel bestaat nu uit de weerlegging door zwart van 1. W₁, dus uit de variant 1. W₁, Z₁₄ enz. De 3 andere zwarte vertakkingen Z₁₁, Z₁₂, Z₁₃ hebben nu voor de redeneering geen waarde meer, het zijn ‘doode takken’ geworden⁹.

Aan het optreden der vertakkingen, bij zetten van wit of zwart, en aan de bewoordingen, waarmee de proefpersoon een nieuwe variant begint, is dikwijls wel te zien of hij zijn berekeningen als poging tot een positief bewijs, als een zuiver empirisch onderzoek naar de beste mogelijkheden voor beide partijen, of als een negatief bewijs opzet. Het eerste van deze drie gevallen is wel het meest frequent, zooals we zullen zien.

In ieder geval zien we hieruit, dat bekendheid met het algemeene bewijsschema voor den ‘besten zet’ zijn nut heeft voor het psychologische onderzoek naar het schaakdenken (vgl. hoofdstuk V § 43 en VII § 54).

9 Voor de bewijsschema's van het schaakspel met hun ‘vertakkingen’ ligt de metaphoor van den ‘logischen boom’ zoo mogelijk nog meer voor de hand dan voor een wiskundig bewijs. G. Pólya spreekt in een artikel over dit laatste onderwerp (A 34) eveneens van ‘doode takken’. In het vervolg zal ik de boom-vergelijking nog meer dan eens ter verduidelijking toepassen.