Het denken van den schaker

C. Het Probleem van de Zetkeuze.

§ 6. De variabiliteit van dit probleem.

Het is eigenlijk misleidend om van ‘het’ zetkeuzeprobleem te spreken. Immers het karakter van het vraagstuk, waarvoor de schaakspeler die aan zet is zich geplaatst ziet, is uiterst variabel, zoowel van psychologisch als van schaaktechnisch standpunt en geheel afhankelijk van den stand op het bord. Het maakt een groot verschil of hij een plan moet opmaken of alleen nog maar uitvoeren, of hij een combinatie moet bedenken of pareeren, of hij eenvoudig moet terugnemen, een schaak moet dekken, moet zoeken naar een reddingsmogelijkheid in een bedreigde stelling, of moet ‘laveeren’ om zijn kans af te wachten. Het maakt verschil of hij - in opening of eindspel, of in een stereotiepe middenspelsituatie - hoofdzakelijk volgens bekende schema's kan te werk gaan, of zelfstandig nieuwe mogelijkheden moet ontdekken en uitwerken.

Het interessantst zijn natuurlijk de knooppunten in de ontwikkeling van den strijd, de momenten, waarin de speler een diepe combinatie ontdekt en gaat uitvoeren, of een plan op langen termijn uitdenkt, de momenten dus, die gewoonlijk ook in een diagram bij de partij worden vastgelegd. Het meest belangwekkend, zeker voor den psychologischen leek, zou het zijn bijvoorbeeld iets naders te weten te komen omtrent het denkproces van Anderssen tijdens zijn ‘onsterfelijke partij’ tegen Kiezeritsky, toen hij besloot zijn beide torens te laten nemen ten behoeve van den voortgang van zijn aanval.

Twee dingen zijn het voornamelijk die men zich hierbij afvraagt, nl. hoe de speler ‘op het idee komt’, en in hoeverre hij de komende ontwikkeling van het spel wel voorzien heeft. Hoe kwam Euwe op het idee in de beroemde 26ste (Zandvoortsche) partij in zijn eerste match om het wereld-

[p. 14]

kampioenschap tegen Aljechin een stuk tegen drie pionnen te offeren? En hoeveel van de fraaie combinatoire mogelijkheden zou Aljechin in zijn schitterende partij te Baden-Baden 1925 tegen Réti wel berekend hebben toen hij zijn toren op e3 en prise zette?

Dergelijke vragen betreffende de spanningshoogtepunten van het wedstrijdspel zijn het, die schaakliefhebber èn -leek het meest interesseeren - naast die naar de psychologische verklaring van speciale kunststukken, zooals blindsimultaanspel. Het behoeft echter geen betoog, dat zulke sensationeele momenten zeldzaam zijn en zeker niet representatief voor het zetkeuzeprobleem in het algemeen. Gewoonlijk is dit veel nuchterder van aard, en het zou dan ook bepaald een ernstige fout geweest zijn, als ik alleen maar geëxperimenteerd had met stellingen waarin brillante combinaties mogelijk zijn. Ik heb ernaar gestreefd eenzijdigheid te vermijden door met stellingsproblemen van zeer uiteenloopend karakter te werken, die alleen in zooverre een selectie vormen, dat er geen regelrecht triviale bij zijn.

Een voor ons doel belangrijk variabel kenmerk in de veelheid van mogelijke stellingsproblemen is dat van de keuzevrijheid van den speler. De keuze der in aanmerking komende zetten kan ruimer of minder ruim zijn, tot en met het extreme geval, dat er heelemaal geen sprake is van kiezen.

Deze kwestie kan men van drie kanten bekijken, namelijk van formeel, van objectief schaaktechnisch en van psychologisch standpunt. Men kan namelijk vragen:

A.	naar het aantal volgens de spelregels mogelijke zetten,
B.	naar het aantal goede zetten, en
C.	naar het aantal zetten, waaruit de speler resp. proefpersoon realiter zijn keuze doet - àls er sprake is van kiezen.

Om later punt C, het belangrijkste, recht te doen wedervaren, is het noodig vooraf iets te zeggen over de eerste twee.

§ 7. De reglementaire keuzevrijheid (K).

Het aantal zetmogelijkheden volgens de spelregels (A) in schaakstellingen, die vanuit den beginstand reglementair kunnen ontstaan, varieert van o (in een pat- of matstelling) tot over de 100. Practisch liggen de grenzen echter dichter bij elkaar: stellingen met meer dan 70 reglementaire mogelijkheden laten zich wel construeeren, maar komen in de practijk nauwelijks voor, terwijl de lage aantallen, onder de 8, vrijwel alleen optreden als de koning schaak staat. In dit laatste bijzondere geval schrijft het reglement de opheffing van het schaak voor, wat slechts op een beperkt aantal manieren kan gebeuren.

Hoe groot is nu de reglementaire keuzevrijheid in doorsnee, d.w.z. als we het universum van alle stellingen, voorkomend in gespeelde tournooi- en matchpartijen beschouwen?

Het antwoord op deze vraag is langs statistischen weg te benaderen,

[p. 15]

wanneer men maar een voldoende aantal ongeselecteerde stellingen hierop onderzoekt. Daartoe zou men b.v., bij wijze van steekproef, alle stellingen uit alle partijen van een paar tournooiboeken onder handen moeten nemen. Maar dat is een omslachtig werk, dat bovendien tenslotte alleen een algemeen gemiddelde als resultaat zou opleveren, zonder dat er iets over de afhankelijkheid van de ‘gemiddelde bewegingsvrijheid’ van het aantal voorafgegane zetten uit zou blijken. Ik ben daarom eenigszins anders tewerk gegaan. Van de diagramstellingen⁶ uit enkele rijk daarmee geïllustreerde partijen-verzamelingen (Tarrasch' ‘300 Schachpartien’, e.a.) heb ik telkens nagegaan:

1.	het nummer van den zet die op dat oogenblik gespeeld moet worden,
2.	het aantal reglementaire zetmogelijkheden in de stelling in kwestie,
3.	het aantal reglementaire zetmogelijkheden voor de tegenpartij, nadat de werkelijk gekozen zet is uitgevoerd.

Deze drie getallen werden telkens gerubriceerd in groepen - 11de tot en met 15den zet, 16de tot en met 20sten zet, verder: 21-25, 26-30, 31-40, 41-50, 50 en hooger -, naar gelang van de grenzen waarbinnen het nummer van den te spelen zet viel. De stellingen waarin een schaak moest worden opgeheven (†-stellingen) werden van de verwerking uitgesloten en afzonderlijk onderzocht, en voor het overige werd er zooveel materiaal verzameld, dat de eerste 5 groepen elk 20 stellingen met wit-aan-zet en 20 met zwart-aan-zet bevatten. Zoo vond ik b.v. voor de groep 21ste tot en met 25ste zet:

gemiddeld zetnummer (gemiddelde van de onder 1. genoemde getallen): 23,4

gemiddeld aantal mogelijkheden voor wit: 38,0⁵ } totaal gem.: 38,0.

gemiddeld aantal mogelijkheden voor zwart: 37,9 } totaal gem.: 38,0.

De bepaling der laagste en hoogste waarden (l en h), en van de mediaan en de quartielen leverde op:

l.	q1.	m.	q3.	h.
21	32,5	38,0	42,5	65

Blijkbaar valt de mediaan m in dit geval juist samen met het gemiddelde.

We kunnen nu, in de gewettigde aanname, dat de steekproef in groote trekken representatief is, de gevonden uitkomsten als volgt interpreteeren:

‘Omstreeks den 23sten en 24sten zet (gem. 23,4) ligt in ongeveer 50 % van alle aan wedstrijdpartijen ontleende stellingen waarin géén schaak wordt gegeven, de reglementaire keuzevrijheid tusschen de 32 en 43 zetmogelijkheden. Aantallen onder de 21 en boven de 65 zijn zeldzaam.’

De resultaten van alle groepen zijn in de grafiek van figuur 1 samengevat. De numerieke resultaten van iedere groep zijn af te lezen op één

6 Deze vormen een selectie, n.l. van critische situaties in den strijd. Het is echter niet waarschijnlijk, dat er verband bestaat tusschen dit moment en her formeele punt van het aantal zetmogelijkheden, vooral niet als we steeds de mogelijkheden van wit èn zwart beschouwen. (Zie onder 2. en 3.)

[p. 16]

der verticale lijnen; de verschillende medianen en quartielen zijn onderling verbonden. Men kan grofweg zeggen, dat in 50 % van alle stellingen bij den x-sten zet de keuzevrijheid, voor wit en zwart gemiddeld, is te vinden bij x tusschen de quartiellijnen. De uiterste waarden zijn sterker dan de quartielen van toeval afhankelijk, zoodat het geen zin heeft deze punten door lijnen te verbinden. Wanneer het aantal stellingen (n) in een groep b.v. vertienvoudigd zou worden, dan moesten gemiddelde, mediaan en quartielen ongeveer op hun plaats blijven, maar maximum en minimum zouden zich naar buiten verplaatsen.

Bij de diagramstellingen bevonden zich te weinig exemplaren uit de eerste openingsphase, vóór den tienden zet, om daarop het linkerdeel van de grafiek op te bouwen. Daarvoor heb ik dan ook ander materiaal gebruikt, en wel alle stellingen voorkomend in een zestal veel gespeelde openingsvarianten: daarop berusten de drie ‘doorsneden’ bij x = 3, 0; x = 6,0; en x = 9,0. De aansluiting met de rest van de grafiek klopt behoorlijk.

Tot zoover over de opstellingswijze van de grafiek.

De volgende resultaten laten zich uit de figuur aflezen:

1. Het gemiddeld aantal zetmogelijkheden op den x-sten zet K̄(x), varieert van 20 - bij den eersten zet, en tegen den 65sten zet van lange partijen - tot ongeveer 40, omstreeks den 17den zet. Onder de 20 komt dit aantal merkwaardigerwijze niet vóór een zeer vergevorderd stadium.

2. De verandering van het gemiddeld aantal zetmogelijkheden met den ‘ouderdom’ van de partij blijft dus binnen bescheiden grenzen, vertoont echter een kenmerkend verloop, waarin b.v. de ontwikkeling der strijdkrachten gedurende de eerste 10, 15 zetten duidelijk gedemonstreerd wordt.

3. Wil men komen tot een schatting van het gemiddeld aantal zetmogelijkheden over het geheele universum van schaakstellingen uit gespeelde meesterpartijen, dan moet men met gewichten werken, daar er b.v. veel meer stellingen op den 12den zet dan op den 74sten zet bij zijn: verreweg de meeste partijen loopen immers na den 12den, maar voor den 74sten zet ten einde. Zoodoende moeten de aantallen bij de eerste 20 zetten het zwaarste tellen. Houdt men daarmee rekening, dan is uit de grafiek af te lezen, dat het totale gemiddelde ergens tusschen de 30 en 35 zetmogelijkheden moet liggen. Inderdaad leverde een berekening op grond van de op bladz. 11 in de noot genoemde verdeeling der partijlengten als ‘gemiddelde keuzevrijheid’ het getal 32,3 op.

4. Aan de dicht bij elkaar liggende quartiellijnen en aan de uiterste waarden kan men zien, dat de spreiding op ieder moment betrekkelijk gering is. In mijn geheele materiaal vóór den 26sten zet (226 stellingen) komt er - afgezien van de †-stellingen, die hierin niet verwerkt zijn - niet één geval van minder dan 20 zetmogelijkheden (K<20) voor; en vóór den 51sten zet niet één geval van minder dan 10 zetmogelijkheden. Ook naar boven toe is de spreiding van matigen omvang. Het geval van 65 mogelijkheden (bij x = 23,4) staat in mijn materiaal alleen; het daarop volgende is de 57 bij x = 17,5.

[p. 17]

5. In dit diagram kan men iedere partij als een gebroken lijn, en iedere stelling als een punt weergeven. Dit laatste heb ik gedaan voor de drie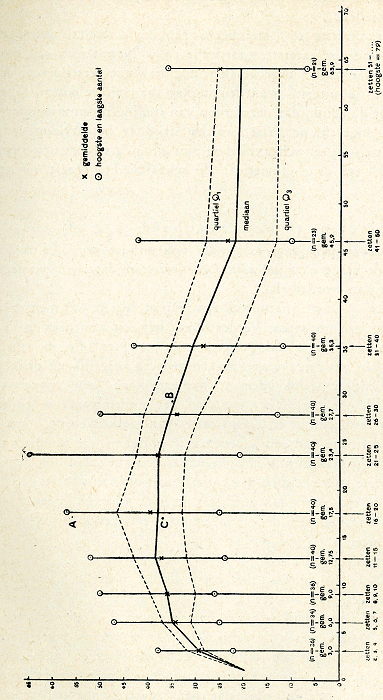

Fig. 1. Het verloop van de reglementaire keuzevrijheid K met het aantal gespeelde zetten
(toelichting zie tekst).

stellingen A, B, en C, waarmee ik hoofdzakelijk geëxperimenteerd heb. Blijkbaar is A. een extreem ‘rijke’ stelling, terwijl B en C normaal zijn.

Nog een enkel woord over de †-stellingen, waarbij dus de noodzaak om het schaak op te heffen een sterke beperking van het aantal zetmogelijkheden met zich meebrengt. In de 45 partijen uit het tournooiboek van

[p. 18]

Margate 1938 werd op een totaal van 3640 ‘halve’ zetten 171 maal schaak gegeven: dus 1 op de 21,3 zetten was een schaakbieding. Grofweg kunnen we dit wel generaliseeren door de relatieve frequentie van de †-stellingen op een 5 % te stellen.

Mijn materiaal bevatte 16 †-stellingen; gemiddeld aantal zetmogelijkheden 3,8; mediaan 3,5; uiterste waarden 2 en 9. Neemt men een grooter aantal gevallen, dan zullen deze getallen nog wel wat verschuiven, in het bijzonder zullen de uiterste waarden sterker gaan uiteenloopen. Maar in ieder geval is het duidelijk, dat deze groep van stellingen een uitzonderingspositie inneemt, ongeacht de phase van den strijd. In het verloop van een partij versmalt zich bij een schaakbieding plotseling de stroom der formeele mogelijkheden tot een drie- of viertal: de schaakbieding heeft dwingend karakter.

§ 8. De ‘objectieve’ keuzevrijheid.

Voor ons onderwerp belangrijker, maar ook minder gemakkelijk te beantwoorden, is de vraag naar het aantal goede zetten, dat er in een gegeven stelling gespeeld kan worden (B).

‘Een goede zet’ - dat is natuurlijk een relatief begrip, dat men strenger of minder streng kan opvatten. Verder houdt het een waardeering in, die degelijke kennis van het schaakspel vooronderstelt, en die in moeilijke gevallen alleen kan worden gegeven na een grondig vergelijkend onderzoek van de verschillende mogelijkheden en hun gevolgen (een zoogenaamde ‘analyse’ van de stelling). Voor ons doel, het vinden van een bruikbaar criterium ter onderscheiding en classificatie van zetkeuzeproblemen, zal ik een speciale definitie van een ‘goeden zet’ opstellen, die eenigszins van het begrip uit het spraakgebruik afwijkt, maar daarvoor dan ook de voordeelen van grootere strengheid en principieele toetsbaarheid bezit:

‘Een zet is dan en slechts dan goed, als het niet mogelijk is een anderen aan te wijzen, waarvan men door analyse op overtuigende wijze kan aantoonen, dat hij beter is.’

Of, anders uitgedrukt:

‘Een zet is dan en slechts dan nièt goed, als het mogelijk is overtuigend aan te toonen dat een andere beter is.’

Hierin komt de betrekkelijkheid van het begrip en de noodzaak van een vergelijking met andere zetten duidelijk uit. Wat de analyse betreft stel ik me op practisch standpunt: de stelling moet te analyseeren zijn door een meester, zonder dat daar nu maanden van onderzoek mee gemoeid zijn, en het resultaat moet zoodanig zijn, dat het iederen onbevooroordeelden kenner vermag te overtuigen. Volkomen streng is deze definitie niet - de diepte van de analyse laat eenige speelruimte - maar dat is ook niet noodig; als de omstandigheden het eischen, kan zij naar believen worden verscherpt.

Nu blijft echter nog de vraag, wannéér zet a eigenlijk beter dan zet b mag heeten, en hoe men die superioriteit bewijst. Het antwoord is: als men

[p. 19]

d.m.v. zet a tegen elk tegenspel betere resultaten kan bereiken dan d.m.v. zet b mogelijk is. Dit lijkt een tautologie, maar geeft in werkelijkheid den gang van zaken weer bij het bewijs dat a beter is dan b. ‘Resultaten bereiken’ wil namelijk zeggen: stellingen bereiken, welker waarde door een kenner op objectieve wijze getaxeerd kan worden, als ‘gewonnen voor wit’, ‘zeer gunstig’, ‘remise’, ‘gelijk spel’, ‘iets minder’ en dgl. Men geeft a.h.w. aan de stelling een cijfer (gewonnen = 10, gunstig = 7, gelijk = 5, b.v.). Geheel vrij van subjectiviteit is zoo'n ‘cijfer’ natuurlijk nooit; maar de veronderstelling, dàt men de superioriteit van a boven b kan bewijzen, impliceert, dat het practisch mogelijk moet zijn in alle varianten eindstellingen te bereiken, die zich met een behoorlijke objectiviteit laten taxeeren.

Een paar voorbeelden ter toelichting.

Zet a is beter dan zet b,

als a tegen elk tegenspel leidt tot een ‘gewonnen’ stelling, terwijl na b hoogstens ‘gunstige’ stellingen kunnen worden bereikt;

als a tegen elk tegenspel minstens ‘gelijk spel’ oplevert, en b niet meer dan een ‘minder goede’ stelling; enz.⁷.

Hiermee is het woordgebruik wel voldoende vastgelegd.

We kunnen nu dus de schaakstellingen classificeeren naar het aantal goede zetten, dat er gespeeld kan worden. Hierover laten zich niet zoo gemakkelijk statistische onderzoekingen uitvoeren - iedere stelling zou immers geanalyseerd moeten worden -, maar het is wel zeker dat de aantallen hierbij van een geheel andere grootte-orde zijn dan zooeven onder A. Zeker 9 van de 10 reglementair mogelijke zetten komen niet serieus in aanmerking; in het algemeen zullen er van de 30, 40 mogelijkheden misschien 3 of 4 overblijven.

Bij het analyseeren van een oude tournooipartij Halic-de Groot, uit het landentournooi te München in 1936 vond ik als gemiddeld aantal goede zetmogelijkheden zelfs niet meer dan 2. Het maximum was 5, en in ongeveer 40 % van de stellingen van deze heel gewone, niet bijzonder brillante of heftige partij was er niet meer dan één goede zet. Blijkbaar is deze laatste categorie belangrijk, reden waarom ik haar eerst zal behandelen.

‘Eén goede zet.’ Dit is dan dus tegelijk ‘de beste zet’: zijn superioriteit boven alle andere moet immers aantoonbaar zijn.

Dit geval doet zich b.v. voor:

a. bij een schaak, dat slechts op één manier gepareerd kan worden (dan is er dus maar één reglementaire mogelijkheid, en a fortiori ook één goede

7 Men kan desnoods het woordgebruik ‘a is beter dan b’ nog uitbreiden tot enkele gevallen, waarin de eindresultaten geen duidelijk verschil vertoonen. Namelijk: a is ook beter dan b, als hetzelfde gunstige resultaat (b.v. de winststelling of de matzetting) d.m.v. a sneller dan d.m.v. b kan worden bereikt. En: a is beter dan b, als beide zetten bij het beste tegenspel weliswaar tot hetzelfde resultaat leiden, maar na a het vinden van de beste tegenzetten veel moeilijker is dan na b. In de practijk rekent men deze gevallen er ook bij. Hier doe ik het niet om de zaak niet onnoodig te compliceeren.

[p. 20]

zet), of dat slechts op één manier zonder onmiddellijk nadeel gepareerd kan worden;

b. bij een ‘afruil’: de tegenpartij neemt een stuk of pion weg, die teruggenomen moet worden (d.w.z. het nemende stuk wordt op zijn beurt geslagen);

c. bij de aanwezigheid van een ‘dreiging’, die maar op één manier behoorlijk kan worden gepareerd (de tegenpartij dreigt b.v. in twee zetten mat te geven, of valt een belangrijk stuk aan, of dreigt door een ‘vork’ een stuk te winnen, en dgl.);

d. in stellingen waarin juist een voordeel brengende combinatie kan worden uitgevoerd (d.i. een reeks van dwingende zetten, die de speler vooraf heeft ‘berekend’);

e. in stellingen waarin er groote haast is bij de uitvoering van een bepaald plan, dat met de zet in kwestie moet beginnen (b.v. als men de tegenpartij vóór moet zijn, en zijn tegenmaatregelen moet voorkomen). Enz., enz.

Hierbij hebben we dus te doen met soortgelijke vernauwingen van den stroom der mogelijkheden als in § 7 bij de †-stellingen. In de practijk heeft inderdaad niet alleen een schaak dwingend karakter; ook een fout van de tegenpartij b.v. kan den speler moreel dwingen tot een bepaalde, onmiddellijke reactie: de weerlegging van die fout namelijk.

In moeilijkheid kunnen de zetkeuzeproblemen van deze groep natuurlijk sterk uiteenloopen: bij alle gevallen a tot en met e kan men triviale en uiterst ingewikkelde voorbeelden geven. Zij hebben echter dit gemeen, dat er één, objectief juiste oplossing bestààt. Men kan objectief aantoonen, dat een bepaalde zet de beste is: het zetkeuzeprobleem is objectief oplosbaar. Voor den speler (proefpersoon) gaat het erom of hij deze eene oplossing zal kunnen vìnden, en niet, of hij gedeeltelijk op grond van persoonlijke motieven een zet zal kunnen kièzen.

‘Twee of meer goede zetten.’

Het ligt na het bovenstaande voor de hand te meenen, dat stellingen waarin meer dan één goede zet kan worden gespeeld, noodzakelijk nièt objectief oplosbaar zijn. Dit is echter niet het geval, of liever gezegd: het is beter het begrip der objectieve oplosbaarheid niet hieraan te verbinden. Stel, er zijn twee goede zetten, a en b. Dat beteekent dus, dat het niet mogelijk is de ongelijkwaardigheid van a en b te bewijzen - maar het kan zijn dat hun gelijkwaardigheid kan worden bewezen. In dat geval moet men het zetkeuzeprobleem ook objectief oplosbaar noemen: een vierkantsvergelijking is tenslotte niet minder objectief oplosbaar dan een lineaire vergelijking.

Dubbele en meervoudige oplossingen zijn in het schaakspel verre van zeldzaam; zij komen b.v. voor in:

a. stellingen, waarin de volgorde der zetten van een combinatie kan worden gevarieerd, zonder dat dit het resultaat verandert;

b. †-stellingen, waarin de koning op twee of meer manieren kan uitwijken, die in verband met het noodzakelijke vervolg volkomen op hetzelfde neerkomen;

[p. 21]

c. stellingen, waarin men de tegenpartij door willekeurige ‘tempozetten’ in het nauw kan brengen;

d. defensieve stellingen, waarin men zelf niets kan ondernemen, maar rustig de komende dingen kan en moet afwachten door de niet aan hun plaats gebonden stukken heen en weer te schuiven. Enz., enz.

Naast deze categorie bestaat er echter nog een andere, die der niet objectief-oplosbare stellingen. Daarin zijn twee of meer goede zetten mogelijk, waarvan zich noch de ongelijkwaardigheid noch de gelijkwaardigheid practisch laat bewijzen, omdat de stelling zich niet volledig laat analyseeren. Specimina daarvan zijn b.v. te vinden:

a. in de openingsphase, als men tusschen verschillende varianten kan kiezen, die (nog) geen van alle weerlegd zijn;

b. in het middenspel, als men tusschen verschillende systemen kan kiezen (b.v. de stelling openen of gesloten houden), omtrent de waardeverhouding waarvan men zelfs in een uitgebreide analyse niets tastbaars kan bewijzen. Enz., enz.

Zulke niet objectief oplosbare stellingsproblemen bezitten dus niet zooals een wiskundevraagstuk een objectief geldige, ‘juiste’ oplossing. Althans: niemand kent die oplossing of kan die naar menschelijke berekening vinden⁸, zoodat het onmogelijk is zonder subjectieve overwegingen tot een keuze te komen. Dergelijke stellingen hebben, vooral als het aantal goede voortzettingen groot is (3 of meer zetmogelijkheden), een typisch eigen karakter.

Het behoeft geen betoog, dat de ‘objectieve keuzevrijheid’ - het aantal speelbare goede zetten -, en in het bijzonder de vraag of de stelling objectief oplosbaar is of niet, van psychologisch standpunt van meer belang is dan de reglementaire keuzevrijheid K. Deze laatste is, psychologisch gezien, slechts een zuiver formeel maximum, zoowel voor het mogelijke aantal goede zetten als voor het aantal zetten, dat realiter door den speler wordt overwogen. Dit maximum wordt slechts zelden en bijna alleen in †-stellingen bereikt. Tusschen de reglementaire keuzevrijheid en de objectieve oplosbaarheid bestaat weinig verband: een reglementair rijke stelling met 60 of meer zetmogelijkheden kan evengoed objectief oplosbaar zijn als een arme stelling met K = 10.

Zooals we objectief oplosbare en niet objectief oplosbare stellingen, of, korter gezegd, dwingende en vrije stellingen naast elkaar kunnen stellen,

8 Men merke op, dat het verschil relatief is. Een nòg niet weerlegde openingsvariant kan later, op grond van de gezamenlijke ervaringen en analysen der schaakmeesters tòch weerlegd worden; een nù niet objectief oplosbare stelling kan het later worden. Inderdaad zijn er gevallen te over van openingsstanden, waarin de 19de-eeuwsche meester nog de vrije keuze had uit verscheidene ‘goede’ zetten a, b en c, terwijl zijn moderne collega zich gedwongen ziet a te kiezen, daar b en c inmiddels weerlegd zijn. De ontwikkeling van de openingstheorie heeft zoodoende ten gevolge, dat gaandeweg steeds meer ‘vrije’ stellingen objectief oplosbaar worden.

[p. 22]

zoo kunnen we ook grofweg tweeërlei houding, tweeërlei instelling van den schaker ten opzichte van zijn probleem onderscheiden. Houdt de speler de situatie op het bord voor objectief oplosbaar, althans meent hij haar zoo te moeten behandelen, dan zal hij zoeken naar den besten zet, naar de ‘juiste’ voortzetting; bij een ‘vrije’ opvatting van het speelprobleem daarentegen stelt hij zichzelf veeleer de vraag: ‘Wat zal ik eens spelen?’, in het bewustzijn van zijn vrijheid en van het persoonlijke element in zijn keuze en tegelijk zonder de pretentie dat deze de ‘juiste’ zal zijn. Zoo kunnen we opgave-situatie en speel-situatie tegenover elkaar stellen, als uitersten van de reeks van werkelijk voorkomende gevallen. Karakteristiek voor het schaakspel is, dat de opvatting van het probleem der zetkeuze door den speler zich steeds tusschen deze twee extremen beweegt.

De opvattingswijze van den speler correspondeert natuurlijk niet altijd met de objectieve geaardheid van het stellingsprobleem. Soms meent men den eenigen juisten zet te hebben gevonden en gespeeld, terwijl men in werkelijkheid even goed op andere voortzettingen had kunnen ingaan; in andere gevallen ‘kiest’ men volgens persoonlijke voorkeur, niets vermoedend, een zet, die achteraf de eenig juiste, of, wat erger is, juist nièt de eenig juiste blijkt te zijn geweest. Verder wordt de opvattingswijze van den speler mede bepaald door diens persoonlijke denkmethodiek en instelling ten opzichte van het schaakspel in het agemeen: er bestaan op dit punt typologische verschillen (vgl. o.a. § 59). Dit alles neemt echter niet weg, dat het criterium van de objectieve oplosbaarheid psychologisch van belang is.

De bespreking van de belangrijke psychologische vraag in hoeverre het streven naar een bewijs van de juistheid van den te spelen zet bij de objectieve opvatting van het stellingsprobleem met succes kan worden bekroond, moet ik tot later uitstellen: daartoe zullen we moeten nagaan of de bij objectief oplosbare stellingen verkregen protocollen een bewijskrachtige redeneering inhouden. Een laatste voorbereiding tot dit probleem behoort echter nog in dit hoofdstuk thuis: we moeten weten hoe een dergelijke redeneering er formeel zou moeten uitzien. Hòe bewijst men eigenlijk dat een bepaalde zet de beste is?