Het verbetert en vermeerdert natuurlyk toover-boek. Of 't nieuw speel-toneel der konsten (onder ps. Simon Witgeest)

[p. 166]

Het Verbetert en vermeerdert Natuurlyk Toover-boek, of Speel-toneel der Konsten.
Het Sevende Boek.
Begriepende de voornaamste dingen in de Tijdrekeningen en eenige andere vermakelijke Reekeningen.

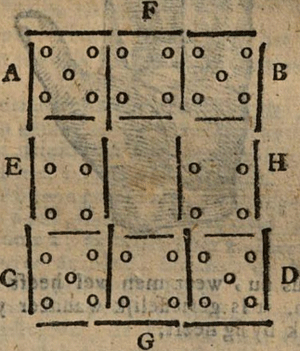
I. Om 32 Soldaten in een sekere ryen gesteld, agt uyt te nemen en vier in een andere plaats te setten, te doen schijnen dat ʼer geen gemist worden.

In ʼt volgende vierkant A. B, C. D, zijn in den omtrek acht kleinder vierkant, F, A. B, C, D, E, F, G, H, in yder set men vier man. Welke in yder linie recht of neerwarts geteld, altijt 12 Man zijn. Nochtans van de binnenste E, F, G.

[p. 167]

H, twee Man weg genomen zijnde, als 2 uyt E. 2 uyt F, 2 uit G, en twee uyt H, welke tʼsamen 8 Men maeken, en in plaats van dese 8, soo set men 4 Man, in yder hoek, van, A een, B een, C een, en D een, soo blijven in de linien eevenwel 12 Mannen als te vooren.

II. Hoe men op de hand tellen kan hoe veel dagen yder Maend heeft.

Om dit te weten, soo houd u duym, middelste vinger en pink om hoog, en de twee andere vingers om laag. Al de vingers die nu opsteken, zijn 31, en die neder leggen 30, teld dan van Maart af, laat de duym Maart zijn, de voorste vinger April, de middelste Mey, de volgende Junnius, de pink Julius, de duym wederom Augustus. Gaat soo tot de pink toe, welk December is, komd dan weder tot de duym Januarius

[p. 168]

Februarius nu, weet men wel heeft altijd 28 of 29. dagen. ʼt Is gerieffelijk wanneer ymant geen Almanack by sig heeft.

III. Wanneer dryederley persoonen uyt driederley glasen drinken, te weten uyt welke een yder gedronken heeft.

Wanneer dit gedaan werd, moeten daar drie glasen zijn, elk met verscheyde vogt gevult, als Bier, Mee en Wijn, yder getekent met een besonder getal, 1, 2, 3, laat het Bier getekent zijn 1, de Mee met 2, en de Wijn met 3, diergelijk getal schrijf ik mede de persoon toe, als Peterus 1, Cladius 2, en Maarten 3, nu seg ik tegens den eersten, namelijk Pieter, als hy uyt sijn glas drinkt, dat hy het getal verdubbele: Maar Claudius de

[p. 169]

tweede, sal het getal van sijn glaas met 9 multipliceeren, en Marten de derde met 10, dese drie getallen by een geteld zijnde, hiet ik die van 60 af trekken: Vraagt dan hoe veel getal dat ʼer uyt gekomen is, dat divideert men met 8, so sal de quotient het eerste glas aanwijsen, de rest dat na de divisie over gebleven is, het twede, waar door dat dan ook het derde betekent is.

By exempel: Peterus drinkt uyt het glas met Mee, so verdubbeld hy het getal des glas, welk 4 uyt brengt.

Claudius drinkt ook uyt het Wijn-glas, en multipliceert sijn getal 3 met 9 ʼt welk 27 uytbrengt.

Marten nu drinkt uyt het bier-glas, soo multipliceert hy 1 met 10, ʼt welk 10 blijft.

De somme by een geteld zijnde, brengen 41 uyt, trekt die van 60 af, soo blijft ʼer 19 over, divedeert die met een 8. komt 2, en blijft over 3. hier uyt volgt dan dat Peterus de Mee, Claudeus de Wijn, en Maarten het Bier gedronken heeft.

Of men hier het getal des eersten drinkers glas met 3 multepliceren, de tweede met 10 en de derde met 12, welke getallen alle drie te samen geteld werden, ʼt welk van 72 af getrokken, en het overige met 9 gedivideerd vverd, soo vvijst u den quotient het aan gelijk het genomen is.

IV. Om ʼt Gulden-getal te vinden van de geboorte Christi af, tot nu toe, en in ʼt toekomende.

Merkt dat het Gulden getal alle Jaren niet meer dan een vermeerderd, en niet hooger en komt dan 19: vvant als se 19 is, soo is het jaar daar aan vveder 1, en vervolgens also van jaar tot jaar, altijd gedeurende, ende is in Alexandrijnschen en Roomschen Almanak zijn beginsel gegeven in ʼt

[p. 170]

eerste Jaar des Concilums van Nicenen, Anno Christi 323 van welke te rugge gerekend, soo word bevonden als dat se in ʼt eerste jaar na Christi geboorte geweest is twee, daarom dat se gevonden kan werden na dien regel: doet 1, tot den jare onses Heeren geboorte, deeld dan het selve door 19, het overschot van de delinge geeft te kennen het Gulden getal: soo daar niets overblijft, so is het getal, 19.

By voorbeeld.

Neemt het jaar 1678, en teld by ʼt selve een getal, ʼt welk 1679 uytbrengt, deeld het selve door 19, soo schiet ʼer 7 over, ʼt welk het gulden getal is van ʼt jaar 1678.

Neemt ʼt jaar 1690 hier by doet 1 komt 1691 dievedeert dit door 19 komt.

Als het 0 is soo is het gulden getal 19.

Het getal van 89 wijst aan, dat ʼer soo veel omkeeren van gulden getal geweest zijn van Christi Geboorte af tot nu toe, het jaar van 1691 heeft 1 voor ʼt Gulden Getal.

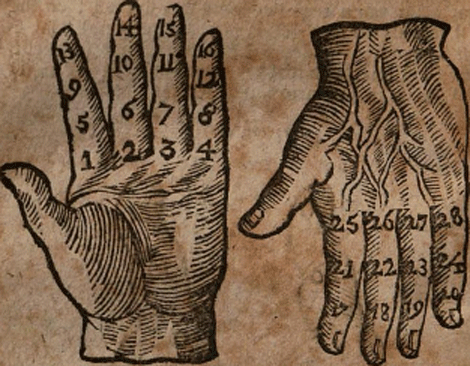
V. Om het gulden getal op de leden van uw vingers te tellen.

In dese Figuur siet ghy dat al de leden binnens hand just 10 uytmeten: daarom soo beeld alle de gulden getal op de selve leden, in sulken vervolg en

[p. 171]

order als ghy hier siet: teld dat op de selve leden by 100 jaren, op volgende maniere Steldt het jaar onses Heeren op ʼt onderste lit van de kleynste vin-

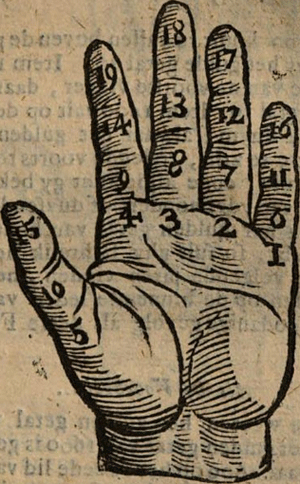
ger of pinke, en het jaar van 100 op ʼt tweede lid des selfs, dan 200 op ʼt derde lid, en 300 boven op de pinke, dan 400 op ʼt onderste lid van de ringvinger, 500 op tweede lid des selfs, 600 op ʼt derde lid, 700 boven op de selfde, dan 800 weeder beneden op ʼt nederste lid van de middelste vinger, also voorts tellende, dat ghy koomt op de bovenste van den duym, op welke dan komt te vallen 1800, so mag men dan voorts als men wil 1900 setten van voren aan op ʼt nederste lid der pinke, en van daar wederom gaande voorts, als van begin aan

[p. 172]

rondom tellen tot eeuwigheyd toe, en en sult verstaan, alleen tʼ elken reyse ygelijk jaar te gevallen komt op fijn gulden getal, vooren geteykent.

By Voorbeeld.

Het jaar 300 komt te vallen boven de pinke, aldaar vind ghy het gulde getal 16. Item 1500 komt op ʼt uyterste van de voorste vinger, daar vind ghy het gulden getal 19. Item 1600 valt op de benedenste lid van de duym, alwaar het gulden getal gevonden wert 5 te zijn, tellende voorts rondom tot in toe komende, ende alsoo kunt gy bekomen het gulden getal van yder hondert of duysend.

Als ghy nu het gulden getal van hondert jaren gevonden hebt, so sult ghy lichtelik het guldengetal van de volgende jaren vinden, herstellende de 19 getallen op de binnenste leden van uw linkerhand in soodanige gevolg als deese Figuur uytwijst

Als by Voorbeeld..

Om nu te weeten het gulden getal van ʼt Jaar 1678 want het gulden getal van 1600 is gevonden 5, so steld dat jaar 1600 op het tweede lid vande voorste vinger, al waar 5 getekent staat, ende teld van daar voorts van jaar tot jaar een lid rondom in des selve onder als die getallen op dese hand staat getekent, soo sal het jaar veertien ten eynde komen, boven op de pink, steld het volgende jaar 15, van vooren aan op het onderste lid van de duym, en de resterende jaren vervolgt voortaan tot het jaar 78, van welke gy het gulden getal begeert te hebben, en valt het eynd van de voorsz: alwaar 7 staat, ʼt welk het gulden getal is, en het naast-komende jaar sal het gulden getal 8 zijn en dat moet gy alsoo vervolgen.

[p. 173]

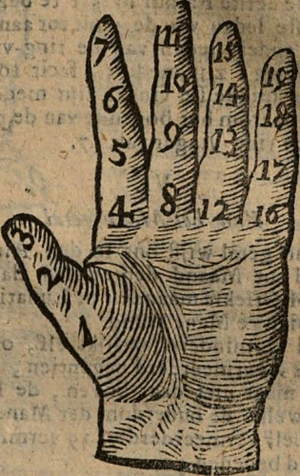
Dit selve hebt gy ook tot allen tijden lichtelijk te volgen op dʼ eygen hand, want al staan de gulden getallen daar juyst niet op geteykend, so wijst dat lid dat selvige genoegsaem uyt.

By voor-beeld.

Ik begeer by memorie te weten wat guldengetal op het bovenste van de ring-vinger valt: de leden van de duym houden in vervolgens 3 getallen, de voorste vinger 4, maken tʼ samen 7, de middelst vinger 4 komt 11, dan op het benedenste lid van de ring-vinger komt 12: ende de andere 13, de derde 14 het bovenste 15.

[p. 174]

Om te weeten wat gulden getal ʼt selve lid moet hebben na de eerste Figuur so is ʼt te bemerken dat de benedenste leden van de punt tot aan den duym zijn 3, de andere leden van de ring-vinger, van gelijken vervolg, zijn mede 5, facit 10. de derde leden van de middelste vinger zijn mede 5. maken 15. Soo is daarom het bovenste van de pink 16, en boven op den ring-vinger valt 17.

VI. Van het Maan-getal.

Het Maan getal wijst ons in den Almanak van Maand tot Maand den eersten dag der Hebreeusche of Griekse maanden of Lunatië, op welke dag de nieuwe Mane komd.

Dit getal verminderd jaarlijks elf, of ʼt welk al even veel is, vermeerderd negentien, en mag wel 30 wesen, maar niet daar boven, de Epacta regt contrari, welke de ouderdom der Manen aanwijst, en jaarlijks elf vermeerderd of 19 verminderd, blijvende altijd beneden 30.

Dit Maan-getal verloopt alle 312 jaren, en 208 dagen, een geheelen dag, die zy verminderd, gelijkerwijs de rekeninge van de anticipatie der nieuwe Mane is mede brengende.

VII. Om het Maan-getal op de drie leden van den duym te vinden.

Hier toe zijn drie getallen van noden, op de drie leden van u duym, welke veranderlijk zijn na de anticipatie of verloop der nieuwe Manen, ontrent alle 312 jaren een, als boven verhaald is.

Om dan de selve te stellen na dese tijd, beginnen van 1583 aan Anno 1700 na den nieuwen Gregori-

[p. 175]

aensen stijl, soo neemd voor de wortel of eerst Maan-tal 23, en addeert tot de selve 11, komt 34, want de sommen mag niet boven 30 klimmen, steld de resterende 4 op ʼt onderste lid van den duym, dʼ andere getallen werden bekomen door gedurige toedoeninge van 10, daarom tot de 4 zijnde gesteld op ʼt benedenste lid van den duym, addeerd 10, soo komt 14 op ʼt middelste lid, hier toe dan weder 10, komt 24 op den duym.

Nota. Na den ouden stijl te rekenen, soo is de wortel of eerste Maan-getal 12 van Anno 1577 af, tot 1881 te geduurende, daarom so doet 11 daar toe, so hebd gy beneden op den duym 25 om te hebben de andere getallen, soo teld 10 tot 23 weg werpende 30, blijft voor het middelste lid 3. daar toe weder 10, soo hebd gy 13. boven op den duym, tot den ouden stijl dienstig.

Om hier uyt te vinden het Maan-getal, soo trekt het gulden getal van u jaar 20 de rest steld op de drie leden van u duym, settende op ʼt benedenste lid 1, tellen soo voorts opwaarts dat boven drie komd dan beneden weder 4 so lange rondom gaande, tot dat gy de reste vol-teld hebt, merkende dat dat lid daar de tellinge op ge-eyndigt is, addert dat getal te samen, op ʼt selfde lid getekent met u gestelde reste, weg werpen de 30 indien u omme is, so krijgt gy het Maan-getal des selve jaars.

By voorbeeld.

Het jaar 1687 van welke het gulden getal geweest is, en de rest uyt 20 is 13, welke na de tellinge op den duym is eyndigende onder op den duym al-

[p. 176]

waar 4 getekent staat, addeert 13, tot vier, maakt op welk het Maan-tal of Epacten zijn, maar soo de somme hooger is als 30, soo snijd 30 af en de rest is het maan-tal na den nieuwen Gregoriaansen stijl.

VIII. Om altijd te vinden op wat dag van de Maanden van January en Maart dat het nieuwe Maan is, soo min of meer na den nieuwen of ouden stijl verschelende.

Als gy nu in ʼt voorgaande het Maan-getal geleerd hebt, soo doet nu de selve 7, werpende 30 weg, soo de somme meer komt te bedragen, ʼt geene daar uyt komt, wijst aan den dag wanneer het nieuwe Maan in January en Maart zijn sal.

By Voorbeeld.

Anno 1678 na den nieuwen stijl is het Maan-getal 17, teld daar 7 by, soo hebt gy op den 24 Maart en January nieuwe Maan volgens de stelling van A. Metius, dat als men daar by doet in plaats van 7, komt het met onsen Almanak op 22, en na den ouden stijl op 12.

IX. Den dag der nieuwen Mane van Januari en Maart noch lichter te bekomen.

In ʼt voorgaande hebbe wy drie getallen op den duym gesteld, als, 4, 14, 24, om door den selven op deese tegenwoordige tijd van honderd jaren het Maan-tal te vinden, na den nieuwen

[p. 177]

Gregoriaanse stijl, waar door voorts bekend gemaakt werd op wat dag in January en Maart het nieuwe Maan zal zijn, welke dag der nieuwe Mane ligter te bekomen sal zijn, als gesteld werd op de duym deese drie volgende getallen 10, 20, 0, gelijk als dese Figuur aanwijst, trekt nu het gulden getal van u tegenwoordig jaar uyt 20, en de rest teld als vooren geleert is, en het getal daar u rest op eyndigt, addeert tot de selve rest, soo hebt gy na den Nieuwen stijl gevonden den dag der nieuwe Manen in Januarius en de Maart.

By voorbeeld.

Anno 1678 is het gulden getal 7, dese van 20 getrokken rest 13, welke op de drie leden des duyms getelt als vooren, soo eyndigt de selve op ʼt onderste eynde des duyms, alwaar 20 staat deese met 13 geaddeert, wijst den dag van de nieuwe Maan in Januario en Maart volgens Metius.

Maar om na den ouden stijl te werken soo stelt de drie getallen op de drie leden van de duym op volgende ordre 0, 10, 20, en werkt als vooren gesegt is.

[p. 178]

X. Den Sonnen cirkel te vinden op de hand na dʼ Oude en Nieuwe stijl.

Anno 1621 is na den Ouden stijl de Sonne cirkel 1 volgens Metius, daarom steld ʼt selve jaar op ʼt onderste lid van u voorste vinger, en teld van daar voorwaarts van Vinger tot Vinger; eerst de onderste leden, en dan de bovenste toppen of nagelen, vervolgende voorts meede alle die krakelen buytens hands, welke alle te samen zijn met 28 tʼ elken reyse, springende van de pinke op de voorste Vinger, gelijk in de Figuren staat afgebeeld. Merkt dan op wat lid, dan u jaar is eyndigende, en die wijst u aan het Sonne-cirkel.

Van den Jare 1625 tellende na de ordeninge der

[p. 179]

getallen van den Jare 1621 af, soo bevind gy dat het Jaar 1625 is eyndelijk op het vierde lid van de voorste vinger, namelijk op het getal van 5, welke dan sal zijn het Sonne-cirkel, maar rond tellende tot 78, soo krijgt gy het getal 2, welke het Sonne-cirkel van ʼt jaar 1678 is, volgens Metius. Maar soo gy ʼt selve begeert na den nieuwen stijl, soo addeert by ʼt selve 20, en soo het selve hooger komt als 28, soo trekt daar 28 af en het overige blijft het Sonnen-cirkel na den nieuwen stijl.

XI. Drie persoonen, drie verscheyden dingen onder haar verborgen hebben, te raden wat een yeder heeft.

Drie persoonen als Piet, Kees, en Klaas, hebben onder haar lieden verborgen een ring, een silveren beker, en een goude kroon; om nu te raden welk een yeder verborgen heeft; soo laat den ring een, de beker twee, en de kroon drie zijn.

Laat daar na het getal des dings, dat den eersten heeft genomen multipliceeren met drie, des anderen met tien, en ʼt getal des dings dat den derden heeft met twaelf, de somme van het geene dat daar af komt laat u seggen, dat gy trekken suld van 72, ʼt blijvende divideert door 9, ʼt komende, seyd u ʼt geene dat den eersten heeft verborgen, en ʼt half deel van ʼt overblijf ʼt geene den tweeden heeft genomen, het derde meld sich selfs.

By voorbeeld.

Laat Piet hebben genomen den Beeker, Kees den Ring, en Klaas de Kroon, dat is 2, 1, 3, mul-

[p. 180]

tipliceert nu 2 met 3, een met tien, en drie met twaalf, komt 6, 10, 36, addeert, die komt 52. trekt die van 72 blijft twintig, deeld die door 9 komt 2 voor de beeker die Piet heeft, dʼ overblijvende twee neemd half, komt een voor den ring die Kees genomen heeft, en by gevolg heeft Klaas de goude Kroon verborgen.

XII.Vier persoonen, vier verscheyde dingen onder haar verborgen hebbende, te raden wat elk heeft.

Daar zijn vier persoonen, Steven, Klaas, Kees, Matthijs, de welke onder haar verborgen hebben een Schelling, Ducaton, Rijxdaalder, en een Rosenobel, om nu te raden welk een yder sal genomen hebben, soo laat de Schelling zijn een, de Ducaton twee, de Rijxdaalder drie, en de Rosenobel vier.

Daar na laat het getal van de schelling multipliceren met twee, ʼt getal van de ducaton met 21, van de Rijksdaalder met 25, en van de Rosenobel met 26, laat dan dese vier uytkomsten by een tellen, de somme seggen, trekkende de selve van 260, het resteerende deeld door 24, het quotient seyd u ʼt geene dat den eersten heeft genoomen, het resterende divedeert met 5, en het quotient segt dat den tweden heeft genomen, en ʼt overblijvende van dese twee divisie, meld ʼt geene dat den derden heeft verborgen, het resterende sal dan de vierde moeten verborgen hebben.

By Voorbeeld.

Laat Steven hebben de Rjiksdaalder, Klaas de

[p. 181]

Rosenobel, Kees de Ducaton, en Matthijs den Schelling, soo koomen dese vier getallen, 3, 4, 2, 1 nu multipliceert 3 met 2, 4 met 21, 2 met 25 en 1 met 26, sal komen 6, 84, 50, en 26, die tʼ samen geaddeert, koomt 166, dit u gesegt zijnde, trekt het van 260 rest 94 die door 24 gedivideert, komt 3 voor de Rijksdaalder die Steven genomen heeft. en dʼ overige 22 divideerd vorders met 5, komt 4; voor den Rosenobel, die Klaas genomen heeft; maar het overblijvende van dese tweede divisie te weten twee, meld dat de derde Ducaton had genomen, de resterende schellingen sal Matthys dan moeten verborgen hebben.

XIII. Om te vinden hoe veel boonen de vier-en-twintigste knoop soude mogen bedragen.

Soo steld sommige getallen drievuldig opklimmende na malkanderen aldus;

0.	1.	2.	3.	4.	5.	6.	7.	8.
1.	3.	9.	27.	81.	243.	729.	2187.	6561.

Multipliceert nu 6561 (staan onder 8) met 2187 (daar 7 boven staat) komt 14348907 voor het getal daar 15 boven staat behoord te staan; want 8 en 7 maaken 15.

Multipliceert vorders 14348907 met 6561, (daar 8 boven staat) sal komen 94143178827 voor het getal daar 23 behoord boven te staan. Want vijftien en acht maaken drie-en-twintig, zijnde van het beginsel het vier-en-twintigste getal, en soo veel boonen beloopt de vier-en-twintigste of de laaste knoop.

Wijders multipliceert deese 94143178827 met 3 (de proportie) komt 282429536481, hier van

[p. 182]

neemt een, de waarde des eerste knoops, deelende de rest als 282429539536480 door twee (de proportie min een) sal komen 141214768240 voor de somme aller boonen van de vier-en-twintig knoopen, ʼt selve divideert nu met 200 tot penningen, en de penningen met sestien tot stuyvers, met dertig tot daalders sal komen 1470987 daalders 5 stuyvers: een en een vijfde penningh.

XIV. Vrage.

Hesiodes eens aan Homerus vragende hoe veel Griekse Soldaten dat ʼer tegens Troyen opgetrokken waren? Homerus antwoorde: de Grieken hebben seven keukens, en in ider keuken leggen vijftig braatspitten, en het vleis dan aan elk spit gebraden werd, is voor 900 menschen. Vrage hoe veel Soldaten dan dat ʼer voor Troyen opgetrokken zijn geweest? Antwoord 315000 zijnde drie maal honderd duysend, en 15000 Soldaten.

XV. Vrage.

Op een Hofstee werden vier jonge Dames van haare Vryers 483 stuks boom-fruit vereert. En dat van vierderley soorte onder een geleyd: Waar af dʼ eene neemt een seeker getal, dʼ andere neemt een vierde des getals (min twee stuks) meer, de derde neemd een vierde des getals (meer 15 stuks, min als dʼ eerste, de vierde neemd eens soo veel (min tien stuks) als de derde: Vrage hoe veel stuks yder Dochter nam? Antwoord de eerste honderd, de tweede 123, de derde 90, de vierde 170.

[p. 183]

XVI. Manier om behendige Brieven te schrijven door verplaatsingen van Letteren of door Cyfergetal.

Wanneer gy yets geheyms aan malkanderen schrijven wild dat een ander niet leesen mag, soo weet men de letteren te verplaatsen, als een A voor een B, en een B voor een C, en soo voorts.

Aldus heeft den Keyser Julius Caesar gedaan: siet hier van Suetonius in ʼt leven van Julius Caesar, desgelijks ook Octavius Augustus, die A voor D, en B voor C settende.

Voorbeelden voor deese.

ABCDEFGHIKLMNOPQRSTVUWXYZ

Neemt.

BCDEFGHIKLMNOPQRSTVUWXYZA

Of

ZYXWUVTSRQPONMLKIHGFEDCBA

Tot een Voorbeeld.

Deo optimo debemus Optima.

Koomt.

Efp pruknp efcfnwt prukb.

Of neemd Cijffer-getal in plaats van de Vocalen als,

1 b c d 2 F g h 3 K L m n 4 p q r S T 5 W x 6 z.

Tot een Voorbeeld

Een yder te verpligten en niet verplicht te zijn: is meer als menschelijk.

Koomt.

22n 6d2r t2 v2rpl3cht2n 2n n32t v2rpl3cht t2 z6n: 3s m22r 1ls m2nsch2l6k.

Men maakt ook de letters die dubbeld staan met een streek boven op.

[p. 184]

XVII. Om acht kannen Wijn in twee even deelen te deelen, sonder meer als deese drie ongelijke Flessen te gebruyken, dʼ een van acht kan, d' ander van vijf, en de laatste van drie kannen.

De drie letters ABC, betekent drie Flessen A van 8 kan, B van 5 kan, en C van drie kan; schenkt de flesse B eerst vol uyt de Flesse A, en ʼt geene noch in B over is, namelijk twee kan schenkt die in C, vuld nu wederom de Fles B uyt A, en ʼt geene in B is, doet daar van C voort vol, Dewijl nu in C alreeds twee kannen waren, soo moet volgen dat uyt B in welke 5 kannen waren, maar een in C geschonken is, en derhalven in B alleenig vier kannen zijn gebleven, het welk de begeerde helft was.

XVIII. Om te raden wat getal ymand gedagt heeft.

Doet yemand een getal denken, by exempel 8, doet dit vermenigvuldighen met drie, komt 24, laat dit midden door doen, komt 12, dit weder met

[p. 185]

3 vermenigvuldigd, komt 36; nu moet men vragen hoe veel maal negen in de uytkomst is, soo sal hy antwoorden 4 maal dit getal met twee verdubbelende, maekt het gedagte getal 8 of

Wanneer ymand nog eens gedagt heeft, by voorbeelt 7. doet het met drie vermenigvuldigen, komt 21. (ʼt welk wanneer dit getal oneven is so moet ʼer altijd een by gevoegd werden, maakt dan 22, midden door gedaan zijnde, maekt elf, laat andermaal 3 vermenigvuldigen, maakt 33. vraegd nu wederom hoe veel negen daar in is, antwoort driemaal, soo verdubbeld dese drie en maakt 6, doed daar noch een by, en komt seven het gedagte getal.

XIX. Om te raden hoe veel oogen yemand onder en boven geworpen heeft.

Laat ymand werpen hoe dikmaals hy ook wil, soo sal yder dobbel steen onder en boven altijd 7 hebben. Soo hy nu met 2 steenen ses maal geworpen heeft, soo moeten daar onder en boven 84 oogen geweest zijn.

XX. Een andere Manier.

Laat ymand 3 gedagt hebben, doet het hem verdubbelen, maackt 6. teld daar 4 by komt 10. multipliceert met 5, maackt 50, teld daar twaalf by komt 62, multipliceert het selve met tien, komt 620, trekt hier van 320 af, rest 300, doet hier de laatste letters aan de regterhand weg, rest alleenlijk drie, welk het gedagte-getal is.

[p. 186]

XXI. De oogen te raden die met drie, vier of meer dobbel steenen geworpen zijn.

Om dit te doen, soo weet dat de oogen van yder steen altijd onder de tien zijn, en men kan de oogen van elke steen, ook voor een getal nemen dat ymand denkt. By exempel, ymand werpt met drie stenen, wanneer gy nu begerig zijt te weten, hoe veel ogen dat op elke steen in ʼt bysonder zijn, en op alle drie te samen, soo segd dat hy de ogen van de eene steen verdubbelde, en daar nog vijf by telle, en met vijf multiplicere, laat by yder uytkomst elf doen, laat dan de ogen van de andere steen by deese somma vergaderen, en dat dan met tien multipliceren. Eyndelijk, laat daar de ogen van de derde dobbel-steen by tellen; dit alles behoorlijk gedaan zijnde, soo vraagd na de uytkomst, trekt daar dan 350 af, en ʼt geen daar over is, zijn de ogen.

XXII. Om te raden verscheyde getallen die yemand denkt mits dat het getal minder zy dan tien.

Laat ymant gedagt hebben 3, 5, 8, 2, het eerste getal verdubbeld of met twee gemultipliceert komt 6, daar by 5 geteld komt 11, die met vijf gemultipliceert komt 55, daar by geteld maakt 65, hier by gedaan het tweede getal vijf, komt 70, dat door 10 gemultipliceert, brengt 700, hier by gevoegd het derde gedagte getal 8 komt 708, dit met 10 gemultipliceert, geeft 7780 daar by het vierde gedagte getal geteld, maakt 7082,

[p. 187]

trekt daar van af 3500, soo is ʼer overig 3582. Dit getal in ordre gesegt, is het eerste getal 3, het twede 5, het derde 8, en het laatsten 2.

XXIII. Een ander manier.

Laat yemand drie gedagt hebben, doet het verdubbelen, maakt ses, doet daar 5 by, komt 11, multipliceert het selve met 5 maakt 55, by welke tien vergadert, multipliceert nog eens met tien, rest 650 trekt daar 350 af, blijft 300 van welke het getal aan de linker-hant het gedagte getal is, te weeten drie.

Exempel.

[p. 188]

Een ander.

Laat yemand 9 gedagt hebben, doed hem dan noch een twede getal denken dat minder is als het eerste als 7, dat hy dan noch een getal denke dat soo veel meerder is als het eerste, als elf, doed hem dan dese twee laaste getallen te samen adderen, en die u seggen. Soo is de helft daar van het eerste gedachte getal, of soo gy al de getallen laat te samen rekenen soo is de derde part het gedagte getal.

Exempel.

9

___

7

11 addeert

___

18 de helft is

___

9

XXIV. Een ander.

Laat ymant 10 gedagt hebben, laat dat getal hem verdubbelen, komt 20, seghd dat hy daar 6, of meer na uw believen by teld, maakt 26, laat dit dan midden door delen, komt 13, dit gedaan zijnde, laat'er dan soo veel af doen als eerst gedagt is, blijft 3, als men nu begeert te raden hoe veel daar overigh blijft, soo doet midden door dat getal, dat gy daar hebt laten by doen 't welk dan drie is, en met dit overige getal drie over een komt.

[p. 189]

Exempel.

verdubbelt	10
	___
	20
teld	6
	___
de helft	___
	13
	___
	3

XXV. Om te weeten als men verscheyde dobbelstenen geworpen heeft, hoe veel het getal der oogen uytbrenght.

Laat ymand met drie stenen werpen, die geworpen heeft moet dan het getal van de ogen te samen rekenen, laat dan een steen leggen, en doed hem rekenen, de onderste ogen van de twee andere stenen, 't selve getal by het vorige rekenen. Laat dan noch eens werpen met de twee steenen, en rekend de ogen die boven zijn by het ander getal, laat dan weder een steen leggen, en rekend dan de ogen die onder de andere steen zijn, by het voorige getal. Doed dan noch eens werpen met de derde steen, en vergadert de ogen die boven zijn by de vorige somme, laat dese steen dan ook stil leggen gelijk de andere. Dit gedaan zijnde, moet ghy sien de oogen die boven op de steenen zijn, en teld daar 21 by, soo suld gy het kunnen raden.

By Exempel.

Soo in de eerste werp zijn geweest 3, 4, 2 welker somme negen maakt. Laat dan een steen alleen

[p. 190]

leggen, soo hy leyd, te weten drie, neemd dan de twee onderste oogen van de twee andere stenen, welk maaken de 3 en 5, teld die by de 9, maken 17, werpt dan weder met dese twee steenen, de bovenste oogen zijnde 6, 1 teld die by de 17, en maakt 24. Laat dan een apart leggen, teld dan de andere ogen van de andere steen by 24 en brengen uyt 25. werpt dan weder met de laatste steen, welk zijnde vergaderd die by 25, en maaken 26 besiet nu de oogen van de steen die boven leggen, welke zijn 5, teld daar 21 by, maekt 26. Welk het geraden getal is.

XXVI. Een Eeuwigh-duurende Almanach.

Dese Almanach werd aldus gesteld: Voor eerst dan stel ik de Sondaghs letters welke zijn volgende van yder jaar in 't toekomende.

Sond. Lett.	Jaren.
D	1682
C	1683
B A	1684
―	―
G	1656
F	1686
E	1687
D C	1688
—	—
B	1689
A	1690
G	1691
F E	1692
―	—
D	1693
G	1694

Jaren.	Sond. Lett.
1695	B
1696	A G
―	—
1697	F
1698	E
1699	D
1700	C B
—	—
1701	A
1702	G
1703	F
1704	E D
—	―
1705	C
1706	B
1707	A
1708	G E
―	―
1709	E
1710	D

[p. 191]

Nu volgen de Maanden, dagen en Sondagsletters in haar order.

April.	September.	Junius.	Augustus.	Majus.	January
30	30	30	31	31	31
			November.
			30
Juilius.	Decemb.	Februarius.	Maart.	October.
31.	31.	28.	31.	41.

			29
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	28
22	23	24	25	26	27	27
29	30	31
G	F	E	D	C	B	A
Sond.	Maand.	Dingsd.	Woensd.	Donder.	Vryd.	Sater.

Om nu te sien wat datum van het Jaar is, so weet men voor eerst het hoe veelste Jaar het is na Christi Geboorte, als ook de maand en dag der weke, als ymand dit in sijn hoofd heeft, kan hy lichtelijk te rechte komen.

By voorbeeld: Ik sie in de Tafel op het Jaar 1682 dat de Sondags letter een D is, so ga ik met dese D en sie wat voor een dag daar onder staat, so bevind ik Woensdag. Dan soo soek ik in de Maand in wat voor een regel hy staat en bevinde in de sevende October. Nu weet ik ten naasten by of ik in 't begin midden of eynde der Maand ben, en dewijl wy nu dit schrijvende op het eynde lopen, en heden Dingsdagh is, soo tel ik met mijn Woensdagh

[p. 192]

daar de sondags letter D op stond, en kom tot 21, welk is Woensdag, 22 Donderdag 23 Vrydag 24 Saturdag, 25 Sondagh, 26 Maandagh, ergo heden Dingsdag den 27 October.

Indien 't nu geheel aan 't eynde van de Maand is, dat is den 31 October, en ik wil weten den hoeveelsten ik morgen kan soeken. Soo speurt eerst uw Maand op, die November is in de vierde reye of order. Dan soo kom ik wederom tot mijn Woensdag, die in de reeks van die Maand op 4 vald, soo tel ik voort tot het eynd welke is Saturdag, en keer my weder tot het begin, soo vald Sondag op 1, want gisteren was het Saturdag den lesten October:

Noch dien ik hier te spreeken van de Schrickel-Jaren: al waar in de order twee letters gevonden werden: By voorbeeld, in 't jaar 1684 is B en A twee Sondags letters, soo regeerd B alleen tot Maart en A begint met de Sondag in Maart. Hier moet sorgvuldig opgelet werden, anders soude men ligtelijk konnen dwalen.

XXVII. Om de getallen op verscheyde manieren in Versen uyt te spreken.

In het duyts begrijpt de volgende Rijm alle de getallen.

1. 2. 3. 4. 5. 6. 7. 8. 9 t'saam,

Steld men alle de tallen sonder nul bequaam.

Vijf, twee, acht, negen, drie, seven, een, vier, ses

Vier, drie, seven, een, vijf, twee, acht, negen.

5. 2. 8. 9. 3. 7. 1. 4. 6.

4. 3. 7. 1. 5. 2. 8. 9.

Deese zijn alsoo te lesen in 't Latijn

[p. 193]

Quinque, duo, octo, novem, tria, septem, unum, quatuor, sex:

Sex, tri, septem, unum, quinque, duo, octo, novem.

Op die manier telt men ook in 't Neerduyts.

1, 2, 3, 4, 5, 6, 7, 8, 9 siet,

Ontrecht in maat-getal dat vliet.

XXVIII Een sonderlinge wens van een vogelaar.

Seeker Vogelaar gaande uyt schieten, vangt twe vogels, siende nog verscheyde anderen, wenschte dat hy noch soo veel, en dubbel soo veel hadde, soo souw hy met sijn twee honderd kunnen maken. Nu is de vrage hoe veel Vogels daar geweest zijn? Antwoord.

De vogels zijn geweest	14
Noch soo veel doen	28
En noch soo veel	56
Daar by getelt	2
	___
Maaken	100

XXIX. Het getal eenes Osses voetstappen te rekenen.

Imant vraegd my of ik wel tellen en na rekenen kan de voetstappen die sijn ploegende Os dien dag gedaan heeft, op het ploegde Land? hier een weynigh overpeynsende geef ik tot antwoord dat de voetstappen, die hy de gantsche dagh gedaan heeft, niet meer te sien zijn, veel minder te tellen en uyt te rekenen, dewijl de ploeg, de selve alles bedekt heeft So dat dit een vraag is om een konstig Reken meester te bedriegen.

[p. 194]

XXX. Waarom dat ʼer minder Wolven sijn dan Schapen.

Dit schint yet wonders te wesen, dewijl de Wolven veele in 't getal voortbrengen, en de Schapen maar een gelijk, en de Schapen gedurig tot nut van de menschen geslacht werden.

Maar men moet weten, dat al is't dat de Wolven veele te gelijk baren, de Schapen nochtans dikwijlder baren dan de wolven. Item dat de Wolven malkanderen in hongers-noot op eten, want sy komen in kringen by malkanderen loopen en vegten, die dan dood blijft is een aas voor de levende, welk gevegt soo lange duurt tot sy alle versadigt zijn.

XXXI. Hoe een egte Soon, zijnde de vierde binnen het Jaar dat zijn Vader trouwde, kan gebooren werden.

Wanneer ymand trouwd, kan het gebeuren, dat de Vrouw in d' eerste drie Maanden, elke staag een misval heeft, 't welk alle Maanden een zijnde, drie uyt maakt, nu als sy in de vierde Maand weder swanger is, en de negen Maanden vol uyt draagd, soo heeft sy vier kinderen binnen het Jaar gehad.

XXXII. Een aardige inhoud en uytcyferinge op een Bort by een Meester die de Cijfer-konst leerde, in School opgehangen.

Op dit Bort stond dan aldus geschreven.

Hoort Arithmeticasche geesten,
Twaalef Buyk-rommelingen maken een veeste.

[p. 195]

 

Twaalf Veesten gevangen in Neus of Mond,

 

Maken een wel-gesalmeerde Stront,

 

Twaalf Stronten, let hier wel op,

 

Maken soo veel Stront als een Schop.

 

Twaalf Schoppen Stronts afgestreeken met een Lemmer.

 

Vullen gesamentlijk eenen Emmer.

 

Twaalf Emmeren Stront, 't sy van Wiesen of Narren,

 

Maken uyt een volle Karre,

 

Twaalf Karren Stronts; 't sy klein of groot,

 

Vullen een volkomen Boot.

 

Twaalf Booten Stronts van Borgers oft Eelen,

 

Maaken uyt een heele Karveele,

 

Nu doet men weten en verstaan

 

Hoe veel Buyk-rommelinge in een Karveele Stront gaan?

Facit 3583 1808. Buyk-rommelingen

Uytscijferinge van de nevenstaande voorstellinge.

1 Veest maakt	12 Buykrommelingen,
	12
	—
	144 Stront
	12
	___
	288
	144
	___
	1728 Schop.
	12
	___
	3456
	1728
	___
	20736 Em:
	12
	___

[p. 196]

	41442
	20736
	___
	248832 Karren.
	12
	___
	497664
	248832
	___
	2985984 Boot.
	5971968
	12
	___
	5971968
	2985984
	___
Facit	35831808 Karvelen.

XXXIII. Van de Progressien en van de wonderbare meenigvuldige der dieren, planten, vrugten, Gout en Silver, als men altijt argumenteert met sekere proportie.

Hier sal ik u voorstellen niet min sekere ative als admirable dingen, maar soo seker en soo licht te bewijsen, dat men niet en behoeft al de getallen te multipliceeren, om daar van proeve te doen, en voor eerst.

XXXIV. Van de Mostert Saatjes.

Ik segge dat al het Saat dat in twintig jaar van een Mostert saatje sal voor komen, en soude niet konnen blijven in het geheele begrijp des Weerelts

[p. 197]

wanneer die schoon duysent maal grooter was als se is, en anders niet en hielde als kleyne mostert saatjens, van het middelpunt af tot boven aan het Firmament; dit wort beweesen als volgt, een plante van Mostert saat, kan alleen lichtelijk voortbrengen meer dan duysent korlen, maar later ons maar duysent nemen, en geduurende twintig jaaren, dat is 20 maal 1000 gemultipliceert, mits dat men al de Saatjes die yder jaar voort komen wederom saayt, die elkens een plant voortbrengen van 1000 saatjes, dit soo zijnde sal daar ten eynde van 17 jaaren een getal komen, dat soo veel sandts te boven gaan sal alsser leggen kan, tot het Firmament toe, want volgens de Rekening van Archimedes, en de aldersekerste opinie van de groote des Firmamends die ons Ticho Braht nagelaten heeft, soo kan het getal der sanden uytgedrukt worden met 49 cyfers, in plaats dat men voor het getal der Mostert saatjens in 17 jaare alreede 52 cyfers vint. En alsoo een Mostert saatje ongelijk grooter is als een sant korentje, 't is wel te gelooven dat voor de 17 jaar al het saat dat successivelijk van een saatje kan voort komen in het begrijp des heele Werelts niet soude konnen worden begrepen, en wat soude het dan zijn, soo men continueerde te multipliceeren elke reys met duysent tot 20 jaaren toe, 't is een saak soo klaar als den dag, dat de veelheyt der Mosters kroontjes honderd duysentmaal grooter soude zijn als de geheele Weerelt.

XXXV. Van de Biggens.

Is het niet een geneugelijke en een admirable propositie, dat men seyt dat de groote Turk met alle sijn inkomste niet een jaar lank soude konnen voe-

[p. 198]

den, alle de biggen, die in twaalf jaar tijds van een sog en van haar geslacht voort komen, en nogtans is het een waaragtige saake, want laat ons nemen datter een sog t'ener dragt 6 voort brengen kan, als twee Mannekens en 4 Vroukens, en dat yder Vrouke 12 jaaren lank soo veel Biggens voort brengt, men sal bevinden na experientie des tijts, meer dan drie en dertig miljoenen Biggens en soggen, en alsoo een kroon des jaars niet te veel is om soo een Beest te onderhouden en te voeden, want het geen twee penningen des daags en bedraagt, moest men ten minsten soo veel kroonen hebben om die een jaar lank te onderhouden, en alsoo den grooten Turk geen 33000 milioenen des jaars in te komen en heeft, is de propositie waaragtig.

XXXVI. Van de Graan Koorentjes.

Gy sult alle verwondert zijn, zoo ik segge dat een graantje Koorens, met al dat in den tijt van 11 Jaaren successivelijk of voort koomen kan, die getal Koorentjes uytbrengen sal 244.140.625.000.000.000.000. welke bedraagt 244 quintilioenen.

De sake gestelt dat men alle Jaar saayden, en dat yder saatje 50 Koorentjes voortbracht, het welke weynig is, want sy brengender somwijle 70, 80 ja 100 voort, ook wel meer, deese somme sal een cubyk Lichaam maaken van 244140 Fransche mijlen, gevende aan yder hondert Korentjes voor lenkte en diepte, en dien volgens soo gy naamd 244, 1400. Steeden soo groot als Parijs, haar gevende een mijl in 't vierkant, en hondert voeten in de hoogte, en de selve soude vol Kooren zijn van boven tot beneden, schoon dat daar anders niet in waar als Kooren, neemt nu dat een Maat

[p. 199]

ofte een Schepel soo veel water als een cubijkse voet, begrijpende een milioen Korentjes, soo komender 244. 140. 624. 000. 000. 000. Scheepels, een getal dat soo groot is, dat soo men het wilde laden in Scheepen, een 1004 Scheepels in elk Schip deede, men soude soo veel Scheepen behoeven, dat se de Oceaan qualijk soude konnen dragen, te weten 244: 140: 624: 000. 000. 000. En rekende yder Schepel teegen het vierde deel van een kroon, sullen de selve beloopen, 61: 635: 156: 250: 000: kroonen die ik niet geloove datter in de gantsche weerelt zijn, is het dan niet wel gemenageert, dat men een zaatje saaydt, met al daar in een heel jaar van voort komt, mids dat men Landryen hadden daar toe van noeden, en onder dien niets en consumeerden.

XXXVII. Van de Erweten.

Ik wil dat elke erwete 30 anderen voort brenge, en dat men al die daar van komt 12 jaren saayde; dit soo sijnde sal men bevinden 531: 441: 000: 000: 000: 000: Erweten, als men der 50 geeft voor de lengte, breete en dikte van een voet in 't vierkant, sullen de selve uytbrengen 4, 251. 528. 000. 000. Teerlingen voeten, laat uw een teerling voet: dat is een vierkante voet waardig zijn: een vierendeel van een kroon, soo sullen se meerder kroonen beloopen als der in de geheele Weerel zijn: namentlijk 1: 620: 882: 000: 000: kroonen, en soo ymant deese Erwete wilde verspreyde door de geheele Wereld, en soude het gantsche vlak van de Kloot der Aarde en van het water niet meede konnen bedekken, als, hy die maar leyde een erweet dik op malkanderen.

[p. 200]

XXXVIII Van de menigvulding der Menschen.

Daar zijn ʼer die niet begriepen konnen hoe het wesen mag, dat van 8 Personen die na de Sont-Vloed overbleven, te weeten vier Mans ende vier Vroewen, soo veel Menschen gesproten zijn, alsser behoefde om een monargie te beginnen onder Nimrots, en een Armade toe te rusten van 200 duysent Menschen, om trent 200 jaren na de Sont-vloet, maar de saake is so wonderlijk niet, als men neemt een van de Kinderen Noê, want merkende, dat de generatie sich over dertigh jaaren vernieuwen, en seven voudig vermeerderen konnen, van een familie vermenigvuldigen agtmaal hondert duysent Zielen ofte Menschen, in dese vernieuwinge des Werelds, waar in de Menschen doenmaals langer leefden, en meerder vrugt-baar waren; daar zijnder ook die het wonder geeft, het geen men leest van de Kinderen Israëls, dat sy van 70 in ʼt getal na 120 jaren soo vermeenigvuldigen, dat se sterk waren over de 600 duysent comparant personen sonder de Vrouwen, Kinderen, en ander oude, die bequaam waaren tot den oorlog: maar die anders effen rekeninge wilde maken, sal bevinden, dat de Familie van Joseph alleen bestant genoegh was om dit getal uyt te brengen, hoe veel te meer dan noch alle de huysgesinnen t' samen.

XXIV. Progressie of Voortgank lopende tot 64 toe.

Noch is het goed Matimaticus te zijn, om niet bedrogen te worden! Gy sult Luyden vinden, soo simpel, dat sy eenige koop sullen maken, met conditie van soo veel koorens te geven alsser van nooden sijn om te vullen 64 plaatse, leggende een

[p. 201]

koorentje in de 1 plaatse, 2 in de tweede, 4 in de derde, en so voorts, en sy en sien niet de goede luyden, dat alleen haar Solders, maar alle de Magesinen der Weereld, daar toe niet genoeg en zijn, want het getal van de koorentjes bedraaght over de somme van 184467440951615, het welk so groot is, dat men daar meede soude konnen laden 1779199825 Schepen, als yder Schip konde houden 2500 mudden koorn, dat lichtelik te ondersoeken is, en soo men wilde tellen soo veel Deniers alsser Greynen sijn, en dat reduceert, tot groot Gelt, het sal soodanigen schat uytbrengen, dat nog Crassus, nog Cresus, nog Thinnoyse, nog Spanjaarts, nog al de Prinsen der weerelt, het tiende deel daar van niet soude kunnen voortbrengen, daar sijn meer graan korentjes als deniers, nochtans is het kennelijk, datter in de gantsche Weerelt niet genoeg en zijn, om alle de voorgemelde Scheepen te laden. Nog was het een saake vry wat absurter, soo ymant aannam te vullen 64 Plaatsen, te weten soo veel alsser sijn in het Schaak-spel, ofte op het Dam-bort, voortgaande met 3 voudige proportie, want hy behoeven moeste 14456127343093749488594646427 graan koorentjes ofte deniers, en so dit weyt korentjes waren, en dat men daar de Scheepen meede wilden laaden, men soude een sulken schrikelijken getal Scheepen van doen hebben, dat se niet alleen den Oceaan souden bedekken, maar meer dan hondert milioenen golven, die so groot waren als het water en de Aarde t' samen, soo de Graan van Coriander waaren, men souden der meer dan 70 globen meede konnen stoffeeren, so groot als het Aartrijk, 't welk alles lichtelijk te reekenen is, soo men de Graantjes reduseert in eenige maten, en de lading der Scheepen considereert, vergelijkende een Graen Coriander met een ander dat grooter is, alles na de geometrische proportie.

[p. 202]

XL Van een Dienaar op sekere conditie aangenomen.

Een Dienaar seyt aen zijn Heer, dat hy te vrede is te dienen soo lank als hy leeft, als alleenlijk dat hy hem geve soo veel plaats Aarde als hy behoeft om te saayen een korentje Graans, met alles datter in acht jaaren van voort komen sal, meent ghy dat dit goede koop sy voor my, ik achte dat het een diefagtige koop is, want wanneer hy maar van doen had de vierde van een duym voor de plaatse tot yder korentie, en dat elk niet meer teffens voort bragt als 40 Graanen yder jaar, soo salder ten eynde van acht jaaren, koomen voor het getal der Koorentjes, ofte Granen 6553600000000, deese met 4 tot duymen gemaakt, alsoo het vierendeelen zijn, koomt 163840000000 duymen, laat nu 12 duymen een voet maken, soo gaander 144 duymen in het vierkant, in een voet door welke de voorige genoemde 163840000000 gedeelt zijnde, komt 11377777777 vierkant voeten, neemt nu dat een uure gaans in 't vierkant doen 324000000 voeten, hier door de vierkant voeten gedeelt zijnde, so komter voor het quotient over de 35 uren in 't vierkant, die mijn Heer den knegt om sijn kooren te saayen van doen sal hebben, dat by na een heele proventie is.

Vervolgh.

Deese laatste questie hebbe ik doorgaans moeten veranderen, en na onse styl voegen, alsoo die van den Auteur defect en vol fouten was, gelijk ik ook by na alle de anderen hebbe moeten veranderen, hier kon ik niet na laten een exempel by te

[p. 203]

voegen, dat eertijts gestelt is by Luddolf van Keulen, sijnde de laatste questie van zijn Algebra ofte konst vrage, staande in het Boek van den Sirkel, daar hy aldus spreekt.

Een Man brenght uyt Indien 40 Diamanten, welke meer dan hondert Ducaten waardig sijn, dese wil hy aan een ander verkopen, alsoo dat den kooper betaalen sal voor den eersten Diamant een Sant koorentie, voor den tweeden tien voor den derden 100 voor den vierden duysent, voor den vijfden 10000 en soo voort altijt voor de volgende Diamanten, tien maal soo veel sandt kornen als de naaste-voorgaande, en dat tot den veertigsten Diamant toe. De vraag is, of de kooper wel mogelijk is de Diamanten met het beloofde Sant te betalen? Antwoord onmogelijk.

Volght de bewijsinge.

Laat A…………………...B de lengte zijn van een duym breet, dese wert gedeelt in 30 gelijke deelen, dan werden gesien 30 spasien waar van tussen elk gaan 20 santies kornen in de lengte aan malkanderen rakende, en konnen leggen, nu ik neeme dat daar 100 leggen konnen, dat is, tusschen A ende B 300 leggen, als nu een voet lank is twaalf duym, dan komt voor een voet in de lengte 3600 sandt koornen, Item een grooten Duytse mijlen doet 22500 voeten, desen gemultipliceert met 36000 komt 810000000, en soo veel Sant-kornen digte aan malkanderen geleyt, sullen langer linen maken als een duytse myle, dese multipliceert met 5000 soo komt voor 5000 mylen lengte 40500000000000 sandt kornen diens quadraat is 16402500000000000000000000, dit quadraat is een korn dik, het welk gemultipliceert met sijn radix, maakt 6943012500000000000000000000000000-

[p. 204]

00000000, dit is een corpus van 4050000000000 sant koorn hoog, en dik, en grooter dan 5 Duysent duytse mylen, dik, lank, en breedt, het welk veel groter is dan de gantsche Weereldt, en by soo verre het Aartrijk met alles dat daar op ofte aanklevende is; Sant waaren, soo soud men nochtans den Diamant-koper niet kunnen betalen na sijn voorgaande begeeren.

Soo dat den laatsten Diamandt soude komen op 1000000000000000000000000000000000000000, dat veel meer is als het voorgevonde getal, en voor alle de Diamanten souden komen 1111111111111111111111111111111111111111 sant koornen, welk getal onmogelijk is te bekomen, ofte voor Menschen handen te tellen, maar een getal te vinden, dat de begeerde sanden te booven gaat, en veel duysent maal meer betekent, is ligt om te doen. Imand heeft bedongen een Put te graven 100 voeten diep, voor 50 Guldens, nu gebeurt het als den Put 80 voeten diep gegraven is, dat sy beyde onder malkanderen oneens worden, de vraag is hoe veel den Arbeyder van sijn arbeyt ontfangen sal? Facit 32 111/8 guldens, hier vallen twee progressie, de een beginnende van 1 tot 100, de andere van 1 tot 10, daar van soekt by de somme als 't volgt.

vergadert	1	1
tot	100	80
	___	___
komt	101	81
multipliceert met	50	40
	___	___
komt	5050	3240 somme.

[p. 205]

XLI. Hoe veel Silver draad men van doen heeft om die rondtom den gantschen Aertkloot te doen.

Om dit te doen, moet men weeten, dat uyt een loot Silver ses honderd voeten lang draad kan gemaakt werden. Soo men nu meent dat de Wereld in sijn omtrek 216000 mijlen heeft, soo geeven 14 Mijlen een pond, en 216000 mijlen 154 pond en vier veertiende pond, uyt welke men soo veel draat kan maaken, dat men sulks om de geheele Wereeld-kloot kan winden.