Streven. Jaargang 59

[p. 1187]

Een inleiding
Het quantumtheoretische debat
Etienne Klein

‘Papa, volgens Einstein... - Zwijg over die Einstein: ik wil geen ruzie met de buren’
Fernand Reynaud

In de eerste decennia van de twintigste eeuw hebben twee revoluties - de ontdekking van het quantum en van de relativiteit - de fysica tot in haar grondvesten doen trillen. Daarna is die fysica weer een machtige, bijna triomfantelijke wetenschap geworden. Zij behaalde ook echt indrukwekkende resultaten, zowel theoretisch als experimenteel. Maar paradoxaal genoeg is ze nu minder triomfalistisch, minder in zichzelf gekeerd dan in haar vroegere versie, de klassieke fysica: deels omdat ze weer op de grote vragen van de traditionele wijsgerige kenleer gestoten is (wat kan men kennen? wat is waarnemen?), deels omdat zij de metafysische vragen niet kan ontwijken waarop zij stoot aan de basis zelf van haar theorie en haar methode: wal is meten, wat is een object, wat is een verschijnsel?

De fysica beschrijft ons universum en levert dus stof voor een wijsgerige reflectie. Wil zij meer zijn dan loutere techniek of techno-wetenschap dan moet zij aantonen dat haar eigen kennis haar niet boven het hoofd groeit, dat zij ze scherp kan verwoorden en erover kan reflecteren, dat haar de fundamentele vragen niet ontgaan die opgeroepen worden door haar nieuwe vondsten. Het is duidelijk dat de quantumfysica - bijvoorbeeld - belangrijke theoretische consequenties heeft; eerlijkheidshalve moet men die onder ogen zien, ook als de studie ervan een moeilijke, riskante en soms esoterische arbeid is.

De grondleggers van de quantumfysica (met name Einstein, Bohr, Schrödinger, Heisenberg) hebben een berg wijsgerige arbeid verzet; zij schreven veel artikelen, die meer wetenschappelijk dan technisch waren en waarin zij blijk gaven van groot meesterschap over het vocabularium en de concepten van de klassieke wijsbegeerte. Allen hadden zij een gedegen kennis van Kant. Dit moet de hedendaagse fysici wel verbazen die volledig in beslag genomen zijn door een arsenaal van mathematische formules, het machtige instrumenta-

[p. 1188]

rium waarmee zij werken en de toenemende complexiteit van de organisatie van het onderzoek. Het is jammer dat zij nog zo zelden tijd vinden voor wijsgerige reflectie. Want (1) op die manier verzaken zij aan een brede cultuur waarin wetenschap, kunst en wijsbegeerte een samenhangend geheel vormen. En (2) nemen zij genoegen met het feit dat de methodes doeltreffend zijn en stellen zij zich niet meer de vraag wat er achter die doeltreffendheid steekt. Nu is het wel zo dat de grondleggers tot de filosofie kwamen omdat zij ertoe gedwongen werden en niet omdat zij er uit zichzelf zo naar verlangden. De quantummechanica heeft al met haar eerste aarzelende stapjes verwarring gezaaid in de geest van de fysici. Ze stonden voor reuzegrote vragen. Enkele hiervan dreven hen naar het terrein van de wijsbegeerte; er was geen ontsnappen mogelijk. Dit was geen dwaalweg, het was een doortocht die hun opgedrongen werd. Om dit te beseffen volstaat een wat uitvoeriger beschrijving van wat bekend staat als de proef van de twee spleten. De quantumfysica omvat wel meer dan de begrippen die men nodig heeft om deze proef nauwkeurig te beschrijven, maar alle vragen die bij de studie van de quantenleer opduiken komen al in aanzet voor bij deze proef, met name de centrale vraag over het meten. Bovendien staan alle quantumparadoxen, b.v. die van de kat van Schrödinger en vooral de beroemde EPR-paradox er min of meer direct mee in verband¹.

1 Einstein wees al vlug de gangbare interpretatie van de quantenleer af (‘Kopenhaagse’ interpretatie genoemd omdat zij vooral door de Deen Niels Bohr voorgestaan werd). Zijn bezwaren zijn het best verwoord in een beroemd artikel van 1935 dat de kern beschrijft van wat sindsdien de EPR-paradox (Einstein, Podolsky, Rosen) heet. Met een methode die hij graag gebruikte - nl. het ontwerpen van zogeheten gedachtenexperimenten - probeerde Einstein daarin aan te tonen dat de quantenmechanica niet af was.

De proef met de twee spleten

‘Courons à l'onde en rejaillir vivant!’
Paul Valéry, Le Cimetière marin

Licht is altijd beschouwd als een zonneklaar, éénduidig fenomeen; het is trouwens het symbool van helderheid. In het boek Genesis staat dat het licht geschapen is op de eerste dag; het was in de wereld voor alle complexiteit, die daarna alsmaar toenam. Toch is dit verschijnsel, dat voor ons zo onmiddellijk in verband staat met de zintuiglijke waarneming van de wereld en onze visuele indrukken, algauw een mysterieus gegeven. ‘Er zou voor ons veel duidelijk worden’, zegt Louis de Broglie, ‘als we wisten wat een lichtstraal is’.

Waaruit bestaat licht? Isaac Newton dacht dat het samengesteld is uit deeltjes omdat hij zag dat schaduwen scherp afgelijnd zijn, niet wazig. De weerkaatsing in een spiegel b.v. verklaarde hij als het terug stuiten van deeltjes op het spiegeloppervlak. Zijn tijdgenoot de Hollandse fysicus Christiaan Huyghens daarentegen meende dat licht een soort golf is.

Als wij een touw spannen en één uiteinde ervan op en neer bewegen, zien wij een golf die zich voortplant in de lengterichting door het touw, zonder dat dit ons uit de hand glipt om achter de golf aan te gaan. In tegenstelling tot deeltjes vervoeren de golven ‘niets’; zij brengen alleen energie en informatie

[p. 1189]

over. Omdat er verschil is tussen het werpen van een steen en de beweging van een golf, lijken de golftheorie en de deeltjestheorie volkomen onverenigbaar. De natuur heeft moeten kiezen tussen de twee.

De deeltjestheorie van Newton heeft eerst de golftheorie verdrongen, vooral (maar niet uitsluitend) vanwege het overweldigende gezag van de man die de geheimen van de zwaartekracht ontsluierd had. Maar dit was geen blijvende overwinning. In 1800 reeds kwam de Engelse fysicus Thomas Young er tegen op. Hij was tot de bevinding gekomen dat het licht wel op een heel vreemde manier het plusteken van de wiskunde verstond. Licht dat aan licht toegevoegd wordt kan duisternis geven! Dit was maar één van de verschijnselen (hij gaf ze de naam lichtinterferenties) die blijkbaar niet door de deeltjestheorie te verklaren waren (Hoe zou een deeltje een ander deeltje kunnen teniet doen?). De golftheorie kan dit verschijnsel wel verklaren: wanneer twee stelsels golven in het water elkaar ontmoeten, zijn op bepaalde punten de golven altijd tegengesteld in fase (de golfberg van de ene valt samen met het golfdal van de andere, en omgekeerd). Op die punten heffen de golven elkaar dus altijd op. Als het nu om lichtgolven gaat, zullen - door hetzelfde effect - die punten donker zijn. De golftheorie geeft dus wel een verklaring van het verschijnsel dat het voegen van licht bij licht duisternis kan veroorzaken.

Na veel tegenkantingen haalde de golftheorie het met glans. Maar tegen het einde van de 19e eeuw brachten proefnemingen een aantal fenomenen aan het licht waar zij geen verklaring voor had (het meest bekende is het foto-elektrisch effect). Omwille van die verschijnselen stelde Einstein in 1905 een gedurfde terugkeer naar de deeltjestheorie voor: de interactie tussen een elektromagnetische golf en de materie verloopt in elementaire ondeelbare stappen, waarbij de straling als het ware uit deeltjes bestaat, de fotonen, die elk een hoeveelheid energie dragen evenredig aan de gegeven frequentie. Moeten we dan de golftheorie opgeven? Men is geneigd ja te antwoorden, want we hebben gesteld dat de twee theorieën elkaar uitsluiten. Wint de ene, dan verliest de andere. Maar het antwoord is ‘nee’: Newton had bijna gelijk, Huyghens had niet helemaal ongelijk! Dat is de paradox die lange tijd² voor verwarring zou zorgen, tot de quantenleer in de jaren twintig de fysica uit het sukkelstraatje zou halen. Om te begrijpen waaruit precies de paradox bestaat in de hypothese van het foton, moeten we teruggaan naar de verrassende proef met de twee spleten, waaruit Young zijn doorslaggevende argumenten geput had.

Stel je een machine voor die knikkers afschiet naar een muur waarin twee evenwijdige spleten zijn, dicht bij elkaar. Laten we aannemen dat zij al de knikkers afschiet met dezelfde snelheid maar in alle mogelijke richtingen. Een eind verderop worden dozen opgesteld om de knikkers in op te vangen die door de spleten gingen. Zij geven ons een aanwijzing waar de knikkers terechtgekomen zijn. De meeste knikkers slaan tegen de muur; een aantal schieten door de eerste spleet, rechtdoor of na terugkaatsing op een van de

2 Einstein besefte dat hier een historisch debat uit zou groeien. In 1909 al zei hij: ‘Ik ben overtuigd dat wij in een volgende ontwikkelingsfase van de fysica tot een theorie over het licht zullen komen die kan beschouwd worden als een soort fusie van de golftheorie en de deeltjestheorie’ (aangehaald door Abraham Pais in Subtle is the Lord). Deze bedenking is destijds nauwelijks opgemerkt; ze was echter de aanzet van de quantentheorie.

[p. 1190]

randen; en nog een aantal gaan zo door de tweede spleet. Als na een groot aantal schoten de knikkers in iedere doos geteld zijn, leidt men uit het aantal knikkers in de verschillende dozen af met welke waarschijnlijkheid de knikkers op een bepaalde plaats terecht komen. Het totale aantal knikkers in een doos is de som van het aantal knikkers die door spleet 1 en het aantal knikkers die door spleet 2 geschoten zijn. Als men nu afspreekt de eerste wit te kleuren en de tweede zwart, bekomt men een resultaat als getekend is in figuur 1. In dit geval komen er geen interferenties voor.

Bestaat, zoals Einstein beweert, het licht uit fotonen, dus a.h.w. uit kleine knikkers, dan moet het resultaat zijn zoals we het net beschreven hebben, d.i. zonder interferenties. Maar Young had heel bepaald gemerkt dat het licht wel interferenties geeft. Hoe kunnen deeltjes interfereren zoals golven?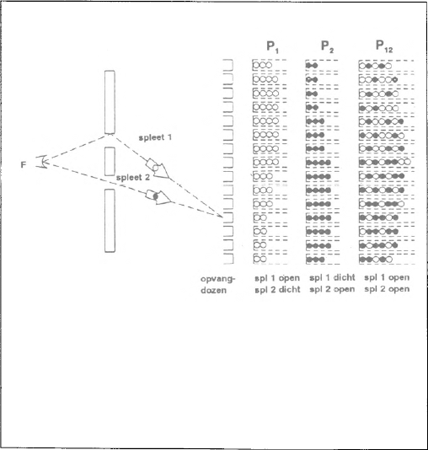

FIGUUR 1: Proef van de twee spleten, uitgevoerd met knikkers. Omdat iedere knikker slechts door één spleet schiet, kan men in het wit de knikkers tekenen die door spleet 1 en in het zwart de knikkers die door spleet 2 gegaan zijn. De waarschijnlijkheid P₁₂ dat een knikker in een bepaalde doos terecht komt als de 2 spleten open zijn is de som van de waarschijnlijkheid P₁ dat hij er terechtkomt als alleen spleet 1 open is en de waarschijnlijkheid P₂ dat hij er terechtkomt als alleen spleet 2 open is. Interferenties treden niet op.

[p. 1191]

Laten we de proef opnieuw doen, maar nu met elektronen. Een elektronenkanon schiet tegen een plaat met twee spleten elektronen af die allen dezelfde energie bezitten. De detector achter de plaat is een scherm, bedekt met een chemisch produkt dat wit wordt waar een elektron inslaat. Hoe ziet die plaat eruit na het afschieten van een groot aantal elektronen? We verwachten hetzelfde resultaat als bij de knikkers omdat we aannemen dat elektronen niets anders zijn dan heel kleine knikkertjes. Maar tot onze verrassing zien we op het scherm interferenties ontstaan, analoog aan de interferenties bij licht (zie fig. 2). Hoe moeten we dit nu begrijpen? Einstein zegt wel: ‘het licht, dat interferenties veroorzaakt in de vorm van golven, bestaat uit fotonen’, maar elektronen, die men altijd rangschikt bij de deeltjes, doen interferenties ontstaan! Zitten er dan knikkertjes in de golven en golven in de knikkertjes?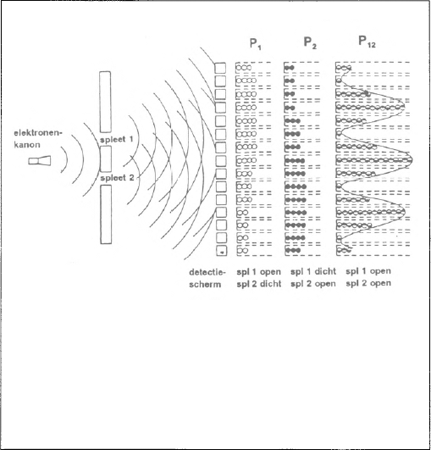

FIGUUR 2 Proef van de twee spleten, met elektronen. Sluit men spleet 2 dan is de verdeling van de inslagen der elektronen op de detector zoals bij de knikkers. Omdat we dan zeker weten dat ze door spleet 1 geschoten zijn, kunnen we afspreken ze wit te kleuren. Sluit men spleet 1 en laat men spleet 2 open dan gaan ze noodzakelijk door spleet 2 en we kleuren ze zwart. Maar als we beide spleten open laten, weten we niet meer door welke spleet ieder elektron gekomen is (we kleuren ze half wit en half zwart) en zien we een figuur met interferenties ontstaan.

[p. 1192]

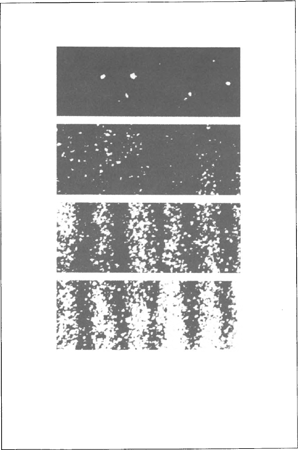FIGUUR 3 Resultaat van de proef van de twee spleten, uitgevoerd met elektronen die één voor één uitgestuurd worden. De inslagen van de eerste elektronen lijken elk afzonderlijk ontstaan en willekeurig gespreid te zijn. Gaandeweg echter ziet men een figuur van interferenties ontstaan, wat altijd beschouwd is als een eigenschap van golven.

[p. 1193]

Laten we het eens meer in detail bekijken. We laten het kanon langzamer schieten: de elektronen vertrekken één voor één, zodat de start en de inslag van ieder afzonderlijk kan worden waargenomen. Dan ziet men (fig. 3) dat ieder elektron inslaat op een heel bepaald punt van de detector. Het valt niet uiteen. Het is dus geen louter golfverschijnsel; een golf zou zich over het hele oppervlak uitbreiden. We zien ook dat de inslagen willekeurig verspreid liggen: hier één, daar één. Is het elektron dan een soort wispelturig deeltje dat grappen uithaalt? Maar gaandeweg, naarmate het aantal inslagen van elektronen toeneemt, verschijnt op het scherm weer een figuur van interferentiebanden! De elektronen worden dus individueel gedetecteerd, zoals deeltjes, maar tussen het kanon en het detectiescherm lijken zij zich te gedragen als golven!

We zetten nu onze inzichten ordelijk op een rijtje en doen beroep op een beetje ‘gezond verstand’.

a) De elektronen zijn één voor één uitgestuurd; het gaat dus om fenomenen die onafhankelijk zijn van elkaar.

b) Ieder elektron moet wel door één van de spleten geschoten zijn.

c) We kunnen meten door welke spleet ieder elektron ging.

d) Door die meting vallen de elektronen in twee groepen uiteen: die door spleet 1 gingen en die door spleet 2 gekomen zijn.

e) Voor degene die door spleet 1 gingen is alles verlopen alsof spleet 2 dicht was (en omgekeerd voor de andere groep).

f) Op ieder punt van de detector zou men dus (zoals bij de knikkers) een aantal elektronen moeten vinden gelijk aan de som van de elektronen die door spleet 1 gingen plus de elektronen die door spleet 2 gingen.

Maar we hebben gezien dat de proef helemaal niet dit resultaat geeft. En, vreemd genoeg, het openen van een tweede spleet - d.i. een tweede doorgang bieden aan het elektron - belet dit elektron bepaalde plaatsen te bereiken (dan verschijnen er namelijk donkere banen). Dus moet onze manier van redeneren ergens fout zijn.

Om meer duidelijkheid te verkrijgen, doen we de proef opnieuw, maar nu meten we eerst door welke spleet elk elektron gaat, door er een lichtstraal op te richten. We plaatsen daarom een lichtbron achter de plaat met de spleten en zorgen ervoor dat bij de doorgang van een elektron door de eerste spleet een foton dat uit spleet 1 vertrekt als zodanig gedetecteerd wordt: hetzelfde geldt voor de doorgang van een elektron door de tweede spleet dat als een foton uit spleet 2 herkend wordt. Deze opstelling stelt ons in staat om alle elektronen te ‘kleuren’, wit als ze door de eerste spleet en zwart als ze door de tweede spleet geschoten zijn. We sluiten eerst spleet 2. De witte elektronen verspreiden zich zoals in fig. 4 afgebeeld is. Nu sluiten we spleet 1 en maken spleet 2 open. De zwarte elektronen verspreiden zich symmetrisch ten opzichte van de witte elektronen. Nu maken we de twee spleten tegelijk open. Het resultaat is alweer verbijsterend: we wéten nu wel door welke spleet elk van de elektronen geschoten is, maar de interferentiepatronen zijn verdwenen!

[p. 1194]

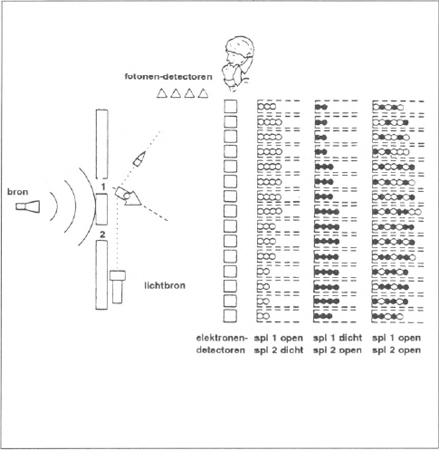FIGUUR 4 We willen meten door welke spleet ieder elektron geschoten is: dan kunnen we het wit of zwart tekenen naargelang de spleet waar het door ging. Maar het interferentiepatroon is verdwenen!

We zien nu net hetzelfde fenomeen als bij de knikkers! (fig. 1)

Samengevat: als we meten door welke spleet de elektronen gaan, zien we geen interferentie meer. Het is een andere proef. En omgekeerd, wanneer interferenties te zien zijn is fysisch niet uit te maken ‘door welke spleet het elektron gegaan is’. Men mag dus niet langer vooropstellen dat het waarnemen van interferenties kan samengaan met het meten door welke spleet de elektronen gegaan zijn. Zo komen we tot vier fundamentele bedenkingen:

- We moeten aannemen dat het voor een elektron dat door een van de spleten gaat een essentieel verschil maakt of de andere spleet al dan niet gesloten is.

- Vóór wij maten door welke spleet de elektronen gingen, waren zij nog in staat om te interfereren. Na het meten waren zij daar niet meer toe in staat. Zij zijn ‘verstoord’ door het meten. In de quantumfysica brengt een meting een verstoring teweeg in het gemeten systeem. Dit is een nieuwe wetmatigheid:

[p. 1195]

voordien namen wij algemeen aan dat het altijd mogelijk is meetinstrumenten te ontwerpen waarvan wij de invloed op het systeem zo klein konden maken als wij maar wilden.

- Het begrip baan, een van de fundamentele elementen in de fysica van Newton, heeft zijn betekenis verloren. Wanneer wij interferenties waarnemen, kunnen wij niet bepalen waar de elektronen een ogenblik daarvoor voorbij gekomen zijn.

- Van een bepaald elektron kan men niet vooruit met zekerheid zeggen waar het op het detectiescherm zal inslaan. Toch zijn de omstandigheden bij het afschieten voor ieder elektron gelijk. Dus geldt niet meer de klassieke opvatting dat de initiële omstandigheden volledig de verdere beweging van een deeltje bepalen. Dit is het einde van het klassieke determinisme.

De quantenleer verklaart deze vreemde feiten door het concept in te voeren van de dualiteit golf - deeltje, waarvan Louis de Broglie al in 1923 een vermoeden had. Dit concept is een aanvulling van Einsteins idee dat er deeltjes zijn in de golven, door te stellen dat er, omgekeerd, golven voorkomen in de deeltjes. Alle deeltjes, zowel van licht als van materie, vertonen een facet dat afhankelijk is van onze manier van waarnemen. Zij zijn niet te herleiden tot het éne aspect van hun verschijningsvormen. Vandaar het idee dat Niels Bohr opperde: de twee aspecten van de dualiteit golf - deeltje zijn complementair.

De epistemologische schok

‘Les inventions d'inconnus réclament des formes nouvelles’
Arthur Rimbaud in een brief aan Paul Demeny

De omwentelingen in de fysica hadden onvermijdelijk een weerslag op het domein van de epistemologie. Vier grondbeginselen van de epistemologie. gebaseerd op de klassieke fysica, komen weer op de helling te staan.

Het eerste: de algemene geldigheid van de natuurwetten. Volgens de klassieke leer zijn de wetten van de fysica van toepassing op alle grootteschalen. De quantumfysica doet deze hypothese teniet. We vinden in het universum niet tot in het oneindig kleine een verkleinde afbeelding van het oneindig grote. Er is een breuk tussen die twee schalen. Er gaapt een kloof tussen het atoom en het planetair model dat men aanvankelijk gebruikte om het atoom af te beelden. Begrippen die totaal evident leken, die niemand ooit zou gewaagd hebben a priori in twijfel te trekken, blijken alle betekenis te verliezen aan de grenzen van de materie. Zo moesten de begrippen ‘plaats’ en ‘snelheid’ radicaal herzien worden wegens de onzekerheidsrelatie van Heisenberg, die stelt dat men op het niveau van de quanten niet meer kan spreken van een welbepaalde plaats en snelheid: het is niet mogelijk dat beide tegelijk een

[p. 1196]

precieze waarde hebben. De elementaire begrippen blijken tekort te schieten om het oneindig kleine te beschrijven.

Tweede aangevochten beginsel: in wezen zijn de krachten in de natuur niet discontinu. Met de quantumfysica wordt een fundamentele discontinuïteit ingevoerd die behoort tot het begrip zelf van het quantum van activiteit. Max Planck bedacht dit in 1900 om het veelbesproken raadsel van de straling van een ‘volmaakt zwart lichaam’ te verklaren. Het probleem was het volgende: iedere brok materie begint te stralen als men het verhit, van rood tot wit naarmate de temperatuur stijgt. De verandering van kleur wordt niet bepaald door de stof waaruit het oppervlak bestaat: voor een volmaakt zwart lichaam is ze uitsluitend afhankelijk van de temperatuur. Dus is de straling van het zwarte lichaam bij hoge temperatuur een eenvoudig fenomeen waarvoor een eenvoudige verklaring moet mogelijk zijn op basis van de bekende wetten van straling en warmte. Maar wanneer men deze wetten toepaste, was het resultaat helemaal niet in overeenstemming met de metingen. Vanaf 1895 probeerde Planck het spectrum van de thermische straling met een eenvoudige mathematische formule weer te geven. Hij vond er een die perfect de meest nauwkeurge metingen weergaf op voorwaarde dat er een minuscule constante h - de constante van Planck - ingevoerd werd. Wat kon de verklaring zijn van deze nieuwe formule? Planck ontdekte dat alles verliep alsof de stralende atomen aan de oppervlakte van het lichaam hun energie maar konden uitwisselen in de vorm van kleine pakketjes, de quanten. Dit ging zo fundamenteel in tegen het idee dat alle uitwisselingen van energie een continu verloop kennen dat hij zelf nauwelijks kon geloven dat zijn ‘oplossing’ iets meer was dan een louter mathematische constructie. In de daaropvolgende jaren veroverde de constante h de hele fysica. Nu blijft er maar één domein meer over dat de aanvallen van de quantentheorie doorstaan heeft, dat van de zwaartekracht.

Derde beginsel van de klassieke epistemologie: er bestaat, onafhankelijk van de waarnemer, een werkelijkheid die door de fysica beschreven kan worden. Die overtuiging heeft men moeten opgeven. Wat de fysica bestudeert zijn geen gebeurtenissen die niet reageren op de blik van de mens die ze bestudeert, maar ‘fenomenen’, d.i. ondeelbare entiteiten bestaande uit het object én de meetapparatuur. De waarnemer in de generische betekenis (niet als afzonderlijk individu) maakt deel uit van het ‘schouwspel’. In het begrijpen van ieder denkbaar fenomeen speelt de meetapparatuur een essentiële rol. Zo bleek uit de proef met de twee spleten dat het de omstandigheden van de proefneming zijn die bepalen of het golf-aspect dan wel het deeltjes-aspect van de partikels waarneembaar is.

Het vierde in twijfel getrokken beginsel: De fysische wereld kan beschreven worden met behulp van de gewone taal. De ontwikkeling van de moderne fysica heeft aangetoond dat gezond verstand niet toereikend is voor het opstellen van theorieën en het begrijpen van de resultaten van bepaalde experimenten. Het lijkt wel of de fysici er een spelletje van gemaakt hebben

[p. 1197]

om stuk voor stuk al wat wij eenvoudig en voor de hand liggend vinden om te keren. Elementaire inzichten, die ons de zuivere logica leken, blijken nu niet meer te zijn dan het bezinksel in onze geest van ervaringen uit het dagelijkse leven. Eenvoudige ideeën, die dag in dag uit hun deugdelijkheid bewijzen, zijn afgewezen als fout of onbruikbaar en de droom om het gebouw van de wetenschap op te trekken met de ruwe bouwstenen van de waarneembare wereld is verzwonden. De Meccano heeft afgedaan. De wereld van de partikels is geen apparaatje, geen horloge in het klein. Het atoom heeft de fysici ertoe gedwongen uiterst ingewikkelde wiskundige methodes te gebruiken. De basis van de moderne fysica is geen materieel object meer, maar een geheel van wiskundige structuren, formules en symmetrieën, scheppingen van de geest waarbij moeilijk uit te maken is wat er in de werkelijkheid aan beantwoordt. Alleen de wiskunde lijkt in staat om de echte samenhang van de werkelijkheid ‘weer te geven’. Die ontwikkeling roept veel vragen op: duidt ze op een soort verwantschap tussen de materie en de geest? Of is de wiskunde maar ten tonele verschenen omdat de fysica een nauwkeurige, niet ambivalente taal vereist?

Tenslotte is er het probleem van het meten in de quantenmechanica. Dit is veruit het neteligste en het laat ons pas goed de omvang van het probleem zien. Bij de proef van de twee spleten zagen we dat de interferenties maar optraden wanneer er niet gemeten werd door welke spleet de elektronen gingen. Zij ontstaan doordat de fenomenen ‘een elektron gaat door spleet 1’ en ‘een elektron gaat door spleet 2’ elkaar overlappen, ook al gaat ieder elektron afzonderlijk door een spleet. De quantumfysica geeft dit weer met een wiskundige functie, de golf-functie. waarvan de structuur op beide fenomenen slaat. Die overlapping blijft duren zolang we geen meting uitvoeren op het systeem. Doen we dit wel, dan houdt ze onmiddellijk op. Proberen we te weten te komen door welke spleet het elektron geschoten is, dan doen we het elektron zich gedragen als een knikker. Bovendien heeft het elektron, voor het het detectiescherm bereikt, het voorkomen van een golf die zich door de hele ruimte voortplant, maar bij het bereiken van het scherm blijkt het in te slaan op een wel omschreven plaats. A priori kon het elders inslaan, omzeggens overal buiten de donkere banen. De kans dat het op dit bepaalde punt inslaat viel overigens te berekenen vanuit de gegeven golffunctie. Maar van alle mogelijkheden wordt er telkens maar één gerealiseerd; wanneer een elektron op een bepaald punt inslaat, ziet het af van alle andere mogelijkheden. De veelheid aan mogelijkheden bestaat niet meer. Bestaat er een mechanisme dat verantwoordelijk is voor de reductie van de bundel golven, dat de overgang zou kunnen veroorzaken van mogelijkheid naar werkelijkheid? Wat valt er over een elektron te zeggen vóór het waargenomen is? Ieder antwoord op deze vragen (waarin het probleem van het meten verwoord is) is ingegeven door een bepaalde voorstelling van de realiteit en van de kennis die men ervan kan hebben. Geen enkel antwoord vindt algemene instemming.

[p. 1198]

Over al deze thema's, die de kern raken van de fysica van de twintigste eeuw, wordt er nog voortdurend gedebatteerd. Verrassende experimenten maken dat ze actueel blijven en dat de fysica afstand neemt van de materialistische kijk op de wereld die haar tegen het einde van de 19e eeuw kenmerkte. Zijn wij erin geslaagd deze nieuwe gegevens te integreren in ons denken? Hopelijk zal er in de toekomst meer aandacht besteed worden aan deze inzichten, want ze zijn een deel van de hedendaagse cultuur.