De Gids. Jaargang 147

H.J.M. Bos
Over de rekenkunde by de Romeinen

[Ik verzamel ingrediënten voor een verhandeling of een opstel, eerst uit Guitel, Hist. comp. d. num. écr., hoofdstuk ‘Rome’:] De Romeinse getalnotatie (i, ii, iii, iv, v, ...); het is geen handig systeem [inderdaad]; de oorsprong van de getaltekens is zeer onzeker, wellicht zijn het letters van een eerder alfabet die niet meer gebruikt werden. werd ⊥ werd L voor 50; ⊕ werd C voor honderd, ↀ werd M voor 1000, de rechterhelft van ↀ, dus ⫐, werd D voor 500; de oorsprong van x en v is duister. Het ‘aftreksysteem (iv voor 4, n.l. 5-1, ix voor 9 et cetera) is een latere toevoeging. Varianten van de tekens [dat zijn er heel veel en boven de 5000 wordt het helemaal een jungle] - [Dit is niet leuk, Guitel babbelt maar door en wordt soms zelfs geëxalteerd: ‘En vérité, notre indulgence vient de ce que nous ne pouvons dissimuler la joie que nous éprouvons en découvrant que les Latins...’ et cetera (p. 220) Ik ga hier niet mee verder.]

[Tropfke, Gesch. elem. Math., geeft bruikbaarder informatie:] Uit ↀ voor duizend ontstonden de letterkombinaties CIƆ (de laatste letter is dus een omgedraaide c) en IƆ voor 1000 en 500; de schrijfwijzen M voor CIƆ, D voor IƆ en het aftreksysteem zijn pas in de middeleeuwen ingeburgerd. Dat M voor Mille en C voor Centum staat zou een toevalligheid zijn.

[Boeiend is het niet; over dus naar de breuken

[p. 640]

bij de Romeinen, uit Friedlein, Zahlzeichen u. elem. Rechnen d. Griechen u. Römer (‘Herrn Schulrath Dr. Christoph Elsperger zur bevorstehenden Feier fünfzigjährigen verdienstvollsten Wirkens im Schulamte in aufrichtigster Verehrung gewidmet’ - geen gevaar voor exaltatie daar):] Het belangrijkste systeem is gebaseerd op deling van de munt as in 12 unciae; de notatie heeft niets met die der gewone getallen te maken; de namen der breuken. [Die namen zijn interessant vanwege de gecompliceerde structuur der twaalfdeling die erachter zit, een aftreksysteem en een curieuze uitdrukking voor 2/3, namelijk ‘twee delen’, blijkbaar bedoeld bij deling in drieën. Ik maak een tabel met zo letterlijk mogelijke vertaling:]

breuk	notatie	naam	vertaling
1/12	-	uncia	ons
2/12 = 1/6	=-	sextans	zesde
3/12 = 1/4	=-	quadrans	kwart
4/12 = 1/3	==	triens	derde
5/12	==-	quincunx	vijfons
6/12 = 1/2		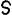semis	half
7/12		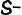septunx	zevenons
8/12 = 2/3		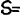bes	tweedeel
9/12 = 3/4		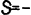dodrans	kwarteraf
10/12 = 5/6		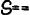dextans	zesderaf
11/12		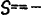deunx	onseraf
(12/12 = 1)		(as)	(hele)

Nog een paar kleinere breuken, ook aan geld ontleend, hadden aparte namen, bijvoorbeeld 1/8 (sescuncia, anderhalfons), 1/24 (semuncia, halfons) 1/72 (sextula, zesdetje). Dat was genoeg voor breukrekenen [het systeem is zeker rijk genoeg voor de meeste in de praktijk voorkomende berekeningen]. Deze breuken werden eeuwenlang op scholen aangeleerd, vermenigvuldiging werd erg moeilijk gevonden, er waren tafels [om uit het hoofd te leren en dat zou dus, vertaald, bijvoorbeeld zo klinken:

Breuktafel van 5: vijf keer ons is vijfons/ vijf keer zesde is zesderaf/ vijf keer kwart is een en kwart/ vijf keer derde is een en tweedeel/ vijf keer vijfons is twee en ons/ vijf keer half is twee en half/ vijf keer zevenons is twee en onseraf/ vijf keer tweedeel is drie en derde/ vijf keer kwarteraf is drie en kwarteraf/ vijf keer zesderaf is vier en zesde/ vijf keer onseraf is vier en zevenons/ vijf keer een is vijf.

Dat zou ik een klas wel eens willen horen opzeggen.] Tropfke vermeldt nog (p. 104) enige dichtregels van Horatius waarin een rekenles beschreven wordt: ‘... Dicat/ Filius Albini: si de quincunce remota est/ Uncia, quid superat? Poteras dixisse! “Triens”. Eu!/ Rem poteris servare tuam. Redit uncia, quid fit?/“Semis!”’ [‘Jouw beurt, de Wit: Als je een ons van vijfons aftrekt wat houd je dan over? Kom, je had het al kunnen zeggen! “Derde.” Best, jij wordt een goede zakenman. En als je er een ons bij doet, wat krijg je dan? “Een half!”’]

[Verder zijn er natuurlijk allerlei varianten van woorden en notatie en rekenwijzen geweest - voer voor feitenweters. Ik stop; het wordt anders te veel en zeker te vervelend. Het zou leuk zijn als er nu een meneer was (uit Schiedam, stel ik me voor) die aan ‘Wie Weet Waar Willem Wever Woont’ vraagt wat zo'n omgedraaide C in Romeinse cijfers nou betekent, of waarom er op de klok iiii staat in plaats van iv, en als er een schoolklas was (vijfde klas Christelijke Basisschool uit Mussel in Drente, om maar wat te noemen) die vraagt: hoe schrijf je 1/2 in Romeinse cijfers? Dan zou dit net een bruikbaar verhaaltje opleveren.]