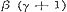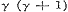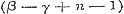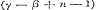De Gids. Jaargang 13
(1849)– [tijdschrift] Gids, De–
[pagina 373]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bibliographisch album.Gronden der Hoogere Algebra, door W. Smaasen, Math. Mag. Phil. Nat. Dr., Leeraar in de Wiskunde aan het Gymnasium te Kampen. Rotterdam, 1849.1. De ontwikkeling der functien in reeksen, wier termen, hetzij naar de opklimmende magten van de veranderlijke grootheid, of naar die van eenige functie derzelve gerangschikt zijn, - hetzij door eenige goniometrische functie van de opvolgende veelvouden dier grootheid worden voorgesteld, werd reeds door de oudere Analytici als een hoogst belangrijk onderwerp behandeld. Dan de wijze dier behandeling strookte niet met het doel, dat men zich voorstelde: men wilde toch tot mathematische, dat is, ware uitdrukkingen geraken, en zocht dit langs wegen en door middelen, die de wiskundige zekerheid misten. Het gebruik der reeksen, zonder van hare convergentie verzekerd te zijn, - de toepassing van de theorie der onbepaalde coefficienten, zonder vooraf het bestaan van den onderstelden vorm der reeks betoogd te hebben, geven er zoo vele voorbeelden van. Eerst sedert Cauchy de convergentie en divergentie der reeksen aan eene bijzondere, wiskundige beschouwing onderwierp, en anderen het voetspoor van dien geleerde zijn gevolgd, is ook dat gedeelte der Wiskunde tot dien trap van juistheid en volkomenheid opgevoerd, die noodig was, opdat het tot grondslag van verdere redenering zoude kunnen strekken. Dit onderzoek is daarenboven ook niet zonder vrucht gebleven ter vermeerdering van onze kennis omtrent andere gewigtige deelen van de theorie der functien. Niet alleen toch geeft nu de theorie der reeksen, overeenkomstig haar oorspronkelijk doel, de noodige hulpmiddelen aan de hand tot het beoordeelen der reeks, die eenige functie moge voorstellen; maar uit haar worden tevens de kenmerken van convergentie afgeleid voor de gedurige produkten, uit een oneindig aantal factoren bestaande, waarin enkele functien kunnen omgezet worden; en nog onlangs werd door Dr. Stern ook de leer der oneindig voortloopende gedurige breuken, wat hare convergentie betreft, tot de theorie van de convergentie der reeksen teruggebragt. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 374]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Zoo is dan de theorie der reeksen een van die belangrijke hoofdonderwerpen der Wiskunde geworden, wier behandeling en bewerking voor den beoefenaar dezer wetenschap allernoodzakelijkst is. De meeste stukken over dit onderwerp zijn evenwel in Tijdschriften verspreid, en er bestaan, behalve de oudere ‘Cours d'Analyse Algébrique’ van Cauchy en het nieuwere ‘Handbuch der algebraischen Analysis’ van Prof. Schlömilch, zoo verre mij bekend is, geene genoegzaam uitgebreide handboeken over dit onderwerp. Het is dus voorzeker een nuttig doel, dat Dr. Smaasen zich heeft voorgesteld, om in dit gebrek door zijne ‘Gronden der Hoogere Algebra’ te voorzien. 2. Na eene korte Inleiding behandelt de Schrijver achtervolgens de ontwikkeling der functien in de drie vormen van reeksen, produkten en gedurige breuken, waardoor het werk van zelf in drie Afdeelingen wordt verdeeld; elke Afdeeling behelst eerst eene korte theorie van den vorm en van de regelen zijner convergentie, en daarna eene toepassing van het gevondene op de meest voorkomende functien. - De korte opgave der onderwerpen zal ons doen zien, welke belangrijke punten worden behandeld.
Terwijl wij nu tot de nadere beschouwing overgaan, zij het hier aangemerkt, dat daarbij de notatien van den Schrijver zullen behouden blijven, ook waar zij van de meer gebruikelijke mogten afwijken, en dat de straks op te geven druk- en schrijffouten voorshands reeds verbeterd worden ondersteld. 3. In het eerste Hoofdstuk vinden wij het begrip en de verdeeling der functien, hare limieten en continuiteit behandeld, waarop eenige stellingen uit de theorie der limieten, en eindelijk beschouwingen over het karakter van het veelvoud en de magt eener veranderlijke, en van de exponentiele en logarithmische functien volgen. Dit laatste punt is vooral van gewigt, daar het karakter in het vervolg dikwijls als toets moet dienen van de verkregene uitkomsten. 4. Met het tweede Hoofdstuk neemt de behandeling der reeksen eenen aanvang. In § 7 ontwikkelt Schr. het begrip van eene convergente en eene divergente reeks. De bepaling door hem van eene divergente reeks (pag. 27) gegeven, is tweeledig. De eigenschap van ‘zich van eene bepaalde waarde meer en meer te verwijderen’ komt alleen aan de eigenlijk divergerende reeksen toe, waaronder de overwogene wel is waar behoort; terwijl ‘eene | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 375]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
reeks van termen, wier som tot geen' bepaalden limiet nadert,’ slechts tot de niet-convergerende moet gerekend worden. Nu vormen de eersten slechts eene ondersoort der tweeden, welke tegenover de convergente reeksen staan: behalve deze divergente reeksen toch zijn er andere, die niet convergeren en oscillerende genoemd worden; zij zijn die, welke bij afwisseling tot twee grenzen naderen, naar mate men telkens eenen term verder bijtelt; tot voorbeeld mogen de volgenden strekken:
Bovendien heeft men nog zoogenaamde half-convergente reeksen, waarvan een zeker aantal termen convergeert, de volgenden evenwel naderhand divergeren; terwijl de reeks zelve in sommige gevallen, als ware ze convergent, gebruikt mag worden. Deze verschillende soorten zijn alle niet-convergent, en werden voorheen onder de divergenten begrepen, hetgeen echter, bij den tegenwoordigen stand der wetenschap, niet geoorloofd is. Wanneer Schrijver evenwel bepaaldelijk de divergentie van reeksen betoogt, bedoelt hij alleen de zoodanige, die zich meer en meer van eene bepaalde waarde verwijderen, de eigenlijk divergente reeksen namelijk; terwijl overigens door divergente reeksen in het algemeen niet-convergente worden bedoeld. 5. Nadat in § 8 de sluitterm of de rest der reeks tot de beoordeeling van de convergentie diende, wordt daartoe in § 9 de vergelijking met eenige bekende reeks aangewend. Op pag. 30, na reg. 18, had hier wel de even eenvoudige opmerking behoord, waarvan dan ook naderhand gebruik wordt gemaakt, dat eene reeks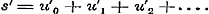 , wier termen, van eenen bepaalden term te beginnen, grooter zijn, dan die der divergente reeks , wier termen, van eenen bepaalden term te beginnen, grooter zijn, dan die der divergente reeks 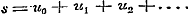 , a fortiori divergent is.
Verder wordt de stelling aangaande de reeks , a fortiori divergent is.
Verder wordt de stelling aangaande de reeks 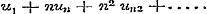 hier in het algemeene geval van n bewezen, terwijl men haar meestal voor het bijzondere geval n = 2 aantreft. § 10 bevat de kenmerken van convergentie en divergentie, afgeleid uit de waarden van hier in het algemeene geval van n bewezen, terwijl men haar meestal voor het bijzondere geval n = 2 aantreft. § 10 bevat de kenmerken van convergentie en divergentie, afgeleid uit de waarden van 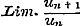 of of 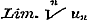 < of > 1, en de toepassing van beide stellingen op acht merkwaardige voorbeelden. Voor het zevende is de gevolgtrekking < of > 1, en de toepassing van beide stellingen op acht merkwaardige voorbeelden. Voor het zevende is de gevolgtrekking 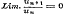 slechts waar, zoo lang slechts waar, zoo lang
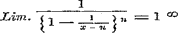
niet ∞ is, hetgeen niet dadelijk blijkt, daar deze waarde (zie pag. 8) niet gelijk de eenheid behoeft te zijn. Men heeft echter 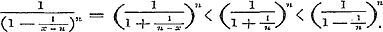
Maar in § 23 wordt bewezen, dat 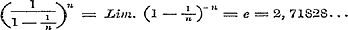 is, derhalve
is, derhalve 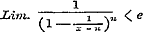 , dus endig, en nu is , dus endig, en nu is 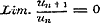 . .
6. Omtrent de reeksen met negatieve teekens worden in § 11 algemeene wenken gegeven. Men kan ook dikwijls, wanneer althans de positieve en ne- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 376]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gatieve teekens elkander volgens zekere eenvoudige wet opvolgen, met vrucht de kunstgreep aanwenden, om, door verbinding der termen, enkel positieve te verkrijgen, in welk geval namelijk de bepaling der convergentie en divergentie meer algemeen mogelijk wordt. Zie tot voorbeeld pag. 51, waar men volgens dezen regel is te werk gegaan. In § 12 gaat de schr. over tot het twijfelachtige geval der eerste stelling van § 10, dat namelijk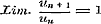 is (welks behandeling eigenlijk § 11 had behooren vooraf te gaan, als betreffende de reeksen met enkel positieve teekens) en bewijst pag. 44 het Theorema van Bonnet (Journ. de Liouville, T. VIII, pag. 77), en pag. 46 dat van Raabe (Journ. von Crelle, XI Bd., S. 309) en Duhamel (Journ. de Liouville, T. IV, pag. 214), waarop eenige belangrijke toepassingen volgen. is (welks behandeling eigenlijk § 11 had behooren vooraf te gaan, als betreffende de reeksen met enkel positieve teekens) en bewijst pag. 44 het Theorema van Bonnet (Journ. de Liouville, T. VIII, pag. 77), en pag. 46 dat van Raabe (Journ. von Crelle, XI Bd., S. 309) en Duhamel (Journ. de Liouville, T. IV, pag. 214), waarop eenige belangrijke toepassingen volgen.
Kon al het Theorema van de Morgan, ‘Differential and Integral Calculus, p. 326,’ hier niet geplaatst worden, zonder de hulp der Differentiaalrekening in te roepen, dat van Cauchy, ‘Analyse Algébrique, T. I, p. 137’, levert die moeijelijkheid niet op, en had hier wel eene plaats verdiend. Hoewel nu deze Theoremata in de toepassing dezelfde uitkomsten van convergentie en divergentie leveren, en dezelfde gevallen van twijfel aanbieden, toch behooren zij nevens elkander te staan, daar elke algemeene vorm der termen de eene of andere dezer stellingen voor de toepassing doet verkiezen. Bovendien wordt door het slechts gedeeltelijk overnemen van het Theorema van Bonnet, en het weglaten van de regels van Bertrand (Journ. de Liouville, T. VII, pag. 43), welke bij dat van Raabe behooren, de schijn gegeven, alsof er werkelijk twijfelachtige gevallen bestonden, hetgeen echter, één enkel geval uitgesloten, niet plaats heeft; - en het komt ons voor, dat in een werk, als het onderhavige, waar de gronden voor de beoordeeling der convergentie en divergentie van reeksen worden aangegeven, juist die regels in hun geheel moeten gelaten, en de loop der bewerking, ook in twijfelachtige gevallen, moet aangetoond worden. - Soortgelijke aanmerking geldt omtrent de stelling in § 10, pag. 35. Omtrent de stellingen van Cauchy en Raabe zij, voor het geval van de Lim. gelijk de eenheid, nog aangemerkt, dat, wanneer de grootheid onder dit teeken voor alle waarden van n steeds < 1 blijft, men alsdan van de divergentie der reeks verzekerd is. 7. In § 13 geeft Schr. eene beschouwing over de gevallen, waarin de optelling en vermenigvuldiging van convergente reeksen geoorloofd is, en in § 14 iets over dubbele reeksen. Eigenaardig had nog in dit Hoofdstuk, en wel na § 12, het bewijs kunnen opgenomen worden van de onmeetbaarheid der waarde van sommige reeksen, dat door Dr. Stern, ‘Journ. von Crelle, XXXVII Bd., S. 95’, gegeven is, inzonderheid in overeenstemming met dezelfde eigenschap van sommige gedurige breuken in § 65 behandeld. 8. Nadat in § 15 over de ontwikkeling der functien in reeksen gehandeld is, volgt in §§ 16 en 18 een bewijs voor het zoogenaamde Binomium van Newton, in de gevallen van positieve geheele, of van willekeurige exponenten; voor deze laatste wordt het met behulp van enkele der in § 17 ontwikkelde eigenschappen der Binomiaal-coefficienten, uit het karakter der magt afgeleid. Hierop worden in § 19 eenige andere vormen van dezelfde formule | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 377]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gegeven, en daaronder voornamelijk die, welke hare toepassing bij de worteltrekking vinden. Nu gaat Schr. over tot het ontleden van breuken, wier teller en noemer uit geheele, rationele functien van eene veranderlijke bestaan, in reeksen van enkelvoudige gebrokens, van zulke dus, wier noemer in het algemeen een binomium is. Hij onderscheidt de gevallen, waarin de factoren van den noemer der te ontleden breuk alle ongelijk (§ 20) of ten deele gelijk zijn, (§ 21) - past de, op eene allezins eenvoudige wijze afgeleide, regels op eenige voorbeelden toe - en herleidt (§ 22) de daarbij gevondene enkelvoudige breuken in reeksen. Wij zagen deze methode van §§ 20 en 21 liever bij de theorie der hoogere magtsvergelijkingen gevoegd, daar zij toch op de eerst later te bewijzen stelling berust, dat iedere rationele functie van den nden graad steeds n eerste magtsfactoren heeft, en zij alzoo met die theorie in een naauw verband staat. In hoeverre echter de behandeling dezer methode in dit boek, zoo als het daar ligt, te huis behoort, zal later worden overwogen; daar evenwel in allen gevalle haar praktisch nut en de toepassing van hare uitkomsten hier moesten worden aangetoond, zoo staat, aan het einde van § 22, de benaderde ontwikkeling eener functie volgens de opklimmende of afdalende magten van x, naar mate deze veranderlijke zeer klein of zeer groot is, wel op zijne plaats, evenzeer als de opmerking, dat de reeks, waardoor een gebroken wordt voorgesteld, tot de wederkeerige behoort, dat is, tot die reeksen, wier coefficienten, van eene bepaalde te beginnen, eene zekere gegeven functie der voorgaanden zijn. 9. Uit de reeks voor het Binomium worden in § 23 die voor de constante e en voor de exponentiele functie afgeleid, en tevens wordt a posteriori aangetoond, dat voor deze laatste de reeks aan het karakter der functie voldoet; terwijl verder, in § 24, uit deze voor de exponentiele functie gevonden reeks, die voor den Neperiaanschen Logarithmus wordt ontwikkeld. In § 25 wordt over de verschillende Logarithmenstelsels gehandeld, en in § 26 over onderscheidene vormen der Logarithmische reeks en hunne toepassing op de berekening der Logarithmen zelve. Men had hier echter, om den Logarithmus van groote getallen in eene reeks uit te drukken, dadelijk in (8) kunnen stellen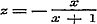 of of 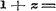 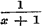 , waarin, daar z > - 1 moet zijn, x alle mogelijke waarden kan hebben; dewijl nu , waarin, daar z > - 1 moet zijn, x alle mogelijke waarden kan hebben; dewijl nu 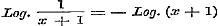 is, volgt hieruit: is, volgt hieruit:
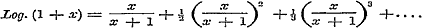 ,
welke reeks, hoewel zij niet naar de magten van de enkele x opklimme, echter merkwaardig genoeg is, om hier eene plaats te vinden. ,
welke reeks, hoewel zij niet naar de magten van de enkele x opklimme, echter merkwaardig genoeg is, om hier eene plaats te vinden.
10. Na een overzigt over de goniometrische functien in § 27, wil Schr. aantoonen, waarin hun karakter gelegen is; maar hierin faalt hij onzes inziens. Vooreerst houde hij mij een paar aanmerkingen op den gang van zijne redenering zelve ten goede. a). Uit het onderstelde in 4o volgt, wel is waar, dat Sin. x en Cos. x beide constanten en tevens onderling gelijk zijn, hetgeen dan ook met regt in Voorstel 27, pag. 246, als eene te bewijzen stelling wordt opgegeven; maar zij zijn niet gelijk nul, zoo als daarenboven in 4o wordt beweerd, daar het gemakkelijk valt aan te toonen, dat hunne waarde ½ is. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 378]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b). Eene nadere beschouwing van de onderstellingen 3o en 4o is geheel overbodig, indien men met den Schrijver de vergelijking (2) als tot het karakter behoorende wil aangemerkt hebben; want dan volgt al dadelijk, dat voor 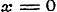 , ook , ook 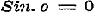 moet zijn, waardoor die onderstellingen terstond worden uitgesloten.
c). Eindelijk is ook de gevolgtrekking aan het begin van pag. 100 niet juist, dat moet zijn, waardoor die onderstellingen terstond worden uitgesloten.
c). Eindelijk is ook de gevolgtrekking aan het begin van pag. 100 niet juist, dat 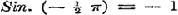 en en 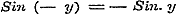 zoude zijn; want met hetzelfde regt kan men uit de aldaar gebezigde vergelijkingen besluiten tot zoude zijn; want met hetzelfde regt kan men uit de aldaar gebezigde vergelijkingen besluiten tot 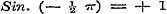 en en 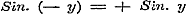 .
Maar wanneer wij, ten tweede, de redenering des Schrijvers nader beschouwen, dan valt het ligtelijk in het oog, dat wij hier alleen het bewijs aantreffen van de stelling, dat de vergelijking (1) eene eigenschap is der functien Sinus en Cosinus, waarbij deze door de betrekking .
Maar wanneer wij, ten tweede, de redenering des Schrijvers nader beschouwen, dan valt het ligtelijk in het oog, dat wij hier alleen het bewijs aantreffen van de stelling, dat de vergelijking (1) eene eigenschap is der functien Sinus en Cosinus, waarbij deze door de betrekking 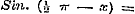 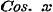 zijn verbonden; terwijl hier in geenen deele betoogd wordt, dat genoemde eigenschap, verbonden met vergelijking (2), uitsluitend aan die functien zoude toekomen, hetgeen toch voor het bestaan van een karakter noodzakelijk is. (Zie § 6). Naar wij meenen, zoude men gevoegelijk op de volgende wijze hierin kunnen voorzien.
11. Men vraagt de functie te bepalen, die voldoet aan de betrekking: zijn verbonden; terwijl hier in geenen deele betoogd wordt, dat genoemde eigenschap, verbonden met vergelijking (2), uitsluitend aan die functien zoude toekomen, hetgeen toch voor het bestaan van een karakter noodzakelijk is. (Zie § 6). Naar wij meenen, zoude men gevoegelijk op de volgende wijze hierin kunnen voorzien.
11. Men vraagt de functie te bepalen, die voldoet aan de betrekking:
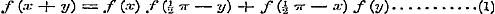 Voor
Voor 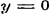 wordt zij wordt zij 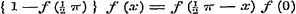 , aan welke vergelijking in vier gevallen kan voldaan worden: , aan welke vergelijking in vier gevallen kan voldaan worden:
a). 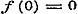 , , 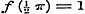 . .
b). 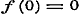 , , 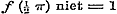 , dan is , dan is 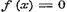 of of 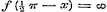 , voor alle x, dus geene functie van x. , voor alle x, dus geene functie van x.
c). 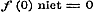 , , 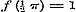 , dan is of , dan is of 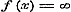 , dus geene functie van x: - of , dus geene functie van x: - of 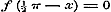 , dus voor , dus voor 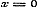 ook ook 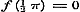 , terwijl zij = 1 was ondersteld. , terwijl zij = 1 was ondersteld.
d). 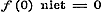 , , 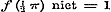 ; dan moet ; dan moet 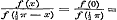
Constante = a zijn. Daardoor wordt (1) 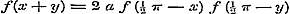 , of voor , of voor 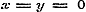 , , 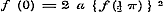 ; maar ; maar 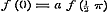 , dus , dus 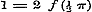 , , 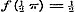 , , 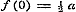 .
Stel in (1) verder voor x, .
Stel in (1) verder voor x, 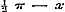 , dan wordt zij , dan wordt zij 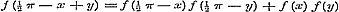 , en deze voor , en deze voor 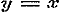 , , 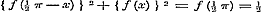 .
Stel hierin .
Stel hierin  , dan wordt , dan wordt 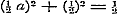 , dus , dus 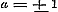 of of 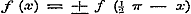 ; derhalve 2 ; derhalve 2 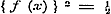 en en 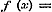  , zoodat , zoodat 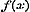 en en 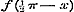 standvastige grootheden en dus onafhankelijk van x zijn, hetgeen tegen het begrip van functie strijdt.
Men heeft dus slechts het geval, dat standvastige grootheden en dus onafhankelijk van x zijn, hetgeen tegen het begrip van functie strijdt.
Men heeft dus slechts het geval, dat 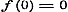 en en 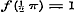 is.......(a)
Stel nu in (1) is.......(a)
Stel nu in (1) 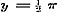 , dan is: , dan is:
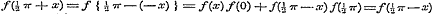 .(b)
Zij in (b) .(b)
Zij in (b) 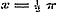 , zoo is , zoo is 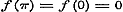 .
Stel in (1) .
Stel in (1) 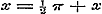 en en 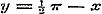 , dan is: , dan is:
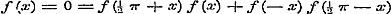 , ,
en dus volgens (b) 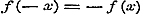 .................................(g)
Neem verder in (1) .................................(g)
Neem verder in (1) 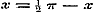 , zoo is: , zoo is:
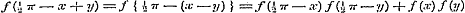 ,.(e) ,.(e)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 379]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
en hierin 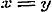 stellende, stellende, 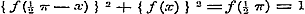 ......(f)
Wordt in (e) y negatief, dan is naar (b) en (g): ......(f)
Wordt in (e) y negatief, dan is naar (b) en (g):
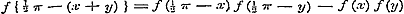 .............(d)Ga naar voetnoot1
Stel nu in (b) achtervolgens .............(d)Ga naar voetnoot1
Stel nu in (b) achtervolgens 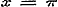 , , 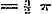 , , 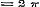 , , 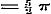 , enz., dan is naar (g): , enz., dan is naar (g):
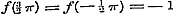 , , 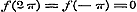 , , 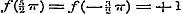 , enz. dus , enz. dus 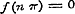 , , 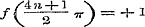 , , 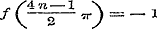 ............(i)
Wordt in (1) en (d) ............(i)
Wordt in (1) en (d) 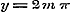 , , 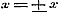 genomen, dan is naar het voorgaande: genomen, dan is naar het voorgaande:
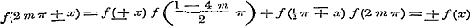 ;(k) ;(k)
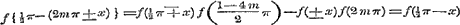 ;(l) zoodat door de formulen (i), (k) en (l) bewezen is, dat de functien ;(l) zoodat door de formulen (i), (k) en (l) bewezen is, dat de functien 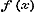 en en 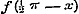 periodiek zijn.
Laat ons nu, gedeeltelijk op het voetspoor van Cauchy, nagaan, welke die functie zal zijn. Omdat bewezen is, dat periodiek zijn.
Laat ons nu, gedeeltelijk op het voetspoor van Cauchy, nagaan, welke die functie zal zijn. Omdat bewezen is, dat 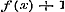 en - 1 tot grenzen heeft, kan blijkbaar, voor eenige waarde van x, de functie door eenen Sinus worden voorgesteld, dat is: en - 1 tot grenzen heeft, kan blijkbaar, voor eenige waarde van x, de functie door eenen Sinus worden voorgesteld, dat is: 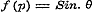 . Dan geeft (e) . Dan geeft (e) 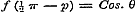 , en (1) , en (1) 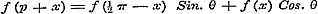 . Stel hierin achtervolgens . Stel hierin achtervolgens 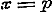 , , 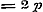 , , 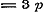 , enz., dan is: , enz., dan is:
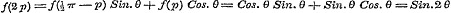 ; en uit (e) ; en uit (e) 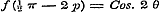 ; ;
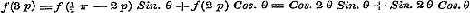
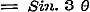 , enz. , enz.
dus voor geheele, positieve 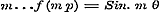 .....................(A) .....................(A)
Voor 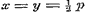 geeft (1) geeft (1) 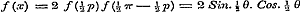 , en (e).......... , en (e).......... 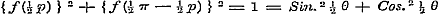 , waarvan de som en het verschil geven: , waarvan de som en het verschil geven:
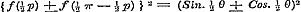 , dus , dus 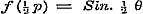 , ,
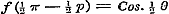 .
Evenzoo, door .
Evenzoo, door 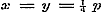 , , 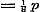 , enz. te stellen, , enz. te stellen, 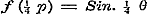 ; ; 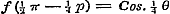 , enz.; dus , enz.; dus
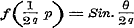 ,............................................(B)
derhalve volgens ,............................................(B)
derhalve volgens 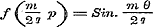 ;............................(C) en, dewijl door de uitdrukking ;............................(C) en, dewijl door de uitdrukking 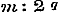 ieder positief getal wordt voorgesteld, voor alle positieve ieder positief getal wordt voorgesteld, voor alle positieve 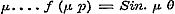 ..........................(D) Volgens (g) is verder ..........................(D) Volgens (g) is verder 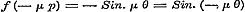 ;..........(E) dus geldt eindelijk voor alle mogelijke μ de vergelijking.. ;..........(E) dus geldt eindelijk voor alle mogelijke μ de vergelijking..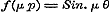 ,.(F) zoodat er tusschen p en θ eene standvastige betrekking blijkt te bestaan. - Stel dan nu deze standvastige reden = z, zoo moet ,.(F) zoodat er tusschen p en θ eene standvastige betrekking blijkt te bestaan. - Stel dan nu deze standvastige reden = z, zoo moet 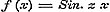 zijn, welke voor zijn, welke voor 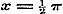 , , 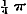 , enz. achtervolgens wordt: , enz. achtervolgens wordt:
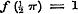 , maar , maar 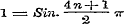 , dus z van den vorm , dus z van den vorm 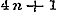 ; ;
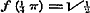 , maar , maar 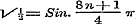 , dus z van den vorm , dus z van den vorm 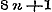 , enz.. , enz..
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 380]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Stelde men eindelijk 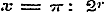 , dan zoude men even zoo vinden, dat z van den vorm , dan zoude men even zoo vinden, dat z van den vorm 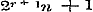 moest zijn. Daar men nu r steeds grooter kan nemen, zoo zoude z tot ∞ divergeren, hetgeen niet zijn kan. Om dus aan al deze vormen van z te voldoen, moet men overal n gelijk nul aannemen, dus moest zijn. Daar men nu r steeds grooter kan nemen, zoo zoude z tot ∞ divergeren, hetgeen niet zijn kan. Om dus aan al deze vormen van z te voldoen, moet men overal n gelijk nul aannemen, dus  , en men heeft alzoo eindelijk............ , en men heeft alzoo eindelijk............ 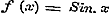 , hetgeen met de gevondene formulen (a), (b), (g), (e), (f), (d), en met de bewezene periodiciteit geheel overeenstemt. - Derhalve blijkt het, dat de (1) op zich zelve reeds uitsluitend aan de functie Sinus toekomt, en dus volkomen haar karakter uitdrukt.
En wat overigens aangaat de vergelijking (2), die nu gebleken is niet tot het karakter te behooren, en toch voor het vervolg van een uitgestrekt nut is, en voor verder onderzoek ten grondslag moet strekken, deze verkrijgt men op de volgende wijze. Wanneer men de geometrische beteekenis, welke wij nu voor die functie hebben gevonden, nagaat, dan blijkt het, dat, daar Sin. x meer en meer tot den Boog x nadert, naar mate beide afnemen, ook , hetgeen met de gevondene formulen (a), (b), (g), (e), (f), (d), en met de bewezene periodiciteit geheel overeenstemt. - Derhalve blijkt het, dat de (1) op zich zelve reeds uitsluitend aan de functie Sinus toekomt, en dus volkomen haar karakter uitdrukt.
En wat overigens aangaat de vergelijking (2), die nu gebleken is niet tot het karakter te behooren, en toch voor het vervolg van een uitgestrekt nut is, en voor verder onderzoek ten grondslag moet strekken, deze verkrijgt men op de volgende wijze. Wanneer men de geometrische beteekenis, welke wij nu voor die functie hebben gevonden, nagaat, dan blijkt het, dat, daar Sin. x meer en meer tot den Boog x nadert, naar mate beide afnemen, ook 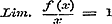 moet zijn, hetgeen dan ook geheel met de formule moet zijn, hetgeen dan ook geheel met de formule 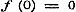 instemt. instemt.
12. In § 28 wordt het Theorema van Moivre voor alle geheele, gebrokene, positieve en negatieve exponenten bewezen, hetgeen zeker voor het algemeen gebruik dezer vruchtbare formule noodzakelijk is. Daarna vindt men in § 29 vooreerst eene vlugtige behandeling van de onbestaanbare (imaginaire) grootheden en uitdrukkingen, van hare herleiding, van den modulus en de herleide uitdrukking, van haar produkt en quotient. Zij, die een ander bewijs verlangen voor de gevolgtrekking en en 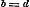 uit de vergelijking uit de vergelijking 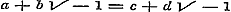 , kunnen daaruit besluiten tot , kunnen daaruit besluiten tot 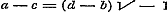 , en dus , en dus 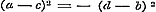 ; daar nu een vierkant nimmer negatief kan zijn, moet zoowel ; daar nu een vierkant nimmer negatief kan zijn, moet zoowel  als als 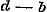 nul zijn, dat is nul zijn, dat is 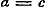 , , 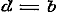 . .
Verder behandelt Schr. in § 29 nog de convergentie van reeksen voor het geval, dat het argument onbestaanbaar is, - het voldoen eener onbestaanbare exponentiele uitdrukking aan het karakter, - eindelijk de geldigheid van Newton's Binonium ook voor eenen onbestaanbaren wortel. Hoezeer dan ook de bedoelde eigenschappen, die uit het gebruik der onbestaanbare grootheden haren oorsprong ontleenen, zeer dienstig zijn tot eene geleidelijke en gemakkelijke ontwikkeling der circulaire functien in reeksen, zij zijn daarom (hetgeen men uit het begin van § 28 zoude opmaken) nog niet noodzakelijk om den Sinus en den Cosinus uit te drukken in reeksen, volgens de opklimmende magten van den boog gerangschikt, zoo als zij in het vervolg (§ 31) met behulp dier grootheden worden afgeleid. Want deze reeksen kunnen zonder tusschenkomst der onbestaanbare grootheden uit het Binonium van Newton worden ontwikkeld, waartoe men de bekende betrekkingen: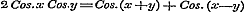 , , 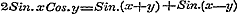 , verder eene eigenschap der Binomiaal-coefficienten: , verder eene eigenschap der Binomiaal-coefficienten:
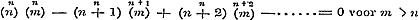 , ,
en = 1 voor  ; ;
en eindelijk de vergelijkingen: 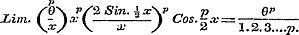 , , 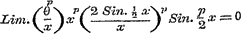 noodig heeft. noodig heeft.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 381]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13. De reeksen, die den Sinus en den Cosinus van eenig veelvoud eens boogs, door middel van deze goniometrische lijnen van den enkelen boog uitdrukken, hadden meer regtstreeks en korter uit het Theorema van Moivre kunnen zijn afgeleid, dan dit wel in § 30 geschied is. Men had immers het tweede lid dier vergelijking slechts volgens het Binomium te ontwikkelen, om dan den Cosinus gelijk te stellen aan de bestaanbare termen der reeks, den Sinus aan de onbestaanbare, gedeeld door √ - 1; terwijl alsdan de beoordeeling der convergentie dezelfde blijft. Uit deze reeksen worden, in § 31, die voor den Sinus en den Cosinus van x, en, na de opgave van eenige cyclometrische formulen in § 32, verder in § 33 de reeks voor Boog Tang., in § 34 die voor Boog Sin. ontwikkeld. Hierbij valt op te merken, dat in § 33 de reeks van Leibnitz en de uitdrukking van Machin voor π worden afgeleid. De reeks voor Boog Sin. z wordt hier slechts bewezen voor de grenzen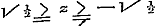 , maar had, bij eene andere afleiding, ook zonder Differentiaalrekening (zie pag. 123), voor de grenzen , maar had, bij eene andere afleiding, ook zonder Differentiaalrekening (zie pag. 123), voor de grenzen 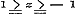 kunnen worden ontwikkeld. Om dit aan te toonen, moeten wij eerst opmerken, dat de in § 39 alleen als eindige bewezen reeksen voor bepaalde waarden van n, ook als oneindige gelden voor bepaalde waarden van θ.
Wanneer men in de reeksen (6) en (7) van § 30 de ontwikkeling overbrengt der formule kunnen worden ontwikkeld. Om dit aan te toonen, moeten wij eerst opmerken, dat de in § 39 alleen als eindige bewezen reeksen voor bepaalde waarden van n, ook als oneindige gelden voor bepaalde waarden van θ.
Wanneer men in de reeksen (6) en (7) van § 30 de ontwikkeling overbrengt der formule 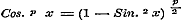 , dan zullen daardoor, met behulp van de volgende eigenschappen der Binomiaal-coefficienten: , dan zullen daardoor, met behulp van de volgende eigenschappen der Binomiaal-coefficienten:
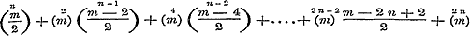
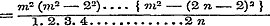 , ,
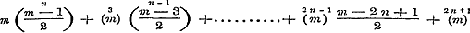
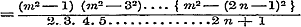 ; ;
de functien Cos. nx, Sin. nx, Cos. nx: Cos. x, Sin. nx: Cos. x, kunnen worden ontwikkeld in oneindige reeksen, welke naar de evene of onevene magten van Sin. x zijn geordend en voor alle n gelden, wier termen met die der in § 39 gevonden eindige reeksen (12), (13), (10) en (11) volkomen identisch zijn, en waarin 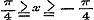 is. - Stelt men nu in deze reeksen 2 m en ½ z voor n en x, zoo worden de grenzen is. - Stelt men nu in deze reeksen 2 m en ½ z voor n en x, zoo worden de grenzen 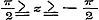 ; ontwikkelt men dan naar de formulen ; ontwikkelt men dan naar de formulen 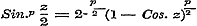 , en , en 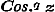 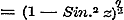 , zoo wordt eindelijk Sin. z het argument der reeksen, terwijl verder de coefficienten berekend moeten worden naar de methode, op pag. 120 gebezigd; hierdoor worden dan de oneindige reeksen, wier termen met die der reeksen (10)-(13) van § 39 overeenkomen, bevonden te gelden voor , zoo wordt eindelijk Sin. z het argument der reeksen, terwijl verder de coefficienten berekend moeten worden naar de methode, op pag. 120 gebezigd; hierdoor worden dan de oneindige reeksen, wier termen met die der reeksen (10)-(13) van § 39 overeenkomen, bevonden te gelden voor 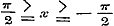 , waarbij n willekeurig is. , waarbij n willekeurig is.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 382]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Als men nu in de formule (13) van § 39, beide leden door n deelt, en tot den Limiet 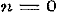 overgaat, zoo is overgaat, zoo is 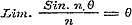 , en dus: , en dus:
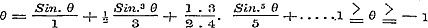 , welke nu dezelfde formule is, die in § 34 slechts voor , welke nu dezelfde formule is, die in § 34 slechts voor 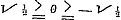 bewezen was. bewezen was.
14. In § 35 worden uit de reeksen voor de circulaire en exponentiele functien de merkwaardige formulen afgeleid, waardoor een Sinus of Cosinus in eene functie van exponentiele grootheden wordt voorgesteld, terwijl in § 36 hetzelfde wordt gedaan voor het geval van een onbestaanbaar argument. De uitdrukkingen, welke door dit onbestaanbaar stellen van de veranderlijke verkregen worden, namelijk: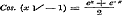 , , 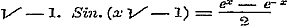 , ,
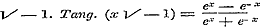 , enz., , enz.,
pleegt men den Hyperbolischen Cosinus, Sinus, Tangens, enz., of Cosh. x, Sinh. x, Tangh. x, enz., te noemen; men ziet uit het door Schr. behandelde, dat er tusschen deze en de gewone goniometrische functien merkwaardige betrekkingen bestaan. Verder wordt de Sinus van een onbestaanbaar binonium getransformeerd in eene uitdrukking, welke de onbestaanbare grootheid explicite bevat; en daarna de weg aangewezen tot dezelfde bewerking ten aanzien van Boog Sin. eener onbestaanbare grootheid. Hier hadden de vergelijkingen: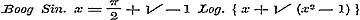 en en
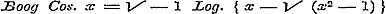 , ,
waar x > 1 is, en 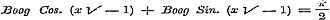 , ,
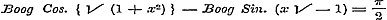
wel eene plaats verdiend. Uit haar blijkt, dat de formule 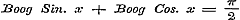
nog blijft gelden, wanneer x > 1 of onbestaanbaar wordt. § 37 handelt over den onbepaalden Logarithmus, naar de notatie van Cauchy, in het bijzonder over dien van eene onbestaanbare grootheid, en eindelijk over den Log. Sin. van zulk een argument. Hier had men ligtelijk, door in (3) b negatief te nemen, nog de volgende merkwaardige betrekking kunnen afleiden: 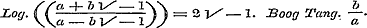 . .
15. In § 38 wordt de sommatie der reeksen, wier algemeene termen an ρn Cos. nθ of an ρn Sin. nθ zijn, afgeleid uit de reeks, wier algemeene term is an xn, en daaruit veel belangrijke formulen ontwikkeld. Van deze | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 383]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
formulen worden er in § 39 twee gebezigd, om de reeds hierboven (No. 13) behandelde reeksen te vinden, evenwel slechts in de onderstelling van geheele, beurtelings evene en onevene, waarden van n. Men had trouwens ook daar ter plaatse reeds dezelfde uitkomsten kunnen verkrijgen, dewijl de reeksen (6) en (7) van § 30 voor geheele n eindig zijn, en in deze onderstelling blijkbaar voor alle waarden van Tang. z gelden. Vóór wij van de behandeling en het gebruik der onbestaanbare vormen afstappen, moeten wij den lezer opmerkzaam maken, dat hij §§ 29, 35, 36 en 37 bewezen vindt, dat de karakters der functien xn, an, Sin. x en Log. x ook voor onbestaanbare waarden van x geldig blijven. Hiermede sluit de Eerste Afdeeling, die over de reeksen en de ontwikkeling van functien in dezelve handelt. Volgen wij den Schrijver nu, als hij in de Tweede Afdeeling de gedurige produkten uit hetzelfde oogpunt behandelt. 16. In Hoofdstuk VI, §§ 40-47 behandelt Schr. de wortels en wortelfactoren eener vergelijking, - de noodzakelijkheid, dat iedere vergelijking minstens éénen wortel moet hebben (voor welke stelling wij hier Cauchy's betoog aantreffen), - de betrekkingen tusschen de coefficienten eener vergelijking en hare wortels, - het Theorema van Girard, - dat van Cotes, - en eindelijk de algemeene oplossing van de derde en vierde magtsvergelijkingen. 17. Naar aanleiding van het ontwikkelde worden in § 48 de reeksen van § 39 herschapen in eindige produkten, en deze onder verschillende vormen voorgesteld. Om echter tot oneindige produkten te kunnen geraken, wordt in § 49 eene stelling gegeven ter beoordeeling van hunne convergentie, en deze in § 50 op de straks gevonden produkten toegepast; terwijl, als bijzonder geval, de uitdrukking van Wallis voor ½ π wordt aangegeven. In § 51 worden, na eenige ontwikkelingen, enkele functien van exponentiele grootheden in produkten herleid. Deze vier laatste formulen zijn de ontwikkelingen van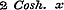 , , 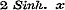 , , 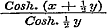 , , 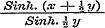 .
Men had hier gevoegelijk nog eenige andere merkwaardige produkten kunnen opnemen, die uit (17) en (18) gevonden worden, door .
Men had hier gevoegelijk nog eenige andere merkwaardige produkten kunnen opnemen, die uit (17) en (18) gevonden worden, door 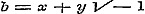 te stellen, en verder de Logarithmen van de functie zelve en van de verschillende factoren te nemen, daarbij lettende op de formulen (4) en (3) van § 37 - en door eindelijk de bestaanbare en onbestaanbare deelen der alzoo verkregen functien en ontwikkelingen gelijk te stellen. Men zal dan o.a. een merkwaardig verband leeren kennen tusschen de hyperbolische en circulaire functien.
18. Niet minder belangrijk is hetgeen nu volgt over de reeksen, die geboren worden uit de onderlinge vergelijking van de reeksen en de produkten, waartoe eene zelfde functie wordt herleid. Nadat in § 52 eene beschouwing is voorafgegaan der gevallen, waarin zulk eene vergelijking geoorloofd is, komen wij in § 53 tot de Bernouillaansche coefficienten en sommige reeksen, welker waarde door de eersten wordt voorgesteld. In overeenstemming met (2) hadden wij achter (4) nog de volgende gewenscht: te stellen, en verder de Logarithmen van de functie zelve en van de verschillende factoren te nemen, daarbij lettende op de formulen (4) en (3) van § 37 - en door eindelijk de bestaanbare en onbestaanbare deelen der alzoo verkregen functien en ontwikkelingen gelijk te stellen. Men zal dan o.a. een merkwaardig verband leeren kennen tusschen de hyperbolische en circulaire functien.
18. Niet minder belangrijk is hetgeen nu volgt over de reeksen, die geboren worden uit de onderlinge vergelijking van de reeksen en de produkten, waartoe eene zelfde functie wordt herleid. Nadat in § 52 eene beschouwing is voorafgegaan der gevallen, waarin zulk eene vergelijking geoorloofd is, komen wij in § 53 tot de Bernouillaansche coefficienten en sommige reeksen, welker waarde door de eersten wordt voorgesteld. In overeenstemming met (2) hadden wij achter (4) nog de volgende gewenscht:
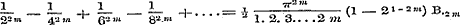
In § 54 worden ½ Tang. ½ y en ½ Cot. ½ y ontwikkeld in reeksen, waar- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 384]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
van de termen zijn van den vorm 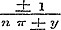 , ten einde daaruit in § 55 voor Tang. z:z en Cot. z anderen te kunnen afleiden, welke dan naar de magten van z zijn geordend, en wier coefficienten de Bernouillaansche tot factoren hebben. Aan het einde dezer § behoorde nog de opmerking, dat de waarheid der reeksen , ten einde daaruit in § 55 voor Tang. z:z en Cot. z anderen te kunnen afleiden, welke dan naar de magten van z zijn geordend, en wier coefficienten de Bernouillaansche tot factoren hebben. Aan het einde dezer § behoorde nog de opmerking, dat de waarheid der reeksen 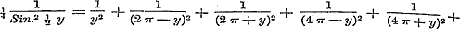 .., .., 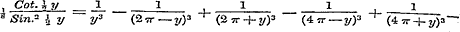 .., even als vroeger (pag. 193) voor soortgelijken het geval was, slechts uit de differentiering van form. (6) kan volgen. .., even als vroeger (pag. 193) voor soortgelijken het geval was, slechts uit de differentiering van form. (6) kan volgen.
Verder vindt men in § 56 voor Cosec. y en ½ Sec. y reeksen, met die van § 54 overeenstemmende, waardoor, na dergelijke behandeling als boven, die functien worden ontwikkeld in reeksen, die naar de magten van y opklimmen; de coefficienten der reeks voor Cosec. y worden uit de Bernouillaansche afgeleid, terwijl de reeks voor Sec. y ons eene nieuwe, hoewel met de vorige naauw verbonden, soort van constanten, de Secanten-coefficienten namelijk, leert kennen. Men had hier, dunkt ons, dergelijke reeksen voor enkele exponentiele functien mogen verwachten, welke nu in dit Hoofdstuk geheel ontbreken, en gemakkelijk waren te vinden geweest door in de formulen (7), (8), (11) en (13) het argument onbestaanbaar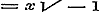 te nemen, en daarbij tevens dezelfde grensbepaling te nemen, en daarbij tevens dezelfde grensbepaling 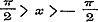 te laten gelden.
§ 57 bevat de herleiding van te laten gelden.
§ 57 bevat de herleiding van 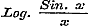 , , 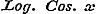 , en , en 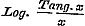 in reeksen, welke, naar de magten van x geordend zijnde, de Bernouillaansche coefficienten als factoren hunner coefficienten hebben. Eindelijk wordt in § 58 eene betrekkingsvergelijking afgeleid voor de Bernouillaansche coefficienten uit de formule in reeksen, welke, naar de magten van x geordend zijnde, de Bernouillaansche coefficienten als factoren hunner coefficienten hebben. Eindelijk wordt in § 58 eene betrekkingsvergelijking afgeleid voor de Bernouillaansche coefficienten uit de formule 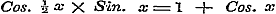 , en eene dergelijke voor de Secanten-coefficienten uit de formule , en eene dergelijke voor de Secanten-coefficienten uit de formule 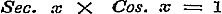 , door namelijk voor deze circulaire functien hare ontwikkeling in reeksen (ten deele zoo als zij in dit Hoofdstuk gevonden zijn) in plaats te stellen, de vermenigvuldiging uit te voeren, en de coefficienten van dezelfde magten der veranderlijke gelijk te stellen. Daardoor verkrijgt men eenvoudige formulen ter berekening dier merkwaardige constanten, welker invoering zulk eene regelmatigheid in de reeksen teweegbrengt, en die in de Hoogere Analyse van zulk een uitgestrekt en gewigtig gebruik zijn. , door namelijk voor deze circulaire functien hare ontwikkeling in reeksen (ten deele zoo als zij in dit Hoofdstuk gevonden zijn) in plaats te stellen, de vermenigvuldiging uit te voeren, en de coefficienten van dezelfde magten der veranderlijke gelijk te stellen. Daardoor verkrijgt men eenvoudige formulen ter berekening dier merkwaardige constanten, welker invoering zulk eene regelmatigheid in de reeksen teweegbrengt, en die in de Hoogere Analyse van zulk een uitgestrekt en gewigtig gebruik zijn.
Wij zijn dan nu genaderd tot het ontleden der functien in gedurige breuken, wier behandeling de Derde Afdeeling uitmaakt. 19. Nadat in § 59 de waarde van den teller en noemer der naderingsbreuken is bepaald, worden in § 60 uit den vorm van het verschil tusschen twee volgende naderingsbreuken eenige stellingen afgeleid omtrent de onderlinge betrekking der naderingsbreuken van evene en onevene rangorde, die echter alleen gelden voor het geval, dat alle termen der gedurige breuk positief zijn. In § 61 stelt Schr. eerst, dat alle termen, behalve de eerste, negatief zijn, en vervolgens, dat de termen, wier teeken onbepaald blijft, alle ware breuken zijn. Bij de behandeling van dit laatste geval zijn in de re- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 385]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
denering eenige misslagen ingeslopen, die ook op het volgende invloed uitoefenen. Opdat toch de termen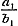 , , 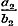 , enz., ware breuken zijn, is het niet noodzakelijk, dat , enz., ware breuken zijn, is het niet noodzakelijk, dat 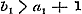 , , 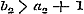 , enz. zij, zoo als pag. 213 wordt aangevoerd; slechts moet , enz. zij, zoo als pag. 213 wordt aangevoerd; slechts moet 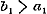 , , 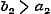 , enz., wezen. Men kan dus ook hebben , enz., wezen. Men kan dus ook hebben 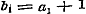 , , 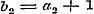 , enz. In dit, wel is waar, zeer bijzondere geval wordt, wanneer nog daarenboven de termen alle negatief zijn, de gedurige breuk van dezen vorm: , enz. In dit, wel is waar, zeer bijzondere geval wordt, wanneer nog daarenboven de termen alle negatief zijn, de gedurige breuk van dezen vorm:
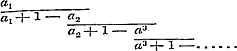 ;..........................(a) ;..........................(a)
waaruit 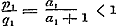 ; ; 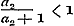 , , 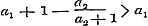 , dus , dus 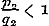 ; enz. volgt, zoodat hier, even als in het algemeene geval, de naderingsbreuken ; enz. volgt, zoodat hier, even als in het algemeene geval, de naderingsbreuken 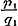 , , 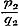 , enz. alle < 1 zijn. Mag men nu, met den Schrijver, uit deze eigenschap besluiten, dat ‘ook de waarde der gedurige breuk kleiner dan de eenheid’ zij? Wij zullen zien, dat het antwoord ontkennend is.
20. Volgens den regel § 59, pag. 208, is hier, in het bijzondere geval, dat alle termen, behalve de eerste, negatief, en hunne noemers juist één grooter zijn dan de overeenkomstige tellers, , enz. alle < 1 zijn. Mag men nu, met den Schrijver, uit deze eigenschap besluiten, dat ‘ook de waarde der gedurige breuk kleiner dan de eenheid’ zij? Wij zullen zien, dat het antwoord ontkennend is.
20. Volgens den regel § 59, pag. 208, is hier, in het bijzondere geval, dat alle termen, behalve de eerste, negatief, en hunne noemers juist één grooter zijn dan de overeenkomstige tellers,
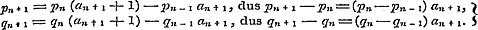 ..(b)
Verder is ..(b)
Verder is 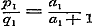 en en 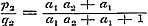 , derhalve , derhalve  , , 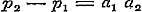 , , 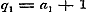 , , 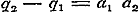 .
Nu geven de vergelijkingen (b) voor n achtervolgens = 2, 3, 4..... .
Nu geven de vergelijkingen (b) voor n achtervolgens = 2, 3, 4..... 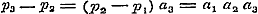 , , 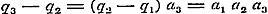 ; ; 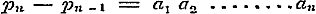 , , 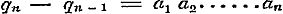 . .
De sommen van de beide leden in ieder stel vergelijkingen geven: 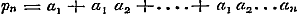 , , 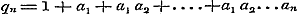 , dus , dus 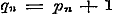 . Daar nu alle n geheele getallen zijn, wordt . Daar nu alle n geheele getallen zijn, wordt 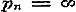 voor voor  , dus: , dus:
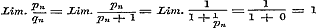 , zoodat eindelijk de waarde van de behandelde gedurige breuk de eenheid zelve is.
Overigens is het duidelijk, dat deze bijzondere gesteldheid der breuk verdwijnt, zoodra slechts één der noemers den overeenkomstigen teller meer dan ééne eenheid overtreft. Men hebbe dan bijv. , zoodat eindelijk de waarde van de behandelde gedurige breuk de eenheid zelve is.
Overigens is het duidelijk, dat deze bijzondere gesteldheid der breuk verdwijnt, zoodra slechts één der noemers den overeenkomstigen teller meer dan ééne eenheid overtreft. Men hebbe dan bijv. 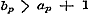 , zoo zal in deze gedurige breuk, in vergelijking met (a): , zoo zal in deze gedurige breuk, in vergelijking met (a):
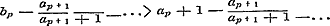
zijn, en nu van iederen term tot zijnen voorgaanden overgaande, wordt in de eerste gedurige breuk de noemer van den term telkens met een kleiner getal verminderd, dan in de tweede, zoodat het complement telkens | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 386]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
grooter wordt. Dewijl echter, volgens de stelling op pag. 212, de naderingsbreuken steeds grooter worden, en volgens het hier betoogde, de waarde der eerste gedurige breuk kleiner dan die der tweede moet zijn, zoo volgt, dat, in het onderhavige geval, de waarde der breuk zelve kleiner dan de cenheid is. Gemakkelijk is het in te zien, dat, wanneer bij negatieve termen meerdere noemers de overeenkomstige tellers meer dan ééne eenheid overtreffen, a fortiori de waarde der gedurige breuk kleiner dan één zal zijn. Op gelijke wijze kan men zich gereedelijk overtuigen, dat, ingevalle eenige termen positief worden, dat is in het algemeene geval, uit dezelfde redenering volgt, dat ook dan de waarde der breuken kleiner dan de eenheid zal wezen. Men ziet, dat deze, slechts ter loops geschetste, vergelijking van verschillende gedurige breuken met de breuk (a) eenige overeenkomst heeft met de methode, welke Schr. in § 9 ten aanzien van de reeksen bezigt. 21. Overeenkomstig het zoo even aangevoerde, zoude men dus op pag. 213, reg. 2 (indien men deze stelling hier behouden wil, die nu evenwel eerder tot § 65 zoude te brengen zijn) na de woorden: ‘de eenheid zijn’ behooren bij te voegen: mits niet alle termen negatief en hunne noemers juist één grooter zijn dan de overeenkomstige tellers, in welk bijzonder geval de waarde der breuk de eenheid zelve is. Verder zoude men, met weglating der woorden: ‘en ook de waarde der gedurige breuk,’ pag. 213, reg. 4 van ond., aan het einde der § het vorige No. kunnen doen volgen. - De wijzigingen, die deze verandering in het volgende medebrengt, zullen wij daar ter plaatse aangeven. In § 62 worden de gewone gedurige breuken, waarbij de termen de eenheid tot teller en een geheel getal tot noemer hebben, - de ontwikkeling van grootheden in zulke breuken, - en ten laatste hare betrekkingsschalen en naderingsbreuken behandeld. In § 63 betoogt Schr., dat die naderingsbreuken de waarde der gewone gedurige breuk het naauwkeurigst voorstellen, en wendt deze eigenschap vervolgens aan tot het uitdrukken bij benadering van onmeetbare grootheden; terwijl hij door middel van het complement den graad van naauwkeurigheid bepaalt. 22. In § 64 vinden wij eene algemeene beschouwing van de oneindige gedurige breuken, van de onmeetbare grootheden, die zij voorstellen, en van het begrip van convergentie eener zoodanige breuk. In § 65 wordt de convergentie nagegaan der oneindige gedurige breuken, wier termen alle positief zijn, waarbij, pag. 223, eene stelling hieromtrent voorkomt, door Prof. Schlömilch, ‘Handb. der algebraischen Analysis, I Th.S. 315’, gegeven. In het geval dat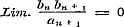 is, kan het door Dr. Arndt, ‘Disquis. nonn. de fractionibus continuis, 1845’, gegeven kenmerk dienen:
De gedurige breuk convergeert in dat geval, wanneer de reeks divergeert, wier algemeene term is is, kan het door Dr. Arndt, ‘Disquis. nonn. de fractionibus continuis, 1845’, gegeven kenmerk dienen:
De gedurige breuk convergeert in dat geval, wanneer de reeks divergeert, wier algemeene term is 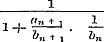 . .
Maar gelijk wij bij de reeksen, behalve het convergeren en eigenlijk divergeren, ook nog het oscilleren deden opmerken, zoo heeft dit ook ten aanzien der oneindige gedurige breuken plaats; wannneer de breuk namelijk twee verschillende grenzen heeft, naarmate de naderingsbreuken van evene of onevene rangorde zijn. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 387]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ook met het oog hierop is de theorie van de convergentie der oneindige gedurige breuken zeer uitgebreid door de Verhandeling van Dr. Stern, ‘Journ. von Crelle, XXXVII Bd., S. 255’, welke Schr. aangehaald heeft. In dit stuk worden zeer belangrijke kenmerken over de convergentie of niet-convergentie dier breuken ontwikkeld, door ze te herleiden in de identieke reeks
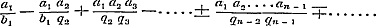 , ,
waarop de regels omtrent het convergeren en divergeren der reeksen worden toegepast. Men vindt als slotsom der behandeling de volgende stelling: Eene gedurige breuk convergeert, als minstens ééne der reeksen 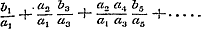 of of 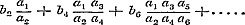 divergeert. - Indien geene dezer reeksen divergent is, dan oscilleert de gedurige breuk.
23. Wat betreft de stelling over de convergentie van oneindige gedurige breuken, wier termen, behalve de eerste, alle negatief en tevens ware breuken zijn, men houde daarbij onder het oog, dat, ten gevolge van hetgeen wij boven (No. 20) omtrent de stelling van § 61 hebben aangemerkt, hier noodzakelijk het geval moet uitgesloten worden, waarin alle termen van den vorm divergeert. - Indien geene dezer reeksen divergent is, dan oscilleert de gedurige breuk.
23. Wat betreft de stelling over de convergentie van oneindige gedurige breuken, wier termen, behalve de eerste, alle negatief en tevens ware breuken zijn, men houde daarbij onder het oog, dat, ten gevolge van hetgeen wij boven (No. 20) omtrent de stelling van § 61 hebben aangemerkt, hier noodzakelijk het geval moet uitgesloten worden, waarin alle termen van den vorm 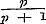 zijn; want uit het daar behandelde toch blijkt, dat de waarde der brenk voor dit bijzondere geval de eenheid zelve is. zijn; want uit het daar behandelde toch blijkt, dat de waarde der brenk voor dit bijzondere geval de eenheid zelve is.
Verder moet men ook bij het bewijs voor de onmeetbaarheid der waarde van gedurige breuken, wier termen alle ware breuken zijn, ten eerste opmerken, dat dit niet geldt, indien, van eenigen term te beginnen, alle volgenden negatief zijn, en daarbij hunne noemers de overeenkomstige tellers juist ééne eenheid overtreffen; want in dit geval kan men voor het complement de eenheid nemen; waardoor de gedurige breuk eindig, en te gelijker tijd meetbaar zal worden. Ten tweede behoorde reeds hier de opmerking te huis, die op het begin van pag. 240 wordt aangetroffen, dat namelijk eene gedurige breuk immer onmeetbaar is, zoodra slechts na eenen zekeren term alle volgenden ware breuken zijn (met uitzondering alleen van het zoo even vermelde bijzondere geval); want indien het complement van eenigen noemer onmeetbaar is, dan wordt die term, en bij gevolg ook tevens de gedurige breuk zelve onmeetbaar. Ten derde geldt hetgeen Schr. pag. 225, reg. 13-15, zegt, slechts van de getallenwaarde van A, B, C, D,... waarbij dus niet op de teekens wordt gelet; want elke dezer grootheden kan in het algemeen positief of negatief zijn, naar mate de term, waarmede eenig complement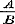 ,....... aanvangt, positief of negatief is; - en bij die beperking alleen geldt ook eerst de gevolgtrekking, dat ‘eene oneindige reeks van steeds afnemende geheele getallen, die allen grooter dan nul zijn,’ zoo als dit hier bij de getallenwaarde van A, B, C,..... het geval is, ‘niet bestaanbaar is, derhalve enz.’. ,....... aanvangt, positief of negatief is; - en bij die beperking alleen geldt ook eerst de gevolgtrekking, dat ‘eene oneindige reeks van steeds afnemende geheele getallen, die allen grooter dan nul zijn,’ zoo als dit hier bij de getallenwaarde van A, B, C,..... het geval is, ‘niet bestaanbaar is, derhalve enz.’.
Uit het aangevoerde kan men verder afleiden, dat een meetbaar gebroken kan worden voorgesteld door eene gedurige breuk van een eindig aantal termen, welke alle ware breuken zijn, terwijl daarentegen eene onmeetbare grootheid zou worden aangeduid door eene breuk, wier teller en noe- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 388]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
mer beide ∞ zijn (daar toch de reeks der geheele positieve getallen A, B, C,...... om tot in het oneindige te kunnen blijven verminderen, wel met het ∞ moet aanvangen), en derhalve, bij ontwikkeling, eene gedurige breuk van een oneindig aantal termen zal leveren. 24. In § 66 overweegt Schr. de reeks van Gausz, wier gevallen van convergentie en divergentie reeds § 12, pag. 48, (stellende aldaar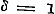 ) zijn behandeld. Vooreerst diende hier aangemerkt te worden, dat zij, bij bijzondere waarden van hare constanten, de meeste der reeksen zal voorstellen, waarin de functien kunnen worden ontwikkeld, die in de Analyse voorkomen. Ten einde dit, althans voor de in dit boek behandelde functien, eenigzins meer volledig aan te wijzen, kunnen, behalve de reeds gegeven, nog de volgende formulen dienen, waarbij wij telkens de reeksen opgeven, met welke zij zamenhangen: ) zijn behandeld. Vooreerst diende hier aangemerkt te worden, dat zij, bij bijzondere waarden van hare constanten, de meeste der reeksen zal voorstellen, waarin de functien kunnen worden ontwikkeld, die in de Analyse voorkomen. Ten einde dit, althans voor de in dit boek behandelde functien, eenigzins meer volledig aan te wijzen, kunnen, behalve de reeds gegeven, nog de volgende formulen dienen, waarbij wij telkens de reeksen opgeven, met welke zij zamenhangen:
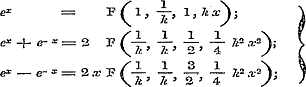 ....§ 23, pag. 89; ....§ 23, pag. 89;
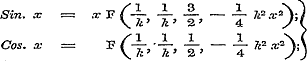 ....§ 31, pag. 115; ....§ 31, pag. 115;
waarin k, na de herleiding, gelijk nul worde gesteld; 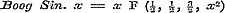 ..............§ 34, pag. 122; ..............§ 34, pag. 122;
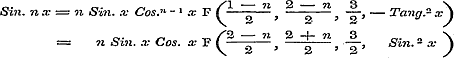 ; ;
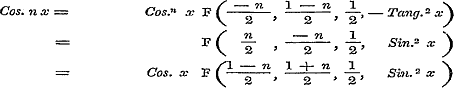 . .
De beide eersten voor Sin. nx en Cos. nx stemmen overeen met de formulen (6) en (7) § 30, pag. 111, 112; de vier overigen voor die zelfde grootheden respectivelijk met de formulen (11) en (13), (10) en (12), § 39, pag. 141. - Omtrent de formule voor 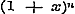 merke men op, dat β daarin geheel willekeurig is. merke men op, dat β daarin geheel willekeurig is.
Verder bepaalt Schr. de verschillen tusschen eenige waarden, welke de algemeene functie F verkrijgt, wanneer enkele der constanten juist met de eenheid worden vermeerderd of verminderd, om in § 67, met behulp dezer verschillen, die functie te kunnen herleiden in eene gedurige breuk, waarvan in § 68 de convergentie wordt aangetoond. Daarna worden, volgens het gevondene, de functiën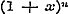 en ex herleid tot gedurige breuken. Die voor ex wordt vereenvoudigd, en verder wordt uit en ex herleid tot gedurige breuken. Die voor ex wordt vereenvoudigd, en verder wordt uit
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 389]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dit vereenvoudigde gedurige gebroken, na de substitutie 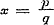 , de onmeetbaarheid van ex bewezen. Daar evenwel, na de verbetering der schrijffout, alle onevene termen gelijk zijn aan ½ p, zoo geldt het hier gegevene bewijs niet, daar ½ p niet meer eene ware breuk is. Men kan echter deze eigenschap van ex betoogen uit de herleiding van , de onmeetbaarheid van ex bewezen. Daar evenwel, na de verbetering der schrijffout, alle onevene termen gelijk zijn aan ½ p, zoo geldt het hier gegevene bewijs niet, daar ½ p niet meer eene ware breuk is. Men kan echter deze eigenschap van ex betoogen uit de herleiding van 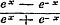 .
25. Volgens het aangevoerde toch wordt, na aanwending der formule op pag. 232, daar .
25. Volgens het aangevoerde toch wordt, na aanwending der formule op pag. 232, daar 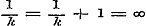 is, is,
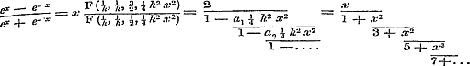 en hierin
en hierin 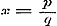 stellende, waarbij p en q geheele getallen zijn, en herleidende, verkrijgt men, daar stellende, waarbij p en q geheele getallen zijn, en herleidende, verkrijgt men, daar
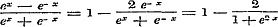 is, is,
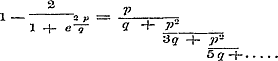 Daar nu de tellers der termen, p2, standvastig blijven, de noemers daarentegen vermeerderen, zoo zullen, nadat eens nq > p2 geworden is, alle termen ware breuken worden; volgens het vroeger bewezene verkrijgt dan de gedurige breuk zelve eene onmeetbare waarde, en moet eindelijk ook
Daar nu de tellers der termen, p2, standvastig blijven, de noemers daarentegen vermeerderen, zoo zullen, nadat eens nq > p2 geworden is, alle termen ware breuken worden; volgens het vroeger bewezene verkrijgt dan de gedurige breuk zelve eene onmeetbare waarde, en moet eindelijk ook 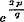 onmeetbaar zijn, welke de geheele waarden van p en q mogen zijn; dat is, ex is onmeetbaar, welke ook de meetbare waarde van x zij.
26. In § 69 wordt vervolgens de onmeetbaarheid van π uit de meetbaarheid van onmeetbaar zijn, welke de geheele waarden van p en q mogen zijn; dat is, ex is onmeetbaar, welke ook de meetbare waarde van x zij.
26. In § 69 wordt vervolgens de onmeetbaarheid van π uit de meetbaarheid van 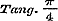 bewezen; hierop volgt nog een bewijs der onmeetbaarheid van π2, hetgeen echter, zoo als het daar gegeven wordt, alleen de onmeetbaarheid van π zelve kan aantoonen, maar met eene geringe wijziging evenwel tot het gestelde doel kan leiden.
Ware bewezen; hierop volgt nog een bewijs der onmeetbaarheid van π2, hetgeen echter, zoo als het daar gegeven wordt, alleen de onmeetbaarheid van π zelve kan aantoonen, maar met eene geringe wijziging evenwel tot het gestelde doel kan leiden.
Ware 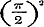 meetbaar meetbaar 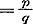 , dan zoude de waarde van de gedurige breuk , dan zoude de waarde van de gedurige breuk
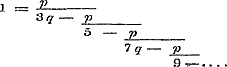
- welker termen standvastige tellers p, en klimmende noemers hebben, en dus, van eenen zekeren term af, als n > p, dus ook nq > p geworden is, ware breuken zijn, - onmeetbaar zijn, hetgeen met de waarde 1 in strijd is; derhalve is  onmeetbaar. onmeetbaar.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 390]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Wij hebben dus nu verscheidene vormen leeren kennen, waarin de algebraische en meest eenvoudige transcendentale functien kunnen ontwikkeld worden: de reeks, het gedurige produkt, de gedurige breuk, die ieder, als het ware, zoo veel voorstellingen zijn van gedurige optelling en aftrekking, gedurige vermenigvuldiging, gedurige deeling. Een niet minder belangrijk middel om de functien te ontwikkelen, bezitten wij in de zoogenoemde bepaalde Integralen, waarvan de theorie echter eerst in de Integraalrekening wordt geleerd, en die dus hier, waar wij den invloed der verandering van het argument op de functie zelve nog niet nagaan, geene plaats konden erlangen. 27. De voorgaande wijze, om het behandelde werk van Dr. Smaasen te doorloopen, is door ons gekozen, eensdeels, omdat zij geschikte aanleiding gaf tot het plaatsen en uiteenzetten der grootere en kleinere aanmerkingen, die onder de lezing bij ons oprezen, - ten andere, omdat zij het best kon doen oordeelen over het aantal en de natuur der onderwerpen, in dit Handboek vervat, en over de geleidelijke methode, waarop deze zijn voorgedragen. Er blijft nu nog eene vraag ter beantwoording over: voldoet het boek aan zijnen titel? of liever: past de titel voor het boek? - Naar den tegenwoordigen omvang der wetenschap, die Algebra genoemd wordt, dient men wel met Cauchy en Schlömilch de Algebraische Analyse van de Hoogere Algebra te scheiden, zoodanig dat deze de theorie der hoogere magtsvergelijkingen, gene daarentegen de leer van de ontwikkeling en van de eigenschappen der functien bevat. Als wij nu zamenvatten, hetgeen wij in dit behandelde werk gevonden hebben, zoo zullen wij het tot de Algebraische Analyse moeten brengen, die dan ook in zijn geheel daarin wordt opgenomen en afgehandeld. Maar hieruit vloeit dan ook voort, dat, gelijk wij reeds boven aanstipten, hoezeer de resultaten van de theorie der hoogere magtsvergelijkingen hier gebezigd moeten worden, toch de §§ 20-22, 40-46, in zoo verre zij ter loops die theorie behandelen, - evenzeer als § 47, waarin de algemeene oplossing der derde en vierde magtsvergelijkingen wordt nagegaan, - hier gevoegelijk konden worden gemist. - Hoewel nu deze wijze van beschouwing afwijkt van die des Schrijvers, zoo blijft toch uit zijn oogpunt dezelfde aanmerking aangaande bedoelde §§ gelden, die evenmin behooren tot hetgeen hij Hoogere Algebra noemt, als tot hetgeen wij onder Algebraische Analyse verstaan. Overigens kwam het ons minder gepast voor, de theorie der hoogere magtsvergelijkingen tot de Lagere Algebra te brengen; van daar dat wij uitsluitend voor haar den naam van Hoogere Algebra wilden bezigen. Eene enkele aanmerking zij ons vergund over eenige notatien van den Schrijver, die den Neperiaanschen Logarithmus door het teeken Log. de Bernouillaansche Coefficienten door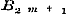 , en de Secanten-coefficienten door , en de Secanten-coefficienten door 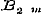 voorgesteld, in plaats van de meer algemeen gebruikte teekens l, voorgesteld, in plaats van de meer algemeen gebruikte teekens l, 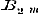 , , 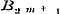 te bezigen. te bezigen.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 391]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
28. Wij hebben dan gezien, dat het onderhavige werk van Dr. Smaasen, wezenlijk veel belangrijks over de theorie der ontwikkeling van functien bevat, hetgeen daarin op eene zeer geleidelijke en bevattelijke, meestal vrij volledige wijze wordt voorgesteld. Viel er al het een en ander aan te merken omtrent de wijze van ontwikkeling van sommige punten, het al of niet opnemen van andere, men bedenke, dat deze handleiding, toch immer de meest volledige over dit deel der Wiskunde, uit zoo veel bronnen moest putten, en zoo veel zaken van belangrijken inhoud en verschillenden aard moest zamenvatten. Wij mogen en moeten dit werk aan de beoefenaars der Wiskunde aanbevelen, niet alleen wegens de belangrijkheid van het onderwerp, dat, gelijk wij reeds boven aanmerkten, tegenwoordig een van de hoofdonderwerpen der Wiskunde is geworden, en dat tot onmisbaren grondslag van zoo veel deelen der Hoogere Analyse moet strekken, - maar ook wegens de methode, waarnaar deze stof hier is bewerkt, en die gevoegelijk tot een rigtsnoer kan dienen bij ieder met dit onderwerp verwant onderzoek; terwijl de lezing van dit boek, mede in verband met enkele onzer aanmerkingen, de overtuiging zal doen ontstaan, dat genoemde deelen der Wiskunde nu ook wel met regt op eene wiskundige juistheid mogen aanspraak maken.
Om alle volgende lezers te gemoet te komen, willen wij hier nog op des Schrijvers lijst van Errata laten volgen eene korte opgave der voornaamste druk- en schrijffouten, die ons nog bij de lezing zijn voorgekomen, en die wij aan den afstand des Schrijvers van de pers, en aan den haast, waarmede het boek schijnt afgedrukt te zijn, toeschrijven.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 392]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 393]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deventer, Junij 1849. D. BIERENS DE HAAN,
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 394]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Oud en Nieuw. Nasporingen en opmerkingen, ter zake van de heemraadschappen en wat daartoe betrekking heeft, door A. Elink Sterk, Jr. ‘Het onderwerp trekt mij. Het is moeijelijk, maar de moeite waard.’ (Thorbecke.) Utrecht, C. van der Post, Jr., 1849.Dit werkje is een herdruk van stukken, in 1847 en 1848 in de ‘Politieke Bijdragen’ geplaatst en daarvoor oorspronkelijk geschreven. Het bevat deels eene schets van de geschiedenis onzer vroegere heemraadschappen, dijk- en polderbesturen, deels voorslagen tot betere regeling van hunnen tegenwoordigen toestand. Het geschiedkundige deel komt ons voor het minst belangrijk te zijn en in bijna geen verband te staan met hetgeen volgt. Het lag zeker wel niet in het plan van den schrijver den oorsprong der onderscheidene waterkeeringen, de instellingen der besturen, het gezag, de regtsmagt en den werkkring der Heemraden, Dijkgraven, enz., volledig te beschrijven en uit de geschiedenis te bewijzen; maar, zoude hetgeen hij daaromtrent zegt eenig nut hebben, dan moesten zijne opmerkingen toch tot eenige algemeene begrippen leiden, die het standpunt aangaven, vanwaar hij den tegenwoordigen toestand zou beschouwen. En dit is het geval niet. Het eenige besluit, dat hier uit de geschiedenis getrokken wordt, is: dat er groot gebrek aan orde en éénheid in die zaken heerschte; maar in het oordeel bij voorbeeld over den invloed, dien de regering zich billijkerwijze kan toeëigenen, en over de autonomie, welke zoo velen voor de polders als een regt inroepen, doet de schrijver volstrekt niets afhangen van den verschillenden oorsprong, welken hij aan de onderscheidene waterkeeringen en vereenigingen daartoe in zijn eerste stuk heeft aangewezen. Zoo als gemis aan orde en regelmaat de hoofdtrek is in het tafereel van de vroegere besturen, door den schrijver gegeven, zoo is éénheid, orde en spaarzaamheid de groote eisch, welken hij aan het tegenwoordige doet. Vaste beginselen in de reglementen en wetgeving, opheffing van vele overbodige betrekkingen, uitroeijing van een aantal nog bestaande misbruiken en ongeregeldheden, zijn daartoe de middelen, die in het laatste en grootste gedeelte van dit werkje nader worden uitééngezet. Veel daarvan zal men, gelooven wij, geheel kunnen beämen, ofschoon men vele stellingen over de centralisatie, waardoor die éénheid moet geboren worden, met voorzigtigheid zal behooren toe te passen op onderwerpen, waar plaatselijk verschil eene verschillende behandeling allezins noodig maakt, en waarbij onmiddelijke, vrije werking te dikwerf vereischt wordt, dan dat men zonder gevaar de bevoegdheid daartoe slechts aan een verwijderd bestuur zou kunnen toekennen. Waar zoo herhaald op zuiverheid van taal wordt aangedrongen, als hier 't geval is, springen germanismen als beduidend, goedbezitters, tweeduidigheid, des te meer in het oog. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 395]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Gedenkschrift der inhuldiging van Z.M. Koning Willem III, in de Nieuwe Kerk te Amsterdam, op Zaturdag den 12den Mei 1849, door J.F. Bosdijk. Te Haarlem, bij J.B. van Loghem, Junior. 1849.Zijn wij wel onderrigt, dan had Alexandre Dumas destijds, door eenen brief aan den Hofmaarschalk, om een plaatsje verzocht, ‘pour voir couronner le dernier des rois.’ - Dat onze oppervlakkige polygraaf hier wel weêr den bal zal hebben misgeslagen, ligt buiten elken redelijken twijfel, en de plegtigheden, aan eene inhuldiging verbonden, zal men nog wel niet dadelijk na ons uit de gedenkschriften daarvan alleen behoeven te leeren kennen. Het hier aangekondigde zou anders veel tot die studie kunnen bijdragen, nog half geholpen daarbij door eene uitslaande, en overigens vrij leelijke, steendrukplaat, het oogenblik voorstellende, waarop de Koning in de Nieuwe Kerk den eed aflegt. - Het boekske bestaat verder uit twee gedeelten, van nagenoeg dezelfde grootte: het eerste, dat in eene soort van voorrede eene gezwollene voorafspraak bevat; het andere, hetwelk de bloote beschrijving geeft van hetgeen de titel vermeldt. - Hetgeen in die voorafspraak wordt bij elkander gehaald, komt voornamelijk hierop neêr: dat er een groot onderscheid bestond tusschen het vernemen van den dood van den stadhouder Willem II, voor bijna twee eeuwen, en nu, bij dien van den koning; - hoe bij den prins die aanslag op Amsterdam dwars in de maag bleef zitten, terwijl men dadelijk na het overlijden van onzen Willem II van standbeelden sprak; - hoe tóen de gemoederen lang aan 't gisten bleven, en nu reeds ‘in vier dagen slechts, iedere zweem van onzekerheid, van twijfel - zoo die al met eenigen grond kon bestaan - verdwenen was.’ - ‘Reeds toen,’ dus gaat de S. voort, ‘had het handschrift van dien zoon (van nu Willem III namelijk) de tijding bekrachtigd, dat hij de teugels der regering in handen nam. Wat meer zegt, bij die verzekering werd iedere ademhaling nog vrijer; want elk, die in de dienst van den lande ambt of rang bekleedde, kon het hoofd tevreden neêrleggen; blijmoedig, vol erkentenis kon hij danken; men liet hem, wat hij door verdienste, voorspraak of geboorte verkregen had,’ enz. Wij laten al hetgeen hieromtrent die voorafgaande algemeene officiers-en ambtenaarsbenaauwdheid gezegd wordt, geheel voor rekening van den S., en zouden hem alleen willen vragen: of die fraaije zin ook welligt dienen moest, om aan het slot daarvan eenige ironie te kunnen inlasschen of een coup fourré te geven? Zoo kunnen wij het mede moeijelijk met elkander vereenigen, wanneer hij, na eerst gezegd te hebben: dat hij geene pligten wil voorschrijven, over geene regelen van bestuur wil spreken, spoedig evenwel daarin vervalt en eindelijk zelfs speciaal er op aandringt, om liever met opoffering van Maastricht en Venlo de Marine te versterken! Maar dit alles en nog eenige gekunstelde redeneringen daarbij, is ook slechts toegift op de eigenlijke beschrijving van de inhuldigingsplegtigheid, die wij trouwens gaarne aannemen, dat tot in de minste bijzonderheden naauwkeurig is, want wij hebben niet tot de aanschouwers behoord, en zelfs dan nog zouden wij in dit geval er lastig mede zitten. In vertrouwen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 396]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gezegd, komt het ons zelfs vreemd voor, hoe de geachte redactie van ‘de Gids’ niet liever de aankondiging van dit ‘Gedenkschrift’ aan eenen gemoedelijken stadgenoot heeft opgedragen, van wien zij met eenige zekerheid mogt veronderstellen, dat hij zich met alle détails in dezen haarfijn had bekend gemaakt. Nu lezen wij b.v., hoe de hoogte tot aan het attiek van den eereboog op de Reguliers-Breestraat 8,63 el bedroeg, - en al scheelde dat ook ettelijke duimen, toch moesten wij er ligtvaardig over heen loopen, en speelt ons daarbij dat spreekwoord van eene kat in een vreemd pakhuis door het hoofd. Zoo regent het insgelijks eigennamen in dit relaas en van de leden der cerewacht en van iedereen, om kort te gaan, die op de eene of andere wijze, al ware het dan ook slechts door de bijzondere versiering van den gevel van zijn huis, op die feestdagen mede heeft uitgeblonken; maar hoe weten wij hier, ‘procul negotiis,’ of al die namen wel goed geschreven, of geene anderen, die even zoo mogten aanspraak maken, om der vergetelheid te worden ontrukt, daaronder vergeten zijn? Niet dat wij voor ons zelven aan dergelijke fouten zouden blijven hangen; maar er werd in deze beschrijving wel eenigzins gerekend op de ijdelheid, en zoo die soms niet in ieder opzigt bevredigd was, kon het debiet er wel onder lijden. Dat willen wij trouwens wel zoeken te bevorderen, door nog even de annonce af te schrijven, die voor het titelblad gevoegd is; zij luidt aldus: ‘de uitgever dezes heeft eenige weinige exemplaren van dit werk, enz., doen binden in cartonnen banden, met de plaat op Chineesch papier gedrukt, welke hij, zoolang de voorraad strekt, à ƒ 1.50 zal afleveren.’ - Bespottelijk weinig voor zoo vele zaken! - ‘Heeren Leden der Eerewacht, zoowel als andere belangstellende personen, worden hierop opmerkzaam gemaakt, en verzocht hunne bestelling ten spoedigste aan hunnen gewonen Boekhandelaar op te geven, daar de voorraad zeer klein is.’ - En daarom: zegt het voort!! want het kon wel eens periculum in mora worden.
C.A.E. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mars, Jaarboekje voor het Nederlandsche leger. Eerste Jaargang, 1849. Breda, Broese en Comp.Wij zouden der waarheid te kort doen, wanneer wij aan dit Jaarboekje eene hooge waarde wilden toeschrijven; maar wij kunnen toch gerustelijk zeggen, dat het zeer veel bevat, hetgeen niet onbelangrijk is. Het is de eerste Jaargang, de eerste stap; en men heeft dus niet het regt, die te streng te beoordeelen. Wij hopen, dat de uitgevers genoegzame deelneming en ondersteuning zullen vinden om hunne moeijelijke taak voort te zetten, en dat hun Jaarboekje, zoo door het belang der onderwerpen, die het bevat, als door de grondige en bezadigde behandeling daarvan, meer en meer eene getrouwe afspiegeling moge geven van de kennis en van de denkwijze van het Nederlandsche leger. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


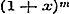 , ex en
, ex en 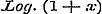 in reeksen.
in reeksen.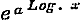
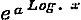
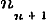 ,
, 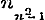
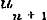 ,
, 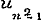
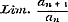
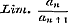
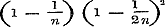
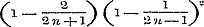
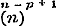
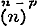
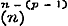
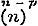
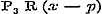
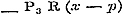
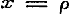 ,
,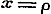 , of dit blijft
, of dit blijft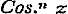
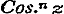
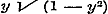
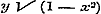
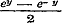
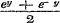
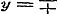
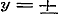
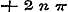
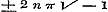
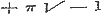
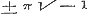
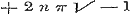
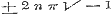
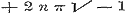
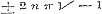
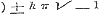
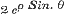
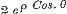
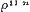
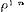
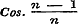
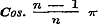
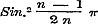
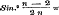
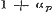
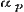
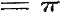
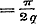
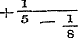
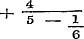
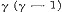 in het verschil.
in het verschil.