Vermogensverhoudingen in Nederland

Ontwikkelingen sinds de negentiende eeuw

[p. 410]

Appendix 2 Berekening van vermogensgrenzen en totaal privé-vermogen

1 Vermogensgrenzen en deeltotalen

In de berekening van de ondergrens van de vermogens van de rijkste p % van de bevolking (v_p) is er van uitgegaan dat de vermogens binnen de gegeven vermogensklasse waarin deze grens ligt Pareto-verdeeld zijn, dat wil zeggen voldoen aan de formule:

log N_v = log A - αlog v

Hierin is v het variërende vermogen per bezitter, is N_v het aantal bezitters met een vermogen v of meer, en zijn α en A constanten. De constante α voor elke vermogensklasse kan berekend worden door de waarden van N_v en v voor de beide klassegrenzen in te vullen. De werkelijke verdeling binnen een klasse bleek op deze wijze redelijk goed benaderd te worden: het naar dit uitgangspunt berekende totale vermogen in de vermogensklasse (zie hieronder: V_kth) week steeds weinig af van het voor die klasse gegeven vermogen (V_k).

Af te leiden is nu dat

Hierin is v_p de te berekenen ondergrens van de vermogens van de rijkste p%, N_p het aantal bezitters dat tot deze p% behoort, v_h de bovengrens van de gegeven vermogensklasse, N_h het aantal dat een vermogen v_h of meer bezit en α de Pareto-constante uit de eerstgenoemde formule.

Het vermogenstotaal van de rijkste p % dat tot de vermogensklasse behoort waarin v_p valt, is eveneens berekend door uit

[p. 411]

te gaan van de Pareto-verdeling, volgens welke



V_kth is hier het totale vermogen van klasse k (theoretisch verondersteld volgens de Pareto-verdeling), v_o en V_h zijn respectievelijk de onder- en bovengrens van deze klasse, en N_o en N_h de bijbehorende aantallen bezitters met een vermogen groter dan of gelijk aan dat van de klassegrenzen. Toegespitst op de rijkste p%, is het gezamenlijke (ongecorrigeerde) vermogen van deze categorie binnen klasse k:



Hierop is nog een correctie aan te brengen, en wel een die gelijk is aan de verhouding tussen het feitelijk geregistreerde vermogen van de gehele klasse (V_k) en het theoretisch veronderstelde vermogen van deze klasse volgens de Pareto-verdeling (V_kth):



Het totale vermogen van de rijkste p% is dan:



waarbij Σ V_i de som is van de totaalvermogens van de vermogensklassen boven de klasse waarin v_p valt.

2 Totaal privé-vermogen

De lognormale verdeling waarvan in de berekening van het totale privé-vermogen is uitgegaan, wordt beschreven door twee parameters: ten eerste het gemiddelde van de logarith-

[p. 412]

men van de vermogens μ = Σx_i/N_pop (waarbij x_i de logarithme van vermogen v_i is, N_pop het aantal bezitters in de hele populatie); en ten tweede de standaarddeviatie σ van dezelfde logarithmische vermogens. Gezocht is nu naar zodanige waarden van μ en σ dat de afstand tussen de gegeven waarden x_i en de bijbehorende frequenties p_i= N_i/N_pop (waarbij N_i het aantal bezitters met een vermogen v_i of meer is) enerzijds en de lognormale verdeling anderzijds minimaal is. De theoretisch veronderstelde verdeling kan worden weergegeven in een lineaire functie x = μ + σ.z, waarin z de z-waarde is die hoort bij het gedeelte van de populatie dat een gegeven vermogen of meer bezit (z_i is zodanig gekozen dat P(u ≥ z_i) = p_i, waarbij u een standaardnormaal verdeelde grootheid voorstelt). Het kwadraat van de loodrechte afstand van een door gegeven waarden bepaald punt P(z_i, x_i) tot de door deze functie beschreven rechte lijn is dan: (x_i - μ - σ.z_i)²/(1 + σ²). Als nu de som van al deze gekwadrateerde afstanden minimaal is, dan is de standaarddeviatie:



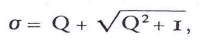
waarbij

Hierin is var(x) de variantie van de waarden x_i, var(z) de variantie van z_i en covar(x,z) de covariantie van x_i en z_i. Het gemiddelde van de logarithmen van alle vermogens volgens de lognormale verdeling is nu:

μ = x̅ - σ.z̅,

waarin x̅̅ het gemiddelde van de x_i-waarden is, z̅ het gemiddelde van de bijbehorende z_i-waarden.

De basisgrootheden van de lognormale verdeling, μ en σ, zijn, zo kan worden afgeleid, als volgt bepalend voor het gemiddelde van alle vermogens (v̅) en daarmee ook voor de (ongecorrigeerde) som van alle vermogens (V_tot(o)):

[p. 413]

log v̅ = μ + 1/2 σ² ln10

waarin ln10 de natuurlijke logarithme van 10 is.

V_tot(o) = v̅. N_pop

Voorts kan worden bewezen dat bij een zuivere lognormale verdeling het totale vermogen boven vermogensgrens v_g gelijk is aan:



waarbij Φ (x) = P(u ≥ x) bij standaardnormale verdeling van u, dat wil zeggen de rechtseenzijdige overschrijdingskans volgens z-waarden.

Met behulp van deze formule (vgl. Aitchison/Brown 1963, p. 87) kan op het berekende totale vermogen een correctie worden toegepast, die rekening houdt met de constateerbare afwijking van de zuivere lognormale verdeling: waar het berekende totale vermogen boven de benedengrens van de geregistreerde vermogens groter was dan het totaal van de geregistreerde vermogens, is het verschil tussen beide van het ongecorrigeerde totale vermogen afgetrokken, waar de eerste grootheid kleiner was dan de tweede, is het verschil bij het ongecorrigeerde totale vermogen opgeteld. In formule:

V_tot = V_tot(o) + V_g(f) - V_g(th)

V_g(f) is hier de som van de feitelijk geregistreerde vermogens, V_g(th) het theoretisch veronderstelde, naar de lognormale verdeling berekende totale vermogen boven de registratiegrens. Deze correctie komt erop neer, dat de som van de geregistreerde vermogens als gegeven is aangenomen en dat het uitgangspunt van de lognormale verdeling alleen gebruikt is om het totaal van de niet-geregistreerde vermogens te schatten.

Het proportionele verschil tussen V_g(f) en V_g(th) is tevens een indicator van de mate waarin de bekende gegevens voldoen aan de veronderstelling van een lognormale verdeling. Een andere, wat preciezere maatstaf daarvoor is de gemiddel-

[p. 414]

de procentuele afwijking van de geregistreerde aantallen die een gegeven vermogen of meer bezitten van de aantallen volgens de zuivere lognormale verdeling. Deze gemiddelde fout is voor ieder jaar berekend. Zoals is aangegeven in hoofdstuk iv (zie met name Tabel 4, kolom 5) en nader wordt toegelicht in appendix 3, is de correspondentie tussen de gegeven en de veronderstelde verdeling steeds bevredigend, voor sommige jaren zelfs bijzonder groot te noemen. In appendix 3 volgen meer argumenten voor de hier gevolgde werkwijze.

De in deze paragraaf weergegeven formules zijn (op de laatste na) ontwikkeld door de wiskundige R. Potharst. Schrijver dezes heeft er dankbaar gebruik van gemaakt.

Voor de in deze en de vorige paragraaf van deze appendix beschreven berekeningswijze is een computerprogramma geschreven. Hierdoor was het mogelijk de aandelen van de rijkste zoveel procent van de bevolking (variërend van o,1% tot 5%) in het totale privé-vermogen te schatten voor alle jaren tussen 1894 en 1974 waarover vermogensstatistieken beschikbaar zijn. Dezelfde berekeningswijze is ter controle ook op gegevens over andere landen en aan de Nederlandse successiestatistieken ontleende gegevens toegepast. Meer hierover in de volgende appendix.