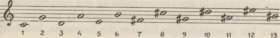Princiepen der Europese muziek
(1949)–Matthijs Vermeulen–
[pagina 14]
| |
Vroegste beginselen en grondslagen der muziekIk ben teruggegaan tot de oudst denkbare aanvangen, tot de seconde waarin de eerste mens vibrerend werd en zong, tot die hemelse seconden welke door alle volkeren, in alle tijden, en in allerlei fabels, werden toegedicht aan de tussenkomst van een God. En ik moest mij wel terug verplaatsen naar die fantastische leegte, toen er nog niets was, naar het ogenblik dat er onloochenbaar geweest moet zijn, waarin het zwijgen werd opgeheven door een menselijk gezang. Want het schijnt me logisch dat er muziek moet zijn alvorens men muziek tot iets kan laten dienen. Philosophen, geschiedschrijvers en andere geleerden zeggen mij dat de muziek ontstond wijl de mens haar nodig had voor zijn religieuze plechtigheden, wijl de chamans (de tovenaars) haar nodig hadden voor hun magische bezweringen, wijl zij zeer doelmatig was voor het regelen, het disciplineren van collectieven arbeid gelijk het roeien ener galei, het voortslepen van een zware last, wijl alle levende wezens wanneer zij verliefd zijn hun wijfje trachten te bekoren met bijzonder gemoduleerde tonen, of wijl de mens een ingeboren, een physiologische behoefte heeft aan spel en dans. Ik geloof dit alles gaarne. Doch hoe rudimentair ook het ritueel kon zijn waarmee de mens zijn eerste doden in de aarde legde, hoe primitief ook de ceremonie waarin hij voor de eerste maal zich richtte naar de goddelijke kracht, of de hulp inriep, of de bedreiging poogde af te wenden van welwillende, van kwaadgezinde geesten, en hoe simplistisch ik mij ook de gebaren verbeeld van de allereerste gezamenlijke menselijke werkzaamheid (en ik zou hier kunnen opmerken dat de bevers bijv., of de mieren, of de bijen zeer goed en schrander arbeiden zonder erbij te zingen) - er moet een min of meer georganiseerde muziek aanwezig, beschikbaar geweest zijn alvorens iemand eraan denken kon haar voor iets te gebruiken. Toen bijgevolg de muziek werd aangewend, gebezigd voor wat dan ook, was zij reeds. Zij was misschien, zij was waarschijnlijk zeer fragmentarisch, zeer schematisch, maar | |
[pagina 15]
| |
zij was. En zij was, zij moet geweest zijn vóór alle utilitaristische toepassing. Ik ben gedwongen mij nogmaals te werpen in de afgronden van het ontstaan der dingen. Ik keer terug naar mijn oertijd, naar mijn oervorm. Ik ben een wilde. Ik draag een vacht, een knots. Ik heb een stem en gebruik mijn stem. Maar de gewone gewaarwordingen mijner lange dagen nopen mij tot geen enkelen bepaalden, geaccentueerden klank. Ik murmel, ik grom, in vage, onverschillige intonaties. Wat gebeurt er echter en wat gebeurt telkens weer wanneer die vreemde, teder-wrede siddering mij overvalt, wanneer ik loop in den gierenden orkaan, wanneer ik in vollen gang jaag achter een buit, achter een vijand, de harde en weke, schroeiende siddering waarin mijn kracht verdubbelt, waarin ik kunnende word, mij koning voel, waarin mijn ganse wezen zich bevelend rekt naar de verre horizon? Mijn stem zet uit, breekt open in een roep, een vraag zonder rust, in een vaart zonder einde, in een signaal van storm, strijd en begeren dat zich millioenen malen kan en zal herhalen zonder dat zijn klank ooit raakt uitgeput. Ik beveel dan:
En wat gebeurt er, wanneer ik een prooi naar de keel vlieg, of, hetgeen dikwijls hetzelfde is, wanneer die prooi mijzelf bespringt, wat gebeurt er telkens wanneer ik den hoogsten nood of den hoogsten lust tegemoet ijl? Mijn stem slaat hijgend over in mijn toegesnoerden strot; zij krijt, schreeuwt, juicht, gilt: Zij kermt of jubelt, joelt of klaagt een luide, woeste, opperste smeking, uitrazing van smart of vreugde, van een leed of van een geluk dat geen verpozing, geen stilling wil noch willen kan, en waarbij zij, in pijn of in genot, wachtend, luisterend, zoekend, wensend, steeds verlangend en onbevredigd, terugvalt naar een geluid dat nog bidt of nog gebiedt: Zij kermt of jubelt, joelt of klaagt een luide, woeste, opperste smeking, uitrazing van smart of vreugde, van een leed of van een geluk dat geen verpozing, geen stilling wil noch willen kan, en waarbij zij, in pijn of in genot, wachtend, luisterend, zoekend, wensend, steeds verlangend en onbevredigd, terugvalt naar een geluid dat nog bidt of nog gebiedt: 
Deze vier tonen heb ik nergens kunnen horen, noch in het woud, noch in de lucht. Zij wellen op uit mijzelf, telkens als ik een heftigen schok onderga, telkens als de omringende wereld mij dwingt tot een daad, telkens als een gevaar, een smart mij dreigt of als een geluk, een vreugde mij wenkt, mij roept. Deze vier tonen (drie stembuigingen) zijn on- zijn on- | |
[pagina 16]
| |
afscheidelijk verbonden aan mijn machtigste en onvermijdelijkste impulsen. Ik kan hun orde wijzigen. Ik kan ze omkeren en eerst den roep laten klinken, daarna het antwoord:  , altijd en overal wanneer ik mij bevind in dezelfde hachelijke of verrukkende omstandigheden komen zij automatisch weerom. Eeuwen lang. Alom. Bij alle mensen der aarde. Ik zou kunnen zeggen dat hun voortdurende wederkeer tijdens honderden, duizenden jaren ze in mijn geheugen grifte. Maar neen. Dat is het niet. Zij behoren mij toe. Zij rijzen spontaan op uit mijn binnenste, telkens wanneer ik méér moet zijn dan ik ben in mija gewone, kalme doen, telkens wanneer ik meer moet worden dan mijn alledaagse zelf. Het zijn de vier klanken van wat ik vaag en gissend noem mijn hart, mijn ziel. Het zijn de vier klanken welke ik uitstoot wanneer ik beveel, wanneer ik vecht, wanneer ik begeer. Zij zijn mijn eigenste echo. Alle geluiden welke ik tussen die vier tonen kan verbeelden, eronder of erboven, lijken mij onderweg te zijn, onbesloten, onbeslist, besluiteloos, zonder noodzaak, zonder die grote, innerlijke spanning; afhankelijk van mijn keus, van mijn gril. Maar die vier andere worden mij opgelegd; zij worden mij gedicteerd door dat zeldzame, geheimzinnige, raadselachtige binnenste van mijn eigen lichaam tijdens de ervaringen welke het wonderlijk zingend maken. Zij vormen twee verschillende samenklanken in mijn gehoor, in mijn geheugen, in mijn bewustzijn: , altijd en overal wanneer ik mij bevind in dezelfde hachelijke of verrukkende omstandigheden komen zij automatisch weerom. Eeuwen lang. Alom. Bij alle mensen der aarde. Ik zou kunnen zeggen dat hun voortdurende wederkeer tijdens honderden, duizenden jaren ze in mijn geheugen grifte. Maar neen. Dat is het niet. Zij behoren mij toe. Zij rijzen spontaan op uit mijn binnenste, telkens wanneer ik méér moet zijn dan ik ben in mija gewone, kalme doen, telkens wanneer ik meer moet worden dan mijn alledaagse zelf. Het zijn de vier klanken van wat ik vaag en gissend noem mijn hart, mijn ziel. Het zijn de vier klanken welke ik uitstoot wanneer ik beveel, wanneer ik vecht, wanneer ik begeer. Zij zijn mijn eigenste echo. Alle geluiden welke ik tussen die vier tonen kan verbeelden, eronder of erboven, lijken mij onderweg te zijn, onbesloten, onbeslist, besluiteloos, zonder noodzaak, zonder die grote, innerlijke spanning; afhankelijk van mijn keus, van mijn gril. Maar die vier andere worden mij opgelegd; zij worden mij gedicteerd door dat zeldzame, geheimzinnige, raadselachtige binnenste van mijn eigen lichaam tijdens de ervaringen welke het wonderlijk zingend maken. Zij vormen twee verschillende samenklanken in mijn gehoor, in mijn geheugen, in mijn bewustzijn:  en en 
Hier keer ik uit mijn voorvaderlijk verleden terug naar dezen tijd en dezen dag, waarop ik het muzikale phenomeen tracht te beredeneren en te begrijpen. Met opzet plaatste ik geen sleutels voor de noten welke mij opklonken uit de menselijke oer-ziel. Ik had zelfs, de zaken strikt historisch beschouwend en weergevend, geen noten mogen gebruiken en geen noten-balken, zelfs geen accenten of andere grafische tekens. Want vergeet niet, als gij u helder en tastbaar wilt voorstellen in hoe hogen graad de muziek een tevens normaal, tevens supranormaal product is van den menselijken geest, en als gij u een reëel, feitelijk begrip wilt vormen van haar geleidelijk ontstaan, vergeet dan nooit dat de prehistorische Homo Faber, die haar grondslagen legde, over geen enkel middel beschikte om andere tonen voort te brengen dan welke hijzelf voortbracht, en dat er geen enkele mogelijkheid bestond om de tonen welke hij nergens vond dan in zichzelf, | |
[pagina 17]
| |
te fixeren, te imiteren, te controleren, te meten, te vergelijken met iets hoorbaars. Vergeet ook niet dat onze zonderlinge voorvader, als 't ware haveloos, naakt en hulpeloos te vondeling gelegd in een alom en op allerlei wijzen vijandige omgeving, steeds bedreigd in zijn eigen leven, steeds bedreigd in het leven zijner dierbaren, (want hij beminde reeds vanaf zijn eersten dag) steeds in 't verweer, steeds op zijn hoede, steeds op de loer, vergeet niet dat deze deerniswekkende, bewonderenswaardige, nooitversagende voorvader een in de uiterste mate oplettend, speurend, sensitief, intuïtief, nerveus, ontvankelijk, om zo te zeggen geniaal wezen geweest moet zijn, schranderder, listiger, sluwer en dapperder dan al wat hem belaagde. Het is meer dan waarschijnlijk, het is zo goed als zeker (hoewel ik dit nimmer zal kunnen bewijzen) dat die onvergelijkelijke voorvader (zijn wandschilderingen in de grotten van Dordogne zijn inderdaad totnutoe weergaloos) gezongen heeft alvorens hij een gedachte leerde uitdrukken in georganiseerde spraak. Men kan nog sporen van dit eerste zingen terugvinden in de accentuatie van alle oude talen, in de melodisch geïntoneerde zegging waarmee de Romeinen en Grieken hun redevoeringen en al hun poëzie voordroegen, in de oorspronkelijke onafscheidelijkheid van vers en muziek. Maar zeker is het, en wetenschappelijk bewijsbaar, dat hij gezongen moet hebben in deze formule:  of omgekeerd: of omgekeerd:  vermoedelijk vocaliserend op de klinkers en den dubbelklinker a, e, o, oe, welke den edelsten gemoedstoestand vertolkten en welke de rijkste sonoriteit bezitten.
Wat nu zie ik, wanneer ik aan de vier fundamentele, ingeboren klanken van den vroegsten mens een zin, een betekenis, een melodische, harmonische, tonale of modale verstaanbaarheid tracht te geven in onze hedendaagse muzikale taal? Ik noteer ze volgens onze methoden in een rangorde vermoedelijk vocaliserend op de klinkers en den dubbelklinker a, e, o, oe, welke den edelsten gemoedstoestand vertolkten en welke de rijkste sonoriteit bezitten.
Wat nu zie ik, wanneer ik aan de vier fundamentele, ingeboren klanken van den vroegsten mens een zin, een betekenis, een melodische, harmonische, tonale of modale verstaanbaarheid tracht te geven in onze hedendaagse muzikale taal? Ik noteer ze volgens onze methoden in een rangorde  en bemerk dat ze ongedefinieerd zijn. Ik kan ze lezen, duiden, begrijpen in verschillende intonaties zonder hun structuur te wijzigen. In zichzelf hebben zij geen naam. Ik kan ze noemen gelijk ik wil. Als ik de interpretatie neem welke mij machinaal 't eerst voor den geest komt, en een zgn. sol-sleutel voorteken en bemerk dat ze ongedefinieerd zijn. Ik kan ze lezen, duiden, begrijpen in verschillende intonaties zonder hun structuur te wijzigen. In zichzelf hebben zij geen naam. Ik kan ze noemen gelijk ik wil. Als ik de interpretatie neem welke mij machinaal 't eerst voor den geest komt, en een zgn. sol-sleutel voorteken  zal zij Dorisch heten en machinaal zal ik de gapingen tussen de hoofd-klanken zo aanvullen dat zal zij Dorisch heten en machinaal zal ik de gapingen tussen de hoofd-klanken zo aanvullen dat
| |
[pagina 18]
| |
zij een geleidelijke reeks vormen:  . Ik weet dat ik aldus een zuiver intellectuele operatie verricht, die mij gesuggereerd kan zijn door mijn aangeleerde kennis, maar zij is niet in tegenspraak met een historisch feit en bevredigt mijn atavistisch geheugen, mijn instinct. De vier hoofd-klanken zijn geworden een kader, een raam, een lijst, wat Aristoteles definieerde als het lichaam der harmonie, en de verkregen reeks vormt een aaneenschakeling welke in gebruik was bij de Doriërs en die de Grieken later adopteerden als hun nationale toonsoort, onder den naam van Doristi.
Ik kan deze cerebrale operatie voortzetten met alle sleutels van ons tegenwoordig systeem dat groeide uit eeuwenlange menselijke overwegingen. Wanneer ik den tweeden sleutel neem welke mij machinaal in 't brein komt en ik schrijf, de leegten werktuiglijk completerend . Ik weet dat ik aldus een zuiver intellectuele operatie verricht, die mij gesuggereerd kan zijn door mijn aangeleerde kennis, maar zij is niet in tegenspraak met een historisch feit en bevredigt mijn atavistisch geheugen, mijn instinct. De vier hoofd-klanken zijn geworden een kader, een raam, een lijst, wat Aristoteles definieerde als het lichaam der harmonie, en de verkregen reeks vormt een aaneenschakeling welke in gebruik was bij de Doriërs en die de Grieken later adopteerden als hun nationale toonsoort, onder den naam van Doristi.
Ik kan deze cerebrale operatie voortzetten met alle sleutels van ons tegenwoordig systeem dat groeide uit eeuwenlange menselijke overwegingen. Wanneer ik den tweeden sleutel neem welke mij machinaal in 't brein komt en ik schrijf, de leegten werktuiglijk completerend  dan heb ik de toon-serie, welke na den Doristi het meest gebezigd werd in de Helleense oudheid, en die de Grieken Ionisti noemden, of ook Iasti, omdat zij in gebruik was bij de Ioniërs. De lezing dan heb ik de toon-serie, welke na den Doristi het meest gebezigd werd in de Helleense oudheid, en die de Grieken Ionisti noemden, of ook Iasti, omdat zij in gebruik was bij de Ioniërs. De lezing  verschaft mij de toonsoort der Phrygiërs, welke de Griekse theoretici classeerden als Phrygisti. Wanneer ik interpreteer verschaft mij de toonsoort der Phrygiërs, welke de Griekse theoretici classeerden als Phrygisti. Wanneer ik interpreteer 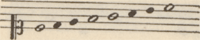 verkrijg ik de gamma welke gezongen werd door de Lydiërs en getiteld Lydisti. Lees ik verkrijg ik de gamma welke gezongen werd door de Lydiërs en getiteld Lydisti. Lees ik  dan hoor ik de serie welke inheems was bij de Eoliërs en die de Grieken daarom registreerden als Eolisti. Zo ontstaan uit vijf interpretaties reeds vijf gamma's zonder dat de externe structuur van het Aristoteleaanse kader verandert en te zamen vormen haar aanvangsnoten de antieke pentatonische (vijftonige) scala dan hoor ik de serie welke inheems was bij de Eoliërs en die de Grieken daarom registreerden als Eolisti. Zo ontstaan uit vijf interpretaties reeds vijf gamma's zonder dat de externe structuur van het Aristoteleaanse kader verandert en te zamen vormen haar aanvangsnoten de antieke pentatonische (vijftonige) scala  , gebruikt door een menigte volken en stammen. De Grieken bezaten nog twee toonsoorten, de mixolydisti: , gebruikt door een menigte volken en stammen. De Grieken bezaten nog twee toonsoorten, de mixolydisti:  en de hypolydisti: en de hypolydisti:  welke zij om obscure reden gemengd en getint achtten, misschien omdat de opeenvolging een modificatie en lichten troebel veroorzaakte in de grond-formule. De aanvangsnoten si en fa maakten de pentatonische reeks tot een volledige zeven-tonige welke zij om obscure reden gemengd en getint achtten, misschien omdat de opeenvolging een modificatie en lichten troebel veroorzaakte in de grond-formule. De aanvangsnoten si en fa maakten de pentatonische reeks tot een volledige zeven-tonige 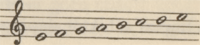
| |
[pagina 19]
| |
In dit retrospectieve spel van den geest, dat bevestigd wordt door de feiten, gebeurt dus de constitutie der zeven oude toonsoorten, alsof de oer-formule, welke resoneerde uit de borst van den Homo Faber en Homo Sapiens, op zeven verschillende wijzen gehoord is door zeven verschillende kleine naties van het Peloponesisch schiereiland en Klein-Azië, die instinctief maar logisch in deze vier klanken een zevenvoudig gekarakteriseerde zielsuitdrukking legden, een zevenvoudig verschillend ethos, pathos, of gemoedswaarde. Het is dus zeer waarschijnlijk dat een wording, welke ik arbitrair doch rationeel construeer, op de meest organische wijze ontstond, aanwezig was, gegroeid is, als de zeven kleuren van den regenboog of van een kristal in het witte licht der zon. Want het is volstrekt zeker, dat het gehele muziek-materiaal vanaf de verste tijden in de natuur voorhanden lag, gelijk vanaf de verste eeuwen de electriciteit en de atomische energie beschikbaar lagen voor den mens. Maar ook tegenover de muziek werd de mens geplaatst gelijk tegenover de rest der natuur, welke zijn roeping hem te doordringen gaf, en om de muziek te ontcijferen moest hij haar, gelijk de overige natuur, eerst kunnen meten. De eerste Europeaan, en vermoedelijk de allereerste mens der vijf werelddelen, die er aan dacht de muziek, een klank te meten, was Pythagoras. Hij leefde in de zesde eeuw voor Christus, doch wijl hij geen enkel materieel document naliet, wordt hij, evenals Homerus en een aantal andere van de uitnemendste vertegenwoordigers der mensheid, door vele geleerden beschouwd als een fabelachtige figuur. Maar of hij mythologisch was, of een wezen van vlees en bloed, is van weinig belang. Zoals gedurende de regering van Tiberius zich op de aarde een verschijnsel openbaarde dat het Christendom bleek te zijn, zo manifesteerde zich omstreeks 600 vóór onze jaartelling een geestesstroming, welke dezelfde duurzaamheid bezat, en die onder den naam van pythagorisme een der machtigste impulsen werd van het menselijk denken. Hij had in de Oudheid een aantal leerlingen die redeneerden op dezelfde theoretische basis, van welke hij traditioneel als uitvinder gold, en die grote beroemdheid verwierven als wiskundigen en meetkundigen. Het verschijnsel Pythagoras is dus volstrekt onloochenbaar, al bezitten wij geen betrouwbare inlichtingen omtrent zijn burgerlijken stand. Het kan met voldoende nauwkeurigheid gedateerd worden om van Pythagoras te spreken als van den eerste die op het idee kwam om muziek wetenschappelijk te meten. | |
[pagina 20]
| |
Wat zag en hoorde Pythagoras in de wereld waar hij leefde en toen hij zijn arbeid begon? Het Archaïsche en het Oude Rijk der Egyptenaren, waarvan de eerste geschreven documenten stammen welke een einde maakten aan de prehistorie, en ook het Midden Rijk behoorden tot een verleden dat onpeilbaar was geworden en dat wij schatten op veertig, vijftig eeuwen. Het nieuwe Egyptische rijk, toen Pythagoras geboren werd, telde reeds een bestaan van duizend jaren. Gedurende deze fantastische, grondeloze lengte van tijd hadden de Egyptenaren de civilisatie geleid en beheerst der Middellandse zee. Zij vereerden goden in tempels, en met een liturgische, muzikale pracht welke al wat men op de aarde vinden kon in ordening, schittering en schoonheid overtrof. Zij hadden ook het geloof dat het leven hiernamaals onmogelijk mooier, zaliger kon zijn dan het leven op hunne aarde, en daarom begroeven zij hun doden als levenden, in hun dagelijkse doen. Zij waren de enigen in de oudheid die zo dachten, en daarom zijn ze de enigen van wie ons een spoor rest van wat hun muziek geweest kan zijn. In hun mastaba's, hun graven, legden zij naast de overledenen slag-instrumenten (castagnetten, bekkens), fluiten met drie, vier, vijf, zes en acht gaten, zelfs een met elf gaten, waarop men onze gehele chromatische toonladder kan spelen, dubbel-fluiten, tokkel-instrumenten (harpen met weinig of met veel snaren) en zelfs een trompet. Zij schilderden deze speeltuigen ook met een zekere nauwgezetheid en in onbederfelijke kleuren op de muren hunner onderaardse tomben. Al die instrumenten klonken reeds sinds eeuwen toen Pythagoras op de wereld verscheen. Zonder enigen twijfel drongen hun echo's en de procédé's hunner fabricatie door tot Griekenland, want Grieken en Egyptenaren onderhielden een druk verkeer. De legende beweert dat Pythagoras zich in de Egyptische tempels heeft laten onderrichten. Dit is zeer wel mogelijk doch geenszins nodig. Alom hoorde hij min of meer Egyptische fluiten en harpen, en kon ze bestuderen, onderzoeken. Ten overvloede: al had hij niets gekend van de Egyptische muziek, toen hij in de geschiedenis trad van het menselijk denken was Homerus reeds drie honderd jaar dood en de verzen van Homerus werden voorgedragen op muziek; de Grieken hadden reeds al hun fabels van Amphion die de muren van Thebe bouwde, van Orpheus die de wilde dieren temde met de tonen hunner lier. De muziek welke Pythagoras ging meten, gelijk men een driehoek of een cirkel meet, was dus reeds volledig georganiseerd. Maar was hij metterdaad de allereerste Europese mens, wiens intelligentie | |
[pagina 21]
| |
zich in maten en getallen rekenschap poogde te geven van het geheimzinnige phenomeen dat klank heet? Tot nader order, en volgens alle waarschijnlijkheid, moet het antwoord op deze vraag bevestigend luiden. Want onder de duizenden papyrussen en andere grafische documenten, welke gedurende de laatste twee eeuwen ontdekt werden in de Egyptische mausolea of andere ruïnes, onder de ontcijferbare overblijfselen der Elamieten, Chaldaeërs en Assyriërs, heeft men tot nu toe niets aangetroffen, dat wijst of wijzen kan op enige theoretische, wetenschappelijke conceptie, waarneming van het geluid, dat uit de tempels opsteeg naar den hemel, uit de huizen en hutten naar de aarde. Pythagoras was dus de eerste die muziek gemeten heeft. Zelfs de acoustische berekeningen van Chinezen en Hindoes, voor zover zij chronologisch met enige zekerheid kunnen worden vastgesteld, dateren allen na den tijd waarin het pythagorische idee ontsprong uit een menselijk brein. Welk nu was het materiaal waarop Pythagoras zijn onderzoekingen baseerde? Nergens bestond een noten-schrift. Nergens bestond een diapason, een vaste toonshoogte, een norm. Men heeft de Egyptische fluiten zo zorgvuldig mogelijk nagebootst en laten bespelen door hedendaagse deskundigen. Maar het is niet gelukt er een toonladder uit af te leiden, of iets wat op een toonladder lijkt, uitgezonderd die ene fluit met elf gaten. Alle overige staan in een verschillende stemming. De tokkel-instrumenten plaatsen ons voor hetzelfde raadsel: wij kennen niet de doorsnede, noch de densiteit (soortelijk gewicht) noch de spanning hunner snaren, de drie voorwaarden welke het geluid bepalen, en wij zullen ze nimmer kunnen kennen. De harpen van het Oude Rijk (ongeveer vijf en twintig eeuwen vóór Pythagoras) waren reeds circa twee meter hoog en droegen zes of acht snaren. In de tomben van het Nieuwe Rijk heeft men harpen aangetroffen welke twintig snaren telden, vervallen, helaas, in stof. Er waren ook kleine, portatieve harpjes, welke later onze cither en guitaar zijn geworden. En 't is mogelijk dat de Egyptenaren op deze instrumenten een toonladder speelden. Maar 't is ook mogelijk dat zij slechts enkele min of meer geordonneerde intervallen erop uitvoerden. Men heeft in de Egyptische ruïnes handleidingen ontdekt over akkerbouw, financiën, krijgskunde en nog andere dingen. Onder de ontelbare teksten echter welke spreken over muziek, vond men er geen enkele die het bestaan aanduidt ener muzikale theorie. Alle muziek vóór Pythagoras schijnt zuiver empirisch be- | |
[pagina 22]
| |
oefend te zijn geworden, op den tast, instinctief, uitsluitend geleid door de ervaring. Wie ook Pythagoras geweest zij, in dezen sonoren chaos trad hij op als stichter van orde. Hij nam een koord en spande het op twee vaste kammen, zodanig dat het, wanneer men het aanraakte, klinkend werd. Hij tokkelde het koord (want de manier van klinkend-maken ener snaar door middel van aanstrijken was in de wereld der Middellandse zee onbekend) bracht een toon voort en gaf hem den naam van No. 1. Hij redeneerde zeer eenvoudig (simplistisch gelijk alle grote geesten) en vroeg zich: Welke is de eenvoudigste verdeling welke ik maken kan van dit koord? Natuurlijk de helft. Door middel van een verschuifbaren kam verdeelde hij het koord in twee gelijke delen en bracht een toon voort aan welken hij den naam gaf van No. 2. Hij beluisterde dezen nieuwen toon en bevond dat hij bijna eensluidend klonk, in een volmaakte harmonie stond met No. 1, en enkel hoger was. Met opzet spreek ik hier niet van trillingen en leid ik uit dit eerste experiment geen enkele onzer moderne physische wetten af; dat bijv. het aantal trillingen ener snaar in omgekeerde verhouding staat tot haar lengte. Want noch Pythagoras, hoe grote geest hij ook was, noch een der Ouden der onmetelijke periode welke ligt tussen het verschijnen van den mens en het verschijnen van Galileï die den slinger ontdekteGa naar voetnoot1, heeft de aanwezigheid gekend of vermoed van longitudinale of transversale trillingen, en ik heb daarom geen recht de experimenten van Pythagoras uit te drukken in deze hedendaagse termen. Hij vroeg zich toen: welke is, na dit ½, de eenvoudigste verdeling welke ik maken kan van mijn koord? Het antwoord kon niet anders luiden dan ⅓. Pythagoras verschoof dus zijn verplaatsbaren kam naar het derde gedeelte zijner snaar, tokkelde, bracht een toon voort, en luisterde. Hij gaf dezen toon den naam van No. 3 en het scheen hem toe dat ook deze No. 3 in een bijna perfecte verhouding, onovertrefbare concordantie stond tot No. 1. Hij ging verder en stelde zich de vraag: welke is, na dit ⅓, de volgende, simpelste verdeling van mijn koord? Natuurlijk ¼. Hij mat dus zo nauwkeurig mogelijk het vierde gedeelte zijner snaar, verschoof zijn kam naar dit punt, tokkelde, hoorde een nieuwen klank en onderzocht wat hij beluisterde met de verrukking van een God die ene wereld schept. Want ook deze vierde verdeling bracht | |
[pagina 23]
| |
een toon voort die in volmaakte, weergaloze harmonie stond tot No. 1. Aan de vier verschillende en toch eensluidende klanken gaf hij den familienaam van symphonieën, d.w.z. samen-klinkers. In modern notenschrift uitgedrukt had hij de formule verkregen van te lezen in een sleutel naar verkiezingGa naar voetnoot1. te lezen in een sleutel naar verkiezingGa naar voetnoot1.
Pythagoras keek rond zich, luisterde naar wat hij getokkeld, gezongen hoorde in de tempels, in de paleizen, huizen en hutten zijner wereld, en van overal echode hem de formule 2. 3. 4 als weerklank van altijd énen grondtoon. En als hij had kunnen luisteren tot in de tempels, paleizen, huizen en hutten van Hindoes en Chinezen dan zou hij wederom en immer de formule 2. 3. 4 vernomen hebben, als echo van een onveranderlijken eersten klank. Toen hij gekomen was bij No. 4 had Pythagoras verder kunnen gaan tot 5, tot 6, enz. Hij deed 't niet. En sinds wij het physieke phenomeen van den klank kennen in zijn gehelen omvang (die de arithmetische voortzetting is van 1, 2, 3, 4, 5, 6, 7, 8, 9 etc.) vragen wij ons af: waarom bleef Pythagoras stilstaan terwijl hij zo goed op weg was? Twee hypotheses kunnen gevormd worden om dit zonderlinge raadsel op te lossen. Men kan veronderstellen dat Pythagoras nergens in de hem omringende (zingende, tokkelende) wereld den klank van No. 5 gehoord heeft, die onze hedendaagse grote terts is. En men kan zich verbeelden, wanneer hij No. 5 vernam, bijv. in de signalen der krijgshaftige trompet welke onmogelijk een anderen toon van haar grondtoon kon voortbrengen dan onze grote terts, dat die No. 5 bij hem automatische, onafweerbare gedachten-associaties opwekte van discordantie, dissonantie, verstoring, verbreking der fundamentele eenheid. Het is een feit dat de gehele Oudheid, zowel de gewone, zingende mens als de geleerde philosooph en rekenaar, de natuurlijke grote terts, instinctmatig, in zijn diepste binnenste, nimmer heeft kunnen aanvaarden. De antieke mens heeft No. 5 niet gehoord. Hij heeft zich gedurende tientallen eeuwen tegenover dezen klank verhouden alsof de constitutie, de inwendige bouw van zijn oor voor deze intonatie ontoegankelijk was, alsof zich, 't zij in het uiterst gecompliceerde, gedeeltelijk nu nog onbekende oor-mechanisme eerst een geleidelijke, eeuwendurende evolutie en verfijndere bewerktuiging moest ontwikkelen, alvorens in de twaalfde | |
[pagina 24]
| |
eeuw na Christus No. 5, de natuurlijke grote terts, waarneembaar, aanvaardbaar en duldbaar kon worden voor het menselijk gehoororgaan. Ik waag deze biologische verklaring van een overigens ondoordringbaar muzikaal geheim omdat zij mij de enig plausiebele lijkt. Doch daar elk verificatie-middel ontbreekt, want alle vroegere oren vervielen in stof gelijk alle vroegere snaren, is zij onbewijsbaar. Ik kan eveneens veronderstellen dat Pythagoras met voorbedachten rade No. 5 nergens heeft willen horen. Hij was immers niet enkel wiskundige en meetkundige, maar tevens, en in de eerste plaats, theoloog, uitvinder van een goddelijk systeem. Het voornaamste zijner dogma's leerde dat alles besloten lag, dat alles - Schepper, werelden, geest en materie, ziel en lichaam, intellect, kennen, weten, voelen - dat al het mogelijke en denkbare bevat was in de verhouding 1. 2. 3. 4, in het quaternarium, wat de Grieken noemden de tetractis. Om te begrijpen, of liever om enigermate te benaderen welk een mystieken, dwingenden invloed de cijfers 1. 2. 3. 4 gedurende meer dan duizend jaren uitgeoefend hebben op de oriëntering van het menselijk intellect, moet men de commentaren lezen, die Hiërocles van Alexandrië in de vijfde eeuw onzer jaartelling nog maakte op de Gulden verzen, het Carmen Aureum, den edelen levensregel der Pythagoraeërs, waarvan de redactie werd toegeschreven aan Pythagoras. Het was onmogelijk in de wereld-conceptie, in het goddelijk systeem der Pythagorici, om de 4 te overschrijden. Zij plaatsen ons daarmee voor een ander historisch feit, dat wij hier niet hebben te onderzoeken, maar dat wij kunnen karakteriseren in deze uitdrukking: wat toenmaals niet bereikbaar was voor de natuur was evenmin bereikbaar voor de theologie. Natuur en theologie liepen parallel. Dit alles is zeer merkwaardig en mysterieus. Zo eenvoudig Pythagoras en zijn school maten en rekenden tot de 4, zo ingewikkeld begonnen zij te meten en te rekenen vanaf dit cabalistisch getal. De één-koord, het monochord van Pythagoras, dat de sonometer is geworden der moderne acoustiek, openbaarde de verhoudingen 1,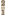 , , 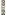 , ,  , voor unisono, octaaf, quint, quart, en , voor unisono, octaaf, quint, quart, en 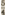 , , 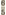 voor grote terts en kleine terts, hetgeen zeggen wil dat, wanneer ik twee gelijke en gelijk-gespannen snaren tot klinken breng waarvan de ene 50 cm en de tweede 40 cm lang is, zij te zamen in een klank-verhouding staan welke den naam ontving van grote terts, wat op 't zelfde neerkomt als te zeggen in hedendaagse termen: wanneer de ene snaar in dezelfde tijdsruimte vijftig trillingen maakt, terwijl een andere snaar voor grote terts en kleine terts, hetgeen zeggen wil dat, wanneer ik twee gelijke en gelijk-gespannen snaren tot klinken breng waarvan de ene 50 cm en de tweede 40 cm lang is, zij te zamen in een klank-verhouding staan welke den naam ontving van grote terts, wat op 't zelfde neerkomt als te zeggen in hedendaagse termen: wanneer de ene snaar in dezelfde tijdsruimte vijftig trillingen maakt, terwijl een andere snaar
| |
[pagina 25]
| |
veertig trillingen maakt, zij tezamen een klank voortbrengen welke grote terts heet. En de grandioze eenvoud der structuur van hetgeen wij tegenwoordig een klank-atoom zouden kunnen noemen, was niet aan de rekenende Pythagoraeërs ontsnapt. ArchytasGa naar voetnoot1 had zeer goed gezien dat de quint, of 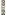 , een optelling is van een grote en een kleine terts, of van , een optelling is van een grote en een kleine terts, of van 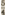 en en 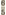 . En toen hij deze intervallen optellend volgens den regel der vermenigvuldiging van breuken, waarbij men de gezamenlijke noemers en tellers vermenigvuldigt, becijferde: . En toen hij deze intervallen optellend volgens den regel der vermenigvuldiging van breuken, waarbij men de gezamenlijke noemers en tellers vermenigvuldigt, becijferde:
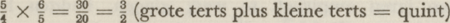 en toen hij, een terugwaartse operatie verrichtend, en van de quint een grote terts aftrekkend, (wat geschiedt volgens den regel der deling van breuken, waarbij men de gedeelde breuk vermenigvuldigt door de omgekeerde delende breuk), toen hij becijferde: 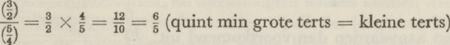 en toen hij, van de quint 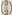 een kleine terts een kleine terts 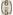 aftrekkend, dus een grote terts aftrekkend, dus een grote terts  moetende vinden, becijferde: moetende vinden, becijferde:
 , toen heeft hij zonder enigen twijfel geconstateerd met verbazing, ik denk zelfs met verrukking, dat een logische verhouding van een voudige cijfers muziek is en dat muziek een cijfer is. Waarom dan constateerden deze musicerende philosophen niet onmiddellijk onze harmonische toonladder, waar de grote en de kleine terts hare nauwkeurige arithmetische waarde hebben? Enerzijds zaten de Pythagoraeërs gevangen in hun dogma van de mystieke tetractis 1. 2, 3. 4, welke alle mogelijke getallen en alle mogelijkheden van getallen behelsde, anderzijds druisten hun logische becijferingen in tegen de muziek welke hun allerwegen opklonk uit de wereld van hun tijd, een muziek die geboren was, die zich gevormd had buiten alle geleerde berekeningen om. Sinds mensenheugenis immers hadden de Griekse Kitharoden hun lier gestemd op de formule der vier tonen welke ik in 't begin van dit hoofdstuk psychanalytisch heb getracht te doorvorsen, en | |
[pagina 26]
| |
die zonder twijfel nog andere interpretaties toelaat, doch die alle van dezelfde orde zullen zijn en denzelfden psychologischen inhoud zullen bezitten. Deze formule:  welke Aristoteles, ongeveer drie eeuwen na Pythagoras, definieerde als het lichaam der harmonie, werd structuraal geregeerd door de wiskundig volmaakte intervallen van octaaf, quint en quart, 2. 3. 4. Welke der vier tonen kon hier No. 1 zijn dezer reeks? De kitharisten, die sinds duizenden jaren empirisch te werk gingen, hadden het zich nimmer afgevraagd. Maar zij stemden hun instrumenten alsof zij het antwoord der Pythagoraeërs reeds gehoord hadden, en de Pythagoraeërs zeiden: de dominerende toon, de grondtoon, No. 1 dezer reeks is: welke Aristoteles, ongeveer drie eeuwen na Pythagoras, definieerde als het lichaam der harmonie, werd structuraal geregeerd door de wiskundig volmaakte intervallen van octaaf, quint en quart, 2. 3. 4. Welke der vier tonen kon hier No. 1 zijn dezer reeks? De kitharisten, die sinds duizenden jaren empirisch te werk gingen, hadden het zich nimmer afgevraagd. Maar zij stemden hun instrumenten alsof zij het antwoord der Pythagoraeërs reeds gehoord hadden, en de Pythagoraeërs zeiden: de dominerende toon, de grondtoon, No. 1 dezer reeks is: 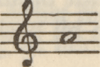 omdat zij haar wiskundig niet anders konden aanvaarden dan voortkomend uit: omdat zij haar wiskundig niet anders konden aanvaarden dan voortkomend uit: 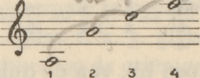 Zij regelden bijgevolg al hun berekeningen naar dezen grondtoon.
Die la ontving bij de Grieken den naam van mesos (wat in 't midden ligt) en behield deze plaats en hare functie van diapason tot op onzen dag. En daar de la 1 was, moest de hoogste mi Zij regelden bijgevolg al hun berekeningen naar dezen grondtoon.
Die la ontving bij de Grieken den naam van mesos (wat in 't midden ligt) en behield deze plaats en hare functie van diapason tot op onzen dag. En daar de la 1 was, moest de hoogste mi 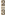 der lengte zijn, uitgaande van 1, welke een gegeven snaarlengte voorstelt: der lengte zijn, uitgaande van 1, welke een gegeven snaarlengte voorstelt:
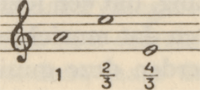 Welke was, deze la de grondtoon, de gegeven lengte blijvend, de eerstvolgende, meest-eenvoudige, meest-volmaakte verhouding? Zonder twijfel de quart of  wier lengtemaat is wier lengtemaat is 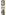 .
Welke was daarna, op dezelfde logische wijze redenerend, de meest natuurlijke, aannemelijke voortzetting? Het was de benedenquint dezer .
Welke was daarna, op dezelfde logische wijze redenerend, de meest natuurlijke, aannemelijke voortzetting? Het was de benedenquint dezer  . Hoe wordt, wanneer . Hoe wordt, wanneer  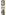 is, een quint verkregen? Eenvoudig door de is, een quint verkregen? Eenvoudig door de 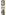 te vermenigvuldigen met het cijfer der nederwaartse quint dat te vermenigvuldigen met het cijfer der nederwaartse quint dat 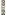 is. Zij vermenigvuldigden dus is. Zij vermenigvuldigden dus  en verkregen en verkregen 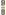 of of  . Daar de volgende meest aangewezen verhouding wederom de quart was, vermenigvuldigden zij . Daar de volgende meest aangewezen verhouding wederom de quart was, vermenigvuldigden zij  en verkregen en verkregen 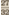 voor de voor de  . Uitdeze . Uitdeze 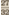 leidden leidden
| |
[pagina 27]
| |
zij een dalende quint 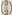 af, cijferden af, cijferden 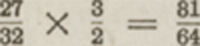 en verkregen de en verkregen de  . Zij hadden toen nog slechts de . Zij hadden toen nog slechts de  te berekenen, die in verhouding der stijgende quint te berekenen, die in verhouding der stijgende quint 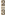 staat tot de staat tot de   . Zij vermenigvuldigden dus . Zij vermenigvuldigden dus  en verkregen en verkregen 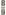 . Zo vormden zij de dalende diatonische toonladder en de snaar-afmetingen: . Zo vormden zij de dalende diatonische toonladder en de snaar-afmetingen: 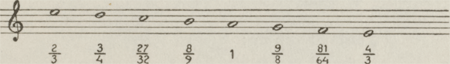
Deze getallen geven in lengte-maten de verhoudingen weer van elken toon tot zijn mesos, zijn centraal-toon la. Toen de Pythagorici de werkelijke intervallen, de toonshoogten wilden kennen die deze klanken scheidt, en verbindt, deelden zij elk der lengte-verhoudingen door de lengte-verhouding welke haar voorafgaat, dus de langste door de kortste, de laagste noot door de hoogste, en ook in deze zuiver-wiskundige operatie werden de cijfers wederom muziek. Zij rekenden dus, en dit werd hun nationaal-Griekse, Dorische toonladder: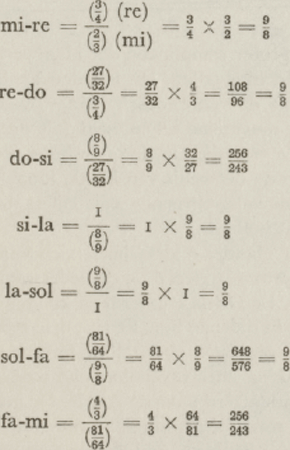 Zij zagen dat de twee helften der toonladder (de twee tetrachor- | |
[pagina 28]
| |
den) elkaar volkomen gelijk waren, alsof zij elkaar herhaalden:
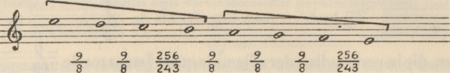 Zij zagen eveneens dat men ter verkrijging dier toonshoogten kon uitgaan van onverschillig welke snaar. Zij namen de hoogste mi tot lengte-eenheid en becijferden als volgt: 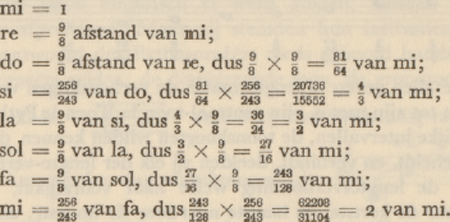 Deze toon-reeks: 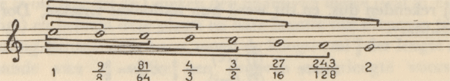 bracht een nog groter complicatie der klankverhoudingen, tot uitdrukking komend in getallen. Dit is onloochenbaar. En voor onze begrippen schijnt dat onpractisch. Maar welk een intellectuele pracht, staatsie, souvereine schoonheid (als de regelmaat van het firmament) in de ordening, in de onderlinge verwantschap, in het evenwicht, en in de betekenis van klank, inhoud van klank, welke die logische, eenvoudige groepen van cijfers bevatten, vertolken, versluieren en onthullen! De Griekse toonladder onderscheidt zich van de Middeleeuwse en tegenwoordige toonladders door de nederwaartse richting waarin zij zich beweegt. De Grieken inderdaad konden de toonladder niet anders zien dan in dalende lijn. Er zijn drie redenen om de eigenaardigheid dezer plastische voorstelling te verklaren. Zij is de symbolische uitdrukking ener psychologische tendentie. De geest der Grieken was georiënteerd naar de Aarde. De geest der Middeleeuwers, evenals de torenspitsen hunner kathedralen, was georiënteerd naar de verten van het uitspansel. Naast deze psychologische motivering der dalende beweging zijn er nog twee technische. Daar de | |
[pagina 29]
| |
leidtoon, de voorlaatste halve toon welke in een scala naar het rustpunt, den grondtoon voert, in de laagte lag, kon de grafische vorm der toonladder logischerwijze niet anders verbeeld worden dan door een dalende figuurGa naar voetnoot1. Vervolgens was het mechanisch onmogelijk de toonladder anders te construeren dan in nederwaartse beweging, toen de Pythagorici uit de klanken der onveranderlijke formule, welke hun bouw-materiaal was  de la kozen als uitgangspunt, en moesten kiezen, wijl deze grond-toon hun allerwegen opklonk uit de omringende muziek. Op deze la immers kon rationeel slechts volgen de re. Pas vijftien eeuwen daarna kon in dezelfde formule de mi genomen worden als uitgangspunt, en uit deze verwisseling van grondtoon resulteerde even logisch, even organisch, gelijk wij later zullen zien, de opwaartse lijn, de stijgende toonladder. de la kozen als uitgangspunt, en moesten kiezen, wijl deze grond-toon hun allerwegen opklonk uit de omringende muziek. Op deze la immers kon rationeel slechts volgen de re. Pas vijftien eeuwen daarna kon in dezelfde formule de mi genomen worden als uitgangspunt, en uit deze verwisseling van grondtoon resulteerde even logisch, even organisch, gelijk wij later zullen zien, de opwaartse lijn, de stijgende toonladder.
Er schuilt in het uitgangspunt der pythagorische besommingen niet de geringste willekeur, en het wonderlijke is, dat uit eenvoudige, primitieve lengte-metingen ener snaar niet enkel een bruikbaar muziek-systeem werd afgeleid, doch tegelijk een muziek-systeem dat zonder enigen twijfel gedurende vele eeuwen gecorrespondeerd heeft met de praktijk, en deze praktijk vernuftig eerst wettigde en daarna bevestigde. Want nadat eenmaal de Pythagoraeërs becijferd hadden, hebben hun volgelingen gedurende bijna tweeduizend jaren niet anders meer becijferd dan op de basis der Pythagoraeërs. Er schuilt in die besommingen daarentegen een niet geringe oorzaak van verwarring, welke aan de rekenende philosophen niet ontsnapt is. Want zij zagen even goed als wij dat de grote terts, die zij aldus verkregen en welke zij diton noemden (of de som van twee hele tonen), gevoelig verschilde van de natuurlijke terts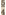 en veel minder eenvoudig was. Daar hun hele toon en veel minder eenvoudig was. Daar hun hele toon 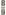 telde, moest hun grote terts (diton) telde, moest hun grote terts (diton) 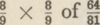 zijn. Het verschil tussen natuur-terts en rationeel berekende grote terts bedroeg dus: zijn. Het verschil tussen natuur-terts en rationeel berekende grote terts bedroeg dus:
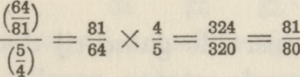 Wanneer men een snaar neemt van 1 m lengte, die onder een zekere spanning de do voortbrengt, dan mat de pythagorische mi 80 cm, de natuurlijke mi daarentegen 81 cm, wat een aanzienlijk en gemakkelijk | |
[pagina 30]
| |
hoorbaar onderscheid oplevert. Tezelfder tijd was hun becijferde kleine terts, welke zij verkregen tussen de 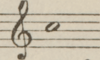 en de en de  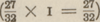 , kleiner dan de natuurlijke kleine terts , kleiner dan de natuurlijke kleine terts 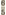 . En rekenend: . En rekenend:
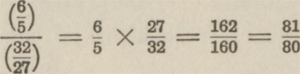 vonden zij wederom hetzelfde verschil, dat den naam kreeg van syntonisch of didymischGa naar voetnoot1 comma. Zulke aldus verworven tertsen waren onbruikbaar als ‘symphonieën’, d.w.z. als samenklinkers, als consonanten. Zij waren niet verenigbaar in de volmaakte quint en konden nimmer een zuiveren drieklank vormen. Maar zij bezaten een hoge, intellectuele schoonheid. Die onevenheid 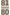 , de Pythagoraeërs vonden haar overal terug. Zij had iets eeuwigs, als de onenigheid van geest en stof. In vele arithmetische formules, die immer snaren-lengten, dus klanken waren, verscheen zij op den horizon van het denken als een magisch getal. De Pythagoraeërs hadden een groten helen toon , de Pythagoraeërs vonden haar overal terug. Zij had iets eeuwigs, als de onenigheid van geest en stof. In vele arithmetische formules, die immer snaren-lengten, dus klanken waren, verscheen zij op den horizon van het denken als een magisch getal. De Pythagoraeërs hadden een groten helen toon 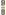 en de latere zeventiende-eeuwse physici een kleinen helen toon en de latere zeventiende-eeuwse physici een kleinen helen toon 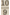 en het verschil tussen beide bedroeg: en het verschil tussen beide bedroeg:
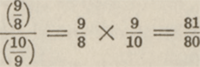 Er was een grote pythagorische sext 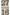 naast een natuurlijke grote sext naast een natuurlijke grote sext 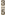 en hun verschil was: en hun verschil was:
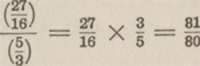 Er was een grote pythagorische septiem  naast een natuurlijke grote septiem naast een natuurlijke grote septiem 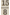 en hun verschil bedroeg: en hun verschil bedroeg:
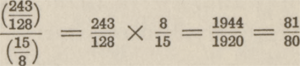 Wanneer de Pythagoraeërs de ganse rij doorliepen ener ideeëlgedachte reeks van stijgende octaven, parallel gaande met de ganse klimmende rij der zuivere quinten, wanneer zij deze beide muzikale voorstellingen transformeerden in een gelijkwaardige wiskundige afbeelding, en toen zij, het cijfer der octaaf 2 zijnde, | |
[pagina 31]
| |
het cijfer der quint 3 zijnde, voor die wiskundige afbeelding der dubbele reeks van octaven en quinten een dubbele geometrische progressie moesten kiezen, de ene - voor de octaven - in de verhouding 2, de andere - voor de quinten - in de verhouding 3, en dus berekenden voor de octaven: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, En voor de twaalf quinten: 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049, 177147 531441, dan zagen zij dat de eindpunten van beide reeksen nimmer konden samentreffen en dat de twaalfde quint van doGa naar voetnoot1, welke si ♯ is, nooit gelijkluidend kon zijn aan de do van het uitgangspunt, doch dat die twee klanken verschilden in de proportie: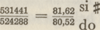 het zgn. pythagorisch comma, waarin zij met een geringe nuance het syntonisch (of didymisch) comma 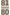 terugherkenden.
Zij vonden hetzelfde cijfer wanneer zij van de eerste do stegen naar de hoogste si ♯ langs een ladder van pythagorische grote hele tonen terugherkenden.
Zij vonden hetzelfde cijfer wanneer zij van de eerste do stegen naar de hoogste si ♯ langs een ladder van pythagorische grote hele tonen
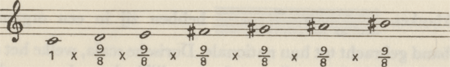 hetgeen gaf  en zij behoefden de uitkomst dezer som slechts te delen door 2 (verhouding van 1ste do tot si ♯) om te verkrijgen: en zij behoefden de uitkomst dezer som slechts te delen door 2 (verhouding van 1ste do tot si ♯) om te verkrijgen:
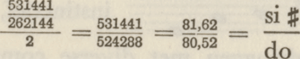 Als zij drie pythagorische tertsen  aaneenschakelden aaneenschakelden
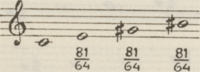 hetgeen gaf 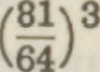 , vonden zij hetzelfde cijfer, want , vonden zij hetzelfde cijfer, want  wat gedeeld door 2 wederom oplevert wat gedeeld door 2 wederom oplevert 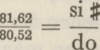
| |
[pagina 32]
| |
En zonderlinger nog: wanneer zij het verschil hadden kunnen berekenen tussen den pythagorischen halven toon  en wat vijf en twintig eeuwen later de halve toon en wat vijf en twintig eeuwen later de halve toon 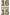 zou worden der moderne physici, dan hadden zij verkregen: zou worden der moderne physici, dan hadden zij verkregen:
 Het zijn deze getallen-ordeningen, grandioos-eenvoudig en tegelijk grandioos-gecompliceerd, nimmer willekeurig, nimmer gefantaseerd, maar volgens de strengste wiskundige logica, voortvloeiend uit de gewijde formule 1. 2. 3. 4, gelijk al wat wij aanschouwen en beminnen is voortgekomen uit het ene begin, het zijn deze sublieme getallen-verhoudingen, die Pythagoras, Pericles, Plato, Aristoteles verrukten wanneer zij aan muziek dachten, en die Pindarus, Aeschylus, Sophocles vervoerd hebben wanneer zij hunne muziek componeerden. Op hun theologisch dogma (de tetractis) en luisterend naar het geluid dat uit de omringende wereld tot hen opklonk, hadden de Pythagorici een nationale toonladder geconstrueerd. De zes andere uitheemse (‘barbaarse’) toonsoorten, afgeleid uit de primordiale klanken hebben zij in een organisch verband gebracht tot hun nationale, Dorische scala, welke het centrum, de basis, bleef van alle tonale mogelijkheden, als een zelfde middelpunt van verschillende cirkels. Toen de zangers, de kitharisten, de virtuozen van keel en lier, de intervallen der twee onwrikbare tetrachorden hebben zij in een organisch verband gebracht tot hun nationale, Dorische scala, welke het centrum, de basis, bleef van alle tonale mogelijkheden, als een zelfde middelpunt van verschillende cirkels. Toen de zangers, de kitharisten, de virtuozen van keel en lier, de intervallen der twee onwrikbare tetrachorden 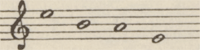 instinctief, expressief, creatief gingen vullen, overbruggen met diverse combinaties van halve tonen instinctief, expressief, creatief gingen vullen, overbruggen met diverse combinaties van halve tonen  of: of:  en zelfs in kwart-tonen, waarvoor de oude Grieken reeds tekens bezaten, want de Hellenen der Olympische Spelen (voor wie Aristophanes zeer grove grappen maakte), hadden een buitengewoon fijn gehoor en een sensitief gemoed, toen virtuozen immer nieuwe raffinementen ontdekten in een chromatische en een enharmonische vulling der tetrachorden, immer nieuwe, subtielere zenuwen verleenden aan het onveranderlijke lichaam der harmonie, keurden rigo- en zelfs in kwart-tonen, waarvoor de oude Grieken reeds tekens bezaten, want de Hellenen der Olympische Spelen (voor wie Aristophanes zeer grove grappen maakte), hadden een buitengewoon fijn gehoor en een sensitief gemoed, toen virtuozen immer nieuwe raffinementen ontdekten in een chromatische en een enharmonische vulling der tetrachorden, immer nieuwe, subtielere zenuwen verleenden aan het onveranderlijke lichaam der harmonie, keurden rigo- | |
[pagina 33]
| |
ristische philosophen als Plato deze inventies af. Zij veroordeelden ze als symptomen van ontaarding. Maar de Pythagorici, steeds luisterend naar het oneindig geruis der wereld, namen hun éénsnaar, hun monochord, en becijferden alle hoorbare variaties te midden van dat ‘lichaam’ in exacte maten en getallen. Die spitsvondigheden der virtuozen waren onuitputtelijk en 't heeft geen belang ze hier in cijfers weer te geven. Zij bewezen dat alles mogelijk, denkbaar, uitvoerbaar en aannemelijk was in het onverzettelijk geraamte. Dit geraamte kan worden uitgebouwd naar boven, naar beneden, in een omvang van vier tetrachorden, twee octaven, het kreeg den naam van groot volmaakt systeem en bevatte alle toonsoorten. Het kon in zijn middelpunt (door verlaging van si in si♭) voorzien worden van een modulerend mechanisme, dat transposities veroorloofde welke wij overgangen naar de onderdominant zouden noemen. De vorm zelf echter, vastgelegd in 1. 2. 3. 4, bleef onveranderlijk, onaantastbaar. Gedurende bijna twee duizend jaar na Pythagoras zal hij niet gewijzigd worden. |
|