Logo DBNL
Geschiedenis van de wiskunde (1990)

Geschiedenis van de wiskunde

(1990)–D.J. Struik–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

VI. De zeventiende eeuw

De snelle ontwikkeling van de wiskunde tijdens de Renaissance berustte niet alleen op de ‘Rechenhaftigkeit’ van de gegoede burgerij. Men begon geld te beleggen in industrie en daarmee in het gebruik en het verbeteren van werktuigen en machines. Deze waren reeds vanouds bekend, zij hadden Archimedes' genie en Heroons vernuft geïnspireerd. In die tijden moedigde evenwel noch de slavernij noch het stedelijk handwerk het gebruik van arbeidsbesparende mechanismen aan, en een economisch vooruitstrevende burgerklasse heeft de Oudheid (en het Oosten) slechts sporadisch bezeten. Bij Heroon vinden wij wel machines beschreven, doch alleen voor amusement of voor goocheltoeren. In de latere Middeleeuwen begint in deze toestand verandering te komen, machines worden aangewend in werkplaatsen, bij openbare werken en in het mijnbedrijf, niet zelden in het bezit van kooplieden, bankiers of vorsten, en door stedelijke gilden met tegenzin begroet. Transatlantische scheepvaart en krijgsbedrijf stimuleren ook uitvinding en verbetering van werktuigen en machines.

‘De constante bedrijvigheid die gij Venetianen in uw beroemde arsenaal tentoon spreidt, biedt de leergierige geest een groot gebied voor studie, vooral dat gedeelte van het werk dat betrekking heeft op de mechanica’ (Galilei 1632, Dialogi, eerste dag).

Reeds in de veertiende eeuw en nog vroeger bestond er in Lucca en Venetië een gevestigde zijde-industrie, gebaseerd op arbeidsverdeling en waterkracht. In Vlaanderen bloeide de lakenindustrie. In de vijftiende eeuw begon in Centraal Europa de mijnbouw zich te ontwikkelen tot een volledig kapitalistisch georganiseerde industrie, waarbij pompen en hijsmachines al een belangrijke technische rol speelden, zodat steeds dieper liggende lagen konden worden aangeboord. De voor Europa nieuwe uitvindingen van vuurwapens, boekdrukkunst, windmolens, de verbetering van schepen en het graven van kanalen, maakten ook op hun beurt weer brede lagen van de bevolking technisch bewust. We beginnen mannen aan te treffen die we nu ingenieurs zouden noemen. Uurwerken werden verbeterd en gebruikt in scheepvaart en sterrenkunde, en zo kreeg het publiek soms prachtige mechanismen te

zien. De regelmatigheid van de loop der uurwerken en de mogelijkheid daarmede de tijd precies aan te geven maakten op velen een diepe indruk. Menig wijsgeer der Renaissance en van later ziet in het uurwerk een model van het heelal. Deze filosofische opvatting heeft medegewerkt tot de ontwikkeling van het mechanische wereldbeeld.

Het gebruik en de studie van machines voerden tot theoretische werktuigkunde, tot de studie van de beweging en de begrippen van snelheid en versnelling. Uit de Oudheid waren reeds geschriften over de statica bekend - b.v. die van Archimedes - en de hernieuwde studie der statica ging van deze klassieke geschriften uit. Er bestonden reeds vóór de uitvinding van de boekdrukkunst boeken over werktuigen en machines (b.v. van Kyeser, begin 15e eeuw), aangevuld door meer theoretisch opgezette studies, als het boek over bouwkunde van Leon Battista Alberti (ca. 1450) en sommige geschriften van Leonardo da Vinci. Leonardo's manuscripten bevatten het begin van een uitgesproken mechanistische natuurleer. Later in de zestiende eeuw verschijnen de mooie technische boeken van Vannoccio Biringuccio (Pirotechnia, 1540, Engelse vertaling 1943) en van Georg Agricola (De re metallica, 1556, Engelse vertaling 1912).

Wat de wiskundigen betreft, Tartaglia behandelde in zijn Nuova scienzia (1537) de constructie van uurwerken en de baan van projectielen, ofschoon hij nog niet inzag dat deze baan (zonder wrijving) een parabool moet zijn. Dit werd eerst door Galilei in de Vierde Dag van zijn Discorsi (1638) bewezen. Deze soort van onderzoekingen werden ook door de uitgave van de werken van Archimedes gestimuleerd, vooral door die van de Italiaan Federigo Commandino (1558). Zo werden de antieke integratiemethoden binnen het bereik van vele wiskundigen gebracht. Commandino paste deze methoden zelf toe op de berekening van zwaartepunten (1565), al deed hij dit ook minder streng dan zijn meester.

De berekening van zwaartepunten bleef nog lang een geliefkoosde bezigheid van hen die hun kennis van Archimedes zochten te verdiepen, en zodoende hun studie van de statica wisten te verbinden aan een beoefening van praktijken die we thans als de beginselen van de integraalrekening zien. Onder deze volgelingen van Archimedes treffen we de Nederlander Simon Stevin aan, die in zijn Weeghconst en Waterwicht (1586) over zwaartepunten en hydraulische problemen schreef, verder de Italiaan Luca Valerio, die in 1604 de berekening van zwaartepunten en in 1606 de kwadratuur van de parabool behandelde. In de Centrobaryca van de

Zwitser Paul Guldin (3 dln, 1635-'41) vinden we de zgn. theorema's van Guldin, die verband leggen tussen oppervlak en inhoud van omwentelingsoppervlakten en het zwaartepunt van het vlak uit wier wenteling ze ontstaan.1

Deze auteurs hebben wegen bewandeld waarlangs Kepler, Cavalieri, Torricelli en anderen tot methoden kwamen die tot de uitvinding van de differentiaal- en integraalrekening hebben geleid.

2.

Kenmerkend voor deze wiskundigen was hun bereidheid om de Archimedische strengheid van bewijs op te geven voor beschouwingen die veel minder streng, soms ‘atomisch’ waren - waarschijnlijk zonder te weten dat Archimedes in zijn brief aan Eratosthenes juist soortgelijke methoden om hun aanschouwelijke waarde had toegepast. Deze mindere scherpte was voornamelijk het gevolg van het verlangen naar resultaten, die met de Griekse methode moeilijk snel waren te verkrijgen, en zeker op omslachtige wijze. Ten dele speelde ook een zekere ontevredenheid met de scholastiek en haar subtiliteiten een rol, waarvan althans sommigen dezer wiskundigen goed op de hoogte waren, zeker de Katholieke priesters onder hen. Reken- en scheepvaartmeesters, ingenieurs en loodsen zochten naar methoden die gemakkelijk te begrijpen waren.

De revolutie in de sterrenkunde, die met de namen Copernicus, Tycho Brahe en Kepler is verbonden, opende nieuwe visies over de plaats van de mens in het heelal en zijn vermogen deze met behulp van de wiskunde nader te bestuderen. Twijfel begon te rijzen aan de manier waarop in het Aristotelisme verband werd gelegd tussen de bewegingen en de krachten bij ‘ondermaanse’ en hemelse lichamen. Hoezeer de wiskunde bij deze revolutie een rol speelde, kan men in het werk van Johannes Kepler zien, waarin geweldig rekenwerk verbonden is met scherpzinnige meetkundige beschouwingen, waarin ook infinitesimalen een belangrijke rol speelden. Kepler, wiens Astronomica nova van 1609 zijn elliptische planetenbeweging bevat, heeft ook een boek over inhoudsberekeningen geschreven, zijn Nova stereometria doliorum vinariorum (‘nieuwe stereometrie van wijnvaten’, 1615), waarin hij, in Archimedes' voetstappen voortschrijdende, de inhoud afleidde van lichamen

die ontstaan door rotatie van kegelsneden om een lijn in hun vlak gelegen. Hij brak met het Archimedische strenge doch indirecte bewijs, voor hem was een cirkelomtrek een veelhoek met oneindig veel zijden en de inhoud van een bol de som van de inhouden van oneindig veel spitse piramiden met gemeenschappelijke top in het middelpunt van de bol. Kepler zag in dat de bewijsvormen van Archimedes streng waren absolutae et omnibus numeris perfectae (absoluut en in elk opzicht volmaakt), maar hij liet ze gaarne over aan lieden die daar plezier in hadden. Iedere auteur van die dagen en nog veel later behield zich de vrijheid voor, zijn eigen maat van strengheid of gebrek aan strengheid te bepalen. Er bleven natuurlijk altijd wiskundigen die het met de strengheid van hun bewijsvoering heel ernstig namen.1

Op Copernicus en Kepler had Plato met zijn Pythagoreïsche verering van de wiskunde een diepe invloed. Bij Galileo Galilei neemt de verwerping van het Aristotelische wereldbeeld scherper en meer polemischer vormen aan. Aan hem hebben wij de nieuwe kinematica van vrij vallende lichamen, het begin van de elasticiteitsleer en een van geest tintelende verdediging van het Copernicaanse stelsel te danken. Hij is een der voorgangers van de moderne wetenschap, die op de harmonsiche samenwerking van theorie en experiment berust, waarbij nadruk wordt gelegd op wiskundige en in 't algemeen kwantitatieve beschouwingen - ook al speelt het experiment bij Galilei niet zulk een belangrijke rol als men soms wel aanneemt: zijn redenering is vaak a priori, terwijl het experiment (soms alleen een gedachtenexperiment) als verificatie dient. In de Discorsi van 1638 vindt men, in de Derde Dag, een scherp-

zinnige wiskundige afleiding der wetten van de eenparige en eenparig versnelde beweging (alles geheel meetkundig); in de Vierde Dag wordt de parabolische beweging van het projectiel afgeleid met tabellen over hoogte en worpswijdte als functie van aanvangshoek en aanvangssnelheid. Galilei heeft echter nooit zijn ideeën over de infinitesimaalrekening systematisch uiteengezet, doch dit aan zijn leerlingen Cavalieri en Torricelli overgelaten. Hij had ook over het oneindige zeer oorspronkelijke ideeën, zoals we ook in de Discorsi kunnen zien (Eerste Dag), waarin hij aantoont dat ‘het aantal kwadraatgetallen niet kleiner is dan het aantal van alle natuurlijke getallen, maar dit aantal ook niet groter is dan het eerste’, zoals blijkt uit de mogelijkheid van de één-éénduidige toevoeging der getallen

1 2 3 4 5 6...
1 4 9 16 25 36...

Dit was een verdediging van het actueel oneindige, bewust gevoerd tegen de meningen van Aristoteles en de Scholastici (Salviati, in de Discorsi, de woordvoerder van Galilei, verdedigt zijn standpunt tegenover Simplicio, de Aristoteliaan). Salviati maakt ook de opmerking dat de kettinglijn er uitziet als een parabool, doch berekent de kromme niet. Galilei heeft ook het eerst de cycloïde beschouwd (1590).

Galilei schreef zijn hoofdwerken in het Italiaans, Stevin in het Nederlands, Bacon in het Engels en Descartes in het Frans (doch niet altijd). Ze schreven hun werken in de landstaal waarmee zij het breder publiek wilden bereiken, dat in deze periode bereid was van de nieuwe wetenschap kennis te nemen. De grote wetenschappelijke revolutie was in gang. En de wiskunde speelde daarin een belangrijke rol.

De tijd was dus gekomen voor een eerste systematische samenstelling van de resultaten die men op het gebied der infinitesimaalrekening had bereikt. Het was Bonaventura Cavalieri, professor aan de universiteit van Bologna, die deze taak op zich nam. In zijn Geometria indivisibilibus continuorum nova (1635) ontwikkelde hij het begin van een integraalrekening, die gebaseerd was op het scholastieke begrip van het indivisibile.1 Volgens deze opvatting

ontstond een lijn uit de sommatie (of beweging) van punten, en een oppervlak uit die van lijnen. Cavalieri had daarom geen oneindig kleine grootheden van ‘atomische’ vorm nodig. Men kan zijn gedachtengang leren kennen uit de stelling die we nog steeds als het ‘beginsel van Cavalieri’ in onze leerboeken aantreffen. Uit dit beginsel wordt geconcludeerd, dat de oppervlakten van twee driehoekachtige figuren met dezelfde basis en dezelfde hoogte gelijk zijn als de doorsneden, op gelijke afstand van de basis getrokken, gelijk zijn.

Met zijn optelling van lijnen kon Cavalieri berekeningen voltrekken die equivalent waren met de integratie van rationale veeltermen, doordat hij het equivalent bezat van de integraal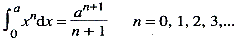



illustratie

Maar als men lijnen optelt, blijft men lijnen krijgen, en geen oppervlakken, evenmin als men door optelling van punten een lijn verkrijgt (hiervoor moet men b.v. een begrip als beweging invoeren). Cavalieri zag dat ook wel in. Toen Torricelli hem eens aantoonde, dat met zijn methode om oppervlakken als sommen van lijnsegmenten te beschouwen, men ‘bewijzen’ kon dat iedere driehoek door een hoogtelijn in twee gelijke helften kon worden verdeeld, veranderde Cavalieri zijn lijnen in ‘draden’, dus in oppervlakken van zeer geringe dikte, doch eerst andere wiskundigen trokken daaruit de nodige consequenties, door niet lijnen l, maar vlakelementen ldx op te tellen, om Leibniz' notatie te gebruiken.

3.

De verschijning van Descartes Géométrie, in 1637, kwam de ontwikkeling van de infinitesimaalrekening zeer ten goede. Door deze Géométrie werd de gehele klassieke meetkunde binnen het bereik van de algebra gebracht, zodat van nu af aan meetkundige en algebraïsche methoden elkaar konden bevruchten. Het boek was gepubliceerd als een der appendices tot Descartes' Discours de la Méthode, zijn te Leiden verschenen verhandeling over de methode van het juiste redeneren. Réné Descartes (Cartesius) was een Fransman van lagere adel, uit de Touraine geboortig, die een tijdlang in het leger van Prins Maurits had gediend. In 1629 keerde hij naar de Republiek terug en bleef daar tot 1649, nogal eens van woning veranderende. Hier ontwikkelde en publiceerde hij zijn wiskunde en zijn wijsbegeerte. Hij stierf in 1650 te Stockholm, waar hij op uitnodiging van Koningin Christina naartoe was gereisd.

In overeenstemming met vele andere denkers van de 17e eeuw



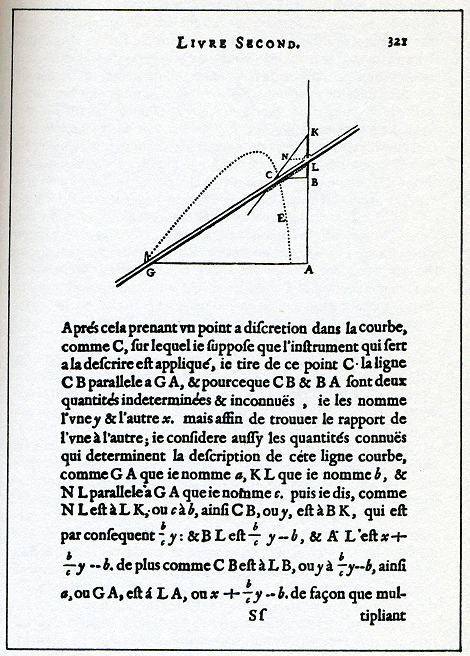illustratie
Bladzijde uit La géometrie van Descartes.


zocht Descartes naar een methode om de waarheid in de wetenschappen te vinden en daardoor zowel de wereld door de rede te begrijpen alsook het maken van uitvindingen te bevorderen. Deze methode leidde in Descartes' handen tot een wijsbegeerte die voor vele tijdgenoten die van Aristoteles verving en tot op de huidige dag zijn invloed laat voelen. Voor deze wijsbegeerte was de sleutel tot de kennis der natuur de mechanica, en de sleutel tot de kennis der mechanica de wiskunde. Zo werd de wiskunde van een werkmethode voor loodsen, landmeters en rekenmeesters tot het belangrijkste wetenschappelijke denkgebied van de wijsgeer verheven. Hierbij speelde, naast de algemene kwantitatief gerichte geest des tijds, ook het feit mee dat de enige natuurwetenschappen die enigszins stelselmatig waren ontwikkeld, de astronomie en de statica, op wiskundige leest geschoeid waren. Daar kwam bij dat de wiskunde zelf, met haar overtuigende waarheden, een schitterend voorbeeld was van het feit dat de waarheid in de wetenschappen door de rede kon worden gevonden. Zo kwam de mechanistische filosofie van deze periode tot conclusies die veel overeenkomst hadden met die van de Platonici, al was hun uitgangspunt heel anders. De Platonici, die in de harmonie van het heelal, en de Cartesianen, die aan een op de rede gevestigde methode geloofden, vonden beiden in de wiskunde de koningin der wetenschappen.

Descartes publiceerde zijn Géométrie als een voorbeeld van zijn rationalistisch denken, dat hier tot een nieuwe verbinding van de algebra en de meetkunde had gevoerd. Volgens een vaak verkondigde mening bestaat de verdienste van dit boek voornamelijk hierin, dat Descartes de analytische meetkunde schiep. Het is waar dat dit gebied van de wiskunde in de loop der tijden onder de sterke invloed van het werk van Descartes is ontstaan. De Géométrie zelf kan echter nauwelijks als een eerste leerboek over dit onderwerp worden beschouwd. Wij vinden er geen ‘Cartesiaanse assen’ en geen afleiding van de vergelijkingen van de rechte lijn en de kegelsneden, al werden enige kwadratische betrekkingen ingevoerd die kegelsneden weergaven. Daar komt bij dat een aanzienlijk deel van het boek uit een theorie over de algebraïsche vergelijkingen bestaat, die o.a. de zgn. ‘regel van Descartes’ over het aantal positieve en negatieve wortels van een vergelijking bevat.

Wij moeten niet vergeten dat reeds Apollonios kegelsneden karakteriseerde met wat we nu (met Leibniz) coördinaten noemen, een karakterisering die natuurlijk geheel in meetkundige taal was vervat. Ook had Pappos in zijn Verzameling een Analuomenos, een ‘analyse’, gebruikt die men slechts heeft te moderniseren om

een consequente toepassing van de algebra op de meetkunde te kunnen afleiden. Bij Ptolemaios in zijn Geografia vinden we de punten op de bol door lengte en breedte, dus door numerieke coördinaten, aangegeven. Zelfs vindt men vóór Descartes nu en dan iets wat op een grafische voorstelling lijkt (Oresme). De verdiensten van Descartes liggen in de eerste plaats in de consequente toepassing van de in zijn tijd door Cardano en Viète ontwikkelde algebra op de geometrische analyse van de Grieken, waardoor deze een grote hoeveelheid nieuwe toepassingen vond. Descartes kon dit presteren omdat hij definitief met de homogeniteitsvoorwaarden van zijn voorgangers brak; voorwaarden die o.a. typisch waren voor Viète's logistica speciosa, zodat x2, x3, xy nu evenals x en y als lijnsegmenten konden worden beschouwd. Zo kon men uit de vergelijking 1: a = a : a2, de term a2 als een lijnsegment uit een evenredigheid construeren, indien een eenheidssegment en het segment a waren gegeven. Een algebraïsche vergelijking tussen x en y werd nu een betrekking tussen getallen, die lijnsegmenten voorstelden: een nieuwe wiskundige abstractie die de algemene algebraïsche behandeling van algebraïsche krommen mogelijk maakte.

Descartes' notatie is in vele opzichten modern, men vindt in zijn boek uitdrukkingen als ½a +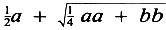 illustratie, die wat schrijfwijze betreffen, slechts hierin van onze schrijfwijzen verschillen dat Descartes aa schrijft waar wij a2 zetten, en aaa waar wij a3 zetten. De notatie a, b, c voor bekende grootheden en x, y, z voor onbekende is ook van Descartes. Het is niet moeilijk de Géométrie te lezen, maar men zal er onze analytische meetkunde niet in vinden.1

Iets dichter bij onze analytische meetkunde staat het werk van Pierre Fermat, een advocaat in Toulouse, die enkele vrij korte meetkundige verhandelingen schreef, zeer waarschijnlijk reeds vóór de publikatie van Descartes' boek, doch die pas in 1679 werden gepubliceerd. In een ervan, de Isagoge vinden we stelselmatige afleidingen van de vergelijkingen van de rechte lijn en de kegelsneden, zodat we hier de vergelijkingen y = mx + a, xy = k2, x2 + y2 = a2, x2 ± p2y2 = b2 vinden, vergelijkingen die zijn afgeleid aan de hand van een stelsel van (gewoonlijk rechthoekige) assen. Deze

vergelijkingen waren echter volgens Viète's notatie geschreven, en werden dus ook homogeen geïnterpreteerd. Fermats verhandelingen zien er dus veel ouderwetser uit dan die van Descartes.

Toen eindelijk Fermats werk in druk verscheen, was het werk van Descartes voortgezet door anderen die meer stelselmatig de algebra op de antieke meet kunde hadden toegepast. Wij denken hier b.v. aan de Tractatus de Sectionibus Con̄icis (1655) van John Wallis en een deel van de Elementa Curvarum Linearum (1659) van Raadpensionaris Jan de Witt. Voor de verspreiding van Descartes' wiskundige ideeën deed vooral de Leidse professor Frans van Schooten, leraar van De Witt en Huygens, veel moeite. Toch was er slechts matige vooruitgang in deze tak van wetenschap, zelfs L'Hospital's Traité analytique des Sections coniques (1707) was niet veel meer dan een vertaling van Apollonios in de taal van Descartes' algebra. Alle schrijvers aarzelden om aan hun coördinaten, die toch lijnen waren, negatieve waarden toe te kennen. De eerste, die onafhankelijk van de Grieken met algebraïsche vergelijkingen werkte, was Newton, in zijn studie over derdegraadskrommen (1703). De eerste analytische meetkunde van kegelsneden die niet meer afhankelijk was van Apollonios, vindt men in Eulers Introductio van 1748, waarin ook ruimtefiguren worden behandeld.

4.

Het verschijnen van Cavalieri's boek droeg ertoe bij, dat de belangstelling van wiskundigen in verschillende landen voor vraagstukken uit infinitesimale beschouwingen voortgekomen groter werd. Beïnvloed door Descartes begonnen zij de fundamentele problemen meer abstract te formuleren, waardoor zij in algemeenheid wonnen. Naast de oudere vraagstukken over inhouden en zwaartepunten, die we nu bij de integraalrekening behandelen, kwam nu ook het vraagstuk: de raaklijn aan een kromme door een gegeven punt te vinden. Dit raaklijnenvraagstuk was door de Grieken nooit fundamenteel aangepakt, zodat, om moderne termen te gebruiken, de differentiaalrekening eerst tweeduizend jaar na de integraalrekening is ontwikkeld. Verwant met het raaklijnenvraagstuk is het probleem, snelheid en versnelling precies te formuleren, waarmee Galilei in de Derde Dag van zijn Discorsi (1638) begonnen is. In deze verhandelingen over beide soorten van infinitesimaalrekening vinden we twee stromingen, een meetkundige en een algebraïsche. De volgelingen van Cavalieri, in het bijzonder Torricelli en Isaac Barrow, Ieraar van Newton, hielden van de Griekse meetkundige manier van redeneren, al had hun redenering niet altijd de Griekse scherpte. Ook Christiaan Huygens hield van

de Griekse methode. Daarentegen zien we bij Fermat, Descartes en John Wallis een neiging de nieuwe algebra te gebruiken. Bijna alle auteurs in deze periode van ca. 1630 tot ca. 1660 beschouwden algebraïsche krommen, in het bijzonder krommen met de vergelijking amyn = bnxm, en ieder op zijn manier vond de formules die equivalent zijn aan onze formule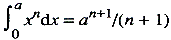

illustratie

eerst voor positieve gehele n, dan voor positief gebroken n. Ook het geval van negatieve n werd beschouwd. Hier gaf het geval n = - 1 bijzondere moeilijkheden, die eerst werden opgelost toen het verband met logaritmen en dat van logaritmen met exponentiële functies volkomen werd begrepen, dus niet voor het einde van de eeuw.

Soms vinden we ook een niet-algebraïsche kromme, zoals de cycloïde. Deze cycloïde was zelfs zo populair en gaf aanleiding tot zoveel discussie en twistgeschrijf dat men haar wel eens de kibbelkromme (curve of contention) heeft genoemd. We vinden haar o.a. behandeld door Descartes en Pascal; Pascals Traité général de la roulette (1658) - de ‘roulette’ is de cycloïde - een deel van een boekje dat onder de naam A. Dettonville verschenen is, heeft o.a. de jonge Leibniz beïnvloed.1

In deze periode beginnen we ook andere gebieden van de infinitesimaalrekening aan te treffen. Fermat ontdekte in 1638 een methode om maxima en minima te vinden door de veranderlijke in een eenvoudige algebraïsche vergelijking een weinig te veranderen en dan te eisen dat de verandering nul werd; deze methode wordt voor meer algemenere algebraïsche krommen gebruikt door Van Schootens leerling, Johannes Hudde (1658), die later burgemeester van Amsterdam zou worden. Men vindt berekeningen van raaklijnen, oppervlakken, inhouden, zwaartepunten en ook van booglengten (die zowel differentiatie als integratie eisen). De betrekking tussen differentiatie en integratie als inverse bewerkingen, werd eerst in haar algemeenheid door Barrow in 1670 ontdekt, doch in een voor ons ongewone meetkundige vorm. Pascal, die formules opstelde die met de integratie van sin x en sin2 x en met partiële integratie equivalent zijn, werkte ook wel met ontwikkelingen in kleine grootheden waarin hij de termen van de kleinste

dimensies verwaarloosde, iets wat we later bij Newton en Leibniz terug vinden, als ze de bedenkelijke formule

(x + dx)(y + dy) - xy = xdy + ydx

(of een equivalente formule) gebruiken. Pascal verdedigde zijn methode door zich meer op zijn intuïtie (esprit de finesse) dan op zijn logica (esprit de géométrie) te beroepen; we vinden hiervan later in Berkeley's kritiek op Newton een weerklank terug.1

De invloed der scholastiek kan men niet alleen bij Cavalieri vinden, doch ook in het werk van de Belgische Jezuïet Grégoire de Saint Vincent en zijn collega's Paul Guldin en André Tacquet. Deze wiskundigen bestudeerden zowel het werk van hun tijdgenoten als de Middeleeuwse geschriften over de natuur van het continuüm en over de latitudo van vormen. In De Saint Vincents en Tacquets boeken vinden we voor het eerst de uitdrukking ‘exhaustie’ voor de indirecte bewijsmethode van Eudoxos en Archimedes (zie bldz. 59). Tacquets boek Cylindricorum et annularium liber (1651) heeft o.a. invloed op Pascal uitgeoefend. De jonge Huygens heeft De Saint Vincents cirkelkwadratuur bekritiseerd.

Deze constante bedrijvigheid van wiskundigen in verschillende delen van Europa in een tijdperk waarin er nog geen wetenschappelijke tijdschriften bestonden, leidde tot een aanzienlijke briefwisseling (waarvan thans heel wat is gepubliceerd) en tot discussiegroepen. Sommige geleerden maakten zich verdienstelijk door als bemiddelaar tussen verschillende correspondenten op te treden. De meest bekende van deze bemiddelaars was de Minderbroeder Marin Mersenne, die ook zelf een verdienstelijk wiskundige was, en naar wie de getallen van Mersenne zijn genoemd (2 n - 1, als n priem is, b.v. 3, 7, 31, enz.) getallen die eigenlijk al bij Euklides voorkomen. Met Mersenne correspondeerden Descartes, Fermat, Desargues, Pascal en vele anderen. ‘Mersenne van een ontdekking te verwittigen betekende dat ze door heel Europa bekend werd gemaakt’.2 Uit die discussiegroepen hebben zich in Parijs en elders wetenschappelijke genootschappen en academies ontwikkeld. Hun oorsprong hangt ten dele samen met een oppositie tegen de universiteiten die nog in menig opzicht hun scholastiek karakter had-

den behouden - niet zozeer de Leidse universiteit die eerst in 1575 was opgericht - en daardoor de gewoonte behielden om reeds verworven kennis in oude vaste vormen door te geven. De nieuwe academies daarentegen vertegenwoordigden de nieuwe manier van onderzoek.

Zij waren de uitdrukking van de geest van het nieuwe tijdperk: ‘verzadigd in de roes van nieuwe kennis, bezig met het verbreken van verouderd bijgeloof, zich ontworstelend aan de tradities van het verleden, en met de uitbundigste hoop voor de toekomst. Hier leerde elke man van wetenschap er niet alleen tevreden mee, maar zelfs trots op te zijn als hij een individuele bijdrage, hoe klein ook, aan de totale som van kennis toe kon voegen. Hier ontwikkelde zich de moderne man van wetenschap’.1 De eerste Academie was in Napels opgericht (1560), ze werd gevolgd door de ‘Accademia dei Lincei’ in Rome (1603). De Royal Society van Londen dateert van 1662, de Franse Académie van 1666. Tot de stichters van de Royal Society behoorde Wallis, tot die van de Franse Académie Christiaan Huygens.

5.

Een van de belangrijkste boeken na dat van Cavalieri in deze periode van voorbereiding was de Arithmetica infinitorum van John Wallis (1655). De schrijver was van 1643 tot aan zijn dood in 1703 Savilian-professor in de meetkunde te Oxford. Reeds de titel van het boek laat zien dat Wallis boven het boek van Cavalieri van de ‘meetkunde der indivisibilen’ uit wilde gaan: hij wilde tonen wat de nieuwe ‘arithmetica’, de algebra, vermocht te doen zonder de oude meetkunde. Zodoende ontwikkelde Wallis de algebra tot een echte analyse: de eerste wiskundige die dit deed. Zijn manier om met oneindige processen om te gaan is voor onze begrippen vaak gewaagd, maar hij kon resultaten boeken: hij werkte met oneindige reeksen en oneindige produkten en was niet bang voor imaginairen, voor negatieve en gebroken exponenten. Hij schreef ∞ voor 1/0 (en beweerde dat - 1 > ∞). Uit zijn integraties van machten en produkten van goniometrische functies (hij gebruikte uitdrukkingen die wij nu Beta-integralen noemen), die hij voor het bepalen van het cirkeloppervlak toepaste, vond hij het oneindige produkt dat zijn naam draagt: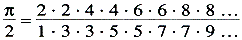



illustratie

Wallis was slechts één van die hele reeks scherpzinnige geleerden die in hun dagen de wiskunde met ontdekking na ontdekking verrijkten. De stuwende kracht voor deze bloei van scheppende wetenschap, ongeëvenaard sinds de grote Griekse tijd, was slechts ten dele de ontdekking van de nieuwe technieken waarmee nieuwe en moeilijke vraagstukken schijnbaar gemakkelijk konden worden opgelost. Vele denkers werden gedreven door diepere problemen: zij zochten, zoals Descartes, naar een ‘algemene methode’, soms in de meer beperkte vorm van een wiskundige methode, soms in een meer algemene vorm als een methode om de natuur te begrijpen om tot nieuwe uitvindingen en ontdekkingen te komen. Daarom waren in deze periode alle wijsgeren van betekenis ook wiskundigen en vrijwel alle wiskundigen van betekenis tevens wijsgeren. Het zoeken naar nieuwe uitvindingen leidde vaak direct tot wiskundige ontdekkingen. Een beroemd voorbeeld is het Horologium oscillatorium van Christiaan Huygens (1673), waarin het onderzoek naar verbeterde uurwerken niet alleen tot het slingeruurwerk voerde, doch ook tot de studie van de slingerbeweging en van evoluten en involuten van vlakke krommen. Christiaan was de zoon van Constantijn, dichter en diplomaat, vermogend en veelzijdig aristocraat, vriend van de Oranjes en van geleerden onder wie Descartes. Christiaan studeerde bij Van Schooten in Leiden, woonde verscheidene jaren in Parijs waar hij een leidende figuur in de nieuwe Académie werd; later keerde hij naar Nederland terug en hij overleed in 1695 op Hofwijck bij Voorburg. Hij was fysicus, astronoom, instrumentmaker en wiskundige, ontdekte de ring van Saturnus en verklaarde het gedrag van het licht uit zijn golfkarakter. Zijn boek over de slingeruurwerken bevat ook belangrijke bijdragen tot de mechanica; zowel door deze bijdrage als door zijn wiskundig werk heeft hij grote invloed uitgeoefend zowel op Newton als op Leibniz, die beiden naar Huygens, hun oudere tijdgenoot, opzagen en hem beschouwden als hun leermeester en criticus. Het boek van Huygens en dat van Wallis bevatten wel de meest geavanceerde infinitesimaaltheorieën vóór de publikaties van Newton en Leibniz. Huygens bestudeerde de tractrix, de logaritmische kromme, de kettinglijn en de cycloïde, waarvan hij het tautochrone karakter aantoonde: de tautochrone is de kromme, die verticaal opgesteld in het zwaartekrachtsveld als een goot, de eigenschap heeft dat een massapunt dat in deze goot rolt steeds in dezelfde tijd beneden in het laagste punt komt, onafhankelijk van de plaats van zijn uitgangspunt. Doch ondanks deze rijkdom van ontdekkingen, waarvan sommige dateren van een tijd toen Leib-

niz zijn methoden van differentiëren en integreren alreeds had gevonden, behoort Huygens toch tot de periode van voorbereiding. Hij bekende aan Leibniz dat hij zich met alle respect toch met diens methoden niet vertrouwd kon maken. Hetzelfde gebeurde overigens met Wallis wat betreft de methoden van Newton. Huygens meende het met de wiskundige strengheid ernstig en sympathiseerde met Archimedische methoden al vond hij die vaak toch te omslachtig voor de praktijk.

Deze uitvinding van de slingeruurwerken staat in nauw verband met één van de grote technische problemen van de vijftiende tot achttiende eeuw, de bepaling van de geografische lengte op zee. De oplossing van dit probleem, dat voor het transoceanische verkeer een levensvraagstuk was, vereiste òf goede uurwerken, òf goede tabellen van zekere hemelverschijnselen als eclipsen of de plaats van de maan tussen de sterren. Regeringen en vermogende heren loofden prijzen uit voor een bevredigende oplossing, en vooraanstaande geleerden van Stevin en Galilei tot Newton en Euler toe hebben aan deze oplossing meegewerkt. Dit heeft op vele takken van wetenschap bevruchtend gewerkt: op de wiskundige cartografie, de infinitesimaalrekening, de sterrenkunde, de werktuigkunde, de elasticiteitsleer, de optica en de instrumentenkunde. Men ziet de sporen van dit onderzoek bij Huygens, in Newtons Principia, in Hookes ontdekking van de wet die zijn naam draagt en later in Eulers theorie van de maan. In het midden van de achttiende eeuw heeft tenslotte een goede tabellering van de positie van de maan, tezamen met de uitvinding van de chronometers, het vraagstuk aan een oplossing geholpen, die bevredigend was tot de tijd van de radiosignalen.

6.

De wiskundigen van deze tijd hebben klassieke problemen met nieuwe oplossingen verrijkt na er een geheel nieuw licht op te hebben doen vallen. Zij hebben ook geheel nieuwe terreinen geopend. Een voorbeeld van een nieuw en bevruchtend bewerken van klassieke problemen is de studie die Fermat van Diofantos heeft gemaakt. Een voorbeeld van een geheel nieuwe zienswijze op klassieke theorema's was Desargues' projectieve methode. En de waarschijnlijkheidstheorie was een geheel nieuw gebied.

Diofantos werd voor kenners van het Latijn in 1621 toegankelijk.1

Fermat, die een ijverig bestudeerder van deze uitgave was, verrijkte zijn exemplaar met kanttekeningen, die zijn zoon later heeft uitgegeven. Een van deze kanttekeningen bevat het beroemde ‘grote theorema van Fermat’, dat zegt dat de vergelijking xn + yn = zn voor gehele positieve getallen x, y, z, n en n > 2 geen oplossingen bezit. Fermat's opmerking dat hij hiervoor een fraai bewijs had, berust waarschijnlijk op een vergissing. Het zoeken naar dit bewijs heeft vele nieuwe resultaten opgeleverd, zo heeft de Duitse wiskundige Kummer naar aanleiding van dit theorema in 1847 de theorie der ideale getallen opgesteld. Er bestaat nog steeds geen bewijs van dit theorema voor alle waarden van n, ofschoon bewezen kan worden dat het theorema voor een groot aantal waarden van n juist is, zeker voor priemgetallen.1

Een andere kanttekening van Fermat leert ons dat een priemgetal van de vorm 4n + 1 steeds éénmaal, en niet meer dan éénmaal, als de som van twee vierkanten kan worden geschreven, een theorema dat later door Euler bewezen werd. Het zgn. ‘kleine theorema van Fermat’ dat zegt dat ap-1 - 1 deelbaar is door p als p een priemgetal is en onderling ondeelbaar met a, vindt men in een brief van 1640; dit theorema kan heel eenvoudig worden bewezen. Fermat was ook de eerste die opmerkte dat de vergelijking x2 - Ay2 - 1 (A geheel maar geen vierkant) een oneindig aantal oplossingen heeft.

Fermat en Pascal zijn de grondleggers van de waarschijnlijkheidstheorie. De ontwikkeling van de algemene belangstelling voor dit onderwerp hangt wel samen met de groei van de verzekeringswetenschap en van het loterijwezen, doch de speciale vraagstukken die aanvankelijk grote wiskundigen ertoe brachten om over deze kwesties na te denken, werden gesteld door nobele heren die in dobbelen of kaarten waren geïnteresseerd. Men denke aan de woorden van Poisson: ‘Een vraag over kansspelen, door een man van de wereld aan een ernstige Jansenist gesteld, is het begin geweest van de waarschijnlijkheidsrekening’.2 Deze man van de wereld was Antoine Gombaud, Chevalier de Méré, een geletterde

edelman, en de Jansenist was Pascal. Het vraagstuk dat De Méré aan Pascal voorlegde was het zgn. problème des partis, het partijenvraagstuk: hoe de pot te verdelen als het spel tussen twee spelers voortijdig wordt afgebroken. Pascal begon over dit vraagstuk en over verwante kwesties met Fermat te corresponderen (1654), en aldus begon de waarschijnlijkheidsrekening. De wiskundige problemen waarop Pascal hierbij stootte, zette hij uiteen in zijn Triangle arithmétique (na zijn dood in 1664 gedrukt), waarin de eigenschappen der binomiaalcoëfficiënten aan de hand van de ‘driehoek van Pascal’ worden uiteengezet. Huygens, in Parijs gekomen, hoorde van het bestaan van deze briefwisseling; dit spoorde hem aan naar eigen oplossingen te zoeken en zo kwam zijn Rekeningh in Spelen van Geluck tot stand, dat door zijn leraar Van Schooten in het Latijn werd uitgegeven (1657) als De Ratiociniis in Ludo Aleae, de eerste gepubliceerde verhandeling over de kansrekening.1 De volgende stappen werden gedaan door de Raadpensionaris De Witt in Holland (1671) en de astronoom Halley in Engeland (1693), die verzekeringstafels berekenden. De titel van De Witts verhandeling is Waerdye van Lijfrenten naar proportie van Los-renten.2 Bij de samenstelling heeft Hudde hem geholpen.

Blaise Pascal was de zoon van Etienne Pascal, die met Mersenne een briefwisseling had onderhouden. De ‘Limaçon van Pascal’ heet naar Etienne. Blaise maakte onder zijn vaders oog grote vorderingen, en op zestienjarige leeftijd ontdekte hij het ‘theorema van Pascal’ over de zeshoek in een cirkel ingeschreven, later ook bekend als hexagramma mysticum. Aangezien hij zijn ontdekking (1641) op een enkel blaadje papier, we zouden zeggen een strooibiljet, liet drukken, mogen we blij zijn dat er nog twee exemplaren zijn behouden gebleven, één in Parijs, een ander in Hannover. Pascals bewijs vertoont de invloed van Desargues. Enige jaren later vond Blaise een rekenmachine uit: de oudste waarvan ooit melding is gemaakt.3 Op vijfentwintigjarige leeftijd begon hij deel te



illustratie
Sterk verkleinde weergave van het pamflet uit 1641 waarin Blaise Pascal het ‘theorema van Pascal’ publiceerde.


nemen aan het ascetische leven van de Jansenisten in het convent van Port Royal bij Parijs. Hij bleef zich echter met de wetenschap en de letterkunde bezighouden. Wij hebben alreeds over zijn verhandelingen over de ‘roulette’ en de integratie van goniometrische uitdrukkingen gesproken. Pascal is ook de eerste geweest die het beginsel der volledige inductie in bevredigende vorm heeft uitgedrukt.1

Gérard Desargues was architect in Lyon en de auteur van een boek over perspectief (1636). Zijn wiskundige roem heeft hij voornamelijk te danken aan een boekje met de curieuze titel Brouillon project d'une atteinte aux événements des rencontres d'un cone avec un plan (1639).2 Hierin vinden we een schets van een projectieve meetkunde, waarin we begrippen als oneindig verre punten, involuties, harmonische verhouding en polariteiten vinden, maar dit alles verborgen in een eigenaardige botanische taal. Deze schets raakte ook al spoedig in vergetelheid, tot de Brouillon in de negentiende eeuw herontdekt en naar waarde geschat werd. Van Desargues' terminologie is slechts het woord ‘involutie’ in onze wiskundige taal overgegaan. Het zgn. theorema van Desargues over perspectivische driehoeken komt niet voor in de ‘Brouillon’, maar in een verhandeling van 1648. Ook van dit theorema werd eerst in de negentiende eeuw het belang begrepen.

7.

Een algemene methode om te differentiëren en te integreren, met inbegrip van het feit dat het ene proces het inverse is van het andere, kon slechts worden ontwikkeld door wiskundigen die zowel de meetkundige methoden van de Grieken en van Cavalieri, als de algebraïsche methode van Descartes en Wallis beheersten. Inderdaad treffen wij na 1660 zulke wiskundigen aan in de personen van de jonge Newton en de jonge Leibniz. Er is heel wat geschreven over de prioriteit van de ontdekking der differentiaal- en integraalrekening; heel wat over het twistgeschrijf dat al tijdens het leven van Newton en Leibniz is begonnen. Ik volsta met hier erop te wijzen dat beide mannen hun methoden onafhankelijk van

elkaar hebben ontdekt. Newton heeft zijn methode, de zgn. fluxierekening, het eerste ontwikkeld (1665-'66), Leibniz wat later (1673-'76), doch Leibniz publiceerde zijn methode, de differentiaalrekening (calculus differentialis), het eerst (1684). Zijn integraalrekening werd in 1686 het eerst aangekondigd. Newtons publikaties in de fluxierekening verschenen eerst in 1704 en later. Leibniz heeft veel genialere volgelingen gehad dan Newton, zijn methode was dan ook eleganter en handiger, en is nu algemeen aanvaard.

Isaac Newton was de zoon van een gegoede landman in Lincolnshire. Hij studeerde in Cambridge onder Isaac Barrow, die in 1669 in zijn leerstoel door de zesentwintigjarige Newton werd opgevolgd. Newton bleef tot 1696 in Cambridge, waarna hij zich in Londen vestigde, eerst als Opzichter (Warden), later als Meester (Master) van de Munt, betrekkingen hem aangeboden door Koning-stadhouder Willem iii in verband met zijn reorganisatie van de Engelse financiën. Newtons geweldige autoriteit berust in de eerste plaats op zijn monumentale Philosophiae Naturalis Principia Mathematica (1687), een werk waarin de mechanica axiomatisch wordt gefundeerd, met invoering van de wet van de zwaartekracht - de wet volgens welke de appel ter aarde valt en de maan om de aarde beweegt. Door strenge wiskundige redenering bewees hij dat de wetten van Kepler over de planetenbeweging het gevolg waren van de wet die zegt dat de kracht waarmee massapunten elkaar aantrekken omgekeerd evenredig is met het kwadraat van hun afstand. Dit maakte een dynamische verklaring van de bewegingen der hemellichamen en van de getijden mogelijk. Hij loste het twee lichamenprobleem voor bolvormige lichamen op en legde de grondslag voor een nieuwe maantheorie. Door het vraagstuk van de aantrekking van twee bolvormige lichamen op te lossen maakte hij ook de latere potentiaaltheorie mogelijk. In zijn axiomatiek van de mechanica postuleerde hij een absolute ruimte en een absolute tijd.

De bewijsvoering in de Principia is meetkundig en doet Grieks aan, al gebruikt Newton, die het limietbegrip kent (doch het slechts op tamelijk duistere wijze in zijn leer der ‘eerste en uiteindelijke verhoudingen’ uitdrukt) niet de indirecte methode. Men zou hieruit zeker niet afleiden dat de schrijver reeds lang in het bezit was van zijn fluxierekening, die hij reeds ontwikkeld had in de jaren 1665-'66, toen hij om de pest die in Cambridge en Londen heerste, te ontvluchten, zich in zijn vaderlijk huis had teruggetrokken. In die periode legde de jonge Newton ook de grondslagen van

zijn gravitatietheorie en van zijn theorie van het licht. Een wonderbaarlijk scheppende periode: ‘In de geschiedenis der wetenschappen kennen wij geen voorbeelden van scheppend werk die te vergelijken zijn met die van Newton gedurende die twee gouden jaren’.1

Newtons ontdekking van zijn fluxies was nauw verbonden met zijn studie van oneindige reeksen in Wallis' Arithmetica infinitorum. Zo kwam hij er toe de binomische stelling op gebroken en negatieve exponenten uit te breiden, waardoor hij de binomiale reeks ontdekte. Dit hielp hem weer om een theorie van fluxies op te stellen die geldig was voor ‘alle’ functies, algebraïsch of transcendent. Voor Newton was een fluxie, uitgedrukt door een stip boven een letter, als ẋ, (pricked letters) een eindige waarde, een snelheid. Hij noemde de grootheden voorgesteld door letters zonder stip fluents, als x.

Hier laten we een voorbeeld volgen van de wijze waarop Newton zijn methode verklaarde. Het is uit zijn Method of Fluxions, eerst in 1736 na Newtons dood uitgegeven, doch in Newtons jonge jaren geschreven. Hij geeft de veranderlijken of fluents aan door v, x, y, z, ‘en de snelheden waardoor iedere fluent door zijn beweging wordt vermeerderd (en die wil ik “fluxies” noemen, of eenvoudig snelheden of celeriteiten) zal ik voorstellen door dezelfde letters met een stip er boven, aldus v̇, ẋ, ẏ, ż.’

Newton noemt zijn infinitesimalen ‘momenten van fluxies’, en stelt ze voor door v̇o, ẋo, ẏo, żo, waar o een ‘oneindig kleine grootheid’ is. (In onze notatie - die van Leibniz - is dus v̇o = dv, en v̇ = dv/dt). Dan gaat Newton als volgt verder:

‘Zij daarom een willekeurige vergelijking gegeven, b.v.

x3 - ax2 + axy - y3 = 0.

Zet hierin x + ẋo voor x, y + ẏo voor y, en we verkrijgen

x3 + 3x2ẋo + 3xẋoẋo + ẋ3o3 - ax2 - 2axẋo - aẋoẋo + axy + ayẋo + aẋoẏo + axẏo - y3 - 3y2ẏo - 3yẏoẏo - ẏ3o3 = 0

Nu hebben we verondersteld dat x3 - ax2 + axy - y3 = 0,

en als we deze termen wegnemen en de overblijvende termen door o delen, krijgen we

3x2ẋ - 2axẋ + ayẋ + axẏ - 3y2ẏ + 3xẋẋo - aẋẋo + aẋẏo - 3yẏẏo + ẋ3oo - y3oo = 0.

Maar aangezien o oneindig klein wordt verondersteld opdat het momenten van kwantiteiten kan voorstellen, zullen de termen, die ermee vermenigvuldigd zijn, niets zijn, vergeleken met de overige. Ik laat ze dus weg, en wat overblijft is

3x2ẋ - 2axẋ + ayẋ + axẏ - 3y2ẏ = 0.’

Dit voorbeeld toont ons dat Newton zijn afgeleiden in de eerste plaats als snelheden dacht, maar ook dat er in zijn wijze van uitdrukking een zekere vaagheid was. Zijn nu die symbolen ‘o’ nullen, zijn ze infinitesimalen, of zijn ze eindige getallen? Newton heeft getracht zijn positie duidelijk te maken door zijn reeds vermelde theorie van ‘eerste en uiteindelijke verhoudingen’ (rationes primae et ultimae), die hij in zijn Principia invoerde, en die het limietbegrip bevat, doch in een vorm die zeer moeilijk is te begrijpen:

Die uiteindelijke verhoudingen waarmee grootheden verdwijnen, zijn in waarheid niet de verhoudingen van uiteindelijke grootheden, maar grenswaarden waartoe de verhoudingen van grootheden die onbegrensd verminderen, altijd convergeren; en waartoe zij meer en meer naderen tot op een willekeurig van te voren gegeven verschil, maar die ze, noch ooit overschrijden, noch werkelijk bereiken tot de grootheden tot in het oneindig kleine afnemen. (Principia Boek i, Sect i, laatste scholium).
‘Grootheden, en de verhouding van grootheden, die in een willekeurig eindig tijdsverloop ononderbroken naar gelijkheid streven, en die vóór het einde van dit tijdsverloop elkaar benaderen tot op een willekeurig van te voren gegeven bedrag, worden ten slotte gelijk’ (Principia Boek i, Sect i, Lemma i).1

Wij kunnen wel hieruit zien, dat Newton, evenals eigenlijk ook alreeds Valerio, het limietbegrip had, maar het is niet heel duidelijk uitgedrukt, en voor de tijdgenoot was het nog onduidelijker. Dit maakte het begrijpen van Newtons fluxietheorie een lastig werk, dat tot veel verwarring leidde en aanleiding gaf tot de scher-

pe kritiek van George Berkeley in 1734. Eerst de invoering van het moderne limietbegrip door Cauchy (omstreeks 1820) en latere wiskundigen heeft de misverstanden weggeruimd.

Newton heeft ook over kegelsneden en vlakke derdegraadskrommen geschreven. In zijn Enumeratio linearum tertii ordinis (1704) gaf hij een classificatie van deze kubische krommen in 72 soorten, waarbij hij uitging van de stelling dat elke derdegraadskromme uit een ‘divergente parabool’ y2 = ax3 + bx2 + cx + d door centrale projectie van uit een vlak op een ander vlak kan worden verkregen. Dit was wel het eerste nieuwe resultaat van belang, dat verkregen was door de toepassing van de algebra op de meetkunde, aangezien zoals we reeds vermeld hebben vrijwel al het werk vóór Newton op dit gebied verricht, niet veel meer was dan de vertaling van Griekse resultaten in de taal van de algebra. Een andere bijdrage van Newton was zijn methode om wortels van numerieke vergelijkingen te benaderen, en die hij illustreerde aan het voorbeeld x3 - 2x - 5 = 0, waarvan x = 2,09455147 als oplossing wordt verkregen.

Het is niet altijd gemakkelijk Newtons invloed op zijn tijdgenoten juist te schatten, omdat hij altijd aarzelde zijn ontdekkingen te publiceren. Hij ontdekte zijn wet van de zwaartekracht in 1665-'66, maar maakte die wet eerst bekend nadat hij het manuscript van de Principia aan de drukker had gezonden (1686). Zijn Arithmetica universalis, die verhandelingen over algebra en analyse bevat die tussen 1673 en 1683 zijn tot stand gekomen, werd in 1707 gepubliceerd. Zijn werk over oneindige reeksen, dat van 1669 dateert, vindt men in een brief van 1676 aan Henry Oldenburg (een brief die voor Leibniz was bestemd1) en verscheen in druk eerst in 1711. Zijn kwadratuur van krommen, uit 1671, zag eerst het licht in 1704, en dit was ook de eerste keer dat de fluxierekening werd gepubliceerd. Zijn Method of Fluxions zelf verscheen, zoals wij reeds vermeld hebben, eerst na zijn dood in 1736. Zelfs zijn hoofdwerk, de Principia, zou nooit tot stand zijn gekomen zonder het aandringen en de offervaardigheid van zijn jongere vriend Edmund Halley, de astronoom.

Niet minder dan door de Principia beïnvloedde Newton door zijn Opticks (1704, naar een veel oudere tekst) de geleerde wereld (en de vele amateurs) van de achttiende eeuw. In 1705 sloeg Koningin Anna hem tot ridder en zo werd hij Sir Isaac.

8.

Gottfried Wilhelm Leibniz, geboortig uit Leipzig, bracht het grootste deel van zijn leven door in de buurt van het hof van Hannover en in dienst van de hertogen, van wie er een in 1714 koning van Engeland werd onder de naam van George i. Hij streefde zelfs de grootste denkers van zijn tijd voorbij in de breedte van zijn scheppend werk; zijn wijsbegeerte omvatte behalve de logica en de monadologie ook geschiedenis, theologie, linguïstiek, biologie, geologie, wis- en natuurkunde, diplomatie en de uitvindingskunst. Hij was een der eersten na Pascal die een rekenmachine uitvond, hij voorzag de stoommachine, studeerde Chinese filosofie en werkte aan de eenheid van Duitsland. Zijn gehele wetenschappelijk en wijsgerig streven werd gedragen door zijn zoeken naar een universele methode, waarmee men ware kennis zou kunnen verkrijgen, uitvindingen kon verrichten en het wezen van de eenheid van het heelal kon begrijpen. Wij hebben gezien hoe dit zoeken ook Descartes' denken beheerste. De ‘Algemene Wetenschap’, de Scientia generalis, waarnaar Leibniz streefde, was zeer veelzijdig en bracht hem ook tot zijn wiskundige ontdekkingen. Hij hoopte de Algemene Wetenschap te kunnen uitdrukken in een aparte symboliek, de Characteristica Universalis en op weg daarheen bestudeerde hij permutaties en combinaties, en zocht naar een Algemene Taal, een Lingua Universalis, waarin alle gedachtenfouten als rekenfouten zouden optreden. Dit leidde hem niet alleen tot een begin van de symbolische logica, doch ook tot de infinitesimaalrekening met zijn sprekende notatie. Doch niet alleen hier, maar ook op andere wiskundige gebieden trachtte hij de symboliek te verbeteren, en zo werd Leibniz een van de grootste uitvinders van mathematische notaties. Er zijn weinig mensen geweest die zo diep de eenheid van vorm en inhoud hebben trachten uit te drukken. Zijn uitvinding van de differentiaal- en integraalrekening (ook deze namen zijn van hem en van de Bernoulli's) was gedragen door zijn streven een lingua universalis van de verandering, speciaal van de beweging, te scheppen, al speelde hier natuurlijk ook de liefde tot de wiskunde om haar zelfs wille een belangrijke rol. Leibniz stelde zijn infinitesimaalrekening op gedurende zijn ‘gouden periode’, toen hij in de jaren 1672-'76 te Parijs in diplomatieke dienst was en persoonlijk met Huygens verkeerde. Hier bestudeerde hij ook Descartes, Pascal en andere voorgangers. Ook stimuleerde hem het bericht uit Engeland dat daar Newton een algemene methode had gevonden om problemen met infinitesimalen te beheersen. Terwijl Newtons methode, als later bleek, kinematisch was georiënteerd, was die van Leibniz aller-



illustratie
Begin van Leibniz' eerste publikatie over de infinitesimaalrekening in de Acta Eruditorum van 1684 (herdruk van C.I. Gerhardt uit 1858).


eerst van meetkundige aard: hij dacht in de taal van de zgn. karakteristieke driehoek (dx, dy, ds), die reeds hier en daar in deze of verwante vorm voor de dag was gekomen, speciaal bij Pascal en bij Barrow in diens Lectiones geometricae van 1670.1 Leibniz' eerste publikatie van zijn resultaten geschiedde in 1684 in een artikeltje van zes pagina's in het nieuwe wetenschappelijke tijdschrift, de Acta Eruditorum, dat sinds 1682 in Leipzig was uitgekomen. De titel van het opstel is tekenend: ‘Een nieuwe methode voor maxima en minima alsook voor raaklijnen onafhankelijk of er gebroken of irrationale grootheden in optreden, en een merkwaardige soort symboliek hiervoor’.2 Als een verhandeling was het artikel dor en duister, maar het bevatte onze symbolen dx, dy en de differentiatieregels, zoals d(uv) = udv + vdu en de differentiaal voor het quotiënt, met de voorwaarde dy = 0 voor extreme waarden en d (dy) = 0 voor buigpunten. In 1686 liet Leibniz hierop, eveneens in de Acta Eruditorum, een ander artikel volgen (in de vorm van een boekbespreking), waarin hij de integraalrekening met het ʃ teken invoerde. Hier vinden we de vergelijking van de cycloïde in de vorm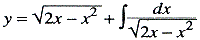



illustratie

Met deze verhandelingen, die door anderen werden aangevuld, opende Leibniz een buitengewone periode van wiskundige produktiviteit. Na 1687 werd hij daarbij vooral door de twee broeders Jakob en Johann Bernoulli geholpen, broeders die zijn methoden ijverig bestudeerden en verwerkten. Het resultaat was, dat nog vóór 1700 deze onderzoekers het voornaamste hadden gevonden van wat we nu de elementaire differentiaal- en integraalrekening noemen, maar daarnaast waren al verscheidene dieper gelegen gebieden aangeboord, zelfs enige vraagstukken uit wat we nu de variatierekening noemen. In 1696 kon alreeds het eerste leerboek der differentiaalrekening verschijnen, dat de titel Analyse des infini-

ment petits voerde. De schrijver, de Markies De L'Hospital, was bij Johann Bernoulli in de leer gegaan wat we o.a. kunnen zien als wij zijn boek met de verhandeling over de differentiaalrekening bekijken die Johann Bernoulli heeft geschreven, doch die eerst in 1922 is gepubliceerd. L'Hospital bracht in zijn boek de stelling, die naar hem genoemd wordt, doch door Bernoulli is gevonden, en waarmee men de grenswaarde van een breuk kan bepalen als teller en noemer beide tot nul naderen.1

Onze voornaamste notaties in de infinitesimaalrekening zijn door Leibniz ingevoerd, ook de namen calculus differentialis en calculus integralis.2 Ook hebben onder zijn invloed tekens als = voor gelijkheid en · voor vermenigvuldiging algemene ingang gevonden. Ook de uitdrukkingen ‘functie’ en ‘coördinaten’, ‘ordinaat’ en ‘abscis’ komen van Leibniz, evenals de ondeugende term ‘osculeren’. De reeksen

arc tg x = x - x3/3 + x5/5 - x7/7 + ...

π/4 = 1 - ⅓ + ⅕ - 1/7 + ...

heten naar Leibniz, ofschoon hij ze niet als eerste heeft ontdekt. Dat is waarschijnlijk gebeurd door James Gregory (zie echter wat we over de Indische wiskunde hebben geschreven). Gregory was een veelbelovende Schotse wiskundige die vóór zijn veertigste jaar is gestorven, en die gewerkt heeft op het gebied van reeksen en de onmogelijkheid met passer en lineaal de kwadratuur van de cirkel te vinden. Zijn brieven, en de drie boeken die hij schreef tijdens zijn verblijf in Italië (1664-'68) voor hij naar St. Andrews University ging, toonden zijn grote originaliteit. Hij kende de binomiale reeks (1670) en in 1671 vinden we reeds de zgn. reeks van Taylor bij hem. Had hij langer geleefd, dan zou hij waarschijnlijk met Newton en Leibniz tot de uitvinders van de differentiaal- en integraalrekening moeten worden beschouwd.

Wat de grondslagen van de differentiaalrekening bij Leibniz be-

treft, die waren even vaag als bij Newton. Vaak waren zijn dx dy eindig kleine grootheden, vaak ook grootheden kleiner dan welk getal hoe klein dan ook, en toch niet nul. Bij gebrek aan een strenge definitie gaf hij analogieën en verwees b.v. naar de verhouding tussen de aardstraal en de afstand van de aarde tot de vaste sterren. Hij gebruikte verschillende manieren om het begrip ‘oneindig’ te benaderen, zo aanvaardde hij in een zijner brieven (aan Foucher, 1693) het actueel oneindige ten einde Zeno's paradoxen te overwinnen, en prees hij De Saint Vincent, die de plaats had berekend waar Achilles de schildpad inhaalt. En evenals Newtons vaagheid de kritiek van Berkeley uitlokte, zo lokte Leibniz' vaagheid de kritiek uit van Bernard Nieuwentijt, arts en burgemeester van Purmerend, die ook tegen Spinoza heeft geschreven. Leibniz heeft Nieuwentijt uitvoerig in de Acta Eruditorum beantwoord.1 We moeten erkennen, dat Berkeley's en Nieuwentijts kritiek recht van bestaan hadden, doch ze was geheel negatief. Beide mannen konden zelf geen strenge opbouw van de infinitesimaalrekening geven. Maar door hun kritiek, vooral door die van Berkeley, zijn andere wiskundigen aangespoord tot werkelijk opbouwend werk op dit gebied.

Literatuur

Men heeft moderne uitgaven van de verzamelde werken van Kepler, Galilei, Descartes, Pascal, Fermat, Torricelli, Huygens en Newton. Er bestaat een oude uitgave van Leibniz' wiskundige werken (die van C.I. Gerhardt), aan nieuwere uitgaven wordt gewerkt (zijn manuscripten bevinden zich in Hannover).

[D.T. Whiteside-M.A. Hoskins, eds.] Mathematical Papers of Isaac Newton (8 dln, Cambridge, 1970-81).
[Id] The Mathematical Works of Isaac Newton (2 dln, New York-Londen, 1964-67, met facsimile reproducties en inleidingen.
[A. Koyré, I.B. Cohen, A. Whitman] Isaac Newton's Philosophiae Naturalis Principia Mathematica. Third Edition (1726) with Variant Readings (2 dln, Cambridge, Mass., & Cambridge, England, 1972).
Correspondence of Isaac Newton, ed. H.W. Turnbull (tot zoverre 3 dln, Cambridge, 1959-61).
[C.I. Gerhardt] G.W. Leibniz' mathematische Schriften (7 dln, Berlin, Halle, 1849-63, opnieuw uitg. Hildesheim 1962, met ‘Register’ van J.E. Hofmann, Hildesheim 1977.

Over de ontdekking van de differentiaal- en integraalrekening zie het reeds enige malen geciteerde boek van C.B. Boyer (New York, 1959), met uitgebreide biblografie. Ook:

G. Castelnuovo, Le origini del calcolo infinitesimale nell' era moderne (Bologna, 1938).
O. Toeplitz, Die Entwicklung der Infinitesimalrechnung i (Berlin, 1949).

Omtrent de historische en technische achtergrond vindt men gegevens in:

H. Grossman, Die gesellschaftlichen Grundlagen der mechanistische Philosophie und die Manufaktur, Zeitschrift z. Sozialforschung 4 (1935) 161-231.
R.K. Merton, Science, Technology and Society in the Seventeenth Century, Osiris 4 (1938). Ook als boek (New York, 1970.)
B. Hessen, The social and economic Roots of Newton's ‘Principia’. In Science at the Crossroads (Londen, 1934). Duitse vertaling in P. Weingart, Wissenschaftssoziologie (Frankfurt, 1972)

en over de wetenschappelijke achtergrond in:

E.J. Dijksterhuis, De mechanisering van het wereldbeeld (Amsterdam, 1950), ook in Engelse en Duitse vertaling verschenen.

Over de leidende wiskundigen:

J.F. Scott, The Mathematical Works of John Wallis, D.D., F.R.S., (Londen, 1938).
A. Prag, John Wallis, Zur Ideengeschichte der Mathematik im 17. Jahrhundert. Quellen und Studies z. Geschichte der Mathematik B1 (1930) 381-412.
I. Barrow, Geometrical Lectures, transl. and edited by J.M. Child (London, 1948).
A.E. Bell, Christiaan Huygens and the Development of Science in the Seventeenth Century (London, 1948).
L.T. More, Isaac Newton. A Biography (New York, London, 1934).
S.I. Wavilow, Isaac Newton (Duitse vertaling uit het Russisch, Berlin, 1951).
R.S. Westfall, Never at Rest. A Biography of I. Newton (New York, enz., 1981).
De beste levensbeschrijving van Newton.
H.W. Turnbull, The mathematical Discoveries of Newton (Glasgow, 1945).

Er bestaan verzamelingen van artikelen over Newton: door de History of Science Society (Baltimore, 1928), de Mathematical Association (London, 1927) en de Royal Society (Cambridge, 1947).

Er bestaat ook een Russische uitgave van Newtons werken.

 

Verder:

H.J.E. Beth, Newton's ‘Principia’ (2 vols, Groningen, 1932). Een gedegen werk in het Nederlands.
J.M. Child, The Early Mathematical Manuscripts of Leibniz, transl. from the Latin texts (Chicago, 1920).
J.E. Hofmann, Die Entwicklungsgeschichte der Leibnizschen Mathematik (München, 1949). Naar een aantal andere studies van J.E. Hofmann over wiskundigen van de 17e eeuw vindt men verwezen in zijn ‘Geschichte der Mathematik’ (Göschen). Ook: Frans van Schooten der Jüngere, (Wiesbaden, 1962).
P. Montel, Pascal Mathématicien (Paris, 1951).
Johann Kepler, A Tercentenary Commemoration of His Life and Work (Baltimore, 1931).
E.J. Dijksterhuis, Descartes als wiskundige. Openbare les Leiden 1932.
G. Milhaud, Descartes Savant (Paris, 1921).
R. Taton, L'Oeuvre mathématique de G. Desargues (Paris, 1951).
[H.W. Turnbull, red] James Gregory Tercentenary Memorial Volume (London, 1939). Zie ook M. Dehn-E.D. Hellinger, Amer. Mathem. Monthly 50 (1943) 149-163.
E.A. Fellman, Die Mathematischen Werke von Honoratius Fabri. Physis 1 (1959) 1-54.
D.T. Whiteside, Patterns of mathematical thought in the later seventeenth century. Arch. for history of exact sc. 1 (1961) 179-388.
J.O. Fleckenstein, Die Prioritätsstreit zwischen Leibniz und Newton (Basel, Stuttgart 1956).
Over deze, vaak beschreven, prioriteitstwist, zie ook, behalve Cantor's Geschichte, P. van Geer, Wiskundig Tijdschrift 10 (1913-14) en de artikelen van D. Mahnke, Abhandl. Akad. Berlin, Phys. Math. Kl. 1 (1925) en Sitzungsber. Ges. z. Beförd. ges. Naturw. Marburg 67 (1932).
Paul Tannery, Notions historiques, in J. Tannery, Notions de mathématiques (Paris, 1903) 324-348.
M.S. Mahoney, The mathematical Career of Pierre Fermat (Princeton N.J., 1970).
C.J. Scriba, James Gregorys frühe Schriften zur Infinitesimalrechnung, Mitt. mathem. Seminar Giessen 55 (1957) 80 bldz.
J.A. Lohne, Thomas Harriot als Mathematiker, Centaurus 11 (1965) 19-45, ook DSBV 1 (1972) 124-129.
H.J.M. Bos, Differentials, Higher-order Differentials and the Derivatives in the Leibnizian Calculus, Dissertatie Utrecht 1963, AHES 14 (1974) 1-90.
R. Taton, L'oeuvre de Pascal en Géométrie projective, Revue Hist. Sciences Appl. 15 (1962) 197-252.
H. Loeffel, Blaise Pascal 1623-1662 (Birkhäusen, 1987) gaat speciaal over Pascal's wis- en natuurkunde.
M.E. Baron, The Origins of the infinitesimal Calculus (New York, 1969).
L. Auger, Un savant méconnu, Giles Personne de Roberval 1602-1675 (Paris, 1962).
D. Bierens de Haan (1822-95), professor te Leiden, schreef tussen 1874 en 1893, 33 artikelen over Nederlandse wis- en natuurkundigen van de ouden tijd voor de Versl. en Med. Kon. Akad. Amsterdam, bijna alle gepubliceerd in de ‘Bouwstoffen’.
G.A. Vorsterman v. Oyen. 144 vraagstukken van Nederlandse wiskundigen der 17e eeuw (Schoonhoven, 1868).
P. van Geer, Hugeniana geometrica i-xii, Nieuw Archief voor Wiskunde (2) 7-10 (1907-13).
P. van Geer, Johan De Witt als Wiskundige, ib (2) 11 (1915) 98-126.
A. Girard, Invention nouvelle en Algèbre. Réimpression (Leiden, 1884).
Zie ook Nieuw Archief voor Wiskunde 11 (1884) 83-152.
C.P. Burger, Amsterdamsche Rekenmeesters en Zeevaartkundigen in de zestiende eeuw (Amsterdam, 1908).
Wiskunde in de Gouden Eeuw, vakantiecursus 1989 (Amsterdam, 1989). Een verzameling opstellen.
Meer algemeen is
D.J. Struik, Het Land van Stevin en Huygens (Amsterdam, 1958, Nijmegen 1979). Ook in het Engels (Dordrecht, enz., 1981).
K. van Berkel, In het voetspoor van Stevin (Amsterdam, 1985).

Over de rekenmeesters en instrumentmakers van deze periode, zie, behalve het boek van Burger en het in Hoofdstuk v geciteerde boek van professor Eva Taylor:

M. Rooseboom, Bijdrage tot de geschiedenis der Instrumentmakerskunst in de noordelijke Nederlanden (Leiden, 1950).
D.J. de S. Price, Science since Babylon (New Haven, 1961), spec. Ch. 3.

Over de belangrijkste wiskundigen vindt men ook vaak een levensbeschrijving in hun verzamelde werken, b.v. een biografie van

Huygens door J.A. Vollgraff in C. Huygens, Oeuvres xxii (La Haye, 1950).

Wat de Nederlandse en Belgische wiskundigen betreft vindt men vele bijzonderheden in de reeds geciteerde werken van H. Bosmans. Wij vermelden artikelen over

Tacquet: Isis 9 (1927-28) 66-83; Stevin: Mathesis 37 (1923), Annales Soc. Sc. Bruxelles 37 (1913) 161-199, Biographie nationale de Belgique 23 (1923-24); Dela Faille: Mathesis 41 (1927) 5-11; van Roomen: Biographie nat. de Belg. 19 (1907); De Saint Vincent: Mathesis 38 (1925) 250-256; van Ceulen: Annales Soc. Sc. Bruxelles 34 (1909-10) 88-139, Mathesis 39 (1925); Nicolaas Pietersz van Deventer: Annales Soc. Sc. Bruxelles 32II (1907-08) 272-301. Over Stevin ook het reeds geciteerde boek van Dijksterhuis en G. Sarton, Simon Stevin of Bruges, Isis 21 (1934) 241-303; zie ook G. Sarton, The first Explanation of decimal Fractions and Measures, Isis 23 (1935) 153-244.

Over Stevin en Huygens (over Huygens zie o.a. ook het reeds geciteerde boek van A.E. Bell. Zie verder J. en A. Romein, Erflaters van onze beschaving, (Amsterdam, 7e dr., 1956)):

D.J. Korteweg, Het bloeitijdperk der wiskundige Wetenschappen in Nederland (Amsterdam, 1894).
D. Bierens de Haan, Bouwstoffen voor de Geschiedenis der wisen natuurkundige Wetenschappen in de Nederlanden i, ii (Amsterdam, 1878-1887).

Vorige Volgende