Geschiedenis van de wiskunde
(1990)–D.J. Struik–
[pagina 105]
| ||||||||||||||||
1.Het Westelijk deel van het Romeinse Rijk is steeds zowel in economisch als in cultureel opzicht bij het Oostelijk deel ten achter gebleven. Hier, in het Westen bestond de intensieve landbouw, door irrigatie georganiseerd, niet of nauwelijks; en daardoor ontbrak een voorname prikkel voor de bestudering van de sterrenkunde. Het Westen was best tevreden met het beetje sterrenkunde, praktische rekenkunde en meetkunde dat voor handel en landmeten nuttig was (sommige handleidingen voor landmeters, agrimensores, zijn bewaard gebleven). Eeuwenlang bleef de inspiratie voor de verdere ontwikkeling of de verdieping van de wiskunde uit het Oosten komen. Toen het Oost-Romeinse Rijk en het West-Romeinse Rijk politiek uiteengingen, leefde deze inspiratie vrijwel geheel niet meer. Vele eeuwen lang bleef de statische beschaving van het West-Romeinse Rijk zonder veel onderbrekingen voortbestaan en werd de eenheid van de cultuur die rondom de Middellandse Zee was ontstaan maar weinig onderbroken, zelfs niet eens door de veroveringen van de zgn. barbaren. In alle Germaanse koninkrijken (misschien die in Brittannië uitgezonderd) bleven de economische verhoudingen, de maatschappelijke instellingen en het geestesleven in beginsel gelijk aan wat ze in het ondergaande Romeinse Rijk waren geworden. Grondslag van het maatschappelijk leven was de landbouw, waarin slaven geleidelijk vervangen werden door vrije boeren of pachters. Steden bleven bloeien, een internationale handel met een geldeconomie bleef gehandhaafd. Nadat het centrale gezag in deze Grieks-Romeinse wereld na de val van het Westelijk Rijk in 476 gedeeld werd door de keizer van Constantinopel en de Paus van Rome, zette de Katholieke Kerk in het Westen zo goed en zo kwaad als ze kon, door haar taal en instellingen de culturele traditie van het Romeinse Rijk binnen de Germaanse koninkrijken voort. Kloosters en geletterde leken hielden althans enige bestanddelen van de Grieks-Romeinse beschaving in leven. Een dezer leken, de diplomaat en wijsgeer Anicius Manilius Severinus Boëthius, schreef enige wiskundige boeken die meer dan duizend jaar in de Westelijke wereld gezag hebben uitgeoefend. | ||||||||||||||||
[pagina 106]
| ||||||||||||||||
Ze zijn een weerspiegeling van de culturele verhoudingen waaronder zij ontstonden, want ze zijn arm aan wetenschappelijke inhoud. Het is niet onmogelijk dat het eeuwenlang aanzien, waarin ze hebben gestaan, samenhangt met het feit dat de schrijver in 524 als martelaar van het Katholieke geloof is gestorven. In Boëthius' Institutiones arithmeticae, een oppervlakkige bewerking van Nikomachos, kon men wat Pythagoreïsche getallentheorie vinden, die op deze manier als een bestanddeel van de zeven artes liberalis, namelijk het ‘quadrivium’ (arithmetica, geometria, astronomia, musica) naast het ‘trivium’ (grammatica, rhetorica, dialectica) in het onderwijs der Middeleeuwen werd opgenomen. Het is moeilijk precies de tijd aan te geven waarin de maatschappijvorm van het oude Romeinse Rijk plaats begon te maken voor de nieuwe feodale orde. Op deze kwestie wordt enig licht geworpen door de hypothese van de Belgische geschiedkundige Henri Pirenne (die overigens niet algemeen wordt aanvaard)Ga naar voetnoot1, volgens welke het einde van de West-Romeinse maatschappijvormen samenhangt met de opkomst van de Islam. De Arabieren beroofden het Byzantijnse rijk van al zijn provincies aan de Oost- en Zuidkust van de Middellandse Zee en maakten het Oostelijk bekken van die Zee tot een mohammedaans binnenmeer. Zij bemoeilijkten vele eeuwen lang de handelsbetrekkingen tussen het Nabije Oosten en het Christelijke Westen. Het intellectuele verkeer tussen de Arabische wereld en het noordelijk deel van het vroegere Romeinse Rijk werd daarbij eveneens aan grote moeilijkheden onderworpen, ofschoon het nooit geheel is stopgezet. Het gevolg was dat in het Frankische Gallië en in andere voormalige delen van het West-Romeinse Rijk de oude instellingen verschrompelden; de steden raakten in verval, de inkomsten uit tollen liepen sterk terug, de internationale geldeconomie werd vervangen door ruilhandel en plaatselijk marktverkeer. West-Europa ging terug tot een tamelijk primitieve landbouweconomie. Het verval van de handel kwam de landelijke aristocratie ten goede en in Noord-Frankenland werden de grondbezitters onder de leiding der Karo- | ||||||||||||||||
[pagina 107]
| ||||||||||||||||
lingers tot heersende klassen. Het economische en culturele middelpunt werd naar het Noorden, naar Noord-Frankrijk en Brittannië verlegd. De scheiding van Oost en West beperkte het feitelijk gezag van de Paus, zodat het Pausdom zich verbond met de Karolingers. Dit verbond werd bezegeld door de kroning van Karel de Grote tot keizer van het Heilige Roomse Rijk in 800. De Westelijke wereld werd feodaal en kerkelijk, haar oriëntering Germaans en naar het Noorden gericht. | ||||||||||||||||
2.Gedurende de eerste eeuwen van het Westelijk feodalisme vinden we zelfs in de kloosters maar heel weinig belangstelling voor de wiskunde. Er ontbraken nu eenmaal de impulsen die tot wiskundig denken prikkelen; ook in het dagelijks leven had men niet meer dan een minimum aan rekenkennis nodig. Het aftellen op de vingers was gewoonlijk wel voldoende. Aan de kloosters bestond de ‘hogere’ wiskunde gewoonlijk uit niet veel meer dan de zgn. computus, die uit een stel regels bestond om de datum van het Paasfeest vast te leggen. Boëthius was op wiskundig gebied de autoriteit. Een mindere autoriteit was de monnik Alcuinus, die uit Brittannië stamde en aan het hof van Karel de Grote leefde; zijn verzameling opgaven ‘voor de verscherping van het verstand’ (zie voetnoot bldz. 90) heeft eeuwen lang stof tot lering en vermaak geleverd. Zo vinden we hierin oude bekenden als de volgende vraagstukken: ‘Een hond achtervolgt een konijn, dat oorspronkelijk een voorsprong heeft van 150 voet. De hond springt elke keer negen voet tegen de zeven voet van het konijn. Na hoeveel sprongen heeft de hond het konijn ingehaald?’ Een andere klerikale wiskundige was de Franse monnik Gerbert, die in 999 de pauselijke troon beklom onder de naam Sylvester ii. Hij schreef enige verhandelingen onder de invloed van Boëthius, doch zijn hoofdverdienste als wiskundige bestaat daarin, dat hij tot de eerste geleerden in de Latijnse wereld behoorde die belangstelling in de wiskunde door zijn invloed in West-Europa verhoogde. Een abacus met een bord met niet minder dan 27 kolommen staat op de naam van Gerbert of zijn invloed. Hij verbleef rondom 968 in Catalonië en kan dus wel door Arabische we- | ||||||||||||||||
[pagina 108]
| ||||||||||||||||
tenschap zijn kennis hebben vermeerderd.Ga naar voetnoot1 | ||||||||||||||||
3.Er bestaan wezenlijk verschillen tussen de ontwikkeling van het Westelijke, het vroeg-Griekse en het Oosterse feodalisme. De landbouw in Westelijk Europa had een extensief karakter en dit maakte een breed opgezette bureaucratie overbodig, zodat de grondslagen voor een Oosterse vorm van despotisme ontbraken. Hier bestond ook geen mogelijkheid grote massa's slaven bijeen te brengen. Dit heeft uitvindersvernuft gescherpt, en zo vinden we nieuwigheden als een meer economisch harnassen van paarden en de invoering van stijgbeugels. Toen de dorpseenheden in West Europa tot steden uitgroeiden, en deze zich ontwikkelden tot zelfstandige bestuurs- en bedrijfseenheden, waarvan de burgers niet in staat waren een gemakkelijk leventje ten koste van slaven te leiden, kwam het uitvindersvernuft ook hun ten goede. Dit is een der voornaamste punten van verschil tussen de ontwikkeling van de Griekse stadstaat en de Westeuropese stad, die toch in het aanvangsstadium sommige gemeenschappelijke trekken vertoonden. De middeleeuwse stadsbevolking kon haar levensstandaard slechts verbeteren door hard werk met scherpe handel en vernuftige techniek te verbinden. In zware strijd met de feodale jonkers - en in veel geharrewar onderling - verkregen de steden in de twaalfde, dertiende en veertiende eeuw steeds grotere macht en zelfbewustzijn. Deze overwinningen berustten niet alleen op de snelle groei van handel, verkeer en geldeconomie, doch vaak ook op een geleidelijke uitbreiding van de industrie. In hun strijd met de landjonkers werden de steden vaak door de vorsten gesteund, waardoor de vorsten hun invloed in de steden versterkten. Botsingen tussen steden en vorsten bleven niet uit. Ten slotte leidde deze ontwikkeling tot de vorming van de eerste nationale staten in Europa. De steden begonnen of hervatten hun verkeer met het Oosten, dat nog steeds een hogere beschaving bezat. Deze betrekkingen | ||||||||||||||||
[pagina 109]
| ||||||||||||||||
tussen Oost en West, Islam en Christendom, Arabische, Griekse en Latijnse wereld waren vaak vreedzaam, doch konden in oorlogen als de kruistochten ook een gewelddadig karakter aannemen. De Italiaanse steden waren de eerste, die de handelsbetrekkingen weer opnamen; zij werden in de loop der tijden door steden in Frankrijk, Duitsland en andere landen gevolgd. De koopman en de soldaat werden voorafgegaan of gevolgd door de geleerde, voor wie het punt van contact op Sicilië of in Spanje, soms ook in Constantinopel, lag. Nadat in 1085 de Christenen Toledo op de Moren veroverd hadden, stroomden van wijd en zijd Latijnse geleerden naar deze stad om de wetenschap van de Arabische wereld te leren kennen. Als tolken traden vaak Joden op, die ook hun bemiddeling bij het vertalen van teksten verschaften. Zo vindt men in het Spanje van de twaalfde eeuw Plato van Tivoli, Gherardo van Cremona, Adelard van Bath en Robert van Chester bezig met het vertalen van wiskundige en sterrenkundige handschriften uit het Arabisch in het Latijn. Op deze manier kreeg Latijns Europa een vermeerderde kennis van de Griekse klassieken door middel van Arabische vertalingen, en dit in een periode waarin deze kennis langzamerhand ook naar waarde kon worden geschat. Een ander cultuurcentrum was Constantinopel (nu Istanbul), meer dan duizend jaren een plaats waar de Griekse wetenschap werd bewaard. Hier kon men de Griekse klassieken zonder Arabische (of Syrische, of Hebreeuwse) tussenkomst studeren. | ||||||||||||||||
4.We hebben reeds vermeld dat de eerste machtige handelssteden in Italië ontstonden. Hier vinden we in de twaalfde en dertiende eeuw Genua, Pisa, Venetië, Milaan en Florence in een bloeiend handelsverkeer met de Arabische wereld en met het Noorden gewikkeld. Italiaanse kooplieden bezochten Egypte en Azië, waarvan zij ook de cultuur bestudeerden; de reizen van Marco Polo naar Centraal Azië en China geven een voorstelling van de onverschrokkenheid van sommige dezer avonturiers. Evenals de Ionische kooplieden van tweeduizend jaren te voren poogden zij de wetenschap en de kunst van een oudere beschaving niet alleen te bestuderen om ze te reproduceren, doch ook om haar te verwerken ten bate van de eigen cultuur, waarin reeds in de twaalfde en dertiende eeuw naast het bankwezen ook kapitalistische vormen van industrie voorkwamen. De eerste koopman van de Latijnse wereld, wiens wiskundige studies een zekere rijpheid vertonen, was Leonardo van Pisa. Leonardo, ook Fibonacci (lid van het huis der Bonacci) ge- | ||||||||||||||||
[pagina 110]
| ||||||||||||||||
naamd,
reisde als koopman naar de Arabische wereld. Na zijn terugkeer schreef hij
het Liber Abaci (1202), een groot handboek over het
rekenen met het Hindoe-Arabische getallensysteem, dat ook
algebraïsche vraagstukken bevat. In zijn Practica
Geometriae (1220) beschreef Leonardo op gelijksoortige wijze wat
hij aan meetkunde en trigonometrie had geleerd. Maar hij is meer dan
leerling, hij is zelfstandig vorser, wiens boeken menig vraagstuk bevatten
waarvan in de Arabische literatuur geen precies voorbeeld voorhanden schijnt
te zijn.Ga naar voetnoot1 Hij citeert speciaal Al-Chwārizmī,
b.v. in zijn discussie van de beroemde vergelijking x2 + 10x = 39. Het probleem
dat tot de zgn. getallen van Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21 ... voert
(waarvan elke term de som is van de twee voorafgaande termen), schijnt nieuw
te zijn, evenals het merkwaardig diep doordachte bewijs van de stelling dat
de wortels van de vergelijking x3
+ 2x2 + 10x = 20 niet met behulp van Euklidische irrationaliteiten
van de vorm 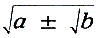 kunnen worden uitgedrukt en dus ook niet met passer en lineaal
kunnen worden geconstrueerd. Leonardo voerde het bewijs door ieder van de
vijftien gevallen, die Euklides in zijn tiende boek van de Elementen heeft behandeld, apart te onderzoeken, waarna hij de
positieve wortel van de vergelijking tot op zes sexagesimale plaatsen
benaderde. kunnen worden uitgedrukt en dus ook niet met passer en lineaal
kunnen worden geconstrueerd. Leonardo voerde het bewijs door ieder van de
vijftien gevallen, die Euklides in zijn tiende boek van de Elementen heeft behandeld, apart te onderzoeken, waarna hij de
positieve wortel van de vergelijking tot op zes sexagesimale plaatsen
benaderde.
De reeks van getallen van Fibonacci wordt verkregen als de oplossing van het volgende vraagstuk in de Liber Abaci: Hoeveel paren konijnen kunnen in één jaar uit een enkel paar woorden gewonnen zo a) elk paar elke maand één nieuw paar gewint dat zichzelf wederom vanaf de tweede maand begint voort te planten, en b) geen enkel konijn sterft? Leonardo stond niet alleen. In de Italiaanse handelssteden bestonden reeds vóór zijn tijd cursussen in het handelswezen, en dus ook in het rekenen, zowel op de abacus als in het Arabisch cijferen. Maar het Liber Abaci heeft aan de verspreiding van het Hindoe-Arabische positiestelsel in West Europa zeker bijgedragen. Deze verspreiding is een langdurig proces geweest, waarin allerhand soort lieden moeten hebben meegeholpen: kooplui, diplomaten, soldaten, pelgrims en geleerden. Het oudste Latijnse manuscript | ||||||||||||||||
[pagina 111]
| ||||||||||||||||
waarin Hindoe-Arabische getallen voorkomen is de Codex Vigilanus, in 976 in Spanje geschreven. Het oudste Franse handschrift waarin ze voorkomen dateert echter eerst van 1275. Langs de Adriatische Zee bleef de Griekse schrijfwijze eeuwenlang nog in gebruik. Gewoonlijk werden rekeningen uitgevoerd op de aloude abacus, het tel- of zandbord, waarbij rekenpenningen of eenvoudig steentjes (calculi) de aantallen aangaven. Men denke hierbij aan de telramen, nog steeds in Japan, China en de Sowjet-Unie in gebruik, en die bij ons nog wel op scholen of aan baby-boxen te zien zijn. Zo nodig werd dan het resultaat van zulk een abacusrekening met behulp van symbolen, b.v. Romeinse cijfers, opgeschreven. Gedurende de Middeleeuwen en nog wel later vindt men in vele koopmansboeken zulke Romeinse cijfers, waaruit blijkt dat op de kantoren telborden werden gebruikt. De invoering van het rekenen met de tien Indisch-Arabische symbolen stuitte zelfs op tegenstand, omdat niet iedereen uit die symbolen wijs kon worden. In de statuten van de Florentijnse ‘Arte del Cambio’, die van 1299 en later dateren, vinden we zelfs een verbod om Arabische cijfers te gebruiken. Op den duur drong het gebruik van zulke cijfers met hun positiewaarde toch door, maar eerst in de vijftiende en zestiende eeuw kan men van een overwinning van het Hindoe-Arabische stelsel spreken.Ga naar voetnoot1 Men vindt wel eigenaardige tussenvormen: op de graftombe van een vrouwe van IJsselstein vindt men het jaar 1471 aangeduid door xiiiiclxxi.Ga naar voetnoot2 | ||||||||||||||||
[pagina 112]
| ||||||||||||||||
5.Met de uitbreiding van de handel en nijverheid breidde zich ook de belangstelling voor de wiskunde naar de Noordelijke steden uit. Eerst had deze belangstelling voornamelijk een praktische kant, zodat het gewoonlijk niet-academisch opgevoede rekenmeesters waren die algebra, rekenkunde en praktische meetkunde onderrichten. Deze rekenmeesters waren praktische mannen, die weinig of geen Latijn kenden, maar wel boekhouden of scheepvaartkunde. Er waren kwakzalvers onder, maar de besten waren schrandere knapen, die ook wel almanakken samenstelden, of instrumenten en kaarten maakten. De wiskunde die zij doceerden behield heel wat sporen van haar Arabische afkomst, hetgeen ook de termen ‘algebra’ en ‘algoritme’ bewijzen. De theoretische wiskunde was gedurende de middeleeuwen in Europa niet volledig ten onder gegaan, doch zij werd niet zozeer door de practici dan wel door de scholastische wijsgeren beoefend. Bij deze, gewoonlijk geestelijke, geleerden leidde de studie van Plato en Aristoteles en speculaties over de natuur van God tot scherpzinnige beschouwingen over de eigenschappen der beweging, der continuïteit en der oneindigheid. De kerkvader Origines volgde Aristoteles in zijn verwerping van het actueel oneindige, doch Augustinus, in zijn De Civitate Dei (De staat Gods, ca. 420) aanvaardde het, schoon in theologisch gewaad. Zijn woorden waren zo goed gekozen dat Georg Cantor heeft opgemerkt dat het transfiniete niet energieker gewenst en niet beter bepaald en verdedigd kan worden dan Augustinus dat heeft gedaan.Ga naar voetnoot1 De scholastieke auteurs, in het bijzonder Thomas van Aquino, namen Aristoteles' stelling ‘infinitum actu non datur’ (actuele oneindigheid bestaat niet) over, en beschouwden ieder continuüm tevens als potentieel deelbaar tot in het oneindige. Voor hen bestond dus geen kleinste lijnsegment, aangezien ieder gedeelte van een lijn weer de deelbaarheidseigenschap van de Jijn bezit. Een punt was dus geen deel van een lijn, omdat het indivisibel, ondeelbaar was: ‘ex indivisibilibus non potest compari aliquod continuum’ (een continuüm kan niet uit indivisibilen bestaan). Een punt kan evenwel door beweging een lijn doen ontstaan. Zulke speculaties hebben later de uitvinders van de infinitesimaalrekening in de zeventiende eeuw en de wijsgeren van het transfiniete in de negentiende | ||||||||||||||||
[pagina 113]
| ||||||||||||||||
eeuw beïnvloed: Cavalieri, Tacquet, Bolzano en Cantor kenden de scholastieke auteurs en schonken veel aandacht aan hun meningen over het oneindig grote en het oneindig kleine. Deze mannen van de kerk hebben af en toe ook wel eens wiskundige resultaten bereikt, die minder speculatief zijn. Thomas Bradwardinus, die in 1348 aartsbisschop van Canterbury werd, onderzocht stervormige veelhoeken nadat hij Boëthius had bestudeerd. Een der meest belangrijke middeleeuwse kerkelijke wiskundigen was Nicole Oresme, bisschop van Lisieux in Norman-dië, die met gebroken exponenten speelde. Uitgaande van het feit dat 43 = 64 = 82 schreef hij 8 als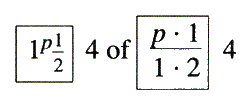 waarmee hij 4 1½ bedoelde. Hij schreef ook een verhandeling De latitudinibus formarum (ca. 1360), waarin hij een afhankelijke veranderlijke (latitudo) tegen een onafhankelijke veranderlijke (longitudo) grafisch afzet wanneer de laatste varieert. Men kan hierin een soort overgang van coördinaten op de bol (reeds aan Ptolemaios bekend) naar coördinaten in het vlak zien, en aangezien deze verhandeling tussen 1482 en 1515 verscheidene malen gedrukt is heeft ze misschien wel enige invloed op de wiskundigen van de Renaissance uitgeoefend, Descartes niet uitgezonderd. Oresme schreef ook over oneindige reeksen en bewees dat de harmonische reeks 1/1 + ½ + ⅓ + ¼ +... divergent is, een merkwaardig, verziend, resultaat voor die dagen! | ||||||||||||||||
6.Nu terug naar de grote handelssteden, waar de wiskunde onder de onmiddellijke invloed van koop- en scheepvaart, sterrenkunde en landmeting wordt bestudeerd in vormen die nog weinig van die der Mohammedaanse wereld verschillen. Deze belangstelling van de stedelijke burgerij in alles wat kwantitatief is en in het bijzonder wat berekend kan worden, heeft de Duitse econoom Werner Sombart met het woord ‘Rechenhaftigkeit’ gekarakteriseerd.Ga naar voetnoot1 Ofschoon men wel zeggen kan dat de rekenmeesters in de beoefening van de praktische wiskunde vooropliepen, vond men onder hen ook wel geleerden met een universitaire opleiding, die door hun kennis van wis- en sterrenkunde de wiskundige methoden van de oudheid en de Islam konden uiteenzetten en ook mee konden | ||||||||||||||||
[pagina 114]
| ||||||||||||||||
helpen bij het verbeteren van het rekenkundig, algebraïsch en meetkundig apparaat. Brandpunten van dit nieuwe leven waren de grote Italiaanse steden, verder Neurenberg, Wenen, Praag, Leipzig, Parijs, Lyon en andere Noordelijke centra. De theoretische belangstelling nam toe toen door de val van Constantinopel in 1453 het Oost-Romeinse Rijk ten einde kwam en vele Griekse geleerden naar de steden van het Westen vluchtten. Daardoor werd het weer gemakkelijker de groeiende belangstelling voor oorspronkelijke Griekse handschriften te bevredigen. Universiteitsprofessoren konden zich met andere humanisten in lezen en vertalen oefenen, eerzuchtige rekenmeesters hielden hun oren open en poogden op hun manier de nieuw verworven kennis te verstaan. Dit is ook de periode waarin de uitvinding van de boekdrukkunst plaatsvindt, gewoonlijk toegeschreven aan Johannes Gutenberg (na 1440). Ze heeft de verspreiding van wiskundige kennis (b.v. rekenboeken) enorm bevorderd. Voor deze periode is Johannes Müller uit Königsberg in FrankenlandGa naar voetnoot1, bekend als Regiomontanus, een karakteristieke figuur. De werkzaamheid van deze veelzijdige man, wiskundige, instrumentmaker, drukker en humanist, die reeds op veertigjarige leeftijd stierf (1476), is tekenend voor de wijze waarop de Europese wiskunde in de twee eeuwen van Leonardo van Pisa was vooruitgegaan. Regiomontanus was ijverig bezig de wiskundige handschriften die hij kon krijgen, te vertalen en verder bekend te maken. Zijn leraar, de Weense astronoom Georg Peurbach, die sterrenkundige en trigonometrische tabellen had samengesteld, was reeds begonnen met de Almagest van Ptolemaios uit het Grieks te vertalen. Regiomontanus zette zijn werk voort en vertaalde ook werken van Apollonios, Heroon en zelfs van Archimedes, de moeilijkste klassieke auteur, in het Latijn. Zijn eigen hoofdwerk, De Triangulis omnimodis (1464, doch eerst in 1533 gedrukt) was een leerboek der trigonometrie, dat voornamelijk hierin van onze tegenwoordige leerboeken verschilt, dat onze handige notatie ontbrak. Alle stellingen worden in woorden uitgeschreven, zodat het boek een meetkundig karakter draagt. Men vindt er de sinusregel van de vlakke en boldriehoek. Van nu af werd de trigonometrie ook in het avondland een wetenschap, onafhankelijk van de sterrenkunde - men zal zich herinneren dat Nasir-Eddin dit reeds vroeger in Perzië had trachten te bereiken. | ||||||||||||||||
[pagina 115]
| ||||||||||||||||
Maar waar de invloed van Nasirs werk naar het schijnt niet heel groot is geweest, heeft Regiomontanus' werk op de verdere ontwikkeling der trigonometrie en haar toepassing op de sterrenkunde en de algebra ten sterkste doorgewerkt. Regiomontanus besteedde ook veel tijd aan de berekening van trigonometrische en sterrenkundige tabellen. In zijn tafels voor de verhouding van de sinus tot de straal R gebruikt hij eerst een sexagesimale schaal voor de straal, later een decimale (R = 6·104 later 6·107, dan 107). Een grotere waarde voor de straal betekende grotere nauwkeurigheid voor de sinus die, zoals we gezien hebben, als een lijnsegment werd opgevat. De overgang tot een decimale schaal bereidde de invoering van decimale breuken voor. | ||||||||||||||||
7.Tot nu toe waren nog geen stappen gedaan om de kennis van Grieken en Mohammedanen niet alleen in te halen, maar voorbij te streven. De klassieke auteurs bleven het nec plus ultra van de wetenschap. Daarom wekte het zulk een blijde verwondering, toen het bekend werd dat Italiaanse wiskundigen erin geslaagd waren een hoofdstuk van de algebra te ontwikkelen, dat aan vroegere generaties was ontsnapt. Dit hoofdstuk behelsde de algemene algebraïsche oplossing van de derdemachtsvergelijkingen, en werd omstreeks 1500 geopend door het werk van Scipio del Ferro en zijn collega's aan de Universiteit van Bologna. Zoals reeds gezegd is waren de Italiaanse steden ook na de dagen van Fibonacci centra van wiskundige bedrijvigheid gebleven, en hun rekenmeesters wisten met kwadratische vergelijkingen en irrationale getallen om te gaan zonder de meetkundige gewetensbezwaren van Euklides te voelen. Hun belangstelling in de wiskunde werd gedeeld door hun schilders en bouwmeesters. In zijn bekende boek over de renaissanceschilders (1550, 1568) legt Giorgio Vasari nadruk op de belangstelling van die schilders voor de meetkunde, een belangstelling die tot de ontwikkeling van de perspectief voerde. Bekende figuren uit de vijftiende eeuw (het Quattrocento) zijn hierbij Leon Battista Alberti en Pier della Francesca; deze laatste schreef niet alleen een boek over perspectief (1482), doch ook een boek over regelmatige lichamen. Deze liefde voor de meetkunde vindt men niet alleen in het werk van Rafael en Leonardo da Vinci, doch ook in dat van Albrecht Dürer, die zelfs een Underweysung der Messung mit dem Zirckel und Richtscheyt (1525) schreef, dat ook orthogonale projectie bevat.Ga naar voetnoot1 | ||||||||||||||||
[pagina 116]
| ||||||||||||||||
De rekenmeesters vonden hun leider in de Franciscaan Luca Pacioli, wiens Summa de Arithmetica in 1494 uitkwam - een der eerste gedrukte wiskundeboeken en het eerste boek dat een volledige uiteenzetting van de hele toenmalig voorhanden wiskunde poogde te zijn.Ga naar voetnoot1 Het boek was in het Italiaans geschreven en leidde tot de drempel van de theorie der derdemachtsvergelijkingen, die Pacioli als nog niet oplosbaar beschouwde. Hij zette ook de kunst van het ‘Italiaans boekhouden’ uiteenGa naar voetnoot2 en in een boek van 1503 ontleende hij aan Pier della Francesca een beschouwing van regelmatige lichamen; hier voegde hij een verhandeling over de gulden snede (‘Divina Proportione’, 1509) aan toe. De figuren worden aan Leonardo da Vinci toegeschreven. Bij Pacioli is het gebruik van Hindoe-Arabische cijfers reeds vast ingeburgerd, en de rekenkundige notatie is niet moeilijk te volgen. De algebraïsche notatie is nog geheel van de onze verschillend. Het oplossen van de vergelijkingen x3 + mx = n, x3 + n = mx leek Pacioli even onmogelijk als het oplossen van het vraagstuk der cirkelkwadratuur. Op dit punt begint nu het werk der wiskundigen aan de universiteit van Bologna, toentertijd een der grootste en beroemdste scholen van Europa. Haar astronomische faculteit alleen telde bij gelegenheid zestien lectoren. Uit alle delen van Europa stroomden studenten naar Bologna om de colleges te horen en zich te verlustigen aan de publieke disputaten, die vaak de belangstelling trokken van grote en sportief ingestelde massa's van toehoorders. Tot deze studenten hebben te hunner tijd Pacioli, Albrecht Dürer en Nicolaas Copernicus behoord. Het lag in de geest der tijden, niet alleen het klassieke erfgoed te aanvaarden, doch het kritisch te waarderen en er zelfs door nieuwe scheppingen bovenuit te groeien. De ontdekking van de boekdrukkunst en de ontdekking van Amerika hadden getoond, dat men verder kon komen dan de Ouden. Waarom niet in de wiskunde? Waar in vroegere perioden sommige derdegraadsvergelijkingen algebraïsch konden worden opgelost, poogden de wiskundigen in Bologna de algemene oplossing te vinden. Deze derdegraadsvergelijkingen konden tot drie soorten worden teruggebracht; in onze tegenwoordige notatie: | ||||||||||||||||
[pagina 117]
| ||||||||||||||||
x3 + px = q, x3 = px + q, x3 + q = px, waar p en q positieve getallen waren. Zij werden door professor Scipio del Ferro (in 1526 gestorven) aan een nauwkeurig onderzoek onderworpen. Op gezag van professor E. Bortolotti kunnen wij aannemen dat Del Ferro werkelijk alle drie de soorten heeft weten op te lossen.Ga naar voetnoot1 De oplossingen werden echter niet gepubliceerd en slechts aan weinige vrienden bekend gemaakt. Doch de mare van de ontdekking verspreidde zich en zo werd de oplossing opnieuw ontdekt door een Venetiaanse rekenmeester die Tartaglia (de Stotteraar) werd genoemd. Omstreeks 1535 maakte hij zijn resultaten bekend, doch hield de methode waarmee hij ze had verkregen, geheim. Ten slotte openbaarde hij haar onder een eed van geheimhouding aan een geleerde arts uit Milaan, Hieronimo Cardano. Toen echter Cardano in 1545 zijn kort maar inhoudrijk boek met de trotse titel Ars Magna het licht liet aanschouwen, ontdekte Tartaglia tot zijn ontsteltenis, dat zijn methode in dat boek volledig was uiteengezet, weliswaar met vermelding van zijn naam, maar desondanks toch gestolen. Hieruit ontstond een bittere strijd, waarin Cardano verdedigd werd door zijn jonge leerling Ludovico Ferrari. Onder de geschriften, die gedurende deze twist geschreven werden, behoorden de Quaesiti van Tartaglia (1546) en de Cartelli van Ferrari (1547-48), waardoor de gehele geschiedenis van deze opzienbarende ontdekking publiek eigendom werd. Men noemt de oplossing nog steeds naar Cardano. De formule van Cardano ziet er in het geval x3 + px = q als volgt uit (in moderne notatie): 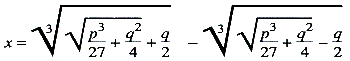 Ze is vervat in een Italiaans rijmpje dat van Tartaglia afkomstig is en waarvan de eerste regels luiden:
| ||||||||||||||||
[pagina 118]
| ||||||||||||||||
Hier ziet men het woord ‘cosa’, dat deze Italianen voor de onbekende x (of een aantal x) gebruikten (‘de zaak’, Latijn ‘res’). In Duitsland werd daarom gedurende de zestiende eeuw de algebra vaak aangeduid met de term ‘Coss’ of ‘De regel Coss’. Men ziet dat in de formule van Cardano vormen van de gedaante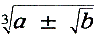 voorkomen in plaats van de Euklidische
voorkomen in plaats van de Euklidische 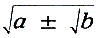 . .
De Ars Magna bevatte nog een andere opzienbarende ontdekking: de methode van Ferrari waarbij de oplossing van een algemene vierdegraadsvergelijking tot die van een vergelijking van de derde graad wordt teruggebracht. Ferrari's voorbeeld was x4 + 6x2 + 36 = 60x, welke vergelijking hij terugvoerde tot y3 + 15y2 + 36y = 450. Cardano beschouwde ook negatieve getallen, die hij fictieve noemde, maar hij wist niets aan te vangen met de zgn. ‘casus irreducibilis’, waarbij de oplossing van de derdegraadsvergelijking weliswaar reëel is, doch verschijnt als de som van getallen die we heden complex noemen.Ga naar voetnoot1 Deze moeilijkheid werd door de laatste der grote Bolognese wiskundigen van de zestiende eeuw, Rafaele Bombelli, onder de ogen gezien. In zijn Algebra, die in 1572 verscheen - en in een toen ongedrukt gebleven meetkunde van ongeveer 1550 - zette hij een theorie van imaginaire en complexe getallen uiteen. Hij schreef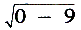 (letterlijk R[0 m. 9], R voor radix, m voor meno) voor onze (letterlijk R[0 m. 9], R voor radix, m voor meno) voor onze
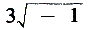 , en behandelde het irreducibile geval op zulk een manier, dat hij
aantoonde dat b.v. , en behandelde het irreducibile geval op zulk een manier, dat hij
aantoonde dat b.v.
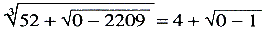
Bombelli's boek werd veel gelezen, we weten dat het gebruikt werd door Stevin, door Leibniz en door Euler. Aan Bombelli is zodoende te danken dat de imaginaire getallen iets van hun bovennatuurlijk karakter kwijtraakten, al duurde het tot de negentiende eeuw voor complexe getallen hun geheimzinnig waas geheel verloren en hun normale plaats in de wiskunde konden innemen. Het is wel merkwaardig dat de complexe getallen het eerst zijn ingevoerd in de studie der derdegraadsvergelijkingen, op die plaats waar reële oplossingen bestaan doch in vermomde gedaante optreden - en niet in de studie van kwadratische vergelijkingen, waar we ze tegenwoordig gewoonlijk het eerst tegenkomen. | ||||||||||||||||
[pagina 119]
| ||||||||||||||||
8.Algebra en praktische rekenkunde bleven vele tientallen jaren het hoofdbestanddeel van het wiskundig dieet. Dit was niet alleen het gevolg van de ‘Rechenhaftigkeit’ van de mercantiele bourgeoisie, doch ook van de eisen die de leiders der zich vormende staten stelden aan landmeetkunde, scheepvaart en het oorlogswezen. Men had ingenieurs nodig voor openbare werken en voor de krijgsvoering. De sterrenkunde, van ouds een belangrijk gebied voor wiskundige studiën, werd nu ook gestimuleerd door de eisen die de wetenschappelijke scheepvaartkunde begon te stellen. De zestiende eeuw werd de tijd der grote astronomen, van Copernicus, Tycho Brahe en Kepler. Een nieuwe opvatting omtrent de samenstelling van het heelal begon zich baan te breken. Het wijsgerig denken weerspiegelde de grote veranderingen in maatschappij, wetenschap en techniek. Plato, met zijn eerbied voor het wiskundig denken en daardoor meer kwantitatief ingesteld dan Aristoteles, wiens natuurleer bijna zuiver kwalitatief is, vond een nieuwe aanhang. Wij zien de invloed van Plato's denken o.a. in het werk van Kepler. Het doorbreken van nieuwe gedachten in de natuurwetenschappen nam vaak een anti-Aristotelisch karakter aan. Van de grote werken die hieraan hebben bijgedragen, noemen wij slechts Andreas Vesalius' De fabrica corporis humani en Nicolaas Copernicus De Revolutionibus orbium celestium, beide van 1543, waarvan de eerste de nieuwe anatomie, de andere de nieuwe sterrenkunde inluidde. Hierbij kunnen wij nog Mercators grote wereldkaart van 1569 voegen, die uitdrukking gaf aan het nieuwe aardbeeld in een projectie met ‘wassende graden’, waarbij lijnen van constante koers als rechte lijnen worden afgebeeld. De eeuw wordt afgesloten met William. Gilberts De Magnete (1600), waarmede de nieuwe natuurkunde zich aankondigt. Ongeveer gelijktijdig met Cardano's Ars magna verscheen nog een ander boek dat grote invloed had op de reken- en stelkunde van deze periode. Dit was de Arithmetica integra (1544) van de Lutherse predikant Michael Stifel, waarin o.a. de driehoek van Pascal, de negatieve getallen, ingevoerd als 0 - 3, 0 - 8, etc., en de oplossing van allerlei vergelijkingen, ook van de derde en vierde graad, worden uiteengezet. Stifels ‘Coss’-notatie is weer zeer verschillend van die van Cardano, die weer van die van Bombelli verschilt. Astronomische en goniometrische tafels met steeds stijgende graad van nauwkeurigheid verschenen vooral in Duitsland. De tafels van G.J. Rhaeticus (die Copernicus' boek voor de uitgave had voorbereid), door zijn leerling Valentin Otho in 1596 voltooid, be- | ||||||||||||||||
[pagina 120]
| ||||||||||||||||
vatten de waarden van alle zes trigonometrische functies, met 10 seconden oplopend, in zes decimalen. De tafels van B. Pitiscus (1613) gingen tot 15 decimalen. Ook was er vooruitgang in de techniek van het oplossen van vergelijkingen en in het begrip van de natuur der wortels. Karakteristiek was de uitdaging, die de Zuidnederlandse wiskundige Adriaen van Roomen in 1593 aan alle belangstellenden zond, en waarin hij de oplossing eiste van een vergelijking van graad 45, die er als volgt uitzag (we geven slechts enige termen aan): x45 - 45x43 + 945x41 - 12300x39 +... - 3795x3 + 45x = A waarbij hij verder vermeldde dat voor 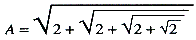 de waarde 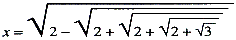 aan de vraag voldeed. Dit was een probleem dat door de studie van regelmatige veelhoeken was geïnspireerd. Het antwoord liet niet lang op zich wachten. In 1594 merkte François Viète (Vieta), een Frans advocaat verbonden aan het hof van Hendrik iv, op, dat de linkerzijde van de vergelijking equivalent is met de ontwikkeling van sin φ naar machten van sin φ/45. De oplossing kan dan herleid worden tot een vergelijking van de 3e, de 3e en de 5e graad (45 = 3 × 3 × 5). Ook kan de oplossing met behulp van tafels worden gevonden. Viète vond 23 oplossingen van de vorm sin (φ/45 - n · 8°), zodat hij geen aandacht schonk aan negatieve wortels. Viète, die de goniometrie met vele formules verrijkte, bracht ook de oplossing van Cardano van de derdegraadsvergelijking over in trigonometrische vorm, waarbij het irreducibile geval zijn afschrikwekkende gedaante verloor, omdat nu geen complexe getallen meer nodig waren.Ga naar voetnoot1 Viètes belangrijkste bijdragen liggen op het gebied der theorie der vergelijkingen. In zijn In artem analyticam isagoge (1591) voerde hij voor het eerst stelselmatig letters in als coëfficiënten van de termen ener vergelijking. Het gebruik van speciale getallen-coëfficiënten, zelfs in de gesyncopeerde algebra van Diofantos, had de algemene discussie van algebraïsche vraagstukken bemoei- | ||||||||||||||||
[pagina 121]
| ||||||||||||||||
lijkt. Viète kwam tot zijn rekening door een kritiek van de methoden der klassieke schrijvers, vooral van de ‘analyse’ en ‘synthese’ zoals die bij Pappos voorkomen. Uit deze kritiek leidde hij de noodzakelijkheid af, een algebra met getallen te vervangen door een algebra met zgn. species (lijnsegmenten, oppervlakken, enz.). In deze logistica speciosa vindt men dus een algemeen symbolisme, waarin lijnsegmenten door een letter, oppervlakken door een wijziging hiervan worden uitgedrukt, b.v. A is een lijnsegment, A quadratum een oppervlak, enz. De logistica speciosa onderscheidt zich dus van onze algebra daarin, dat Viète vasthoudt aan het homogeniteitsbeginsel, waarbij het produkt van lijnsegmenten A en B als oppervlak wordt beschouwd; lijnsegmenten kunnen slechts met lijnsegmenten, oppervlakken met oppervlakken worden vergeleken. Er bestond zodoende enige twijfel of vergelijkingen van hogere graad dan drie nog zin hadden, daar ze tot een ruimte van vier of meer afmetingen konden leiden. Maar Viète (en ook Stevin) vonden wel een driedimensionale interpretatie. De rekentechniek bereikte, zoals reeds is vermeld, nieuwe hoogtepunten. Viète, in Archimedes' geest, berekende π in negen decimalen, kort daarop vond Ludolph van Ceulen, een wiskundige en schermmeester in Delft, π eerst in 20 decimalen (Van den Circkel, 1596), later in 35 decimalen, steeds meer en meer in- en omgeschreven veelhoeken berekenend.Ga naar voetnoot1 Viète slaagde er in π als een oneindig produkt voor te stellen (1593), dat in onze notatie er zó uitziet: 2/π = cos π/4 · cos π/8 · cos π/16 · cos π/32 ... · cos (π · 2-n)... Bij deze verscherping van de techniek speelde de verbeterde notatie (speciaal het systematisch gebruik van het decimale positiestelsel met de tien ons bekende symbolen) een belangrijke rol. De rijkdom van nieuwe resultaten laat duidelijk zien hoe verkeerd het zou zijn te zeggen, dat mannen als Viète ‘alleen maar’ de notatie hebben verbeterd. Aan wie zo iets zegt, ontsnapt het diepliggende verband tussen vorm en inhoud. Vaak zijn nieuwe resultaten ontdekt als een gevolg van een verbeterde notatie. Een voorbeeld is de invoering van de Hindoe-Arabische cijfers, een ander voorbeeld is Leibniz' schrijfwijze voor differentiaalquotiënt en in- | ||||||||||||||||
[pagina 122]
| ||||||||||||||||
tegraal. Een goed gekozen notatie weerspiegelt de werkelijkheid beter dan een onhandige. Daardoor lijkt het wel of een goede notatie een eigen leven heeft, de symbolen ‘denken’ voor ons en zo komen nieuwe resultaten voor den dag. Op Viètes verbetering van de algebraïsche notatie volgt een generatie later die van Descartes, met haar toepassing in de coördinatenmethode. | ||||||||||||||||
9.Het nut van het decimale positiestelsel werd nog aanzienlijk vergroot door de invoering van decimale breuken. Ofschoon deze in het Oosten al lang bekend waren (zie blz. 98, 101), vangt het stelselmatig gebruik van deze breuken in Europa aan met het boekje De Thiende van Simon Stevin (1585). Stevin, een boekhouder uit Brugge, vestigde zich in 1581 te Leiden. Hij werd ingenieur in het Statenleger; Maurits van Oranje waardeerde de wijze waarop Stevin praktische zin met theoretisch inzicht verbond.Ga naar voetnoot1 De Thiende is een voorstel, het gehele toenmaals verwarde stelsel van maten en gewichten in een decimaal stelsel om te zetten, en daarbij laat Stevin ook zien hoe men met decimale breuken even gemakkelijk kan rekenen als met gehele getallen. Stevin schreef ook over statica en hydrodynamica en zijn Arithmétique (1585) is een uitvoerig leerboek der reken- en stelkunde, met een behandeling van hogere-machtsvergelijkingen aan Cardano ontleend, maar met een andere notatie, bij die van Bombelli aanknopend. Stevins manier om decimale breuken te schrijven is nogal omslachtig. Onze tegenwoordige notatie is ontstaan als een gevolg van een andere grote verbetering in de rekentechniek, de uitvinding der logaritmen. Gedurende de zestiende eeuw hadden verscheidene wiskundigen met de mogelijkheid gespeeld, een rekenkundige met een meetkundige reeks in correspondentie te plaatsen (b.v. Stifel), vaak met de bedoeling het werk met de ingewikkelde trigonometrische tafels te vergemakkelijken. Dit was ook het doel van de Schotse burchtheer John Napier (of Neper), die in 1614 een boek uitgaf met de titel Mirifici logarithmorum canonis descriptio. Zijn idee was twee reeksen getallen zodanig met elkaar te verbinden dat steeds, als de ene reeks volgens een rekenkundige reeks groeit, de andere volgens een meetkundige reeks afneemt. Dan bestaat er tussen het produkt van twee getallen in de tweede reeks en de som van de corresponderende getallen van de eerste reeks een eenvoudige betrekking, en zo kon vermenigvuldiging tot | ||||||||||||||||
[pagina 123]
| ||||||||||||||||
optelling worden teruggevoerd, mits men eens en voor altijd de bijbehorende tafels berekende. Door zijn uitvinding kon Napier het rekenen met trigonometrische waarden vereenvoudigen. Napier's eerste poging was nogal onbeholpen, aangezien zijn beide reeksen, in moderne schrijfwijze uitgedrukt, zich verhouden als x en y in y = a e-x/a of x = Nep. log y waarin a = 107.Ga naar voetnoot1 Is dan x = x1 + x2, dan a y = y1y2/a. Dit systeem bevredigde ook Napier niet, en met zijn bewonderaar Henry Briggs, een professor aan het nieuwe Gresham College in Londen, besloot hij een decimaal systeem op te bouwen, berustende op wat wij als y = 10 x zouden schrijven, zodat y = y1y2 als x = x1 + x2.Ga naar voetnoot2 Na Napiers dood in 1617 voerde Briggs dit plan uit in zijn Arithmetica logarithmica (1624), dat de zgn. Briggse logaritmen van de gehele getallen van 1 tot 20.000 en van 90.000 tot 100.000 in 14 decimale plaatsen bevat. In voorbereiding hiervoor had Napier van Stevin de decimale breuken overgenomen, doch de schrijfwijze gewijzigd: gehelen en breukdeel werden door een punt gescheiden (gepubl. 1619). De leemte die nog in de logaritmentafel bestond, werd in Gouda gevuld. Hier had de landmeter Ezechiel de Decker in 1626 een Eerste deel der nieuwe telkonst uitgegeven. Met behulp van zijn stadgenoot Adriaen Vlacq gaf hij in 1627 een Tweede deel van de nieuwe telkonst uit, waarin de logaritmen van alle getallen van 1 tot en met 100.000 in 10 decimalen werden gepubliceerd.Ga naar voetnoot3 Dit werd gevolgd door Vlacqs Arithmetica logarithmica (1628). Met Stevins decimale breuken en Briggs' decimale logaritmen was zo- | ||||||||||||||||
[pagina 124]
| ||||||||||||||||
doende het Hindoe-Arabische stelsel tot dezelfde graad van vervolmaking gebracht als het nu bezit, en de twee boeken van De Decker waren een soort apotheose van dit stelsel. De nieuwe uitvinding werd onmiddellijk door astronomen en wiskundigen met vreugde begroet, vooral door Kepler, die een lange en pijnlijke ervaring met gecompliceerde berekeningen achter de rug had. De uiteenzetting die hier over het ontstaan der logaritmen is gegeven, werkt historisch gesproken een beetje verwarrend, omdat de exponentiële functies die we gebruikt hebben eerst in het laatste deel van de zeventiende eeuw zijn ingevoerd. Napier kende het begrip van een basis niet. Het verband tussen logaritmen, de afstand van breedtecirkels in een kaartprojectie van Mercator, de machten van het getal e en de integraal van x-1 (of het oppervlak tussen hyperbool en asymptoot) is eerst langzaam ontdekt, en wordt eerst door Euler in 1748 helder uiteengezet. Natuurlijke logaritmen, gebaseerd op wat wij nu y = e x schrijven, verschenen bijna gelijktijdig met de logaritmen van Briggs, maar hun fundamentele betekenis werd eerst begrepen toen de differentiaal- en integraalrekening reeds ontwikkeld was.Ga naar voetnoot1 Van de Nederlandse wiskundigen uit het begin van de zeventiende eeuw moeten wij nog Willebrord Snell van Royen (Snellius) vermelden, een leerling van Van Roomen, Tycho Brahe en Kepler, en professor aan de in 1575 gestichte Leidse universiteit. Behalve als vertaler in het Latijn van werken van Van Ceulen en Stevin heeft hij zich op de triangulatie, de trigonometrie en de zeevaart-kunde toegelegd. In zijn Eratosthenes Batavus (1617) vinden wij het resultaat van zijn graadmeting, in zijn Tiphys Batavus (1624) wordt de lijn van gelijke koers op de bol, die een rechte lijn wordt in de Mercatorprojectie, met ‘loxodrome’ aangegeven. Wanneer hij de naar hem genoemde brekingswet heeft ontdekt weten we niet, daar we van het bestaan van het handschrift slechts door anderen weten. | ||||||||||||||||
[pagina 125]
| ||||||||||||||||
LiteratuurOver de verspreiding der Hindoe-Arabische cijfers in Europa:
Over de theoretische wiskunde in de Middeleeuwen:
Over de wiskunde der scholastici:
De Italiaanse wiskunde van de 16e en 17e eeuw vindt men in een aantal verhandelingen besproken:
| ||||||||||||||||
[pagina 126]
| ||||||||||||||||
Men vindt vele gegevens over de wiskundigen van de zestiende en zeventiende eeuw, en in het bijzonder de Vlaamse en Nederlandse wiskundigen, in de vele artikelen van H. Bosmans S.J., waarvan de meesten zijn te vinden in de Annales de la Société Scientifique de Bruxelles 1905-1927. De volledige bibliografie, door A. Rome, in Isis 12 (1929) 88-112. Ook vindt men belangrijke gegevens over Noord-Nederlandse wiskundigen in artikelen van het Nieuw Nederlandsch Biographisch Woordenboek (10 dln., Leiden 1911-37), vele van de hand van C. de Waard.
| ||||||||||||||||
[pagina 127]
| ||||||||||||||||
|
|

