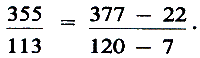Logo DBNL
Geschiedenis van de wiskunde (1990)

Geschiedenis van de wiskunde

(1990)–D.J. Struik–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

IV. Het Oosten na het verval van de Griekse maatschappij

Ondanks alle hellenistische invloed was de oude beschaving van het Nabije Oosten nooit verdwenen: in de Alexandrijnse wetenschap zien we zowel Oosterse als Griekse invloeden duidelijk aan het werk. Oost en West konden elkaar ook ontmoeten in zulke plaatsen als Constantinopel of in India. In 395 stichtte Theodosius i het Byzantijnse Rijk met Constantinopel als hoofdstad, dat, ofschoon zelf Grieks, tegelijk het administratieve centrum was van grote gebieden waarvan de Grieken slechts een gedeelte van de stedelijke bevolking uitmaakten. Dit rijk streed duizend jaar lang tegen machten uit het Noorden, Oosten en Westen, en diende tevens als een bolwerk van Griekse beschaving en als een brug tussen de Arabische en Latijnse wereld. Alreeds in de tweede eeuw na Christus werd Mesopotamië onafhankelijk van de Romeinen, eerst onder de Parthische koningen, na 266 onder de zuiver Perzische dynastie der Sassanieden. In het Indusgebied treffen we enige eeuwen lang Griekse dynastieën aan, die in de eerste eeuw na Christus verdwenen, doch de volgende Indische heersers bleven culturele betrekkingen met Iran en het Westen onderhouden.

Met de plotselinge opkomst van de Islam komt de politieke overheersing van het Nabije Oosten door de Grieken bijna geheel tot een einde. Na 622, het jaar van de Hegira, veroverden de Arabieren stormenderhand grote gedeelten van westelijk Azië en hadden voor het einde van de zevende eeuw niet alleen grote delen van het Oost-Romeinse, doch ook van het oude West-Romeinse Rijk bezet, landen als Sicilië, Noord-Afrika en Spanje. Waar zij kwamen poogden zij de Grieks-Romeinse cultuur door die van de Islam te vervangen. De ambtstaal en wetenschappelijke taal werd Arabisch, in plaats van Latijn of Grieks, maar ook al werden nu geleerde werken in het Arabisch geschreven, toch bleef onder de Arabische heerschappij de continuïteit van de oude Griekse en Oosterse beschaving voor een groot deel bewaard. De oude inheemse culturen hadden onder deze heerschappij zelf een betere kans om bewaard te blijven dan onder de Grieken, wier cultuur altijd een opgelegd karakter had gedragen. Zo bleef bijvoorbeeld Perzië ondanks het Arabische bestuur toch in menig opzicht het oude land der Sassanieden. De wedijver tussen de verschillende

tradities leefde voort, ook al nam hij nieuwe vormen aan. Gedurende de gehele periode van de heerschappij van de Islam bleef ook ononderbroken een Griekse traditie bestaan, een traditie die haar eigen karakter te midden van de inheemse culturen wist te handhaven.

2.

Wij hebben gezien dat gedurende het bloeitijdperk van het Romeinse Rijk de mooiste wiskundige resultaten waren verkregen in Egypte, waar Oosterse en Griekse beschaving enige eeuwen lang vruchtbaar op elkaar konden inwerken. Met de ondergang van het Romeinse Rijk kwam het centrum der scheppende wiskundige bedrijvigheid langzamerhand in India te liggen, en vandaar uit kwam het op den duur weer naar Mesopotamië toe (wij spreken hier niet van China, dat zijn eigen weg ging, doch met India in culturele uitwisseling stond.) De eerste Indische bijdragen tot de exacte wetenschappen, die tamelijk goed bewaard zijn gebleven, zijn de Siddhāntā's, waarvan een gedeelte, de Sūrya, bewaard is in een vorm die misschien nog de oorspronkelijke is. Ze dateert mogelijkerwijze uit de vierde eeuw na Christus. Deze boeken bevatten veel sterrenkundige bijdragen met de epicykeltheorie en sexagesimale breuken. Dit wijst op Griekse invloed, die misschien reeds teruggaat tot de tijd vóór de Almagest, maar een direct verband met de Babylonische astronomie is ook niet uitgesloten. De Siddhāntā's hebben overigens ook vele karakteristieke trekken. De Sūrya Siddhāntā bevat tafels van sinussen en niet, als die van Ptolemaios, van koorden. Die sinussen zijn halve koorden van de dubbele hoek bij een gegeven waarde van de straal R: R sin α = ½ koorde (2α). Eerst bij Euler (1748) wordt stelselmatig R = 1 gesteld en houdt de sinus op een lijn te zijn, maar is een getal.

De resultaten van de Siddhāntā's werden in de Indische scholen van wiskundigen, die men o.a. in Ujjain (Centraal-India) en in Mysore (Zuid-India) vond, stelselmatig bestudeerd en verder uitgewerkt. Nu beginnen wij enige namen van individuele wiskundigen en hun geschriften te verkrijgen; enige dezer geschriften bestaan in een vertaling in een moderne taal.

De meest bekende dezer wiskundigen zijn Āryabhata (wel de ‘Eerste’ genoemd, ca. 500)1 en Brahmagupta (ca. 625). Hoezeer zij door de Griekse, Babylonische of Chinese wetenschap zijn beïnvloed is niet met zekerheid uit te maken, doch het eigen karakter

van hun werk is niet te ontkennen. Dit werk heeft meer een arithmetisch-algebraïsch karakter, en in zijn nadruk op onbepaalde vergelijkingen (vaak ontstaan uit kalenderberekeningen) vertoont het een zekere verwantschap met dat van Diofantos enerzijds en dat van de Chinezen anderzijds. Deze auteurs werden in de volgende eeuwen door anderen gevolgd, die in dezelfde geest werkzaam waren; hun werk had gedeeltelijk een astronomisch, gedeeltelijk een arithmetisch-algebraïsch karakter, zijdelings werden praktische meetkunde en trigonometrie behandeld. Āryabhata had voor π de waarde 3,1416. Een geliefkoosd onderwerp was het vinden van rationale driehoeken en vierhoeken (hierbij moet het oppervlak geheel zijn als de zijden gehele getallen zijn); hierbij denken we in het bijzonder aan Mahāvirā, die tot de wiskundigen van Mysore behoort (ca. 850). En in Ujjain, waar Brahmagupta had gewerkt, vinden we omstreeks 1150 een andere uitstekende wiskundige, Bhāskara, genaamd Bhāskara II.1

Voor de oplossing van onbepaalde vergelijkingen van de eerste graad ax + by = c (a, b, c geheel), zoals we die o.a. bij Brahmagupta vinden, werden gehele getallen vereist. Het is daarom, als men precies wil zijn, niet juist om zulke vergelijkingen Diofantisch te noemen, omdat Diofantos oplossingen met breuken toeliet. De Hindoes waren de eersten die vasthielden aan de eis dat de oplossingen gehele getallen moeten zijn. Een ander verschil met Diofantos was dat in India ook negatieve wortels voor een vergelijking werden aanvaard, al was dit misschien een oudere praktijk, ontleend aan de Chinese wiskunde of misschien aan de astronomie. Hoe dit ook zijn moge, wij weten dat Bhaskara aan de vergelijking x2 - 45x = 250 de wortels x = 50 en x = -5 toekende, al was hij er niet geheel van overtuigd dat zulk een negatieve wortel zin had. Zijn Lilāvati (opgedragen aan een dame, naar men zegt zijn dochter) was eeuwen lang een standaardwerk over reken- en meetkunde in India en ook daarbuiten: Keizer Akbar liet het in het Perzisch vertalen (1587). In 1892 werd het nog weer eens in Calcutta uitgegeven.

Bij de Indische wiskundigen vinden we ook studies in de oplossing van vergelijkingen van de gedaante x2 - Ay2 = 1 (A geheel) in gehele getallen, vergelijkingen die we nu naar Pell noemen. Ook vinden we alreeds bij Āryabhata rekenwijzen die als oplossingsmethoden van vergelijkingen met kettingbreuken kunnen worden opgevat. Bij Brahmagupta vindt men de formule



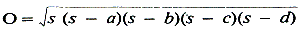illustratie

voor het oppervlak van een koordenvierhoek met zijden a, b, c, d.1

Overigens moeten we erop bedacht zijn, dat het oude India nog wiskundige schatten bezit die eerst nu weer langzaam aan het licht worden gebracht en uit de Sanskrietteksten in moderne wiskundige taal worden vertaald. Zo zijn we b.v. te weten gekomen dat de reeks voor π/4, die we naar Gregory of Leibniz noemen, reeds te vinden is bij Nïlakantha (ca. 1500), natuurlijk in een terminologie die zeer van de onze verschilt.2

3.

Het meest bekende resultaat van de wiskunde der Hindoes is het decimale positiestelsel. Het decimale stelsel is zeer oud, en het positiestelsel zijn we alreeds in het oude Mesopotamië tegengekomen, doch de verbinding van die twee ontwikkelde zich naar het schijnt eerst in China, en daarna in India. Hier verkreeg het geleidelijk de overhand op oudere stelsels, die niet op positie berustten. In India wordt het decimale positiestelsel het eerst gevonden op een inscriptie van het jaar 595 na Chr., waar men de datum 346 aantreft, met de drie tekens voor 3, 4, 6 geschreven. De Indiërs hadden reeds vele eeuwen lang een systeem waarin getallen, ook zeer grote, in woorden werden uitgedrukt volgens een positiebeginsel, en er bestaan teksten uit vroege tijd met de term ‘sūnya’, dat nul betekent.3

Het zgn. Bakshāli-manuscript, dat uit zeventig bladen van berkenschors bestaat, en dat van onzekere ouderdom is (schattingen variëren van de derde tot de twaalfde eeuw na Chr.) en traditioneel Indisch materiaal over benaderingen, onbepaalde vergelijkingen en vierkantsvergelijkingen bevat, heeft een punt om de nul uit te drukken. De eerste keer dat een teken voor nul in een opschrift verschijnt, is de negende eeuw. Dit is veel later dan het optreden van een teken voor nul in Babylonische teksten.

Het teken voor nul dat wij hebben, de 0, kan Griekse invloed verraden (‘oudèn’ is het Griekse woord voor niets, een woord dat met een omikron begint). Terwijl de Babylonische punt voor nul slechts tussen cijfers wordt geschreven, komt de Indische nul ook aan het einde van een getal voor, en dit maakt 0, 1, 2,..., 9 tot gelijkwaardige symbolen.1

Het decimale positiestelsel verspreidde zich geleidelijk langs de karavaanwegen van India uit naar verschillende richtingen en veroverde zich een plaats te midden van allerlei andere stelsels. Details omtrent deze verspreiding kennen we eigenlijk alleen maar uit latere eeuwen, doch we kunnen ons voorstellen dat het decimale positiestelsel onder de Sassanieden (224-641) naar Perzië is gekomen: er bestond toen een vrij nauw contact tussen Mesopotamië, India en Egypte. Het is niet onmogelijk dat in deze periode de herinnering aan het oude Babylonische positiestelsel nog leefde. Ook tot Egypte is het decimale positiestelsel misschien toen al doorgedrongen. De oudste duidelijke vermelding van het Indische positiestelsel buiten India wordt gevonden in een uitlating van de Syrische bisschop Severus Sēbōkht, die van 662 dateert. Dan begint met Al-Fāzarī's vertaling van de Indische Siddhāntā's in het Arabisch (ca. 773) de wereld van de Islam met het Indische stelsel kennis te maken. Dit stelsel begint zich nu over de Arabische wereld en ook daarbuiten te verspreiden, ofschoon ook het Griekse getallensysteem en ook andere systemen in gebruik bleven, zowel als het rekenen op het telbord (abacus). Bij die verspreiding van het decimale positiestelsel kunnen ook maatschappelijke factoren een rol hebben gespeeld, omdat het positiestelsel tegenover het rekensysteem van de Grieken en dat van de Romeinen meer in de Oosterse traditie lag. Op den duur bleek het decimale positiestelsel, ook Indisch-Arabisch stelsel genoemd, van het standpunt van de rekentechniek aanzienlijke voordelen boven alle andere stelsels te

hebben, en dit heeft het doen zegevieren.

De symbolen die men voor het schrijven der tien cijfers gebruikte, lopen nogal uiteen. Men kan evenwel twee hoofdtypen onderscheiden: de symbolen waarmee men in de Oost-Arabische wereld de cijfers aangaf, en de zgn. ġobâr (of ghubär) cijfers, die in de West-Arabische wereld voorkwamen, o.a. in Spanje. Die Oostelijke vormen worden in de Arabische wereld nog steeds gebruikt, doch uit die gobârgetallen schijnt zich het stelsel ontwikkeld te hebben, dat wij gebruiken. Er bestaat ook een (reeds vermelde) theorie van Woepcke, volgens welke de gobâr getallen al in Spanje gebruikt werden voor de Arabieren daar aankwamen. Alexandrijnse Neo-Pythagoreeërs zouden dan reeds ca. 450 na Chr. die getallen naar het Westen hebben gebracht.1

De voornaamste overbrengers van de tien decimale getallen met hun rekenwijze zullen echter wel kooplieden en andere praktisch ingestelde mensen zijn geweest.2

Het woord ġobâr betekent stof, omdat het telbord (abacus) vaak bestond uit een bord met zand bestrooid, waarin de tekens werden aangegeven, dus een stof-bord. Ons woord cijfer komt van het Arabisch sifr, dat ‘leeg, nul’ betekent (vgl. bladz. 91); het woord voor nul werd overgebracht op alle negen andere symbolen.

4.

Mesopotamië, dat onder haar Hellenistische en Romeinse heersers een grensgebied van het Grieks-Romeinse cultuurgebied was geworden, herwon haar centrale positie langs de handelswegen onder de Sassanieden, die als inheemse vorsten over Perzië en aangrenzende gebieden regeerden in de traditie van Cyrus en Xerxes. Over de stand der wetenschap onder de Sassanieden is niet veel bekend, al wijst de legendarische geschiedenis, zoals ze uit de Duizend-en-Een Nacht, de verzen van Firdawsi en Omar Khayyam te voorschijn treedt, op een periode van culturele bloei. Tussen Constantinopel, Alexandrië, India en China gelegen, was het Perzië der Sassanieden een land waar verscheidene beschavingen elkaar

ontmoetten. Babylon was verdwenen om plaats te maken voor Seleukia-Ktesiphon, tot dit na de Arabische verovering van 641 weer plaats moest maken voor Bagdad. Al werd nu Arabisch de officiële taal, veel van het oude Perzië bleef onder de Islam onveranderd bestaan. Zelfs de Islam werd slechts in een gewijzigde vorm aanvaard (het Sjiisme). Christenen, Joden en aanhangers van Zoroaster bleven bijdragen tot het culturele leven onder het kalifaat van Bagdad.

Evenals in Alexandrië en in India nemen we ook onder de Islam een vermenging van allerlei stromingen in de wiskunde waar. De grote tijd der ‘Arabische’ wiskunde1 begint met de kaliefs uit het huis der Abbasieden: Al-Mansor (754-775), Haroen-al-Rasjied (786-809) en Al-Mamoen (813-833), die ook de sterrenkunde en andere wetenschappen aanmoedigden. Al-Mamoen richtte zelfs in Bagdad een ‘Huis der Wijsheid’ op met een bibliotheek en een sterrenwacht. Dit wetenschappelijke werk dat aanving met Al-Fāzarī's reeds vermelde vertaling van de Siddhāntā's, leidde omstreeks 825 tot de activiteiten van Mohammed ibn Moesā Al-Chwārizmī, een wiskundige geboortig uit Khiwa. Van de boeken, die Al-Chwārizmī heeft geschreven, hebben er twee, ook door een Latijnse vertaling, aanzienlijke invloed uitgeoefend. Vooreerst hebben we een elementaire rekenkunde, bewaard gebleven in een Latijnse vertaling van de twaalfde eeuw, die tot de verspreiding van het decimale positiestelsel in de Arabische en later in de Latijnse landen heeft bijgedragen. De Latijnse vertaling met de aanhef ‘Algorismi de numero Indorum’ heeft het woord algoritme, een latinisering van Al-Chwārizmī, blijvend aan onze wiskundige taal toegevoegd.

Iets dergelijks is ook geschied met Mohammeds tweede boek, zijn algebra, waarvan de titel luidde: Hisāb al-jabr wal-moeqābala, hetgeen ‘wetenschap van hergroeperen en tegenover-

stellen’ betekent, wat staat voor de leer der vergelijkingen. Het woord al-jabr heeft, ook door latinisering, tot het woord algebra gevoerd. Inderdaad was algebra tot aan de tweede helft van de negentiende eeuw niets anders dan de leer der vergelijkingen.

Deze Algebra van Al-Chwārizmī bevat een bespreking van eerste- en tweedegraadsvergelijkingen, maar alles in woorden. Zelfs het gesyncopeerde algebraïsche formalisme van Diophantos is afwezig. De vergelijkingen worden in zes categorieën verdeeld, die we in onze notatie als volgt schrijven:

ax2 = bx, ax2 = c, bx = c,

x2 + bx = c, x2 + c = bx, x2 + c = bx, x2 = bx + c,

waarin a, b, c constanten zijn. De manier waarop Al-Chwārizmī ze aangeeft is b.v. ‘kwadraten en getallen zijn gelijk wortels’ voor x2 + c = bx; het woord ‘wortel’, latijn ‘radix’, staat voor de onbekende x. In de gevallen die behandeld worden zijn a, b, c altijd positieve getallen, zodat we als voorbeelden o.a. de vergelijkingen x2 + 10x = 39, x2 + 21 = 10x, x2 = 3x + 4 vinden, die ieder afzonderlijk behandeld worden. Deze drie vergelijkingen komen geregeld in de literatuur voor, zodat L.C. Karpinski eens gesproken heeft over ‘de vergelijking x2 + 10x = 39’, die ‘verscheidene eeuwen lang als een gouden draad door de algebra loopt’.1 De oplossingen van deze vergelijkingen (alleen positieve wortels komen in aanmerking) worden gevonden met behulp van een algebraïsch recept, aangevuld met een meetkundig diagram, direct of indirect aan Euklides ontleend.

Ook Mohammeds astronomische en trigonometrische tafels (met waarden van sinussen en tangenten) zijn later in het Latijn vertaald. Zijn meetkundeboek is een catalogus van meetrecepten, het is van enig belang omdat het de directe invloed toont van een Joodse tekst uit 150 na Chr. Het vertoont overigens geen spoor van sympathie voor de Euklidische traditie. Zijn sterrenkunde was een uittreksel uit de Siddhāntā's en kan daardoor via de tekst in het Sanskriet misschien enige Griekse invloed tonen. Algemeen gesproken zien we bij Al-Khwārizmī de Oosterse invloed veel sterker dan de Griekse2, en best mogelijk is dit opzet geweest.

Het werk van deze wiskundige, ofschoon verre van oorspronkelijk, en nogal elementair, blijft belangrijk omdat het mee heeft geholpen de Indische getallen en de Arabische algebra in Latijns Europa bekend te maken. Dat receptachtige is deze algebra tot in het midden van de negentiende eeuw bijgebleven, ze bleef haar Oosterse oorsprong getrouw door haar gebrek aan axiomatische opbouw, waardoor ze verschilde van de meetkunde zoals Euklides die uiteenzette. Zeer lang kon men dit verschil tussen algebra en meetkunde nog in het schoolonderwijs waarnemen.

5.

Andere Arabisch schrijvende geleerden verdiepten zich in de studie van de wiskunde zoals die door de Grieken was beoefend. Met grote toewijding werden de Griekse klassieken, Apollonios, Archimedes, Euklides, Ptolemaios en anderen in het Arabisch vertaald en becommentarieerd. Het woord Almagest, waarmee we Ptolemaios' sterrenkundig handboek aanduiden, is een mengsel van het Arabische ‘al’ en het Griekse ‘magistë’ (grootst). Dit overschrijven en vertalen heeft menig Grieks werk, dat in het oorspronkelijk is verloren geraakt, voor ons behouden.

Algemeen gesproken was er een voorliefde voor de berekenende en praktische zijde van de Griekse wis- en sterrenkunde, al vinden we ook vele theoretische beschouwingen in de Arabische literatuur. Maar de gonio- en trigonometrie was een gebied waarin de wis- en sterrenkundigen van de Arabische wereld bijzonder waren geïnteresseerd. Zo vinden wij heel wat tabellen van wat we nu goniometrische functies noemen. Met de Indiërs voerden ze de sinus in als de halve koorde van de dubbele hoek. Dit Latijnse woord ‘sinus’, dat ‘bocht’ of ‘boezem’ betekent, is een letterlijke vertaling van het Arabische woord ‘gaib’, dat uit ‘gîb’ ontstond, een woord dat de Arabische manier was om het Indische woord ‘jyā’, koorde, op te schrijven.1

Men vindt heel wat gonio- en trigonometrie in de geschriften van de astronoom Al-Battānī (ca. 858-929), als Albategnius beroemd om zijn planetentheorie. Hij beschouwde niet alleen sinussen, doch beschouwde ook als hoekmaat de schaduw van een gegeven staaf voor invalshoeken van de zon die van graad tot graad opklimmen. Deze ‘umbra extensa’ was dus een cotangens. Rekenregels voor boldriehoeken, die bij Al-Battānī voorkomen, kunnen als de cosinusregel worden geïnterpreteerd.

Het werk van Al-Battānī toont dat de geleerden in de cultuurwereld van de Islam niet alleen kopieerden, doch ook tot nieuwe resultaten kwamen door hun kennis van Griekse, Indische, inheemse en misschien ook Chinese methoden. Dit geldt ook voor Aboe-I-Wafa (940-998), die zijn kennis der trigonometrie gebruikte om (sexagesimale) sinustabellen voor intervallen van 15' samen te stellen, met waarden tot in acht decimalen nauwkeurig.

Hij werkte ook met tangenten en voerde in studies over zonnewijzers de secans en de cosecans in. Hij vergemakkelijkte de studie van boldriehoeken, waarbij hij het equivalent van de sinusregel gebruikte. In zijn Meetkundige Constructies vindt men werkstukken opgelost met behulp van een passer met één vaste opening. Al-Karagi (Al-Karkī), die ca. 1025 is gestorven, heeft een algebra geschreven die bij Diofantos aanknoopt. Men vindt bij hem werk over irrationalen, zoals de formules √8 + √18 = √50, ∛54 - ∛2 = ∛16, verder de sommen Εk2, Εk3 voor k = 1, 2,..., n, en onbepaalde vergelijkingen in de stijl van Diofantos. Hij had een duidelijke voorliefde voor de Grieken, zijn ‘verwaarlozing van de wiskunde der Hindoes moet opzettelijk zijn geweest’.1

6.

Het is hier niet nodig een verslag te geven van alle politieke en etnologische veranderingen die de wereld van de Islam verstoorden. Soms kwamen zij de wetenschap ten goede, dan weer brachten zij achteruitgang, soms gingen centra van studie verloren, dan kwamen weer andere op. Het karakter van de wis- en sterrenkunde bleef in het algemeen onaangetast. Wij kunnen slechts enige hoogtepunten aanstippen.

Omstreeks het jaar 1000 verschenen in Noord-Perzië nieuwe heersers, de Seldsjoekse Turken, wier rijk een tijdlang bloeide rondom het irrigatiecentrum van Merw. Hier leefde Omar Khayyam (ca. 1038/48 tot 1123/24), sinds 1859 in het Westen bekend als de dichter van de Rubaiyat, kwatrijnen zeer vrij vertaald in het Engels door Edward Fitzgerald.2 Omar was een astronoom, wiskundige en (Aristotelisch) wijsgeer.

In een der kwatrijnen (lix) leest men  
  (vrij vertaald)
Ah, but my Computations, Maar mijn Kalenderwerk. Wat is
People say de Reden
Have squared the Year to Van dit gecijfer. Ach, mijn vriend,
human Compass, eh? het Heden
If so, by striking from the Viert in mijn rekening triomfen
Calendar Over afwezend Morgen en het
Unborn tomorrow, dood Verleden
and dead Yesterday.  

Dit schijnt een toespeling te zijn op Omars hervorming van de oude Perzische kalender, die de fout terugbracht op één dag in 5000 jaren (1540 of 3770 jaren volgens andere interpretaties), waar onze Gregoriaanse kalender een fout heeft van één dag in 3330 jaar. Deze hervorming werd in 1079 ingevoerd, doch later weer vervangen door de maankalender. Omar schreef een Algebra, die een systematische studie van derdegraadsvergelijkingen bevat.1 Hierbij gebruikte hij een methode die de Grieken wel eens hebben gebruikt (b.v. bij de constructies voor het vinden van de dubbele evenredigen x, y tussen twee lijnsegmenten a, b, zodat a : x = x : y = y : b), waarbij de oplossing wordt gevonden door de snijpunten van twee kegelsneden te bepalen. Omar was niet in de numerieke berekeningen van oplossingen geïnteresseerd en maakte een onderscheid tussen ‘meetkundige’ en ‘rekenkundige’ oplossingen; de laatste bestonden slechts - net als bij de Grieken - als de wortels positief rationaal waren. Zijn methode was dus in beginsel verschillend van die der latere wiskundigen, die, beginnende met de Bolognezen van de zestiende eeuw, naar een algemene numerieke oplossing streefden. In een ander geschrift over de moeilijkheden bij Euklides verving Omar het parallellenaxioma door een aantal andere veronderstellingen. Hierbij stelde hij de figuur op die we nu verbinden met de zgn. hypothesen van de stompe, de scherpe en de rechte hoek, en waarbij dan de eerste twee (die we tegenwoordig als beginselen van de niet-euklidische meetkunde erkennen) door vernuftige redeneringen ad absurdum werden gevoerd. Omar trachtte ook de euklidische leer der verhoudingen door een getalsmatige theorie te vervangen, waarbij hij tot een benadering van irrationale getallen werd gevoerd en dichtbij het begrip reëel getal kwam.2

Nadat Bagdad in 1256 door de Mongolen was geplunderd, ont-

stond in de omgeving een nieuw centrum van studie in de sterrenwacht van Marāgha, gesticht door de Mongoolse heerser Hoelāgoe voor de astronoom Nasīr-al-dīn at-Toesi (Nasir-eddin, 1201-1274). Hier werd weer getracht alle beschikbare wiskundige wetenschappen, zowel van het Oosten als van de Grieken, bijeen te brengen. Nasir is een der eersten geweest die de gonio- en trigonometrie als zelfstandige tak van wetenschap van de sterrenkunde heeft gescheiden. Zijn pogingen om het parallellenaxioma te bewijzen doen sterk aan die van Omar denken en tonen duidelijk Griekse invloed. De invloed van Nasir (of At-Toesi, zoals hij vaak wordt genoemd) was zeer groot, zowel in de richting van Indië en China als naar het Westen. Zijn werk is aan de Europeanen van de Renaissance-tijd bekend geweest: nog in 1651 en 1663 zien we John Wallis bezig met de studie van het parallellenaxioma volgens Nasir-eddin.

Nasirs onderzoekingen over de leer der verhoudingen en de numerieke benadering van irrationale getallen zijn eveneens in de traditie van Omar Khayyam.

Een andere Perzische wiskundige, Jamsjid Al-Kashi (eerste helft vijftiende eeuw, Samarkand) was bedreven in het maken van grote rekenkundige en algebraïsche berekeningen, zodat we hem kunnen vergelijken met de wiskundigen die we in het Europa van de laatste jaren der zestiende eeuw zullen ontmoeten, zoals Viète of Van Ceulen. Hij loste derdegraadsvergelijkingen op met behulp van iteratieprocessen of van trigonometrische methoden, en benaderde wortels van vergelijkingen van willekeurige graad met de benaderingsmethode die we gewoon zijn te noemen naar de Engelsman W.G. Horner, die ze in 1819 opnieuw heeft ontdekt.1 Bij Al-Kashi vindt men de binomiale formule voor positief gehele exponenten2 en een beheersing niet alleen van berekeningen met sexagesimale, doch ook met decimale breuken (b.v. 25,07 maal 14,3 is 358,501), hetgeen evenals het gebruik van ‘Horners methode’ op Chinese invloed schijnt te wijzen (zie bldz. 101). Om in decimale breuken het gehele deel van het gebroken deel te onderscheiden, gebruikte Al-Kashi verschillende kleuren, en niet zoals wij een

scheidingsteken als komma of punt. Hij kent π in 16 decimalen, en schrijft π ook in sexagesimalen - met een versje om de getallen te onthouden.

Een belangrijke figuur in Egypte was Ibn Al-Haitham (Alhazen, ca. 965-1039). Men beschouwt hem wel als de grootste Islamitische natuurkundige; zijn Optica (of Perspectiva) heeft in een Latijnse vertaling veel invloed in het Westen uitgeoefend, zoals we b.v. bij Kepler zien. Het ‘vraagstuk van Alhazen’ bestaat daarin, door twee punten in het vlak van een cirkel rechte lijnen te trekken die elkaar zó op de cirkelomtrek ontmoeten, dat zij met de cirkel-normaal in het snijpunt gelijke hoeken maken. Het vraagstuk leidt tot een vierdemachtsvergelijking, die door Al-Haitham op Griekse wijze werd opgelost door een cirkel met een hyperbool te snijden.

Alhazen is ook vertrouwd met de exhaustiemethode om de inhoud te vinden van lichamen die ontstaan door de omwenteling van een parabool om een middellijn of een lijn er loodrecht op.

Honderd jaar voor Alhazen vinden we in Egypte Aboe Kāmil, die het algebraïsche werk van Al-Chwārizmī voortzette en uitbreidde. Men kan zijn invloed zowel in Al-Kashi als in Leonardo van Pisa ontdekken.

Andere wetenschappelijke centra bestonden in Spanje, waar de scholen van Cordoba en Toledo eeuwen lang een grote reputatie genoten. Een der beroemdste sterrenkundigen van Cordoba, later van Toledo, was Al-Zarqāli, (Arzaquiel, ca. 1029-ca. 1087), de beste waarnemer van zijn tijd en de samensteller van de zgn. Toledaanse planetentafels. Deze tafels, die ook gedeeltelijk in het Latijn werden vertaald, hebben op de verdere ontwikkeling der astronomie een zekere invloed uitgeoefend, vooral als voorgangers van de zgn. Alfonsinische tafels, naar koning Alfonso x, de Wijze, van Castilië (13e eeuw) genoemd. Ook het trigonometrische gedeelte van deze tafels heeft doorgewerkt tot in de trigonometrie van de Renaissance.

Ofschoon een groot gedeelte van de ‘Arabische’ wiskunde en bijna de gehele Chinese wiskunde het algoritmisch-algebraïsch karakter van de Oostelijke wiskunde behield, betekende ze wel degelijk een fikse stap vooruit vergeleken bij de antieke methoden. West-Europa bereikte eerst tegen het einde van de zestiende eeuw een hoogte die met deze Arabisch-Chinese wiskunde kan worden vergeleken.

7.

Wat deze Chinese wiskunde betreft, het is al wel gebleken dat men haar niet moet beschouwen als een geïsoleerd verschijnsel,

zoals b.v. de wiskunde der Maya's in Centraal Amerika. Reeds ten tijde van de Han-dynastie (ongeveer ten tijde van het Romeinse Rijk), ja, nog wel vroeger, onderhield China commerciële en culturele betrekkingen met andere gebieden van Azië, of zelfs Europa. Indische, Arabische en Chinese wetenschap hebben elkaar wederzijds beïnvloed. We denken b.v. aan de verspreiding van het decimale positiestelsel en de negatieve getallen, die mogelijkerwijze van China naar Indië zijn gekomen. Bij deze beïnvloeding kunnen we ook denken aan de komst van het Boeddhisme in China, die in de eerste eeuw na Chr. plaatsvond.

Van een direct Chinees-Griekse beïnvloeding kunnen wij echter weinig bespeuren, ondanks het bestaan van parallelle ontwikkelingen, b.v. in het berekenen van de waarde van π. De onderzoekingen over de verhouding van omtrek tot middellijn in de cirkel, die typerend zijn voor de eeuwen na de Han-dynastie, zijn waarschijnlijk zonder kennis van Archimedes doorgevoerd. Liu Hui, de schrijver van een overgeleverde commentaar op de Negen Hoofdstukken (263 na Chr.) vond met behulp van in- en omgeschreven regelmatige veelhoeken dat 3,1401 < π < 3,1427, en twee eeuwen later gaven Zu Chong Zhi (Tsoe Chhung-Chih, 430-501) en zijn zoon niet alleen een waarde van π in zeven decimalen, doch ook de waarden π = 22/7 en π = 355/113.1

Onder de T'ang-dynastie (618-907) werd een verzameling van de gewichtigste wiskundige werken samengesteld en gebruikt als officieel tekstboek voor de keizerlijke beambtenexamens. In deze periode begon men boeken te drukken, doch de eerste gedrukte wiskundige werken, die wij kennen, dateren van 1084 of later. In 1115 verscheen een belangrijke gedrukte uitgave van de Negen Hoofdstukken.

Reeds in een boek van Wan Xiaotong (Wang Hsiao Thung, omstreeks 625) vinden we een derdemachtsvergelijking die ingewik-

kelder is dan de vergelijking x3 = a uit de Negen Hoofdstukken. De bloeiperiode van de oud-Chinese wiskunde kwam echter eerst gedurende de Soeng-dynastie (960-1279) en de eerste jaren der Mongolenheerschappij van de Yüan (de ‘Grote Khan’ van Marco Polo's reisbericht). Van de leidende wiskundigen noemen wij Qin Jiushao (Chhin Chioe-Shao), die de toen reeds oude theorie der onbepaalde vergelijkingen verder ontwikkelde (zijn boek is 1247 gedateerd). Een zijner voorbeelden kunnen wij als volgt schrijven:

x ≡ 32(mod 83) ≡ 70(mod 110) ≡ 30(mod 135).

Qin was ook geïnteresseerd in de numerieke oplossing van vergelijkingen van hogere graad, b.v. van

-x4 + 763 200x2 - 40 642 560 000 = 0.

Zulke vergelijkingen loste hij op door een generalisatie van de methode der opvolgende benaderingen, die reeds in de Negen Hoofdstukken gebruikt was om vierkants- en derdemachtswortels uit te rekenen. Deze ‘methode van Horner’, is reeds vermeld bij de bespreking van de wiskunde onder de Islam.

Nog een andere wiskundige van de Soeng-periode is Yang Hui. Hij werkte met decimale breuken en schreef deze in een vorm die wat doet denken aan onze moderne manier van schrijven. In zijn boek, dat van 1261 dateert, vindt men een vraagstuk dat tot de berekening 24,68 × 36,56 = 902,3008 voert. Yang Hui maakt ons ook bekend met de oudste ons overgeleverde afbeelding van de driehoek van Pascal, die we terugvinden in een boek van Zhu Shijie (Choe Chioe-Shao) van 1303 en die op de kennis van binomiale formules voor gehele exponenten wijst. Zhu wordt wel voor de meest vooraanstaande wiskundige van deze periode gehouden; in zijn boeken vindt men de meest uitgewerkte Chinese arithmetisch-algoritmische rekenmethoden.1 Hij generaliseert de ‘matrix’-oplossingen van een systeem van lineaire vergelijkingen op stelsels van vergelijkingen van hogere graad met verscheidene onbekenden en komt zo tot eliminatiemethoden die enigszins aan die van Sylvester herinneren. Voor zulke berekeningen moeten wel verscheidene telborden gebruikt zijn.

In de tijd na de Soeng-dynastie bleef er wel wiskundig werk te doen, maar veel nieuws is er niet meer uitgevonden. Westerse wiskunde en astronomie kwamen tot China gedurende de Ming perio-

de met de Jezuïeten, geleid door Pater Matteo Ricci, die in 1583 kwam en tot zijn dood in 1610 te Peking woonde.1

Algemeen gesproken kan men zeggen dat de Chinese wiskundigen in hun vaardigheid gecompliceerde rekenkundige en algebraische vergelijkingen op te lossen niet alleen de evenknie waren van de Indische geleerden en die van het Arabische taalgebied, doch deze vaak voorbijstreefden. Zo vinden we Horner's methode en de tiendelige breuken weer, als gezegd, terug in het werk van Al-Kashi uit Samarkand (ca. 1420).2

Vanaf de twaalfde eeuw beginnen wij berichten te krijgen over de wiskunde in Japan. Hier ziet men duidelijk de Chinese invloed. Nieuwe vormen van wiskunde worden in de zeventiende eeuw en later ontwikkeld, gedeeltelijk onder Europese invloed, waarbij ook Nederlanders een rol spelen. De wiskundige Seki Kǒwa3 kwam ca. 1683 bij zijn werk over vergelijkingen tot een rekenwijze die met de determinantenmethode equivalent is, en die wij met de aloude ‘matrix’ methode in verband kunnen brengen. Dit was tien jaren voor Leibniz tot soortgelijke beschouwingen kwam.

Literatuur

Behalve de werken genoemd aan het einde van Hoofdstuk 1, noemen we nog over Chinese en Indische wiskunde:

B. Datta, The Science of the Sulba, a Study in Early Hindu Geometry, (Calcutta 1932).
D.E. Smith-L.C. Karpinski, The Hindu-Arabic Numerals (Boston, 1911).
D.E. Smith, Unsettled Questions concerning the Mathematics of China, Scientific Monthly 33 (1931) 244-250.
H.T. Colebrooke, Algebra, with Arithmetic and Mensurations from the Sanskrit of Brahmagupta and Bhascara (London, 1817, herzien door H.C. Banerji, 2e uitg. Calcutta, 1927).
W.E. Clark, The Aryabhatya of Aryabhata (Chicago, 1930).
D.J. Struik, On ancient Chinese mathematics, The Mathematics Teacher 56 (1963) 424-432, herdruk in Euclides 1964, 65-79.
U. Libbrecht, Chinese Mathematics in the thirteenth Century.
The Shu-Shu Chiu-Chang of Ch'in Chiu-Shao (Cambridge, Mass., 1973).
L.Y.A. Lam, A critical Study of the Yang Hui Suan Fa: A thirteenth Century Chinese mathematical Treatise (Singapore, 1977). Vgl. J. Needham, HM 6 (1979) 466-468.
F.J. Swetz, A brief chronological and bibliographical Guide to the History of Chinese Mathematics HM 11 (1984) 39-56. Zie hierbij A.P. Joesjkewitsj, ib. 13 (1986) 36-38.

Over de wiskunde in het Arabisch:

H. Suter, Die Mathematiker und Astronomen der Araber und ihre Werke (Leipzig, 1900, Nachträge, 1902).
zie ook H.P.J. Renaud, Isis 18 (1932) 166-183.
D.S. Kasir, The Algebra of Omar Khayyam (New York, 1931).
Er bestaat nog een andere Engelse vertaling. (Journ. Roy. Asiatic Soc. of Bengali 16 (1950) 27-77) en een Franse vertaling van F. Woepcke (1951).
F. Rosen, The Algebra of Mohammed ben Musa (London, 1931) zie S. Gandz, Quellen und Studien z. Gesch. d. Mathem. 2 A (1932) 61-85.
L.C. Karpinski, Robert of Chester's Latin Translation of the Algebra of Al-Khwārizmī (New York, 1915).
A.P. Joesjkewitsj, Geschiedenis van de Wiskunde in de Middeleeuwen, Moskou, 1963, in het Russisch.
A.P. Joesjkewitsj-B.A. Rosenfeld, Kommentaar op de wiskundige verhandelingen van D.G. Al-Kashi (Istor, Matem. Issled, 7 (1954) 380-449, in het Russisch).
Deze auteurs hebben ook de twee verhandelingen van Al-Kashi met fotografische reproduktie van de tekst en Russische vertaling uitgegeven (Moskou, 1956). In het Duits is van hen vertaald:
A.P. Joesjkewitsj-B.A. Rosenfeld, Die Mathematik der Länder des Ostens im Mittelalter. Sowjetische Beiträge zur Geschichte der Naturwissenschaft (Berlin, 1960) 62-160 (ook afzonderlijk als boek uitgegeven).
P. Luckey, Die Ausziehung der n-ten Wurzel und der binomische Lehrsatz in der islamischen Mathematik. Mathem. Annalen 120 (1947-49) 217-274. Zie ook Abh. Deutsche Akad. Wiss. Berlin, Klasse für Mathem. 1950, Nr. 6 (1953) 95 blz.
D.J. Struik, De tiendelige Breuken bij Al-Kashi. Simon Stevin 33 (1959) 65-71.
J. Macdonald S.J., Jesuit Geometers (Vaticaanstad, 1989).
L.Y. Lam-K.S. Shen, Methods of solving linear equations in traditional China, H.M. 16 (1989) 107-122; met bibliografie van andere artikelen van mevr. Lam.

Vorige Volgende