Geschiedenis van de wiskunde

[p. 47]

III. Griekenland

Gedurende de laatste eeuwen van het tweede millennium v.C. hadden grote economische en politieke verschuivingen plaats in het gebied rondom de Middellandse Zee. In een woelige en ongetwijfeld vaak gewelddadige atmosfeer werd het Bronzen Tijdvak naar het verleden geschoven en vervangen door het IJzeren, het tijdvak waarin we nog heden verondersteld worden te leven. Over deze periode zijn maar weinig bijzonderheden bekend, maar het is de tijd van saga's, de tijd der Homerische liederen, de tijd van Mozes. Tegen het einde van deze periode van volksverhuizingen en oorlogen, misschien omstreeks 900 v.C., blijken de rijken der Minoërs (Kreta), der Myceners en der Hittieten (N. Klein Azië) verdwenen en de macht van Egypte en Babylonië sterk verminderd te zijn. Nieuwe volkeren verschijnen nu op het wereldtoneel op de plaats waar wij ze historisch kennen, volkeren als de Israëlieten, de Foeniciërs, de Assyriërs en de Hellenen of Grieken. Deze vervanging van brons door ijzer voor werktuigen voor dagelijks gebruik veranderde niet alleen de kunst van het oorlog voeren, doch ook het hele economische en politieke leven. Het gebruik van werktuigen werd goedkoper, gemakkelijker en meer doeltreffend, zodat het sociale surplus groter werd, wat weer handel en nijverheid bevorderde en de belangstelling van bredere kringen dan een eng verbonden bureaucratie in politieke, economische en ook technisch-wetenschappelijke vragen vergrootte. Twee grote uitvindingen illustreren deze veranderingen: die van het alfabet en die van het geld. Het alfabet verving de onhandige schrijfwijze die in de oudere periode gebruikelijk was, wat het lezen en schrijven vergemakkelijkte, ook voor niet-geleerden. De invoering van het gemunte geld bracht grote veranderingen in het oude ruilverkeer, wat de handel en ook de belangstelling in het rekenen en in de aardrijkskunde bevorderde. De tijd was aangebroken waarin de beschaving niet zonder meer het uitsluitend bezit van een beambtendom kon blijven.

Aanvankelijk brachten de aanvallen van de ‘zeerovers’, zoals sommige dezer trekkende volkeren in de Egyptische teksten worden genoemd, meer culturele verliezen dan winsten. De Minoïsche beschaving op Kreta verdween, de kunst van Egypte ging achter-

[p. 48]

uit, Babylonische en Egyptische wetenschap stagneerden eeuwen lang. Wij kennen geen wiskundige teksten uit deze overgangsperiode. Toen na eeuwen het leven der volkeren wat stabieler werd, herstelden sommige rijken van het Oude Oosten zich weer, min of meer in traditionele banen. Maar nu was het toneel geopend voor een geheel nieuwe vorm van beschaving, die van de Grieken.

De steden die langs de kust van Klein Azië, van Zuid-Italië en in het eigenlijke Griekenland ontstonden, waren in hoofdzaak niet langer administratieve centra van een irrigatie-economie. Zij waren in de eerste plaats handelscentra, waarin de feodale heren van de oude stempel hadden te strijden met een onafhankelijke, politiek zelfbewuste klasse van kooplieden; een strijd die ze op den duur moesten verliezen. Deze koopliedenklasse werd gedurende de zevende en zesde eeuw v. C. steeds machtiger, maar had nu zelf te kampen met de kleinere handelaren en ambachtslieden, de demos. Zo ontstond de Griekse polis, de zichzelf besturende stadstaat, een nieuw maatschappelijk experiment, verschillend niet alleen van steden zoals Thebe of Babylon, doch ook van vroegere stadstaten als we in Soemerië en andere Aziatische landen hebben aangetroffen. Tot de meest belangrijke Griekse stadstaten behoorden Milete en andere steden in Ionië aan de Klein-Aziatische kust van de Middellandse Zee, wier handel zich uitstrekte tot de kusten van de gehele Middellandse en Zwarte Zee, tot Mesopotamië, Egypte, Scythië (het tegenwoordige Z. Rusland) en nog verder verwijderde landen. Er waren ook steden aan andere kusten die in aanzien en rijkdom de Ionische evenaarden, b.v. Corinthe en later Athene in het eigenlijke Griekenland, Croton en Taras (Tarente) in Zuid-Italië, Syracuse op Sicilië.

Deze nieuwe maatschappelijke orde bracht een nieuw soort mensen voort. De koopman-vaarder en reiziger had zelden zo veel onafhankelijkheid gekend, maar hij wist ook dat deze onafhankelijkheid alleen door constante en harde strijd verkregen en behouden kon worden. In zijn gedachtenwereld was weinig ruimte voor het statische, het behoudende, dat zoveel in het Oosten kenmerkt. Hij leefde in een tijdperk van aardrijkskundige ontdekkingen dat enigszins doet denken aan dat van het zestiende-eeuwse Europa; hij erkende noch absolute monarchie noch enige andere macht geworteld in een statische Godheid. Bovendien kon hij zich tijd gunnen voor verpozing en tot nadenken: het gevolg van rijkdom en althans gedeeltelijk, van slavernij. Hij kon over die nieuwe wereld filosoferen, wat, in de afwezigheid van een diep gewortelde godsdienst, vaak de bewoners van deze kuststeden tot de een of andere

[p. 49]

vorm van mysticisme leidde, doch anderzijds ook juist tot de tegenpool van zulk mysticisme: een groeiend rationalisme en een wetenschappelijke wereldbeschouwing.

2.

In deze geestelijke atmosfeer van het Ionische rationalisme werd een nieuw soort wiskunde geboren, een wiskunde die niet alleen de Oosterse vraag ‘hoe?’, doch ook de hogere wetenschappelijke vraag ‘waarom?’ stelde. We zouden dit het ontstaan van de moderne wiskunde kunnen noemen. De vader van deze nieuwe, deze Griekse, wiskunde is volgens de overlevering Thales van Milete, een koopman uit de eerste helft van de zesde eeuw, die geld en wijsheid had verkregen in verre landen zoals Babylon en Egypte. Zelfs zo men zijn figuur meer legendarisch dan historisch ziet, behoudt ze betekenis omdat ze iets zeer reëels belichaamt. Thales symboliseert de omstandigheden waaronder niet alleen de moderne wiskunde, doch ook onze gehele moderne wetenschap en wijsbegeerte in het leven kwamen.

De vroege Griekse studie der wiskunde had als voornaamste doel de plaats van de mens in het heelal op redelijke wijze te begrijpen. De wiskunde leende daarbij haar hand door orde in de chaos te scheppen, gedachten in logische ketenen te leggen, en dus het vinden van grondbeginselen te vergemakkelijken. Wiskunde is van alle wetenschappen het meest op het redenerende verstand ingesteld, en ofschoon er weinig twijfel bestaat dat de Griekse kooplieden op hun handelswegen ook de Oosterse wiskunde leerden kennen, we kunnen ook begrijpen dat zij ontdekten dat de rationalisatie van de wiskunde nog grotendeels ongedaan was gebleven. Waarom had de gelijkbenige driehoek twee gelijke hoeken? Waarom was het oppervlak van een driehoek gelijk aan dat van de halve rechthoek met gelijke basis en hoogte? Zulke vragen kwamen op natuurlijke wijze op bij mannen en vrouwen die gelijksoortige kwesties stelden in de kosmologie, biologie, natuurkunde en staatsbestuur.

Er bestaan geen bronnen waaruit we de vroege ontwikkeling der Griekse wiskunde uit de eerste hand kunnen bestuderen en na kunnen gaan hoe beslissend het contact met de oude beschavingen van Egypte en Babylonië is geweest. De bestaande wiskundige codices dateren uit Christelijke en Arábische tijden, en we hebben ook enige Egyptische papyri met fragmenten die wat ouder zijn. Uit dit materiaal hebben geleerden, thuis in klassieke talen en in de wiskunde, uitstekende teksten kunnen construeren. De vroegste van deze teksten, voor zover ze geen verspreide aanhalingen, doch

[p. 50]

volledige geschriften zijn, gaan terug tot de vierde eeuw v. C. en niet verder. Op die manier bezitten we nu betrouwbare uitgaven van Euklides, Archimedes, Apollonios en andere grote wiskundigen van de Oudheid. Maar deze geschriften vertegenwoordigen een reeds geheel volwassen wiskunde, waarvan het moeilijk is de historische wortels uit te graven, zelfs met behulp van wat latere commentatoren aan gegevens hebben nagelaten. Om iets van de formatieve periode van de Griekse wiskunde te leren moeten we ons dus tot fragmenten beperken, overgeleverd door latere schrijvers of op verspreide opmerkingen bij wijsgeren en andere niet strikt wiskundige schrijvers. Toch hebben scherpzinnige tekstcritici uit dit materiaal vele duistere punten kunnen ophelderen en ons zo een beeld kunnen geven van de vroegste ontwikkeling van de Griekse wiskunde. We denken hier aan het werk van Paul Tannery, T.L. Heath, H.G. Zeuthen, E. Frank en anderen, die het ons mogelijk hebben gemaakt een samenhangend, zij het vaak hypothetisch beeld van deze periode te schetsen.

3.

Op de ruïnes van het Assyrische Rijk ontstond in de zesde eeuw v. C. een nieuwe macht: het Perzische Rijk der Achaemenieden. Het veroverde de Anatolische steden, doch de maatschappelijke structuur van het eigenlijke Griekenland was alreeds te hecht om ontworteld te worden. De Perzische aanval werd afgeslagen in de beroemde slagen van Marathon, Salamis en Plataeae (490-479). Een belangrijk resultaat van deze overwinningen was de uitbreiding en de hegemonie van de macht van Athene. Onder Perikles, in de tweede helft van de vijfde eeuw, kregen de democratische elementen steeds meer invloed. Zij waren het die achter de militaire en economische expansie stonden, die het Athene van ca. 430 v. C. niet alleen tot de leidende macht van een Grieks Rijk, doch ook tot het middelpunt van een nieuwe en ondanks het bestaan van slavernij toch bewonderenswaardige beschaving maakte.

Hier, temidden van het gewoel der maatschappelijke en politieke twisten, bewogen zich leraars en wijsgeren die hun theorieën verkondigden, en met die theorieën ook de nieuwe wiskunde. Voor het eerst in de geschiedenis hield zich een groep kritisch ingestelde mannen en vrouwen, minder dan ooit voorheen door traditie belemmerd, met wiskundige vraagstukken bezig ter wille van het zuivere begrip, en niet uit directe of indirecte nuttigheidsoverwegingen. Men noemt die kritisch ingestelde leraars vaak ‘sofisten’, een woord dat van ‘sofia’, wijsheid, afkomstig is en dus oorspronkelijk niet ‘drogredenaars’ betekent, al schenen zij die naam

[p. 51]

wel eens door hun paradoxen te verdienen. Van die discussies der sofisten, die tot aan de wortel van het exacte denken reikten, is maar weinig bewaard, al kunnen wij er in de dialogen van Plato wel een indruk van krijgen. Wat de wiskunde betreft bezitten wij slechts één samenhangend fragment uit deze tijd, en dit is geschreven door de Ionische filosoof Hippokrates van Chios (ca. 440). Dit fragment toont al reeds een grote beheersing van de wiskundige redeneerwijze en behandelt, op karakteristieke wijze, een merkwaardig ‘onpraktisch’, doch theoretisch belangrijk onderwerp, de zgn. ‘lunulae’ of maantjes begrensd door twee of drie cirkelbogen.

Dit onderwerp - zekere oppervlakken begrensd door cirkelbogen te vinden die rationaal kunnen worden uitgedrukt in hun middellijnen - hangt direct samen met het vraagstuk van de cirkelkwadratuur, een kernkwestie in de Griekse wiskunde. In de bespreking van zijn maantjes¹ toont Hippokrates dat de wiskundigen van Griekenlands Gouden Eeuw reeds een stelselmatig geordende vlakke meetkunde hadden, waarin het beginsel, door logische gevolgtrekkingen van de ene stelling tot de andere (‘apagoge’) te komen, volledig was geaccepteerd. Men had al een soort axiomatiek, zoals men kan opmaken uit de naam van een boek dat op naam van Hippokrates staat, en dat Elementen (‘Stoicheia’) heet, en dus de naam heeft van alle Griekse axiomatische verhandelingen, ook die van Euklides. Hippokrates onderzocht de oppervlakken van vlakke figuren begrensd door lijnsegmenten of cirkelbogen. Hij leert dat de oppervlakken van gelijkvormige cirkelsegmenten zich verhouden als de kwadraten op hun koorden beschreven. Hij kent het theorema van Pythagoras en de corresponderende ongelijkheid voor niet-rechthoekige driehoeken. Het gehele fragment zouden we haast ‘in de Euklidische traditie’ willen noemen, maar het is meer dan een eeuw ouder dan Euklides.

Het vraagstuk van de cirkelkwadratuur is een van de zgn. ‘drie beroemde wiskundige vraagstukken van de Oudheid’. Deze begonnen in de tijd van Hippokrates een onderwerp van studie te worden. Deze vraagstukken waren:

1 Een moderne onderzoeking van zulke maantjes door E. Landau, Über quadrierbare Kreisbogenzweiecke, Berichte Berliner Mathem. Gesellsch. 2 (1903) 1-6. Zie ook T. Dantzig, The Bequest of the Greeks (New York, 1955), Hoofdstuk 10, en DSB VI (1972) 411-416, zowel als C.J. Scriba, Welche Kreismonde sind elementar quadrierbar?, Mitt. Mathem. Ges. Hamburg 11 (1988) 517-539.

[p. 52]

1.	De driedeling van de hoek, dwz. de vraag een gegeven hoek in drie gelijke delen te verdelen.
2.	De verdubbeling van de kubus, dwz. een kubus te construeren, waarvan de inhoud het dubbele is van de inhoud van een gegeven kubus.
3.	De kwadratuur van de cirkel, dwz. een vierkant te construeren, waarvan het oppervlak gelijk is aan dat van een gegeven cirkel.

Het belang van deze vraagstukken ligt daarin, dat ze niet meetkundig kunnen worden opgelost door een eindig aantal rechte lijnen en cirkels te construeren, behalve dan bij benadering, en daardoor dienden zij als een middel om nieuwe wiskundige gebieden aan te boren.

De twee eerste problemen werden vaak teruggevoerd tot het vraagstuk twee lijnsegmenten x en y te construeren zo dat, voor gegeven lijnsegmenten a en b, de verhouding bestaat a : x = x : y = y : b (het vraagstuk een lijnsegment x te vinden zo dat a : x = x : b kan met passer en lineaal worden opgelost). Dit leidde weer tot de studie van kegelsneden, van sommige krommen van de derde en hogere graad (b.v. de cissoïde en de conchoïde) of van een transcendente kromme, de kwadratrix. De anekdotische vorm waarin die vraagstukken soms zijn overgeleverd (Delphische orakels, enz.) moet ons hun fundamentele betekenis niet doen vergeten. Het gebeurt wel meer dat zulk een gewichtig probleem met een anekdote of een puzzel is verbonden - wij denken b.v. aan Cardano's gebroken belofte, aan Keplers wijnvaten, aan Newtons appel. Wiskundigen van verschillende perioden, ook hedendaagse wiskundigen, hebben op het verband gewezen dat er bestaat tussen deze Griekse vraagstukken en de moderne leer der vergelijkingen, der algebraische getallen en de groepentheorie.¹

1 Zie b.v. F. Klein, Vorträge über ausgewählte Fragen der Elementargeometrie (Leipzig, 1895); F. Enriques, Fragen der Elementarmathematik II (Leipzig, 1907, Italiaanse tekst, Bologne 1906).

4.

Waarschijnlijk buiten de groep der sofisten, die tot op zekere hoogte met de democratische beweging waren verbonden, stond een andere groep van wiskundig geïnteresseerde wijsgeren, die meer tot de aristocratische richting werden aangetrokken. Zij zijn bekend als Pythagoreeërs, zo genaamd naar de min of meer legendarische stichter van de school, Pythagoras, waarvan verhaald wordt dat hij een mysticus, een man van wetenschap en een aristocratische staatsman was. In tegenstelling tot de sofisten, die de

[p. 53]

werkelijkheid van de verandering leerden - dit was althans het geval met de atomisten, volgelingen van Leukippos en Demokritos - vindt men bij de Pythagoreeërs de nadruk op het onveranderlijke in natuur en gemeenschap. In hun streven de eeuwige wetten van het heelal te onderkennen kwamen zij met religieuze eerbied tot de getallenleer, niet als de Babyloniërs en Egyptenaren, omdat ze behoefte hadden praktisch te rekenen, maar omdat zij in het getal het wezen van het heelal zagen. Dus ontwikkelden zij de theoretische getallenleer, zowel als de (theoretische) meetkunde, de astronomie en de muziekleer, die tezamen het latere ‘quadrivium’ zouden uitmaken. Hun meest bekende leider was Archytas van Taras (Tarente), die omstreeks 400 leefde en in wiens school, zo we de hypothese van E. Frank volgen, het voornaamste van de als ‘Pythagoreïsch’ bekende wiskunde moet zijn ontwikkeld. De getallenleer was niet alleen theoretisch, maar zelfs speculatief, en had weinig gemeen met de Babylonische rekentechniek van diezelfde tijd. Getallen werden in klassen verdeeld, even, oneven, even maal even, oneven maal oneven, ondeelbaar, samengesteld, volkomen; ook waren er vriendschaps-, driehoeks-, vierkants-, vijfhoeksgetallen, enz. In de driehoeksgetallen komt de verbinding tussen meetkunde en rekenkunde, zoals de Pythagoreeërs die zagen, duidelijk aan het licht:



enz. Evenzo hadden de Pythagoreeërs vierkantsgetallen



enz.

die wij nog zo noemen (Grieks: tetragona, Lat.: quadrati), en ook vijfhoeks-, en viervlaksgetallen. De figuren zelf zijn vaak veel ouder, en sommige ervan kunnen wij op aardewerk uit de Nieuwe Steentijd zien. De Pythagoreeërs bestudeerden de eigenschappen van zulke polygonale en piramidale getallen, voegden er

[p. 54]

hun soort getallenmystiek aan toe, en gaven hun een wezenlijke rol in hun kosmische filosofie, waarin zij trachtten alle betrekkingen tot getallenbetrekkingen te herleiden (‘alles is getal’). Een punt was ‘eenheid in positie’. Nadruk werd gelegd op de verhouding van getallen (‘logos’, Lat. ‘ratio’). Zo kenden zij een rekenkundige (2b = a + c), een meetkundige (b² = ac) en een harmonische (2/b; = 1/a; + 1/c;) verhouding, die ze ook wijsgerig en maatschappelijk interpreteerden.

De Pythagoreeërs kenden sommige eigenschappen van regelmatige veelhoeken en veelvlakken. Zij toonden aan hoe het vlak kan worden gevuld met mozaïeken van regelmatige driehoeken of zeshoeken, en de ruimte met kubussen, waaraan Aristoteles later ten onrechte de regelmatige viervlakken toevoegde.¹ De Pythagoreeërs hebben waarschijnlijk ook de andere regelmatige veelvlakken gekend. De kennis van het twaalfvlak kunnen zij verkregen hebben doordat pyriet in regelmatige twaalfvlakken kristalliseert. Pyriet wordt in Italië aangetroffen, en was een voorwerp van belangstelling in een periode waarin het ijzer regelmatig verwerkt begon te worden. We vinden reeds bij de Etrusken modellen van regelmatige dodekahedra als sieraden of misschien als magische symbolen.²

Wat het theorema van Pythagoras betreft, de ontdekking hiervan werd door de Pythagoreeërs aan hun Meester zelve toegeschreven, die volgens een (laat) verhaal in dankbaarheid aan de goden een honderdtal ossen (een ‘hekatombe’) zou hebben geofferd - een eigenaardige handeling voor een man die zijn school in strikt vegetarisme moet hebben opgevoed. Wij hebben gezien dat het theorema al reeds in Hammurabi's Babylon bekend was als een getallenbetrekking, doch Pythagoras of een zijner leerlingen kan best het eerste bewijs uit axioma's hebben gegeven. Voor hen was het theorema een meetkundige betrekking tussen oppervlakken.

Een der meest belangrijke ontdekkingen, die aan de Pythagoreeërs wordt toegeschreven, is die van de onderling onmeetbare Iijnsegmenten. Deze ontdekking van het irrationale is wellicht het

1 D.J. Struik, Het Probleem ‘de impletione loci’. Nieuw Archief v. Wiskunde 15 (1925), 121-137.
Zie hiertoe: M. Senechal, Which Tetrahedra fill Space?, Mathematics Magazine 54 (1981) 227-243.

2 F. Lindemann, Sitzungsber. Bayer, Akad. Wiss. München 26 (1897) 625-768; ook 1934, 265-275.

[p. 55]

resultaat geweest van hun studie van de meetkundige verhouding a : b = b : c, die ook als een symbool van de aristocratie diende. Wat nu was de meetkundig evenredige tussen 1 en 2, twee gewijde symbolen? Deze vraag kwam ook op bij de vraag naar de verhouding van diagonaal en zijde van het vierkant. De Pythagoreeërs ontdekten dat deze verhouding niet kon worden uitgedrukt in wat zij ‘getallen’ (arithmoi) noemden, dat is, in wat wij met de naam rationale (dus gehele of gebroken) getallen aanduiden. In andere woorden, wat wij als √2 schrijven, kan niet als breuk worden uitgedrukt.

Dit kan men met Aristoteles als volgt inzien. Veronderstel dat deze verhouding p : q was, waarbij we de getallen p en q als onderling ondeelbaar kunnen aannemen. Dan moet p² = 2q² zijn, dus p² en daarom ook p moet even zijn, b.v. p = 2r. Dan moet q oneven zijn. Maar q² = 2r², waaruit volgen zou dat q even is. Deze tegenspraak werd niet, zoals in het Oosten of in het Europa van de renaissance, opgelost door het getalbegrip te generaliseren, doch door de getallentheorie voor zulke gevallen opzij te schuiven en een nieuwe synthese in de meetkunde te zoeken. Deze ontdekking, die de eenvoudige harmonie tussen de meetkunde en de getallenleer verstoorde, werd vermoedelijk gedurende de laatste tientallen jaren van de vijfde eeuw v. C. gemaakt. Uit die tijd dateert nog een andere moeilijkheid, voortgekomen uit de debatten over de werkelijkheid van de verandering, debatten die toen zowel als later de wijsgeren hebben beziggehouden. De moeilijkheid in kwestie wordt toegeschreven aan Zeno van Elea (ca. 450 v. C.), een leerling van Parmenides, een conservatief filosoof die leerde dat de rede alleen het absolute wezen erkent en dat verandering slechts schijnbaar is. Deze wijsgerige wijze van argumenteren kreeg een wiskundige betekenis toen het bleek dat men oneindige processen moest beschouwen, zoals b.v. bij de bepaling van de inhoud van een viervlak. Zeno's paradoxen kwamen hier in conflict met sommige oude en intuïtieve begrippen omtrent het oneindig kleine en het oneindig grote, en openden de discussie over het probleem der continuïteit. Men had steeds zonder veel bedenken aangenomen dat de som van een oneindig aantal grootheden zo groot kan worden gemaakt als men wil, zelfs als iedere grootheid zeer klein is (∞ × ε = ∞) en ook dat de som van een oneindig aantal grootheden van dimensie nul ook nul is (n × 0 = 0, ∞ × 0 = 0). Hier nu zette Zeno's kritiek in. Met zijn vier paradoxen ondermijnde hij het geloof in die opvattingen en van de steen die hij in de filosofische poel wierp kan men de rimpels nog heden ten dage waarne-

[p. 56]

men. Men kan Zeno's argumenten bij Aristoteles vinden; ze zijn bekend als de Achilles, de Pijl, de Dichotomie en het Stadium. Ze waren zo gekozen dat de tegenstrijdigheden in de begrippen van beweging en tijd scherp worden uitgebracht, en geen poging werd gedaan (zover we weten) om die tegenstrijdigheden te verzoenen.

Wij geven hier de Achilles en de Dichotomie, waaruit we kunnen zien wat de geest is die uit de ‘paradoxen’ spreekt. Wij geven ze weer in onze eigen woorden.

Achilles. Achilles en een schildpad bewegen zich op een rechte weg in dezelfde richting. Achilles is achter de schildpad en wil hem inhalen. Hij loopt veel sneller dan de schildpad, doch om het dier te bereiken moet hij eerst het punt P passeren vanwaar de schildpad begon. Als Achilles in P is aangekomen, is de schildpad in het punt P₁ gekomen. Achilles kan de schildpad niet bereiken voordat hij P₁ passeert, maar dan is de schildpad alweer iets vooruit in P₂ gekomen. Als Achilles in P₂ is, is de schildpad in P₃, enz. Daarom kan Achilles de schildpad nooit bereiken.

Dichotomie. Ik wil van A naar B langs een rechte lijn gaan. Om B te bereiken moet ik eerst B₁ halfweg tussen en A en B bereiken, doch om B₁ te bereiken moet ik eerst in B₂ komen halfweg tussen A en B₁. Dit kan men oneindig vaak voortzetten, zodat we zien dat de beweging zelfs niet kan beginnen.

Uit Zeno's argumenten bleek dat een eindig segment kan worden opgedeeld in een oneindig aantal segmenten, ieder van eindige lengte. Ook bleek daaruit dat er een moeilijkheid was in de uitspraak dat een lijn uit punten is ‘samengesteld’, want uit de samenvoeging van punten kan nooit meer dan een punt, en nooit een stuk lijn, worden gevormd. Het is wel mogelijk dat Zeno zelf niet besefte hoezeer zijn redenering de gedachten der wiskundigen na hem zou verontrusten. En niet alleen de wiskundigen: vraagstukken die verband houden met Zeno's paradoxen zijn ook geregeld in wijsgerige en theologische discussies opgekomen. In zulke discussies spreekt men wel van de tegenstelling tussen het potentieel en het actueel oneindige, dwz. tussen het oneindige beschouwd als een proces, en het oneindige beschouwd als iets voltooids (iets ‘wordt’ oneindig, en iets ‘is’ oneindig). Paul Tannery, de Franse historicus van de wiskunde, geloofde dat het Zeno er vooral om te doen was het Pythagoreïsche begrip van de ruimte als de som van haar punten aan te tasten (‘het punt is eenheid in positie’, volgens de Pythagoreeërs).¹ Wat hiervan ook de

1 P. Tannery, La géométrie grecque (Paris, 1887)217-261. Een andere mening bij B.L. van der Waerden, Mathem. Annalen 117 (1940) 141-161. Zie ook E.J. Dijksterhuis, De Elementen van Euclides (Groningen 1929) I, 41-55, met een uitvoerige bespreking van de Griekse meetkunde vóór Euklides.

[p. 57]

waarheid moge zijn, het is zeker dat Zeno's redenering het mathematisch denken eeuwenlang heeft beïnvloed. Zijn paradoxen kunnen met die van George Berkeley worden vergeleken, toen deze achttiendeeeuwse bisschop aantoonde hoe de vage formulering van de grondbeginselen der differentiaalrekening tot logische absurditeiten leidt, eveneens zonder zelf een betere formulering voor te stellen. Ook in de tegenwoordige discussies omtrent de grondslagen der wiskunde spelen een aantal paradoxen over oneindige verzamelingen een rol (paradox van Russell, van Burali Forti, etc.). En de discussies over de betekenis van de paradoxen van Zeno gaan onverminderd voort.¹

De paradoxen van Zeno kregen een diepere wiskundige betekenis ongeveer terzelfder tijd dat het irrationale werd ontdekt. Was het eigenlijk wel mogelijk de wiskunde als een exacte wetenschap te behandelen? Tannery² heeft als zijn mening geuit dat we hier van een ‘waarlijk logisch schandaal’, van een crisis, in de Griekse wiskunde mogen spreken.³ Zo dit het geval geweest is, is deze crisis opgetreden in de latere jaren van de Peloponnesische oorlog, die eindigde met de val van Athene (404). Het is dan mogelijk een verband te ontdekken tussen de crisis in de wiskunde en de maatschappelijke crisis, aangezien de val van Athene de nederlaag betekende van de slavenhoudende democratie en een nieuw tijdperk inluidde waarin de aristocratie weer de overhand had. De crisis in de wiskunde werd opgelost in de geest van het nieuwe tijdperk.

1 Uitvoerige bespreking met literatuurlijst vindt men in het artikel van K. von Fritz in DSB XIV (1976) 607-612.

2 P. Tannery, ibid. p. 98. Op deze plaats houdt zich Tannery alleen bezig met het bankroet van de oude verhoudingsleer, een gevolg van de ontdekking van onderling onmeetbare lijnsegmenten.

3 Zie hierover H. Freudenthal, Y avait-il une crise des Fondaments des Mathématiques dans l'Antiquité? Bulletin Soc. Mathem. Belgique 18 (1966) 43-55.

5.

Deze nieuwe periode in de Griekse geschiedenis zag de rijkdom der meer gegoeden vermeerderen en de lagere klassen meer en meer in armoede vervallen. De slavernij nam grotere afmetingen aan, wat aan menige vermogende familie de gelegenheid gaf meer aandacht te wijden aan kunsten, wetenschappen, wijsbegeerte of een persoonlijke ethiek, en daarbij tevens neer te zien op alle werk dat handwerkers of slaven konden verrichten. Wij zien deze geesteshouding bij Plato en bij Aristoteles, en het is in Plato's Repu-

[p. 58]

bliek (misschien omstreeks 360 v. C. geschreven), dat wij de helderste uitdrukking vinden van de idealen van de slavenhoudende aristocratie. De ‘wachters’ van Plato's republiek moeten het quadrivium bestuderen, dus de arithmetica, de meetkunde, de astronomie en de muziekleer, teneinde de wetten van het heelal te begrijpen.¹ In zijn Timaeus geeft Plato het voorbeeld van zulk een begrijpen: de dialoog schetst een kosmogonie waarin als bouwstenen van het heelal de elementen vuur, aarde, lucht en water optreden, ieder opgebouwd uit regelmatige veelvlakken, waarbij het twaalfvlak de rol van een soort ether vervult. Zulk een Pythagoreïsche atmosfeer leidde, althans in haar eerste periode, tot de discussie van de meer theoretische kanten van de wiskunde, dus naar onderwerpen die met de grondslagen samenhangen.

Minstens drie belangrijke wiskundigen waren met Plato's Akademie verbonden, Archytas, Theaitetos (die in 369 stierf) en Eudoxos (ca. 408-355). Theaitetos' naam is verbonden met het onderzoek van die irrationaliteiten die we nu met √2, √3, √5,..., √17 aanduiden, een onderzoek dat geheel meetkundig was; misschien is van hem de theorie der irrationale lijnstukken afkomstig die we in het tiende boek van Euklides' Elementen vinden. Eudoxos heeft, naar men met vrij grote stelligheid kan aannemen, de theorie der verhoudingen ontdekt die we in het vijfde boek van deze Elementen vinden, en ook de zgn. ‘exhaustie’-methode, waarmede oppervlak en inhoudsberekeningen streng konden worden behandeld zonder dat de moeilijkheden die lagen in de paradoxen van Zeno optraden.

Dit betekent dat het Eudoxos is geweest die de zgn. crisis in de Griekse wiskunde heeft opgelost en wiens strenge formuleringen de koers van de Griekse axiomatica, en tot op zekere hoogte die van de gehele Griekse wiskunde, hebben bepaald.

Eudoxos' leer der verhoudingen was een breuk met die van de Pythagoreeërs, die alleen voor onderling meetbare grootheden geldig was. Ze was zuiver meetkundig en in haar strikt axiomatische vorm maakte ze elk onderscheid tussen meetbare en onmeetbare grootheden overbodig.

Voor die leer is Definitie 5 van Boek v van Euklides' Elementen karakteristiek:

1 Volgens late bronnen (o.a. Philoponos, 6e eeuw n. C.) was er een opschrift boven de ingang van Plato's school, de Akademia luidend: ‘Laat niemand hier binnentreden die geen meetkunde kent’ (‘ageōmetrêtos’). Zie D.H. Fowler, The Mathematics of Plato's Academy (Oxford, 1987).

[p. 59]

‘Men zegt, dat grootheden in dezelfde verhouding staan, de eerste tot de tweede en de derde tot de vierde, wanneer willekeurige zelfde veelvouden van de eerste en de derde tegelijk groter zijn dan, gelijk aan of kleiner dan willekeurige zelfde veelvouden van de tweede en de vierde, in overeenkomstige volgorde genomen’.

Dit betekent, in onze notatie, dat a : b = c : d, zo tegelijk met ma > nb ook mc < nd, tegelijk met ma = nb ook mc = nd, en tegelijk met ma < nb ook mc < nd, waar m en n gehele getallen zijn. Dat zo iets mogelijk is, moest eerst door het zgn. axioma van Archimedes worden vastgelegd, dat in Euklides als Definitie 4 aan de vorige definitie voorafgaat:

‘Men zegt dat grootheden een verhouding tot elkaar hebben als zij, vermenigvuldigd, elkaar kunnen overtreffen’.

Deze definitie zou dus wel beter als het axioma van Eudoxos aangeduid kunnen worden. De moderne theorie van de irrationale getallen, door Dedekind en Weierstrass ontwikkeld, vertoont grote overeenkomst met die van Eudoxos, ondanks het feit dat de moderne theorie aritmetisch, de klassieke theorie meetkundig is. De aritmetische opzet van de moderne theorie heeft echter wijdere perspectieven geopend.

De ‘exhaustie’-methode (deze naam komt eerst voor in 1647 bij Grégoire de Saint Vincent) was het antwoord van de school van Plato op Zeno. Ze ontdook de struikelblokken van het oneindig kleine door ze te vermijden, door vraagstukken die tot infinitesimalen konden voeren, terug te brengen op vraagstukken die alleen formele logica inhielden. Wanneer, om een voorbeeld te noemen, men had te bewijzen dat de inhoud V van een viervlak gelijk is aan het derde deel van een prisma P met dezelfde hoogte H en hetzelfde grondvlak, dan werd bewezen dat de aannamen V > ⅓P en V < ⅓P allebei tot ongerijmdheden voeren, zodat de enige overblijvende mogelijkheid, V = ⅓P, de waarheid bevat. Om deze ongelijkheden te bewijzen moest weer een axioma worden ingevoerd equivalent aan dat van Archimedes (of Eudoxos). Bij Archimedes luidt het als volgt: ‘dat het verschil, waarmee het grootste van ongelijke oppervlakken het kleinste overtreft, bij zichzelf gevoegd, elk voorgeschreven begrensd oppervlak kan overtreffen’, waarbij dit bij zichzelf toevoegen willekeurig herhaald mag worden. In ons geval van het viervlak werd de hypothese V = A, A > ⅓P dan weerlegd door het viervlak in te sluiten in een omgeschreven trappenpiramide van n prisma's, ieder van hoogte H/n en dan te bewijzen dat n zo groot kan wor-

[p. 60]

den gemaakt dat de inhoud der trappenpiramide & A is. Aangezien de inhoud der trappenpiramide zeker > V is, komen we tot een tegenstrijdigheid. Evenzo bewijst men met een ingeschreven trappenpiramide dat ook V < ⅓P tot een ongerijmdheid voert. Euklides bewijst o.a. op deze manier dat de oppervlakken van twee cirkels zich verhouden als de vierkanten op de diameters.

Deze indirecte behandeling van wat we nu met limietovergangen beredeneren bleef de geaccepteerde vorm van bewijs in de wiskunde der Grieken en later in die van de Renaissance. Zulke bewijzen waren streng, en kunnen zonder veel moeite in een vorm worden gebracht die de moderne analyse accepteert. Maar ze hadden het nadeel dat aan alle indirecte bewijsvoeringen kleeft: men moet eerst het antwoord weten vóór men het bewijs kan geven. Het antwoord zelf moet dus op een andere, meer heuristische en minder exacte methode worden gevonden.

Er bestaan duidelijke aanwijzingen dat zulk een meer tastende methode ook werkelijk werd gebruikt. Wij bezitten een brief, door Archimedes omstreeks 250 v. C. aan zijn vriend Eratosthenes geschreven, en die eerst in 1906 door J.L. Heiberg is teruggevonden in een manuscript dat te Jeruzalem werd bewaard. In deze brief beschrijft Archimedes hoe hij het oppervlak van een segment van de parabool heeft berekend door het oppervlak als som van koorden te beschouwen, dan die koorden op te tellen en deze met behulp van de wetten van de hefboom te wegen. Zulk een methode is niet streng, maar geeft, in de handen van een goede wiskundige, resultaten, die dan later met de ‘exhaustie’-methode streng kunnen bewezen worden. Deze brief is uitgegeven en is bekend onder de naam ‘Methode’ (Ephodos).

Er bestaat een theorie van S. Luria waarin de gedachte wordt uitgesproken dat de gehele gedachtengang van Eudoxos in een soort concurrentieverwantschap stond met die van een andere, de Platonische traditie tegenoverstaande, school, verbonden met de naam Demokritos, met Leukippos de stichter van de atoomtheorie. In deze school, zo zegt deze theorie van Luria, werd voor wiskundige beschouwingen het begrip ‘meetkundig atoom’ ingevoerd. Een lijnsegment, een oppervlak, een inhoud bestond dan uit een groot, doch eindig, aantal ondeelbare (indivisibile) atomen. Wilde men een inhoud berekenen dan moest men de som bepalen van de inhoud van al de atomen waaruit het betreffende lichaam bestaat. Deze theorie doet wel wat vreemd aan, totdat we beseffen dat verscheidene wiskundigen in de jaren vóór Newton, in het bijzonder Kepler, (en ook wel er na) zich eigenlijk van de-

[p. 61]

zelfde gedachtenwijze bedienden als ze, om een voorbeeld te noemen, de omtrek van een cirkel beschouwden als samengesteld uit een oneindig aantal kleine lijnsegmenten. Er bestaan geen documenten die bewijzen dat men in de Oudheid ooit een strenge methode op deze grondslag heeft ontwikkeld, doch ons moderne limietbegrip heeft het mogelijk gemaakt deze ‘atoom’-theorie om te zetten in een theorie die even streng is als die waarop Eudoxos' exhaustiemethode berust. Zelfs heden ten dage gebruiken we geregeld dit begrip van ‘atomen’ als we een vraagstuk uit de theorie der elasticiteit, der natuur- of scheikunde, of zelfs der differentiaalmeetkunde, opstellen, waarna we het strenge bewijs aan de specialist in de analyse overlaten.¹

Het voordeel van de ‘atoom’-methode boven de ‘exhaustie’-methode was dat men er gemakkelijker resultaten mee bereikte. De Oudheid had dus de keuze tussen een strenge maar tamelijk steriele, en een onvoldoend gebaseerde doch veel vruchtbaarder theorie. Het is interessant te zien dat in bijna alle boeken die uit de Oudheid tot ons zijn gekomen de strenge theorie wordt aangewend. Dit heeft wel te maken gehad met het feit dat de wiskunde een lievelingsbezigheid was geworden van mannen en vrouwen die tot een klasse behoorden wier bestaan gedeeltelijk op slavernij berustte, geen belang had in uitvindingen, doch wel in een beschouwende levenswijze. Men moet met zulk een generalisatie evenwel voorzichtig zijn - Archimedes was b.v. wel in uitvindingen geïnteresseerd -, doch zij bevat toch een historische waarheid. Deze kan ook uitgedrukt worden door te zeggen dat het Platonische idealisme op het Demokritische materialisme althans op het gebied der wiskundige filosofie in de Oudheid de overwinning heeft behaald.

1 Zie, om een voorbeeld te noemen, H.B. Phillips, Differential Equations, (New York 1922) bldz. 7 (een boek voor aanstaande ingenieurs): ‘Zo kan men, zolang men zich tot eerste differentialen beperkt, een klein deel van een kromme bij een punt als recht en een klein deel van een oppervlak als vlak beschouwen; voor korte tijdsperioden mag men aannemen dat een deeltje zich met constante snelheid beweegt en een willekeurig fysisch proces in een constant tempo verloopt’.

6.

In het jaar 334 begon Alexander de Grote zijn veldtocht tegen Perzië. Toen hij in 323 in Babylon stierf, behoorde het gehele Nabije Oosten met Egypte en delen van Noord-Indië tot zijn rijk. Zijn generaals verdeelden het veroverde gebied, en tenslotte ontstonden drie grote koninkrijken: Egypte onder Ptolemaios, Meso-

[p. 62]

potamië en Syrië onder de Seleuciden en Macedonië onder Antigonos en zijn opvolgers. Deze vorsten en hun hogere ambtenaren waren Grieken of waren vergriekst. Zelfs in de vallei van de Indus heersten een tijd lang Griekse vorsten. Het tijdperk van het Hellenisme was aangebroken.

Als onmiddellijk gevolg van Alexanders veroveringstochten zien we een grote versnelling in de uitbreiding van de Griekse beschaving over grote gebieden van het Oosten. Egypte, Mesopotamië en een deel van Indië werden gehelleniseerd. De Grieken overstroomden het Oosten als beambten, handelaren, kooplieden, dokters, reizigers, huursoldaten en avonturiers. De steden, waarvan verscheidene, kenbaar aan hun Griekse namen, eerst onder Alexander en zijn navolgers waren gesticht, stonden onder Griekse militaire en ambtelijke controle en hadden een bevolking die een mengsel was van Grieken, Aziaten en Afrikanen. Het Hellenisme was in wezen een stedelijke beschaving; het platteland bleef vrijwel onberoerd of opstandig (men denke aan de Maccabeeën). In de steden kwam de oude Oosterse beschaving met de ingevoerde Griekse cultuur in aanraking, en ofschoon er een gedeeltelijke versmelting van die levenswijzen plaatsvond, een diepe kloof bleef bestaan. De Hellenistische monarchen namen Oosterse gewoonten over, hadden zich bezig te houden met Oosterse administratieproblemen, zoals irrigatie, doch moedigden Griekse kunsten en wetenschappen aan.

De Griekse wiskunde, dus naar vreemde streken overgeplaatst, behield vele traditionele kenmerken, doch ondervond ook de invloed van de vraagstukken in administratie die het Oosten had op te lossen, en die de belangstelling wakker hielden in berekenende arithmetica en astronomie. Dit nauwe verband tussen Griekse en Oosterse wetenschap heeft grote resultaten gehad, vooral gedurende de eerste eeuwen, vóór de Romeinse overheersing begon. Praktisch al die werkelijk scheppende wiskunde die we ‘Grieks’ noemen is ontstaan in het betrekkelijk korte tijdperk van ca. 400-ca. 200, van Archytas en Eudoxos tot Apollonios, en zelfs de resultaten van de eerste decennia van deze periode zijn ons vrijwel alleen bekend door hun interpretaties bij Euklides en de andere Alexandrijnse wiskundigen. En het is ook merkwaardig dat de grootste bloei der Hellenistische wiskunde plaatsvond in Egypte onder de Ptolemeeën, en niet in Mesopotamië, ondanks het feit dat de oude Babylonische wiskunde veel verder ontwikkeld was dan de oude Egyptische, althans voor zover wij weten.

Men kan de oorzaak van deze verschuiving zien in de verander-

[p. 63]

de rol van Egypte, dat in Hellenistische tijden een centrale positie in de gebieden rondom de Middellandse Zee innam. De nieuwe hoofdstad Alexandrië was aan de zeekust gesticht en werd het commerciële en intellectuele middelpunt van de Hellenistische wereld. Babylon bleef nog naleven als een centrum van karavaanwegen op de grens van deze wereld, maar verdween op den duur om plaats te maken voor Seleukia-Ktesiphon, de nieuwe hoofdstad der Seleuciden. Met Babylon, voor zover we weten, zijn nooit grote Griekse wiskundigen verbonden geweest, maar Antiochië en Pergamum, ook steden van het rijk der Seleuciden doch dichter bij de Middellandse Zee, hadden belangrijke Griekse scholen. Maar onder de Seleuciden bloeiden wel de oude Babylonische astronomie en wiskunde, die zelfs hun hoogtepunt in dit tijdperk bereikten, en deze ontwikkeling stimuleerde ook de Hellenistische astronomie. Naast Alexandrië bestonden er nog enige andere Hellenistische wiskundige centra, in het bijzonder Athene en Syracuse. Athene bleef een middelpunt van opvoedkundig werk, Syracuse bracht Archimedes voort, de grootste Griekse wiskundige.

7.

In deze periode zien we de beroepsgeleerde optreden, de man die zijn leven aan de beoefening der wetenschap wijdt en er een salaris voor ontvangt. Enige van de allerbeste vertegenwoordigers van deze groep woonden in Alexandrië, waar de Ptolemeeën in het zgn. Museum (Mousaion) met haar beroemde bibliotheek een groot wetenschappelijk centrum gesticht hadden. Hier werd het grote Griekse erfgoed in wetenschap en letteren bewaard en met groot succes verder ontwikkeld. En zo vinden we onder de eerste geleerden die met dit Museum verbonden waren de figuur van Euklides, een der meest invloedrijke wiskundigen van alle tijden.

Euklides, van wiens leven niets met zekerheid bekend is, leefde vermoedelijk ten tijde van de eerste Ptolemaios (306-283), tot wien hij moet gezegd hebben dat er voor koningen geen speciale weg naar de meetkunde bestaat. Zijn beroemdste en belangrijkste werken zijn de dertien boeken van de Elementen (Stoicheia), maar hem worden nog verscheidene andere werken toegeschreven, waarvan sommige ook bewaard zijn gebleven. Onder deze bevinden zich de Data, dat in zuivere meetkundige vorm toepassingen van de algebra op de meetkunde geeft. We weten niet hoeveel van deze werken van Euklides door hemzelf zijn geschreven en hoevele er compilaties zijn, maar ze tonen op vele plaatsen een treffende diepzinnigheid. De werken zijn de eerste volledige wiskundige geschriften die ons uit de Griekse Oudheid zijn overgeleverd.

[p. 64]

De Elementen is wel, op de Bijbel na, het boek geweest dat in de Westerse wereld het meest is gereproduceerd en bestudeerd. Sedert de uitvinding van de boekdrukkunst zijn er meer dan duizend uitgaven van verschenen, en vóór die tijd waren er vele exemplaren in manuscript en in verschillende talen in omloop. Het grootste deel van onze schoolmeetkunde is, soms letterlijk, aan negen van de dertien boeken ontleend, en de Euklidische traditie weegt nog steeds zwaar op ons onderwijs. Voor de beroepswiskundige hebben deze boeken steeds een grote bekoring gehad (al hebben ze aan zijn leerlingen menige zucht ontlokt), en als model van logische uiteenzetting hebben ze het wetenschappelijk denken door de eeuwen heen misschien meer beïnvloed dan enig ander boek.

Euklides' uiteenzetting is gebaseerd op een aantal definities, postulaten en axioma's, waaruit dan de verdere stellingen streng logisch worden afgeleid. De eerste vier boeken behandelen de vlakke meetkunde voor zover ze niet op de leer der verhoudingen berust, en voeren van zeer elementaire stellingen en constructies (de eerste propositie van het eerste boek, dus i, 1 laat zien hoe men een gelijkzijdige driehoek construeert als een zijde is gegeven) over stellingen omtrent lijnen en hoeken tot de congruentie van driehoeken, de gelijkheid van oppervlakken, de cirkel en de regelmatige veelhoeken. De stelling van Pythagoras (i, 47) en de gulden snede (ii, 11) worden ingevoerd als eigenschappen van oppervlakken. In het vijfde boek vinden wij de leer der verhoudingen van Eudoxos, die zoals wij hebben gezien, geen verschil kent tussen onderling meetbare en onmeetbare grootheden. Deze leer wordt dan in het zesde boek op de gelijkvormigheid van vlakke figuren aangewend; hier vinden we het theorema van Pythagoras en de gulden snede terug (vi, 31, 30) als stellingen over verhoudingen. In deze late invoering van de leer der verhoudingen verschilt de Euklidische behandeling van de vlakke meetkunde van de methode die tegenwoordig gebruikelijk is; dit moet worden verklaard uit het gewicht dat Euklides hechtte aan de in zijn tijd nieuwe leer der onmeetbare grootheden. In dit zesde boek (vi, 27) vinden we ook het eerste maximumvraagstuk dat ons heeft bereikt, en dat, algebraïsch uitgedrukt, leert dat ax - λx² voor x = a/2λ haar grootste waarde bereikt, zodat van alle rechthoeken met gelijke omtrek het vierkant het grootste oppervlak heeft. Het meetkundige vertoog wordt hervat in het tiende boek, vaak als het moeilijkste deel der Elementen beschouwd (Stevin sprak van ‘het kruis der mathematici’), waarin we een meetkundige classificering vinden van de kwadratische irrationalen en hun vierkantswortels, grootheden die we

[p. 65]

Gedeelte van een bladzijde uit de Elementen van Euklides (uitgave van 1482).

[p. 66]

nu met a ± √b, 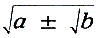aangeven. De laatste drie boeken xi-xiii bevatten de stereometrie en brengen de lezer via ruimtehoeken, de inhouden van blokken, prisma's en piramiden tot de bol tot wat wel als de climax is beschouwd: de leer van de regelmatige (Platonische) lichamen met het bewijs dat hun aantal vijf bedraagt.

De boeken vii-ix zijn aan de getallentheorie gewijd - niet aan rekentechniek doch aan zulke Pythagoreïsche onderwerpen als de deelbaarheid van getallen, de bepaling van volkomen getallen, de sommatie van een meetkundige reeks en sommige eigenschappen van priemgetallen. Ook vindt men hier weer een leer der verhoudingen, nu van (gehele) getallen. De methode waarbij (vii, 2) de G.G.D. van een gegeven aantal getallen wordt bepaald wordt nog steeds de algoritme van Euklides genoemd. Vaak aangehaald is het bewijs (ix, 20) dat het aantal priemgetallen onbeperkt is.

Gegeven de drie eerste priemgetallen α, β, γ. Vorm het produkt αβγ en tel er de eenheid bij op. Dan is αβγ + 1 noch deelbaar door α, noch door β, noch door γ en is dus òf priem, òf deelbaar door een priemgetal groter dan γ. Euklides beperkt zich tot 3 getallen, maar zijn bewijs geldt algemeen.

Van alle postulaten en axioma's in Boek i (het verschil tussen beide is niet zeer duidelijk) heeft het vijfde postulaat het meeste stof doen opwaaien. Het is equivalent met wat gewoonlijk het parallellenaxioma wordt genoemd en dat zegt dat er door een punt P buiten een lijn l één en slechts één lijn in het vlak door P en l kan worden getrokken die l niet snijdt, hoe ver ook verlengd. Gedurende meer dan tweeduizend jaren heeft men getracht dit axioma tot een stelling te maken, dus uit andere axioma's van Euklides af te leiden. In de negentiende eeuw heeft men tenslotte Euklides' wijsheid beseft en begrepen dat geen bewijs van de gezochte aard mogelijk is. Door het parallellenaxioma door een ander te vervangen is hieruit de niet-euklidische meetkunde ontstaan (zie ons hoofdstuk over de Negentiende Eeuw). Verwerping van het axioma van Archimedes heeft later ook tot niet-archimedische meetkunden gevoerd.

We vinden geen algebra bij Euklides, maar in zijn meetkundige redeneringen zit veel dat wij nu liever algebraïsch uitdrukken. Wat wij √A schrijven wordt als de zijde van het vierkant A uitgedrukt, een produkt ab als het oppervlak van een rechthoek met zijden a en b. Lineaire en kwadratische vergelijkingen worden door meetkundige constructies opgelost met behulp van de zgn. leer der ‘aanpassing van oppervlakken’. Deze uitdrukkingswijze was een

[p. 67]

consequent gevolg van Eudoxos' leer der verhoudingen, waarin vermeden werd de lengte van lijnsegmenten door getallen weer te geven.

Wat had Euklides eigenlijk voor met zijn Elementen? Eén antwoord is dat hij in één werk systematisch drie grote ontdekkingen van het recente verleden wilde samenvatten: Eudoxos' leer der verhoudingen, Theaitetos' leer der irrationaliteiten, en de theorie der vijf regelmatige lichamen die zulk een belangrijke rol speelden in Plato's kosmogonie. Deze drie ontdekkingen waren karakteristiek ‘Grieks’.

8.

De grootste wiskundige van het Hellenistische tijdvak - en van de gehele Oudheid - was Archimedes (287-212), die in Syracuse op Sicilië woonde als adviseur van Koning Hieron. Hij is een der weinige wetenschappelijke figuren van de Oudheid die meer is dan een naam: we weten iets van hem als persoon. Zo weten we dat hij gedood werd toen in 212 de Romeinen onder Marcellus Syracuse innamen na een lang beleg waarin de bejaarde geleerde zijn grote technische bekwaamheid in dienst der belegerden had gesteld.

Zulk een ijver voor praktische toepassingen doet ons enigszins vreemd aan als wij aan de minachting denken waarmee de school van Plato op zulk ‘misbruik’ van de wetenschappen neerzag, maar Plutarchus heeft in zijn ‘Marcellus’ een soort verklaring gegeven:

‘Ofschoon deze uitvindingen hem de reputatie van bovenmenselijke wijsheid hadden verschaft, heeft hij het beneden zijn waardigheid geacht enig geschrift over die onderwerpen na te laten - doch, aangezien hij al dit construeren van werktuigen en andere kunsten die nut of winst afwerpen als onedel en minderwaardig verwierp, plaatste hij zijn gehele eerzucht in die speculaties waarvan de schoonheid en de diepzinnigheid buiten contact met de gewone noodzakelijkheden des levens blijven.’

Dat was echter geschreven door een Platonist ongeveer drie eeuwen na Archimedes' dood. Schrijvers als Polybius en Vitruvius, die nader tot Archimedes' tijd stonden, vermelden die gewetensbezwaren niet en zien in hem vooral de grote werktuigkundige.

De belangrijkste bijdragen van Archimedes tot de wiskunde behoren tot het gebied dat we nu de integraalrekening noemen: de bepaling van het oppervlak van vlakke figuren en de inhoud van lichamen. In zijn Cirkelmeting berekende hij benaderingswaarden van de cirkelomtrek met behulp van ingeschreven en omgeschreven regelmatige veelhoeken. Hij berekende achtereenvolgens door een verdubbelingsformule de zijde van de veelhoek met 6, 12, 24,

[p. 68]

48 en 96 zijden, en vond (in onze notatie)

een resultaat dat gewoonlijk geresumeerd wordt door te zeggen, dat Archimedes een waarde van π vond die dicht bij 3 1/7 ligt.¹ In Archimedes' boek Over de bol en de cilinder vinden we de uitdrukking voor het oppervlak van de bol in de vorm dat dit oppervlak gelijk is aan het viervoud van het oppervlak van een grote cirkel, en ook een uitdrukking voor de inhoud van de bol als ⅔ van de inhoud van de omgeschreven cilinder. Archimedes' stelling, dat het oppervlak van een parabolisch segment met de koorde k als basis, gelijk is aan 4/3 maal het oppervlak van de ingeschreven driehoek met basis k en top in dat punt van de parabool, waar de raaklijn evenwijdig is aan k, vindt men in de ‘Kwadratuur van de parabool’. Het bewijs hier is volgens de strikte methode van het indirecte bewijs, doch wij hebben alreeds gezien dat Archimedes het op een meer directe wijze gevonden had (in de ‘Methode’). In het boek over ‘Spiralen’ vinden we berekeningen omtrent de ‘spiraal van Archimedes’, in het boek ‘Over Konoïden en Spheroïden’ vinden we de inhouden van zekere kwadratische omwentelingsoppervlakken. We herinneren ons nog wel uit onze schooljaren het zgn. theorema van Archimedes over ondergedompelde lichamen; dit vinden we in zijn boek over de hydrostatica: ‘Over drijvende lichamen’. Archimedes kende ook de wet van de hefboom. Deze natuurwetten behoren tot de eerste die ooit geformuleerd zijn, en hebben als model gediend toen in de 17e eeuw het begrip natuurwet in zijn moderne vorm werd ontwikkeld.

In al deze werken verbond Archimedes een grote oorspronkelijkheid met een meesterlijke hantering van de rekentechniek ener-

1 Ofschoon π een Griekse letter is, hebben de Grieken daarmee nooit de verhouding van omtrek en middellijn van de cirkel aangegeven. Het symbool komt in enige geschriften van de 18^e eeuw voor, doch werd het eerst algemeen aanvaard nadat. Euler het in zijn veel gelezen Introductio van 1748 geregeld had gebruikt. In decimale notatie betekent Archimedes' benadering:
3,1409... < π < 3,1429...
Het rekenkundig gemiddelde van beide waarden geeft π = 3,1419... Correct is π = 3,14159...
Archimedes gebruikte ook de letter π (of beter, de hoofdletter Π) als een getal. Maar dit getal betekende toen wat wij met 80 aanduiden.

[p. 69]

zijds en de strenge bewijsvoering anderzijds. Kenmerkend voor deze strengheid van wiskundig denken is het reeds vermelde ‘axioma van Archimedes’ en zijn gebruik van Eudoxos' ‘exhaustie’-methode. In zijn hantering van de rekentechniek verschilde Archimedes van de meeste grote Griekse wiskundigen. Zo kreeg zijn werk, door en door Grieks als het is, toch een Oosters trekje: Archimedes was nu eenmaal niet bang alle wiskunde die hij kende, scheppend te gebruiken.

Dit ‘Oosterse’ trekje vinden we ook in het vaak aan Archimedes toegeschreven ‘Runderprobleem’, een ingewikkeld vraagstuk in onbepaalde analyse, dat men kan interpreteren als een probleem dat leidt tot een zgn. vergelijking van Pell

t² - Au² = 1

waarvan de oplossing moet worden gevonden in gehele getallen t en u. In het ‘Runderprobleem’ is A = 4729494 en u is een veelvoud van 9304, het antwoord bestaat uit zeer grote getallen.¹

1 Zulke vergelijkingen van Pell ontmoet men ook in de Pythagoreïsche getallenleer, waar speculaties over de verhouding van diagonaal en zijde van een vierkant tot de studie van t² - 2u² = ± 1 hebben gevoerd. Oplossingen zijn hier (3,2), (7,5), (17,12), enz. die de benaderde breuken 3/2, 7/5, 17/12,... van de kettingbreukenontwikkeling voor √2 geven. Hierover zie men b.v. E.J. Dijksterhuis, De Elementen van Euclides II (Groningen 1930), 20-25; B. v.d. Waerden, Ontwakende Wetenschap (Groningen, 1950) 141, 232.
Dat de vergelijking naar Pell is genoemd berust vermoedelijk op een misverstand van Euler. John Pell (1611-1685) werd in 1643 professor aan de Amsterdamse Illustre Academie, in 1646 aan de pas geopende academie in Breda (waar de jonge Christiaan Huygens studeerde). Later keerde hij naar Engeland terug.

9.

Met de derde grote Hellenistische wiskundige, Apollonios van Perga, (ca. 260-ca. 170) zijn we weer geheel in de meetkundige traditie. Apollonios, die in Alexandrië en in Pergamum gedoceerd schijnt te hebben, schreef acht boeken over kegelsneden, de Konica. Hiervan zijn zeven boeken bewaard gebleven, de laatste drie alleen in een Arabische vertaling. Apollonios voert de kegelsneden in als snijlijnen van vlakken met een rechte of scheve cirkelkegel, en ofschoon zijn behandeling zuiver meetkundig is kan men ze licht herleiden tot de studie van de homogene vergelijkingen y² = px (1 + ε x/d), waar ε = - 1 de ellips, ε = 0 de parabool, ε = + 1 de hyperbool geeft (p en d zijn lijnen). Deze namen, die wij aan Apollonios ontlenen, vinden hun verklaring in

[p. 70]

de ‘aanpassingstheorie’ van oppervlakken die we in Euklides kunnen bestuderen, ε = - 1 is aanpassing met defect (‘elleipsis’), ε = 0 (precieze) aanpassing (‘parabolê’), ε = + 1 aanpassing met exces (‘hyperbolê’).

Apollonios had onze coördinatenmethode niet, omdat hij geen algebraïsche notatie had, die misschien onder invloed van Eudoxos bewust verwerpend. Vele van zijn resultaten kunnen echter onmiddellijk in de taal van onze analytische meetkunde vertaald worden, ook zijn theorie van de evoluten der kegelsneden.¹

Ook vele andere werken van Apollonios, waarvan gedeelten tot ons zijn gekomen, bevatten wat wij algebraïsche meetkunde zouden noemen, doch in meetkundige en dus homogene vorm. Tot die gedeelten behoort het zgn. raakprobleem van Apollonios: een cirkel te construeren die aan drie gegeven cirkels raakt, de cirkels mogen door punten of rechten vervangen worden.² Bij Apollonios vinden we de eis dat men in meetkundige constructies zich moet beperken tot passer en lineaal, expliciet geformuleerd (ofschoon ze impliciet al in de Elementen voorkomt); deze eis was dus niet zo typisch Grieks als men soms wel gelooft.

1 ‘Mijn stelling, dan, is dat het wezen der analytische meetkunde bestaat in de studie van meetkundige plaatsen met behulp van hun vergelijkingen, en dat dit aan de Grieken bekend en de basis van hun studie der kegelsneden was’: J.L. Coolidge, A History of Geometrical Methods (Oxford 1940), bldz. 119. Zie in dit verband onze opmerkingen over Descartes. Coolidge's ‘Stelling’ is onzes inziens onhistorisch, het hele karakter van het wiskundig denken der Grieken verschilde van het onze.

2 Dit probleem heeft door de eeuwen heen wiskundigen beziggehouden, o.a. Viète, Newton en Steiner. Het algemeen probleem heeft 8 oplossingen. Zie b.v. P. Molenbroek, Leerboek der vlakke Meetkunde (10e druk, Groningen, 1948) 544-553.

10.

Het is moeilijk de wiskunde gedurende haar gehele verloop tot op betrekkelijk moderne tijd van de sterrenkunde te scheiden. In de Oosterse en Hellenistische wetenschap nam de sterrenkunde door haar belang voor de landbouw en speciaal de irrigatie een overwegende plaats in - om van de astrologie maar te zwijgen. Daardoor had de ontwikkeling van de astronomie een sterke invloed op die der wiskunde, vooral op de rekentechniek, doch ook op de begripsinhoud van de wiskunde. Anderzijds hing de voortgang der sterrenkunde weer van de beschikbare mathematische kennis af. De bouw van het planetensysteem is zo dat betrekkelijk eenvoudige wiskundige methoden reeds machtige resultaten ople-

[p. 71]

veren, doch terzelfder tijd is ze ingewikkeld genoeg om de verbetering van die methoden te stimuleren, hetgeen dan weer de astronomische theorieën beïnvloedt. Het Oosten had grote vooruitgang in de berekenende sterrenkunde geboekt in die periode die juist aan de Hellenistische voorafgaat, in het bijzonder in Mesopotamië gedurende de laat-Assyrische en Perzische perioden. Hier had de stelselmatige bestudering van waarnemingen over vele jaren tot een opmerkelijk begrip van vele verschijnselen gevoerd, b.v. van de beweging van de maan, die door haar schijnbare grilligheid de wiskundige steeds weer tot nieuwe studie heeft aangespoord, in de Oudheid zowel als in meer moderne tijden. Babylonische (‘Chaldese’) sterrenkundigen hadden tabellen van zulke efemeriden opgesteld, die, als we ze grafisch voorstellen, door trapfuncties kunnen worden voorgesteld. Toen, gedurende de periode der Seleuciden, Griekse en Babylonische wetenschap elkaar ontmoetten, leidde deze kennismaking tot vooruitgang, niet alleen in de berekenende, doch ook in de theoretische astronomie. Doch terwijl de Babylonische wetenschap in haar oude kalendarische tradities bleef voortgaan, behaalde de Griekse wetenschap nieuwe triomfen op theoretisch gebied.

De oudste Griekse bijdrage tot de theoretische sterrenkunde was de planetentheorie van dezelfde Eudoxos die Euklides inspireerde. Ze was een poging om de beweging der planeten (rondom de vaststaande aarde) te verklaren door vier boven elkaar liggende, draaiende, concentrische bollen aan te nemen, ieder draaiende om zijn eigen as waarvan de eindpunten vast zaten in de omgevende bol. Dit was iets nieuws en typisch Grieks: een kinematisch model van het planetenstelsel in plaats van de tabellen waarmee de Babyloniërs zich vergenoegden: een meetkundige verklaring in plaats van een beschrijving. Ondanks haar tamelijk eenvoudige vorm bevat deze theorie van Eudoxos het centrale denkbeeld dat aan alle planetaire theorieën tot de zeventiende eeuw ten grondslag heeft gelegen, en dat daarin bestaat dat de onregelmatigheden in de schijnbare banen van maan, zon en planeten worden verklaard uit de superpositie van cirkelvormige bewegingen. Een moderne analogie is de techniek, waarbij we functies in trigonometrische reeksen ontwikkelen.

Na Eudoxos krijgen we Aristarchos van Samos (ca. 280), de ‘Copernicus van de Oudheid’, waarvan we bij Archimedes lezen dat hij de hypothese opstelde dat niet de aarde, maar de zon het middelpunt is van de planetenbanen. Aristarchos' verhandeling zelf is nooit teruggevonden, wij bezitten van hem alleen een werk

[p. 72]

over de bepaling van de afstand van maan en aarde. Wat zijn heliocentrische hypothese betreft, deze vond weinig bewonderaars in de Oudheid - waarschijnlijk om dezelfde reden waarom Copernicus' leer in den beginne weinig aanhangers had: de moeilijkheid om deze leer met die van Aristoteles in overeenstemming te brengen. In de Oudheid werden Aristarchos' theorieën door die van Hipparchos in de schaduw gesteld.

Hipparchos van Nicaea, vaak als de grootste astronoom van de Oudheid beschouwd, verrichtte zijn observaties tussen 141 en 127 v. C. Directe kennis van zijn werk hebben we niet; wat we weten komt voornamelijk van Ptolemaios, die ongeveer drie eeuwen later leefde. Er is veel in Ptolemaios' groot astronomisch handboek, bekend als Almagest, dat op rekening van Hipparchos komt, speciaal het gebruik van eccentrische cirkels en epicykels om de beweging van zon, maan en planeten te beschrijven. Ook wordt aan Hipparchos de ontdekking van de precessie der nachteveningspunten toegeschreven. Van hem is misschien ook het denkbeeld afkomstig plaatsen op aarde door lengte en breedte aan te geven en deze ‘coördinaten’ door astronomische metingen te bepalen, doch men heeft nooit gedurende de Oudheid de wetenschappelijke organisatie gehad die zulk een geografisch program op grote schaal mogelijk maakte. Mannen van wetenschap waren in de Oudheid nu eenmaal dun gezaaid, zowel in tijd als in plaats. Het werk van Hipparchos stond in nauwe betrekking tot de Babylonische sterrenkunde, die in zijn dagen een periode van bloei beleefde, zodat we in dit werk een uiterst belangrijk wetenschappelijk resultaat van het contact tussen de Griekse en de Oosterse beschaving in het Hellenistische tijdvak kunnen zien.¹

1 O. Neugebauer, Exact Science in Antiquity, Studies in Civilization, Univ. of Pennsylvania Bicentennial Conference (Philadelphia, 1942) 22-31; en The exact Sciences in Antiquity (Princeton, 1952, 2e uitg. 1957, Dover herdruk 1969).

11.

De derde en laatste periode van de klassieke Oudheid is die van de Romeinse overheersing. Rome veroverde Syracuse in 212, Carthago in 146, Griekenland in 146, Mesopotamië in 64, Egypte in 30 v. C. Het Oosten, dat Rome had veroverd, werd een kolonie, beheerd door Romeinse bestuurders en beambten. Deze controle beïnvloedde de economische structuur van de Oosterse landen maar weinig zolang de belastingen en andere tributen maar rustig konden worden geïnd. Verder was het Romeinse Rijk nu op na-

[p. 73]

tuurlijke wijze in twee delen verdeeld, een Westelijk gedeelte met extensieve landbouw die op massale slavenarbeid berustte, en een Oostelijk gedeelte met intensieve landbouw, waarin de slavernij in het algemeen alleen voor openbare werken en voor huisdiensten in aanmerking kwam. Ondanks het bestaan van een aantal steden en een handel die het hele Rijk omvatte, en zelfs het Rijk met landen als China en Indië verbond, vormde de landbouw de economische grondslag. De uitbreiding der slavernij in zulk een maatschappij ondermijnde steeds meer de mogelijkheid van oorspronkelijk wetenschappelijk werk. Slavenhouders zijn als een klasse bitter weinig geïnteresseerd in technische verbeteringen, zolang ze genoeg slaven kunnen vinden om al het werk te doen, en bovendien, het is gevaarlijk om enig werktuig in de hand van een slaaf te geven dat helpen zal zijn kennis te vergroten. Vele leden van de slavenhoudende klasse amuseerden zich met kunsten en wetenschappen, doch zulk een bezigheid gaf meer aanleiding tot middelmatig dan tot scheppend denken. En toen uiteindelijk de toevoer van slaven meer en meer beperkt werd en de gehele Romeinse volkshuisvesting in verval raakte, bleven er slechts weinig mensen over om zelfs de middelmatige wetenschap van de vergane eeuwen voort te zetten.

Zolang als het Romeinse Rijk nog stabiliteit vertoonde, bleef in het Oostelijk deel de wetenschap bloeien in een merkwaardige vermenging van verschillende cultuurelementen, Hellenistische zowel als Aziatische en Egyptische. Het is waar dat scheppingskracht en oorspronkelijkheid langzamerhand minder en minder werden, doch de pax Romana, die verscheidene eeuwen het leven van velen voor grote schokken vrijwaarde, bevorderde wetenschappelijke en wijsgerige speculatie, in grotendeels traditionele banen. Naast de pax Romana genoot een ander deel van de wereld een tijdlang de pax Sinensis: in de gehele geschiedenis heeft het Eurazische continent nooit meer zulk een periode van ononderbroken vrede genoten als onder de Antonienen in Rome en de Han in China. In dit tijdperk kon zich wetenschappelijke en technische kennis gemakkelijker dan voorheen van West naar Oost en van Oost naar West verspreiden. Hellenistische wetenschap kwam naar Indië en misschien ook naar China, en werd zelf door intellectuele stromingen van het Oosten beïnvloed. Zekere trekken van de Babylonische sterrenkunde en de Griekse wiskunde kwamen naar Italië, Spanje en Gallië, zoals b.v. de sexagesimale indeling van uur en hoek, die zich over het gehele Romeinse Rijk verbreidde. Er bestaat een theorie van de Oriëntalist-wiskundige F.W. Woepcke (1863) waar-

[p. 74]

in de verspreiding van de zogenaamde Hindoe-Arabische getallen over Europa alreeds in de latere jaren van het Romeinse Rijk wordt verzet, een verspreiding waarbij misschien neo-Pythagoreïsche invloeden een rol hebben gespeeld. Dit kan wel waar zijn, doch zo de verspreiding van die getallen over de Westerse wereld reeds zo vroeg plaatsvond, is ze waarschijnlijk wel meer door de handel dan door de filosofie beïnvloed.

Alexandrië bleef ook onder Rome het middelpunt van de wiskunde der klassieke Oudheid. Men bleef oorspronkelijk werk verrichten, ofschoon compilatie en exegese hoe langer hoe meer de plaats van scheppend denken begonnen in te nemen. De geleerden van die dagen hebben ons menig wis- en sterrenkundig resultaat overgeleverd, dat anders zou zijn verloren gegaan, en het is niet altijd gemakkelijk om vast te stellen wat zij overgeschreven of wat zij zelf ontdekt hebben. Als we trachten de geleidelijke achteruitgang van de Griekse wiskunde te begrijpen moeten we ook aan haar technische zijde denken, haar vaak omslachtige meetkundige manier van uitdrukken zonder de hulp van een algebraïsche schrijfwijze. In de leer der krommen maakte dit elke systematische vooruitgang boven de kegelsneden bijkans onmogelijk. Algebra en rekentechniek werden aan de volkeren van het Oosten overgelaten, waar een rechtgeaarde Griek op neer zag, ook al was hun beschaving met een Grieks vernisje overdekt. Het is evenwel verkeerd te geloven dat de Alexandrijnse wiskunde zuiver ‘Grieks’ was in de traditionele Euklidisch-Platonische zin: er bleef steeds naast de abstracte meetkundige denkwijze een Egyptisch-Babylonische, algebraïsch-berekenende wiskunde bestaan. We hoeven slechts aan Heroon, Ptolemaios en Diophantos te denken om dit in te zien. Al die verschillende scholen hadden één kenmerk gemeen: ze gebruikten de Griekse taal voor wetenschappelijke doeleinden.

12.

Een der vroegste Alexandrijnse wiskundigen van de Romeinse periode was Nikomachos van Gerasa (ca. 100 n. C.), wiens Inleiding tot de Arithmetica de meest complete uiteenzetting van de rekenkunde der Pythagoreeërs is. Men vindt er, algemeen gesproken, dezelfde onderwerpen die men in de arithmetische boeken van Euklides' Elementen vindt, doch waar Euklides getallen door lijnsegmenten voorstelt, gebruikt Nikomachos een rekenkundige schrijfwijze, waarbij hij de gewone taal gebruikt als onbepaalde getallen moeten worden uitgedrukt. Zijn behandeling van polygonale en piramidale getallen heeft middeleeuwse rekenkunde, in het bijzonder het werk van Boëtius, beïnvloed.

[p. 75]

Een der belangrijkste documenten uit dit tweede Alexandrijnse tijdvak was het Grote Systeem (Megalè Syntaxis) van Klaudios Ptolemaios, beter bekend onder de gearabiseerde naam van Almagest (ca. 150 n. C.). Deze Almagest is het grote astronomische meesterwerk van de Oudheid, een werk dat zowel grote originaliteit als meesterlijke techniek tentoon spreidt, ook al zijn vele van de leidende ideeën afkomstig van Hipparchos of van Babylonische sterrenkundigen als Kidinnu (of Kidenas), die circa 450 v.Chr. zijn observaties verrichte, ongeveer terzelfder tijd als de Ionische filosofen. Voor ons is van belang dat de Almagest ook een goniometrie bevat, met een koordentafel voor verschillende hoeken, die dus equivalent is met een sinustafel volgens de formule:

koorde α - 2R sin α/2, met R = 60.

Ptolemaios' hoeken gaan van 0° tot 90° met inter vallen van 30′, de straal van de cirkel is 60 eenheden en de koorden worden in sexagesimale breuken uitgedrukt. Toegevoegd is een tabel voor interpolatie naar minuten. Als hij dus b.v. voor de koorde van 1° de waarde (1,2,50) geeft, betekent dit dat deze koorde

1/60 + 2/60² + 50/60³ = 0,0174537 van de straal is.

Voor π heeft de Almagest de waarde (3, 8, 30) = 3 17/120 = 3,14166. We vinden in dit boek de zgn. ‘stelling van Ptolemaios’ over de diagonalen en de zijden van een koordenvierhoek, zowel in het vlak als op de bol, en zo men in deze stelling voor de vlakke koordenvierhoek één zijde als middellijn kiest krijgt men een meetkundige betrekking equivalent met de tegenwoordige formules voor de sinus en cosinus van de som en het verschil van twee hoeken. Deze stelling wordt dan bij het berekenen der tafels gebruikt, omdat ze het mogelijk maakt van de koorde van α tot die van α/2 over te gaan. Zo vindt Ptolemaios uit de koorde van 72° en 60° die van 12°, 6°, 1°30′ en 45′, welke waarden dan weer gebruikt worden om de koorde van 1° te benaderen door de ongelijkheid

zodat koorde 1° < 4/3 koorde 45′ en > ⅔ koorde 1°30′.

[p. 76]

In Ptolemaios' boek Planisphaericum vinden we de stereografische projectie. Zijn Geographia heeft nog enige andere kaartprojecties, en voert lengte en breedte op aarde in. Dit zijn dus antieke voorbeelden van een coördinatenstelsel. Met deze stereografische projectie is de constructie verbonden van het astrolabium, reeds in de Oudheid bekend en later door de Arabische beschaving verder ontwikkeld, en in de vorm van werkelijke kunstwerken uitgevoerd.¹

Iets ouder dan Ptolemaios was Menelaos (ca. 100 n. C.), wiens Sphaerica een meetkunde van het boloppervlak bevat. Hier vindt men een bespreking van boldriehoeken, iets wat bij Euklides ontbreekt, waarbij gebruik wordt gemaakt van ‘Menelaos' theorema’ over transversalen van een driehoek, in dit geval een boldriehoek. Waar Ptolemaios' sterrenkunde veel rekenwerk (in sexagesimale breuken) bevat, is de verhandeling van Menelaos meetkundig in de zuivere Euklidische traditie.

Het is zeer waarschijnlijk dat tot deze periode ook Heroon (of Hero) behoort, wij weten althans dat hij een maaneclips van 62 n. C. precies beschrijft.² Heroon was een encyclopedisch schrijver, hij schreef over meetkundige, rekentechnische en mechanische onderwerpen. In zijn Metrica vinden we de ‘Heronische’ formule voor het oppervlak van een driehoek:

in een meetkundige vorm, een formule die ook wel aan Archimedes wordt toegeschreven. Bij Heroon komen Griekse en Oosters-Egyptische elementen beide voor, zo vindt men in de Metrica typische Egyptische stambreuken, als in de benadering voor √63 door 7 + ½ + ¼ + ⅛ + 1/16. Heroon's formule voor de inhoud van een afgeknotte vierzijdige piramide kan herleid worden tot die welke in de oude Moskouse papyrus voorkomt. Zijn uitdrukkingen voor de inhoud van de vijf regelmatige lichamen zijn daarentegen weer in de geest van Euklides.

1 H. Michel, Traité de l'astrolabe (Parijs, 1947), zie ook O. Neugebauer in Isis 40 (1949) 240-256, en P.H. van Cittert over astrolabia in het Utrechts Universiteitsmuseum (1954). Algemeen: Eva G.L. Taylor, The Haven-finding Art (1956).

2 O. Neugebauer, Über eine Methode zur Distanzbestimmung Alexandria-Rom bei Heron. Hist. fil. Medd. Danske Vid. Sels. 26 (1938) No. 2, 28 bldz.

[p. 77]

13.

De invloed van het Oosten is nog veel sterker in de Arithmetica van Diofantos (ca. 250 n. C.). Van de oorspronkelijke boeken zijn er nog zes over, hoeveel er totaal waren weten we niet precies. Uit de bekwame manier waarop bepaalde en onbepaalde vergelijkingen behandeld worden blijkt dat de aloude algebra van Babylon of misschien ook van Indië onder het Griekse vernis niet alleen nog voortleefde, doch ook verbeterd werd. Hoe en wanneer dit gebeurde weten we niet, evenmin als we weten wie Diofantos was, misschien wel een gehelleniseerde Babyloniër. Zijn Arithmetica is een der meest fascinerende verhandelingen die ons uit de Grieks-Romeinse oudheid zijn overgeleverd.

Diofantos' verzameling van vraagstukken omvat vele gebieden en de behandeling is vaak hoogst vernuftig. ‘Diofantische analyse’ bestaat in het vinden van oplossingen van allerlei onbepaalde vergelijkingen, zoals (in onze notatie)

y² = Ax² + Bx + C, of y³ = Ax³ + Bx² + Cx + D

of stelsels van zulke vergelijkingen.

Karakteristiek was Diofantos' verlangen positief rationale oplossingen te vinden, dus niet noodzakelijk oplossingen in gehele getallen. Irrationale oplossingen waren ‘onmogelijk’, en hij zorgde ervoor dat zijn coëfficiënten getallen waren die tot positieve rationale oplossingen voerden. Onder zijn vergelijkingen vinden we x² + y² = z² (de ‘Pythagoreïsche drietallen’), en de vergelijkingen van Pell x² - 26y² = 1, x² - 30y² = 1. Diofantos heeft ook verscheidene stellingen op het gebied der getallentheorie, zoals het theorema (iii, 19) dat als elk van twee gehele getallen de som is van twee vierkanten hun produkt op twee manieren kan gesplitst worden in de som van twee vierkanten. Hij heeft ook theorema's over de splitsing van een getal in de som van drie en vier vierkanten.

In Diofantos vinden we voor het eerst een stelselmatig gebruik van algebraïsche symbolen. Hij heeft een eigen teken voor de onbekende, voor het minteken, voor omgekeerden. De symbolen hebben nog meer de natuur van afkortingen dan van algebraïsche symbolen in onze zin, en zo spreekt men wel van Diofantos' ‘gesyncopeerde’ algebra in tegenstelling tot onze ‘symbolische’. Voor elke macht van de onbekende had hij een eigen symbool. Hier vinden we dus niet alleen, zoals in Babylon, arithmetische kwesties van een duidelijk algebraïsch karakter, doch ook een goed ontwikkelde algebraïsche notatie die meehielp om vraagstukken op te lossen die ingewikkelder waren dan die welke vroeger aan de orde

[p. 78]

waren gesteld.¹ Toen, in het laatst van de zestiende en het begin van de zeventiende eeuw de studie van Diofantos weer werd opgevat, door Stevin, Viète en vooral Fermat, heeft de ‘Arithmetica’ er toe bijgedragen dat zowel algebra als getallenleer een nieuwe bloeiperiode tegemoet ging.

1 Papyrus 620 van de Universiteit van Michigan, in 1921 verkregen, bevat sommige vraagstukken in Griekse algebra die tot een periode vóór Diofantos behoren, misschien tot het begin van de tweede eeuw na Chr. In dit manuscript vindt men al reeds sommige van Diofantos' symbolen. Zie F.E. Robbins, Classical Philology 24 (1929), 321-329, K. Vogel, ibid. 25 (1930) 373-375. De indeling van de algebra in ‘retorische’ (geheel in woorden), ‘gesyncopeerde’ (half en half), en ‘symbolische’ (algebra van heden) komt het eerst voor bij G.H.F. Nesselman, Die Algebra der Griechen (Berlijn, 1842).

14.

De laatste grote Alexandrijnse wiskundige verhandeling was de Verzameling (Synagoge) van Pappos (eind 3^e eeuw). Dit werk, in acht boeken, was een soort inleiding tot de studie van de Griekse meetkunde met historische noten, verbeteringen en veranderingen in bestaande theorema's en bewijsvoeringen. Het behoorde eigenlijk met de oorspronkelijke werken tezamen gelezen te worden, en niet onafhankelijk ervan. Vele resultaten van antieke schrijvers zijn ons echter alleen bekend in de vorm waarin Pappos die aan ons heeft overgeleverd. Voorbeelden zijn vraagstukken die betrekking hebben op de driedeling van een hoek, de verdubbeling van de kubus, en de kwadratuur van de cirkel. In een sectie over isoperimetrische figuren (dat een boek van Zenodorus, misschien ca. 180 voor Chr., volgt) vindt men de uitspraak dat de cirkel een groter oppervlak heeft dan elke regelmatige veelhoek met dezelfde omtrek. Hier vindt men ook een opmerking over het feit dat de cellen in een honingraat een hexagonale vorm hebben, omdat zulk een figuur onder de gegeven voorwaarden van ruimtevulling een maximum aan honing kan bevatten.² De dertien halfregelmatige lichamen van Archimedes (die van de vijf regelmatige lichamen daarin verschillen, dat zij niet door één doch door twee of drie stelsels van congruente regelmatige veelhoeken begrensd zijn), zijn ook door Pappos bekend gemaakt. Sommige eigenschappen die hij vermeldt behoren tot wat we nu de projectieve meetkunde noemen, maar ze zijn geïsoleerd en schijnen er op te wijzen dat de Oudheid nooit aan een systematische projectieve meetkunde is

2 Een uitvoerige discussie van dit probleem vindt men in D'Arcy W. Thompson, Growth and Form (2^e uitg., Cambridge, 1942).

[p. 79]

toegekomen. Maar met zijn verscheidenheid van problemen, en juist door het feit dat hij zoveel vragen aanroert doch slechts ten dele oplost, heeft Pappos, met zijn Verzameling, evenals Diofantos met zijn Arithmetica, een boek achtergelaten dat vele latere geesten tot verder werk heeft aangespoord.

Met het langzame verval van de antieke maatschappij verviel ook de Alexandrijnse school. Ze bleef, globaal gezien, een bolwerk van de heidense filosofie tegen het opdringende Christendom, en sommige wiskundigen van die school hebben zich ook een plaats verworven in de geschiedenis der antieke wijsbegeerte: Proklos (410-485), wiens commentaar tot het eerste boek van Euklides' Elementen een van onze voornaamste bronnen van de geschiedenis der Griekse wiskunde is, was de leidende figuur van een Neo-Platonische school in Athene. Een andere commentator van de Elementen was Theon van Alexandrië (ca. 370). Zijn behandeling van de Elementen is tot aan de negentiende eeuw toe voor de oorspronkelijke tekst aangezien. Theons dochter Hypatia heeft ook commentaren op klassieke wiskundigen geschreven. Ze werd in 415 door aanhangers van de heilige Cyrillus vermoord, hetgeen Charles Kingsley tot het schrijven van de roman Hypatia inspireerde (1853).¹ In deze filosofenscholen met hun commentatoren wisselden eeuwen lang tijden van voorspoed af met tijden van achteruitgang. De Akademie in Athene werd in 529 door Keizer Justinianus als ‘heidens’ opgeheven, doch omstreeks die tijd waren er al weer andere scholen, b.v. in Constantinopel en in (Perzisch) Jundishapur. Vele oude teksten weerstonden de eeuwen in boekerijen van Constantinopel waar Grieks schrijvende commentatoren doorgingen, tot de val in 1453, de herinnering aan de Griekse wetenschap en wijsbegeerte levend te houden. In het jaar 641 werd Alexandrië door de Arabieren veroverd, die de Griekse beschaving van de opperste lagen der maatschappij door een Arabische vervingen. Men behoeft het verhaal dat de Arabieren de beroemde bibliotheek vernield hebben niet te geloven; het is best mogelijk dat er van die bibliotheek al niet veel meer over was.² Aan het karakter van de wiskunde in Egypte hebben de Arabische veroveraars weinig veranderd. Er was een tijdelijke achteruitgang,

1 Ook: F. Mauthner, Hypatia, Roman aus dem Altertum (1892). Zie verder D.J.E. Schrek, Hypatia van Alexandrië, Euclides 21 (1945-46) 164-173.

2 A. Parsons, The Alexandrian Library. Glory of the Hellenistic World (Amsterdam enz., 1952) is anders van oordeel.

[p. 80]

maar als we weer van Egyptische wiskunde horen heeft ze nog steeds het Alexandrijnse half Grieks, half Oosterse karakter (b.v. Alhazen).

15.

Wij eindigen dit hoofdstuk met enkele opmerkingen over Griekse arithmetica en logistica. De ‘arithmetica’ was de leer der getallen (arithmoi), de ‘logistica’ was de praktische rekenkunst. De term ‘arithmos’ werd gebruikt voor wat wij een natuurlijk (dus positief geheel) getal noemen, een getal dat een grootheid is ‘bestaande uit eenheden’ (Euklides vii, Def. 2); één werd dus niet als een getal beschouwd.¹

Ons begrip reëel getal was onbekend, en een lijnsegment had dus niet altijd een lengte, die in getallen kan worden uitgedrukt. Waar wij reële getallen gebruiken, gebruikte de Griekse wiskundige theoreticus meetkundige beschouwingen. Als Euklides wil uitdrukken dat het oppervlak van een driehoek gelijk is aan het halve produkt van hoogte en grondlijn zegt hij dat dit oppervlak de helft is van dat van een parallellogram met gelijke grondlijn dat tussen dezelfde evenwijdige lijnen ligt als de driehoek (Euklides i, 4). De stelling van Pythagoras was een betrekking tussen de oppervlakken van drie vierkanten en niet tussen de lengten van drie zijden. Vierkantsvergelijkingen komen in de Elementen voor, doch als meetkundige constructies op de zgn. ‘aanpassing’ berustende. De wortels zijn dan zekere lijnstukken, en daarom altijd positief. Deze opvatting over lijnen en getallen was een welbewuste daad, die op de overwinning van het Platonische idealisme binnen de Griekse bezittende klasse (voor zover ze in de wiskunde belangstelling had) berustte, en die een afkeer vertolkte tegenover de Oosterse opvattingen, die in de betrekkingen tussen meetkunde, algebra en rekenkunde geen beperkingen aan het getalbegrip oplegden. Er bestaan voldoende redenen om aan te nemen dat deze opvattingen, b.v. dat van het theorema van Pythagoras als een getallenbetrekking, aan de Ionische wiskundigen bekend moeten zijn geweest, en die opvattingen moeten dus later bewust verworpen zijn.

Toch is het gewone getallenrekenen, de logistica, gedurende alle perioden van de Griekse geschiedenis steeds levend gebleven, ook onder wiskundigen. Euklides moge het verworpen hebben en het aan de marktplaats hebben overgelaten, Archimedes en Heroon

1 Wij vinden nog bij Stevin, in zijn Arithmétique van 1585, een bijna hartstochtelijk betoog om ‘één’ als een getal te erkennen.

[p. 81]

gebruikten het met groot gemak en zonder gewetensbezwaren. Dit rekenen was gebaseerd op een notatie die met de tijd veranderde. Oorspronkelijk hadden de Grieken een stelsel waaraan een additief decimaal beginsel ten grondslag lag, als bij de Egyptenaren en later de Romeinen. In de Alexandrijnse periode, en misschien wel vroeger, kwam een methode in gebruik die anderhalf duizend jaar bestaan heeft, en niet alleen door mannen van wetenschap, doch ook door kooplieden en beambten werd aangewend. In dit stelsel gebruikte men de notatie van het Griekse alfabet om getallen uit te drukken¹, eerst 1, 2,..., 9 (dus 1 = α, 2 = β, enz.), dan de tientallen van 10 tot 90, (dus ι = 10, κ = 20, enz.) en eindelijk de honderdtallen van 100 tot 900 (dus ρ = 100, σ = 200, enz.). Soms werd er een streepje boven gezet, b.v. ᾶ = 1. Drie verouderde letters werden aan de 24 letters van het Griekse alfabet toegevoegd om de nodige 27 symbolen te krijgen. Zo kon men elk getal beneden 1000 met ten hoogste 3 symbolen uitdrukken, b.v. 14 als ιδ, 257 als σνζ, getallen groter dan 1000 werden door een eenvoudige toevoeging van symbolen aangegeven, b.v., α voor 1000. Breuken kon men er ook mee uitdrukken. Men vindt dit stelsel zowel in de bestaande manuscripten van Archimedes, Heroon en andere klassieke auteurs, als in koopmanshandschriften. Er bestaat archeologisch materiaal dat laat zien dat het ook op school werd onderwezen.

Dit was een decimaal, maar niet een positiestelsel, ιδ en δι konden beide alleen maar 14 betekenen. Dit ontbreken van een plaatswaarde en het gebruik van niet minder dan 27 symbolen zijn vaak als bewijzen voor de inferioriteit van dit stelsel aangevoerd. Het gemak, waarmee de antieke wiskundigen het gebruikten, het feit dat Griekse kooplui het zelfs voor ingewikkelde berekeningen accepteerden, de lange tijd dat het gebruikt werd (in het Oost-Romeinse Rijk tot aan zijn ondergang in 1453), wijzen er op dat dit Griekse stelsel ook enige voordelen had. Als men zich een beetje oefent in het gebruik, blijkt dat er weinig kunst voor nodig is om de elementaire operaties ermee te verrichten, zodra de betekenis van de 27 symbolen is begrepen (een taak niet moeilijker dan de 26 letters van ons alfabet te leren). Breukenrekening was ook vrij eenvoudig, maar hier waren de Grieken inconsequent, omdat een algemeen aanvaard systeem ontbrak. Ze gebruikten Egyptische

1 Eigenlijk werden hoofdletters gebruikt, dus Α voor α, Γ voor γ, enz. De letters α, β, γ, enz. zijn eerst in de Middeleeuwen ingevoerd, door Byzantijnse geleerden.

[p. 82]

stambreuken, Babylonische sexagesimaalbreuken en ook breuken in een notatie die enigszins aan de onze herinnert (Archimedes schrijft 10/71 als ῖοα´, met een accent om de noemer aan te wijzen). Decimale breuken werden niet gebruikt; deze verschijnen eerst in Europa nadat het rekenapparaat ver was uitgegroeid boven dat van de antieke wereld en in vele schoolboekjes vindt men decimale breuken niet voor de achttiende of zelfs negentiende eeuw.

Men heeft wel beweerd dat deze alfabetische manier van schrijven een slechte invloed heeft gehad op de groei van de Griekse algebra, omdat het gebruik van letters voor bepaalde getallen hun gebruik voor getallen in het algemeen, zoals wij het in onze algebra doen, verhinderde. Wij kunnen zulk een formele verklaring voor de afwezigheid van een Griekse algebra vóór Diofantos moeilijk aanvaarden, ook al waarderen wij ten volle de betekenis van een goede notatie. Indien de klassieke schrijvers de behoefte hadden gevoeld aan een goede algebra hadden ze wel de bijbehorende notatie gevonden, zoals we dat dan ook bij Diofantos zien beginnen. Het vraagstuk dat het bestaan en niet-bestaan van de Griekse algebra opwerpt kan alleen worden benaderd door verdere studies over het verband tussen Griekse en Babylonische wiskundigen, en dit weer in de gehele samenhang van de betrekkingen tussen de Griekse en de Aziatische wereld.

Literatuur

De klassieke Griekse wiskundige auteurs zijn allen in moderne uitgaven te verkrijgen, en van bijna allen bestaan vertalingen in het Engels, het Duits of het Frans. In de Nederlandse taal bezitten wij:

E.J. Dijksterhuis, De Elementen van Euclides (2 dln, Groningen, 1930). Dit boek bevat ook een kritisch overzicht van de literatuur vóór Euclides.

E.J. Dijksterhuis, Archimedes (eerste deel Groningen, 1938; vervolgd in ‘Euclides’ 15-17, 20 (1938-44), het geheel ook in het Engels, Kopenhagen 1956).

B.L. van der Waerden, Ontwakende wetenschap (Groningen 1950, ook in het Duits en Engels).

E.M. Bruins, Fontes mateseos (Leiden 1953). Dit boek bevat een aantal Griekse teksten voor schoolgebruik met verklaringen in het Nederlands.

[p. 83]

Verder in andere talen:

T.L. Heath, A History of Greek Mathematics (2 dln., Cambridge, 1912).

T.L. Heath, A Manual of Greek Mathematics (Oxford 1931, ook in Dover herdruk 1963).

T.L. Heath, The Thirteen Books of Euclid's Elements (3 dln., Cambridge 1908, ook in Dover herdruk 1955).

Al deze boeken van Heath (er bestaan nog andere, o.a. over Aristoteles, Diofantos en Archimedes) zijn standaardwerken.¹

P. Ver Eecke, Oeuvres complètes d'Archimède (Brussel 1921, herdruk Parijs 1961, heeft ook het commentaar van Eutocius).

P. Ver Eecke, Pappus d'Alexandrie. La Collection mathématique, (Parijs-Brugge 1933).

P. Ver Eecke, Proclus de Lycie. Les Commentaires sur le Premier Livre des Eléments d'Euclide (Brugge 1948).

I. Schneider, Archimedes (Darmstadt, 1979).

K. Manitius, Ptolemäus' Handboek der Astronomie, 2e uitg., bewerkt door O. Neugebauer, 2 delen (Leipzig, 1963), eerste uitgave 1912-13. Engelse vertaling met commentaar van J.G.T. Toomer (Springer, New York enz., 1984).

B.L. van der Waerden, Die Pythagoreër, Religiöse Bruderschaft und Schule der Wissenschaft (Zürich, München, 1979).

G. Loria, Le Scienze esatte nell'antica Grecia (2e ed., Milaan 1914).

G.J. Allman, Greek Geometry from Thales to Euclid (Dublin 1889).

J. Gow, A Short History of Greek Mathematics (Cambridge, 1884).

T. Dantzig, The Bequest of the Greeks (New York 1955).

W. Blaschke, Griechische und anschauliche Geometrie (München, 1953).

O. Becker, Das mathematische Denken der Antike (Göttingen, 1957).

G. Hauser, Geometrie der Griechen von Thales bis Euklid (Luzern, 1955).

K. Reidemeister, Die Arithmetik der Griechen, Einzelschriften

1 Thomas Little Heath (1861-1940) was een hoge beambte in het Engelse ministerie van financiën (tot 1926), Hij was een Fellow van de Universiteit van Cambridge. Zijn werken zijn klassieken op het gebied der Griekse wiskunde.

[p. 84]

Hamburger Mathem. Seminar 26 (1939).

K. Reidemeister, Das exakte Denken der Griechen (Hamburg 1959).

H. Wussing, Mathematik in der Antike (Leipzig, 1965) (behandelt ook de voor-Griekse wiskunde).

A.D. Steele, Über die Rolle von Zirkel und Lineal in der griechischen Mathematik, Quellen und Studien A2 (1932) 61-89.

A. Szabó, The Beginnings of Greek Mathematics, (Dordrecht enz., 1978).

W.R. Knorr, Archimedes and the Pre-Euclidean Proportion Theory, Arch. intern. hist. sc. 28 (1978) 183-244.

Vergelijkende Griekse, Latijnse en Engelse teksten in

J. Thomas, Selections illustrating the History of Greek Mathematics. (Londen, Cambridge Mass., 1939).

Verdere tekstkritiek in

P. Tannery, Pour l'histoire de la Science hellène (2e ed., Parijs 1930).

P. Tannery, Mémoires scientifiques (dln. 1-4) (Toulouse Paris 1912-20).

H. Vogt, Die Entdeckungsgeschichte des Irrationalen nach Plato und anderen Quellen des 4ten Jahrhunderts, Bibliotheca mathematica (3e ser.) 10 (1909-10) 97-105.

E. Sachs, Die fünf Platonischen Körper (Berlin 1917).

E. Frank, Plato und die sogenannten Pythagoreer (Halle, 1923).

S. Luria, Die Infinitesimaltheorie der antiken Atomisten, Quellen und Studien zur Gesch. d. Mathem. B 2 (1932) 106-185 vgl. hierbij het in het Russisch geschreven boek van dezelfde schrijver met dezelfde titel. Verh. Inst. v. Gesch. d. Wetenschap en Techniek ii 5 (Akademie der Wetenschappen USSR, 1935).

Over de betrekking tussen Griekse en Oosterse astronomie:

O. Neugebauer, The History of Ancient Astronomy. Problems and Methods, Journ. Near Eastern Studies 4 (1945) 1-38.

Id. A History of ancient mathematical Astronomy (3 dln., Springer, New York enz., 1975).

Vgl. hierbij:

B.L. van der Waerden, Die Anfänge der Astronomie. Erwachende Wissenschaft II (Groningen, 1967).

[p. 85]

Verdere literatuur:

W. Lietzmann, Der Pythagoreische Lehrsatz. Mit einem Ausblick auf das Fermatsche Problem. (Leipzig, 1951).

H.A. Naber, Das Theorem des Pythagoras (Haarlem, 1908).

F. Cajori, The History of Zeno's Arguments on Motion. Amer. Math. Monthly 22 (1915). Acht artikelen. Zie ook Isis 3 (1920-21) 8-20.

M.R. Cohen-J.E. Drabkin, A Source Book in Greek Science (New York, 1948).

T.L. Health, Mathematics in Aristotle (Oxford, 1949).

H.G. Apostle, Aristotle's philosophy of mathematics (Chicago, 1952).

P. Lorenzen, Die Entstehung der exakten Wissenschaften (Berlin 1960).

In het Russisch:

E. Kolman, Geschiedenis van de wiskunde in de Oudheid (Moskou, 1961).

I.G. Bashmakova, Lessen over de geschiedenis van de Griekse wiskunde, Istor.-matem. issledovaniye 11 (1958) 225-438.

De DSB heeft uitvoerige artikelen over Euklides, Archimedes en andere Griekse wiskundigen. In het Lexikon der antiken Welt (Stuttgart, 1965) vindt men ook artikelen over die wiskundigen, door K. Vogel en anderen.

Over Byzantijnse wiskunde, zie

K. Vogel, Der Anteil von Byzanz an Erhaltung und Weiterverbreitung der griechischen Mathematik, in Miscellanea mediaevalae Ia, Berlin 1962, 112-128. Zie ook Istor.-matem. Issled. 10(1973) 249-263 (Russisch).