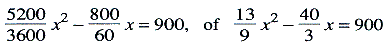Logo DBNL
Geschiedenis van de wiskunde (1990)

Geschiedenis van de wiskunde

(1990)–D.J. Struik–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

II. Het oude Oosten

1.

Gedurende het vijfde, vierde en derde millennium v. C. ontstonden nieuwe en meer ontwikkelde maatschappijvormen uit neolithische gemeenschappen die zich reeds eeuwen lang in subtropische of bijna subtropische gebieden langs de oevers van grote rivieren in Afrika en Azië hadden gevestigd. Deze rivieren waren de Nijl, de Tigris en de Eufraat, de Indus, en later de Ganges, de Hoang-ho en de Yang-tse.

De landerijen langs die rivieren konden overvloedige oogsten opleveren wanneer de rivieren onder controle waren gebracht en moerassen waren drooggelegd. In scherpe tegenstelling tot de woestijnen en berggebieden die deze gebieden omringden, konden de rivierdalen in een paradijs van vruchtbaarheid worden herschapen. Dit werd in de loop der eeuwen volbracht door het bouwen van dijken en dammen, het graven van kanalen en het aanleggen van reservoirs. De regeling van de watertoevoer vereiste samenwerking tussen de verschillende gemeenschappen, ook al lagen die naar toenmalige verhoudingen een heel eind van elkaar verwijderd. Dit bracht centrale administratie-organen in het leven, die niet meer in primitieve dorpen, doch in steden moesten worden gelokaliseerd. Deze steden, op kruispunten van handelswegen in of ook buiten de administratieve centra, werden tegelijkertijd plaatsen waar de produkten van landbouw en veeteelt ter markt konden worden gebracht. Er ontstond een tamelijk hoog overschot van zulke produkten, dat niet alleen de algemene levensstandaard verhoogde, doch ook een stedelijke aristocratie met machtige opperhoofden schiep. Er kwamen vele gespecialiseerde beroepen: handwerkers, soldaten, beambten, priesters. Het beheer der openbare werken werd in de handen van een blijvende bureaucratie geplaatst, een groep die verstand had van het gedrag der jaargetijden, de bewegingen der hemellichamen, de kunst van het landmeten, het opstapelen van voedingsmiddelen, of de heffing van belastingen. Gaandeweg ontstond een schrift waarin de handelingen van de bureaucratie en de daden der opperhoofden konden worden beschreven en bewaard. Zulke handwerkers en bureaucraten verkregen langzamerhand heel wat speciale technische kennis, waartoe ook kennis van de metaalbewerking en van de geneeskun-

de behoorde. En zo begonnen ze ook de kunst van het rekenen en meten te beheersen.

De maatschappij ten tijde van deze opkomst der steden (men spreekt wel van een revolutie: the urban revolution) was ook langzamerhand in klassen gesplitst. Men had opperhoofden, vrije en pachtboeren, handwerkers, schrijvers en andere beambten, horigen en slaven. Plaatselijke hoofden werden soms zo rijk en machtig dat ze van feodale heerschappen met beperkte autoriteit opklommen tot plaatselijke koningen met absolute macht. Twisten en oorlogen tussen allerlei despootjes konden er wel toe leiden dat grote gebieden onder een enkele monarch verenigd werden. Deze althans in de centrale gebieden vaak op irrigatie berustende maatschappijvormen met intensieve landbouw konden op deze manier tot een ‘Oosters’ type van despotisme voeren. Zulk despotisme kon eeuwen lang gehandhaafd blijven en dan weer ineenstorten, soms onder de aanvallen van woestijn- of bergstammen die aangetrokken werden door de rijkdommen der rivierdalen, ook wel door de verwaarlozing van het uitgestrekte, ingewikkelde en levensbelangrijke systeem van irrigatie. Onder zulke omstandigheden kon de macht van het ene koningshuis naar het andere overgaan, of het kon gebeuren dat het staatsverband opgebroken werd in kleinere feodale eenheden, en dan kon het proces van hereniging weer opnieuw beginnen, soms op hogere technische grondslag. Maar ondanks al die dynastieke revoluties en overgangen van feodalisme tot absolutisme en omgekeerd bleven de dorpseenheden, die de basis vormden van die ‘Oosterse’ maatschappijvormen, door de eeuwen wezenlijk onveranderd, en daarmee de wezenlijke economische en sociale structuur. De Oosterse maatschappij beweegt zich vaak in cyclische perioden, doch zelfs tot de huidige dag toe bestaan er nog vele gemeenschappen in Azië en Afrika (of Zuid-Amerika) waarin al eeuwen en eeuwen lang het leven op dezelfde wijze voortgaat. Onder zulke omstandigheden blijft de vooruitgang langzaam en aan toevalligheden onderworpen; perioden van culturele groei kunnen door eeuwen van stilstand en verval van elkaar gescheiden zijn.

Dit statische karakter van het Oosten verleende een zekere heiligheid aan zijn eeuwenoude instellingen, en maakte de vereenzelviging van de godsdienst met de staatsinstellingen mogelijk. De ambtenarij deelde vaak in dit godsdienstig karakter van de staat, en zo zien we in vele Oosterse landen de priesters als administrateurs van de domeinen. En aangezien de beoefening van de wetenschap de taak was van de bureaucratie vinden we in vele - maar ze-

ker niet in alle - Oosterse landen priesters als de voornaamste dragers van wetenschappelijke kennis.

2.

Oosterse wiskunde ontstond als een praktische wetenschap, nuttig voor het berekenen van de kalender, het beheren van de oogsten, de organisatie der openbare werken en de inzameling van belastingen. Oorspronkelijk werd uiteraard op praktisch rekenen en meten de nadruk gelegd. Doch wanneer een wetenschap eeuwen lang beoefend wordt door een speciale groep van mensen, wier taak het is, niet alleen die wetenschap toe te passen doch ook zijn geheimen aan leerlingen door te geven, dan ontwikkelen zich neigingen tot grotere abstractie en tot wetenschap om der wille van de wetenschap, zodat men haar als theorie gaat bestuderen. Rekenen ging zodoende over in algebra, niet alleen omdat het sommige praktische berekeningen gemakkelijker maakte, doch ook als de natuurlijke ontwikkeling van een wetenschap die in scholen van schriftgeleerden beoefend en ontwikkeld werd. Dit was ook de oorzaak dat het meten zich ontwikkelde tot een begin - maar ook niet veel meer dan een begin - van theoretische meetkunde.

Ondanks alle handel en verkeer, die in deze oude maatschappijen bloeiden, bleef de landbouw, verspreid over geïsoleerde en traditioneel voortlevende dorpen, de economische basis van de maatschappij. Daarom vindt men, ondanks een zekere gelijkvormigheid in de economische grondslagen en het algemene niveau van de wiskundige kennis, steeds verrassende verschillen tussen de diverse culturen. De afgeslotenheid van de Chinezen en de Egyptenaren was spreekwoordelijk, al was ze bij de Chinezen slechts in zekere perioden van hun geschiedenis een feit. Het is gemakkelijk het verschil te zien tussen de kunstvormen en de schrift van de Egyptenaren, de Mesopotamiërs, de Chinezen en de Indiërs. Men kan dus van Egyptische, Mesopotamische, Chinese en Indische wiskunden spreken, ofschoon zij in hun arithmetisch-algebraïsch karakter veel principiële overeenkomsten vertonen. Zelfs dan, wanneer de wetenschap gedurende een bepaalde periode in één land grotere vooruitgang vertoont dan in een andere periode of een ander land, blijft het algemene karakter en zelfs de symboliek voortbestaan.

Het is moeilijk nieuwe ontdekkingen in het Oosten precies te dateren. Het statische karakter van de economische structuur draagt er toe bij dat een wetenschappelijk leergebied eeuwen lang weinig veranderingen ondergaat. Het komt voor dat ontdekkingen die in het isolement van één stadsgebied worden gemaakt, nooit verder

doordringen of zelfs weer verloren gaan. Grote schatten in wetenschappelijke en technische kennis kunnen door dynastieke veranderingen, door oorlogen of natuurrampen verdwijnen. Zo vertelt men dat in het jaar 221 v.C., toen China voor het eerst onder de heerschappij van een absolute despoot, Shé Hunag Di (Chhin Shih Huang Té, de eerste keizer van China) verenigd werd, alle leerboeken met uitzondering van sommige (b.v. over de geneeskunst) op 's keizers bevel werden vernietigd. Later, zo zegt men, werd heel wat van de verloren schatten uit het hoofd weer opgeschreven, maar men begrijpt hoe moeilijk onder zulke omstandigheden het dateren of zelfs het bewaren van ontdekkingen wordt.

Een andere moeilijkheid bij het dateren van ontdekkingen in de Oosterse wetenschap komt voort uit het materiaal waarin de resultaten werden opgeschreven. De Mesopotamiërs gebruikten kleitafeltjes, die gebakken werden en praktisch onverwoestbaar zijn zolang zij in de puinhopen der oude steden onder de grond liggen.1 De Egyptenaren gebruikten papyrus, en veel hiervan is in het droge klimaat bewaard gebleven. De Chinezen en Indiërs gebruikten materiaal dat veel minder bestand was tegen de tand des tijds, zoals schors of bamboe. In het tweede millennium v.C. begonnen de Chinezen papier te gebruiken, doch er is weinig behouden van wat vóór 700 n. C. is beschreven. Onze kennis van de Oosterse wetenschap is dus uiterst gebrekkig, en voor de eeuwen vóór onze jaartelling zijn we bijna uitsluitend op materiaal uit Egypte en Mesopotamië aangewezen. Het is niet onmogelijk dat nieuwe ontdekkingen onze opinies over de verschillende prestaties van de vóór-Griekse wiskundigen aanmerkelijk kunnen wijzigen. Er was een tijd dat onze rijkste historische bronnen uit Egypte kwamen, en dit was aan de ontdekking, in 1856, van de zgn. Papyrus Rhind te danken.2 Deze Papyrus is omstreeks 1650 v.C. geschreven, doch bevat veel materiaal dat eeuwen ouder is. In de laatste vijftig jaren is door de merkwaardige ontdekkingen van F. Thureau Dangin en O. Neugebauer onze kennis van de Mesopotamische wiskunde aanzienlijk vermeerderd. Deze geleerden hebben, door de ontcij-

fering van vele kleitabletjes, de superioriteit van de Mesopotamische wiskunde boven de Egyptische aangetoond. Dit oordeel is waarschijnlijk wel van een blijvend karakter, aangezien in de Babylonische zowel als in de Egyptische teksten door de eeuwen heen een soort van wiskundige karaktervastheid bestaat. Tot die superioriteit kan hebben bijgedragen dat de economische ontwikkeling van Mesopotamië in het algemeen hoger stond dan die van de andere landen in de zgn. Vruchtbare Halve Maan (‘Fertile Crescent’), die zich uitstrekte van Mesopotamië tot Egypte. Mesopotamië lag op het kruispunt van een groot aantal karavaanwegen, terwijl Egypte betrekkelijk geïsoleerd lag. Bovendien eiste het in bedwang houden van de onberekenbare Tigris en Eufraat meer technische kennis en bestuursbekwaamheid dan het in bedwang houden van de Nijl, de rivier die wel de ‘most gentlemanly of all rivers’, de rivier met de beste manieren, is genoemd (Sir William Willcocks).1 We zouden in het geheel niet verbaasd zijn als b.v. verdere studie van de oudste wiskunde der Hindoes merkwaardige resultaten zou opleveren, al hebben wij daarvan tot nu toe geen overtuigend bewijs gezien.

3.

Wij putten onze kennis van de oud-Egyptische wiskunde voornamelijk uit twee mathematische papyri: allereerst uit de reeds vermelde Papyrus Rhind, die 84 opgaven bevat, en ten tweede uit de zgn. Moskouse Papyrus, die misschien twee eeuwen ouder is, en 25 opgaven heeft. Deze problemen waren al oude kost toen die papyri werden geschreven, doch er zijn papyri gevonden die van veel later, zelfs uit de tijd der Romeinen en Byzantijnen stammen, en die dezelfde methoden gebruiken. Deze methoden zijn gebaseerd op een tientallig getallenstelsel waarin iedere hoge eenheid, 1, 10, 100, 1000 enz. door een apart symbool wordt aangeduid. Aan zo'n systeem zijn wij gewend door de Romeinse schrijfwijze, want daar wordt b.v. 1878 uitgedrukt door mdccclxxviii. Deze notatie is in wezen additief, omdat b.v. dc betekent dat men d = 500 bij c = 100 moet optellen, en zo was ook de Egyptische rekenkunde sterk additief ingesteld. Dit betekent in de eerste plaats dat vermenigvuldiging tot herhaalde optelling werd teruggebracht. Zo werd, bijvoorbeeld, een getal met 13 vermenigvuldigd door het eerst te verdubbelen, dan het resultaat nogmaals, en dit nogmaals te verdubbelen, en de som van de laatste twee uitkomsten bij het oorspronkelijke getal op te tellen.

Voorbeeld van de berekening 13 × 11: /1 11
  2 22
  /4 44
  /8 88

De met een streepje / aangegeven nummers worden opgeteld, hetgeen 11 + 44 + 88 = 143 geeft. Deling van 143 door 11 gaat analoog.

 

Het merkwaardigste kenmerk van de Egyptische rekenkunde was de breukrekening. Breuken met (wat wij zouden noemen) teller 1, zgn. stambreuken, werden aangegeven door het getal van de noemer, met een tekentje erboven, dat wij hier door een streepje aanduiden, zodat wij 1/10 als /10 zullen schrijven. Alleen voor ½ en ⅔ bestonden speciale tekens. Alle breuken werden teruggebracht op sommen van stambreuken en hiervoor werden speciale tafels voor de herleiding van breuken van de vorm 2/n tot stambreuken gebruikt. Met het oog op de dyadische vorm van de vermenigvuldiging was dit voldoende om alle breuken tot stambreuken terug te voeren. De Papyrus Rhind bevat zulk een tafel, die voor alle breuken met oneven n van 5 tot 101 een reductie tot stambreuken geeft. Bijvoorbeeld:

n = 5: /3 /15 (dus ⅖ = ⅓ + 1/15)
  7: /4 /28  
  59: /36 /236 /531
  97: /56 /679 /776

Het principe dat aan deze speciale herleiding tot stambreuken ten grondslag ligt (b.v. waarom voor n = 19 de herleiding /12, /76, /114 en niet /12, /57, /228) is niet geheel duidelijk en men heeft hiervoor verscheidene theorieën ontwikkeld.1 De eerste breuk is echter altijd zo groot mogelijk, zodat de ontbinding in stambreuken tevens een soort benadering is. De tafel is waarschijnlijk eerst in de loop der eeuwen tot stand gekomen. Maar het rekenen met stambreuken heeft, ondanks het gecompliceerde karakter dat het delen erdoor kreeg, duizenden jaren geduurd; we vinden het niet alleen terug bij de Grieken, ook in de Europese middeleeuwen.

Vele problemen waren heel eenvoudig en gingen niet verder dan elementaire rekenkunde en een algebra bestaande uit één lineaire vergelijking met één onbekende:

 

Een grootheid daarbij haar ⅔, haar ½ en haar 1/7, samen opgeteld, geeft 33. Wat is deze grootheid?

 

Het antwoord, 14 28/97, wordt in stambreuken geschreven:

14 /4 /97 /56 /679 /776 /194 /388, hierbij vormen /56 /679 /776 juist /97 × 2.

 

Voor de onbekende in een vergelijking werd een hiëroglief ingevoerd, dat ‘hoop’, Eg. hau, betekende. Men spreekt dus wel van de Egyptische algebra als de ‘hau’ rekening.

De opgaven behandelen onderwerpen als de sterkte van brood en bier, het voederen van dieren en het bewaren van graan, en laten duidelijk de praktijk zien waaruit deze omslachtige en primitieve algebra is voortgekomen. Soms vindt men een vraagstuk van meer theoretische aard, b.v. dat waarin gevraagd wordt 100 broden onder 5 man zó te verdelen, dat hun aandelen een rekenkundige reeks vormen, en 1/7 van de som van de drie grootste aandelen gelijk is aan de som van de twee kleinste (eerst wordt de reeks 23, 17½, 12, 6½, 1 opgezet, de som hiervan is 60, en wordt deze reeks met 100/60 vermenigvuldigd). In één vraagstuk vinden we zelfs een meetkundige reeks: hier hebben we te doen met 7 huizen, in ieder huis zijn 7 katten, iedere kat bespiedt 7 muizen, enz.1

Enige vraagstukken waren meetkundig en ook gewoonlijk van praktische aard. Verscheidene behandelen het meten van oppervlakken. We denken hier aan het bekende verhaal van Herodotus, dat de Egyptenaren de meetkunde hadden uitgevonden omdat ze gedwongen waren iedere keer na de overstromingen van de Nijl de grenzen van de landerijen opnieuw uit te meten. Het oppervlak

van een (gelijkbenige) driehoek werd als het halve produkt van basis en hoogte bepaald. Het oppervlak van de cirkel met middellijn d werd uit de formule (d - d/9)2 berekend, hetgeen tot een waarde van π = 256/81 = 3,1605... leidt. Men vindt ook enige recepten voor de bepaling van inhouden, zoals die van de kubus, een blok en een rechte cilinder, alle beschouwd als voorwerpen, b.v. pakhuizen. Het meest belangwekkende resultaat van deze Egyptische inhoudsbepalingen was de uitdrukking voor het volume van een afgeknotte vierkante pyramide V = h/3 (a2 + ab + b2), waar a en b de zijden zijn van de twee vierkanten en h de hoogte is. Dit resultaat dat tot nu toe nog niet in andere antieke wiskundevormen is aangetroffen, is daarom zo merkwaardig omdat er geen aanleiding is te geloven dat de Egyptenaren zelfs maar het theorema van Pythagoras hebben gekend - ondanks het onbevestigde verhaal, dat Egyptische landmeters - zgn. harpedonaptai, touwspanners -rechte hoeken afzetten met een touw waarin 3 + 4 + 5 knopen zaten.1 Maar we moeten niet vergeten dat de bouwers van de paleizen in Luxor en Karnak heel wat praktische meetkunde moeten hebben gekend.

We moeten hier overigens wel even waarschuwen tegen allerlei overdrijvingen over de hoge ouderdom en diepte van de wiskundige kennis der Egyptenaren. Men heeft aan de bouwers van de piramiden, die omstreeks 3000 v.C. geleefd hebben, allerlei hogere wetenschappelijke kennis toegeschreven, en men treft nogal eens het verhaal aan dat de Egyptenaren in het jaar 4212 v. C. de zgn. Sothische periode voor de kalenderberekening hebben aangenomen. Zulk nauwkeurig wis- en sterrenkundig werk kan moeilijk aan een volk worden toegeschreven, dat zich langzaam uit neolithische verhoudingen ontwikkelt. Vaak komen deze verhalen tot ons doordat de latere Grieken de een of andere Egyptische traditie hebben overgeleverd. Aan oude beschavingen is gemeen dat zij ervan houden aan de grondbeginselen van hun kennis een heel lang bestaan toe te kennen. Wat we aan oorspronkelijke teksten werkelijk bezitten, wijst op een Egyptische wiskunde van beperkte omvang, doch binnen die omvang goed ontwikkeld. Iets dergelijks kan men ook zeggen van de sterrenkunde der Egyptenaren. Doch nu ons respect voor de astronomische kennis van oude volken (zoals Stonehenge) aan het stijgen is, moeten we wel wat voorzichtig zijn met onze oordelen.

4.

De wiskunde van Mesopotamië (of Irak, zouden we nu moeten zeggen) staat op een hoger peil dan de wiskunde van Egypte. We kunnen hier zelfs in de loop der eeuwen vooruitgang ontdekken. Reeds de oudste teksten, die tot de laatste Soemerische periode (de Derde Dynastie van Oer, ca. 2100 v.C.) behoren, vertonen een aanzienlijke bedrijvigheid in het rekenen. Deze teksten bevatten tafels van vermenigvuldiging, waarin een goed ontwikkeld sexagesimaal (zestigtallig) stelsel was geënt op een oorspronkelijk decimaal (tientallig) stelsel. Slechts twee tekens werden gebruikt, het ene stond voor 1, het andere voor 10, en daarmee werden alle getallen gevormd. De manier waarop dit gebeurde, is het meest karakteristieke kenmerk van deze rekenwijze. Waar de Egyptenaren iedere hogere eenheid door een speciaal symbool aanduidden, gebruikten deze Soemeriërs hetzelfde symbool, maar lieten de waarde daarvan door de positie in het getal bepalen. Zo kon het symbool voor 1 door zijn positie zowel 60, 602,... als 60-1, 60-2,... betekenen. Als het symbool voor 1 naast een ander symbool voor 1 stond, had het eerste symbool de waarde zestig, en 11 betekende wat wij door 61 uitdrukken. Een 5, gevolgd door 6, gevolgd door 3 (we zullen dit 5, 6, 3 schrijven) betekende 5 × 602 + 6 × 60 + 3 = 18363 in onze manier van schrijven. Dit sexagesimale positiestelsel, dat dus in beginsel niet verschilt van het stelsel dat wij gebruiken, behalve dan dat wij niet als basis het getal 60, maar het getal 10 hebben (zodat voor ons 563 = 5 × 102 + 6 × 10 + 3), maakt het rekenen veel gemakkelijker dan een stelsel als het Romeinse, iets waarvan men zich licht kan overtuigen door eens in ieder stelsel een vermenigvuldiging te beproeven. Het positiestelsel maakt ook het rekenen met breuken niet moeilijk, zoals we dat weten uit onze praktijk van de decimale breuken. Dit handige sexagesimale stelsel schijnt gegroeid te zijn uit administratieve praktijken. We bezitten althans duizenden teksten van diezelfde periode met verslagen over de aflevering van vee, graan, enz. vergezeld van bijbehorende berekeningen.

Zulk een schrijfwijze bracht dubbelzinnigheden mee, aangezien de waarde van ieder symbool niet altijd uit zijn positie duidelijk was. Het getal (5, 6, 3) kan ook wel 5 × 601 + 6 × 600 + 3 × 60-1 = 306 1/20 betekenen, en 11 niet alleen ons 61, maar ook 2 of 1/30. In zulke gevallen moest de waarde van het getal uit de verdere tekst worden afgeleid. Een andere dubbelzinnigheid kon optreden als een open plaats een nul moest voorstellen, zodat (11, 5) misschien 11 × 602 + 5 = 39605 kon betekenen. In de loop der tijden werd op zo'n plaats een bijzonder symbool voor nul geschreven,

doch dit gebeurde niet vóór de Perzische tijd. De zgn. ‘uitvinding van de nul’ is dus het logische resultaat van het werken met getallen in positiestelsel geschreven, doch deze uitvinding wordt eerst gedaan wanneer er reeds een aanzienlijke bedrevenheid in het rekenen is verkregen.

Zowel het zestigtallig stelsel als het positiesysteem is blijvend bezit van de mensheid gebleven. Onze huidige indeling van een uur en een cirkelgraad in 60 minuten en de minuut in 60 seconden komt via de Grieken en de Babyloniërs van de Soemeriërs. Men gelooft wel dat de keuze van het getal 60 in plaats van 10 als eenheid samenhangt met het feit dat 60 vele delers heeft hetgeen in het stelsel van maten en gewichten een zekere eenheid kon brengen, en bovendien het delen eenvoudiger maakt. De vroege geschiedenis van het positiesysteem, waarvan de blijvende betekenis wel met die van het alfabet is vergeleken1 - omdat bij beide uitvindingen een ingewikkeld stelsel van symbolen vervangen werd door een stelsel dat gemakkelijk te begrijpen is - blijft nog steeds in tamelijk duister gehuld. We kunnen met vrij grote zekerheid vaststellen dat zowel de Hindoes als de Grieken ermee in aanraking kwamen langs de karavaanwegen door Babylon. We weten ook dat Mohammedaanse geleerden later het decimale positiestelsel als een Indische uitvinding beschreven. Wat de mogelijke rol van China, dat reeds vroeg een decimaal positiestelsel bezat, hierbij is geweest, is nog niet duidelijk. Het is niet onmogelijk, dat de Chinese zowel als de Babylonische traditie de gehele verdere ontwikkeling van het positiestelsel heeft beïnvloed.

5.

De volgende groep van spijkerschrift-teksten behoort tot de periode van de eerste Babylonische dynastie, waartoe koning Hammurabi behoorde (1950 v. C.) en waaronder een Semitisch volk de oorspronkelijke bewoners, de Soemeriërs, had overwonnen. In deze teksten vinden we de rekenkunde voortgezet in een ontwikkelde algebra. Terwijl de Egyptenaren in deze periode slechts in staat waren eenvoudige lineaire vergelijkingen op te lossen, waren de Babyloniërs uit de tijd van Hammurabi in het volle bezit van de oplossing van vierkantsvergelijkingen (natuurlijk alleen voor positieve wortels). Ook losten zij lineaire en kwadratische vergelijkingen met twee veranderlijken op, en zelfs vraagstukken waarin derde- en vierdegraadsvergelijkingen optraden. Zij formuleerden zul-

ke vraagstukken slechts met bepaalde getallenwaarden als coëfficiënten, maar hun methode laat geen twijfel bestaan, dat ze een algemeen oplossingsschema hadden. Het volgende voorbeeld vindt men op een kleitafeltje uit die tijd. We geven het met de getallen (als in de oorspronkelijke tekst) sexagesimaal uitgedrukt.

‘Ik heb het oppervlak van twee vierkanten gesommeerd, het is (16, 40). De zijde van het ene is ⅔ van de zijde van het andere. Ik heb 10 van de zijde van het kleine vierkant afgetrokken. Wat zijn de zijden van het vierkant?’
Dit leidt tot de vergelijkingen x2 + y2 = (16, 40); y = ⅔x - 10, waarvan de oplossing kan worden teruggebracht tot die van de vierkantsvergelijking

illustratie

waarvan de oplossing is x = 30, y = 10.
In onze notatie, waarin (16, 40) door 1000 wordt weergegeven, wordt deze vergelijking

illustratie

Voor de oplossing zijn de leden der vergelijking met 5200 te vermenigvuldigen en links het kwadraat te complementeren. Hierbij moet de wortel uit (22,24,26,40) worden getrokken, dit is (36,40). De oplossing in de tekst beperkt zich - zoals altijd in deze Oosterse teksten - eenvoudig tot de opsomming van de stappen, die genomen moeten worden: Neem het vierkant van 10, geeft (1,40), trek (1,40) af van (16,40), geeft (15,0), (1,0)2 = (1,0,0), 402 = (26,40) enz.

Het aritmetisch-algebraïsch karakter van deze Babylonische wiskunde blijkt ook uit de meetkunde. Evenals in Egypte ontstond de meetkunde uit de behoeften van de praktijk, doch de meetkundige vorm van het vraagstuk werd vaak slechts een manier om een algebraïsch praktisch of theoretisch vraagstuk te formuleren. In ons vorige voorbeeld zagen we hoe een vraagstuk omtrent het oppervlak van vierkanten tot een stelsel van twee vergelijkingen voerde, en dat soort vraagstuk is typisch. Uit de teksten blijkt dat de Babylonische meetkundigen van de Semitische periode het oppervlak van eenvoudige rechtlijnige figuren en de inhoud van eenvoudige ruimtefiguren wisten te berekenen. Voor de inhoud van de afgeknotte piramide is de Babylonische formule (nog?) niet gevonden, wel zijn benaderingen bekend. Een benadering voor het oppervlak van een vierhoek met overstaande zijden a,c; b,d was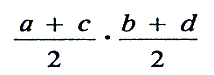



illustratie

Het zgn. theorema van Pythagoras was bekend in volle algemeenheid als een getallenbetrekking tussen de zijden van een rechthoekige driehoek, en we hebben zelfs Pythagoreïsche drietallen uit die tijd, b.v. 120, 119, 169 (d.i. (120)2 + (119)2 = (169)2). Het algemene karakter van deze meetkunde bleef steeds behouden, ook in latere teksten, in het bijzonder die van de derde periode waaruit er een groot aantal aan het licht zijn gekomen, nl. die van de Nieuw-Babylonische, Perzische en Seleucidische rijken (van ca. 600 v. C.-300 n. C.).

De teksten van die latere periode tonen de invloed van de Babylonische astronomie, die in die jaren een veel strenger wetenschappelijk karakter verkreeg door het tabelleren en analyseren van de loop van de maan en de planeten. De rekentechniek verscherpte zich, zodat algebraïsche vraagstukken werden opgelost die zelfs nu nog heel wat numerieke vaardigheid vereisen. Sommige berekeningen uit de Seleucidische tijd gaan tot zeventien sexagesimale plaatsen. Zulk ingewikkeld rekenwerk had niet veel meer te maken met de oude vraagstukken over landmeting of over belastingen, maar was beïnvloed door de sterrenkunde of eenvoudig door het feit dat men zulk werk leerzaam en plezierig vond.

Al dit rekenen was vaak op het gebruik van tabellen gebaseerd. Men heeft tabletten gevonden, die eenvoudige tafels van vermenigvuldiging, en andere die tweede- en derdegraadswortels bevatten. Eén tafel bevat een lijst van getallen van de vorm n3 + n2, die blijkbaar is gebruikt om kubieke vergelijkingen van de vorm x3 + x2 = a op te lossen. Als benaderingswaarden vinden we voor √2 de waarde (1,25) = 1 5/12 (√2 = 1,4142..., 1 5/12 = 1,4167..)1 en voor 1/√2 (= 0,7071) vindt men 17/24 (= 0,7083). Het schijnt dat vierkantswortels berekend werden volgens een formule die we kunnen schrijven als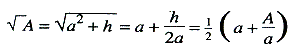



illustratie

(voor A = 2 neme men a = 4/3).

Wat de waarde van π betreft, die wordt in de meeste teksten eenvoudig op 3 gezet, de waarde die we ook in de Bijbel aantreffen (ii Kron. 4:2). Hier wordt dus het oppervlak van de cirkel gelijk

1/12 het kwadraat van de omtrek genomen. Er zijn echter teksten die tot een waarde π = 3⅛ voeren.1

 

De vergelijking x3 + x2 = a wordt in een vraagstuk gevonden waarin de oplossing gezocht wordt van het systeem xyz + xy = 1 + ⅙, y = ⅔x, z = 12x. Dit leidt tot (12x)3 + (12x)2 = 252, of (uit de tabel:) 12x = 6.

 

Er bestaan ook spijkerschriftteksten met vraagstukken over samengestelde interest. Zo wordt berekend hoe lang het zal duren totdat een zekere som geld zich verdubbeld heeft, indien ze tegen 20% samengestelde interest uitstaat. Dit voert tot de vergelijking (1⅕) x = 2, die wordt opgelost door eerst vast te stellen dat x tussen 3 en 4 ligt, waarna het antwoord berekend wordt door lineaire interpolatie. In moderne schrijfwijze: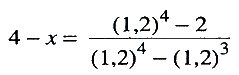



illustratie

hetgeen voert tot x = 4 (jaar)minus (2,33,30) maanden.

Een van de oorzaken van de ontwikkeling der algebra omstreeks 2000 v. C. is, naar het schijnt, het gebruik van het oude Soemerische schrift door de nieuwe Semitische heersers. Het oude schrift was, zoals de hiërogliefen, een collectie van ideogrammen, waarbij ieder teken een speciaal begrip aanduidde. De Semieten gebruikten ze om hun eigen taal fonetisch weer te geven en namen ook enige tekens in de oude betekenis over. Deze tekens drukten nu begrippen uit, doch werden nu anders uitgesproken. Zulke tekens waren zeer geschikt voor een algebraïsch schrift, evenals onze tekens +, -, enz., die ook ideogrammen zijn. In de administratiescholen van Babylon was deze algebraïsche taal gedurende vele generaties in de leercursus opgenomen, en ondanks alle veranderingen in de taal der heersers - Kassieten, Assyriërs, Meden, Perzen - bleef deze traditie bestaan.

Die meer ingewikkelde vraagstukken behoren tot een periode - de Perzische en Seleucidische - waarin Babylon niet langer een politiek centrum was, doch nog steeds het culturele centrum bleef van een groot gebied, waar niet alleen Babyloniërs woonden, doch ook Perzen, Grieken, Joden, Hindoes en vele andere volkeren. In die spijkerschriftteksten kan men door alle eeuwen heen een conti-

nuïteit van wetenschappelijke traditie waarnemen, die er op schijnt te wijzen, dat althans in het centrum nooit veel op cultureel gebied veranderde. Men kan wel aannemen, dat deze plaatselijke ontwikkeling ook de invloed ondervond van andere beschavingen, en dat ook deze weer op hun beurt door de Babylonische wetenschap werden beïnvloed. Wij weten dat de Babylonische sterrenkunde van die periode de sterrenkunde van de Grieken aan materiaal heeft geholpen en dat de Babylonische wiskunde op de rekentechniek van andere volken bevruchtend heeft gewerkt. Griekse en Indische wetenschap hebben elkaar wel in de Babylonische geleerdenscholen ontmoet. Maar we weten nog heel weinig van de rol die Perzisch en Seleucidisch Mesopotamië in de verspreiding van de sterrenkunde hebben gespeeld, maar wat we weten wijst er op, dat die rol belangrijk was. De Middeleeuwse Arabische en Indische wetenschap kregen vele hunner ideeën niet alleen uit Alexandrië, doch ook uit Babylon.

6.

Wij vinden nergens in de wiskunde van het Oosten iets dat op een bewijs lijkt. In plaats van gedocumenteerde redeneringen krijgen we alleen bepaalde voorschriften: ‘Doe het nu zó, dan weer zó!’ We weten niet hoe de theorema's en voorschriften zijn gevonden. Hoe b.v. zijn de Babyloniërs aan het theorema van Pythagoras gekomen? Verscheidene pogingen zijn gedaan om aan te tonen, hoe de Egyptenaren en Babyloniërs hun resultaten konden hebben verkregen, maar zulke pogingen blijven hypothesen. Dit schijnt aan ons, die onze wiskunde anders hebben geleerd en de school van Euclides' meetkunde hebben doorlopen, vreemd en hoogst onbevredigend toe. We begrijpen het echter beter, wanneer we bedenken dat heel wat van de wiskunde die we onze technici en ingenieurs doceren, nog steeds voornamelijk uit recepten bestaat, zonder dat veel werk van strenge bewijzen wordt gemaakt. In het middelbaar onderwijs wordt de algebra ook vaak niet als een deductieve wetenschap doch als een stel voorschriften geleerd. Oosterse wiskunde schijnt in de duizenden jaren van haar bestaan zich nooit hebben kunnen losmaken van de invloed der technologische en administratieve problemen waaruit ze is voortgekomen.

7.

In hoeverre hebben de Grieken, Babyloniërs en Chinezen de oude Indische wiskunde beïnvloed? We weten hier weinig van, maar zeker is dat Indische geleerden van latere dagen nadruk hebben gelegd op de hoge ouderdom van hun wiskunde. Men kent evenwel geen wiskundige teksten die met zekerheid in de tijd vóór

de Christelijke jaartelling teruggaan. De oudste teksten kan men misschien in de eerste eeuwen n. C. plaatsen. Wij weten wel, dat de Hindoes in de oude tijd decimale getallenstelsels zonder positiewaarde gebruikten. Zulk een systeem was b.v. dat van de zgn. Brâhmî-getallen, waarin we speciale symbolen vinden voor de nummers 1, 2, 3,..., 9, 10; 20, 30, 40,..., 100; 200, 300...; 1000; 2000... enz. Deze symbolen gaan op zijn minst terug naar de tijd van Koning Açoka (300 v.C.).

Ook bezitten we de zgn. Sūlvasūtras, die gedeeltelijk tot 500 v.C. of nog vroeger teruggaan, en die wiskundige voorschriften bevatten die van oude inheemse oorsprong zijn. Men vindt die voorschriften te midden van religieuze en ritualistische beschouwingen, waaronder er zich een aantal met de bouw van altaren bezighouden. Hier vindt men recepten voor de constructie van vierkanten en rechthoeken, uitdrukkingen voor de betrekking van diagonaal en zijde van het vierkant, en voor die tussen cirkels en vierkanten. In speciale gevallen is het theorema van Pythagoras bekend, en we ontmoeten enige eigenaardige benaderingswaarden met behulp van stambreuken, zoals b.v. (in onze notatie):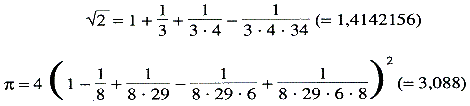



illustratie

Ook π = 18 (3 - 2√2) (= 3,088).

 

Het is merkwaardig dat deze resultaten niet meer in latere geschriften der Hindoes voorkomen. De continuïteit van de traditie, die zo typisch is voor de Egyptische en Babylonische wiskunde, schijnt in die oude Indische wiskunde te ontbreken, en men kan dit misschien verklaren uit de uitgestrektheid van het Indische subcontinent. Er kunnen op verscheidene ver uiteengelegen plaatsen verschillende mathematische scholen hebben bestaan. Wij weten bijvoorbeeld, dat het Jainisme, dat ongeveer even oud is als het Boeddhisme (ca. 500 v. Chr.) de studie der wiskunde aanmoedigde. In heilige boeken van deze godsdienst vinden we b.v. de waarde π = √10.1

8.

De studie van de oud-Chinese wiskunde wordt, evenals die van het oude Indië, bemoeilijkt door de schaarste van vertalingen, zodat we op tweedehands informatie aangewezen zijn, zolang we geen Chinees of Sanskriet kennen. Gelukkig kunnen we in de boeken van Mikami en Needham, die in het Engels zijn geschreven, een goede oriëntatie in de oud-Chinese wiskunde verkrijgen, en er komen nu ook geregeld artikelen over speciale Chinese teksten in vertalingen uit, vooral in het Engels en het Russisch. Wij hebben b.v. een Russische en een Duitse vertaling van de klassieke tekst Jiu zhang suan-shu (Chiu Chang Suan Ching), de ‘Negen Hoofdstukken over de kunst der wiskunde’.1 Dit boek is wel de oudst bewaarde Chinese leercursus in de wiskunde, en in de vorm waarin wij het thans hebben, dateert het van de tijd der Han-dynastie (202 v. C.-220 n. C.), doch kan veel ouder materiaal bevatten. Ditzelfde geldt voor een ander boek, de Zhou bei (‘Chou Pei’), doch dit is slechts gedeeltelijk wiskundig. Die ‘Zhou Pei’ is echter interessant, omdat het het theorema van Pythagoras bespreekt. De ‘Negen Hoofdstukken’ zijn daarentegen geheel wiskundig en ook daarom van belang, omdat ze al reeds geheel het karakter dragen, dat de Chinese wiskunde door de eeuwen heen tot de zeventiende eeuw heeft behouden.

Zeer oud zijn ook zekere diagrammen uit boeken van de Han-periode, zoals de Yi-jing (I-ching, Boek der Veranderingen). Hiertoe behoort het legendarische toverkwadraat (Lo Shu):

4 9 2
3 5 7
8 1 6

De Chinezen hebben steeds decimaal gerekend, en reeds in het tweede millennium v. C. vinden we getallen die door negen symbolen in positie werden uitgedrukt. Deze schrijfwijze moet in de Han-periode of reeds eerder ingeburgerd zijn geraakt. De negen symbolen werden door bamboestaafjes in verschillende orde aangegeven, zo betekende ⊥ ⊤⊤ = ⊤⊤⊤⊤ het getal 6729, en dit was ook de manier waarop het getal werd geschreven. De elementaire rekenoperaties werden uitgevoerd op rekenborden, waarbij lege plaatsen de nul aangaven (eerst in de 13e eeuw n. C. vinden we een

eigen symbool voor nul, 0, doch dit kan best veel ouder zijn).

Bij de berekening van de kalender werd een soort sexagesimaalsysteem gebruikt, dat men vergelijken kan met een combinatie van twee met elkaar verbonden tandraderen, het ene met 12, het andere met 10 tanden. Op die manier ontstond 60 als een hogere eenheid, een ‘cyclus’. (Men denke aan Tennyson's ‘Locksley Hall’: better fifty years of Europe than a cycle of Cathay).1

De wiskundige inhoud van de ‘Negen Hoofdstukken’ bestaat voornamelijk uit vraagstukken en algemene recepten voor de oplossing. Deze vraagstukken hebben hun oorsprong in de praktijk, maar gaan er vaak bovenuit. Vierkants- en derdemachtswortels worden berekend, zo wordt b.v. 751½ als vierkantswortel uit 564752¼ gevonden. In berekeningen met de cirkel werd π = 3 aangenomen.

Heel wat vraagstukken leiden naar algebraïsche vergelijkingen, zoals die worteltrekking die tot de vergelijkingen x2 - a = 0, x3 - b = 0 voert. Interessant zijn de systemen van lineaire vergelijkingen, b.v.

3x + 2y + z = 39
2x + 3y + z = 34
x + 2y + 3z = 26

die geschreven werden met behulp van de ‘matrix’ van de coëfficiënten. De oplossing werd aangegeven in een vorm die we thans een ‘matrixtransformatie’ zouden noemen. In zulke matrices komen ook negatieve getallen voor, voor de eerste keer in de geschiedenis van de wiskunde.

Bij de Chinese wiskunde doet zich het ongewone geval voor, dat een wiskundige traditie van de Oudheid tot bijna de huidige dag zonder onderbreking zich heeft gehandhaafd, zodat men haar ontwikkeling en maatschappelijke rol beter kan bestuderen dan dit het geval is met de wiskunde van Egypte en Babylonië (of der Maya's in Amerika), die tot ondergegane beschavingen behoren. Zo weet men b.v. dat kandidaten voor staatsposities een nauwkeurige kennis van een aantal klassieke werken moesten bezitten, en bij het examen werd nadruk gelegd op geheugenwerk. Zo kon de traditionele theorie onveranderd van generatie tot generatie overgeleverd worden. Zulk een praktijk werkt stagnerend, en maakt

uitvindingen en ontdekkingen moeilijk, ofschoon de traditie gehandhaafd blijft. Grote historische catastrofen konden soms het doorwerken van de traditie verhinderen of vertragen. We hebben een dergelijke toestand ook in Indië aangetroffen, waar we zelfs wiskundige teksten hebben die in stanza's zijn geschreven om het uit het hoofd leren te vergemakkelijken. Misschien is de wiskundige praktijk van de oude Egyptenaren en Babyloniërs niet veel anders geweest.

De verstening van de wiskunde kon slechts voorkomen worden door het ontstaan van een geheel nieuwe beschaving. Die kwam dan ook werkelijk. In de Griekse wereld, met zijn geheel andere levenshouding, werd de wiskunde op een nieuw en hoger wetenschappelijk standpunt verheven.

Literatuur

The Rhind Mathematical Papyrus, uitgeg. door T.E. Peet (Londen, 1923).
The Rhind Mathematical Papyrus, uitgeg. door A.B. Chace, L. Bull, H.P. Manning en R.C. Archibald (2 dln. Oberlin, Ohio, 1927-29).
Dit boek heeft een uitgebreide bibliografie van de Egyptische en Babylonische wiskunde. Een andere bibliografie, voornamelijk over antieke astronomie, in het geciteerde boek van Neugebauer, p. 18.
Mathematischer Papyrus des staatlichen Museums der schönen Künste in Moskou, uitgeg. door W.W. Struve en B.A. Turajeff (Berlijn 1930).
O. Neugebauer, Vorlesungen über Geschichte der antiken mathematischen Wissenschaften i. Vorgriechische Mathematik (Berlijn 1934).
O. Neugebauer, Mathematische Keilschrift-Texte (3 dln. Berlijn, 1935-37).
O. Neugebauer, The exact Sciences in Antiquity (Princeton, 1952, 2e uitg. 1957, Dover uitg., 1969, zie ook E.M. Bruins, Janus 17 (1958) 68-72.
O. Neugebauer-A. Sachs, Mathematical Cuneiform Texts (New Haven, 1945).
E.M. Bruins-M. Rutten, Textes mathématiques de Suse (Paris, 1961).
F. Thureau-Dangin, Sketch of a History of the sexagesimal System, Osiris 7 (1939) 95-141.
F. Thureau-Dangin, Textes mathématiques babyloniens (Leiden, 1938).
R.J. Gillins, Mathematics in the Time of the Pharaos (Cambridge, Mass., 1972, Dover reprint 1982). Zie H.M. 4 (1977) 445-452.
Tussen de hierboven genoemde geleerden bestaan zekere meningsverschillen omtrent de zin van zekere babylonische teksten. Zie daarbij ook
S. Gandz, Conflicting interpretations of Babylonian Mathematics, Isis 31 (1940) 405-425.
Een overzicht over de vóór-Griekse wiskunde vindt men ook in R.C. Archibald, Mathematics before the Greeks, Science 71 (1930) 109-121, 342; zie ook ib. 72 (1930) 36.
D.E. Smith, Algebra of 4000 years ago, Scripta mathematica 4 (1936) 111-125.
K. Vogel, Vorgriechische Mathematik (2 dln. Hannover, Paderborn, 1958, 1959).
Een uitstekende beschrijving door een vooraanstaande autoriteit. De verschillende delen van het Bulletin of the Calcutta Mathematical Society bevatten vele artikelen over de oude Indische wiskunde.

Bovendien:

B. Datta-A.N. Singh, History of Hindu Mathematics (2 dln. Lahore, 1935-38). Zie ook bespreking door O. Neugebauer in Quellen und Studien 3 B (1936) 263-271.
L.v. Gurjar, Ancient Indian Mathematics (Poona 1947, zie ook Mathem. Reviews 9, blz. 73).
G.R. Kaye, Indian Mathematics, Isis 2 (1919) 326-356.
A. Seidenberg, The ritual origin of geometry, Archives for Hist. Exact Sciences (1962) 408-527.
C. Müller, Die Mathematik der Sulvasūtra, Abh. mathem. Sem. Hamburg 7 (1929) 173-207.

Over de Chinees-Japanse wiskunde:

Y. Mikami, The Development of Mathematics in China and Japan (Leipzig 1913, herdruk New York 1961).
Y. Mikami, On the Japanese theory of determinants, Isis 2 (1914) 9-36, zie ook ib. 4 (1921-22) 70-77.
Y. Mikami, Mathematical papers from the far East. Abh. zur Gesch. d. mathem. Wiss. 28 (Leipzig-Berlin, 1910).
J. Needham (with the collaboration of Wang Ling), Science and civilization in China iii (Cambridge, 1959).
T. Hayashi, Brief History of Japanese Mathematics, Nieuw Archief v. Wiskunde, 2e ser., 6 (1905) 296-361, 7 (1907), 105-161. Zie ook ib. 9 (1911) 370-372, 373-386 (Y. Mikami).
L. van Hée, Le classique de l'ile maritime, ouvrage chinois du iii e siècle. Quellen und Studien zur Geschichte der Mathematik B, Studien 2 (1932) 255-280.

In het Russisch:

E.I. Berezkina, De oudchinese verhandeling: ‘Wiskunde in negen boeken’, Istor. Matem. Issled. (Moskou) 10 (1957) 423-584.
Duitse vertaling: Neun Bücher arithmetischer Technik, übersetzt und erläutert von K. Vogel. Ostwalds Klassiken, Neue Folge 4 (Brunswijk, 1968).
R. Wilhelm, ‘I Ging’ [I Ching] Das Buch der Wandlungen, 2 delen, Jena 1924. Engelse vertaling van C.F. Baynes, New York, 1950.

Over de structuur van de Oosterse maatschappij:

J. Needham: Science and Society in East and West, Science and Society 28 (1964) 385-408. Zie ook
bldz. 127-149 van The Science of Science, ed. M. Goldsmith and A. Mackay, Londen, 1964.
K.A. Wittfogel, Die Theorie der orientalischen Gesellschaft, Zeitschrift für Sozialforschung 7 (1938) 90-122. Ook Le mode de production asiatique, La Pensée 114 (1964) 3-78.

Verder nog:

B.L. van der Waerden, Ontwakende wetenschap, Groningen, 1950. Vol. XV, supplement I van DSB, New York 1978, heeft op blz. 531-818 ‘Topical Essays’ artikelen over wis- en sterrenkunde en wetenschap in 't algemeen, in Indië, Mesopotamië, Egypte, Japan en de Maya's.
B.L. van der Waerden, On Pre-Babylonian Mathematics, AHES 23 (1980) 1-26, 27-46.
Zie ook A. Seidenberg, AHES 18 (1978) 301-342.

Zie verder de literatuurlijst na Hoofdstuk iv.


Vorige Volgende