Wisconstighe gedachtenissen. Deel 4: van de weeghconst

[p. 191]

Tweede deel des byvovghs der weeghconst,
vant catrolwicht.

[p. 192]

Cortbegryp⁺ des catrolwichts.

AL soo sijn Vorstelicke Ghenade deursien hadde het bouck Delle fortificationi di Buonaiuto Lorini, en daer in overlesen een handel van catrollen, vvaer in gheseyt vvort van ghevvichten alleenlick rechtopgaende, deur treckende crachtenrecht neer vvaert streckende: En dat nocht ans metter daet dicvvils de selve niet recht op en neer en gaen, so is hy begheerich gevveest oock te verstaen decrachten, reden en oirsaken der scheeve, om alsoo van desen handel volcommen kennis te hebben, vvelcke gheneghentheyt oock in genouchsaem reden ghegront schijnt, ghemerct catrollen dadelick seer ghebruyckt vvorden, tot optrecking van groote ghevvichten, en dattet somvvijlen oirboir cansijn, van te vooren te vveten vvat macht datter behouft om een voorghestelde svvaerheyt op te trecken. Nu alsoo hy hem gheoeffent hadde inde voorgaende VV eeghconst, mettet eerste deeldes Byvoughs, vvaer deur de vvichtighe ghedaenten des Catrolvvichts grondelick connen verstaen vvorden, en dat hy hem dadelick daer toebegaf, soo heb ick t'ghene daer af ghedaen vviert onder sijn vvisconstighe ghedachtenissen vervought, als volght.

+ Argumentum.

[p. 193]

Voorstel.

T'ondersoucken de ghedaenteder ghevvichten opghetrocken met catrollen.

Eer wy totte saeck commen sullen int ghemeen dit segghen: Als wy spreken van een ghegeven ghewicht, men mach sich int ghedacht beelden, om vande saeck met volcommenheyt claerlicker te handelen, dattet ghewicht des ondersten catrols, mettet ghewicht daer an hangende, t'samen maken t'ghegeven gewicht; voort dattet verschil der swaerheyt veroirsaeckt deur de tau, hier voor gheen verschil ghenomen en wort.

1 Voorbeelt met rechtvvichticheyt.

Laet in dees eerste form A een catrol sijn, hanghende daer an t'ghewicht B, de tau sy C D E F, wiens twee deelen C D, F E, evewijt van malcander sijn, of beyde rechthouckich op den^* sichteinder. Dit aldus wesende, en het heel ghewicht B alsoo hanghende ande twee deelen C D, F E, en op yder deel eveveel ghewelts ancommende, soo hangt om de draeyende beweeghlickheyt der schijf



an yder deel den helft van B: Daerom soo ymant sijn hant stelde ant punt F, houdende t'ghewicht in die standt, op sijn handt soude commen den helft der

* Horizontem.

[p. 194]

swaerheyt van B, waer uyt de oirsaeck blijckt, waerom de ghewichten alsoo met een catrol lichter opgetrocken worden dan sonder catrol. Merckt nochdatmen hier siet plaets te houden dese ghemeene weeghconstighe reghel:

Ghelijck wech des doenders, tot wech des lijders,
Alsoo ghewelt des lijders, tot ghewelt des doenders.

Want de hant an F, welcke hier doender is, opgaende 2 voeten, t'ghewicht B, dats hier lijder, en gaet maer op 1 voet, en dat om bekende oirsaken.

Deur t'ghene tot hier toe verclaert is vande eerste form, alwaer t'ghewicht op ghetrocken wort over een schijf, canmen verstaen derghelijcke ghedaente wanneerment treckt over twee schijven, als in dees tweede form, alwaer C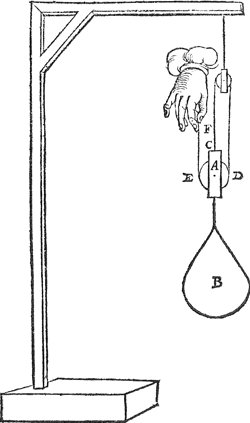



weerom tander uyterste der tau beteyckent: Want het ghewicht B dan hangende an drie tauwen, die elck een derdendeel draghen, soo en heeft de hant an F dan maer de ghewelt te doen van een derdendeel des ghegheven ghewichts.

[p. 195]

Ende over noch een schijf meer loopende als in dees 3 form, want het ghewicht B dan hanghende an vier tauwen die elck een vierendeel draghen van B, soo en heeft de hant an F dan maereen vierendeel des ghewichts B ghewelt te



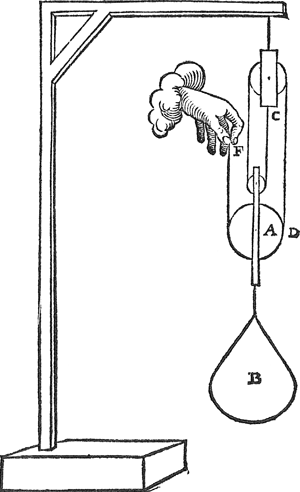doen. Waer me bekent is de ghemeene reghel van ghewichten over meer schijven ghetrocken sijnde.

Hier staet noch te dedencken datmen metter daet selden alsoo an F opwaert treckt, ghelijck wy om claerder bewijs wille inde boveschreven drie formen by voorbeelt ghestelt hebben, maer men doet ghemeenelick de tau loopen over noch een schijf meer, om van boven neerwaert te trecken als in dese 4 form: Doch soo is te weten dat sulcke vierde oft laerste schijf, ande hant F gheen verlichting noch verandering desghewichts en brengt, om dattet gewicht B maer an vier tauwen en hangt ghelijck inde 3 form, want dese laetste tau een vijfde tau schijnende, en is eyghentlick mette vierde al maer een selve. Waer by te verstaen is, dat al liepe die tau over noch hondert sulcke catrollen, dat den trecker daer me gheen verlichting en crijcht.

Maer soomen van t'voornomde dadelicke proef wilde sien, men sal an F deser vierde form, in plaets des hants hanghen een ghewicht als doender, wesende t'vierendeel van het optreckelick ghewicht, en sullen teghen malcander soo int werck gheen faute en is, evestaltwichtich bevonden worden. Macr om dat optreckelick ghewicht heel volcommelick uyt te spreken, het is de somme deser drie, te weten t'ghewicht B, t'onderste carrol A, en t'ghewicht veroirsaeckt deur de swaerheyt der tau. Maer om de selve swaerheyt der tau breeder te verclaren, soo laet D en E sijn de uyterste gheraeckselen der tau teghen de schijf A, en G H

[p. 196]

de uyterste gheraeckselen der tau teghen de bovenste schijf des bovenste catrols, L M de uyterste gheraeckselen der tau teghen de bovenste schijf des ondersten catrols; voort sy N t'middelste punt der tau tusschen G en H, en O t'middelste



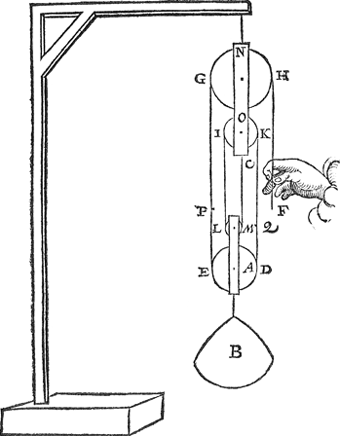punt der tau tusschen I en K, en C t'ander uyterste der tau: Laet voort gheteyckent worden in G E t'punt P, alsoo dat G P even sy met H F: Daer na in K D t'punt Q alsoo dat K Q even sy met I L. Dit so wesende, N G P is even en evewichtich met N H F, en O I L met O K Q: Maer C M en brengt lichticheyt noch swaerheyt by. Sulcx dattet ghegeven gewicht mettet catrol, noch beswaert worden, so veel als veroirsaken de drie sticken taus, te weten des halfronts L M, des halfronts D E, en het recht stick Q D.

Merckt noch dat alsmen met catrollen dadelick yet optreckt, alsoo dattet eynde der voortghetrocken tau inde locht blijft hanghen, sonder vloer te gheraken, soo veel dat voortghetrocken deel taus weeght, soo veel sal openbaerlick den trecker min ghewelt behouven te doen.

2 Voorbeelt met scheefvvichticheyt.

Laet dese eerste form sijn alsins ghelijck d'eerste des eersten voorbeelts, uytghenomen dat de hant hieran F niet recht op en treckt, maer scheefter sijdewaert uyt, t'welck soo sijnde, t'ghewicht op elcke tau ancommende, wort bekent deut het 5 vervolgh des 1 deels deses byvoughs der Weeghconst. Maer om daer af met een wat verclaring te doen; ick treck de lini daer t'ghewicht Ban hangt opwaert tot G, als B G, en F E voorwaert, tot datse de oneyndelicke door B G ontmoet, t'welck sy in H: Daer na uyt eenich punt der lini H F als I, een

[p. 197]

lini gherakende B G in K, als I K evewijdeghe met D C. T'welck soo sijnde, ick segh ghelijck I K tot K H, alsoo t'ghewicht deur de hant F ghetrocken, tottet ghegheven ghewicht B: Voort ghelijck H I tot I K (die in voorbeelden met een schijf als dit altijt evelanck moeten sijn, want C D voortghetrocken wesende moet commen in H, en den houck G H I, valt om bekende redenen altijt even anden houck G H C) alsoo t'ghewelt op de hant F ancommende, tottet ghewelt op C ancommende, welcke twee machten in voorbeelden met een schijfals dit,



altijt even moeten sijn, doende elck den helft eens ghewichts, dat in sulcken reden is tottet ghegheven ghewicht, als H K tot H I deur het voorschreven 5 vervolgh des 1 deels deses Byvoughs der Weeghconst.

Maer by aldien de scheefstreckende tauwe liepe over twee of meer schijven, alles wort oock bekent. Laet by voorbeelt dese tweede form sijn alsins ghelijck de tweede des eersten voorbeelts, uytghenomen dat de hant hier an F niet recht op en treckt, maer scheef ter sijdewaert uyt, t'welck soo sijnde, t'ghewicht op elcke tau ancommende, wort oock bekent deur het boveschreven 5 vervolgh. Maer om daer af met een wat verclaring te doen, ick treck de lini daer t'gewicht an hangt opwaert tot G, als B G, en F E voorwaert tot datse de oneyndelicke door B G ontmoet, t'welck sy in H, teyckenende daer na t'bovenste punt daert bovenste catrol an hangt met I, en treck H I, daer na wt eenich punt der lini H F als K, een lini gherakende H G in L, als K L evewijdighe met H I: T'welck soo sijnde, ick segh ghelijck K H tot L H, also t'ghewelt op de hant ancommende, tottet gegeven ghewicht: Maer K H is in alle voorbeelden met twee schijven als dit, altijt even an den helft van K L, daerom t'ghewelt op Fancommende, is

[p. 198]

den helft des gewelts op I ancommende, waer deur op elck der drie tauwen eveveel ghewelts comt, te weten het derdendeel eens ghewichts, dat in sulcken reden is tottet ghegheven ghewicht, als L H tot H K, daerom segghende in alle



sulcke voorbeelden, K H gheeft H L, wat t'ghegheven ghewicht? het derdendendeel van t'ghene daer uyt comt is voor de ghewelt op de hant F ancommende, en oock op elcke van d'ander twee tauwen.

Maer alsser alsoo drie schijven sijn, soo ist kennelick datmen dan moet nemen het vierendeel van dat uytcommende ghewicht, en soo voort met allen anderen.

De reden waerom K L hier boven meer evewijdeghe moest sijn met H I, dan met eenighe der tauwen, is kennelick deur t'ghene wy van derghelijcke gheseyt hebben int 2 en 3 vervolgh vant 1 deel des Byvoughs der Weeghconst, want de hanghende swaerheyts middellijn des gheheels, streckt deur t'punt H, van welck punt openbaerlick de twee linien moeten commen daer wy ons rekening op maken. Tbeslvyt. Wy hebben dan ondersocht de ghedaente der ghewichten opghetrocken met catrollen, na den eysch.

Catrolwichts

EYNDE.