Wisconstighe gedachtenissen. Deel 4: van de weeghconst

Nv de⁺ voorstellen.

1 Vertooch. 1 Voorstel.

T'ghestelde vvater hout alle plaets diemen hem binnen vvater gheeft.

Tghegheven. Laet het water in t'vlackvat A t'ghestelde water sijn in t'water B C. Tbegheerde. Wy moeten bewijsen dattet water A in die plaets sal blijven.

+ Propositiones.

Tbewys.

En latet water A (soot meughelick waer) sijn plaets niet houden, maer het' sy ghedaelt daer D is; Dit soo toeghelaten, t'water dat daer naer inde plaets van A gecommen is, sal om de selve oirsaeck oock ter plaets van D dalen, t'welck daer naer oock een derghelijcke ander doen sal, inder voughen dat dit water (om dat de reden altijt de selve is) een eewich roersel sal maken, t'welck ongheschickt is.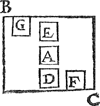



S'ghelijcx sal oock bethoont worden dat A niet rijsen, ofte naer eenighe ander sijden hem begheven en can. T'blijckt oock dat soomen A stelde binnen t'water ter plaets van D,E,F, of G, dat tet om de voornoemde redenen, op yder van die plaetsen, ende over al daerment in B C set, blijven sal.

Tbeslvyt. T'gestelde water dan, hout alle plaets diemen hem binnen water gheeft, t'welck wy bewijsen moesten.

[p. 127]

2 Vertooch. 2 Voorstel.

Een stijflichaem stoflichter dan vvater, en sinckt niet heel daer onder, maer een deel blijfter uyt stekende.

Tghegheven. Laet het stijflichaem A, stoflichter sijn dan t'water B C, diens oppervlack B D. Tbegheerde. Wy moeten bewijsen dat A, gheleyt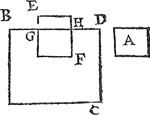



in t'water B C, niet heel daer onder sincken en sal, maer datter een deel buyten t water sal blijven steken.

Tbereytsel. Laet E F een vlackvat sijn, wiens deel dat binnen t'water ende met water ghevult is, sy G F, evegroot ende ghelijck an A, ende sijn oppervlack G H sal in t'vlack B D sijn, overmidts t'vlackvat E F licht noch swaer en is.

Tbewys.

Anghesien A stoflichter is door t'ghegheven dan t'water G F, ende dat G F evegroot is an A, soo is G F swaerder dan A. Laet ons nu t'water G F dat in t'vlackvat E F is, uytgieten, ende legghen daer in t'lichaem A, t'welck die plaets effen vullen sal, overmits A door t'bereytsel gelijck en̄ evegroot is an G F; Maer als vooren geseyt is t'lichaem A is lichter dan t'uytgegoten water; T'vlackvat dan E F en sal van A so diep niet sincken alst van t'water G F dede, door de 3 begheerte; Maer soo veel t'vlackvat E F ondieper sinckt, soo veel moetet lichaem A nootsakelick buyten t'water steken. Tbeslvyt. Een stijflichaem dan stoflichter als water, en sinckt niet heel daer onder, maer een deel blijfter uytstekende; t'welck wy bewijsen moesten.

3 Vertooch. 3 Voorstel.

Een stijflichaem stofsvvaerder dan vvater sinckt tot den grondt.

Tghegheven. Laet A een stijflichaem wesen stofswaerder dan t'water B C, diens oppervlack B D, ende gront E C sijn. Tbegeerde. Wymoeten bewijsen dat A gheleyt in t'water B C, sin cken sal tot den grondt E C.

Tbereytsel. Laet F G een vlackvat sijn met water ghevult, evegroot ende ghelijck an A, wiens oppervlack F H in t'vlack B D sy.

Tbewys.

Anghesien A stofswaerder is door ghestelde dan t'water F G, ende dat F G evegroot is an A, so is A swaerder dan F G. Laet ons nu t'water F G dat in t'vlacvat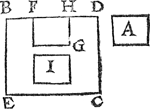



F G is, uytgieten, ende legghen daer in t'lichaem A, t'welck die plaets effen vullen sal, overmits A door t'gestelde gelijck en evegroot is an F G; Maer soo wy vooren gheseyt hebben, A is swaerder dan het uytghegoten water; T'vlackvat dan F G sal van A dieper sincken alst van t'water F G dede door de 3 begheerte. Wy hebben dan bethoont dattet lichaem A sincken sal. Daer rest noch bewesen te worden dattet oock sincken sal tot op den grondt E C, aldus: En latet (soot meu-

[p. 128]

ghelick waer) niet sincken tot E C, maer op den wech tusschen beyden blijven als daer I is, ende laet ons t'stijflichaem datter in t'vlack vat I steeckt, weeren, ende vollen dat met water, t'selve sal door het 1 voorstel op die plaets blijven: Maer dit water is lichter als dat lichaem, een swaerder dan ende een lichter, sullen op een selfde plaets blijven, t'welck ongheschickt ende teghen de 3 begheerte is. T'lichaem A dan, en can tusschen t'oppervlack B D ende den grondt E C niet blijven, t'moet dan nootsakelick sincken tot dattet op den grondt E C rust.

Tbeslvyt. Een stijflichaem dan stofswwerder als water, sinckt tot den grondt, t'welck wy bewijsen moesten.

4 Vertooch. 4 Voorstel.

Een stijflichaem evestofsvvaer an vvater, hout alle plaets diemen hem binnen vvater gheeft.

Tghegheven. Laet het stijflichaem A, evenstofswaer sijn mettet water B C. Tbegheerde. Wy moeten bewijsen dat A in t'water B C gheleyt, alle plaets hout diemen hem daer gheeft. Tbereytsel. Laet D een vlackvat vol waters sijn, evegroot ende ghelijck an A.

Tbewys.

Anghesien A evestofswaer is door t'ghegheven an t'water D, ende dat D evegroot is met A, soo is D oock eveswaer met A; Laet ons nu t'water D dat in t'vlackvat D is, uytgieten, ende leggen daer in sijn evewichtich lichaem A, t'welc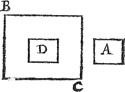



die plaets effen vullen sal, overmits A door t'ghestelde ghelijcken evegroot is an D; T'vlackvat dan D en sal van A niet dieper sincken noch hoogher rijsen dan van t'water D, door de 3 begheerte: Maer t'water D hielt in B C alle plaets diemen hem gaf door het 1 voorstel, t'stijflichaem A dan, hout in t'water B C alle plaets diemen hem gheeft. Tbeslvyt. Een stijflichaem dan evestofswaer an water, hout alle plaets diemen hem binnen water gheeft, t'welck wy bewijsen moesten.

5 Vertooch. 5 Voorstel.

Een stijflichaem stoflichter dan vvater daert in light, is evevvichtich an t'vvater evegroot met sijn deel dat binnen t'vvater is.

Tghegheven. Laet A B een stoflichter stijflichaem sijn dan t'water C D daert in ligt, ende sijn vlackvat sy A B, ende sijn deel binnen t'water sy E B.

Tbegheerde. Wy moeten bewijsen dat het stijflichaem A B, evewichtich is an t'water dat evegroot is met het deel E B dat binnen t'water C D is.

Tbewys.

Laet ons t'stijflichaem A B trecken uyt het vlackvat A B, ende vullen t'vlacvat weder met water, tot dattet soo diep ingesoncken is alst eerst mettet lichaem was. T'welck soo sijnde, t'water E B datter in t'vlackvat A B is, sal (want t'op-

[p. 129]

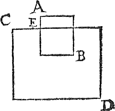pervlack van alle water des vlackvats met een deel buyten t'water stekende, is altijt in t'oppervlack des omvangenden waters, overmits t'vlackvat niet en weeght) evewichtich sijn an t'gegheven lichaem A B, Reden, dat twee ghewichten die een vat evediep doen sincken oock eveswaer sijn, door de 3 begheerte. Tbeslvyt. Een stijflichaem dan stoflichter als water daert in light, is evewichtich an t'water evegroot met sijn deel dat binnen t'water is, t'welckwy bewijsen moesten.

1 Werckstick. 6 Voorstel.

Ligghende t'een deel des stijflichaems bekender grootheyt, in vvater bekender svvaerheyt, ende t'ander deel daer buyten: Te vinden t'ghevvicht des heelen lichaems.

Tghegheven. Laet A B C D een stijflichaem wesen van form soot valt, ende E F een water van t'welck een teerlincksche voet weegt 65 ℔, (so veel weeght naer d'ervaring een Delfsche voet Deifs water, ende daer op sullen wyse inde volgende voorbeelden altijt schatten) ende des lichaems deel binnen t'water sy A C D, wiens grootheyt sy van 10000 teerlijncksche voeten.

Tbegheerde. Wy moeten vinden hoe swaer t'heel lichaem A B C D sy, met al datter in ende op is.

Twerck.

Men sal 10000 menichvuldighen met de 65 ℔ comt 650000 ℔ voor t'begheerde.

Tbewys.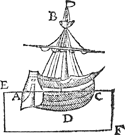

Het heel lichaem A B C D is evewichtich an t'water evegroot met A C D door het 5 voorstel, maer t'water evegroot an A C D weeght 650000 ℔, het heel lichaem dan A B C D weeght 650000 ℔, t'welck wy bewijsen moesten. Tbeslvyt. Ligghende dan t'een deel des stijflichaems bekender grootheyt, in water bekender swaerheyt, ende t'ander deel daer buyten; wy hebben t'ghewicht des heelen lichaems ghevonden naer den eysch.

6 Vertooch. 7 Voorstel.

Wesende tvvee onevestofsvvare vvateren, ende een stijflichaem stoflichter dan eenich van dien: Ghelijck de stofsvvaerheyt des svvaersten vvaters, tot de stofsvvaerheyt des lichtsten, alsoo de grootheyt diens stijflichaems binnen t'vvater in t'lichtste vvater geleyt, tot sijn grootheyt binnen t'vvater in t'svvaerste gheleyt.

Tghegheven. Laet A B een water sijn, stofswaerder dan t'water C D, ende E F sy een stijflichaem stoflichter dan eenich dier twee wateren, t'welck

[p. 130]

eerst gheleyt in t'water A B, soo daelter onder t'water het deel G F, maer t'selve lichaem E F gheleyt in t'water C D, t'welck daer sy H I, so sinckter onder t'water het deel K I. Tbegheerde. Wy moeten bewijsen dat gelijck de stofswaerheyt des waters A B, tot de stofswaerheyt des waters C D, alsoo de grootheyt K I, tot G F.

Tbewys.

T'water des waters A B evegroot an G F, is eveswaer mettet lichaem E F, ende t'water des waters C D evegroot an K I, is eveswaer mettet lichaem H I door het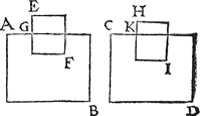



5 voorstel, maer t'lichaem E F ofte H I is al een selfde lichaem door t'ghegheven, daerom t'water des waters A B evegroot met G F, is eveswaer an t'water des waters C D evegroot met K I; Maer wesende twee eveswaere wateren, gelijck haer grootheyt tot grootheyt, also overandert haer stofswaerheyt tot stofswaerheyt, als nootsakelick volght uyt de toeghelaten 5 bepaling, daerom ghelijck de stofswaerheyt des waters A B, tot de stofswaerheyt des waters C D, alsoo de grootheyt K I, tot de grootheyt G F. Tbeslvyt. Wesende dan twee onevestofsware wateren ende een stijflichaem, &c.

7 Vertooch. 8 Voorstel.

Yder stijflichaem is soo veel lichter in t'vvater dan inde locht, als de svvaerheyt des vvaters met hem evegroot.

Tghegheven. Laet A een stijflichaem sijn, ende B C een water.

Tbegheerde. Wy moeten bewijsen dat A in t'water B C gheleyt, aldaer soo veel lichter sal sijn dan inde locht, als de swaerheyt des waters met hem evegroot. Tbereytsel. Laet D een vlackvat vol waters sijn, even ende ghelijck an A.

Tbewys.

T'vlackvat D vol waters, en is in t'water B C licht noch swaer, want het daer in alle ghestalt hout diemen hem gheeft, door het 1 voorstel, daerom t'water D uytghegoten, t'vlackvat sal t'ghewicht des waters lichter sijn dant in sijn eerste



ghedaente was, dat is, van soo veel volcommentlick licht: Laet ons nu daer in legghen t'lichaem A, t'selve sal daer in effen passen, om dat sy even ende ghelijck sijn door t'ghestelde. Ende t'vlackvat mettet lichaem A alsoo daer in, sal weghen t'gewicht van A met sijn voornoemde lichticheyt, dat is t'gewicht van A min t'ghewicht des waters datter eerst uytghegoten was, maer dat water is evegroot an A. Daerom A in t'water B C geleyt, is daer in soo veel lichter dan inde locht, als de swaerheyt des waters met hem evegroot. Tbeslvyt. Yder stijflichaems swaerheyt dan, is soo veel lichter in t'water dan inde locht, als de swaerheyt des waters met hem evegroot, t'welck wy bewijsen moesten.

[p. 131]

2 Werckstvck 9 Voorstel.

Wesende ghegheven de reden der stofsvvaerheyt des vvaters, ende eens stijflichaems, ende des stijflichaems svvaerheyt: Sijn staltvvicht in t'vvater te vinden.

1 Voorbeelt alvvaer t'stijflichaem stoflichter is dan vvater.

Tghegheven. Laet A B een water sijn, ende C een stijflichaem weghende 2 ℔, ende de stofswaerheyt des waters, tot de stofswaerheyt des stijflichaems sy als van 5 tot 1. Tbegheerde. Wy moeten des stijflichaems C staltwicht in t'water A B vinden.

Twerck.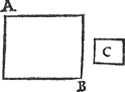

Men sal sien hoe veel een lichaem waters evegroot met C, weghen soude, wort bevonden 5 mael 2 ℔, dat is 10 ℔, de selve getrockē van 2 ℔ des stijflichaems C, rest min 8 ℔, dat is licht ofte rijsendwicht 8 ℔ voor C in t'water A B.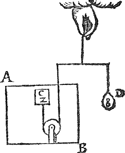

Om t'welck opentlicker te verclaren, soo neemt dat C in t'water A B ghesteken sy, ende daer teghen ghehanghen t'ghewicht D van 8 ℔, als hier nevens, ende D sal met C evestaltwichtich sijn.

2 Voorbeelt, alvvaer t'stijflichaem stofsvvaerder is dan t'vvater, diens vvercking ghelijck is ande voorgaende.

Tghegheven. Laet de reden der stofswaerheyt des waters A B hier boven, tot het stijflichaem C, nu sijn als van 1 tot 4, ende laet C weghen 12 ℔.

Tbegheerde. Wy moeten des stijflichaems staltwicht in t'water A B vinden.

Twerck.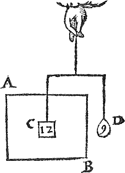

Men sal sien hoe veel een lichaem waters evegroot met C weghen soude; wort bevonden het ¼ van C 12 ℔, dat is 3 ℔, de selve getrocken van 12 ℔ des stijflichaems C, rest 9 ℔ voor t'ghewicht van C in t'water A B.

Om t'welck breeder te verclaren, soo neemt dat C in t'water A B ghesteken sy, ende daer teghen hanghe t'ghewicht D van 9 ℔, als hier nevens, ende D sal met C evestaltwichtich sijn.

[p. 132]

Wy souden oock meughen een derde voorbeelt setten, alwaer de reden der stofswaerheyt des waters ende stijflichaems even waer, maer t'is blijckelick dat (oock volghende de reghel der voorgaender wercking) sulcken stijflichaem in t'water licht noch swaer sijn en sal, van alle welcke t'bewijs openbaer is door t'boveschreven 8 voorstel. Tbeslvyt. Wesende dan ghegheven de reden der stofswaerheyt des waters, ende eens stijflichaems, ende des stijflichaems swaerheyt: Wy hebben sijn staltwicht in t'water ghevonden naer den eysch.

8 Vertooch. 10 Voorstel.

Op yder bodem des vvaters^⋆ evevvijdich sijnde vanden sichteinder, rust eē gevvicht even ande svvaerheyt vvaters die evegroot is met den pylaer, vviens grondt dien bodem is, ende hoochde, de^⋆ hanghende lini van^⋆ t'plat door t'vvaters oppervlack tot den gront.

Tghegheven. Laet A B C D een water sijn, van form een lichamelick rechthouck, diens oppervlack A B is, ende eenighen bodem daer in E F, evewijdich vanden sichteinder; Laet oock G E de hanghende lini sijn van t'plat door t'waters oppervlack totten grondt E F, ende den pylaer begrepen onder den bodem E F ende hoochde E G, sy G H F E. Tbegheerde. Wy moeten bewijsen dat op den bodem E F, rust het ghewicht even ande swaerheyt waters des pylaers G H F E.

⋆ Paralleū cū Horizonte.

⋆ Perpendienlaris.

⋆ Plano.

Tbewys.

Soo op den bodem E F meer ghewicht rust dan des waters G H F E, dat sal moeten commen van weghen t'nevenstaende water; Latet sijn soot meugelick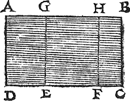



waer, van t'water A G E D ende H B C F; Maer dat so ghenomen, daer sal op den bodem D E, van weghen t'water G H F E, om dat de reden de selve is, ooc meer ghewichts rusten dan des waters A G E D; ende op den bodem F C, oock meer ghewichts dan des waters H B C F, ende vervolgens op den heelen bodem D C sal meer ghewichts rusten, dan des heelen waters A B C D, t'welck (ghemerckt A B C D een lichamelick rechthouck is) ongheschicktwaer. S'ghelijcx salmen oock bethoonen dat op den bodem E F niet min en rust dan t'water G H F E, daer rust dan nootsakelick op t'ghewicht even ande swaerheyt waters des pylaers G H F E.

1 Vervolgh.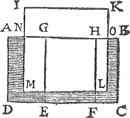

Laet ons nu in t'water A B C D des 10 voorstels, legghen een stijflichaem I K L M, stoflichter dan water, dat is drijvende op t'water, mettet deel N O L M daer binnen, ende mettet deel N O K I daer buyten, welcker gestalt dan sy als hier onder. Dit soo sijnde, t'stijflichaem I K L M is evewichtich mettet water evegroot an N O L M door het 5 voorstel, waer door t'lichaem I K L M, met de rest des waters rondom hem, evewich-

[p. 133]

tich is an een lichaem waters evegroot an A B C D daerom segghen wy noch naer luyt des voorstels, dat teghen den bodem E F een ghewicht rust, even ande swaerheyt waters die evegroot is met den pylaer, diens gront E F is, ende hoochde de hanghende lini G E, van^* t'plat A B, door t'waters oppervlack A N totten grondt F F: Waer uyt blijckt dat eenighe drijvende stof in t'water gheleyt, sy en verswaert noch en verlicht (welverstaende als t'water inde selfde hoochde blijft) den grondt niet.

* Plano.

2 Vervolgh.

Laet andermael int water A B C D, legghen een stijflichaem, ofte verscheyden stijflichamen evestofswaer mettet water, ick neem alsoo, datter maer water en blijft als t'begrepen binnen I K F E L M; T'welck soo sijnde, dese lichamen en beswaren noch en verlichten den grondt E F niet meer dan t'water eerst en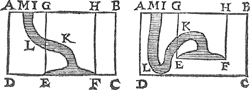



dede: Daerom segghen wy noch naer luyt des voorstels, dat tegen den bodem E F, een gewicht rust even ande swaerheyt waters die evegroot is metten pylaer, wiens gront E F is, ende hoochde de hanghende lini G E, van t'plat A B door t'waters oppervlack M I, totten grondt E F.

3 Vervolgh.

Laet wederom A B C D t'eenemael water sijn, ende E F een bodem daer in, evewijdich vanden sichteinder. T'welck soo wesende, t'water onder den bodem E F, stoot even soo stijf daer teghen opwaert, als t'water boven den bodem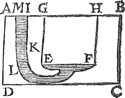



E F, daer teghen neerwaert stoot: Want by aldient so niet en waer, t'cranckste soude voor t'sterckste wijcken, t'welck niet en ghebeurt, want yder hout sijn gegheven plaets door het 1 voorstel. Laet nu eenighe stijflichamen evestofswaer mettet water, alsoo geleyt worden, dattet water I K E F L M, van onder anstoot teghen E F, als hier nevens. Dit soo sijnde, t'water onder den boden E F, stoot nu soo stijf teghen E F, dat is teghen t'stijflichaem, alst te vooren teghen t'water dede; maer t'stack daer teghen soo stijf als t'bovenste teghen E F stiet, so vooren gheseyt is, ende t'bovenste stiet teghen E F naer luyt deses voorstels, daerom t'onderste stoot oock tegen E F naer luyt deses voorstels, dat is soo wy boven gheseyt hebben, dat teghen den bodem E F noch een ghewicht rust, even ande swaerheyt waters die evegroot is metten pylaer, diensgrondt E F is, ende hoochde de hanghende lini G E, van t'plat A B door t'waters oppervlack M I totten grondt E F.

4 Vervolgh.

Laet ons nu de stijflichamen des 2 ende 3 vervolghs tot haer plaets hechten, ende t'water uytgieten, ende daer sal een ledige plaets I K F E L M blijven, ende den grondt E F en sal gheen ghewicht draghen; waer uyt blijckt, dat met die cleyne ledighe plaets weder vol waters te gieten, soo salmen den gront E F even

[p. 134]

soo seer beswaren, als of t'gheheele vat A B C D (de ingheleyde stijflichamen gheweert sijnde) vol waters waer.

5 Vervolgh.

Maer anghesien de ingheleyde stijflichamen des 2 ende 3 vervolghs t'haerder plaets ghehecht sijn, soo en gheeft noch en neemt haeruyterste stof tot de beswaring ofte verlichting des grondts E F, daerom laet ons de stof der selver rondtom afcorten, alsoo datter blijven de inwendighe ongheschickte formen oft vaten met water ghevult M I K F E L, als hier onder.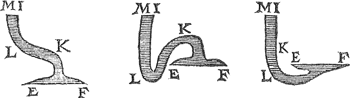

Ende sullen noch segghen naer luyt des voorstels, dat teghen den bodem E F een ghewicht rust, even ande swaerheyt waters die evegroot is metten pylaer, wiens gront E F is, en̄ hoochde de hangende lini van t'plat door t'waters oppervlack M I, totten grondt E F. Ende dit alsoo om de selve reden van alle ander formen diens bodems in een plat sijn evewijdich vanden sichteinder.

Tbeslvyt. Op yder bodem dan des waters evewijdich sijnde, &c.

Leest d'ervaringhen hier af breeder inden Anvang der Waterwichtdaet.

Merckt.

Wy souden t'boveschreven 10 voorstel eyghentlicker aldus uytghesproken hebben:

Op yder bodem des vvaters in een vvereltvlack sijnde, rust een ghevvicht even ande svvaerheyt vvaters die evegroot is mettet clootsdeel begrepen tusschen den bodem ende t'vvereltvlack door t'vvaters hoochste punt, ende t'vlack tusschen die tvvee vlacken, beschreven met de oneyndelicke rechte lini vast in t'vverelts middelpunt, ende ghedraeyt door des bodems^⋆ omtreck.

Daer afbewijsende sulcx als boven bewesen is, maer om de redenen onder de 7 begheerte verclaert, soo ist beter ghelaten.

⋆ Circumserentiam.

9 Vertooch. 11 Voorstel.

Wesende een gheschickt bodem diens hoochste punt in t'vvaters oppervlack is: T'ghevvicht daer teghen rustende is even anden helft des pylaers vvaters, diens gront even an dien bodem is, ende hoochde, de^⋆ hanghende lini van

⋆ Perpendicularis.

[p. 135]

des bodems hoochste punt, tot het^⋆ plat evevvijdich van den^⋆ sichteinder door des bodems leeghste punt.

⋆ Plano.

⋆ Horizonte.

1 Voorbeelt.

Tghegheven. Laet A B een vat waters wesen, en̄ den bodem A C D E sy ten eersten een evewijdich vierhouck, onevewijdich vanden sichteinder, daer op rechthouckich, diens hoochste sijde A C in t'waters oppervlack A C F G is, ende A E sy de hanghende lini van des bodems hoochste punt, tot het plat evewijdich vanden sichteinder door des bodems leeghste punt, dat is door E D, en̄ A G sy soo lanck alst valt. Laet oock de lini D B evewijdich sijn vanden sichteinder, ende daer in gheteeckent H, alsoo dat D H even sy an D C, oock getrocken worden C H, ende met A C H D E sy beteeckent den helft des pylaers diens gront A C D E, ende hoochde D H even an A E.

Tbegheerde. Wy moeten bewijsen dattet ghewicht waters teghen den bodem A C D E rustende, even is anden voornoemden halven pylaer A C H D E; Dat is (om t'selve opentlicker te verclaren) ghenomen dat I een scheefwicht sy, eveswaer met A C H D E, diens trecklini K L, evewijdich is met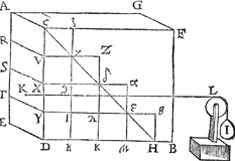



D H, ende dat K swaerheyts middelpunt sy vande macht des gheprangs vergaert inden bodem (wiēs middelpunts vinding door t'volghende 18 voorstel bekent wort) t'ghewicht I staet teghen t'gheprang des waters evewichtich, houdende den bodem A C D E (ghenomen datse beweeghlick waer) in die stant. Ofte tot meerder claerheyt, laet M N O P een bodem sijn, even ende ghelijck an A C D E, te weten de sijde M P^* lijckstandige met A C, ende M N met A E,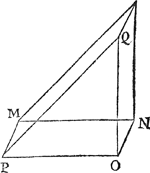



op welcken bodem M N O P, ligt een stijflichaem M N O P Q, even, ghelijck, ende eveswaer met den halven pylaer A C H D E, ende de lini Q O even an D H, sy rechthoukich op den sichteinder. Ick seg dat alsulcken gheprang als dat stijflichaem M N O P Q, doet teghen den bodem M N O P, te weten meer pranghende naer N O dan naer M P, om dattet aldaer dicker en swaerder is dan alhier, even soodanigen gheprang doet t'water A B, oock teghen den bodem A C D E, meer pranghende naer E D dan naer A C.

Tbereytsel. Laet de sijde A E ghedeelt worden in vier even deelen, met de punten R, S, T, ende daer uyt ghetrocken worden R V, S X, T Y, evewijdighe met A C; Laet oock ghetrocken worden V Z, X α, Y β evewijdige met D H, ende snyende C H inde punten γ, δ, ε, ende alsoo, dat yder der linien γ Z, δ α, ε β, even sy an V γ; Laet daer naer door t'punt γ ghetrocken worden de lini ζ η, evewijdighe met C D, snyende X α in ς, ende Y β in ι, sghelijcx de lini Z ϰ, door δ, snyende Y β in λ, sghelijcx de lini α μ door ε, ende ten laetsten β H.

* Homologa.

[p. 136]

Tbewys.

Teghen den bodem A C V R rust meer ghewichts dan niet, want waer dien bodem in t'waters oppervlack, soo souder niet teghen rusten, maer sy comt nu leegher, daer rust dan meer teghen als niet: Ten anderen segh ick datter min teghen rust dan t'lichaem waters A C ζγ V R, want waer sy evewijdich vanden sichteinder door R V, soo souder dat lichaem A C ζ γ V R teghen rusten, door het 10 voorstel, maer sy comt nu hoogher, daer rust dan min teghen. S'ghelijcx segh ick dat teghen den bodem R V X S, meer ghewichts rust dan des lichaems A C ζ γ V R, want waer dien bodem evewijdich vanden sichteinder door R V, daer soude dat lichaem teghen rusten door het 10 voorstel, maer sy comt nu leegher, daer rust dan meer tegen, maer t'lichaem R V γϑ X S is even an t'lichaem A C ζγ V R, daerom teghen den bodem R V X S, rust meer ghewichts dan des lichaems R V γ ϑ X S. Ten anderen seg ick datter min tegen rust dan t'lichaem A C ζ ϑ X S, want waer dien bodem evewijdich vanden sichteinder door S X, soo souder dat lichaem A C ζτ X S teghen rusten door het 10 voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer t'lichaem R V Z δ X S is even an t'lichaem A C ζ ϑ X S, daerom rust teghen den bodem R V X S min als t'lichaem R V Z δ X S. S'ghelijcx segh ick dat teghen den bodem S X Y T meer gewichts rust dan des lichaems A C ζϑ X S, want waer dien bodem evewijdich vanden sichteinder door S X, daer soude dat lichaem teghen rusten door het 10 voorstel, maer sy comt nu leegher, daer rust dan meer teghen, maer t'lichaem S X δλ Y T is even an t'lichaem A C ζϑ X S, daerom tegen den bodem S X Y T rust meer ghewichts dan des lichaems S X δλ Y T. Ten anderen segh ick datter min teghen rust dan t'lichaem A C ζι Y T, want waer dien bodem evewijdich vanden sichteinder door T Y, soo souder dat lichaem A C ζ ι Y teghen rusten, door het 10 voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer r'lichaem S X α ε Y T is even an t'lichaem A C ζ ι Y T, daerom rust teghen den bodem S X Y T min als t'lichaem S X αε Y T. S'ghelijcx segh ick dat tegen den bodem T Y D E, meer ghewichts rust dan des lichaems A C ζ ι Y T, want waer dien bodem evewijdich vanden sichteinder door T Y, daer soude dat lichaem teghen rusten door het 10 voorstel, maer sy comt nu leegher, daer rust dan meer teghen, maer t'lichaem T Y ε μ D E is even an t'lichaem A C ζ ι Y T, daerom teghen den bodem T Y D E rust meer gewichts dan des lichaems T Y ε μ D E. Ten anderen segh ick datter min teghen rust dan t'lichaem A C ζη D E, want waer dien bodem evewijdich vanden sichteinder door E D, soo souder dat lichaem A C ζ η D E teghen rusten, door het 10 voorstel, maer sy comt nu hoogher, daer rust dan min tegen, maer t'lichaem T Y β H D E, is even an t'lichaem A C ζη D E, daerom rust teghen den bodem T Y D E min als t'lichaem T Y β H D E. Nu anghesien als vooren bewesen is, dat teghen den bodem A C V R meer rust dan niet, ende teghen den bodem R V X S meer als t'lichaem R V γ ϑ X S, ende teghen den bodem S X Y T meer dan t'lichaem S X δ λ Y T, ende teghen den bodem T Y D E meer als t'lichaem T Y ε μ D E, soo rust teghen den heelen bodem A C D E meer dan t'ghewicht van alle die lichamen t'samen, t'welck is t'binneschreven lichaem R V γ ϑ δ λ ε μ D E inden halven pylaer A C H D E: Tis oock bewesen dat teghen den bodem A C V R min rust dan t'lichaem A C ζ γ V R, ende teghen den bodem R V X S min als t'lichaem R V Z δ X S, ende teghen den bodem S X Y T min dan t'lichaem S X αε Y T, ende teghen den bodem T Y D E min als t'lichaem T Y β H D E, daerom rust tegē den heelen bodem A C D E min dan t'gewicht van alle die lichamen t'sa-

[p. 137]

men, dat is t'omschreven lichaem A C ζ γ Z δ α ε β H D E. Maer datmen nu den bodem A C D E welcke hier boven ghedeelt is in vier even deelen, alsoo deelde in acht even deelen, tis kennelick dat het binneschreven lichaem inden halven pylaer A C H D E, ende het omschreven, alsdan van dien halven pylaer maer den helft soo veel verschillen en souden als sy nu doen, tis dan openbaer door sulcke oneyndelicke deeling des bodems, datter gheen ghewicht soo cleen ghegheven en can worden, oft men sal bethoonen dattet verschil(sooder eenich waer)des ghewichts teghen den bodem A C D E rustende, tot het ghewicht des halven pylaers A C H D E noch minder is, waer uyt ick aldus^* strye:

A.	Alle swaerheyt die min verschilt van t'ghewicht tegen den bodem A C D E rustende dan ghegheven can worden, is even mettet ghewicht tegen den bodem A C D E rustende;
I.	T'ghewicht des halven pylaers A C H D E, is een swaerheyt die min verschilt van t'ghewicht teghen den bodem A C D E rustende dan ghegheven can worden;
I.	T'ghewicht dan des halven pylaers A C H D E, is even mettet gewicht tegen den bodem A C D E rustende.

* Argumentor.

2 Voorbeelt.

Tgegheven. Laet A B andermael een vat waters wesen, en̄ den bodem A C D E sy een evewijdich vierhouck des selfden, onevewijdich vanden sichteinder, en̄ daer op scheefhouckich, diens hoochste sijde A C in t'waters oppervlack A C F G is; T'selve water ende bodem sy also gedeelt ende geteeckent als t'water des 1 voorbeelts, ende A ν sy hanghende lini van des bodems hoochste sijde, tot het plat evewijdich vanden sichteinder door des bodems leeghste sijde E D. Tbegheerde. Wy moeten bewijsen dattet ghewicht waters teghen den bodem A C D E rustende, even is anden helft des pylaers diens bodem A C D E, ende hoochde A ν. Tbereytsel. Laet de sijde A ν gedeelt worden in vier even deelen met de punten ο, π, ϱ.

Tbewys.

Teghen den bodem A C V R, rust meer ghewichts dan niet, want waer dien bodem in t'waters oppervlack, soo souder niet teghen rusten, maer sy comt nu leegher, daer rust dan meer teghen als niet: Ten anderen segh ick datter min tegen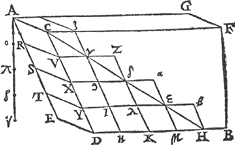



rust dan den pylaer diens grondt A C V R is, ende hoochde A ο, want waer sy evewijdich vanden sichteinder door R V, soo souder dien pylaer tegen rusten door het 10 voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer A C ζ γ V R is⁺ even an dien pylaer, daerom teghen den bodem A C V R rust min gewicht dan des pylaets A C ζγ V R. S'ghelijcx

+ 31. v.11.b.E.

[p. 138]

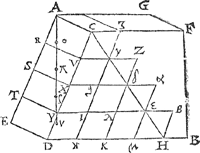salmen oock al de rest bethoonen even so sy in t'eerste voorbeelt bewesen was, waer uyt besloten sal worden dattet ghewicht teghen den bodem A C D E rustende, ev῭ is an t'lichacm A C H D E, maer dat lichaem is even anden helft des pylaers diens bodem A C D E, ende hoochde A ν, (want A ν is even ande hanghende van H rechthouckich op t'plat door A C D E) Daerom t'ghewicht teghen den bodem A C D E rustende, is even anden helft des pylaers waters diens gront even is an A C D E, ende hoochde A ν.

3 Voorbeelt.

Tghegheven. Laet A B eenich gheschickt bodem sijn; Ick neem een^* scheefrondt, diens hoochste punt A in t'waters oppervlack is, ende B sy t'leegste punt, ende A C de hanghende lini van t'hoochste punt A, tot het plat evewijdich vanden sichteinder door B. Tbegheerde. Wy moeten bewijsen dattet ghewicht waters teghen den bodem A B rustende, even is anden helft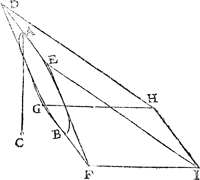



des pylaers diens grondt den bodem A B is, ende hoochde A C.

Tbereytsel. Laet ghetrocken sijn een evewijdich vierhouck D E F G, in wiens plat begrepen sy t'scheefrondt A B, alsoo dat D E in t'waters oppervlack sijnde, naecke an t'punt A, ende dat G F naecke an t'punt B; Laet daer naer ghetrocken worden F I even an A F ende rechthouckich op F G, maer evewijdich vanden sichteinder, ende uyt G F ende F I sy beschreven den rechthouck F G H I, voorts de linien E I ende D H.

Laet daer naer een ander form gestelt sijn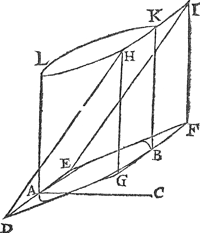



even, ghelijck, ende eveswaer met de voorgaende, maer alsoo dat F I rechthouckich sy op den sichteinder ghelijck hier neven. Ende laet in dese tweede form t'lichaē D E F G H I een stijflichaem wesen, rustende op den boden D E F G.

* Ellipsim.

Tbewys.

Alsulckē drucsel als t'stijflichaem DEFGHI der tweeder form, veroirsaeckt teghen den bodem D E F G, even soodanighen drucksel veroirsaeckt het water des eersten forms teghen sijn bodem D E F G, soo boven

[p. 139]

bewesen is, ende vervolghens alsulcken drucksel alsser valt teghen t'scheefrondt A B der tweede form, even soodanighen drucksel valter oock teghen t'scheefrondt A B der eerste form, maer het drucksel op t'scheefrondt der tweede form is den helft des pylaers (soo wy hier onder verclaren sullen) diens grondt dat scheefrondt is, ende hoochde even an A C, (want ghetrocken een hanghende lini van K rechthouckich op t'plat door t'scheefront A B, sy is even an A C) daerom het drucksel des waters teghen t'scheefrondt A B der eerste form, is even anden helft des pylaers wiens grondt dat scheefrondt is, ende hoochde A C.

Maer dattet ghewicht rustende in dese tweede form teghen t'scheefront A B, even is anden helft des pylaers diens gront dat scheefront is, ende hoochde even an A C, wort aldus bethoont: Laet ghetrocken worden de lini B K even ende evewijdighe met F I; Laet nu het onderste B der selver lini B K, ghedraeyt worden inden omtreck des scheefrondts A B, tot dat sy weder ter plaets comt daer sy begon te roeren, ende blijvende int roeren altijt evewijdich van F I, de selve sal tusschen de twee bodems een pylaer A B K L beschrijven, welcke mettet plat D E I H, ghesneen wort door twee lijckstandighe punten A, K, schuens teghen over malcander staende inde omtrecken der bodems; Maer alle pylaer diens grondt een gheschickt bodem sijnde, ghesneen wort met een plat door twee lijckstandighe punten inde omtrecken der bodems schuens teghen over malcander staende, die pylaer wort van dat plat in twee even deelen ghedeelt, daerom het deel diens pylaers onder t'plat D E I H, is den helft des heelen pylaers A B K L rustende op t'scheefrondt A B, maer dat den pylaer A B K L even is anden pylaer diens grondt A B ende hoochde A C, blijckt daer an, dat sijn hoochde even is an A C, daerom t'ghewicht rustende teghen t'scheefront A B, is even anden helft des pylaers diens grondt dat scheefrondt is, ende hoochde even an A C.

4 Voorbeelt.

Wy hebben hier boven drie voorbeelden ghegheven met^* Wisconstich bewijs, t'welck, wel is waer, den grondt volcommentlicker verclaert als ander; doch anghesien t'bewijs door ghetalen tot opentlicker kennis van alles, niet en verachtert, sullen dit 4 voorbeelt door ghetalen stellen.

Tghegheven. Laet A B een vat waters sijn, diens bodem A C D E wy nemen te wesen een rechthouckich vierhouck, rechthouckich op den sichteinder, ende d'hoochste sijde A C doende een voer, sy int waters oppervlac A C F G, ende A E doe oock een voet, maer A G sy soo lanck alst valt.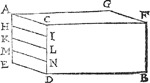

Tbegheerde. Wy moeten door getalen bewijsen, dattet ghewicht waters rustende teghen den dodem A C D E, even is anden helft des pylaers waters, wiens gront even is an dien bodem, ende hoochde de hanghende lini A E: Maer dien pylaer is een teerlinck doende een voet, wy moeten dan bethooneu dat teghen den bodem A C D E rust het ghewicht van een halve voet waters. Tbereytsel. Laet door den bodem getrockē worden drie evewijdige linien met A C, als H I, K L, M N, alsoo dat A H even sy an H K, ende an K M, ende an M E.

* Mathematica demonstratione.

[p. 140]

Tbewys.

Tis blijckelick dat op den bodem A I meer rust dan 0, want alwaer sulcken bodem door A C evewijdich vanden sichteinder, soo souder 0, op rusten, maer sy comt nu leegher daer rust dan meer op als 0. Ten anderen seg ick datter min op rust dan 1/16, voets, want al waer sulcken bodem door H I evewijdich vanden sichteinder, soo souder 1/16 voets op rusten, maer sy comt nu hoogher, daer rust dan min op als 1/16, ende om dergelijcke reden ist oock openbaer, dat op den bodem H L meer rust dan 1/16, ende min als 2/16, ende op den bodem K N meer dan 2/16, ende min als 3/16; maer op den bodem M D meer dan 3/16 ende min als 4/16. Nu dan vergaert de vier ghewichten (ghenomen dat 0 gewicht waer) die lichter sijn d'ander op elcken bodem rust, als 0. 1/16. 2.16. 3/16. maken t'samen 6/16: Insghelijcx vergaert de vier ghewichten die swaerder sijn d'ander op elcken bodem rust, als 1/16. 2/16. 3/16. 4/16. maken t'samen 10/16: Tis dan openbaer dat op den heelen bodem A C D E meer rust dan 6/16 voets, ende min als 10/16 voets, tusschen welcke twee den ½ voet is, die wy noch bewijsen moeten op den bodem A C D E te rusten.

Nu ghelijck den bodem hier boven door de drie evewijdighe linien ghedeelt is in vieren, alsoo meughen wijse deelen in soo veel deelen alst ons belieft, latet sijn in thienen, ende om de voorgaende redenen, de thien ghewichten die lichter sijn d'ander op elcken bodem rust, sullen sijn 0. 1/100. 2/100. 3/100. 4/100. 5/100. 6/100. 7/100. 8/100. 9/100. t'samen 45/100. S'ghelijcx de thien ghewichten die swaerder sijn d'ander op elcken bodem rust, als 1/100. 2/100. 3/100. 4/100. 5/100. 6/100. 7/100. 8/100. 9/100. 10/100. maken t'samen 55/100; tis dan kennelic dat op dē bodem A C D E meer rust dan 45/100 voets, ende min als 55/100 voets, tusschen welcke twee den halven voet is die wy noch bewijsen moeten op den bodem A C D E te rusten: Maer dese twee^* palen sijn naerder den halven voet dan d'eerste twee, want min verschilt 45/100 van ½, dan 6/16, alsoo oock verschilt 55/100 min van ½, dan 10/16; Waer uyt blijckt dat hoe wy den bodem A C D E in meer sulcke even deelen snyen, hoe dat wy den halven voet altijt naerder commen.

T'wlck soo verstaen sijnde, laet op den bodem A C D E min of meer rusten 1/1000 voets (waert meughelick) dan een halve voet, ende laet ons de waerheyt daer af ondersoucken, deelende den bodem door de gedacht in 1000 even deelen alsvooren. Ende om de voorgaende redenen, de duysent ghewichten die lichter sijn d'ander op elcken bodem rust, sullen sijn 0, 1/1000000. 2/1000000 ende soo voorts tot het laetste, dat sijn sal van 999/1000000, alle welcke ghetalen t'samen, sullen maken (wiens corte manier om te vergaren wy hier onder verhalen sullen) 499500/1000000. S'ghelijcx de duysent ghewichten die swaerder sijn d'ander op elcken bodem rust als 1/1000000. 2/1000000. 3/1000000. ende soo voorts tot het laetste, dat sijn sal van 1000/1000000, maken t'samen 500500/1000000, daer rust dan meer op den bodem als 499500/1000000 voets, ende min dan 500500/1000000 voets; Maer 499500/1000000 en is maer 1/1000 minder dan ½. daer en rust dan gheen 1/1000 voets min op den bodem dan ½ voet. Alsoo en is 500500/1000000 maer 1/2000 meerder dan ½. daer en rust dan geen 1/1000 meer op den bodem dan ½ voet. Ende alsoo salmen dierghelijcke bethoonen over alle ghestelt deel hoe cleen het sy. Het blijckt dan, dat het verschil (sooder eenich waer) tusschen t'water op den bodem A C D E rustende, ende een halve voet waters, minder soude moeten sijn dan meughelick is ghestelt te worden, waer uyt ick aldus^* strye:

A.	Nevenyder ghewicht dat met een halve voet waters verschil heeft, can een ghewicht ghestelt worden daer af min verschillende;

* Termini.

* Argumentor.

[p. 141]

O.	Neven t'ghewicht waters op den bodem A C D E rustende, en can gheen gewicht ghestelt worden van een halve voet waters min verschillende;
O.	T'ghewicht waters dan op den bodem A C D E rustende, en heeft met een halve voet waters gheen verschil.

Tbeslvyt. Wesende dan een geschickt bodem diens hoochste punt int waters, &c.

DE reden waerom het half hier boven, altijt blijft tusschen de twee getalen, welcke an het half oneyndelick naerderen, maer mimmermeer daer toe en gheraken, is begrepen in sulcken^* vertooch:

Wesende een^⋆ voortganck van getalen malcanderen in^⋆ een heyt te boven gaende, ende beginnende vande eenheyt: Den helft des viercants van t'laetste, is minder dan de somme van al de getalen, maer meerder dan de somme van al de ghetalen min t'laetste.

Maer om te verclaren (als boven belooft is) de manier om door cortheyt te vergaren die groote menichte der ghetalen; Soo is ten eersten kennelick, dat haer noemers al even sijn, waer door wy alleenelick op der ghetalen telders te letten hebben, de selve sijn in oirdentlicke voortganck beginnende van de eenheyt, ende met eenheyt malcanderen te boven gaende, daeromme vermenichvuldicht t'laetste met sijn helft, ende an t'uytbreng noch gevoucht sijn helft, gheeft de begeerde somme. By voorbeelt ick wil weten hoe veel de somme is van 1,2,3,4,5,6; Ick segh 6 mael 3 is 18, met 3 maeckt 21 voor de begeerde somme. Laet het laetste nu oneven ghetal sijn, als 1,2,3,4,5,6,7; Ick segh 7 mael 3½ is 24½, met 3½ maeckt, 28, voor de begheerde somme. Maer als t'laetste aldus oneven is, soo vallet lichter om door gheen ghebroken te wercken, datmen t'laetste menichvuldicht door den helft der somme van t'laetste met 1, als andermael willende weten de somme van 1,2,3,4,5,6,7; Ick doe 1 tot 7, maect 8, sijn helft is 4, die vermenichvuldicht door 7, comt alsboven 28, voor de begheerde somme, ende alsoo met allen anderen.

* Theoremata.

⋆ Progressio.

⋆ Vnitate.

Merckt.

Anghesien de boveschreven helft des pylaers even is anden heelen pylaer diens grondt den ghegeven bodem is, ende hoochde den helft der hangende lini van des bodems hoochste punt, tottet plat evewijdich vanden sichteinder door des bodems leegste punt, men soude t'boveschreven 11 voorstel oock meughen aldus uyten.

Wesende een gheschickt bodem diens hoochste punt in t'vvaters oppervlack is: T'ghevvicht daer teghen rustende is even anden pylaer vvaters diens grondt even an dien bodem is, ende hoochde den helft der hangende lini van des bodems hoochste punt, tottet plat evevvijdich vanden sichteinder door des bodems leeghste punt.

Ende na sulcke wijse sullen wy t'laetste deel deses 12 voorstels formen.

[p. 142]

10 Vertooch. 12 Voorstel.

Wesende een gheschickt bodem diens hoochste punt onder t'vvaters oppervlack is: T'ghevvicht daer teghen rustende is even anden pylaer vvaters diens grondt even is an dien bodem, ende hoochde de^⋆ hanghende lini van^⋆ t'plat door t'vvaters oppervlack, tot des bodems hoochste punt, ende boven dien den helft der hangende lini van des bodems hoochste punt, tottet plat evevvijdich vanden^⋆ sichteinder door des bodems leeghste punt.

⋆ Perpen dicularis.

⋆ Plano.

⋆ Horizonte.

1 Voorbeelt.

Tghegheven. Laet A B C D een geschickt bodem sijn, als ten eersten een evewijdich vierhouck diens hoochste sijde A B onder t'waters oppervlack is, evewijdich neem ick, vanden sichteinder, ende E A sy de hanghende lini van t'waters oppervlack, tot des bodems hoochste punt A, ende A F de hanghende lini van A, tot het plat evewijdich vanden sichteinder door D C, ende A G sy den helst van A F. Tbegheerde. Wy moeten bewijsen dattet ghewicht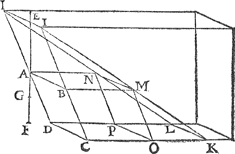



waters teghen den bodem A B C D rustende, even is anden pylaer diens grondt dien bodem is ende hoochde G E. Tbereytsel. Laet D A ende C B voortghetrocken worden tot H ende I, beyde in t'waters oppervlack; laet oock ghetrocken sijn H I, daer naer C K evewijdich vanden sichteinder, ende even an C I, maer rechthouckich op D C, sgelijcx D L even endeevewijdighe met C K, voort L K, daer naer I K ende H L, voort B M evewijdige met C K, ende alsoo dat Minde lini I K sy, daer naer A N even ende evewijdighe met B M, voort M O ende N P beyde even ende evewijdighe met B C.

Laet daer nae een ander form ghestelt worden, even, ghelijck, ende evewichtich mettet water even ande voorgaende C D H I K L, maer also dat C K rechthouckich sy op den sichteinder als hier neven.

Tbewys.

Alsulcken drucksel als t'stijflichaem C D H I K L der tweede form, veroirsaeckt teghen den bodem C D H I, even soodanigen drucksel veroirsaeckt t'water des eersten forms teghen sijn bodem C D H I soo bewesen is int 11 voorstel, ende vervolghens sulcken drucksel alsser valt teghen het deel A B C D der tweede form, even soodanighen drucksel valter oock teghen het deel A B C D der eerste form, maer het drucksel teghen A B C D der tweede form is t' lichaem

[p. 143]

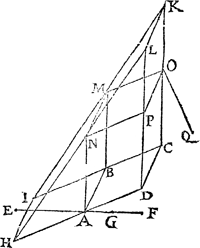A B C D L K M N, t' welck even is anden pylaer diens bodem A B C D en̄ hoochde G E, ghelijck wy terstont segghen sullen, daerom t'gewicht des waters rustende tegen A B C D der eerste form, is even anden pylaer diens grondt A B C D, ende hoochde G E. Maer dattet lichaem A B C D LK N M even is anden pylaer diens bodem A B C D en̄ hoochde G E blijckt aldus: Ghetrocken O Q rechthouckich op t'plat door A B C D, de selfde O Q is d'hoochde des pylaers A B C D P O M N, daerom dat lichaem is even anden pylaer diens gront A B C D ende hoochde O Q: Maer angesien A H even is an O C, ende den houck H A E even anden houck C O Q, ende dat A E rechthouckich is op t'plat door de punten H, E, sghelijcx O Q rechthouckich op t'plat door de punten C, Q, soo is A E even an O Q, daerom t'lichaem A B C D P O M N is even anden pylaer diens grondt A B C D, ende hoochde A E. Maer t'lichaem M N P O K L is even anden pylaer diens grondt A B C D ende hoochde A G door t'vervolgh des 11 voorstels, daerom die twee lichamen makende t'samen t'lichaem A B C D L K N M, sijn even anden pylaer diens bodem A B C D ende hoochde G E.

Ander bewys.

Ghenomen datter in t'water der eerste form hier boven een bodem sy, even ende ghelijck met A B C D, maer evewijdich vanden sichteinder in t' plat daer A B in is: Teghen den selven bodem sal rusten t'ghewicht even anden pylaer waters diens grondt even is an A B C D, ende hoochde A E door het 10 voorstel, t'selve ghewicht rust oock teghen alle bodem die even is an dien bodem en̄ leegher; Daer rust dan voor al teghen A B C D, een pylaer diens grondt even is an A B C D, ende hoochde A E: Nu gheweert al t'water datter boven den voornomden bodem is, die wy even stelden an A B C D, alsoo dat A B in t'waters oppervlack sy soo ruster teghen A B C D door t'vervolgh des 11 voorstels, den pylaer diens gront even is an A B C D, ende hoochde A G, welcke twee pylaren maken t'samen den pylaer diens gront A B C D, ende hoochde E G, voor t'ghewicht rustende teghen den bodem A B C D als vooren.

2 Voorbeelt.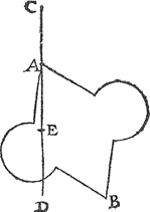

Laet A B eenich geschickt bodem wesen, dienshoochste punt onder t'waters oppervlac sijnde, is A, ende t'leegste B, ende de hanghende lini van t'waters oppervlack tot des bodems hoochste punt sy C A, ende van des bodems hoochste punt tot het plat evewijdich vanden sichteinder door des bodems leeghste punt B, sy A D, diens helft A E. Ick segh dattet ghewicht waters teghen den bodem A B rustende, even is anden pylaer waters diens bodem even is ande selve A B, ende hoochde E C, waer af t'bewijs sijn sal als van t'voorgaende. Tbeslvyt. Wesende dan een gheschickt bodem diens hoochste punt, &c.

[p. 144]

Merckt.

Wy hebben hier boven bethoont t'ghe wicht teghen een gheschickt bodem rust ende, mettet behulp der hanghende lini door des bodems hoochste punt; Maer alst een ongheschickt bodem is, soo en wort dat ghewicht door die hanghende lini niet bekent: Tis wel waer, datter altijt voor al op rust t'gewicht even an den pylaer waters diens grondt den bodem is, ende hoochde de hangende lini van t' waters oppervlack tot des bodems hoochste punt, maer t' ander deel en is niet even anden helft des pylaers wiens gront dien bodem is, ende hoochde de hanghende lini van des bodems hoochste punt, tottet plat evewijdich vanden sichteinder door des bodems leeghste punt, waer af d'oirsaeck is, dat den pylaer met een ongeschickt bodem niet nootsakelick in twee even deelen (ghelijck den pylaer met een gheschickt bodem) ghedeelt en wort, met een plat, door twee lijckstandighe punten scheuns teghen over malcanderen staende inde omtrecken des bodems. Maer op dat wy t' ghewicht teghen alle ongeschickt plat bodem oock bekent maken, sullen daer af soodanighen eysch beschrijven.

3 Werckstvck 13 Voorstel.

Wesende in t'vvater een platte bodem van form soot valt: Te vinden een lichaem vvaters evesvvaer an t'ghevvicht teghen dien bodem rustende.

Tghegheven. Laet A B een platte bodem in t'water sijn, geschickt ofte ongheschickt soot valt. Tbegheerde. Wy moeten een lichaem waters vinden eveswaer an t'ghewicht rustende teghen A B.

Twerck.

Ick treck het plat A B over allen sijden oneyndelick voort, diens gemeen sne mettet waters oppervlack sy C, uyt de selve sne C treck ick een lini door t'plat A B als C D, maer alsoo dattet plat rechthouckich op den sichteinder door C D, oock rechthouckich sy op t'oneyndelick plat door den ghegheven bodem; Daer naer treck ick de lini D E, even ande lini D C, maer evewijdich vanden sichteinder, ende rehthouckich op de ghemeene sne der twee platten, t'een het boveschreven door den bodem A B, t'ander door D E evewijdich vanden sichteinder, Daer na treck ick door C en E een oneyndelick plat, rechthouckich opt plat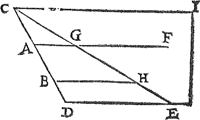



C D E, voort, uyt eenich punt vanden omtreck des ghegheven bodems als uyt A, een oneyndelicke lini A F, draeyende de selve mettet punt A in des bodems A B omtreck, tot datse weder ter plaets comt daerse begon te roeren, maer alsoo datse int roeren altijt evewijdich blijft met de lini D E, beschrijvende also een lichaem begrepen tusschen de twee deelen der oneyndelicke platten, ende t'vlack van die roerlicke lini beschreven, als t'lichaem A G H B. Ick seg dat een lichaem waters evegroot an t'lichaem A G H B, eveswaer is an t'ghewicht rustende teghen den ghegheven bodem.

Tbereytsel. Laet beschreven sijn dese tweede form even ende gelijck

[p. 145]

an d'eerste, ende eveswaeran water, maer alsoo dat de lini D E rechthouckich sy op den sichteinder.

Tbewys.

Alsulcken ghewicht alsser rust teghen den bodem A B der tweede form, even soodanighen ruster oock teghen den bodem A B van d'eerste, als vooren bewesen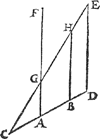



is, maer teghen A B der tweeder form, rust het ghewicht des lichaems A G H B, daerom teghen den bodem A B der eerste form, rust oock een ghewicht even an t'lichaem waters A G H B, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan int water een platte bodem van form soot valt, wy hebben een lichaem waters ghevonden eveswaer an t'ghewicht teghen dien bodem rustende, naer den cysch.

11 Vertooch. 14 Voorstel.

Wesende tvvee evevvijdige vierhouckighe bodems van even breeden, ende evediep intvvater, ende haer hoochste sijden int vvaters oppervlack: Ghelijck der bodems langde tot langde, alsoo haer gheprang des vvaters, tot gheprang des vvaters.

Tghegheven. Laet A B C D een water sijn, daer in twee evewijdighe vierhouckighe bodems wesende, E F ende G H, van even breeden, ende evediep int water, te weten, dat de^* hanghende I F, even sy ande hanghende K H, ende haer hoochste sijden E en G, sijn int waters oppervlack.

Tbegheerde. Wy moeten bewijsen dat ghelijck de langde E F, tot de langde G H, alsoo t'gheprang des waters teghen den bodem E F, tottet gheprang des waters teghen den bodem G H.

* Perpendicalaris.

Tbewys.

T'ghewicht des waters teghen den bodem E F rustende, is even anden helft des pylaers waters diens hoochde I F, ende grondt het plat E F, door het 11 voorstel; S'ghelijcx is t'ghewicht des waters teghen den bodem G H rustende, even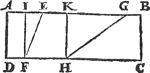



anden helft des pylaers waters diens hoochde K H, ende grondt het plat G H: maer dit sijn twee pylaren met even hoochden^* daerom sijnse inde reden haerder gronden; maer ghelijck de langde E F, totte langde G H, alsoo den grondt E F, totten grondt G H, want sy^* door t'ghestelde van even breeden sijn, daerom ghelijck de langde E F totte langde G H, also diens pylaer tot desens pylaer, ende wijder also diens halven pylaer tot desens halven pylaer, ende vervolgens also diens gewicht des waters teghen haer rustende, tot desens ghewicht des waters teghen haer rustende. Tbeslvyt. Wesende dan twee evewijdighe vierhouckige

* 32. v.11.b.E.

* Per hypothesin.

[p. 146]

bodems, van even breeden, ende evediep int water, ende haer hoochste sijden int waters oppervlack: Ghelijck der bodems langde tot langde, alsoo haer gheprang des waters, tot gheprang des waters, t'welck wy bewijsen moesten.

4 Werckstick. 15 Voorstel.

Wesende den bodem des vvaters een evevvijdich vierhouck onevevvijdich vanden^⋆ sichteinder, met sijn bekende hoochste sijde in t'vvaters oppervlack, ende bekent vvesende de lini vande hoochste sijde rechthouckich op de voortghetrocken leeghste, oock de^⋆ hanghende vande hoochste sijde tot het^⋆ plat evevvijdich vanden sichtemder door de leeghste sijde: Te vinden t'ghevvicht vvaters daer teghen rustende.

⋆ Horizonte.

⋆ Perpendicularis.

⋆ Plano.

Merckt.

Alle evewijdich vierhouck onevewijdich vanden sichteinder met sijn hoochste sijde int waters oppervlack, is of rechthouckich of scheefhouckich, ende elck van desen is op den sichteinder rechthouckich oft scheefhouckich, daerom vallender vier verscheyden ghestalten, daer wy soo wel inde volghende twee voorstellen als in dit, vier voorbeelden af beschrijven sullen: T'eerste van een rechthouck op den sichteinder rechthouckich, wiens drie linien, als de sijde onevewijdich vanden sichteinder, ende de lini uyt het uyterste vande hoochste sijde rechthouckich op de voortgetrocken leegste sijde, ende de hanghendc uyt het uyterste vande hoochste sijde tottet plat evewijdich vanden sichteinder door de leeghste sijde, al een selfde lini sijn: Het tweede voorbeelt sal sijn van een evewijdich scheefhouckich vierhouck op den sichteinder rechthouckich, diens twee linien als de lini vande hoochste sijde rechthouckich op de leeghste sijde, ende de hanghende vande hoochste sijde tottet plat evewijdich vanden sichteinder door de leeghste sijde, beyde een selve sijn: Het derde voorbeelt sal sijn van een rechthouck scheefhouckich op den sichteinder, diens twee linien, als de sijde onevewijdich vanden sichteinder, ende de lini van t' uyterste der hoochste sijde rechthouckich op de leegste sijde, beyde een selve sijn: T'vierde voorbeelt van een evewijdich scheefhouckich vierhouck op den sichteinder scheefhouckich, diens voornoemde drie linien al verscheyden sijn.

1 Voorbeelt.

Tgegheven. Laet A B C D een rechthouck wesen rechthouckich op den sichteinder, diens sijde A B in t'waters oppervlack doe 4 voeten, ende A D 3 voeten. Tbegheerde. Wy moeten t'ghewicht waters vinden rustende teghen A B C D.

Twerck.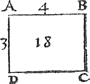

Ick menichvuldighe 3 van A D door 4 van A B, maeckt 12, die andermael ghemenichvuldicht door 3 van A D comt 36 voeten, diens helft voor t'begheerde 18 voeten. Ofte andersins

[p. 147]

ick menichvuldighe t'viercant der 3 van A D, door den helft der 4 van A B, comt als vooren 18 voeten. Nu ghenomen den voet te weghen 65 ℔, soo ruster 1170 ℔ teghen.

2 Voorbeelt.

Tghegheven. Laet A B C D een evewijdich scheefhouckich vierhouck wesen, rechthouckich op den sichteinder, diens sijde A B in t'waters oppervlack doe 4 voeten, ende A E hangende lini vande hoochste sijde A B, tot inde voortghetrocken C D, sy van 3 voeten. Tbegheerde. Wy moeten t'gewicht waters vinden rustende teghen A B C D.

Twerck.

Ick menichvuldighe 3 van A E door 4 van A B,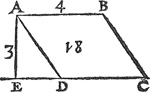



maeckt 12, die andermael gemenichvuldicht door 3 van A E comt 36 voeten, diens helft voor t'begheerde 18 voeten. Oft andersins ick menichvuldighe als boven t'viercant der 3 met den helft der 4 van A B.

3 Voorbeelt.

Tghegheven. Laet A B C D een rechthouck wesen scheefhouckich op den sichteinder, diens sijde A B in t'waters oppervlack sijnde doet 6 voeten, ende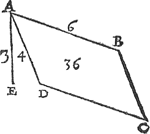



A D 4 voeten, maer A E hanghende van A tot in t'plat evewijdich vanden sichteinder door C D doet 3 voeten.

Tbegheerde. Wy moeten t'ghewicht waters vinden teghen A B C D rustende.

Twerck.

Ick menichvuldighe 4 door 6 comt 24, de selve door 3 maeckt 72 voeten, diens helft voor t'begheerde 36 voeten. Ofte andersins ick menichvuldighe den uytbreng van 3 met 4, door den helft van 6, comt als vooren 36 voeten.

4 Voorbeelt.

Tghegheven. Laet A B C D een evewijdich scheefhouckich vierhouck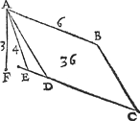



sijn, scheefhouckich op den sichteinder, diens sijde A B in t'waters oppervlac sijnde doet 6 voeten, ende A E rechthouckich op de voortghetrocken C D doet 4 voeten, ende A F hangende van A tot het plat evewijdich vanden sichteinder door D C doet 3 voeten.

Tbegheerde. Wy moeten t'ghewicht waters vinden teghen A B C D rustende.

[p. 148]

Twerck.

Ick menichvuldige 4 van A E, met 6 van A B comt 24, t'selve met 3 van A F, comt 72 voeten, diens helft voor t'begheerde 36 voeten. Ofte andersins, ick menichvuldighe, als vooren, den uytbreng van 3 met 4, door den helft van 6, comt oock 36 voeten.

Tbewys.

Wesende een pylaer diens gront 12 voeten, ende hoochde 3 voeten, den helft van dien doet 18 voeten; maer sulcken lichaem ruster tegen den bodem A B C D des 1 voorbeelts, door het 11 voorstel, daer rust dan t'ghewicht van 18 voeten waters teghen. S'ghelijcx sal oock t'bewijs sijn van d'ander voorbeelden.

Tbeslvyt. Wesende dan den bodem des waters een evewijdich vierhouck, &c.

1 Vervolgh.

Uyt het boveschreven is blijckelick, hoemen vinden sal t'ghewicht waters teghen een evewijdich vierhouck rustende, wesende d'hoochste sijde des ghegeven vierhoucx onder t'waters oppervlack, want tot het ghewicht ghevonden alsvooren, noch vergaert den pylaer diens grondt dien bodem is, ende hoochde de hanghende lini van t'plat door t'waters oppervlack tot de hoochste sijde des bodems, de somme sal t'begheerde sijn.

Laet by voorbeelt A B C D een evewijdich vierhouck sijn onevewijdich van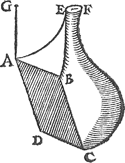



den sichteinder, diens hoochste sijde AB onder t'waters oppervlack E F is, ende G A doende drie voeten sy de hanghende lini van t'plat door E F tot de sijde A B, ende t'plat A B C D sy groot 20 voeten, ende als A B in t'waters oppervlack waer, soo souder op rusten (t'welck ick neem ghevonden te sijne door de voorgaende leering) 40 voeten waters: Vraegh hoe veel datter nu op rusten? Ick menichvuldighe 20 des plats van A B C D, door 3 van G A, comt een pylaer van 60 voeten, die tot de 40 maeckt 100 voeten dieder teghen A B C D rusten.

2 Vervolgh.

Soo den ghegheven platten bodem ongheschickt waer, men sal vinden een lichaem waters eveswaer an t'ghewicht teghen dien bodem rustende door het 13 voorstel, t'selve lichaem gemeten sal de begheerde swaerheyt bekent maken.

5 Werckstvck 16 Voorstel.

Wesende den bodem des vvaters een evevvijdich vierhouc, onevevijdich vanden^⋆ sichteinder, met sijn hoochste sijde intvvaters oppervlack, ende bekent sijnde t'ghevvicht daer teghen rustende, oock de lini vande hoochste sijde rechthouckich op de voortghetrocken leegste sijde, mette^⋆ hangende van de hoochste sijde, tottet^⋆ plat eve-

⋆ Horizonte.

⋆ Perpendiculari.

⋆ Planum.

[p. 149]

vvijdich vandē sichteinder door de leegste sijde: D'hoochste sijde bekent te maken.

1 Voorbeelt.

Tghegheven. Laet A B C D een rechthouck wesen rechthouckich op den sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende



d'hoochste sijde A B in t'waters oppervlack sy onbekent, maer AdD doet 3 voeten. Tbegheerde. Wy moeten de sijde A B bekent maken.

Twerck.

Ick deel de 18 door t'viercant der 3 van A D comt 2 voeten, diens dobbel A B 4 voeten.

2 Voorbeelt.

Tghegheven. Laet A B C D een evewijdich scheefhouckich vierhouck wesen, rechthouckich op den sichteinder, daer tegen rustende t'gewicht



van 18 voeten waters, ende de hoochste sijde A B in t'waters oppervlack sy onbekent, maer de lini A E vande hoochste sijde rechthouckich op de voortghetrocken leeghste sijde doet 3 voeten.

Tbegheerde. Wy moeten de sijde A B bekent maken.

Twerck.

Ick deel de 18 door t'viercant der 3 van AE comt 2 voeten, diens dobbel voor A B 4 voeten.

5 Voorbeelt.

Tghegheven. Laet A B C D een rechthouck wesen scheefhouckich op



den sichteinder, daer teghen rustende t'ghewicht van 36 voeten waters, ende d'hoochste sijde A B in t'waters oppervlack sy onbekent, maer de lini A D doet 4 voeten, ende A E hanghende vande hoochste sijde tot het plat evewijdich vanden sichteinder door de leeghste sijde doet 3 voeten.

Tbegheerde. Wy moeten de sijde A B bekent maken.

Twerck.

Ick menichvuldighe 3 van A E door 4 van A D comt 12, daer door ghedeelt de 36 comt 3 voeten, diens dobbel voor A B 6 voeten.

[p. 150]

4 Voorbeelt.

Tghegheven. Laet A B C D een evewijdich scheefhouckich vierhouck sijn scheefhouckich op den sichteinder, daer teghen rustende t'ghewicht van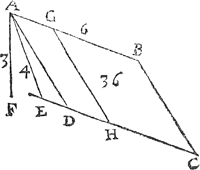



36 voeten waters, ende de hoochste sijde A B in t'waters oppervlack sy onbekent, maer A E lini vande hoochste sijde rechthouckich op de voortghetrocken leegste sijde C D, doet 4 voeten, ende A F hanghende vande hoochste sijde tot het plat evewijdich vanden sichteinder door de leeghste sijde, doet 3 voeten.

Tbegheerde. Wy moeten de sijde A B bekent maken.

Twerck.

Ick menichvuldighe 3 van A F, met 4 van A E, comt 12, daer door gedeelt de 36, comt 3 voeten, diens dobbel voor A B 6 voeten.

Tbewys.

Soo A B des 1 voorbeelts langher of corter waer als 4 voeten, t'ghewicht waters teghen den bodem rustende soude moeten meerder of minder sijn dan 18 voeten, t'welck teghen t'ghestelde waer, daerom A B is van 4 voeten. S'gelijcx sal oock t'bewys sijn van d'ander voorbeelden. Tbeslvyt. Wesende dan den bodem des waters een evewijdich vierhouck onevewijdich, &c.

1 Vervolgh.

Uyt het voorgaende is blijckelick, hoemen d'hoochste sijde bekent sal maken, als sy onder t'waters oppervlack is, want van t'gheheel ghewicht waters teghen den bodem rustende, ghetrocken den pylaer diens grondt dien bodem is, ende hoochde de hanghende lini van t'plat door t'waters oppervlack tot de hoochste sijde des bodems, daer sal resten t'ghewicht waters op den bodem rustende als haer hoochste sijde in t'waters oppervlack is, waer door sy alsdan bekent sal worden als vooren gheleert is.

Maer om in dit 1 vervolgh dien aftreckelicken pylaer te vinden, men sal nemen een deel des heel ghegheven gewichts, of des heelen pylaers, in sulcken reden totten selven heelen pylaer, als de hanghende lini tusschen t'waters oppervlack en des bodems hoochste sijde, totte ghegheven hanghende lini tusschen t'waters oppervlack en de bodems hoochste sijde, metten helft der hanghende lini tusschen des bodems hoochste sijde, en t'plat evewijdich door des bodems leeghste sijde. Om t'welck te verclaren door de form des 1 voorbeelts van het 12 voorstel, soo laet dit aftreckelick deel daer te vinden sijn: Ick segh E G gheeft E A, wat het ghegheven ghewicht? t'ghene daer uyt comt is den aftreckelicken pylaer.

2 Vervolgh.

Soomen inden bodem een lini wilde trecken evewijdich met de sijde die van den sichteinder onevewijdich is, de noodighe langde der hoochste sijde can bekent worden. Laet by voorbeelt inde form des boveschreven 4 voorbeelts, te

[p. 151]

ken sijn een lini als G H, evewijdich met A D, alsoo dat op A G H D ruste t'gewicht van 12 voeten waters. Ick sie wat deel dese 12 sijn vande 36 dieder teghen rusten, wort bevonden het derdedeel, daerom oock sal A G ⅓ wesen van AB dat sijn 2 voeten.

6 Werckstvck. 17 Voorstel.

Wesende den bodem des vvaters een evevvijdich vierhouck onevevvijdich vanden^⋆ sichteinder, met sijn bekende hoochste sijde in t'vvaters oppervlack, ende bekent sijnde t'ghevvicht daer teghen rustende, oock de^⋆ hanghende lini vande hoochste sijde tot het^⋆ plat evevvijdich vanden sichteinder door de leeghste sijde: De lini vande hoochste sijde rechthouckich op de voortgetrocken leegste sijde bekent te maken.

⋆ Horizonte.

⋆ Perpendicularis.

⋆ Planum.

1 Voorbeelt.

Tghegheven. Laet A B C D een rechthouck wesen, rechthouckich op den sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende



d'hoochste sijde A B in t'waters oppervlack sijnde, doet 4 voeten. Tbegheerde. Wy moeten de sijde A D bekent maken.

Twerck.

Ick deel de 18 door 2, helft van A B, comt 9, diens viercantighe sijde voor A D doet 3 voeten.

2 Voorbeelt.

Tghegheven. Laet A B C D een evewijdich scheefhouckich vierhouck wesen, rechthouckich op den sichteinder, daer teghen rustende t'gewicht



van 18 voeten waters, ende d'hoochste sijde A B in t'waters oppervlack sijnde doet vier voeten.

Tbegheerde. Wy moeten de lini A E bekent maken.

Twerck.

Ick deel de 18 door 2 helft van A B, comt 9, diens viercantighe sijde voor A E is 3 voeten.

3 Voorbeelt.

Tghegheven Laet A B C D een rechthouck wesen scheefhouckich op den sichteinder, daer teghen rustende t'gewicht van 36 voeten waters, ende

[p. 152]

de hoochste sijde A B in t'waters oppervlack sijnde doet 6 voeten, ende A E doende 3 voeten, sy de hanghende lini vande hoochste sijde tot het plat evewijdich vanden sichteinder door de leeghste sijde. Tbegheerde. Wy moeten A D bekent maken.

Twerck.

Ick deel de 36 door 3 helft van A B, comt 12, de selve ghedeelt door 3 van A E, comt 4 voeten voor A D.

4 Voorbeelt.

Tgegheven. Laet A B C D een evewijdich scheefhouckich vierhouck sijn scheefhouckich op den sichteinder, daer op rustende t'ghewicht van 36 voeten waters, en̄ de hoochste sijde A B in t'waters oppervlack sijnde doet 6 voeten, ende A E sy de lini van d'hoochste sijde rechthouckich op de voortghetrocken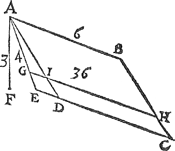



leeghste sijde, ende A F doende 3 voeten, is de hanghende vande hoochste sijde tot het plat evewijdich vanden sichteinder door de leeghste sijde. Tbegheerde. Wy moeten de lini A E bekent maken.

Twerck.

Ick deel de 36 door 3 helft der 6 van A B, comt 12, de selve door 3 van A F comt 4 voeten, voor A E.

Tbewys.

Soo A D des 1 voorstels langher of corter waer als 3 voeten, t'ghewicht waters teghen den bodem rustende soude moeten meerder of minder sijn dan 18 voeten, t'welck teghen t'gestelde is, A D dan is van 3 voeten, S'gelijcx sal oock t'bewijs sijn van d'ander voorbeelden. Tbeslvyt. Wesende dan den bodem des waters een evewijdich vierhouc onevewijdich vanden sichteinder, &c.

1 Vervolgh.

Uyt het voorgaende is blijckelick hoemen de lini vande hoochste sijde rechthouckich op de leeghste sijde, bekent sal maken, als de hoochste sijde onder t'waters oppervlack is, want van t'gheheel ghewicht waters teghen den bodem rustende, ghetrocken den pylaer diens grondt dien bodem is, ende hoochde de hanghende lini van t'plat door t'waters oppervlack, tot de hoochste sijde des bodems, daer sal resten t'ghewicht waters op den bodem rustende als haer hoochste sijde in t'waters oppervlack is, waer door sy alsdan bekent sal worden als voren gheleert is.

2 Vervolgh.

Soomen inde ghegheven bodem een lini wilde trecken evewijdich met de hoochste sijde, alsoo datse afsne een deel des bodems daer een begheert gewicht

[p. 153]

teghen ruste, de noodighe langde der lini vande hoochste sijde rechthouckich op de voortghetrocken leeghste sijde can bekent worden. Laet by voorbeelt in de form des boveschreven 4 voorbeelts, te trecken sijn een lini als G H, snyende A D in I, evewijdich met A B, alsoo dat op A B H I rust t'ghewicht van 24 voeten waters; Ick deel die 24 door 3, helft van A B, comt 8, daer naer vinde ick twee getalen tot malcanderen in sulcken reden als 3 van A F, tot 4 van A E, ende dat haer uytbreng de voornoemde 8 make, die ghetalen sijn √ 6 ende √ 10⅔, t'laetste is voor A G, want uyt G ghetrocken G H evewijdighe met A B, daer sal teghen A B H I rusten t'ghewicht van 24 voeten waters door het 15 voorstel.

Merckt.

Wy moeten nu naer luyt des Cortbegrijps, inde volghende 18, 19, 20, voorstellen, schrijven vande swaerheyts middelpunten der gheprangselen des waters in bodems vergaert; alwaer niet onbillichlijck eerst soude meughen gheseyt worden, vande bodems evewijdich sijnde vanden sichteinder, maer overmidts der selver swaerheydts middelpunten (welcke ghevonden worden nae de leering des 2 boucx vande beginselen der Weeghconst) oock de swaerheyts middelpunten sijn der voornoemde haer gheprangselen, soo en beschrijven wy daer afom cortheyts wil, gheen besonder voorstel. Sullen dan beginnen ande bodems onevewijdich vanden sichteinder als volght.

12 Vertooch. 18 Voorstel.

Wesende den bodem des vvaters een evevvijdich vierhouc onevevvijdich vanden^⋆ sichteinder, diens hoochste sijde in t'vvaters oppervlack is, uyt vvelcke sijdens middel een lini ghetrocken is, tot in t'middel vande leeghste sijde:^⋆ T'svvaerheyts middelpunt des geprangs inden bodem vergaert, deelt die lini alsoo, dat haer opperste stuck dobbel is an t'onderste.

⋆ Horizonte.

⋆ Centrum gravitatis.

1 Voorbeelt.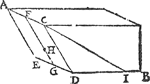

Tghegheven. Laet A B een water sijn, ende den bodem A C D E sy een evewijdich vierhouck onevewijdich vanden sichteinder, diens hoochste sijde A C in t'waters oppervlack is, ende F sy t'middel van A C, ende G t'middel van E D, ende tusschen de punten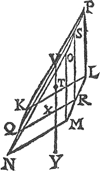



F G sy getrocken de lini F G, welcke in Halsoo ghedeelt is, dat F H dobbel is tot H G.

Tbegheerde. Wy moeten bewijsen dat H t'swaerheyts middelpunt is des geprangs inden bodem vergaert.

Tbereytsel. Laet ghetrocken worden de lini C I, also dat D I even sy an D C, ende mettet lichaem A C I D E sy beteeckent den helft des pylaers diens gront A C D F, en̄

[p. 154]

hoochde de hangēde van A tot in t'plat evewijdich vandē sichteinder door E D.

Laet daer naer ghetrocken worden t'stijflichaem K L M N O P even ende ghelijck ende eveswaer an t'lichaem A C I D E, te weten K L M N^* lijckstandich plat met A C D E, ende M O rechthouckich op den sichteinder, sy lijckstandighe lini met D I, ende Q R sy lijck standighe lini met F G, ende van S in t'middel van O P, sy getrocken de lini S Q, ende S R, ende des driehoucx Q S R swaer heyts middelpunt sy T, door t'welck ghetrocken is de lini V X rechthouckich op den sichteinder.

* Homologum planum.

Tbewys.

Alsulcken gheprang als t'lichaem K L M N O P doet teghen den boden K L M N, even sulcken gheprang doet t'water A B tegen den bodem A C D E door het 11 voorstel, daerom ghelijck t'swaerheyts middelpunt des gheprangs inden bodem K L M N valt, alsoo salt oock vallen inden bodem A C D E. Om dan tottet bewijs te commen, soo is ten eersten blijcklick dat T, welcke door^* t'ghestelde swaerheyts middelpunt is des driehoucx Q S R, oock swaerheyts middelpunt is (door het 15 voorstel des 2 boucx der beginselen vande Weeghconst) des lichaems K L M N O P, maer V X is door T rechthouckich op den sichteinder, V X dan is des lichaems swaerheyts middellini, daerom soo wy de lini X Y neerwaert trecken, t'lichaem K L M N O P sal mettet punt X op de lini X Y,^* Wisconstlick verstaen, sijn gegheven stant houden, daerom X is swaerheyts middelpunt van des lichaems gheprang, vergaert inden bodem K L M N, maer V X is door t'swaerheyts middelpunt T rechthouckich op den sichteinder, daerom oock evewijdich met S R, ende vervolghens sy snijt Q R (door het 5 voorstel des 2 boucx vande beginselen der Weeghconst) alsoo dat Q X dobbel is an X R; Maer soo boven gheseyt is, t'swaerheyts middelpunt valt inden bodem A C D E, in sulcken ghestalt ghelijckt inden bodem K L M N doet, het valter dan also in, dattet bovenste deel der lini F G, dobbel is an t'onderste, maer dat is in H, daerom H is t'swaerheyts middelpunt van t'gheprang des waters in den bodem A C D E vergaert.

* Hypothesin.

* Mathematicè.

2 Voorbeelt.

Om alsulcke redenen als int 4 voorbeelt des 11 voorstelsgheseyt sijn, sullen wy hier boven t'voorgaende^* Wisconstich bewijs, noch een voorbeelt door ghetalen stellen, aldus:

Laet A B C D een bodem sijn, daer in ghetrocken is de lini E F, tusschen de middelen van A B, ende D C, deelende dien bodem in ettelicke even deelen (die wy maten noemen) met linien evewijdich van A B, ick neem ten eersten in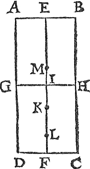



tween, mette lini G H, snyende E F in I, ende t'punt K sy alsoo, dat E K dobbel is an K F, welcke K wy bewijsen moeten t'swaerheyts middelpunt des gheprangs te sijn aldus: Genomen dat teghen A B H G, ruste 1 pont, ofte ghewicht waters, soo salderteghen G H C D sulcke 3 ghewichten rusten: Dit soo sijnde, ick acht ten eersten al oft t'swaerheyts middelpunt des gheprangs van A B H G, waer in I, ende van G H C D in F, (tis seker dat sy hoogher sijn) soo sal I F balck wesen, welcke ghedeelt in haer ermen tot malcanderen in sulcken reden als de voornoemde gewichten van 3 tot 1, t'welck in t'punt L valle, so sal F L doen ¼ eender maet, dat is ¼ van I F. Ten tweeden soo acht ick, al of t'swaerheyts middelpunt des gheprangs van A B H G waer in E, ende van G H C D in I, (tis seker

* Mathematicam demonstrationem.

[p. 155]

dat sy leegher sijn) so sal haer ghemeen swaerheyts middelpunt vallen een maet boven I als in M. Tis dan blijckelick dattet ware begheerde swaerheyt middelpunt is tusschen M ende L. Maer ghelijck wy den bodem hier boven ghedeelt hebben in tween, alsoo canmense deelen in oneyndelicke stucken, daer af vindende twee swaerheyts middelpunten als boven, tusschen de welcke altijt is, het ware begheerde swaerheyts middelpunt. Wy connen dan door sulcke middel altijt oneyndelick naerderen, daerom als wy door dese ervaring bevinden, dattet punt als L nimmermeer tot K en comt, maer seer by en̄ altijt daer onder blijft; S'ghelijcx dattet punt als M nimmermeer tot K en comt, maer altijt daer boven blijft, wy besluyten uyt sulcx, dat K het ware begheerde swaerheyt middelpunt is. Maer want het moeylicke rekening soude sijn t'ghemeene swaerheyts middelpunt van alle die bodems also te vinden, wy sullen daer af een corte manier verclaren aldus, ick schrijf een^* voortganck als 1. 3. 5. 7. 9. ende so voort altijt met tween opclimmende, want in sulcken voortganc ende reden sijn de prangselen der even deelen eens bodems A B C D door het 15 voorstel, daer naer stel ick ¼, (t'welck hier boven bevonden is voor F L) boven het tweede getal 3, als hier onder.

	¼
1.	3.	5.	7.	9.	11.

Daer naer vergaer ick 4, noemer van ¼, met de 5 derde in d'oirden, comt 9, die stel ick als noemer boven de 5, ende boven de 9 set ick 5, dat is de somme des noemers en telders van het ¼ welcker ghestalt dan aldus is:

	¼	5/9
1.	3.	5.	7.	9.	11.

S'ghelijcx vinde ick oock alle d'ander, want om t'ghetal te hebben dat boven 7 comen sal, ick vergaer den telder 9 ende 7, maeckt 16, daer boven stel ick de somme van 9 ende 5 (die noemer ende telder sijn vande 5/9) maeckt 14. Inder voughen dat boven de 7 comen sal 14/16, wiens ghestalt dan aldus sijn sal:

	¼	5/9	14/16
1.	3.	5.	7.	9.	11.

Ende soo voortgaende, boven de 9 ende 11 sullen ghetalen comen als hier onder:

	¼	5/9	14/16	30/25	55/36
1.	3.	5.	7.	9.	11.

Dit soo verstaen sijnde, men wilt weten neem ick, waer t'punt als L vallen sal, wanneer den bodem ghedeelt is in vijf even deelen: Ick sien wat ghetal dat ter boven t'vijfde in d'oirden staet, dat is boven de 9, ende bevinde 30/25 diens eerste ghebroken doet 6/5, daer uyt besluyt ick dat de lini als L F van sulcken bodem in vijven ghedeelt, sijn sal van 6/5 eender maet, der maten daer den bodem in ghedeelt is, maer dat die min sijn dan ⅓ van EF, ende dat haer uyterste als L vallen sal onder K, wort aldus bethoont: De 6/5 eender maet der maten daer den bodem in ghedeelt is, dat is 6/5 van ⅕ doen 6/25, vande heele lini als E F, welcke 6/25 minder sijn als ⅓ F K, want ghetrocken 6/25 van ⅓, blijft 7/75 der lini E F, ende soo verre sal dan t'punt als L van K vallē. Maer om t'punt als M te vinden, ick doe eē maet tot de 6/5 maets, comt 11/5 eender maet, de selve doen 11/25 vande heele lini E F, welcke 11/25 meerder sijn dan ⅓ van F K, want getrocken ⅓ van 11/25 blijft 8/75 der lini

* Progreßionē.

[p. 156]

E F, ende soo verre sal dan t'punt als M van K vallen, dat is 1/75 verder dander L afviel, ende alsoo met allen anderen, want soomen den bodem A B C D deelde in 40 even deelen, de lini als F L soude bevonden worden van 20550/1600 eender maet, dat is eens veertichstendeels der lini E F, door t'welcke men de punten als L, M, veel naerder soude bevinden dan boven, maer nimmermeer daer toe comen, waer af de nootsakelicheyt int bovenschreven 1 voorbeelt Wisconstelick betoocht is. De reden vande boveschreven corte manier der vindingh des ghemeen swaerheyts middelpunts van die verscheyden prangselen, sal den ghenen lichtelick connen bemercken, diese in t'lange souckt naer de leering des 2 voorstels van het 1 bouck der beginselen vande Weeghconst.

Tbeslvyt. Wesende dan den bodem des waters een evewijdich vierhouck onevewijdich, &c.

13 Vertooch. 19 Voorstel.

Wesende den bodem des vvaters een evevvijdich vierhouck onevevvijdich vanden^⋆ sichteinder, diens hoochste sijde onder t'vvaters oppervlack is, maer evevvijdich vanden sichteinder, uyt vvelcke sijdens middel een lini getrocken is, tot in t'middel vande leeghste sijde: T'svvaerheyts middelpunt des geprangs inden bodem vergaert, is inde lini tusschen t'middelpunt des bodems, ende t'punt dat het onderste derdendeel dier liniafsnijt; ende tusschen die tvvee punten in soodanigen punt, t'vvelck t'onderste deel alsoo afsnijt, dattet sulcken reden heeft tottet bovenste, ghelijck de^⋆ hanghende lini van t'vvaters oppervlack in des bodems hoochste sijde, tot den helft der hanghende lini van des bodems hoochste sijde, tottet^⋆ plat evevvijdich vanden sichteinder door des bodems leeghste sijde.

Tghegheven. Laet A B C D een bodem sijn onevewijdich vanden sichteinder diens hoochste sijde A B onder t'waters oppervlack E F is, maer evewijdich vanden sichteinder, ende G A sy de hanghende lini van t'waters oppervlack tot de hoochste sijde A B, ende A H de hanghende lini van A, tottet plat evewijdich vanden sichteinder door D C, ende A I sy den helft van A H, ende K L sy de lini ghetrocken tusschen de middelen van A B ende D C, ende L M sy het derdendeel vande lini L K, ende N t'middelpunt des bodems A B C D, en̄ O een punt tusschen M ende N, alsoo dat O M sulcken reden heeft tot O N, gelijck A G tot H I. Tbegheerde. Wy moeten bewijsen dat O t'swaerheyts middelpunt is van t'gheprang des waters inden bodem A B C D vergaert.

Tbereytsel. Laet C B ende D A voortghetrocken worden tot in t'waters oppervlack, als tot P ende E, daer naer C Q even an C P, maer evewijdich vanden sichteinder, ende rechthouckich op C D, daer naer B R evewijdige met

⋆ Horizonte.

⋆ Perpendicularis.

⋆ Planum.

[p. 157]

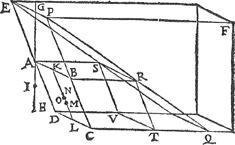C Q, wesende R inde lini P Q: S'ghelijcx A S even ende evewijdighe met B R, voort R T, ende S V even ende evewijdige met B C. Laet daer naer een ander form ghestelt worden, even ghelijck ende evewichtich ande voorgaende E P C D Q, maer alsoo dat C Q rechthouckich sy op dē sichteinder, ende X sy swaerheydts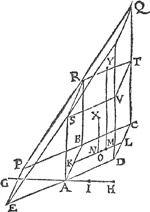



middelpunt des pylaers A B C D R S V T, en̄ Y swaerheyts middelpunt des lichaems R S V T Q, Laet oock ghetrocken worden de linien X N ende Y M.

Tbewys.

Anghesien in dese tweede form, X swaerheyts middelpunt is des pylaers A B C D R S V T, ende N swaerheyts middelpunt haersgrondts A B C D, ende dat C T rechthouckich is op den sichteinder, soo is X N haer evewijdighe, oock rechthouckich op den sichteinder, ende vervolgens heur swaerheyts middellini, daerom oock is N swaerheyts middelpunt des gheprangs diens pylaers; Maer M swaerheyts middelpunt te wesen des gheprangs van t'lichaem S R T V Q dat is int 18 voorstel betoocht: T'welck soo sijnde, M N is Weeghconstighen balck, die in O alsoo ghedeelt is, dat ghelijck A G tot A I, alsoo O M tot O N door t'ghegheven, maer ghelijck A G tot A I, alsoo den pylaer A B C D R S V T, tottet lichaem S R T V Q, daer om ghelijck den pylaer A B C D R S V T, tottet lichaem S R T V Q, also O M tot O N, waer door O t'swaerheyts middelpunt is deser tweede form, door het 1 voorstel des 1 boucx vande beginselen der Weeghconst, maer t'swaerheyts middelpunt van d'eerste form, om de redenen alsvooren, valt aldaer gelijck in de tweede, O dan der eerste form, is t'begheerde swaerheyts middelpunt.

Tbeslvyt. Wesende dan den bodem des waters een evewijdich vierhouck onevewijdich vanden sichteinder, &c.

7 Werckstvck 20 Voorstel.

Wesende den bodem in t'vvater een rechtlinich^⋆ plat van form soot valt: Te vinden het svvaerheyts middelpunt des gheprangs daer in vergaert.

Tghegheven. Laet A B een water wesen, diens oppervlack A C, ende D E een bodem, welcke een rechtlinich plat sy. Tbegheerde. Wy moe-

⋆ Planum.

[p. 158]

ten het swaerheyts middelpunt vinden van t'gheprang des waters in dien obdem vergaert.

Twerck.

Men sal eerst vindē eē lichaem waters eveswaer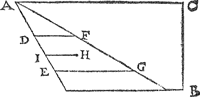



an t'geprang tegē den bodem D E, na de leering des 13 voorstels, t'selve sy DEFG, vindende daer naer sijn swaerheydts middelpunt door het 21 voorstel des tweeden boucx vande beginselen der Weeghconst, t'welck H sy, daer naer ghetrocken H I evewijdighe met G E, diens uyterste punt I inden bodem D E sy; Ick seg t'selve punt I te wesen t'begeerde swaerheyts middelpunt, waer af t'bewijs gelijck sal sijn ande bewijsen des voorgaenden 18 ende 19 voorstels. Tbeslvyt. wesende dan den bodem int water een rechtlinich plat, &c.

8 Werckstvck. 21 Voorstel.

Wesende ghegeven een vvater onbekender grootheyt, maer bekender svvaerheyt: Sijn grootheyt door sijn eyghenvvicht te vinden.

Merckt.

Men soude des waters grootheyt meughen^* Meetconstlick vinden naer de ghemeene reghel van dien, maer want het in cleyne menichvuldicheyt, Weegconstlick ghereeder ende sekerder wercking is, voornamelick inde ongeschickte formen, wy sullense daer door beschrijven.

Tghegheven. Laet A een water sijn diens grootheyt onbekent is, maer tis bekender swaerheyt, dat is (door de 1 bepaling deses boucx) dat sijn bekende grootheyt door bekent ghewicht can gheuytet worden; ick neem dat een voet des selfden weghe 65 ℔. Tbegheerde. Wy moeten de grootheyt van A door haer eyghenwicht vinden.

* Geometricè.

Twerck.

Men sal t'water A weghen, t'welck ick neem bevonden te worden van 5 ℔, die ghedeelt door de voornoemde 65 ℔, comt 1/13; dat is 1/13, voets voor de begeerde grootte van A.

Tbewys.

Anghesien t'water A 5 ℔ weeght, ende dat een voet des selfden



weeght 65 ℔, ende dattet over al eenvaerdigher swaerheyt is door de 2 begheerte, soo heeft sijn gewicht sulcken reden tot 65 ℔, als sijn grootheyt tot een voet, maer 5 ℔ heeft tot 65 ℔, de reden van 1 tot 13, daerom sijn grootheyt heeft sulcken reden tot 1 voet, als 1 tot 13, de grootheyt dan des waters A is 1/13 voets, t'welckwy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven een water onbekender grootheyt maer

[p. 159]

bekender swaerheyt, wy hebben sijn grootheyt door sijn eyghenwicht ghevonden, naer den eysch.

9 Werckstvck. 22 Voorstel.

Wesende ghegeven tvveer lichamen redenen der grootheyt, ende stofsvvaerheydt, ende t'ghevvicht van t'een lichaem: T'ghevvicht van t'ander te vinden.

Tghegheven. Laet A B t'een lichaem wesen, ende C t'ander, ende de reden der grootheyt van A B tot C, sy van 3 tot 1, ende der stofswaerheyt van 1 tot 2, ende A B weghe 6 ℔. Tbegheerde. Wy moeten t'ghewicht des lichaems C vinden.

Twerck.

Ick teecken D B evegroot met C, de selve D B dan is het derdendeel van A B 6 ℔, daerom D B weeght 2 ℔, maer de stofswaerheyt van D B tot C, is als van 1 tot 2, daerom soo weeght C 4 ℔.

Tbewys.

Laet C (soot meughelick waer) meer dan 4 ℔ weghen; T'welck soo ghenomen heur swaerheyt sal meerder dan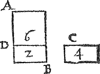



dobbel reden hebben tot de swaerheyt van D B, want D B weeght 2 ℔, ende vervolghens de stofswaerheyt van C (anghesien C ende D B even groot sijn) sal in meerder dan dobbel reden sijn tot D B, t'welck teghen t'gestelde is, daerom en weeght C niet meer dan 4 ℔. S'ghelijcx salmen oock bethoonen dat sy niet min en weeght, sy weeght dan nootsakelick 4 ℔ t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven tweer lichamen redenen der grootheyt, ende stofswaerheyt, ende t'ghewicht van t'een lichaem, wy hebben t'ghewicht van t'ander lichaem ghevonden na den eysch.

Vervolgh.

Tis uyt het voorgaende openbaer dat,

Chetrocken reden der grootheyt, van reden des ghewichts, rest reden der stofswaerheyt.

Ghetrocken reden der stofswaerheyt, van reden des ghewichts, rest reden der grootheyt.

Vergaert reden der stofswaerheyt, tot reden der grootheyt, comt reden des ghewichts.

Waer uyt blijckt dat een gebrekende^* pael der ses, door de vijf gegeven palen altijt bekent can worden. Maer om t'selve by voorbeelt te verclaren,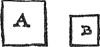

Ghewichten.	6 ℔.	4⅕ ℔
Grootheden.	5 voet.	2 voet
Stofswaerheden.	4	7

laet A weghen 6 ℔, ende groot sijn 5 voeten; ende t'gewicht van B sy onbekent, maer heur grootheyt is van 2 voeten, ende de reden der stofswaerheydt van A tot B, sy van 4 tot 7. Nu om t'onbekende ghewicht van B te vinden, ick vergaer reden der stofswaerheyt, dat is Reden 4/7 tot reden der grootheyt, dat is Reden 5/2, comt reden des ghewichts Reden 10/7, t'ge-

* Terminus.

[p. 160]

wicht dan van A heeft sulcken reden tottet ghewicht van B, als 10 tot 7, maer A weeght 6 ℔, daerom segh ick 10 gheeft 7, wat 6 ℔? comt voor t'ghewicht van B 4⅕ ℔.

Laet ten tweeden de grootheyt van B onbekent sijn, welcke wy door d'ander vijf palen vinden willen. Ick treck reden der stofswaerheyt, dat is Reden 4/7 van reden des gewichts, dat is Reden 10/7, rest reden der grootheyt Reden 5/2; de grootheyt dan van A, heeft sulcken reden tot de grootheyt van B, als 5 tot 2, maer A is groot 5 voeten, daerom segh ick 5 gheeft 2 wat 5 voeten? comt voor B 2 voeten.

Laet ten laetsten de reden der stofswaerheyt onbekent sijn, welcke wy door d'ander twee ghegheven redenen bekent willen maken. Ick treck reden der grootheyt, dat is Reden 5/2, van reden des ghewichts, dat is Reden 10/7, rest reden der stofswaerheyt van 4 tot 7.

Dit voorstel is gemeen over alle stoffen, doch schijnt sijn grootste gebruyck in^* watersche verschillen te bestaen.

vierde bovcx

EYNDE.

* Aquaticis questionibus.