Wisconstighe gedachtenissen. Deel 4: van de weeghconst
(1605)–Simon Stevin–
[pagina 13]
| |||||||
Het ander deel
| |||||||
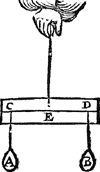
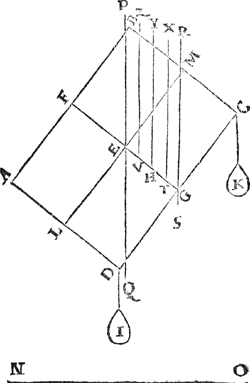
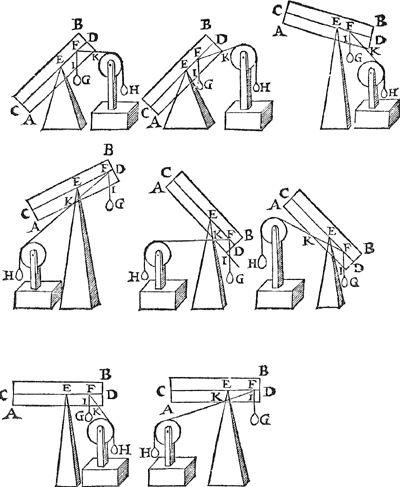
1 Voorbeelt.Tghegheven. Laet A B C D een pylaer sijn weghendeGa naar margenoot+ 6 ℔. welcke ghedeelt sy in 6 even deelen, doorGa naar margenoot* platten evewijdich van sijn grondt A D, als E F, G H, I K, L M, N O, snyende den as P Q in R, S, T, V, X: Laet ons nu nemen L M D A voor de swaerste swaerheyt, wiens swaerheyts middelpunt is S, ende L M C B voor de lichste swaerheydt, wiens swaerheydts middelpunt is X, ende S X is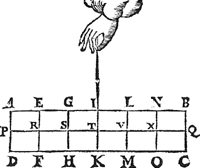 dier deelen balck door de 7 bepaling, ende T is t'swaerheydts middelpunt des heelen pylaers, ende T I d'hanthaef, waer an L M D A ende L M C B evestaltwichtich hanghen, ende T X is den langsten erm, ende T S den cortsten door de 8 bepaling. Tbegheerde. Wy moeten bewijsen Quaesitum. dat ghelijck de swaerste swaerheydt L M D A, tot de lichtste L M C B, alsoo den langsten erm T X, tot den cortsten T S. | |||||||
Tbewys.Ga naar margenoot+De swaerste swaerheyt L M D A weeght 4 ℔, ende de lichtste L M C B 2 ℔, ende den langsten erm T X heeft sulcken reden tot de cortste T S, ghelijck 2 tot 1 door t'ghegheven: Maer ghelijck 4 tot 2, also 2 tot 1, ghelijck dan de swaerste swaerheyt L M D A, tot de lichtste L M C B, alsoo den langsten erm T X, tot den cortsten T S.
Maer op datmen niet en dencke dit daer alsoo by ghevalle gheschiet te sijne, wy sullenderGa naar margenoot* Wisconstich bewijs af doen aldus: | |||||||
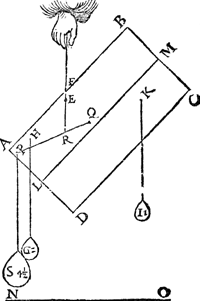
2 Voorbeelt.Tghegheven. Laet A B C D wederom een pylaer sijn, ghedeelt met een plat evewijdich van A D, als E F, snyende den as G H, waert sy in I, ende het swaerheyts middelpunt van het deel E F D A sy K, int middel van G I, ende van het deel E F C B, sy L int middel van I H, ende des heels A B C D sy M int middel van G H, ende M N sal der deelen E F D A ende E F C B hanthaef sijn, daer an sy evestaltwichtich hanghen. Tbegheerde. Wy moeten bewijsen dat ghelijck het lichaem ofte de swaerheydt (t'welck hier een selfde is om haer | |||||||
[pagina 14]
| |||||||
everedenheydt, want ghelijck t'lichaem
 E F D A, tot t'lichaem E F C B, also diens swaerheydt tot desens, overmidts den pylaerGa naar margenoot+ door t'ghestelde overal eenvaerdiger swaerheydt is) van E F D A, tot E F C B, alsoo den langsten erm M L, tot den cortsten M K. | |||||||
Tbewys.1 Lidt.M H is even an M G door t'ghegheven, laet tot elck doen K M, soo sal dan K H even sijn an M G met K M; daer naer van d'eene getrocken G K, ende van d'ander K I (welcke G K ende K I even sijn door t'ghegheven) soo sal K M met K M even blijven an I H; Ende haer helften als K M ende I L sullen oock even sijn. | |||||||
2 Lidt.Laet tot elck (te weten K M ende I L) doen M I, Ende M L sal even sijn an I K. | |||||||
3 Lidt.Ghelijck G I tot haer helft K I, alsoo I H tot haer helft I L, ende doorGa naar margenoot* overanderde everedenheyt ghelijck G I tot I H, alsoo K I tot I L, maer K I is even an M L door het 2 lidt, ende I L an M K door het 1 lidt, daerom ghelijck G I tot I H, alsoo M L tot M K; Maer ghelijck G I tot I H, alsoo het lichaem ofte de swaerheyt E F D A, tot E F C B. Ghelijck dan de swaertste swaerheyt E F D A, tot de lichtste E F C B, also den langsten erm M L, tot den cortsten M K. NV mocht yemant segghen, ghy hebt dat voorstel wel bewesen in deelen die t'samen een heel pylaer maken een vaerdigher swaerheyt, maer wie weet of dat alsoo plaets sal houden in allen anderen verscheyden deelen van ongeschicter form, ende oneveswaerder stof, daerom sullen wy de gemeenheyt des voorstels aldus bethoonen: Laet ons achten dat den balck K L der 1 ghestalt hier boven, in haer plaets blijve, ende dat het stick E F D A neerghetrocken wort, ende dat het blijve hangende met een lini uyt sijn swaerheyts middelpunt an t'punt K, ende dat insghelijcx oock neerghetrocken 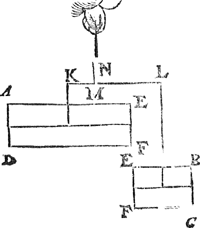 sy het ander stick E F C B, ende dat het blijve hanghende by sijn swaerheyts middelpunt an t'punt L, ende dat E F C B niet en ghenake an E F D A, ende haer gestalt sy dan soo dees form uytwijst. Nu doen het lichaem in d'eerste gestalt hinck ande hanthaef M N, alsdoen was E F D A evestaltwichtich met E F C B; Maer t'ghewicht E F D A in dees tweede ghestaltGa naar margenoot+ neerghetrocken sijnde, en brengt an K L gheen meerder noch minder swaerheydt dan in d'eerste ghestalt door de 3 begeerte. S'ghelijcx en brengt t'ghewicht E F C B | |||||||
[pagina 15]
| |||||||
der tweede ghestalt, an L K gheen meerder swaerheyt dan in d'eerste ghestalt, waer door de ghewichten der tweede gestalt an K L de selfde sijn die sy in d'eerste waren, daerom oock de balck K L blijft noch inde selve eerste ghestalt, waer door E F D A noch evestaltwichtich blijft met E F C B. De sticken dan des pylaers blijven so wel evestaltwichtich verscheyden, als doen sy an malcanderen waren, ende de ermen oock inde selve reden. 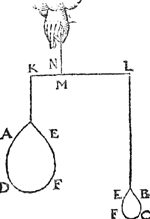 Dit soo sijnde, laet ons de lichamen E F D A ende E F C B der tweede ghestalt ander formen gheven, die alsoo duwende (neemt dat de stof sy van was, cleye, ofte yet soodanich t'welck sulcx lijde) dat E F D A der tweede ghestalt, sy E F D AGa naar margenoot+ deser derde ghestalt, ende dat E F C B der tweede ghestalt, sy E F C B deser derde ghestalt; Ende is openbaer dat K L noch in haer selve ghestalt sal blijven, ende de ermen M L, M K, inde selve reden, ende vervolgens E F D A noch evestaltwichtich met E F C B, want dees verandering der form (al de stofblijvende) en veroirsaeckt gheen verandering des ghewichts. Laet ons ten laetsten weeren E F D A der derde ghestalt ende hanghen in diens plaets een lichaem van loot des selfden ghewichts, ende inde plaets van E F C B een houten lichaem des selven ghewichts,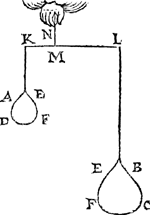 wiens vierde gestalt alsdan sy als hier nevens. Ende is kennelick dat K L noch inde selve gestalt sal blijven, ende vervolgens E F D A noch evestaltwichtichGa naar margenoot+ met E F C B, ende de ermen noch inde selve reden. | |||||||
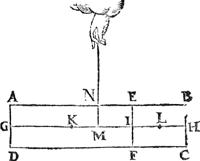
3. Voorbeelt.Men can t'voorgaende oock bethoonen, blijvende twee swaerheden hanghende an eenen lichamelicken balck, in deser voughen: Laet den pylaer A B C D ghesneen sijn in twee deelen, met een plat door den as E F, ende den as des ondersten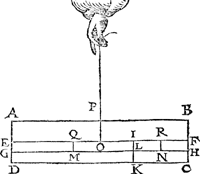 deels E C sy G H, ende E C sy doorsneen met een plat I K evewijdich vanden gront E D, snyende den as G H in L, ende het swaerheydts middelpunt van het deel I K D E sy M int middel van G L, ende van het deel I K C F sy N int middel van L H, en̄ des heels A B C D sy O int middel van E F, ende O P sy swaerheyts middellini des heels A B C D, ende M Q van I K D E, ende N R van I K C F. Dit soo sijnde tis kennelick dat des heels pylaers rechter sijde, evewichtich is teghen haer slincker. Laet ons nu het onderste deel E F C D neertrecken, alsoo dat het blijve hanghende ande linien M Q ende N R, als hier nevens. Ende is openbaer dat den lichamelicken balck A B F E noch in haer eerste ghestalt sal blijven. Laet ons | |||||||
[pagina 16]
| |||||||
nu achten dat het deel I K D E, ghesneen sy
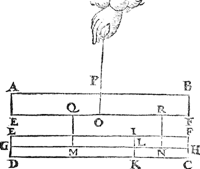 van I K C F, ende dat elck deel vallen mach daert wil, maer sy hanghen an haer swaerheydts middelpunten M, N, sy houden dan haer eerste ghegheven gestalt door de 4 bepaling, daerom A B F E blijft oock noch in sijn eerste gedaente. Maer I K D E, sulcken reden te hebben tot I K C F, als den erm O R, tot den erm O Q, is vooren beproeft; Inder voughen dat t'ghene eerst betoocht was anden weeghconstighen balck (dat is een lini) sulcx hebben wy hier ververclaert an een lichamelicken. Tbeslvyt. Wesende dan twee evestaltwichtigeGa naar margenoot+ swaerheden, de swaerste heeft sulcken reden tot de lichtste (van wat stof ofte form oock de lichamen sijn) als den langsten erm tot den cortsten, t'welck wy bewijsen moesten. | |||||||
Vervolgh.uyt het verkeerde des voorgaenden voorstels volght, dat hebbende de swaerste swaerheyt sulcken reden tot de lichtste, als den langsten erm tot den cortsten, dat die twee swaerheden evestaltwichtich sijn. | |||||||
1 Werckstick. 2 Voorstel.Ga naar margenoot+Wesende ghegheven bekende svvaerheden, haer hanthaef te vinden. | |||||||
1 Voorbeelt.Tghegheven. Laet d'een swaerheyt A sijn weghende 3 ℔, hanghende an C, d'ander B van 1 ℔ hanghende an D, ende C D sy balck. Tbegheerde. Wy moeten haer hanthaef vinden. | |||||||
Twerck.Men sal C D alsoo deelen, dat haer meeste stick naest de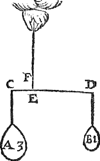 hanghende swaerheytds middellini van de minste swaerheydt, sulcken reden hebbe tot het minste stick, ghelijck de meeste swaerheyt tot de minste, t'welck sy in E, te weten dat E D sulcken reden hebbe tot E C, als 3 ℔ van A, tot 1 ℔ van B. Ick seg dat de hangende door E, als E F, d'hanthaef is. | |||||||
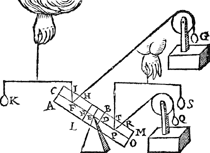
2 Voorbeelt.Tghegheven. Laet d'een swaerheyt sijn den pylaer A B C D weghende 6 ℔, ghedeelt als den pylaer int begin des eersten voorstels; En̄ an Q hanghe een ghewicht Y van 12 ℔. Tbegheerde. Wy moeten d'handthaef vinden. | |||||||
[pagina 17]
| |||||||
Twerck.De hangende swaerheyts middellini des pylaers is I T, en̄ vā t'gewicht Y is B Q, en̄ T Q is balck, de selve salmen in tween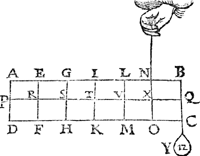 deelen, alsoo dat de sticken de reden hebben als 12 ℔ van Y, tot 6 ℔ vanden pylaer, welverstaende t'cortste stick naer de hangende swaerheyts middellini vande swaerste swaerheyt Y, t'welck vallen sal in X, indervoughen dat N X de begheerde hanthaef is. | |||||||
3 Voorbeelt.Tghegheven. Laet A B C D wederom den pylaer sijn, gedeelt als vooren, hanghende nu Y 6 ℔ an X. Tbegheerde. Wy moeten d'hanthaef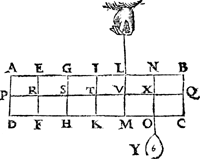 vinden. | |||||||
Twerck.De hangende swaerheyts middellini des pylaers is I T, ende van Y is N X, ende T X is balck: de selve salmen in tween deelen, alsoo dat de sticken de reden hebben als 6 ℔ van Y, tot 6 ℔ des pylaers, t'welck vallen sal in V, inder voughen dat V L de begheerde hanthaef sijn sal. | |||||||
Tvoornoemde werck op een ander manier.DE hanghende swaerheydts middellini van M L B C Y, is N X, ende van M L A D is S G, ende S X is balck, de selve salmen in tween deelen, also dat de stucken de reden hebben als 8 ℔ van M L B C Y, tot 4 ℔ van M L A D: welverstaende t'cortste stick naer de hanghende swaerheyts middellini van t'swaerste deel, t'welck vallen sal in V, inder voughen dat V L wederom de begheerde handthaef sijn sal als vooren. | |||||||
4 Voorbeelt.Tghegheven. Laet A B C D wederom den pylaer sijn, ghedeelt als vooren, hanghende Y 6 ℔ an X, ende Z 24 ℔ an R. Tbegheerde. Wymoeten d'hanthaef vinden. | |||||||
Twerck.De hanghende swaerheydts middellini van A B C D Y, is L V door het | |||||||
[pagina 18]
| |||||||
3 voorbeelt, ende van Z is R E, daerom is
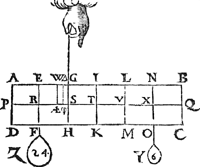 R V balck; de selve salmen in tween deelen, alsoo dat de sticken de reden hebben als 12 ℔ van A B C D Y, tot 24 ℔ van Z: welverstaende t'cortste stick naer de hanghende swaerheyts middellini van t'swaerste deel, t'welck vallen sal in S, inder voughen dat S G de begheerde handthaef sijn sal. | |||||||
Tvoornoemde werck op een ander manier.DE hanghende swaerheydts middellini van A B C D Z is AE W door het 3 voorbeelt, alsoo dat S AE doet ⅗ van S R, ende de hanghende swaerheyts middellini van Y is X N, ende AE X is balck, de selve salmen in tween deelen, alsoo dat de sticken de reden hebben als 30 ℔ van A B C D Z, tot 6 ℔ van Y: welverstaende t'cortste stick naer de hanghende swaerheyts middellini van t'swaerste deel, t'welck vallen sal in S, inder voughen dat S G wederom de begheerde handthaef is als vooren. | |||||||
Tvoornoemde werck op een ander manier.DE hanghende swaerheyts middellini van Y Z, is (door het eerste voorbeelt) Φ Δ, alsoo dat S Φ doet ⅕ van S R, ende de hanghende swaerheyts middellini vande pylaer T I, ende T Φ is balck: de selve salmen in tween deelen, alsoo dat de sticken de reden hebben als 30 ℔ van Y met Z, tot 6 ℔ vande pylaer, te weten t'cortste stick naer de hangende swaerheyts middellini van t'swaerste deel, t'welck vallen sal in S, inder voughen dat S G wederom de begheerde hanthaef is als vooren. | |||||||
5 Voorbeelt.Tghegheven. Laet A B C D wederom den pylaer sijn ghedeelt als vooren, hanghende Y 6 ℔ an X, ende Z 24 ℔ an R, ende AE 12 ℔ an Q. Tbegheerde. Wy moeten d'hanthaef vinden. | |||||||
Twerck.De hangende swaerheyts middellini van A B C D Y Z is S G door het 4 voorbeelt, ende van AE is Q B, ende S Q is balck:de selve salmen in tween deelen, alsoo dat de sticken de reden hebben als 36 ℔ vanden pylaer met Y ende Z, tot 12 ℔ van AE, te weten t'cortste stick naer de hanghende swaerheydts middellini van t'swaerste deel, t'welck vallen sal in T, inder voughen dat T I de begheerde hanthaef sal sijn. Ende soomen noch hinghe an P 24 ℔, d'hanthaef soude S G sijn, ende soo voorts met allen anderen swaerheden diemen anden pylaer soude meughen hanghen. | |||||||
[pagina 19]
| |||||||
Tbewys.De swaerste swaerheyt A int eerste voorbeelt,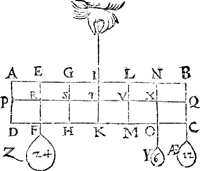 heeft sulcken reden tot de lichtste B, als den langsten erm E D, tot den cortsten E C, daerom E F door de 9 bepaling is d'hanthaef. S'ghelijcx sal oock t'bewijs sijn van al d'ander voorbeelden, t'welck wy om de cortheyt achterlaten. Tbeslvyt. Wesende dan ghegheven bekende swaerheden, wy hebben haer handthaef ghevonden naer den eysch. | |||||||
Merckt.Soomen t'ghewicht Y des 2 voorbeelts verswaerde van 1 ℔, ende datmen an V hinge 1 ℔, inder vougen dat haer ghestalt dan waer als hier onder, Tis kennelick uyt het voorgaende dat X N noch handthaef blijft, ende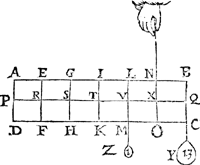 alles an haer evest altwichtich hangt. T'selve sal X N oock blijven, soomen Z 1 ℔ hangt an T, ende dat Y doe 14 ℔, ofte Z 1 ℔ an S, ende dat Y doe 15 ℔, ofte Z 1 ℔ an R, ende dat Y doe 16 ℔, ofte Z 1 ℔ an P, ende dat Y doe 17 ℔, ende soo oir dentlick voort by aldien den pylaer langher waer; te weten, verswarende Y altijt van 1 ℔, voor elcke langde als XV, daermen Z voorder an verschuyft. Waer uyt deGa naar margenoot* Ghedaenten des Onsels bekent sijn, als inde Weeghdaet breeder daer af sal ghehandelt worden. | |||||||
2 Werckstick 3 Voorstel.Wesende ghegeven tvvee evestaltvvichtighe svvaerheden, d'een bekent d'ander onbekent, ende d'hanthaef: Die onbekende bekent te maken. | |||||||
1 Voorbeelt.Tghegheven. Laet A ende B twee evestaltwichtighe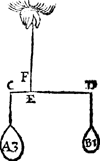 swaerheden sijn, welcker A hanghende an C weeght 3 ℔, maer B hangende an D is onbekent, ende E F sy d'hanthaef, Tbegheerde. Wy moeten t'ghewicht van B bekent maken. | |||||||
Twerck.Men sal ondersoucken wat reden den erm E D heeft, tot den erm E C, wort bevonden, neem ick, als van 3 tot 1, daer om segh ick, E D 3, gheeft E C 1, wat A 3 ℔? comt voor B 1 ℔. | |||||||
[pagina 20]
| |||||||
2 Voorbeelt.Tghegheven. Laet inde form des 2 voorbeelts van het 2 voorstel den pylaer A B C D voor d'een swaerheyt weghen 6 ℔, ende d'ander onbekende swaerheyt sy t'ghewicht daer an hanghende Y, ende d'hanthaef sy X N. Tbegheerde. Wy moeten t'ghewicht van Y bekent maken. | |||||||
Twerck.Anghesien T I hanghende swaerheyts middellini is des pylaers, ende Q B, van Y, soo sal T Q balck sijn, diens cortsten erm X Q, ende langsten X T; Daerom salmen ondersoucken wat reden den erm X Q, heeft tot X T, wort bevondē neem ick, als van 1 tot 2. Ick segh dan, X Q 1, geeft X T 2, wat den pylaer 6 ℔? comt voor Y 12 ℔. Der gelijcke voorbeelden mochten wy hier stellen op d'ander formen der voorbeelden des 2 voorstels, ten waer die door de voorgaende kennelick ghenouch sijn. | |||||||
Tbewys.Laet B int eerste voorbeelt, soot meughelick waer, swaerder sijn dan 1 ℔, de swaerste swaerheyt dan en sal niet sulcken reden hebben tot de lichtste, als den langsten erm tot den cortsten; t'welck teghen het 1 voorstel is; B dan en is niet swaerder dan 1 ℔. S'ghelijcx salmen oock bethoonen dat sy niet lichter en is, sy weeght dan effen 1 ℔, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven twee evestaltwichtige swaerheden, d'een bekent d'ander onbekent, ende d'hanthaef: Wy hebben die onbekende bekent ghemaeckt, naer den eysch. | |||||||
3 Werckstick 4 Voorstel.Wesende ghegheven tvvee bekende evestaltvvichtighe svvaerheden met de langde van d'eenen erm: De langde des anderen erms te vinden.
Tghegheven. Laet A ende B twee evestaltwichtighe swaerheden sijn, welcker A hanghende an C weeght 3 ℔, ende B hanghende an D 1 ℔, ende de langde des erms D E sy 6 voeten. Tbegheerde. Wy moeten de langde des anderen erms vinden. | |||||||
Twerck.Men sal segghen A 3 ℔, gheeft B 1 ℔, wat D E 6 voeten?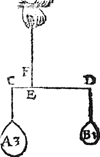 comt voor E C 2 voeten. Ende derghelijcke voorbeelden mochten wy stellen op de formen der voorbeelden des 2 voorstels, ten waer die door t'voorgaende kennelick ghenouch sijn. | |||||||
Tbewys,Laet E C, soot meughelick waer, langher sijn dan 2 voeten; den langsten erm sal dan minder reden hebben tot den | |||||||
[pagina 21]
| |||||||
cortsten, dan de swaerste swaerheyt tot de lichtste, t'welck tegen het eerste voorstel is, E C dan en is niet langher dan 2 voeten; S'ghelijcx salmense oock bewijsen niet corter te sijn, sy is dan effen van twee voeten, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven twee evestaltwichtighe swaerheden met de langde van d'eenen erm, wy hebben de langde des anderen erms ghevonden, naer den eysch. | |||||||
4 Werckstick. 5 Voorstel.Wesende ghegheven een pylaer: te vinden een gevvicht in ghestelde reden tot des pylaers ghevvicht.
Tghegheven. Laet A B C D een pylaer wesen, diens as E F, ende haerGa naar margenoot* middelpunt G, ende de ghestelde reden sy van 2 tot 3. Tbegheerde. Wy moeten een ghewicht vinden in sulcken reden tot den pylaer, als van 2 tot 3, dat is even an sijn ⅔. | |||||||
Merckt.Ghelijck deGa naar margenoot* Meetconstighe ende Telconstighe voorstellen verscheyden werckinghen hebben, alsoo oock de Weeghconst, want men soude vanden pylaer een stuck connen snyen in sulcken reden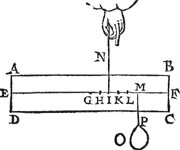 tot den heelen pylaer, als van 2 tot 3, Oft andersins om den pylaer heel te laten, men mocht hem teghen ander stof wegen, daer af nemende de ⅔, maer wy willent Weeghconstlicker doen in deser voughen. | |||||||
Twerck.Men sal van t'middelpunt G af, naer F, teeckenen eenighe vijf punten (te weten 5 voor de somme der ghegheven palen 2.3) als H, I, K, L, M, van malcanderen evewijt; Ende van het tweede punt I (van het tweede om dat 2 het ander der ghegheven getalen is) salmen den pylaer ophanghen by de hanghende swaerheydts middellini I N; Daer naer salmen an t'vijfde punt M een ghewicht hanghen als O, even so swaer dat alles in evestaltwichticheyt sy, t'welck so wesende, ick segh dat t'ghewicht van O, in sulcken reden is tot t'ghewicht des pylaers, als 2 tot 3, ofte dat O even is ande ⅔ des pylaers. | |||||||
Tbewys.G isGa naar margenoot* swaerheyts middelpunt des pylaers A B C D, ende M P hanghende swaerheyts middellini van O, daerom ghelijck den erm I G tot den erm I M, alsoo O tot den pylaer door het 1 voorstel, maer I G heeft sulcken reden tot I M, als 2 tot 3, daerom O heeft sulcken reden tot den pylaer, als 2 tot 3, t'welck wy bewijsen moesten, Tbeslvyt. Wesende dan ghegheven een pylaer, wy hebben ghevonden een ghewicht in ghestelde reden tot des pylaers ghewicht, naer den eysch. | |||||||
[pagina 22]
| |||||||
Merckt.Wy souden oock meughen voorbeelden stellen met Redenen vanGa naar margenoot* onmetelicke palen, maer sulcx is openbaer ghenouch door t'voorgaende, metsgaders t'ghene wy vande onmetelicke grootheden elders gheschreven hebben. | |||||||
2 Vertooch. 6 Voorstel.Wesende een hanghende pylaer ghesneen door sijn svvaerheydts middelpunt, met een plat evevvijdich van den gront, ende vvesende t'vastpunt in dat plat boven het svvaerheyts middelpunt: Den as des pylaers blijft evevvijdich vandenGa naar margenoot⋆ sichteinder. Tghegheven. Laet A B C D een 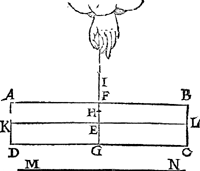 pylaer sijn, ghesneen door sijn swaerheyts middelpunt met een plat F G, evewijdich vanden grondt A D, ende laet H vastpunt inde hanghende swaerheyts middellini I G wesen, boven het swaerheyts middelpunt E, ende K L sy as, ende M N sichteinder. Tbegheerde. Wy moeten bewijsen dat den as K L evewijdich blijft vanden sichteinder M N. | |||||||
Tbewys.Laet K L soot meughelick waer, onevewijdich sijn vanden sichteinder M N, als in dees tweede form, ende laet I H voortghetrocken worden tot in O, snyende A B in P, ende laet het stick des pylaers P O C B alsoo evewichtich blijven hanghen teghen P O D A, maer dat is grooter ende swaerder dan dit (want F G D A, is even an F G C B, ende minder is den driehouck F H I ghesneen van F G C B, als de driehouck O H G gesneen van F G D A, dacrom, &c.) het swaerder dan sal evewichtich sijn an een lichter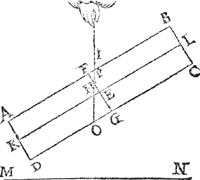 t'welck ongeschickt is, K L dan blijft evewijdich vanden sichteinder M N, als in d'eerste form. Tis oock te anmercken als voor gemeenen Weeghconstighen Reghel, dat Alle swaerheyts middelpunt eens hangenden lichaems is in sijn hanghende swaerheydts middellini. Maer t'swaerheyts middelpunt hier boven E en is inde tweede form niet in sijn hanghende swaerheyts middellini I O, tis dan een onmeughelicke ghestalt. Tbeslvyt. Wesende dan een pylaer ghesneen, &c. | |||||||
[pagina 23]
| |||||||
3 Vertooch. 7 Voorstel.Wesende t'vastpunt het svvaerheyts middelpunt des hanghenden pylaers, hy hout alle ghestalt diemen hem gheeft. Tghegheven. Laet A B C D een 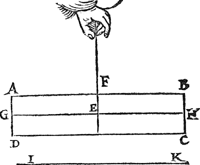 pylaer wesen, diens swaerheyts middelpunt E vast sy, daer by hanghende ande lini E F, ende den as G H sy evewijdich vandē sichteinder I K. Tbegheerde. Wy moeten bewijsen dat den pylaer A B C D alle ghestalt hout diemen hem gheeft. | |||||||
Tbewys.Laet ons den ghegheven pylaer (t'punt E vast blijvende) een ander ghestalt geven dan d'eerste, als in dees tweede form, ende laet F E voortghetrocken worden tot in L, snyende A B in M, ende en laet den pylaer soot meughelick waer niet in die ghestalt blijven, dan het stick M L D A,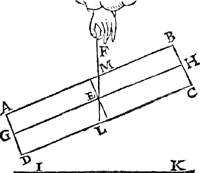 ofte M L C B neervallen; Maer dees twee deelen sijn gelijc evegroot, en̄ daerom oock eveswaer, het eene dan van evewichtighe sal swaerder sijn dan t'ander, t'welck ongeschickt is: Den pylaer dan blijft in die ghestalt, ende sghelijcx in allen anderen diemen hem soude meughen gheven. Tbeslvyt. Wesende dan t'vastpunt het swaerheyts middelpunt des pylaers, hy houdt alle ghestalt diemen hem gheeft, t'welck wy bewijsen moesten. | |||||||
4 Vertooch. 8 Voorstel.Wesende den pylaer ghesneen door sijn svvaerheydts middelpunt, met een plat evevvijdich vanden gront, ende vvesende t'vastpunt in dat plat beneden het svvaerheyts middelpunt: Den pylaer (natuerlick verstaen) keert om tot dat sijn svvaerheyts middelpunt is in sijn hangende svvaerheyts middellini. 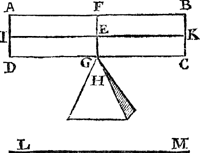 Tgheghe ven. Laet A B C D een pylaer wesen, ghesneen door sijn swaerheyts middelpunt E, met een * plat F G evewijdich vanden grondt A D, ende laet G vastpunt sijn, beneden t'swaerheyts middelpunt E, met welck punt G den pylaer light ofte rust op t'punt des pins H, ende I K sy as, evewijdich van- | |||||||
[pagina 24]
| |||||||
denGa naar margenoot* sichteinder L M. Tbegheerde. Wy moeten bewijsen dat den pylaer omkeeren sal, tot dat sijn swaerheyts middelpunt is in sijn hangende swaerheyts middellini: maer dit natuerlick verstaen, wantGa naar margenoot* Wisconstelick ghenomen soo can hy daer op rusten. | |||||||
Tbewys.
DesGa naar margenoot* Bewijsredens tweede voorstel is daer uyt openbaer, dat het punt gheen grootheyt en is, ende vervolghens gheen grondt: wel is waer dat wy dickmael nemen door t'ghestelde een lichaem also te rusten, maer metter daet en connen wy dat niet te weegh brenghen. Inder voughen dat hoe wel den as I K evewijdich ghestelt is vanden sichteinder L M, soo sal nochtans den pylaer (t'punt G vast blijvende)omkeeren over die sijde daer hy eerst begint. Maer dat hy so lang keeren sal tot dat sijn swaerheyts middelpunt inde hanghende swaerheyts middellini sy, is door het 6 voorstel openbaer. Tbeslvyt. Wesende dan den pylaer ghesneen, &c. | |||||||
1 Merck.Yemant mocht hier noch de verclaring begheeren des verschils tusschen hanghen en ligghen, waer op d'antwoort is dat wy een lichaem voor hanghende houden, als sijn swaerheyts middelpunt is onder, oft in t'ghenaecksel daert opt rust; Maer t'swaerheyts middelpunt daer boven sijnde, alsdan houden wijt voor ligghen, staen, oft sitten; Ligghen, als de langste sijde des lichaems haer streckt langs den sichteinder: Staen, als sy daer op rechthouckich is; daerom ist oock dat wy den teerlinck (overmidts sijn sijden al even lanck sijn) soo eyghentlick segghen te staen als te ligghen, ende te liggen als te staen. Sitten is wat tusschen ligghen en staen. | |||||||
2 Merck.Soo ymant t'inhout der voorgaende drie voorstellen door eenighe ervaring wilde sien, hy mocht nemen een reghel van houdt ofte ander stof eenvaerdigher dickte ende swaerheyt, als A B C D, teeckenende de punt eu E, F, G, H, inde middelen der linien A B, B C, C D, D A, treckende E G, ende H F, malcander snyende in I, maeckende daer naer een seer cleen gaetken an I, ende daer boven een gaetken als K, ende onder I een gaetken als L. Ende stekende een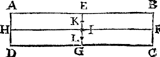 naelde door t'gaetken K, die vryelick daer in drayen mach, d'ervaringh sal bethoonen dat H F altijt evewijdich sal blijven vanden sichteinder. Maer de naelde in I stekende, de reghel sal daer op alle ghestalt houden diemen haer gheeft. Ende de naelde in L ghesteken, alles sal omkeeren over die sijde daert eerst begint, tot dat I is in haer swaerheydts middellini, waer af d'oirsaeck inde voornoemde 6, 7, 8, voorstellenGa naar margenoot* Wisconstlick blijckt. | |||||||
[pagina 25]
| |||||||
5 Vertooch. 9 Voorstel.D'hanthaef oneyndelick voortghetrocken, deelt alle balcken tvveer svvaerheden in haer ermen.
Tghegheven. Laet A B twee swaerheden sijn ende haer middellinien C D, E F, ende haer balck C E, ende d'hanthaef G H, inder voughen dat C G is tot G E, als de swaerheyts B tot A, Laet I K noch een balck wesen, onevewijdich van C E, ende laet G H oneyndelick voortghetrocken worden naer L, snyende den balck I K in M. Tbegheerde. Wy moeten bewijsen dat I M, ende M K, oock de ermen sijn der swaerheden A B; dat is ghelijck B tot A, alsoo M I tot M K. Tbereytsel. Laet ghetrocken worden C N, evewijdich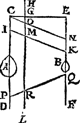 van I K, snyende H L in O. | |||||||
Tbewys.Ghelijck C G tot G E, alsoo C O tot O N, Maer C O is even an I M, ende O N an M K, daerom ghelijck C GGa naar margenoot+ tot G E, alsoo I M tot M K, maer ghelijck B tot A, alsoo C G tot G E, door t'ghegheven, daerom ghelijck B tot A, alsoo M I tot M K, t'selfde sal alsoo bewesen worden van allen balcken tusschen C D ende E F, als P Q, doorsneen in R, ende allen anderen diemen soude meughen trecken. Tbeslvyt. D'hanthaef dan oneyndelick voortghetrocken, deelt alle balcken tweer swaerheden in haer ermen, t'welck wy bewijsen moesten. | |||||||
1 Vervolgh.Hier uyt blijckt datmen om te vinden de hanghende swaerheyts middellini tweer swaerheden, niet nootsakelick en moet nemen eenGa naar margenoot* evewijdige vandenGa naar margenoot* sichteinder, maer alsulcke alsmen wil, ende als best te pas comt. | |||||||
2 Vervolgh.Anghesien alle swaerheyts middelpunt inde hanghende swaerheyts middellini is, soo volght dat alle rechte lini begrepen tusschen twee swaerheyts middelpunten, oock dier swaerheden balck is, ende het onderscheyt der ermen diens balçx, oock het swaerheyts middelpunt te wesen der twee swaerheden. | |||||||
5 Werckstick 10 Voorstel.Wesende ghegeven een vastpunt des bekenden pylaers, ende bekende evestaltvvichtige svvaerheden an hem hanghende: Te vinden of den as evevvydich sal blijven vandenGa naar margenoot⋆ sichteinder, ofte alle ghestalt houden diemen hem gheeft, ofte omkeeren tot dat sijn svvaerheydts middelpunt is in sijn hanghende svvaerheyts middellini. | |||||||
[pagina 26]
| |||||||
Tghegheven. Laet A B C D een pylaer sijn weghende 4 ℔, ende ghesneen door sijn swaerheyts middelpunt E, met een plat F G evewijdich vanden grondt A D, ende laet H vastpunt wesen beneden t'middelpunt E int middel
 van E G; Ende anden pylaer twee ghewichten hanghen als I, K, elck wegende 4 ℔, welcker middellinien vastpunten sijn D, C, ende laet L M den as, ende N O sichteinder wesen. Tbegheerde. Wy moeten vinden of den as L M evewijdich sal connen blijven vanden sichteinder N O; ofte alle ghestalt houden diemen haer gheeft; Ofte ommekeeren tot dat haer swaerheyts middelpunt E is inde hanghende swaerheydts middellini door H, welcke verscheydenheden vallen connen naer de reden der swaerheyt des pylaers, tot de ghewichten dieder anhanghen. | |||||||
Twerck.Men sal trecken door E de hanghende swaerheyts middellini P Q des pylaers, daer naer door G de hanghende swaerheyts middellini R S der ghewichten I, K, ende E G sal balck sijn, daer naer salmen sien door het 2 voorstel waer t'vastpunt der hanthaef valt: want commet onder H, soo keert L M tot sy evewijdich blijft vanden sichteinder N O; Maer commet in H, sy houdt alle ghestalt die men haer geeft; Commet boven H, alles keert om. Maer den pylaer weeght 4 ℔, ende I, K, elck 4 ℔ t'samen 8 ℔ door t'ghegheven, daerom ghedeelt E G in T, alsoo dat E T, sulcken reden heb tot T G, als 8 tot 4: Ick segh dat L M keeren sal (overmidts T onder H comt) tot sy evewijdich is vanden sichteinder. Laet nu den pylaer weghen 4 ℔, ende I en K elck 2 ℔, t'samen 4 ℔, daerom ghedeelt E G in H (welcke H t'middel van E G is door t'ghegheven) alsoo dat E H sulcken reden heb tot H G, als 4 tot 4: Ick segh dat L M (overmidts het in H viel) alle ghestalt sal houden diemen haer gheeft. Laet nu den pylaer weghen 4 ℔, ende I, K, elck 1 ℔, t'samen 2 ℔, daerom ghedeelt E G in V, alsoo dat E V sulcken reden hebbe tot V G, als 2 tot 4, Ick segh dat den pylaer met al de rest omkeeren sal (overmits V boven H comt) tot dat H is in haer hanghende swaerheyts middellini. | |||||||
Tbewys.Ten eersten I en K elck 4 ℔ weghende, dat dan L M keert tot sy evewijdich is vanden sichteinder, blijft aldus: De hanghende door T ghelijck T X, is hanghende swaerheyts middellini des heels, daerom die latende, ende hanghende t'gheheel andeGa naar voetnoot* hanghende door H, als H Y (welcke H ons ghegheven vastpunt is) soo sal de sijde naer B C, K, swaerder sijn dan naer A D I, daerom oock | |||||||
[pagina 27]
| |||||||
sal de sijde B C K neerdalen, tot dat H inde hanghende swaerheyts middellini is des heels, ende dan sal L M evenwijdich sijn vanden sichteinder N O. Ten tweeden I, K, elck 2 ℔ weghende, dat dan L M alle ghestalt hout, wort aldus bethoont: Laet ons achtē dat I ende K opgeschorst sijn, also dat D t'swaerheyts middelpunt sy van I, ende C van K, ende door de 3 begheerte sy en sullen anden pylaer gheen oirsaeck van verandering der swaerheyt wesen; T'welck soo sijnde, H is t'swaerheyts middelpunt van soodanighen lichaem vergaert uyt den pylaer rnde de twee gewichten I K, ende door de 4 bepaling t'sal daer op alle gestalt houden diemen hem gheeft, t'selfde sal alsoo bewesen worden in alle ghestalten daermen L M in soudc connen stellen. Ten laetsten I, K, elck 1 ℔ weghende, dat dan alles omkeert, wort aldus bethoont: De hanghende door V ghelijck V Z, is hanghende swaerheyts middellini des heels, daerom die latende, ende hanghende t'gheheel ande hanghende H Y door H ghegheven vastpunt, soo sal de sijde naer A D I, swaerder sijn dan naer B C K, daerom oock sal de sijde A D I neerdalen, tot dat H inde hanghende swaerheyts middellini is des heels, ende ofmen schoon L M (alles op t'vastpunt H draeyende) evewijdich stelde vanden sichteinder N O, sy en can soo niet blijven door het 8 voorstel, maer alles sal omkeeren, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven een vastpunt des bekenden pylaers, &c. Uyt het voorgaende is ghenouch blijckelick den ghemeenen voortganck in allen anderen, als van pylaren welcker vastpunt is buyten de lini als F G, ende der gewichten vastpunten op ander plaetsen dan D C; Maer overmidts wy hier voornamelick trachten de oirsaecken vande ghedaenten des waeghs grondelick te openbaren (daer af inde Weeghdaet bree der sal gheseyt worden) soo en geven wy van sulcke ongheschicte ghestaltheden gheen besonder voorbeelden. | |||||||
6 Werckstick 2 Voorstel.Wesende ghegheven een bekende pylaer, ende bekende svvaerheden daer an hanghende: Te vinden het vastpunt daer op hy alle ghestalt houdt diemen hem gheeft. | |||||||
1 Merck.
Soo tweer evewichten als A, B, vast punten C, D, waren in des
| |||||||
2 Merck.Tis openbaer dat wesende de twee vastpunten der ghewichten als C D, ende t'vastpunt des hanthaefs als E, alle drie in een rechte lini als hier boven, ende an C D even ghewichten ghehanghen, soogroot ofte cleen alst valt: E sal altijt t'vastpunt blijven, daer sy alle ghestalt op houden diemen haer geeft. Maer so die drie punten als C E D in een rechte lini wesende C ende D niet evewijt en waren van E, ende datmen an haer ghewichten hingheGa naar margenoot* everednich met de ermen, dat E noch altijt t'vastpunt sal blijven daer sy alle ghestalt op houden diemen haer geeft. | |||||||
[pagina 28]
| |||||||
Tghegheven. Laet A B C D een pylaer sijn weghende 10 ℔, diens swaerheyts middelpunt E, ende laet de ghewichten daer an hanghende wesen F 1 ℔, diens vastpunt G, ende H 4 ℔, wiens vastpunt I. Tbegheerde. Wy moeten het vastpunt vinden daer op sy alle ghestalt houden diemen haer gheeft. | |||||||
Twerck.Men sal trecken G I balck der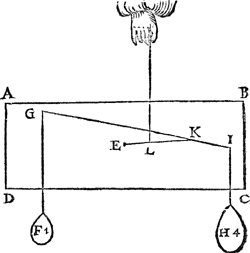 gewichten F H, daer naer salmen vinden haer crmen door het 2 voorstel, dat is ghelijck F 1 ℔, tot H 4 ℔, alsoo den erm K I, tot K G, daer naer salmen trecken E K balck des pylaers ter eender, ende der ghewichten F H ter ander sijden, de selve E K ghedeelt in L, alsoo dat den erm E L sulcken reden hebbe tot L K, als 5 ℔van F H, tot 10 ℔ des pylaers, L sal t'begeerde punt sijn op t'welck sy alle ghestalt sullen houden diemen haer gheeft, waer af t'bewijs openbaer is door het 7 voorstel. | |||||||
7 Werckstick. 12 Voorstel.Wesende ghegheven een bekende pylaer, met sijn vastpunt ende bekende ghevvichten daer an hanghende die den as evevvijdich houden vandenGa naar margenoot⋆ sichteinder: Te vinden een ghevvicht hanghende ter begheerder plaets des pylaers, dat den as in ghegheven ghestalt houde. | |||||||
1 Voorbeelt.Tghegheven. Laet A B C D een pylaer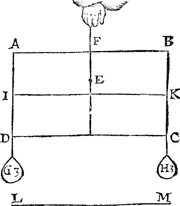 sijn weghende 6 ℔, diens vastpunt E, ende hanthaef E F, ende twee ghewichten G, H, elck 3 ℔ weghende, welcker vastpunten C, D; ende I K, sy as, evewijdich vanden sichteinder L M, ende D sy t'punt voor de begheerde plaets. Daer naer wort den as I K (alles draeyende op E) verheven als inde tweede form. Tbegheerde. Wy moeten een ghewicht an D vinden, dat den as I K in die gestalt houde. | |||||||
[pagina 29]
| |||||||
Twerck.Men sal vinden door het 11 voorstel, t'vastpunt daer op den as alle ghestalt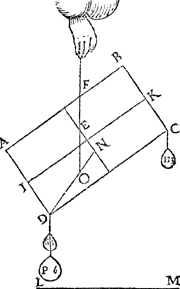 houde diemen haer gheeft t'welck N sy: Daer naer salmen trecken D N, ende deGa naar margenoot* hanghende E O, snyende N D in O, daer naer salmen sien wat reden N O heeft tot O D, ick neme als van 1 tot 2, daerom hanghe ick an D een ghewicht P van 6 ℔, te weten in sulcken reden tot den pylaer met de twee ghewichten G, H, al t'samen 12 ℔, als van 1 tot 2; Ick segh P 6 ℔, te wesen het begheerde ghewicht. | |||||||
Tbewys.T'swaerste ghewicht 12 ℔ des erms O N, heeft sulcken reden tot het lichtste 6 ℔ des erms O D, ghelijck den langsten erm O D, tot den cortsten O N; Daerom hanghet al evestaltwichtich ande handthaef E F door het 1 voorstel. Ende vervolghens den as I K blijft in haer ghegeven ghestalt. | |||||||
2 Voorbeelt.Laet A B C D een pylaer sijn weghende 6 ℔, diens vastpunt E, ende hanthaef E F, ende G een gewicht van 2 ℔, diens vastpunt H, ende I een gewicht van 1 ℔,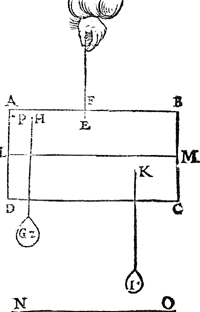 diens vastpunt K, ende den as L M sy evewijdich vanden sichteinder N O, endeGa naar margenoot+ P sy een punt inden pylaer voor de begheerde plaets. Daer naer wert den as L N (alles draeyende op E) verheven, als inde tweede form. Tbegeerde. Wy moeten een ghewicht an P vinden, dat den as L M in die ghestalt houde. | |||||||
Twerck.Men sal vinden door het 11 voorstel t'vastpunt dat op t'ghegeven alle gestalt hout diemen hem gheeft, t'welck Q sy, daer naer salmen trecken P Q, ende deGa naar margenoot* hanghende E R, snyende P Q in R: siende daer naer wat reden R Q heeft tot R P, ick neem als van 1 tot 2, soo hang ick an P een gewicht S van 4½ ℔, te weten in sulcken reden tot den pylaer met de twee ghewichten G, I, al t'samen | |||||||
[pagina 30]
| |||||||
9 ℔, als van 1 tot 2; Ick segh S 4½ ℔ te
 wesen het begheerde ghewicht. | |||||||
Tbewys.T'swaerste ghewicht 9 ℔ des erms R Q, heeft sulcken reden tot het lichtste gewicht 4½ ℔ des erms R P, gelijck den langsten erm R P, tot den cortsten R Q, daerom hanghet al evestaltwichtich ande handthaef E F door het 1 voorstel, ende vervolghens den as L M blijft in haer ghegheven ghestalt, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven een bekenden pylaer met sijn vastpunt, &c. | |||||||
6 Vertooch. 13 Voorstel.Een daelvvicht ende een hefvvicht an hem even, doen met even houcken an even ermen even ghevvelden. | |||||||
1 Voorbeelt met rechtvvichten.Tghegheven. Laet A des balcx B C vastpunt, ende A B met A C twee even ermen sijn, ende an B hanghe het rechtdaelwicht D, ende an C sy het rechthefwicht E, evewichtich an D, ende sijn balck sy F G, diens vastpunt H, ende even ermen H F, H G, ende den houck A B I, sy even anden houck A C F. Tbegheerde. Wy moeten bewijsen dat het rechtdaelwicht D, ende t'rechthefwicht E, ande even ermen A B, A C, even ghewelden doen. Tbereytsel. Laet an C een ghewicht K hanghen, even an D. | |||||||
Tbewys.Laet ons weeren E, ende is blijckelick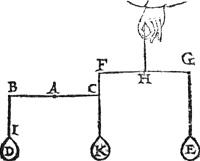 dat de macht van D is de ermen A B, A C, in die ghegheven ghestalt te houden, want D is even an K, ende A B an A C. Laet nu D weeren, ende E wederom anhanghen, ende de macht van E is oock de ermen A B, A C, in die ghegeven ghestalt te houden, want K is even an E, ende H F an H G, daerom E ende D, doen an even ermen A B, A C, even ghewelden. | |||||||
[pagina 31]
| |||||||
2 Voorbeelt met scheefvvichten.Tghegheven. Laet A des hanthaefs vastpunt, ende A B met A C twee even ermen sijn, ende an B hanghe t'scheefdaelwicht D, diens scheefdaellini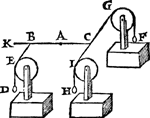 B E, ende an C sy t'scheef hefwicht F, even an D, ende sijn scheefheflini sy C G, ende den houck A B E, sy even anden houck A C G. Tbegheerde. Wy moeten bewijsen dat het scheefdaelwicht D, ende t'scheefhefwicht F, ande even armen A B, A C, even gewelden doen. Tbereytsel. Laet an C een scheefdaelwicht H hanghen even an D, diens scheefdaellini C I,Ga naar margenoot* evewijdich sy van B E, ende C B sy wat voortghetrocken tot in K. | |||||||
Tbewys.Laet ons weeren F, ende is kennelick dat de macht van D teghen H, is de ermen A B, A C, in die ghegheven ghestalt te houden, want D is even an H, ende den erm A B, an A C, ende den houck A C I, anden houck K B E. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen A B, A C, in die ghegheven ghestalt te houden, overmits H even is an F. | |||||||
3 Voorbeelt.Tghegheven. Laet A des hanthaefs vastpunt, ende A B met A C twee even ermen sijn, ende an B hanghe het scheefdaelwicht D, diens scheefdaellini B F, ende an C sy het scheefhefwicht F, even an D, diens scheefheflini sy C G, ende den houck K C G, sy even anden houck K B E. Tbegheerde. Wy moeten bewijsen dat het scheefdaelwicht D, ende het scheef hefwicht F, ande even ermen A B, A C, even ghewelden doen. Tbereytsel. Laet an C een scheefdaelwicht H hanghen even an D, diens scheefdaellini C I, alsoo dat den houck A C I, even sy anden houck A B E. | |||||||
Tbewys.Laet ons weeren F, ende is kennelick dat de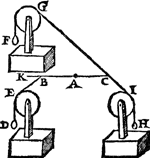 macht van D is de ermen A B, A C, in die ghegheven ghestalt te houden, want D is even an H, ende den erm A B an A C, en̄ den houck A C I, anden houck A B E. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen A B, A C, in die ghegheven ghestalt te houden, overmidts H even is an F. Tbeslvyt. Een daelwicht dan ende een hefwicht an hem even, doen met even houcken an even ermen even ghewelden, t'welck wy bewijsen moesten. | |||||||
[pagina 32]
| |||||||
8 Werckstick. 14 Voorstel.Wesende ghegheven een pylaer, ende tvvee punten in den as, t'een vast t'ander int langste deel verroerlick: Te vinden een rechthefvvicht an t'verroerlick, dat den pylaer in sijn ghegheven standt houde.
Tghegheven. Laet A B C D een pylaer sijn, weghende 6 ℔, ende die ghedeelt als int begin des 1 voorstels, ende vastpunt sy R, ende roerlick V, int langste deel des as R Q, want int cortste R P ist onmeughelick dat eenich rechthefwicht den as in haer ghegheven stant houde. Tbegheerde. Wy moeten een rechthefwicht an V vinden, dat den pylaer in die stant houde. | |||||||
Twerck.Men sal de lini Q R voorttrecken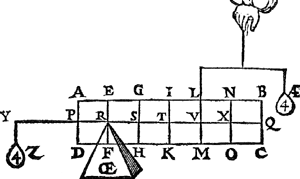 tot in Y, also dat R Y even sy an R V: Daer naer salmen vinden t'ghewicht Z an Y, evestaltwichtich met den pylaer, t'selve (ghedenckende dat R vastpunt is) sal van 4 ℔ wesen door het 3 voorstel; Ick segh daerom dat het begheerde rechthefwicht t'welck AE sy, van 4 ℔sal wesen. | |||||||
Tbewys.Overmidts den erm R V des rechthefwichts AE, even is anden erm R Y des ghewichts Z, ende AE even an Z, soo is de ghewelt AE even an de ghewelt van Z door het 13 voorstel. Maer de ghewelt van Z is (AE gheweert sijnde) den pylaer in die standt te houden, die ghewelt dan van AE (Z gheweert sijnde) is oock den pylaer in die standt te houden, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegeven een pylaer, ende twee punten inden as, t'een vast, t'ander int langste deel verroerlick: Wy hebben ghevonden een rechthefwicht an t'verroerlick, dat den pylaer in sijn ghegheven stant hout naer den eysch. | |||||||
Merckt.Men soude oock meughen segghen metten cortsten VR 3, gheeft R T2, wat den pylaer 6 ℔? comt voor AE 4. ℔ als vooren, waer af de reden int volghende 15 voorstelblijcken. sal. | |||||||
1 Vervolgh.Anghesien den heelen pylaer door t'ghestelde 6 ℔ weeght, waer af ae de 4 ℔ verheft, soo volght nootsaeckelick datter opt punt R, dat is op t'sop des keghels OE, 2 ℔ rusten. | |||||||
[pagina 33]
| |||||||
Ofte soomen an R een rechthefwicht ii voughde, inde plaets des kegels OE, als hier neven, dat ii sal weghen 2 ℔. 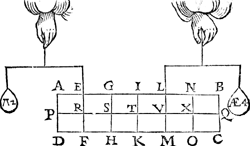 Ofte somen an V een kegel ϕ voughde, inde plaets des rechthefwichts AE, als hier neven, dat op den kegel OE rusten sal 2 ℔, ende op den keghel ϕ 4 ℔. 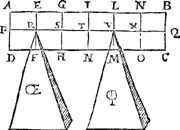 Ofte soomen den pylaer ophinge an tweeGa naar margenoot* evewijdige linien OE R, ende ϕ V, als hier neven, dat ande lini OE R hanghen sal 2 ℔, ende ande lini ϕ 4 ℔. 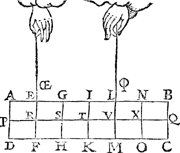 | |||||||
2 Vervolgh.SO anden pylaer (t'punt R vast sijnde als vooren) eenich ghewicht ofte gewichten hinghen, t'rechthefwicht sal oock bekent worden. Laet by voorbeelt an X hanghen 6 ℔, soo sal Z moeten wegen 12 ℔ door het 3 voorstel, ende vervolgens AE 12 ℔. 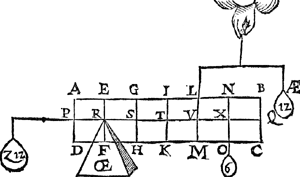 | |||||||
[pagina 34]
| |||||||
7 Vertooch. 15 Voorstel.Wesende tvvee punten inden as des pylaers, t'een vast t'ander verroerlick: T'rechthefvvicht an t'verroerlick met den pylaer evestaltvvichtich, heeft sulcken reden tot den pylaer als het asstick tusschen het svvaerheyts middelpunt des pylaers, ende het vastpunt, tot het asstick tusschen t'vastpunt ende t'verroerlick punt. | |||||||
Verclaring.Laet ons nemen de formen des 14 voorstels, al waer blijckt dat ghelijck AE 4 ℔, tot t'ghewicht des pylaers 6 ℔, alsoo T R tot R V. Maer om d'oirsaeck hier afGa naar margenoot* Wisconstelick te verclaren, soo is te weten dat ghelijck t'ghewicht Z, tottet ghewicht des pylaers, alsoo R T tot R Y door het 1 voorstel; Maer AE is even an Z, ende R V is even an R Y door t'ghegheven, ghelijck dan AE tot den pylaer, alsoo T R tot R V. Tbeslvyt. Wesende dan twee punten inden as des pylaers t'een vast t'ander verroerlick, &c. | |||||||
8 Vertooch. 16 Voorstel.Wesende tvvee punten inden as des pylaers t'een vast t'ander verroerlick: T'rechthefvvicht an t'verroerlick dat den pylaer in een ghestalt houdt, sal hem in alle gestalten houden.
Tghegheven. Laet ons den pylaer met sijn ghewichten des 14 voorstels wat verkeeren op t'vastpunt R, ende dat AE 4 ℔ noch sy rechthefwicht, also dat dan alles van ghestalt sy als hier neven. Tregheerde. Wy moeten bewijsen dattet rechthefwicht AE den pylaer oock in die ghegheven ghestalt houdt. | |||||||
Tbewys.Laet ons weeren AE ende anhanghen Z 4 ℔, ende door het 10 voorstel den pylaer sal in die ghestalt blijven: Maer AE doet by V so grooten ghewelt anden pylaer als Z by Y door het 13 voorstel, daerom gheweert Z, ende AE angehangen, soo sal AE den pylaer oock in die ghestalt houden. 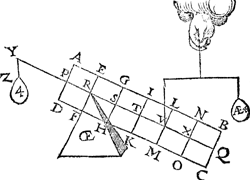 Tbeslvyt. Wesende dan twee punten in den as des pylaers t'een vast t'ander verroerlick, t'rechthefwicht an t'verroerlick, dat den pylaer in een ghestalt houdt, sal hem in alle ghestalten houden, t'welck wy bewijsen moesten. | |||||||
[pagina 35]
| |||||||
9 Vertooch. 17 Voorstel.Rustende een pylaer op tvvee punten in den as: Gelijck het asstick tusschen t'svvaerheyts middelpunt ende t'slinckerpunt, tottet asstick tusschen t'svvaerheytds middelpunt ende t'rechterpunt, alsoo t'ghevvicht des pylaers rustende op t'rechterpunt, tottet ghevvicht rustende op t'slinckerpunt.
Tghegheven. Laet A B C D een pylaer sijn wegende 6 ℔, gedeelt als int 1 voorstel, rustende met de twee punten R, V, op de punten van OE, AE. Tbegheerde. Wy moeten bewijsen dat ghelijck het asstick T R, tottet asstick T V, alsoo t'ghewicht rustende mettet punt V op t'punt van AE, tottet ghewicht rustende mettet t'punt R op t'punt van OE. | |||||||
Tbewys.T R is dobbel an T V door t'ghestelde, ende op t'punt van AE rust 4 ℔, ende van OE 2 ℔ door 1 vervolgh des 14 voorstels, maer 4 ℔ is tot 2 ℔ oock dobbel, ghelijck dan T R tot T V, alsoo t'gewicht rustende op t'punt van AE, tot t'ghewicht rustende op t'punt van OE. 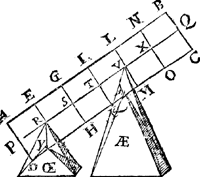 Maer om t'ghemeen nootsaeckelick vervolgh in allen te bewijsen, laet ons voorttrecken V R tot in Z, alsoo dat R Z even sy an R V; aensiende daer naer R voor t'vastpunt, 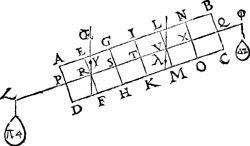 soo sal an Z moeten hanghen Π 4 ℔, om de pylaer in die ghestalt te houden door het 3 voorstel. Maer t'ghene an V den pylaer in die ghestalt houdt als AE, doet daer an alsulcken gewelt als Π, door het 13 voorstel; An AE dan rust een gewicht even an Π. Laet ons insghelijcx voorttrecken, R V tot in ϕ, alsoo dat V ϕ even sy an V R, ansiende daer naer V voor vastpunt, so sal an ϕ moeten hanghen Δ 2 ℔, om den pylaer in die ghestalt te houden door het 3 voorbeelt, maer r'ghene an R den pylaer in die ghestalt houdt als OE, doet daer an alsulcke ghewelt als Δ door het 13 voorstel, An OE, dan rust een ghewicht even an Δ. Nu anghesien Π evestaltwichtich is teghen den pylaer op t'ghemeen vastpunt R, soo heeft den erm T R, sulcken reden tot den erm R Z, als Π tot den pylaer door i voorstel. Insghelijcx nemende V voor t'vastpunt, soo heeft den erm T V sulcken reden tot den erm V ϕ, als Δ tot den den pylaer, maer R Z is altijt even an V ϕ: Wy hebben hier dan tweeGa naar margenoot* evere- | |||||||
[pagina 36]
| |||||||
denheden elck van vierGa naar margenoot* palen, welcker tweede palen an malcanderen even sijn, en̄ welcker laetste palē an malcanderen oock even sijn. Maer alle twee everedenheden elck van vier palen, welcker tweede palen an malcander even sijn, ende welcker laetste palen an malcander oock even sijn, die hebben d'ander palen oock everednich, daerom ghelijck T R tot T V, alsoo Π tot Δ; maer Π is even an t'ghewicht des pylaers rustende met t'punt V op t'punt van AE, ende t'ghewicht Δ is even an t'ghewicht des pylaers rustende met t'punt R op t'punt van OE, daerom gelijck T R tot T V, alsoo t'ghewicht rustende mettet t'punt V op t'punt van AE, tottet gewicht rustende mettet punt R op t'punt van OE. Tbeslvyt. Rustende dan een pylaer op twee punten inden as, &c. | |||||||
Vervolgh.Soo de twee punten daer den pylaer op rust, waren indeGa naar margenoot* hanghende linien door R en V, de selve gewichten die hier vooren op elck rustende punt waren, soudender nu oock op sijn. Laet by voorbeelt door de punten R, V, hanghende linien ghetrocken worden, ende punten inde selve ghestelt als Y λ, Genomen nu dat Y ende λ de punten sijn daer den pylaer op rust, tis kennelick dat op Y rusten sal 2 ℔, ende op λ 4 ℔, waer uyt alsulcken vertooch openbaer is. | |||||||
10 Vertooch. 18 Voorstel.Rustende een pylaer op eenighe tvvee punten, ghelijck het asstick tusschen t'svvaerheydts middelpunt ende de hanghende door t'slinckerpunt, tottet asstick tusschen t'svvaerheyts middelpunt ende de hangende door t'rechterpunt, alsoo t'gevvicht des pylaers rustende op t'rechterpunt, tottet ghevvicht rustende op t'slinckerpunt. Tghegheven. Laet A B C D een 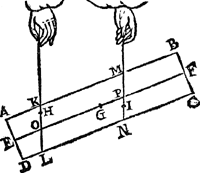 pylaer wesen, diens as E F, ende swaerheyts middelpunt G, ende de twee punten daer d'een pylaer op rust H I, waer door ghetrocken sijn de hangende linien K L, M N, snyende den as in O, P; Ick segh dat gelijck G O tot G P, alsoo de swaerheyt rustende op t'punt I, tot de swaerheyt rustende op H, waer af t'bewijs openbaer is door t'vervolgh des voorgaenden 17 voorstels, nochtans om alhier wat breeder vande nootsakelickheyt 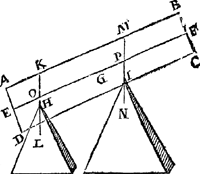 te segghen, soo laet ons achten al of H ter plaets van O waer, t'welck soo ghenomen t'ghewicht alsdan op H rustende, heeft sulcken reden tottet ghewicht op P rustende, ghelijck G P, tot G O, door het 17 voorstel; Laet ons voort nemen dattet punt H vast blijvende, den pylaer in haer ghegheven ghestalt neerghetrocken worde, soo verre als van | |||||||
[pagina 37]
| |||||||
H tot O, ende door de 3 begheerte, de swaerheyt an H rustende blijft de selve. S'ghelijcx salmen bethoonen de swaerheyt dieder op P rust, oock te rusten op I, daerom ghelijck G O tot G P, alsoo de swaerheyt rustende op I, tot de swaerheyt rustende op H. Tbeslvyt. Rustende dan een pylaer op eenighe twee punten, &c. | |||||||
Vervolgh.Tblijckt uyt het voorgaende dat soomen begheerde te weten de reden van t'ghewicht rustende op I, tottet ghewicht rustende op H, datmen trecken soude de hangende linien K L, M N, snyende den as E F in O, P, ende de reden van G O tot G P soude de begheerde sijn, waer uyt oock openbaer is, dat des pylaers swaerheyt bekent wesende, soo is oock t'ghewicht bekent rustende op yder punt als H ende I. | |||||||
Tot hier toe siin de ghedaenten der rechtwichten verclaert: int volghende sullen de eyghenschappen der scheefvvichten beschreven vvorden, vviens gemeene grondt dit volghende vertooch begrijpt.11 Vertooch. 19 Voorstel.Wesende een driehouck vviensGa naar margenoot⋆ plat rechthouckich op denGa naar margenoot⋆ sichteinder is, met sijn gront daer af evevvijdich, ende op elck der ander sijden een cloot met malcanderen evevvichtich: Ghelijck des driehoucx rechter sijde tot de slincker, alsoo t'staltvvicht des cloots op de slincker sijde, tottet staltvvicht des cloots op de rechter sijde. Tghegheven. Laet A B C een driehouck wesen diens plat sy rechthouckich op den sichteinder, ende den gront A C evewijdich vanden sichteinder, 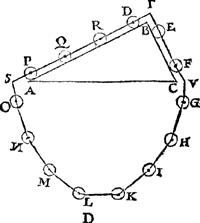 ende op de sijde A B, die dobbel sy an B C, ligge een cloot D, ende op de sijde B C een cloot E, evewichtich ende evegroot met den cloot D. Tbegheerde. Wy moeten bewijsen dat ghelijck de sijde A B 2, tot B C 1, also t'staltwicht des cloots E, tottet staltwicht des cloots D. Tbereytsel. Laet ons maken rondtom den driehouck A B C eenen crans van veerthien clooten, evegroot, evewichtich, ende evewijt van malcanderen, als E, F, G, H, I, K, L, M, N, O, P, Q, R, D, al ghesnoert an | |||||||
[pagina 38]
| |||||||
een lini, streckende door haerGa naar margenoot* middelpunten, alsoo dat sy op die middelpunten draeyen meughen; Datter oock twee clooten passen op de sijde B C, ende vier op B A, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, over welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die boven den driehouck staen,Ga naar margenoot* evewijdich sijn vande sijden A B, B C; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertreckt, soo rollen de clooten op de linien A B, B C. | |||||||
Tbewys.Soo t'staltwicht der vier clooten D, R, Q, P, niet even waer met het staltwicht der twee clooten E, F, t'een of t'ander sal swaerder sijn, latet wesen (soot meugelick waer) der vier D, R, Q, P; Maer de vier clooten O, N, M, L, sijn evewichtich met de vier clooten G, H, I, K, de sijde dan der acht clooten D, R, Q, P, O, N, M, L, is swaerder na de ghestalt dan de sijde der ses clooten, E, F, G, H, I, K: maer want het swaerste altijt het lichtste overweeght, de acht clooten sullen neerwaert rollen, en̄ d'ander ses rijsen: Latet so wesen, ende D sy gevallen daer nu O is, en̄ E, F, G, H, sullen sijn daer nu P, Q, R, D, ende I, K, daer nu E, F, sijn. Maer dit so wesende, den crans der clooten sal sulcken gestalt hebben als sy te vooren dede, ende sullen om de selve redenen de acht clooten ter slincker sijde wederom staltwichtigher sijn dan de ses clooten ter rechter, waer door de acht clooten wederom neer sullen rollen, ende d'ander ses rijsen, welcke valling ter eender, ende rijsing ter ander, om dat de reden altijt de selve is, altijt ghedueren sal, ende de clooten sullen uyt haer selven een eeuwich roersel maken, t'welck valsch is. Het deel dan des crans D, R, Q, P, O, N, M, L, is evestaltwichtich met het deel E, F, G, H, I, K: Maer van sulcke evewichtighe ghetrocken evewichtighe, de resten sijn evewichtich, laet ons dan van dat deel trecken de vier clooten O, N, M, L, ende van dit de vier clooten G, H, I, K, (welcke even sijn ande voornoemde O, N, M, L,) de resten D, R, Q, P, ende E, F, sullen evestaltwichtich sijn, Maer wesende dese twee evestaltwichtich met die vier, E sal tweemael staltswaerder sijn als D. Ghelijck dan de sijde B A 2, tot de sijde B C 1, alsoo t'staltwicht des cloots E, tottet staltwicht des cloots D. Tbeslvyt. Wesende dan een driehouck wiens plat, &c. | |||||||
1 Vervolgh.Laet A B C een driehouck sijn als vooren, wiens sijde A B dobbel sy an B C, ende laet op A B ligghen een cloot D, ende op de sijde B C een cloot E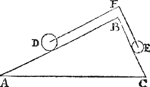 evewichtich anden helft van D, ende an F sy een vastpunt daer over de lini D F E (te weten uyt hetGa naar margenoot* middelpuut des cloots D over F tot int middelpunt des cloots E) slieren mach, also dat D F evewijdich blijve van A B, ende F E van B C. Dit alsoo sijnde, anghesien de vier clooten P, Q, R, D, hier vooren, evestaltwichtich waren met de twee clooten E, F, soo sal desen cloot D, evestaltwichtich sijn teghen den cloot E: want ghelijck die P, Q, R, D, tot E, F, also dese D tot E: Daerom ghelijck de lini A B, tot B C, alsoo den cloot D tot den cloot E. | |||||||
[pagina 39]
| |||||||
2 Vervolgh.Laet ons nu d'een sijde des driehoucx als B C (ande welcke A B dobbel is) rechthouckich stellen op A C als hier neven; Ende den cloot D die dobbel is an E, sal noch met E evestaltwichtich sijn, want gelijck A B tot B C, alsoo den cloot D tot den cloot E. 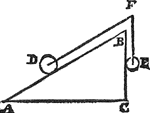 | |||||||
3 Vervolgh.Laet ons nu inde plaets van t'punt F, stellen een caterol als hier neven, also dat de scheefheflini van D naer F evewijdich blijve van A B, ende inde plaets van den cloot E sy eenich wicht van form soot valt, maer evewichtich anden cloot E: t'selve is noch evestaltwichtich met D, Daerom ghelijck A B tot B C, alsoo noch den cloot D tottet ghewicht E. 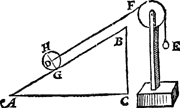 | |||||||
4 Vervolgh.Anghesien den cloot des 3 vervolghs naeckt de lini A B, in t'punt G, als vastpunt, so sal den as G H rechthouckich sijn op A B; Daerom laet onsGa naar margenoot+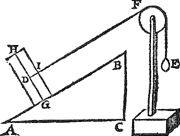 weeren den cloot, ende stellen in die plaets den pylaer D evewichtich met den cloot, alsoo dat den as G H (diens vastpunt G) rechthouckich sy op A B, ende de scheefheflini tusschen D F noch evewijdich van A B, ende snyende de sijde des pylaers in I, Als hier nevens. Ende is openbaer dat ghelijck A B tot B C, (dat is dobbel als vooren) alsoo den pylaer D tottet ghewicht E. | |||||||
5 Vervolgh.Laet ons trecken de hanghende lini uyt hetGa naar margenoot* middelpunt des pylaers D als D K, snyende de sijde des pylaers in L, t'welck so sijnde, den driehouck L D I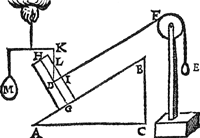 is ghelijck an den driehouck A B C, want de houcken A C B ende L I D sijn recht, ende L D is evewijdich van B C ende D I van A B: Daerom ghelijck A B tot B C, alsoo L D tot D I; Maer ghelijck A B tot B C, alsoo den Pylaer tot t'gewicht E door het 4 vervolgh, daerom ghelijck L D tot D I, alsoo den pylaer tot E. Laet ons nu ande lini K D vougen t'rechthefwicht M met den pylaer evestaltwichtich, t'selve gewicht M sal met den pylaer evewichtich sijn door het 14 voorstel: Daerom gelijck L D tot D I, also M tot E. | |||||||
[pagina 40]
| |||||||
6 Vervolgh.Laet ons trecken B N, snyende de voortghetrocken A C in N: Insghelijcx D O, snyende de voortghetrocken L I dat is de sijde des pylaers in O, ende alsoo dat den houck I D O, even sy an den houck C B N. Laet ons oock voughen an D O t'scheefhefwicht P, dat den pylaer (de ghewichten M, E gheweert sijnde) in die stant houde. Nu angesien D L, des driehoucx D L I,Ga naar margenoot* lijckstandighe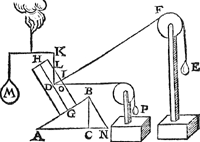 is met B A des driehoucx B A C, ende D I met B C, men besluyt daer uyt aldus: Ghelijck B A tot BC, alsoo t'staltwicht van B A tottet staltwicht van B C (door het 2 vervolgh,) Ende oock ghelijck D L tot D I, alsoo t'staltwicht van D L tot t'staltwicht van D I, dat is alsoo M tot E. Maer de lijckstandighe linien van dese ghelijcke driehoucken A B N, L D O, sijn A B met D L, ende B N met D O, Daerom segghen wy als vooren, Ghelijck B A tot B N, alsoo het staltwicht van B A tot het staltwicht van B N (door het 1 vervolgh,) Ende oock ghelijck D L tot D O, alsoo het staltwicht van D L tot het staltwicht van D O, dat is alsoo M tot P. Maer by aldien de lini B N, ghetrocken waer van B af over d'ander sijde van B C, soo soude de lini D O, dan oock vallen van D over d'ander sijde vā D I, dat is, daer D O nu valt onder D I, sy souder dan boven vallen, ende t'voorgaende bewijs soude oock dienen tot sulcke gestalt, te weten, dat wy noch segghen souden, ghelijck B A tot B N, alsoo t'staltwicht van B A, tottet staltwicht van B N; Ende ghelijck D L tot D O, also t'staltwicht van D L, tottet staltwicht van D O, dat is, alsoo M tot P. Inder voughen dat deseGa naar margenoot* everedenheydt niet alleen en bestaet inde voorbeelden, alwaer de heflini als D I rechthouckich is op den as, maer op allen houcken. Tvoorgaende mach oock verstaen worden van een cloot ligghende op een lini A B als hier nevens, alwaer wy segghen als vooren, gelijck L D tot D O, alsoo M tot P(welverstaende dat C L rechthouckich ghetrocken is op 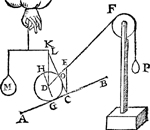 A B, dat is evewijdich met den as G H des cloots D,) maer t'ghewicht M is even an den cloot D, daerom segghen wy gelijck L D tot D O, alsoo t'ghewicht des cloots, tot P. Maer want L D ende D O binnen t'lichaem des cloots metter daet niet bequamelick en connen beschreven worden, soo laet ons trecken de hanghende C E, ende sullen dan hebben buyten t'lichaem een driehouck C E O, ghelijck an den driehouck L D O, welckerGa naar margenoot* lijckstandighe sijden sijn L D met C E, ende D O met E O, daerom ghelijck L D tot D O, alsoo C E tot E O, ende vervolghens ghelijck C E tot E O, alsoo t'ghewicht des cloots, tot P. | |||||||
[pagina 41]
| |||||||
Laet ons nu tot meerder claerheyt dit alleen stellen sonder d'ander linien als hier neven, alwaer wy segghen ghelijck C E tot E O, alsoo t'ghewicht des cloots D tot P. 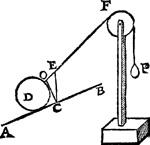 Ende dit niet alleen van clooten maer van ander lichamen slierende, ofte rollende, op punten ofte linien als hier onder, (daer wy eygentlicker af handelen sullen inde Weeghdaet) 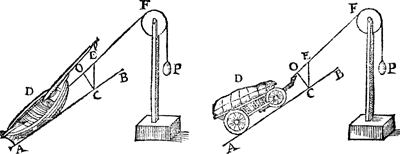 alwaer wy noch segghen ghelijck C E tot E O, alsoo t'ghewicht des lichaems D tottet ghewicht P. Waer uyt oock blijct, dat wesende de lini A B evewijdich vandenGa naar margenoot* sichteinder als hier nevens, dat C E ende C O dan in een selfde lini sullen vallen, waer door tusschen E en O gheen langde en sal sijn, ende vervolghens C E 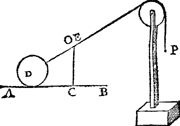 en sal tot E O gheen reden hebben, daermen by verstaen sal dat een swaerheyt inde plaets van P hoe cleen sy mocht wesen, en sal niet evestaltwichtich connen sijn teghen t'lichaem D, maer salt (Ga naar margenoot* Wisconstelick verstaende) voorttrecken hoe swaer het sy: Waer uyt volght, dat alle swaerheden voortghetrocken langs den sichteinder, als schepen int water, waghens langs t'platte lant, &c. en behoeven gheen vliegesterctens macht tot haer verroersel, meer dan de omstaende verhindernissen en veroirsaecken, als Water, Locht, Naecksel der assen, teghen de bussen, naecksel der rayers teghen de straet, ende dierghelijcke.
Maer anghesien den driehouck A B N int 6 vervolgh, tot deseGa naar margenoot* everedenheyt niet en gheeft noch en neemt, laet ons hem weeren, ansiende G voor vastpunt des pylaers rustende op een pin als hier neven, ende sullen noch segghen gelijck L D tot D O, alsoo M tot P. 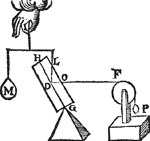 | |||||||
[pagina 42]
| |||||||
7 Vervolgh.Maer op dat nu blijcke deseGa naar voetnoot* everedenheyt niet alleen alsoo te bestaen inde pylaren alwaer de rechtheflini als D L, comt uyt t'middelpunt des pylaers, ende diens vastpunt is des assens uyterste, als hier vooren G int 6 vervolgh; Soo laet A B C een driehouck sijn, wiens sijde A B dobbel is an B C, ende B C syGa naar voetnoot* hanghende op A C: Ende laet D E een pylaer sijn diens as F G rechthouckich op A B, ende snyende A B in t'punt H, ende I sy eenich ander punt in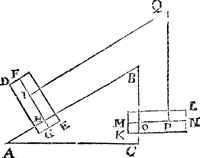 den selven as; Laet oock K L een ander pylaer sijn, even ende ghelijck anden pylaer D E, wiens as M N, ende O een punt des as naeckende B C, ende van ghelijcke ghestalt in sijn pylaer, als H inden pylaer D E; Laet oock P een ander punt sijn van sulcker gestalt inden pylaer K L, als I inden pylaer D E; Ende laet Q een vastpunt sijn daer over de lini I Q P slieren mach, alsoo dat de lini I QGa naar margenoot* evewijdich sy van A B, ende Q P evewijdich van B C. Ende om de redenen die int 19 voorstel vande 14 clooten verclaert sijn (t'welck wy hier door soodanighe veel slierende pylaren oock souden connen bewijsen, maer want sulcx uyt t'voorgaende kennelick is, wy slaent over) het staltwicht des pylaers K L, sal dobbel sijn an t'staltwicht des pylaers D E. | |||||||
8 Vervolgh.Laet ons nu an I des 7 vervolghs voughen t'rechtheswicht R evestaltwichtich met den pylaer, diens rechtheflini sy I S, snyende de sijde des pylaers in T, ende I Q snye de sijde des pylaers in V, ende laet an de lini P Q hanghen een gewicht X, inde plaets vanden pylaer K L, t'welck even sy anden helft van t'staltwicht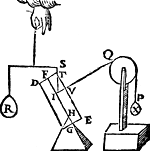 des selfden pylaers K L, Laet ons oock weeren den driehouck A B C, ende den pylaer D E doen rusten op t'punt H als hier neven. Ende om de redenen als vooren, ghelijck T I tot I V, alsoo R tot X. Ende dit niet alleen als I V rechthouckich is op den as F G, maer cromhouckich soot valt, waerafmen besonder betooch soude meughen doen, maer tis openbaer ghenouch door het 6 vervolgh. | |||||||
9 Vervolgh.WY hebben int 8 vervolgh deseGa naar margenoot* everedenheyt verclaert, alwaer t'roerende punt I, hooger was dan t'vastpunt H, ende alwaer de scheefheflini I V helde naer de sijde des vastpunts H, Wy moeten nu betoogen de selve everedenheyt oock soo te bestaen in d'ander gestalten, ende eerst alwaer t'roerende punt leegher sy dan t'vastpunt, ende alwaer de scheefheflini afwijckt vande sijde des vastpunts in deser voughen. Laet A B een pylaer sijn, diens as C D, ende vastpunt E, ende t'verroerlick | |||||||
[pagina 43]
| |||||||
 punt F, ende t'scheefhefwicht dat hem in die gestalt hout sy G, diens scheefheflini F H, ende F I sy rechtheflini, diens rechthefwicht K. Laet L M oock een pylaer sijn, even en̄ gelijck an den pylaer A B, wiens as sy N O, ende vastpu nt E, ende verroerlick punt P, alsoo dat E N even sy an E D, ende E F an E P, ende t'scheefhefwicht Q sy evē an G, ende sijn scheefheflini sy P R,Ga naar margenoot* evewijdich van F H, ende t'rechthefwicht S sy even an K, ende sijn rechtheflini sy P T. Dit soo sijnde laet ons vergaren de twee pylaren A B ende L M, ansiende A M voor een heel pylaer, wiensGa naar margenoot* swaerheyts middelpunt ende vastpunt sal E sijn door t'ghestelde. Laet ons nu weeren de ghewichten K, G, S, Q, ende den pylaer A M sal op E alle gestalt houden diemen hem gheeft door het 7 voorstel, hy sal dan soo blijven, ende den pylaer A B sal alsoo evewichtich blijven tegen den pylaer L M. Laet ons nu de ghewichten Q G weder andoen, hanghende evewichtighe van ghelijcke ghestalt, an evewichtighe, ende door het 13 voorstel, Q sal anden pylaer A M even sulcken macht doen als G:ende vervolgens Q doet sulcken macht an heur pylaer L M, als G an heur pylaer A B; maer de macht van G is A B in die ghestalt te houden door het 6 vervolgh, de macht dan van Q is oock L M in die ghestalt te houden. Insghelijcx soo is oock de macht van K, den pylaer A B in die gestalt te houden, daerom oock is de macht van S den pylaer L M in die gestalt te houden; Nu ghelijck I F tot F H, alsoo K tot G door het 8 vervolgh, Maer T P, is even an I F, ende P R an F H, ende S an K, ende Q an G, ghelijck dan T P tot P R, alsoo S tot Q. Dese everedenheydt dan, als wy gheseyt hebben, is soo wel inde voorbeelden alwaer t'roerende punt P leegher is dan t'vastpunt E, ende alwaer de scheefheflini P R afwijckt vande sijde des vastpunts E, als daert hoogher is, ende daer de scheef heflini helde naer t'vastpunt. | |||||||
10 Vervolgh.Laet ons stellen een form ghelijck an die des 9 vervolghs, alleen daer in verschillende dat dese F H wijckt over d'ander sijde van F I, ende dat den houck H F C, even sy anden houck R P O, waer door G anden pylaer A M even soo grooten ghewelt doet als Q, ende om de redenen des 9 vervolghs (die wy om cortheyt overslaen) G doet even sulcken ghewelt anden pylaer A B, als Q anden pylaer L M; Nu ghelijck T P, tot P R, alsoo S tot Q door het 9 vervolgh, maer I F is even an T P, ende F H an P R, ende K an S, ende G an Q, daerom ghelijck I F tot F H, alsoo K tot G. 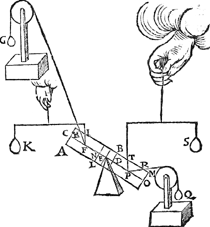 | |||||||
[pagina 44]
| |||||||
11 Vervolgh.Laet ons stellen een form ghelijck an die des 10 vervolghs, alleen daer in verschillende dat dese P R wijckt over d'ander sijde van P T, ende dat P R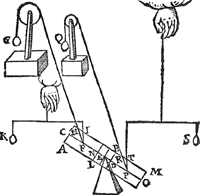 evewijdich sy met F H, waer door Q an den pylaer A M, even soo grooten gewelt doet als G, ende om de redenen des 9 vervolghs, Q doet even sulcken ghewelt anden pylaer L M, als G anden pylaer A B; Nu ghelijck I F tot F H, alsoo K tot G door het 6 vervolgh: Maer T P is even an I F, ende P R an F H, ende S an K, ende Q an G, daerom ghelijck T P tot P R, alsoo S tot Q. Ende inder selver voughen salmen van den anderen ghestalten door haer contrarien altijt dese everedenheyt bewijsen. | |||||||
12 Vervolgh.Maer dat deseGa naar margenoot* everedenheyt oock bestaet inde ghestalt daer den as evewijdich is vandenGa naar margenoot* sichteinder, wort aldus bethoont: Laet A B een pylaer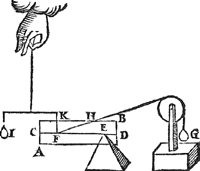 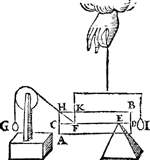 sijn, diens as C DGa naar margenoot* evewijdich sy vanden sichteinder, ende t'vastpunt daer in E, ende t'roerlick punt F, ende G t'scheefhefwicht dat den pylaer in die ghestalt hout, wiens scheefheflini F H, ende I t'rechthefwicht dat den pylaer oock in die ghestalt houdt, wiens rechtheflini F K; T'welck soo sijnde, Laet K F tot F H een ander reden hebben (soot meughelick waer) dan I tot G, By voorbeelt K F sy tot F H, als 1 tot 2, maer I tot G, als 3 tot 7. Dit soo ghenomen, laet ons den pylaer der eerste form neerduwen, ofte der tweeder form oplichten tot dat K F sulcken reden hebbe tot F H, als 3 tot 7, ende alsdan sal G oock evestaltwichtich sijn teghen den pylaer door de voorgaende vervolghen; Inder vougen dat den pylaer hoogher ende leegher verheven, sal teghen G evestaltwichtich blijven, t'welck openbaer onmeughelick is, als oockGa naar margenoot* wisconstlick sal blijcken door t'volghende 22 voorstel. K F dan en heeft tot F H gheen ander reden dan I tot G.
Uyt dese voorgaende beschrijven wy een vertooch soodanich. | |||||||
[pagina 45]
| |||||||
12 Vertooch. 20 Voorstel.Wesende inden as des pylaers een vastpunt, ende een roerlick, daer an hy door een rechthefvvicht ende scheefhefvvicht in seker standt gehouden vvort: Ghelijck rechtheflini tot scheefheflini, alsoo rechthefvvicht tot scheefhefvvicht.
Tghegheven. Laet A B een pylaer sijn diens as C D, ende t'vastpunt E, ende roerlickpunt F, daer an den pylaer door t'rechthefwicht G in die gestalt gehouden wort, daer an oock den pylaer door t'scheefhefwicht H (welverstaende G gheweert sijnde) in die ghestalt ghehouden wort, ende de rechtheflini snye de sijde des pylaers in I, maer de scheef heflini snye de selve sijde in K: Ick segh dat ghelijck de rechtheflini I F, tot de scheefheflini F K, alsoo t'rechthefwicht G, tot het scheefhefwicht H, waer af t'bewijs uyt de voorgaende openbaer is. 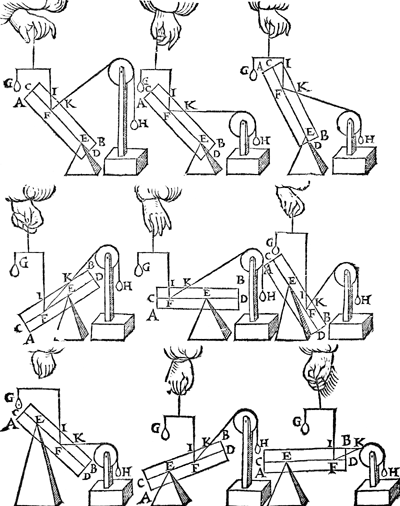 | |||||||
[pagina 46]
| |||||||
Tbeslvyt. Wesende dan inden as des pylaers een vastpunt, &c. | |||||||
Merckt.Soo eenighe der linien als I F, F K, de sijde des pylaers niet en sneen, men sal die sijde voorder trecken tot dat sy ghesneen wort, als inde voorgaende laetste form. | |||||||
13 Vertooch. 21 Voorstel.Wesende inden as des pylaers een vastpunt, ende een roerlick, daer an hy door een rechtdaelvvicht ende scheefdaelvvicht in seker stant ghehouden vvort: Gelijck rechtdaellini tot scheefdaellini, also rechtdaelvvicht tot scheefdaelvvicht.
Tghegheven. Laet A B een pylaer sijn, diens as C D, ende vastpunt E, ende roerlick punt F, daer an den pylaer door t'rechtdaelwicht G in die ghestalt ghehouden wort, daer an oock den pylaer door t'scheefdaelwicht H (welverstaende G gheweert sijnde) in die ghestalt ghehouden wort, ende de rechtdaellini snye de sijde des pylaers in I, maer de scheefdaellini snye de selve sijde in K. Tbegheerde. Wy moeten bewijsen dat gelijck de rechtdaellini I F tot de scheefdaellini F K, alsoo t'rechtdaelwicht G tot het scheefdaelwicht H. Tbereytsel. Laet ons teeckenen t'punt L, alsoo dat E L even sy an E F, ende voughen an t'punt L t'rechthefwicht M, dat den pylaer in die ghestalt can houden, diens rechtheflini L N: Insghelijcx t'scheefhefwicht O, dat den pylaer oock in die ghestalt can houden, wiens scheefheflini L P evewijdich sy met F K. | |||||||
Tbewys.Ghelijck N L tot L P, alsoo M tot O, door het 20 voorstel, maer de macht van G is anden pylaer even met de macht van M, en̄ de macht van H met die van O door het 13 voorstel, ende I F is even an L N, en̄ F K, an L P; Daerom gelijck de rechtdaellini I F tot de scheefdaellini F K, also t'rechtdaelwicht G tottet scheefdaelwicht H, S'ghelijcx sal oock t'bewijs sijn van alle d'ander ghestalten als inde formen hier na volghende. 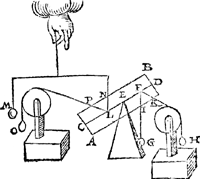 | |||||||
[pagina 47]
| |||||||
 Tbeslvyt. Wesende dan inden as des pylaers een vastpunt ende een roerlick, &c. | |||||||
9 Werckstick. 22 Voorstel.Wesende ghegheven een bekende pylaer, met een vastpunt inden as, ende een roerlick punt, an t'vvelck eenich onbekent ghevvicht den pylaer in ghegheven ghestalt houdt: Dat ghevvicht bekent te maken,
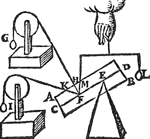
Tghegheven. Laet A B C D een pylaer sijn wegende 6 ℔, ende gedeelt als int 1 voorstel, ende t'vastpunt sy X, ende het roerende punt S, an t'welck ghevoecht sy een onbekent scheefhefwicht Y, met den pylaer evestaltwichtich, ende sijn scheefheflini snie de sijde des pylaers A B in OE. Tbegheerde. Wy moeten dat onbekende scheefhefwicht Y bekent maken. | |||||||
Twerck.Men sal sien wat rechthefwicht an S den pylaer in die gestalt soude houden, wort bevonden door 14 voorstel, van 4 ℔, daer naer salmen ondersoucken wat reden eenigheGa naar margenoot* hanghende lini als Z AE, heeft tot Z OE, ick neme als van 2 tot 1, daer uyt segh ick 2 gheeft 1, wat t'rechthefwicht van 4 ℔? comt voor Y 2 ℔, | |||||||
[pagina 48]
| |||||||
t'welck ick segh sijn waer ghewicht te sijne. Tbereytsel. Laet ons trecken de hanghende door S welcke sy A S. 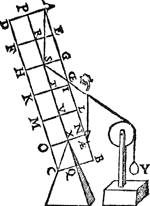 | |||||||
Tbewys.Ghelijck A S tot S OE, alsoo t'rechthefwicht tottet scheef hef wicht Y door het 20 voorstel, maer den driehouck OE Z B, is gelijck anden driehouck OE S A, welckerGa naar margenoot* lijckstandige linien sijn OE Z met OE S, ende Z AE met S A: Daerom gelijck A S tot S OE, also AE Z tot Z OE, ende vervolghens gelijck AE Z 2, tot Z OE 1, alsoo t'rechthefwicht 4 ℔ tot Y, daerom Y weghende 2 ℔ is bekent ghemaeckt, t'welck wy bewijsen moesten. Ende sghelijcx sal den voortganck sijn in allen anderen voorbeelden. Tbeslvyt. Wesende dan ghegheven een bekenden pylaer met een vastpunt inden as, &c. | |||||||
1 Merck.Wy souden inde wercking hebben meughen segghen, A S 2, gheeft S OE 1, wat t'rechthefwicht 4 ℔?comt voor Y 2 ℔, maer op dat sy lijckformigher souden sijn an t'ghene inde daet gheschiet (want men can binnen int lichaem qualick de linien A S, S OE trecken) wy hebben de hanghende lini Z AE int voorbeelt uytwendich genomen. | |||||||
2 Merck.Tis openbaer door deGa naar margenoot* verkeerde ende overanderde Everedenheyt, hoe dat elck van d'ander onbekendeGa naar margenoot* palen als Rechthefwicht, Rechtheflini, Scheefheflini, Pylaer, door drie bekende palen altijt bekent sullen worden, welcker beschrijving wy om de cortheyt achterlaten. | |||||||
14 Vertooch. 23 Voorstel.Even ghevvichten der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as even houcken makende; doen anden pylaer even ghevvelden. Tghegheven. Laet A B een pylaer sijn diens as C D, ende vastpunt daer in E, ende t'roerlick punt F, an t'welck een scheefhefwicht G sy, dat den pylaer 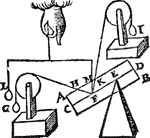 in die ghestalt houde, ende diens scheefheflini F H. Laet oock an t'selve punt F ghevoucht wesen een scheefhefwicht I, over d'ander sijde, ende met G evewichtich, ende diens scheefheflini F K, den houck K F D even make anden houck H F C. Tbegheerde. Wy moeten bewijsen dat I anden pylaer even sulcken gewelt doet als G, te weten dat I (G geweert sijnde) den pylaer oock in die gestalt sal houden. Tbereytsel. Laet an t'punt F ge- | |||||||
[pagina 49]
| |||||||
voucht worden t'rechthefwicht L dat den pylaer oock in die ghestalt can houden, ende sijn rechtheflini sy F M. | |||||||
Tbewys.Want de linien F H, F K, sijn tusschen de *Parallela. evewijdighe H K, C D, ende dat den houck H F C, even is (door t'ghegheven) an den houck K F D, soo sijn F H ende F K even, waer uyt volght dat ghelijck M F tot F H, alsoo M F tot F K, Maer ghelijck M F tot F H, also L tot G, daerom oock ghelijck M F tot F K, also L tot G; maer I is even an G door t'ghestelde, ghelijck dan M F tot F K, alsoo L tot I. T'welck soo sijnde, I hout den pylaer in die ghestalt door het 20 voorstel. S'gelijcx sal oock t'bewijs sijn in alle ander voorbeelden. Tbeslvyt. Even ghewichten dan der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as even houcken maken de; doen anden pylaer even ghewelden, t'welck wy bewijsen moesten. | |||||||
15 Vertooch. 24 Voorstel.Als des ghevvichts trecklini rechthouckich op den as is; Soo doedet anden pylaer ghegevener gestalt de grootste ghevvelt.
Tghegheven. Laet A B een pylaer sijn diens as C D, ende vastpunt E, ende roerlick punt F, waer an ghevoucht is t'scheefhefwicht G, dat den pylaer in die ghestalt hout, ende alsoo dat sijn scheefheflini H F rechthouckich op den as C D is, Laet oock an F ghevoucht worden t'scheefhefwicht I, even an G, ende sijn scheefheflini sy K F. Tbegeerde. Wy moeten bewijsen dat G meerder gewelt doet anden pylaer, dan I, oock geen meerder gewelt daer an doen en can. Tbereytsel. Laet ons an F vougen t'rechthefwicht L dat den pylaer in die ghestalt houden can, diens rechtheflini F M. | |||||||
Tbewys.
 I is even an G, ende K F is meerder dan F H,Ga naar margenoot+ daerom I heeft minder reden tot L, dan K F tot F M, waer door soo wy boven gheseyt hebben, t'ghewicht I is te licht om den pylaer in die ghestalt te houden; maer G cander hem in houden, G dan doet anden pylaer meerder gewelt dan I. Maer dat G daer an gheen meerder doen en can, is daer uyt openbaer, dat van F op de sijde des pylaers gheen corter lini en can ghetrocken worden dan F H, angesien sy daer op rechthouckich is. | |||||||
[pagina 50]
| |||||||
Tbeslvyt. Als dan des ghewichts trecklini rechthouckich op den as is, soo doedet an den pylaer gheghevener ghestalt de grootste ghewelt, t'welck wy bewijsen moesten. | |||||||
Vervolgh.Het blijckt dat hoe de houcken der trecklinien vande ghewichten op den as den rechthouck naerder sijn, hoe de ghewichten meerder ghewelt doen; Ende ter contrarie hoe sy vanden rechthouck meer verschillen, hoe de ghewichten minder ghewelt doen. | |||||||
16 Vertooch. 25 Voorstel.Tvvee onevevvijdighe linien daer een pylaer an hangt beyde oneyndelick voortghetrocken, snyen malcanderen inde hanghende svvaerheyts middellini des pylaers. | |||||||
1 Voorbeelt.Tghegheven. Laet A B een pylaer sijn hanghende ande twee onevewijdige linien C D, E F, welcke voortgetrocken sijn tot G, H, snyende malcander in I. Tbegeerde. Wy moeten bewijsen dattet punt I inde hangende swaerheyts middellini is des pylaers A B. | |||||||
Tbewys.Den houck F E C, ofte I E C, ofte H E C, is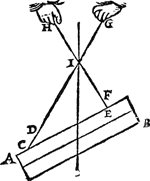 al een selfden houck, alsoo oock is D C E, ofte I C E, ofte G C E, daerom wat punten wy inde linien H E, ende C G voor uytersten nemen, den pylaer hout daer an sijn ghegheven standt. Laet ons nemen I, ghemeen uyterste punt van d'een ende d'ander lini, den pylaer dan hout daer an sijn ghegheven stant. Maer hanghende den pylaer an t'punt I, soo is deGa naar margenoot* hanghende door I des pylaers hanghende swaerheyts middellini inde welcke I is. | |||||||
2 Voorbeelt.Tghegheven. Laet A B een pylaer sijn hangende ande onevewijdige linien C D, E F, welcke voortgetrocken sijn tot G, H, snyende malcander in I. Tbegheerde. Wy moeten bewijsen dattet punt I, inde hangende swaerheyts middellini is des pylaers A B. | |||||||
Tbewys.Laet ons D G ende F H ansien voor stijlen ofte stijve linien daer den pylaer op rust, welcke door de 2 begeerte niet en breken noch en buygen, der selver gewelt is even ande gewelt der linien C D, E F, want gelijck dese den pylaer in sijn gegeven stant houden alsoo oock die. Ende wat punten wy inde linien D G, F H voor uytersten nemen, den pylaer hout daer op sijn gegeven stant. Laet ons | |||||||
[pagina 51]
| |||||||
nemen I, ghemeen uyterste punt van d'een
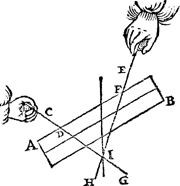 en d'ander lini; den pylaer dan hout daer op (Ga naar margenoot* Wisconstlick verstaende) sijn ghegeven standt, maer rustende den pylaer op t'punt I, soo is de hanghende door I des pylaers hanghende swaerheydts middellini, inde welcke I is. | |||||||
3 Voorbeelt.Tghegheven. Laet A B een pylaer sijn welcke in die standt ghehouden wort door de scheefdaellini C D, ende scheefheflini E F, de selve sijn voortghetrocken tot G, H, snyende malcanderen in I. Tbegheerde. Wy moeten bewijsen dat I inde hanghende swaerheyts middellini is des pylaers A B. | |||||||
Tbewys.Laet ons G C ansien voor stijl, ofte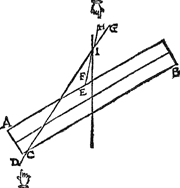 stijve lini ende nemen dat de macht die an D int neertrecken was, nu neersteeckende sy in yder punt tusschen C en G daermen haer stelt, ende den pylaer A B, sal alsoo op allen punten diemen tusschen C, G, ende E, H voor uytersten neemt, sijn ghegheven standt houden. Laet ons nemen I ghemeen uyterste van d'een en d'ander lini, den pylaer dan hout daer an sijn ghegheven stant; maer hangende den pylaer an t'punt I, de hanghende door I is des pylaers hanghende swaerheyts middellini, inde welcke I is. | |||||||
4 Voorbeelt.Tghegheven. Laet A B een pylaer sijn, welcke in die standt gehouden wort door de scheefdaellini C D, ende de scheefheflini E F, de selve sijn voortghetrocken tot G H, snyende malcanderen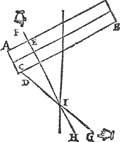 in I. Tbegheerde. Wy moeten bewijsen dat I inde hanghende swaerheyts middellini is des pylaers A B. | |||||||
Tbewys.Laet ons H E ansien voor stijl, ofte stijve lini, en̄ nemēe dat de macht die an E int opheffen was, nu opstek ende sy in yder punt tusschen E en H, daermen haer stelt, ende den pylaer A B sal alsoo op allen punten | |||||||
[pagina 52]
| |||||||
diemen tusschen C G ende E H voor uytersten neemt, sijn ghegheven standt houden. Laet ons nu nemen I ghemeen uyterste punt van d'een en d'ander lini, den pylaer dan hout daer op sijn ghegheven standt, maer rustende den pylaer op t'punt I, soo is de hanghende door I des pylaers hanghende swaerheyts middellini, inde welcke I is. Tbeslvyt. Twee onevewijdighe linien dan, daer een pylaer an hangt beyde oneyndelick voortghetrocken, snyen malcanderen inde hangende swaerheyts middellini des pylaers, t'welck wy bewijfen moesten. | |||||||
17 Vertooch. 26 Voorstel.Soo d'eene der tvvee linien daer een pylaer an hangt rechthouckich op denGa naar margenoot⋆ sichteinder is, d'ander salder oock rechthouckich op sijn: Ende sooder d'een scheefhouckich op is, dander salder oock scheefhouckich op vvesen: Ende soo dese naer die neycht, die sal naer dese neygen: Maer so dese van die vvijckt, die sal oock van dese vvijcken.
Tghegheven. Laet A B een pylaer sijn hangende an twee linien, d'een C D rechthouckich op den sichteinder, d'ander E F (soot meughelick waer) scheefhouckich, ende G H sy des pylaers hanghende swaerheyts middellini. Tbegheerde. Wy moeten bewijsen t'inhout des voorstels. Tbereytsel. Laet C D ende EF voortghetrocken worden, snyende malcander in I. | |||||||
Tbewys.Soo den pylaer in die ghestalt blijft hanghende ande linien C D, E F, sy sal op alle vastpunten in die voortghetrocken linien de selve ghestalt houden, overmidts de houcken I C E, ende I E C, niet en veranderen: Daerom ghenomen I ghemeen vastpunt dier twee linien, den pylaer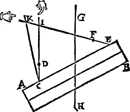 sal daer an in sijn ghegheven standt blijven hanghende, ende I C sal hanghende swaerheydts middellini sijn: maer dat is onmeugelick, wanttet G H haer evewijdeghe is. T'selve sal oock also bethoont worden als de lini E F over d'ander sijde neycht. Wesende dan I C rechthouckich op den sichteinder, d'ander lini als E F en cander niet scheefhouckich op sijn; nootsaccklick dan rechthouckich: Ende vervolghens sooder E F scheefhouckich op is, d'ander moeter ooc scheefhouckich op sijn. Voorder, anghesien E F neycht naer de sijde van A, soo sal de lini die den pylaer in dieghestalt hout moeten neyghen naer E F. Want laetse (soot meugelick waer) daer van wijcken, als C K, snyende de voortghetrocken E I in K, inder voughen dat de hanghende lini door K, sal om de redenen als boven hanghende swaerheyts middellini wesen des pylaers, t'welck noch ongheschicter is dan doen wy die seyden door I te vallen: D'ander lini dan die den pylaer in de gheslalt can houden, en wijckt van E F niet, sy en is met haer oock gheen evewijdighe als boven bethoont is, ende ter sijden uyt te wijcken is openbaer on- | |||||||
[pagina 53]
| |||||||
meughelick, sy neycht dan nootsaecklick naer E F. Ende soo E F over d'ander sijde neychde, men sal insghelijcx bethoonen dat d'ander lini van haer wijcken sal. Tbeslvyt. Soo d'eene dan der twee linien, &c. | |||||||
18 Vertooch. 27 Voorstel.Hanghende een pylaer evestaltvvichtich teghen tvvee scheefhefvvichten: Ghelijck scheefheflini tot rechtheflini, alsoo elck scheefhefvvicht tot sijn rechthefvvicht.
Tghegheven. Laet A B een pylaer sijn wiens as C D, ende twee punten daer in E, F, welcker scheefhefwichten die hem in die standt houden sijn G, H, ende rechthefwichten I, K, ende scheefheflinien E L, F M, ende rechtheflinien E N, F O. Tbegheerde. Wy moeten bewijsen dat gelijck L E tot E N, alsoo G tot I, ende ghelijck M Ftot F O, alsoo H tot K. | |||||||
Tbewys.Laet ons Fansien voor vastpunt, ende E voor t'roerlick, daerom (door het 20 voorstel) ghelijck L E tot E N, alsoo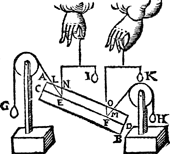 G tot I. Laet ons ten tweeden E ansien voor vastpunt, ende F voor t'roerlick, Daerom (door t'voornoemde 20 voorstel) ghelijck M F tot F O, alsoo H tot K. Tbeslvyt. Hanghende dan een pylaer evestaltwichtich teghen twee scheefhefwichten: Gelijck scheefheflini tot rechtheflini, alsoo elck scheefhefwicht tot sijn rechthefwicht, t'welck wy bewijsen moesten.  | |||||||
Vervolgh.Hangende een bekende pylaer an twee onevewijdige linien als hier neven; T'blijct dat bekent sal worden hoe veel ghewichts an yder lini hangt, ofte hoe veel ghewelts yder lini doet.  | |||||||
[pagina 54]
| |||||||
Merckt.Wy hebben tot veel voorbeelden der voorstellen deses boucx, genomen den pylaer, als bequaemste form tot de verclaring des voornemens, oock vastpunt ende roerlickpunt ghestelt inden as, wy sullen nu door dit laetste voorstel, bethoonen de reghelen van dien gemeen te wesen over alle formen der lichamen hoedanich sy sijn, met vastpunt ende roerlickpunt daert valt. | |||||||
19 Vertooch. 28 Voorstel.Alle deGa naar margenoot⋆ everedenheden, vvelcke hier vooren beschreven sijn vanden pylaer tot de ghevvichten an hem hanghende, ende dier ghevvichten linien: De selve te vvesen van yder lichaem tot de ghevvichten an hem alsoo hanghende, ende dier ghevvichten linien. Tghegheven. Laet ons t'voorbeelt nemen der everedenheydt des 20 voorstels aldus: Het sy een pylaer A B, diens as C D, ende swaerheyts middelpunt E, ende vastpunt daer in F, ende 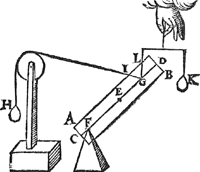 roerlick punt G, an t'welck ghevoucht sy een scheefhefwicht H, dat den pylaer in die gestalt houde, diens scheefheflini G I. Daer naer t'rechthefwicht K, dat den pylaer oock in die ghestalt houde, diens rechtheflini G L, alwaer wy segghen, gelijck I G tot G L, alsoo H tot K. Tbegheerde. Wy moeten bewijsen dat dese everedenheyt niet alleenlick alsoo en bestaet in t'lichaem A B een pylaer sijnde, maer van sulcke form alst valt. | |||||||
Tbewys.Laet ons den pylaer A B (blijvende de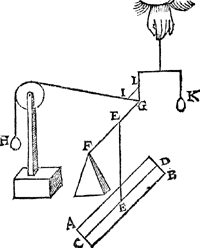 linien F G ende I L op haer plaetsen) neertrecken, alsoo dat hy blijve hanghende an sijnGa naar margenoot* swaerheyts middelpunt E, wiens ghestalt dan sy als hier nevens. Ende door de 3 begheerte den pylaer en veroirsaeckt op de punten F, G, gheen ander swaerheyt dan d'eerste; ende alles blijft noch evestaltwichtich, ende ghelijck I G tot G L, alsoo noch H tot K. | |||||||
[pagina 55]
| |||||||
Laet nu de form des pylaers (al de stof
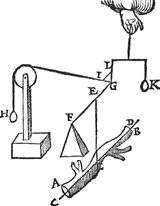 blijvende) verandert worden in eenighe ander ongheschickte form, als A B hier nevens, diens swaerheytds middelpunt Esy, ende een rechte lini daer door C D (welcke vinding des swaerheyts middelpunts ende rechter linien inde Weeghdaet verclaert sal wordenGa naar margenoot* werckelick, niet Wisconstelick) ende alles blijft noch evestaltwichtich, ende ghelijck I G tot G L, alsoo noch H tot K. Laet nu t'lichaem A B opghetrocken 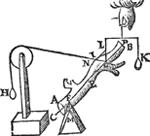 worden, tot dat F G is inde lini C D, wiens ghestalt dan sy als hier nevens, ende alles blijft noch evestaltwichtich: want het lichaem A B hoogher ofte leegher hangende, blijft van een selfde ghewicht door de 3 begheerte, ende vervolghens ghelijck I G tot G L, alsoo noch H tot K. De everedenheyt dan des 20 voorstels en is niet alleenelick alsoo met den pylaer, maer met yder lichaem: Ende der ghelijcke salmen oock alsoo bethoonen van al t'ghene hier vooren in alle d'ander voorstellen vanden pylaer gheseyt is. Tbeslvyt. Alle de everedenheden dan, welcke hier vooren beschreven sijn vanden pylaer tot de ghewichten an hem hanghende, ende dier gewichten linien; de selve sijn van yder lichaem tot de ghewichten an hem alsoo hangende, ende dier ghewichten linien, t'welck wy bewijsen moesten. | |||||||
Vervolgh.Tis oock openbaer dat de gegeven punten als F, G, niet nootsakelick en moeten inde lini C D sijn, maer daert valt by voorbeelt ande uytersten des lichaems M, N, want voortgetrocken de lini I N tot inde rechte C D, t'welck ick neem te vallen in G; sghelijcx getrocken door M deGa naar margenoot* hangende tot inde lini C D, welckeick neem te vallen in F, de voornoemde everedenheyt, te weten ghelijck I G tot G L, alsoo H tot K, blijft noch staende.
EERSTEN BOVCX EYNDE.  |
|