Wisconstighe gedachtenissen. Deel 3: van de deursichtighe
(1605)–Simon Stevin–Nv de Voorstellen.Ga naar margenoot+ | |
1 Werckstick. 1 Voorstel.Ga naar margenoot+Wesende ghegheven een oneyndelicke platspieghel, en een verschaeulickpunt: Sijn schaeu te vinden.
Tghegheven. Laet A B een oneyndelicke platspieghelsijn, ende C een verschaeulickpunt daer voor. Tbegheerde. Wy moeten sijn schaeu vinden. 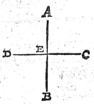 | |
Twerck.Men sal trecken de lijn C D rechthouckich op A B, snyende deselve in E, ende alsoo dat E D even sy an E C: Ick segh | |
[pagina 98]
| |
t'punt D de begheerde schaeu te sijn, waer af t'bewijs deur d'eerste begheerte openbaer is. Tbeslvyt. Wesende dan ghegeven een oneyndelicke platspieghel, en een verschaeulickpunt, wy hebben sijn schaeu ghevonden na der eysch. | |
Vervolgh.Anghesien de lijn uyt oneyndelicke menichte van punten bestaet, ende da de schaeu van yder dier punten ghevonden wort deur t'boveschreven 1 voorstel; Soo volght dat de beschrijving des schaeus van alle lijn in een platspieghel bekent is. Laet tot voorbeelt A B een platspieghel sijn, ende C D een cromme lijn met oneyndelicke menichte van punten daer in gheteeckent als C, E, F, G, D: Nu ghevonden haer schaeuwen H, I, K, L, M, alsboven, de lijn ghetrocken deur sulcke oneyndelicke menichte van punten als de lijn H I K L M, is de begheerde schaeu. Voort anghesien yder lichaems vlack, uyt oneyndelicke menichte van linien bestaet, en yder lichaen in vlacken begrepen is, soo volght uyt redenen alsvooren, dat de beschrijving de schaeus van yder lichaem in een platspieghel oock openbaer is.  | |
2 Werckstick. 2 Voorstel.Wesende ghegheven een oneyndelicke platspieghel met een verschaeulickpunt en t'oogh: T'keerpunt vinden.
Tghegheven. Laet A B een oneyndelicke platspieghel sijn, C t'ver schaeulickpunt, ende D het oogh. Tbegheerde. Wy moeten t'keerpunt vinden. | |
Twerck.Men sal vinden de schaeu van C, als E, deur het I voorstel, dat is treckende de lini C E rechthouckich op A B, snyende de selve in F, ende also dat F E even sy an F C, daer na de rechte E D, snyende A B in G, welcke sne G ick segh t'begheerde keerpunt te wesen.  | |
Tbewys.Angesien E schaeu is des verschaeulickpunts C deur het 1 voorstel, ende D oogh deur t'ghegheven, soo is E D ooghstrael deur de 5 bepaling, en daerom G keerpunt deur de 6 bepaling. Tbeslvyt. Wesende dan ghegheven een oneyndelicke platspiegel me een verschaeulickpunt, en t'oogh; Wy hebben t'keerpunt ghevonden nae der eysch. | |
[pagina 99]
| |
1 Vertooch. 3 Voorstel.Ga naar margenoot+T'verschaeulickpunt en sijn schaeu, staen evevvijtvant oneyndlick plat des voortghetroken platspieghels.
Tghegheven. Laet A B een platspieghel sijn, wiens oneyndlick voortghetrocken plat C D is, ende E sy enn verschaeulickpunt, alsoo dat de lijn E F rechthouckich op C D, niet en streckt deur de spieghel A B, ende E F snye C D in G. Tbereytsel. Laet ghenomen worden C D teenemael een platspieghel te wesen, ende eenich oogh ghestelt worden als H siende de schaeu F deur t'keerpunt linde spieghel A B.  | |
Tbewys.Wesende C D aldus een platspieghel, ende schaeu des verschaeulickpunts E, so sijn E ende F evewijt van G deur de 1 begheerte. Laet ons nu wech doen de spigheldeelen A C ende B D, soo datter maer spieghel en blijve A B: T'welck so sijnde, het oogh H siet noch de schaeu F want blijvende t'keerpunt des spiegels I onveradert ende ongheroert, de wechdoening van al de rest des spieghels, en belettet oogh niet deur I t'punt F te sien: Maer de schaeu F van t oogh H daer alsoo ghesien wesende, soo isse in die plaets niet tegenstaende tusschen E F geen spieghel en is, oock even soo wijt vant oneyndelick plat des voortghetrocken platspieghels, als sijn verschaeulick punt E. Tbeslvyt. T'verschaeulickpunt en sijn schaeu dan, staen evewijn vant oneydelick plat des voortghetrocken platspieghels, t'welck wy bewijsen moesten. | |
2 Vertooch. 4 Voorstel.Des verschaeulickpunts keelijn, ende d'oogh keerlijn, maken op den platspieghel even houcken.
Tghegheven. Laet A B een platspieghel sijn, ende C t'verschaeulickpunt, D de schaeu, C D verschaeulickpunts strael, snyende A B in E, ende F het oogh, D F ooghstrael; G keerpunt, G C verschaelickpunts keerlijn, G F ooghkeerlijn. Tbegheerde. wy moeten bewijsen dat den houck C G A; even is anden houck F G B. | |
Tbewys.Anghesien E G rechthouckich op D C, ghemeene sijde is der drichoucken D E G, ende C E G, oock dat D E even is an E C deur de 1 begheerte, so is D G even an C G,Ga naar margenoot+ voort is den houck C G E even anden houck D G E; MaerGa naar margenoot+ den houck F G B, is oock even anden houc D G E, daerom den houck C G E, is even anden houck F G B. Maer den houck C G E oste C G A is al een selfde, daerom den houck C G A, is even anden houck F G B.  Tbeslvyt. Des verschaeulickpunts keerlijn dan, ende d'ooghkeerlijn, maken op den platspiegel even houcken, t'welck wy bewijsen moesten. | |
[pagina 100]
| |
3 Vertooch. 5 Voorstel.Wesende een clootspieghel en verschaeulick punt, van t'vvelck deur des clootspieghels middelpunt een oneyndelicke lini ghetrocken is: De schaeu in die lijn, en t'verschaeulickpunt, sijn evevvijt vande clootspieghel.Ga naar margenoot+
Tghegheven. Laet A B twee clootspieghels sijn, d'een bol, d'ander hol, diens middelpunt C is, ende D sy t'verschaeulickpunt, van t'welck deur C ghetrocken is, de oneyndelicke D E, snyende de spieghel in F. Tbergheerde. Wy moeten bewijsen dat de schaeu inde lijn D E, even soo wijt is vande clootspieghel, dat is vant t'punt F, als t'verschaeulick punt D. Tbereytsel. Laet getrocken worden de platspiegel G H, deur t'punt F, ende rechthouckich op C F, daer na sy geteyckent t'punt I, alsoo dat I F even sy an F D.  | |
Tbewys.Anghesien C F rechthouckich is op G H, soo gheraeckt G H de lijn A B int Ga naar margenoot+punt F, daerom F is ghemeen punt des platspieghels ende clootspieghels, deur welck punt F het verschaeulick punt D verschijnt; Daerom oock is de schaeu in d'een en d'ander spieghel op een selsde plaets: Maer de schaeu des platspieghels is I deur het 1 voorstel, de schaeu dan des clootspieghels is oock I: Maer I is inde platspieghel even soo wijt van t'punt F, als D, daerom de schaeu des clootspieghels A B, is even soo wijt vande clootspieghel, dat is van t'punt F, als sijn verschaeulickpunt D. | |
Ander bewys.Laet ons nemen dat de clootspieghel A B, recht ghetrocken worde tot inde platspieghel G H, alsoo datse beyde in een selve plat staen; t'welck soo wesende, I is ghemeene schaeu van d'een en d'ander spieghel des verschaeulickpunts D deur het 1 voorstel, ende F ghemeene sne der spieghels, met des verschaeulickpunts strael I D. Laet ons nu nemen dattet plat A B, blijvende t'punt Fonverroerlick, weder ghecromt worde in sijn eerste clootsche ghestalt: Dit soo sijnde, de schaeu I is noch op haer selve plaets, want blijvende de punten F en D (die alleenlick des schacus oirsaeck sijn, overmidts d'ander stof des spieghels buyten t'punt F, tot de saeck en gheeft noch en neemt) on verroert, soo moet de schaeu I inde clootspieghel oock op haer plaets onbeweeghlick blijven, dat is in sulcke wijde van F, alsser D af is. Tbeslvyt. Wesende dan een clootspiegel, en een verschaeulickpunt, van t'welck deur des clootspieghels middelpunt een oncyndelicke lijn ghetrocken is: de schaeu in die lijn en t'verschaeulickpunt, sijn evewijt vande clootspieghel, t'welck wy bewijsen moesten. | |
[pagina 101]
| |
Merckt.Hier boven wort eyghentlick gheseyt vande schaeu inde lijn D E, want met al d'ander schaeuwen die inde clootspiegel van oneyndelicke menichte connen sijn, ist anders ghestelt, soo int volghende blijcken sal. | |
3 Werckstick 6 Voorstel.Wesende ghegeven een clootspieghel, t'verschaeulickpunt, en t'oogh t'vvelck de schaeu sien can: T'keerpunt te vinden.
Oogh dat de schaeu sien can, is diens rechte lijn tusschen t'oogh en t'verschaeulickpunt, den cloot niet en raeckt, noch daer deur en lijdt: Oock diens keerlijn op t'ghegheven deel des clootspieghels even houcken connen maken, en dat om bekende redenen. | |
1 Voorbeelt alwaer t'verschaeulickpunt en het oogh, evewijt van t'middelpunt des cloot spieghels sijn.Tghegheven. Laet A B een clootspieghel wesen, diens middelpunt C is, en t'verschaeulickpunt sy D, maer het oogh E, welcke D ende E evewijt van t'middelpunt C sijn. Tbegheerde. Wy moeten t'keerpunt vinden. | |
Twerck.Men sal trecken de lijn D E, ende uyt haer middel F, de lijn F C, snyende A B in G: t'welck soo sijnde, ick segh G t'begheerde keerpunt te wesen. Tbereytsel. Laet ghetrocken worden G D, G E, voort H I, als platspieghel gherakende A B in t'punt G. | |
Tbewys.Anghesien D F des driehoucx D F G, even is an F E des driehoucx E F G, ende haer ghemeene G F daer op rechthouckich, so is den driehouck D F G, even ende ghelijck an den driehouck E F G, daerom oock den houck D G F, even anden houck E G F: Voort, na dien H I den booch A B in G gheraeckt, soo is H I rechthouckich op G F: Daerom oock den houck F G H, even anden houck F G I: Nu van dese twee even houcken, ghetrocken de twee even houcken D G F, E G F, de blijvende houcken D G H ende E G I sijn oock even, ende vervolghens soo is G keerpunt des platspieghels H I deur het 2 voorstel: Maer G is ghemeen punt des clootspieghels A B, ende platspieghels H I, daerom de schaeu van D, welcke vant oogh E ghesien wort deur G des platspieghels, de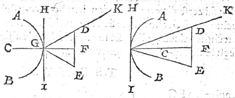 | |
[pagina 102]
| |
selve schaeu worter oock afghesien deur G des clootspieghels: G dan is oock keerpunt des clootspieghels A B, t'welck wy bewijsen moesten. | |
2 Voorbeelt, alwaer t'ver schaeulickpunt ende het oogh, onevewijt van t'middelpunt des clootspieghels staen.Tghegheven. Latet verschaeulickpunt nu inde boveschreven sorm K wesen, verder vant middelpunt des spieghels C, dant oogh E. Tbegheerde. Wy moeten t'keerpunt vinden. | |
Merckt.Alsoo my hier af alsnu gheen wisconstighe manier te vooren en comt, wy sullentGa naar margenoot* tuychwerckelick doen in deser voughen. | |
Twerck.Men sal trecken eenighe twee linien K G, E G, makende eenighen houck K G E, die t'begheerde soo na comt als uyt het oogh mach gheoirdeelt worden, daer na salmen deur t'punt G, trecken de lini C G F, welcke soo sy den houck K G E even in tween deelt, soo heeftmen t'begheerde keerpunt, dies niet, soo salmen de twee linien als K G, E G, trecken uyt een punt als G so veel opwaert of neerwaert, ende dat soo menichmael doen, tot dat soodanighe linie als C F, den houck ghelijck K G E, even in tween doorsnijt, t'welck soo wesende t'bewijs is deur t'voorgaende openbaer. | |
4 Werckstick. 7 Voorstel.Wesende ghegeven een clootspieghel, t'verschaeulickpunt, en het oogh dat de schaeu sien can: De schaeu te vinden.
Tghegheven. Laet A B een clootspieghel sijn, C t'verschaeulickpunt, D het oogh dat de schaeu sien can. Tbegheerde. Wy moeten de schaeu vinden. | |
Twerck.Men sal eerst t'keerpunt vinden deur het 2 voorstel, t'welck E sy, treckende de rechte lijn F G, alsoo datse den booch A B gherake int punt E, daer na de lijn C H rechthouckich op F G, die snyende in I, ende alsoo, dat I C even sy an I H. Ick segh H de begheerde schaeu te wesen. | |
Tbewys.Anghesien F G den booch A B in E gheraeckt, soo is F G rechthouckich op des clootspiegels bedochte middellijn deur E, de selve middellijn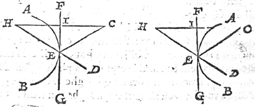 | |
[pagina 103]
| |
soude den houck C E D openbaerlick int middel deelen, daerom oock is den houck C E F, even anden houck D E G: T'welck soo wesende, H is schaeu des verschaeulickpunts C, inde platspieghel F G deur het 1 voorstel: Maer t'keerpunt E des platspieghels F G, is oock t'keerpunt des clootspieghels A B, daerom valt de schaeu van d'een en d'ander spieghel op een selve plaets, want by aldient op een ander viel, soo soude de stof des clootspieghels buyten E daer af d'oirsaeck moeten wesen; t'welck onmeughelick is, overmidts die tot de saecken gheeft noch en neemt. H dan is de begheerde schaeu, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan gegeven eē clootspiegel t'verschaeulickpunt en t'oogh welck de schaeu sien can, Wy hebben de schaeu gevonden na den eysch. | |
5 Werckstick 8 Voorstel.Wesende ghegheven een spieghel van form soot valt, t'verschaeulickpunt en t'oogh, t'vvelck de schaeu sien can: T'keerpunt te vinden.
Tghegheven. Laet A B eenich cromvlackich spieghel sijn van sorm soot valt, C t'verschaeulickpunten D het oogh. Tbegheerde. Wy moeten t'keerpunt vinden. | |
Merckt.Alsoo my hier af (ghelijck oock vant 2 voorbeelt des 6 voorstels) gheen wisconstighe manier te vooren en comt, wy sullentGa naar margenoot* tuychwerckelick doen in deser voughen. | |
Twerck.Ick teycken inde spieghel A B eenich punt als E, ter plaets daer my uyter oogh dunckt het keerpunt te willen vallen, treck daer na deur t'selve punt E de lini F G als platspieghel, gherakende sonder snyen de spieghel A B, treck daer na E C en E D. By aldien, nu den houck C E F, even bevonden wort anden houck, D E G, soo is E t'begheerde keerpunt. Maer by aldien die twee houcken oneven bevonden wierden, men sal het punt als E hoogher oflegher stellen tot dat sulcke twee houcken even vallen, t'welck ick neem te ghebeuren wesende dat punt an E: Dit soo sijnde ick segh E t'begheerde keerpunt te wesen.  | |
Tbewys.Anghesien de platspieghel F G, de cromvlackighe spieghel A B in t'punt E gheraeckt, soo is t'punt E ghemeen in d'een en d'ander spiegel, daerom de schaeu des verschaeulick punts C, die vant oogh D ghesien wort deur E als keerpunt des platspieghels F G, de selve schaeu worter oock ghesien deur E als keerpunt des ghegheven cromvlackighe spieghels A B, en daerom is E oock keerpunt des selven spiegels A B, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven een spieghel van form soot valt, t'verschaeulick punt, en t'oogh t'welck de schaeu sien can, wy hebben t'keerpunt ghevonden, na den eysch. | |
[pagina 104]
| |
6 Werckstick. 9 Voorstel.Wesende ghegheven een spieghel van form soot valt, t'verschaeulicklickpunt, en het oogh t'vvelck de schaeu sien can: De schaeu te vinden.
Tghegheven. Laet A B eenich cromvlackich spieghel sijn van form soot valt, C t'verschaeulickpunt, D het oogh. Tbegheerde. Wy moeten de schaeu vinden. | |
Twerck.Men sal eerst het keerpunt vinden deur het 8 voorstel t'welck E sy, en de lini die int vinden des selven punts E ghetrocken wort als platspieghel sy F G, daer na sy ghetrocken de lini C H rechthouckich op F G die snyende in I, also dat I C even sy an I H. Dit soo wesende ick segh H de begheerde schaeu te wesen. | |
Tbewys.Anghesien de platspieghel F G, de cromvlackighe spieghel A B int punt E gheraect, soo is t'punt E ghemeen in d'een en d'ander spieghel: Daerom de schaeu des verschaeulickpunts die vant oogh D ghesien wort deur E als keerpunt des platspieghels F G, de selve schaeu wort oock ghesien deur E als keerpunt des gegeven cromvlackighe spieghels A B, en daerom is H oock schaeu inde selve spieghel A B.  Tbeslvyt. Wesende dan ghegeven een spieghel van form soot valt, t'verschaeulickpunt en het oogh t'welck de schaeu sien can, wy hebben de schaeu gevonden, na den eysch. | |
Vervolgh.Wesende deur dit 9 voorstel openbaer de vinding des schaeus van yder verschaeulickpunt sienlick in een spieghel van form alst valt, soo volght oock in alle spiegel bekent te wesen de vinding des schaeus van yder lini, vlack en lichaem, te weten de lini deur oneyndelicke beschrijving van punten, en t'vlack deur beschrijving van linien, t'lichaem deur beschrijving van vlacken. |
|

