Wisconstighe gedachtenissen. Deel 2: van de meetdaet
(1605)–Simon Stevin–11 Voorstel.Een ghegheven rechtlinich plat te meten. | |||||||||||
1 Voorbeelt vant meten eens driehoucx.Tghegheven. Laet A B C een driehouck sijn. Tbegheerde. Wy moeten t'begrijp des selfden vinden. | |||||||||||
Twerck.Ick meet eenighe sijde als B C, bevinde die neem ick van 8, en treck A D hanghende op de selve B C die ick bevinde van 6, welcke gemenichvuldicht deur 4 helft van C B, comt voor t'begheerde plat 24, waer af t'bewijs openbaer is deur het 41 voorstel des 1 boucx van Euclides. Maer die hier af eenighe dadelicke proef begheerde te sien, mach vanden houck B trecken een hanghende op A C, die menichvuldighende deur den helft van haer gront A C, wantmen alsoo siet hoe na die verscheyden werckinghen met malcander overcommen. | |||||||||||
MercktDat wy hier boven de hanghende A D ghemenichvuldicht hebben metten helft des gronts C B: Doch machmen oock andersins den helft der hanghende dats 3, menichvuldighen deur den heelen gront 8, en comt oock 24. Oft andersins segghen 6 mael 8 is 48, diens helft alsvooren 24. Ende mach sulcken helft bequamelicxt ghenomen worden van die lini der twee diens ghetal parich is, om wercking int ghebroken te schuwen. | |||||||||||
[pagina 74]
| |||||||||||
By aldien de hanghende vanden houck na de gront buyten den driehouck viel, soo machmen dan nemen de hanghende vanden houck op den voortghetrocken gront menichvuldighende de selve deur den helft des
 gronts. Als by voorbeelt, te meten sijnde den driehouck A B C; wiens hanghende vanden houck A op de voortgetrocken C B sy A D, de langde der selve ghemenichvuldicht deur den helft van C B, gheeft het begrijp des driehoucx A B C. | |||||||||||
2 Voorbeelt vant met en eens bijls.Tghegheven. Laet A B C D een bijl wesen, diens twee evewijdeghe sijden sijn A B, C D. Tbegheerde. Wy moeten t'begrijp des selfden vinden. | |||||||||||
Twerck.Men soude de bijl meughen deelen in twee driehoucken met een lini van A tot C, of van B tot D, metende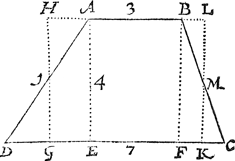 elck van dien na de manier des 1 voorbeelts, en de somme dier twee driehoucken soude t'begeerde sijn, maer want de meting corter can vallen, soo sullen wy die verclaren als volght: Ick meet de twee evewijdege sijden, bevinde A B van neem ick 3, en C D van 7, maken t'samen 10, diens helft 5 ghemenichvuldicht dent de hanghende A E doende neem ick 4, comt voor t'begheerde plat des bijls A B C D 20. Tbereytsel. Laet ghetrocken worden B F rechthouckich op D C, daer na sy t'punt G ghestelt int middel van D E, en ghetrocken G H even en evewijdeghe met E A snyende A D in I, daer na H A: S'ghelijcx sy int middel van F C ghestelt het punt K, en ghetrocken K L, even en evewijdeghe met F B snyende B C in M, daer na L B. | |||||||||||
Tbewys.Want den driehouck I A H even is anden drichouck I D G, en den driehouck M B L, even anden driehouck M K C, soo is den rechthouck H L K G, even anden bijl A B C D, en H L is even anden helft der twee linien D C, A B, daerom den rechthouck begrepen onder A E, of onder H G en den helft der twee evewijdeghe sijden des bijls, is altijt even anden bijl: En daerom is t'plat alsoo int werck ghevonden voor de begheerde grootheyt der bijl A B C D. | |||||||||||
3 Voorbeelt vant meten eens rechtlinich plats soot valt, deur deeling in driehoucken.Tghegheven. Laet A B C D E F een rechtlinich plat sijn, als een seshouck van form soot valt. Tbegheerde. Wy moeten t'begrijp des selfden vinden. | |||||||||||
[pagina 75]
| |||||||||||
Twerck.Ick treck de drie linien A C, A D, A E, deelende den seshouck in vier driehoucken: Meet daer na elcke driehouck na de leering des 1 voorbeelts, en de somme der vier driehoucken is t'begheerde. Merckt noch datmen cortheyts halven twee hanghende linien die op een selve gront vallen, t'samen vergaren mach, en daer me den helft des gronts menichvuldighen. Als by voorbeelt om de twee driehoucken A E D, A E F beyde t'samen met een menichvulding te vinden, ick mete de hanghende D G, bevinde die van 4 en F H van 3, welcke alsoose beyde vallen op een selve gront A E, ick vergaerse, maken t'samen 7, daer me ghemenichvuldicht den helft des grondts A E doende neem ick 5, comt voor t'begrijp der boveschreven twee driehoucken 35. S'ghelijcx machmen oock doen met d'ander twee driehoucken, vergarende daer na de twee gevonden vierhoucken A D E F, A D C B. Waer af t'bewijs openbaer is. | |||||||||||
4 Voorbeelt vant meten eens rechtlinich plats deur rekening der platte driehoucken.T'ghebeurt int dadelick lantmeten, datmen de langden van ettelicke linien diemen behouft int rekenen na de manier des 3 voorbeelts, niet meten en can, deur belet van water, huysen of dierghelijcke, doch dat eenighe ander linien wel connen ghemeten worden, maer t'werck moet deur rekening der platte driehoucken afgheveerdicht sijn, daer af wy nu segghen sullen, stellende een voorbeelt dat sijn Vorstelicke Ghenade gheteyckent seer nauwe ghemeten en berekent heeft, als volght. Tghegheven. Laet A B C D E een rechtlinich plat sijn, te weten een vijfhouck van form soot valt. Tbegheerde. Wy moeten t'begrijp des selfden vinden. | |||||||||||
Twerck.Ghenomen datmen de inwendighe linien als A C, A D, met hanghende daer op vallende, om eenich belet, opt landt niet meten en can, maer wel de uytwendige sijden, die gevonden sijn gelijck de ghetalen daer op staende anwijsen: Genomē voort dat ick vande baec A, sien can tot d'ander vier baecken B, C, D, E, om daer op te vinden de drie houcken B A C, C A D, D A E, elck van grootheyt ghelijck daer op gheteyckent staet. Dit soo sijnde, den Meter can het inhoudt deses plats berekenen sonder ander kennis daer af te hebben in deser voughen: Voor al om te meten het plat des driehoucx A B C, ick treck B F rechthouckich op A C, en heb inden driehouck A B F drie bekende palen, te weten den houck F A B 47 tr. den houck B F A recht, en de sijde A B van 954 ②.
| |||||||||||
[pagina 76]
| |||||||||||

| |||||||||||
[pagina 77]
| |||||||||||
| |||||||||||
1 Merck.Soot niet gheleghen en waer gheweest datmen vande baeck A hadde connen sien tot d'ander vier baecken B, C, D, E, om te vinden de drie houcken B A C, C A D, D A E, maer datmen wel had connen nemen de grootheyt der vijf uytwendighe houcken A, B, C, D, E, tis kennelick datmen daer me oock deur rekening der platte driehoucken t'begheerde soude ghevonden hebben, want de driehouck A B C soude drie bekende palen hebben, te weten de twee sijden A B, B C, mette sijde A C, en hanghende B F, waer me ghevonden wort t'plat des driehoucx A B C. Om daer na te vinden t'plat des driehoucx A C D, men treckt den voorschreven ghevonden houck B C A, vanden ghemeten houck B C D, de rest is voor den houck A C D des driehoucx A C D, die dan oock drie bekende palen heeft, te weten totten selven houck A C D, noch de twee sijden C A, C D, waer me voort gevaren alsmen metten driehouck A B C ghedaen heeft, en derghelijcke oock doende metten driehouck A D E, het heel plat wort bekent alsvooren. | |||||||||||
2 Merck.T'mach ghebeuren datmen niet sien en can van een deser vijf baecken A,B,C,D,E, tot al d'ander, maer wel van eenighe seste baeck ontrent het middel des landts ghestelt: Als neem ick in dees vijfhouck A B C D E sy ghestelt een seste baeck F, van waermen d'ander vijf can sien, en meten de vijflinien F A,F B,F C,F D,F E mette vijf houeken A F B, B F C, C F D, D F E, en E F A, T'welck soo sijnde elcke driehouck heeft drie bekende palen, waer me yders hanghende in elcken driehouck, als D G inden driehouck D F E ghevonden wort alleenelick deur een menichvulding sonder deeling, om dat inde evereden heyts reghel d'eerste der drie palen altijt 100000 doet, welcke hanghende ghevonden sijnde, en ghemenichvuldicht deur den helft des gronts, men heeft het plat van dien driehouck, en sulcke vijf driehoucken t'samen maken het heel begheerde plat. | |||||||||||
3 Merck.In dit 3 en 4 voorbeelt sijn ghemeene reghelen beschreven om alle rechtlinighe platten te meten deur deyling in driehoucken, doch soo vallender op sekerGa naar margenoot* afcomsten corter weghen, diemen daert te pas comt gebruycken mach als volght. | |||||||||||
[pagina 78]
| |||||||||||
 Ten eersten, het viercant als A wort gevonden menichvuldighende een sijde in sich. Ten 2, den rechthouck als A B C D wort ghevonden menichvuldighende langde deur breede, dats A B deur A D.  Tē 3, de ruyt en scheefruyt, als A B C D, worden ghevonden menichvuldighende den gront D C, deur een hanghende daer op als A E.  Ten 4, de gheschickte veelhoucken als A, worden ghevonden menichvuldighende de lini A B, vant middelpunt des forms A tot int middel van een der sijden als C D, deur den halven omtreck, of den heelen omtreck deur den helft van A B. Maer hoe men de lini A B in yder gheschickte form deur de bekende C D vindt, is int 7 voorstel van desen verclaert. | |||||||||||
5 Voorbeelt vant meten eens rechtlinich plats soot valt deur deeling inbijlen.Tghegheven. Laet A B C D E F G een rechtlinich plat sijn, t'welckmen wil meten deur deeling in bijlen met linien evewijdich streckende vande lini H I. Tbegheerde. Wy moeten deur sulcke manier van meting het inhoudt des ghegheven plats vinden. | |||||||||||
Twerck.Ick treck evewijdeghe linien met H I, uyt al de houcken daer linien uyt commen connen die t'plat snyen als G K, B L, F M, C N, E O, die de ghegheven form deelen in vier bijlen en twee driehoucken, daerom die twee driehoucken ghemeten na de manier des 1 voorbeelts, en de bijlen na de manier des 2 voorbeelts, de somme van als is openbaerlick t'begheerde plat, sulcx dat daer af gheen bewijs en behouft. Dese deyling in bijlen comt dickwils te pas om landen in seker cavels te deelen, diemen met evewijdeghe linien begheert te scheyden. Maer hoemen die cavels alsoo elck van begheerde grootheyt crijcht, sal t'sijnder plaets int 11 voorstel des 5 boucx vande Everedentlicke snyding der grootheden verclaert worden. | |||||||||||
[pagina 79]
| |||||||||||
Ymant mocht nu segghen dat onder de bijlen daer t'rechtlinich in ghedeelt wort, formen mochten vallen gheen bijlen sijnde, maer byghevalle viercanten, ruyten, of scheefruyten: T'welck ghebeurende, de voorgaende reghel der bijlen is daer af ghemeen: Want den helft van twee evewijdeghe sijden die even sijn, is een der selve evewijdeghen, welcke ghemenichvuldicht deur de hanghende, gheeft ghelijck inde bijl het inhoudt des plats. Tbeslvyt. Wy hebben dan een rechtlinich plat ghemeten na den eysch. | |||||||||||
12 Voorstel.Wesende ghegheven de middellijn eens rondts: Het plat te vinden.
Tghegheven. Laet A B C D een rondt sijn diens middelpunt E is, en de middellijn B D doet 12. Tbegheerde. Wy moeten de grootheyt des plats vinden. | |||||||||||
Twerck.Ick vinde den omtreck deur het 8 voorstel deses 2 boucx van 37 5/7 (want segghende 7 gheeft 22 wat 12? comt alsboven 37 5/7) den helft van dien als 18 6/7. ghemenichvuldicht deur de halfmiddellijn 6, comt voor begheert plat des rondts 113 1/7. T'bewijs daer af is openbaer deur het 1 voorstel der rondtmeting van Archimedes. Tbeslvyt. Wy hebben dan een ghegheven rondt ghemeten, na den eysch. | |||||||||||
13 Voorstel.Een ghegheven halfmiddellijndeel des rondts te meten.
Daer gheschien int rondt twee besonder vermaerde sneen, d'eene met twee halfmiddellijnen, wiens deel ick halfmiddellijndeel noem, d'ander met een peez ick peezdeel heete: Tis waer datmen daer voor int Latijn seght sector en sectio, dat snijder en sne bediet, maer het onderscheyt en dunckt my niet eyghen ghenouch, welverstaende voor den ghenen die in een beter tael de saken eerst namen gheeft, want anders is de ghewoonte veel toe te laten. Angaende de meting des halfmiddellijndeels, die verclaren wy in dit voorstel, ende des peezdeels sullen wy int volghende beschrijven. Tghegheven. Laet A B C een halfmiddellijndeel sijn diens halfmiddellijn A B doet 6, ende den booch B C 8. Tbegheerde. Wy moeten t'plat vinden. | |||||||||||
Twerck.Ick menichvuldighe den helft des boochs C B als 4, deur A B 6, comt voor begheert plat 24, waer af t'bewijs openbaer is deur dien dat het heel rondt even is anden uytbreng der halfmiddellijn ende des halven omtrecx, deur t'boveschreven bewijs van Archimedes, ende dat boven dien ghelijck des rondts booch totten heelen omtreck, alsoo het middellijndeel tottet heel rondt. | |||||||||||
[pagina 80]
| |||||||||||
Tbeslvyt. Wy hebben dan een ghegheven halfmiddellijndeel des rondts ghemeten, na den eysch. | |||||||||||
Merckt.Ghelijck ghemeten wort dit halfmiddellijndeel A C B cleender dant halfrondt, alsoo wort oock ghemeten het grooter deel A C D B, want den helft des boochs C D B, ghemenichvuldicht deur de halfmiddellijn, gheeft het begeerde halfmiddellijndeel. | |||||||||||
14 Voorstel.Een ghegeven peezdeel des rondts te meten.
Tghegheven. Laet A B C een peezdeel sijn diens booch A B C lanck is 6 6608/15120, ende de peez A C 6. Tbegheerde. Wy moeten t'plat des peezdeels A B C vinden. | |||||||||||
Twerck.Ick vinde des heelen rondts middel punt D, daer na de langde der halfmiddellijn A D, die deur het 8 voorstel sijn sal van 5, ende de hanghende D E (om dat des rechthouckighen driehoucx D E A twee sijden A D 5, A E 3 bekent sijn) van 4. Dit soo sijnde, het halfmiddellijndeel D A B C doet deur het 13 voorstel 16 5/54: Daer af ghetrocken den drichouck D A C doende deur het 11 voorstel van desen 12, blijft voor het begeerde peezdeel 4 5/54: Waer af t'bewijs deur t'werc openbaer is. Tbeslvyt. Wy hebben dan een ghegheven peezdeel des rondts ghemeten, na den eysch. | |||||||||||
1 Vervolgh.T'voorbeelt hier boven is vant peezdeel A B C cleender dant halfrondt, waer deur het peezdeel A F C grooter dant halfrondt openbaer is, want tottet halfmiddellijndeel D A F C, vergaert den driehouck A D C, men heeft t'begheerde. | |||||||||||
2 Vervolgh.Sooder te meten waer een deel des rondts, als hier nevens het stuck A B C, men sal meten het peezdeel C B na de leering deses voorstels, daer toe vergarende den rechtlinigen driehouck C B A, ende men sal t'begheerde hebben. | |||||||||||
3 Vervolgh.Om te meten een rinck als A, te weten het plat begrepen tusschen de twee omtrecken, men meet eerst het grootste rondt: Daer afghetrocken het cleenste, t'is kennelick de rest den begheerden rinck te wesen. | |||||||||||
[pagina 81]
| |||||||||||
15 Voorstel.Een ghegheven lanckrondt te meten.
Tghegheven. Laet A B C D een lanckrondt sijn, diensgrootste middellijn A C doet 12, ende de cleenste D B 6. Tbegeerde. Wy moeten het plat vinden. | |||||||||||
Twerck.Ick vinde t'plat eens rondts diens middellijn A C 12, t'welck doet deur het 12 voorstel van desen 113 1/7: Segh daer na A C 12, gheeft D B 6, wat 113 1/7? Comt voor begheert plat des lanckrondts 56 4/7. Andersins machmen oock mette cleenste middellijn D B beginnen aldus: Ick vinde t'plat eens rondts diens middellijn D B 6, t'welck doet 28 2/7. Segh daer na D B 6, gheeft A C 12, wat 28 2/7? Comt voor begheert plat des lanckrondts als boven 56 4/7. T'bewijs daer af is openbaer deur het 6 voorstel vant bouck der kegelsche ende clootsche van Archimedes. Tbeslvyt. Wy hebben dan een lanckrondt ghemeten na den eysch. | |||||||||||
16 Voorstel.Een ghegheven brantsnees plat te meten. Tghegheven. Laet A B C  een brantsne sijn, diens sop A, en gront B C. Tbegheerde. Wy moeten het plat vinden. | |||||||||||
Twerck.Ick treck A B, A C, meet daer na den driehouck A B C, die bevindende neem ick van 20, daer toe by ghemeene regel sijn helft als 10, maeckt voor t'begheerde plat des brantsnees 30; waer af t'bewijs openbaer is deur het 24 voorstel vande viercanting der brantsne van Archimedes. Tbeslvyt. Wy hebben dan een ghegheven brantsnees plat ghemeten na den eysch. | |||||||||||
17 Voorstel.Te meten een gegheven ⋆ slangtreckplat, bestaende uyt Planum spirale. een of meer heele keeren.
Tghegheven. Laet A B C een slangtrecx eersten omkeer sijn, diens eerste lini A C, en t'plat daer in begrepen sy D, Tbegheerde. Wy moeten t'selve plat D vinden. | |||||||||||
[pagina 82]
| |||||||||||
 | |||||||||||
Twerck.Ick meet d'eerste lini A C, die bevindende neem ick van 21, de selve aenghesien voor halfmiddellijn eens rondts ick souck hoe groot dat soude sijn het plat des rondts daer me beschreven, wort bevonden deur het 12 voorstel 1386; Daer af altijt het derdendeel, comt voor begheert plat D 462. Maer by aldiender meer keeren te meten waren, soo is te weten dattet tweede slangtrecxplat 6 mael soo groot is alst eerste: En het derde 12 mael soo groot als t'eerste: Het vierde 18 mael soo groot als t'eerste, en alsoo int oneyndelick van d'ander, altijt met 6 vermeerderende voor yder keer, waer me elck plat bekent wort. Laet by voorbeelt C E de tweede lini wesen, En den tweeden keer des omtrecx sy C F E, En het tweede plat datter begrepen is tusschen den eersten en tweeden omkeer sy G. Nu volghende de boveschreven ghemeene reghel, soo doet het plat G sesmael soo veel als t'plat D, dats ses mael 462, die doen voor het tweede plat 2772: Daer toe vergaert het eerste plat D 462, maken t'samen voor het heel plat 3234. Maer waerder een derde keer, die soude volghende de voorgaende reghel doen 12 mael 462 dats 5544, daer toe d'ander twee keeren doende alsvooren 3234, souden t'samen maken voor t'gheheel 8778, en soo voort met d'ander: Waer af t'bewijs ghedaen is int 27 voorstel des boucx der slangtrecken van Archimedes. Tbeslvyt. Wy hebben dan ghemeten een ghegheven slangtreck, bestaende uyt een of meer heele keeren na den eysch. | |||||||||||
18 Voorstel.Een ghegheven clootvlack te meten.
Tghegheven. Laet A B C D een cloot sijn, diens as B D doet 12. Tbegheerde. Wy moeten sijn vlack vinden. | |||||||||||
[pagina 83]
| |||||||||||
Twerck.Ick menichvuldighe B D 12, metten omtreck A B C D, die deur het 8 voorstel van desen doen sal 37 5/7, comt voor begheert clootvlack 452 4/7, waeraf t'bewijs openbaer is deur het 30 voorstel des 1 boucx vande cloot en seul van Archimedes. Tbeslvyt. Wy hebben dan een ghegheven clootvlack ghemeten na den eysch. | |||||||||||
19 Voorstel.Te meten het bultich vlack eens clootdeels, dat met een plat vanden heelen cloot ghesneen is.
Tghegheven. Laet A B C D een cloot wesen, diens middelpunt E sy, en den as B D doet 12. Vanden selven cloot sy gesneen met een plat A C, rechthouckich op den as B D, het clootdeel A C D: En het asstick daer in bestaende als F D, sy lanck 3. Tbegheerde. Wy moeten het clootvlack des clootdeels A C D vinden. | |||||||||||
Twerck.Ick treck of bedenck de lini A D, en die metende, bevindse neem ick van 6 voeten: Sie daer na hoe groot een rondt is diens halfmiddellijn 6 voeten, en wort bevonden deur het 12 voorstel van 112½, En so groot is t'begheerde bultich vlack des clootdeels A C D. Tbewys daer af is ghedaen int 40 en 41 voorstel vant bouck des cloots en seuls van Archimedes. | |||||||||||
1 Vervolgh.Tis deur t'voorgaende kennelick, dat soomen wilde hebben het clootvlack des grootsten deels A B C, datmen dan den heelen omtreck 37 5/7, souden moeten menich vuldighen deur het asdeel daer in bestaende als F B 9, want den uytbreng als 339 3/7 is t'begheerde. | |||||||||||
2 Vervolgh.Soo den cloot doorsneen waer met twee evewijdeghe platten, het clootdeels clootvlack tusschen beyden is oock bekent. Laet by voorbeelt G H een plat sijn snyende des as B D deur t'middelpunt E, ende evewijdich mettet plat A C: Om nu te vinden het clootvlack G H C A, Men menich vuldicht den omtreck des grootsten rondts, deur het asdeel daer in bestaende, als deur E F 3, comt 113 1/7, sulcx dat de riem G H C A, ende het clootvlacxdeel in dit voorbeelt A D C evegroot sijn. | |||||||||||
3 Vervolgh.Maer soo de twee snyende platten onevewijdich waren, als I K onevewijdich met A C, men vindt eerst het clootvlack des grootsten deels I A D C K na de | |||||||||||
[pagina 84]
| |||||||||||
ghemeene reghel: Daer af ghetrocken het clootvlack des cleensten deels A D C, de rest is t'begheerde. | |||||||||||
4 Vervolgh.Men soude hier noch meughen voorstellen beschrijven, van t'meten der bultighe vlacken van seulen en keghels, maer anghesien t'bultichseulvlack ghemeten wort als een platte rechthouck, diens langde is des seuls hooghde, ende de breede des gronts omtreck, soo laten wy dat cortheyts halven daer by blijven. Derghelijcke is oock te verstaen vant bultich keghelvlack, t'welck ghemeten wort als een rondts halfmiddellijndeel, na de leering des 13 voorstels van desen, want een keghelvlack plat ontvouwen of uytghespreyt sijnde, wort van soodanighe form: Daerom ghemenichvuldicht den halven omtreck van des keghels gront, deur de lini van t'sop totten selven omtreck, den uytbreng is t'begheerde. Oft anders soomen int meten des bultich seulvlacx, en bultich keghelvlacx, wilde volghen de vondt van Archimedes int 32 voorstel des 1 boucx vande cloot en seul men sal aldus doen: Om te meten het bultich seul vlack, men sal vinden de middeleveredenighe lini tusschen des seuls hooghde en haer grondts middellijn, metende daer na hoe groot het rondt is beschreven met die middeleveredenighe als halfmiddellijn, wantmen daer me oock de grootheydt van des seuls bultich vlack heeft. Maer om des keghels bultich vlack te meten na Archimedes voorschreven vondt, men sal vinden de middeleveredenighe tusschen de keghels sijde en haer gronts halfmiddellijn, metende daer na hoe groot het rondt is beschreven met die middeleveredenighe als halfmiddellijn, wantmen daer me oock de grootheyt van des keghels bultich vlack heeft. Maer om des ghecorte keghels bultich vlack te meten na de vondt van Archimedes, men sal vinden de middeleveredenighe tusschen de ghecorte keghels sijde, en een lini even ande halfmiddellijn des gronts, met de halfmiddellijn des decksels, metende daer na hoe groot het rondt is beschreven met die middeleveredenighe als halfmiddellijn, wantmen daer me oock heeft de grootheyt des gecorte keghels bultich vlacx. | |||||||||||
20 Voorstel.Een stuck landts Lantmetersche vvijse te meten.
Wy hebben tot hier toe beschreven het meten der vlacken, dienende int ghemeen tot vlacken van alle stoffen, maer want het meten des landts, een der voornamelicke metinghen is die de menschen indeGa naar margenoot* daet ontmoeten daer in sijn Vorstelicke Ghenade hem dadelick heeft willen oeffenen, soo sullen wy daer af noch wat int besonder segghen. Tghegheven. Laet A B C drie punten of teycken opt landt sijn, tusschen welcke verdocht worden drie rechte linien van t'een tottet ander. Tbegheerde. Wy moeten vinden de grootheyt des landts tusschen de voorschreven rechte linien begrepen. | |||||||||||
Twerck.Men sal om te stellen de drie baken an A, B, C, voort om int meten recht te gaen, met ander omstandighen daer by noodich, oversien en volghen t'ghene gheseyt is int 3 voorbeelt des 1 voorstels vant 1 bouck: En doen de meting van een der drie sijden, ick neem B C, na de wijse vant 2 voorbeelt des 1 voorstels | |||||||||||
[pagina 85]
| |||||||||||
vant 2 bouck, en dien volgende, soo wort B C bevonden, neem ick, van 1267 ①: Voort om te vinden t'punt D, van t'welck de verdochte lini tot A, rechthouckich valt op B C, men sal oversien t'ghene van dies gheseyt is int 4 voorbeelt des 2 voorstels vant 1 bouck, en die metende alsvooren, wort bevonden, neem ick, van 536 ① deur den helft der selve dats 268 ①, ghemenichvuldicht de boveschreven
 1267 ①, comt 3395 roen 5 ① 6 ②: Nu gherekent na de hollantsche wijse 600 roen op de morghen, soo is dien driehouck groot 5 morgen 395 roen. 5 ① 6 ②. Maer soomen de 5 ① 6 ② deur voeten en duymen wilde uytspreken na landts ghebruyck, men siet op de roe wat daer me overcomt, en moet sijn 6 voet 8 16/25 duym. En sgelijcx sal den voortganck sijn van alle driehoucken daer de rechtlinighe platten in ghedeelt worden. Doch staet hier te mercken dat de boveschreven 6 voeten 8 16/25 duym, niet en sijn 6 viercante voeten, en 8 viercante duymen, maer tis een rijem landts lanck een roe, breet 6 voet 8 16/25 duym, want nadien de heele viercante roe lanck sijnde 12 voet, doet 144 viercante voeten, soo moet sulcken halve roe van 6 voeten, doen 72 viercante voeten: En hierom ist dat de Lantmeters onderscheyt maken tusschen rijem voeten en viercante voeten. | |||||||||||
Ander voorbeelt van sticken landts in ongheschickte cromme linien omvanghen.Om landen te meten begrepen in ongheschickte cromme linien, ghelijck inde lantmeting dickwils te vooren commen, men stelt soo veel baecken inden omtreck, tot dat de cromte tusschen twee baecken begrepen, gheen hinderlick verschil by en brengt, daer na meetmen die form als een rechtlinich plat met soo veel houcken alsser baecken staen: Als by voorbeelt inde form A B C D E F te sien is: Soo de saeck nauwer rekening vereyschte, men mochter meer baecken stellen, vereyschtse soo nauwe niet, men macher min steken: Want hier staet te bedencken, dat ettelicke dingen van cleen belanck inde lantmeting by der gisse moghen toegaen. Om t'welck by voorbeelt noch wat breeder te verclaren,  te metten sijnde een vierhouck A B C D, waer af een sijde C E F D niet recht en is, maer ghetrocken of bedocht sijnde een rechte lini C D, soo heeft die cromme lini een bocht an E binnewaert streckende, en wederom een bocht an F buytewaert streckende, | |||||||||||
[pagina 86]
| |||||||||||
doch soo dattet landt tusschen E G seer cleen sijnde, en deur gissing by t'oogh, soo groot als t'landt tusschen F H, inder voughen dat soo veelmen op d'een sijde verliest, soo veel wort op d'ander gewonnen: In sulcken ghevalle wort de rechte lini C D als voor derde sijde ghenomen des driehoucx A C D, en den selven driehouck A C D daer op ghemeten; want anders alles heel volcommelick te willen doen, t'soude dickwils meerder moeyte behouven, dant oirboir waer daer an te besteden. Doch soo t'landt tusschen de voorschreven E G, H F begrepen te groot waer, en meerder sekerheyt vereyschte dan om uytet oogh alsoo gedaen te worden, men stelt verscheyden baecken inde cromme lini alsvooren, soo veel noodich is. | |||||||||||
3 Voorbeelt vant meten der berghachtighe Landen.Laet A B C D beteyckenen den omtreck des voets of gronts van een berch: Nu want het verheven bultich vlack des selven berchs op dien grondt staende, een ander en grooter is dan t'plat begrepen in een omtre ck als A B C D, soo moet hier een ander meting toe gebruyckt worden, t'welck geschien mach met op den berch te steken verscheyden baken, welcke hier beteyckent worden mette tippelinghen daer in vervanghen, diem en soo na of verre van malcander stelt als de saeck vereyscht, te weten soo na tot dat elck bultich vlack tusschen vier palen begrepen, geen hinderlick verschil en heeft van een plat, Want alsdan elck dier vierhoucken en ander ghedeelten ghemeten ghelijck platten, en die t'samen vergaert, men heeft t'begheerde. Tbeslvyt. Wy hebben dan een stuck landts landtmetersche wijse ghemeten, na den eysch. | |||||||||||
Merckt ten 1.Wanttet lichtelick ghebeuren can, datmen int meten met groote moeyte seer nau gaslaet, dinghen die soo grooten sekerheyt niet en behouven: En weerom verkeert, datmen ettelicke dinghen niet seer nau en meet, die nochtans nauwer maet vereysschen, soo sullen wy daer af wat verclaring doen als volght. Alen valt int metens eens driehoucx opt landt, de hanghende, als neem ick de verdochte A D, int eerste voorbeelt deses voorstels, niet heel rechthouckich op de gront B C, t'is cleen verlanck, midts datse inde lini B C eyndt. Laet by voorbeelt A D de ware hanghende sijn, en A E een weynich daer buyten, doch inde lini B C: Men siet dat de langde A E vande langde A D gheen verschil van belanck en heeft, En om daer af by voorbeelt te spreken, soomen A D neemt op 100 roen, al waer D E dan van een heele roe(ick laet een voet of twee varen) soo en sal A E gheen duym langher sijn als A D, want deur des driehoucx A D E twee rechthoucksijden A D, D E, ghesocht de schoensche A E, wort bevonden seer na van 100 roen 20736/28801 duym daerom dat men dit opt lant tottet alder uyterste heel nauwe en moeylick passen wil, ten is niet noodich: Maer het metercruys, ofte het punt als E niet even inde lini B C sijnde, ghelijck dan de ghedwaelde hanghende totte ware hanghende, alsoo t'ghedwaelde vlack tottet ware, deur het 1 voorstel des 6 boucx van Euclides: Daerom moetmen toesien t'metercruys wel puntelick inde voorschreven grontlini B C te passen, t'welck met groote sekerheyt licht om doen is, deur t'behulp eens baecx als F, ghestelt inde lini B C, also van dergelijcke breeder geseyt is int 3 voorbeelt des 3 voorstels vant 1 bouc. | |||||||||||
[pagina 87]
| |||||||||||
Ten anderen soo ist int meten van seer langhe smalle landen, betamelick int meten der cortste sijde, scherper toe te sien dan int meten der langste sijde, want een voet daer ghefeylt, grooter missing int plat veroirsaeckt, dan een voet op de langhe sijde ghefeylt. Om t'welck by voorbeelt te verclaren, laet een rechtlinich stick lants sijn lanck 800 voeten, en breet alleenelick 10 voeten, het plat sal sijn van 800 viercante voeten: Ghenomen nu datter op de langste sijde, die eyghentlick van 800 voeten is, int meten een voet ghemist wierde, en gheseyt te wesen van 799 voeten, die ghemenichvuldicht deur de breede 10 voet, comt het plat 7690 voet, t'welck eyghentlick moetende sijn 8000, soo isser alleenelick 10 voeten feyls. Maer sooder op de cortste sijde die eyghentlick van 10 voeten is, int meten een voet ghemist wierde, en gheseyt te wesen van 9 voeten, die ghemenich vuldicht deur de langde 800 voet, comt plat 7200 voeten, t'welck eygentlick moetende sijn 8000 voet, soo isser 800 voet feyls: Een voet dan op de langste sijde, veroirsaeckt missing int plat alleenelick van 10 voeten, maer een voet op de cortste sijde ghemist, veroirsaeckt missing int plat van 800 voeten. En daerom ist betamelick ghelijck wy gheseyt hebben, int meten der cortste sijde van seer lang he smalle landen, scherpst toe te sien. Deur dit voorbeelt van een vierhouckighe rechthouck, is te verstaen dat men int meten des driehoucx, scherpst toe moet sien int meten der cortste lini van tween, te weten de hanghende en de grondt, want deur haer menichvulding het plat des drichoucx oock ghevonden wort. | |||||||||||
Merckt ten 2.Men mach t'begrijp des landts noch vinden sonder landt te meten, of immer deur t'meten van alleenelick een lini, treckende de form des landts tusschen seker palen begrepen op papier, na de manier des 4 voorbeelts vant 16 voorstel des 1 boucx. Die afteyckening daer na op de cleene maet ghemeten sijnde, men seghtten laetsten deur ghemeene reghel daer toe by sijn Vorstelicke Ghenade verdocht: T'viercant van een sijde, gheeft dat ghevonden plat op papier, wat t'viercant vant haer lijckstandighe sijde opt landt ghemeten, en t'gene daer uyt comt is t' begheerde. Om dit by voorbeelt wat opentlicker te verclaren. Laet A B C D E F een stuck lants sijn datmē metē moet: Hier af sy int cleen op papier gheteyckent het plat G H I K L M, ghelijc met A B C D E F, en dat deur de manier vant 16 voorstel des 1 boucx,
| |||||||||||
[pagina 88]
| |||||||||||
| |||||||||||
Tbewys.Ghelijcke platten sijn in ghedobbelde reden van haerGa naar margenoot* lijckstandighe sijden deur het 20 voorstel des 6 boucx van Euclides. Maer de twee viercanten der twee sijden A B, G H ghelijck wesende, sijn in ghedobbelde reden der selve sijden: En ghelijck tot malcander die twee viercanten, alsoo deur t'werck de twee platten, waer deur die twee platten hebben ghedobbelde reden haerder lijckstandighe sijden. En daerom t'plat G H I K L M wel ghemeten wesende, soo moetet plat A B C D E F oock wel ghemeten sijn. Tis wel waer dat sulcke wercking meerder sekerheyt heeft uyt het groot int cleen, dan uyt het cleen int groot, als hier, doch de form opt papier ten grootsten ghenomen datse bequamelick vallen mach, en int werck met goe reetschap wel nauwe toeghesien, men souder hem somwijlen me connen behelpen. |

