Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

[p. 332]

Eerst Ptolemevs byghevoughde spiegheling des Dvvaelders met stelling eens vasten Eertcloots.

1 Voorstel.

Wesende een Dvvaelder gestelt in een uytmiddelpuntichront, of anders in een inront diēs halfmiddellijn even is an dese uytmiddelpuntichronts uytmiddelpunticheytlijn, en dat inront in een middelpuntichront, even in grootheyt en loop ant uytmiddelpuntich, en des Dvvaelders loop int inront ghelijck metten loop des inronts int middelpuntichront, doch op een verkeerde sijde: Die tvvee stellinghen gheven den Dvvaelder een selve plaets.

Anghesien de stelling der Maen in een uytmiddelpuntighe wech na de manier inde voorgaende twee boucken beschreven, en volghens t'ghene inde natuer schijnt te bestaen, heur de selve plaets gheeft diese crijcht met een middelpuntich inront op de wijse deses voorstels, die Ptolemeus vercoos om sijn ghevonden tweede oneventheden bequamelicker te verclaren, en dat ick de selve oneventheden hier beschrijven wil, soo heeft my voughelick ghedocht eerst te bewijsen (ghelijck Ptolemeus oock gedaen heeft int 5 Hooftstick sijns 4 boucx) sulcke twee stellingen alsoo te overcommen, t'welck d'oirsaeck is der beschrijvinghen van dit voorstel tot dese plaets.

T'ghegheven. Laet voor eerste stelling het uytmiddelpuntichront A B C de Dwaelderwech beteyckenen, diens middelpunt D, en E den vasten Eertcloot, t'punt A sy den Dwaelder ten eersten ant verstepunt, welcke daer na ghedaen hebbe een loop van A tot B, dats oock den houck A D B.

Laet nu voor tweede stelling op E als middelpunt, beschreven worden het middelpuntichront F G H, even an A B C, en op F mette halfmiddellijn F A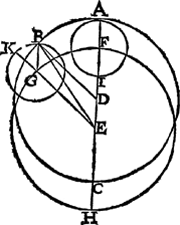



(die even moet vallen met E D) het inront A I, diēs verstepunt A, daer na sy het inronts A I middelpunt F ghecommen an G, sulcx dat sijn loop F G, of houck F E G, even sy anden loop der eerster stelling A D B, en het inront beschrevē opt middelpunt G, sy B K, waer in van E deur G ghetrocken sy E G K, soo dat K des inronts verstepunt beteyckent, van t'welck den Dwaelder daerentusschen gheloopen heb na B (tegen d'eerste loop van F na G) een booch ghelijck met F G, of anders geseyt sulcx dat den houck begrepen tusschen de lini K G, en de lini van G na B tot inden omtreck des inronts, welcke lini men crijcht treckende van G een evewijdeghe met E F. T'begheerde. Wy moeten bewijsen dat dē Dwaelder in dese tweede stelling int selve punt B valt,

[p. 333]

daer hy in d'eerste stelling was. T'bewys. Anghesien D B, E G twee even en evewijdeghe halfmiddellijnen sijn, tusschen welcke E D comt, en dat de lini van G na B even en evewijdeghe met E D is, deur t'gegeven, soo moet de form begrepen tusschen de vier linien B D, D E, E G, en de lini van G na B evewijdeghe met E D, dats de form B D E G een^* evewijdich vierhouck sijn, en vervolghens t'punt B, te weten den Dwaelder, is soo wel uyterste der lini G B int inront K B na d'eerste stelling, als uyterste der lini D B int uytmiddelpuntichront A B na d'eerste stelling, en vervolgens den Dwaelder gesien vanden Eertcloot E an B int inront sonder uytmiddelpuntichront, of an B int uytmiddelpuntichront sonder inront, het is hem al tot een selve plaets ghesien. t'beslvyt. Wesende dan een Dwaelder ghestelt &c.

* Parallelogrammum.

Merckt.

Hoewel dese manier de Manens ware plaets oock anwijst, soo schijnt nochtans datmense niet en behoort te ghebruycken, eensdeels om dat haer duyster plecken die altijt na den Eertcloot ghekeert staen, betuyghen datse in geen inront en draeyt, ten anderen om datmen met meer haspeling twee ronden stelt daert deur een can ghedaen worden: En daerom is by Ptolemeus int stellen des Sonloops, en by Copernicus des Eertclootloops, met reden het uytmiddelpuntichront vercoren, t'welck Ptolemeus int stellen des Maenloops oock soude genomen hebben, ten waer dat, soo hy seght int 5 Hooftstick sijns 4 boucx, de stelling des inronts hem bequamer viel om daer deur sijn voornemen der navolghende tweede oneventheden te verclaren.

2 Voorstel.

Te verclaren d'oirsaeck die Ptolemeus bevveeghde tottet ondersoucken van sijn tvveede oneventheden der Maen, metsgaders de ghedaente van sijn byghevoughde spiegheling int ghemeen.

Alsoo Ptolemeus gheduerlick en seer ernstelick gaslouch de Manens schijnbaer duysteraerlangden, heeft dickwils bevonden die te verschillen mette regelen hier vooren beschreven, en hem van sijn voorganghers naghelaten, welck hy d'eerste oneventheden noemt, sulcx dat hy daer af na sijn goetduncken verbetering ghedaen heeft, ende een tweede onevenheyt daer by vervought. Om hier af sijn meyning te verclaren ick segh aldus: Hy heeft bevonden dat haer uyterste voorofachtringhen in saminghen en tegestanden der Son altijt waren van 5 tr. ghelijck int 30 voorstel des 2 boucx d'eerste oneventheyt mebrengt, maer daer buyten vielder verandering, en dat ten grootsten in vierdeschijn, alwaerse conde vallen van 7 tr. 40 ①, dats 2 tr. 40 ① meer als d'ander, en soo veel mochte int oirdeel der toecommende Maenplaetsen feyl vallen, alsmē int rekenen alleenelick sach na d'eerste oneventheyt. Om nu te verclaren d'oirsaeck die hy stelt van dit verschil, soo is voor al te weten dat hy totte bequaemste uytlegging sijns voornemens (ghelijck hy seght int 5 Hooftstick sijns 4 boucx) eerstelick ghenomen heeft de stelling der Maen niet in een uytmiddelpuntighe wech, ghelijck wy die hier vooren beschreven hebben, maer in een^* middelpuntichinront, dat is te loopen in een inront, en t'selve in een middelpuntighe wech, na de manier beschreven int 1 voorstel deses Anhangs.

* Concentrepiryclo.

[p. 334]

Laet tot breeder verclaring van desen A B C een middelpuntighe inrontwech sijn, diens middelpunt D, inront E B F, wiens middelpunt A, grootste^*



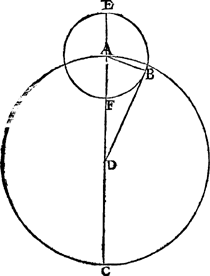voorofachtring dē houck A D B van 5 tr. ghelijckse in samingen en teghestanden bevonden wort. Nu by aldien de hemelē des Maenloops alsoo waren, t'is kennelick dat de grootste voorofachtring overal de selve soude moeten wesen als bovē van 5 tr. Maer want dit strijt tegen de boveschreven ervaringhen, soo heeft Ptolemeus d'oirsaeck van sulcke verscheydenheyt ghestelt dusdanich te wesen: Anghesien des inronts halve grijphouck als A D B, in vierdeschijn bevonden wiert van 7 tr. 40 ①, dats 2 tr. 40 ① meer, so moetet inront ten tijde van vierdeschijn den Eertcloot altijt soo veel naerder sijn dan in teghestant, dat dien halvē grijphouck dan van soo veel vermeerdert, sulcx dat de Maen gaet in een inront, loopende t'selve inront niet in een middelpuntige wech als inde voorgaende form, maer in een uytmiddelpuntighe ghelijck de navolghende tweede anwijst, alwaer A B C andermael den inrontwech beteyckent, diens middelpunt D, inront E B F G, en H een uytmiddelpuntichpunt, dats den Eertcloot, van waer ghetrocken is de lini H B, gherakende het inront an B tewijle het daer met sijn middelpunt an des wechs verstepunt is, ghelijck in samingen en teghenstanden altijt gebeurt,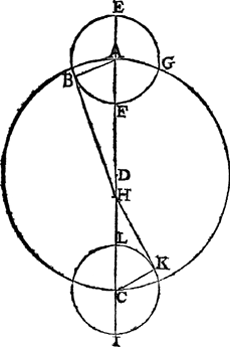



daer af d'oirsaeck volghens sijn stelling ten einde deses voorstels sal beschreven worden, en alsdan doet den houck A H B de voorschreven 5 tr. Voort sy I K L andermael het inront, maer gecommen wesende ant naestepunt C, daert volgende Ptolemeus stelling altijt in vierdeschijn is, en getrocken H K het inront gerakende an K, soo doet den houck C H K de boveschreven 7 tr. 40 ①.

Hier me was wel voorcommē de ongeregeltheyt diemen vande Maen bevant in saming tegestant en vierdeschijn, maer daer buyten en hielt de reghel gheen plaets, als wanneer des inronts middelpunt was int eerste halfront tusschē A en C, of int tweede halfront tusschen C en A: Om t'welck deur

* Prostapheresis.

[p. 335]

een eyghentlicke form te verclaren, laet in dese derde A B C den inrontwech beteyckenen, diens middelpunt D, Eertcloot E, en op B als middelpunt sy beschrevē



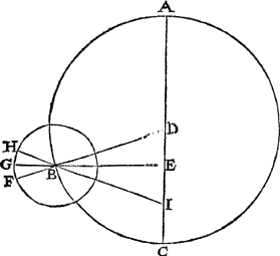het inront F G, int eerste halfront A C, daer na sijn getrockē de twee rechte D B F, E B G, sulcx dat F tot die plaets is t'verstepunt van D, en G van E. Dit soo wesende, en behoorende de Maen volgens t'voorgaende ghestelde, uyt E gesien te worden by voorbeelt an het verstepunt G, sy en wiert dadelick daer niet bevonden, maer, neem ick, an H, daerom heeft hy ghetrocken een rechte lini van H deur B tot I, inde halfmiddellijn D C, en na rekeninghen die hy deur ghetalen daer op maeckte (welckebeschreven sullen worden int 4 voorstel) heeft bevonden E I even te vallen an E D. Dit punt I noemde Ptolemeus het^* onevenheytspunt, soodanich wesende dat sijn verstepunt als H, t'ghene is daermen altijt de Manens inrontloop moet af beginnen te rekenen, en niet van t'verstepunt F, t'welck doende men bevint soo Ptolemeus seght deur rekening ghemaeckt op sulcke stelling, de schijnbaer duysteraerlangde der Maen altijt tot haer behoorlicke plaets, midts welverstaende datmen toelate dese drie saken: Ten eersten des inronts middelpunt B oirdentlick te drayen gesien wesende uyt des Eertcloots middelpunt E, waer uyt volght dattet onoirdentlick moet drayen ghesien wesende uyt des wechs middelpunt D, of anders gheseyt dattet in sijn wech d'een tijt rasscher als d'ander moet loopen: Ten tweeden de Maen int inront oirdentlick te drayen ghesien wesende uyt het onevenheyts punt I, waer uyt volght datse onoirdentlick moet drayen ghesien wesende uyt des wechs middelpunt D, oft anders gheseyt datse in haer inront d'een tijt rasscher als d'ander moet loopen: Ten derden des inronts middelpunt als B in elck middelmaenschijn tweemael om te drayen, sulcx dattet in middelsaming en middelteghestant altijt is an t'verstepunt A, en in middelvierdeschijn altijt an t'naestepunt. Maer hoe dit roersel gheseyt wort toe te gaen wort aldus verclaert.

Den inrontwech met haer inront is ghedregen in een hemel diese noemen^* verstepuntdragher des uytmiddelpuntichronts der Maen, welcke beteyckent wort met een plat begrepen tusschen twee ronden, t'een, te weten het binnenste, beschreven opt middelpunt des inrontwechs deur het inronts verstepunt, t'ander daer boven beschreven op des Eertcloots middelpunt: En draeyt teghen de Sonnens eyghenloop, in sulcker voughen dat soo verre des inronts middelpunt vande Middelson ter eender sijde schijnbaerlick afwijckt, soo verre doetse des inrontwechs verstepunt op de selve tijt ter ander sijde schijnbaerlick af wijcken, daer mede sy in alle middelsaminghen en middelteghestanden het inronts middelpunt ten versten van des Eertcloots middelpunt streckt: Maer in alle vierdesicht ten naesten: En moet hier me des inronts middelpunt in elck middelmaenschijn sijn wechs verstepunt tweemael ontmoeten.

Laet tot breeder verclaring vant boveschreven in dese volgende 4 form A B

* Ptol Punctū inaequalitatis. Purbachius Punctum diametraliter oppositum centro excentrici.

* Deferens augem seu apogaeum excentrici Lunae.

[p. 336]

een plat sijn begrepen tusschen twee ronden C D, E F, het middelpunt van C D is G, opt welck beschrevē is den inrontwech H I. Het middelpunt van E F



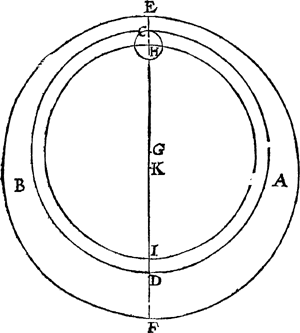is K: Voort is C D den inrontwechdragher, en draeyt (welverstaende metten heelen platten rijnck A B) teghen t'vervolgh der trappen, dat is van C na A: Hier me stiert desen inrondtwechsdrager het inront soo, dat sijn middelpunt H in alle middelsamingen en middeltegestanden ten versten van des Eertcloots middelpunt K is, maer in alle middelvierdeschijn ten naestē: T'welck noch claerder valt alsmen dese rondē van verscheydē stucken op malcander beweeglick maeckt, alwaermen noch siet dattet punt K vast blijvende, soo beschrijft het punt G een rondt daer om. T'beslvyt. Wy hebben dan verclaert d'oirsaeck die Ptolemeus beweeghde tottet ondersoucken van sijn tweede oneventheden der Maen, metsgaders de ghedaente van sijn byghevoughde spiegheling int ghemeen, na den eysch.

Merckt.

De ghedaente van Ptolemeus spiegheling tot hier toe beschreven sijnde sonder ghetalen, wy sullen nu commen tottet vinden dier getalen, daer af beschrijvende het volghende 3, 4 en 5 voorstel.

3 Voorstel.

Te vinden de halfmiddellijn vanden inrontvvech der Maen, de uytmiddelpunticheytlijn, mette Manens meeste en minste verheden, in sulcke deelen alsser de lini vanden Eertcloot tot des inrontvvechs verstepunt 60 doet, deur vvercking ghegront op stelling van Ptolemeus bygevoughde spiegheling.

T'ghegheven. Laet inde 2 form des 2 voorstels den houck A H B doē 5 tr. en C H K 7 tr. 40 ①, met al de rest van sulcke beteyckening als daer geseyt is. T'begheerde. Wy moeten vinden des inrontwechs halfmiddellijn A D, de uytmiddelpunticheytlijn D H, mette Manens meeste verheyt H E, en minste verheyt H L, in sulcke deelen alsser de lini H A vanden Eertloot H tot des wechs verstepunt A, 60 doet.

[p. 337]

t'Werck.

De driehouck H K C heeft drie bekende palen, te weten C K halfmiddellijn des inronts doende deur Ptolemeus 5 voorstel sijns 4 boucx 5 deelen 13 ①, den houck H K C recht, en den houck C H K 7 tr. 40 ① deur t'ghegheven: Hier me ghesocht de sijde H C, wort bevonden deur het 4 voorstel der platte driehoucken van 39 deelen 6 ①, doch latet sijn na Ptolemeus segghen	39 deel 22 ①.
Daer toe vergaert A H 60 deelen deur t'ghegheven, comt voor de heele middellijn A C	99 deel 22 ①.
Diens helft voor D C begeerde halfmiddellijn des inrontwechs	49 deel 41 ①.
Daer af getrockē H C 39 deel 22 ① eerste in d'oirden, blijft voor begheerde uytmiddelpunticheytlijn D H	10 deel 19 ①.
Tot A H 60 deelen deur t'ghegheven, vergaert des inronts halfmiddellijn A E 5 deel 13 ①, comt voor H E begheerde meeste verheyt	65 deel 13 ①.
En van H C 39 deel 22 ① eerste in d'oirden, ghetrocken des inronts halfmiddellijn C L 5 deel 13 ①, blijft voor H L begheerde minste verheyt	34 deel 9 ①.

Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wy hebben dan gevonden de halfmiddellijn vanden inrontwech der Maen, de uytmiddelpunticheytlijn, mette manens meeste en minste verheden, in sulcke deelen alsser de lini vanden Eertcloot tot des inrontwechs verstepunt 60 doet, deur wisconstighe wercking ghegront op stelling van Ptolemeus byghevoughde spiegheling, na den eysch.

Merckt.

De reden der meeste verheyt totte minste, volghens dese bygevoughde spiegeling van Ptolemeus, is als van H E 65 deelen 13 ① vijfde in d'oirden, tot H L 34 deelen 9 ① seste in doirden, welcke reden inde verandering der Manens grijphoucken niet blijckende, soo ist seker, ghelijck wy vooren geseyt hebben, die reden der verheden int wesen soo niet te bestaen, en de spiegheling der eerste oneventheden volghensde beschrijving van Ptolemeus int 6 Hooftstick sijns 4 boucx, hier in vaster te gaen, te weten van 65 deelen 13 ①, tot 54 deelē 47 ①.

4 Voorstel.

Te vinden de lini vandē Eertcloot tottet onevenheyts punt, in sulcke deelen alsser de lini vanden Eertcloot tottet verstepunt des inrontvvechs der Maen 60 doet, deur vvercking gegront op stelling van Ptolemeus bygevoughde spiegheling.

T'gegeven. Ptolemeus heeft int 5 Hooftstick sijns 5 boucx genomen een dadelicke ervaring der Maenplaets deur Hypparchus gagheslaghen en hem nagelaten, welcke was buytē middelsaming, middeltegestant of middelvierdesicht, anders gheseyt wesende des inronts middelpunt buyten sijn wechs verstepunt

of naestepunt, te weten doen de booch vande Middelson totte Middelmaen, dats de middelmaenwinst, dede

45 tr. 15.

[p. 338]

En bevant alsdoen de Manens middelloop int inront van	333 tr. 12.
Welcke plaets alsmen op des inronts verstepunt vanden Eertcloot ghesien rekening maeckt, voordering geeft (ghelijck int volgende werck verclaert sal worden) van	2 tr. 32.
Maer de schijnbaer booch vande ware Son totte ware Maen deur Hypparchus dadelick ghemeten, wiert alleenelick bevonden met voordering van	1 tr. 26.

Deur welcke verscheydenheyt Ptolemeus quam tottet ondersoucken en berekenen der langde vande lini tusschē den Eertcloot en het onevenheytspunt daer ande 3 form des 2 voorstels int ghemeen af gheseyt is: De selve ondersoucking en berekening sullen wy verclaren in twee deelen, t'eerste vant vinden der boveschreven 2 tr. 32 ① derde in d'oirden: Het tweede deel, dat in die plaets ghenomen sal worden 1 tr. 26 ① vierde in d'oirden, waer deur men eyntlick vinden sal de lini tusschen den Eertcloot en het onevenheytspunt te doen 10 deelen 19 ①, even ande uytmiddelpunticheytlijn, doende oock soo veel deur het 3 voorstel deses Anhangs.

T'bereytsel vant eerste deel.

Laet A B C den inrontwech sijn, diens middelpunt D, uytmiddelpuntichpunt of Eertcloot E, van welcke ghetrocken sy de lini E B, soo dat den houck A E B doe 90 tr. 30 ① wesende het dobbel der Maenwinst 45 tr. 15 ① int geghevens eerste des oirdens: De reden waerom hier dit dobbel ghenomen wort, is dat des inronts middelpunt van d'een middelsaming tot d'ander het verstepunt tweemael ontmoet deur de verclaring van dien ghedaen ande 4 form des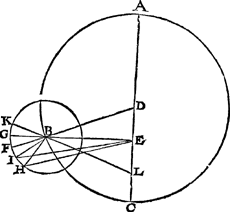



2 voorstels. Op het punt B als middelpunt, sy beschrevē het inront F G, en getrocken van D deur B de lini D B F, sulcx dat F des inronts verstepunt is vā D, en wort by Purbachius^* holheyts punt ghenoemt, om dattet beschrijft de binnenste hollicheyt des inrontwechdragers. Daer na sy getrocken van E deur B de rechte lini E B G, sulcx dat G des inronts verstepunt is van den Eertcloot E: Laet nu voort t'punt H de Maen beteyckenen, diens middelloop int inront dede deur t'gheghevens tweede des oirdens 333 tr. 12 ①, de selve tel ick van t'verstepunt G teghen t'vervolgh der trappen tot H, en trecke H E.

* Punctum concavitatis.

T'begheerde vant eerste deel.

Wy moeten vinden den houck der voordering B E H.

T'vverck vant eerste deel.

De driehouck D E B heeft drie bekende palen, te weten den houck D E B 90 tr. 30 ① deur t'bereytsel, de uytmiddelpunticheytlijn D E 10 deelen 19 ① deur het 3 voorstel, D B halfmiddellijn des inrontwechs 49 deelen 41 ① deur

[p. 339]

t'selve 3 voorstel: Hier me ghesocht de sijde E B, wort bevonden deur het 5 voorstel der platte driehoucken van

48 deel 31 ①.

De driehouck B E H heeft drie bekende palen, te weten de sijde E B 48 deelen 31 ① eerste in d'oirden, B H 5 deelen 15 ① deur het 5 voorstel des 5 boucx van Ptolemeus (t'is wel waer dat int voorgaē. de 3 voorstel ghenomen wiert 5 deel 13 ①, dan wy volghen in elcke plaets Ptolemeus stelling) en den houck H B E 153 tr. 12 ① (want angesien de booch G H doet deur t'gegeven 333 tr. 12 ①, ick treck die vant heel rondt, en blijft voor de booch H G ofte houck H B G 26 tr. 48 ①, die ghetrocken van 180 tr. blijft voor den houck I B E als vooren 153 tr. 12 ①) Hier me ghesocht den begeerden houck B E H, wort bevonden deur het 6 voorstel der plat te driehoucken van 2 tr. 33 ①, latet sijn na Ptolemeus seggen

2 tr. 32.

T'bereytsel vant tvveede deel.

Nu dan desen houck B E H aldus bevonden sijnde van 2 tr. 32 ①, die maer en behoort te wesen ghelijck vooren verclaert is van 1 tr. 26 ①, soo heeft Ptolemeus aldus geseyt: Nadien den houck B E H te groot is, soo en moet de Maen dadelick niet wesen an H, maer meer na G, latet sijn an I, en ghetrocken wesende de lini E I, soo doe den houck B E I de voorschrevē 1 tr. 26 ①. Dit soo sijnde G en mach het middelverstepunt niet blijven, daermen den loop der Maen int inront af moet beginnen te rekenen, ghelijck te vooren ghedaen is, maer sulck verstepunt moet soo verre over G commē, als van H tot I, latet sijn an K, sulcx dat G K even is an H I, daerom ghelijck eerst van G tot H waren 333 tr. 12 ①, alsoo sullē nu van K tot I oock sijn de selve 333 tr. 12 ①: Twelck so wesende, ick treck de rechte K B voorwaert tot inde middellijn A C, vallēde an L.

T'begheerde vant tvveede deel.

Wy moeten nu vinden de lini E L.

T'vverck vant tvveede deel.

De driehouck E B I heeft drie bekende palen, te weten den houck B E I 1 tr. 26 ① deur het bereytsel vant tweede deel, de sijde E B 48 deelen 31 ① deur het eerste des oirdens van t'werck des eerstē deels, en B I des inronts halfmiddellijn 5 deelen 15 ①: Hier me ghesocht den houck I B E, wort bevonden deur het 5 voorstel der platte driehoucken van	165 tr. 13.
Die getrocken van 180 tr. blijft voor den houck I B G of booch I G	14 tr. 47.
De selve getrocken van I K, welcke als rontvervulling van 333 tr. 12 ① doet	26 tr. 48.
Blijft voor de booch G K, of houck G B K, dats oock voor dē houck E B L	12 tr. 1.
De driehouck B E L heeft drie bekende palen, te weten den houck B E L 89 tr. 30 ①, als halfrontschil des houcx B E A, doēde deur t'bereytsel van t'eerste deel 90 tr. 30 ①, voort den houck E B L 12 tr. 1 ① vierde in d'oirden des wercx van dit tweede deel, en de sijde B E 48 deelen 31 ① eerste des oirdens van t'werck des eerstē deels: Hier me ghesocht de begheerde sijde E L, wort bevonden deur het 4 voorstel der platte driehoucken van	10 deel 19 ①.

[p. 340]

Welck ghetal even valt mettet ghetal der uytmiddelpunticheytlijn D E, die int 3 voorstel oock soo veel berekent wiert: En seght Ptolemeus derghelijcke oock te ghebeuren tot alle plaetsen daer des inronts middelpunt in sijn wech mocht wesen, sulcx dat hy daer uyt besluyt een punt als K altijt voor middelpunt te moeten ghenomen worden, daer af men de Manens inrontloop moet beginnen te tellen. T'beslvyt. Wy hebben dan ghevonden de lini vanden Eertcloot tottet evenheyts punt, in sulcke deelen alsser de lini vanden Eertcloot tottet verstepunt vanden inrontwech der maen 60 doet, deur wercking ghegront op stelling van Ptolemeus byghevoughde spiegheling, na den eysch.

5 Voorstel.

Te vinden op een ghegeven tijt de Manens voorofachtring, deur vvercking ghegront op stelling van Ptolemeus byghevoughde spiegheling.

Het sy een tijt op welcke de Manens inrontlangde bevonden is van 333 tr. 12 ①, en de middelmaenwinst 45 tr. 15 ①. T'begheerde. Wy moeten de Manens voorofachtring vindē, gegront op stelling vā Ptolemeus bygevoughde spiegeling. T'bereytsel. Laet A B C dē inrontwech sijn, diens middelpunt D, uytmiddelpuntichpunt of Eertcloot E, van welcke getrocken sy de lini E B, so dat dē houck A E B doe 90 tr. 30 ①, wesende het dobbel der Maenwinst 45 tr. 15 ① des ghegevens: De reden waerom dit hier dobbel genomen wort, is dat des inronts middelpunt van d'eē middelsaming tot d'ander t'verstepunt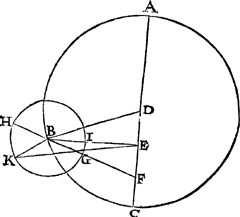



tweemael ontmoet, deur de verclaring van dien gedaen inde 4 form des 2 voorstels deses Anhang, en F is het onevēheyts punt: Voort sy op B als middelpunt beschreven het inront G H I, snyende de lini E B in I, daer na getrockē de rechte F G B H, snyende het inront in G en H, soo beteyckent G het middelnaestepunt, H t'middelverstepunt: En t'punt K sy de Maen, so dat de booch H I G K doe de ghegeven 333 tr. 12 ①, ten laetsten treck ick de twee linien E K, B K, sulcx dat den houck B E K de Manens^* voordering beteyckent. T'begheerde. Wy moeten den houck B E K vinden.

* Additionem.

T'werck.

De driehouck D E B heeft drie bekende palen, te weten den houck D E B 90 tr. 30 ① deur t'ghegheven, de uytmiddelpunticheytlijn D E 10 deel 19 ① deur het 3 voorstel deses Anhangs, D B halfmiddellijn des inrontwechs 49 deelen 41 ① deur t'selve 3 voorstel: Hier me gesocht de sijde E B, wort bevondē deur het 5 voorstel der platte driehoucken van

48 deel 31 ①.

[p. 341]

De driehouck E B F heeft drie bekende palen, te weten E B 48 deel 31 ① eerste in d'oirden, E F 10 deel 19 ① deur het 3 voorstel deses Anhangs, en dē houck B E F 89 tr. 30 ①, als halfrontschil des gegeven houcx D E B 90 tr. 30 ①: Hier me ghesocht den houck E B F, wort bevonden deur het 6 voorstel der platte driehoucken van	12 tr. 1.
Vande booch H I G K doende deur t'bereytsel 333 tr. 12 ①, getrocken de booch H G 180 tr. blijft de booch G K, of houck G B K	153 tr. 12.
Daer toe den houck E B F 12 tr. 1 ① tweede in d'oirden, comt voor den houck E B K	165 tr. 13.
De driehouck E B K heeft drie bekende palen, te weten den houck E B K 165 tr. 13 ① vierde in d'oirdē, E B 48 deel 31 ① eerste in d'oirden, en des inronts halfmiddellijn B K 5 deelen 15 ①: Hier me ghesocht den begheerden houck der voordering B E K, wort bevonden deur het 6 voorstel der platte driehoucken van 1 tr. 25 ①, latet sijn	1 tr. 26.

T'beslvyt. Wy hebben dan ghevonden op een ghegeven tijt de Manens voorofachtring, deur wercking gegront op stelling van Ptolemeus bygevoughde spiegheling, na den eysch.

Vervolgh.

Deur dit vinden der voorofachtring is openbaer hoe bekent sal worden de Manens schijnbaer duysteraerlangde op een ghegeven tijt, want totte Middelmanens duysteraerlangde vervought de voorofachtring men heeft t'begeerde. Merckt noch dat deur Ptolemeus en anderen verscheyden tafels ghemaect sijn, om met lichticheyt te vinden t'ghene hier boven deur rekeninghen der platte driehoucken met meerder moeyte ghevonden wort, welcke tafels wy hier onbeschreven laten, als totte kennis vande gedaente deser tweede oneventheden of byghevoughde spiegheling der Maen van Ptolemeus niet voorderlick. Dit dan t'ghene sijnde t'welck wy vande selve tweede oneventheden voorghenomen hadden te segghen, sullen nu commen tot sijn onbekende oneventheden van d'ander Dwaelders.

6 Voorstel.

Te verclaren de somme van Ptolemeus byghevoughde spiegheling des langdeloops van Saturnus, Iupiter, Mars en Venus.

Anghemerckt wy deser Dwaelders eenvoudighe loop ghelijckse Ptolemeus ter handt quam voor bekent nemen, als int eerste en tweede bouck beschreven sijnde, soo sal t'verclaren van sijn by vouging hier cort en licht vallen.

Voor al is te weten dat hy deser vier Dwaelders schijnbaer duysteraerlangden, in saminghen en teghestanden der Middelson als des inronts middelpunt was an sijn wechs verstepunt of naestepunt, altijt bevant ghelijck me brocht de rekening des eenvoudighen loops soose hem eerst ter handt ghecommen was, want hy in yder Dwaelder op sulcke stelling vant en berekende de langde der uytmiddelpunticheytlijn, en des inronts halfmiddellijn, maer daer buyten vielder verandering.

[p. 342]

Om dan totte saecke te commen laet A B C D den inrontswech sijn, diens middelpunt E, verstepunt A, uytmiddelpuntichpunt of den Eertcloot F, des inronts middelpunt B, waer op beschreven is het inront G H I K, daer na van E en F deur B ghetrocken sijnde de twee rechte linien E L, F K, sy snyen het inront in H en I, soo dat H is t'naestepunt, K t'verstepunt, I middelnaestepunt, L middelverstepunt: Voort neem ick dat den Dwaelder na uytwijsen der rekening des tweeden boucx, dat is volghens den eenvoudigen loop soose Ptolemeus eerst



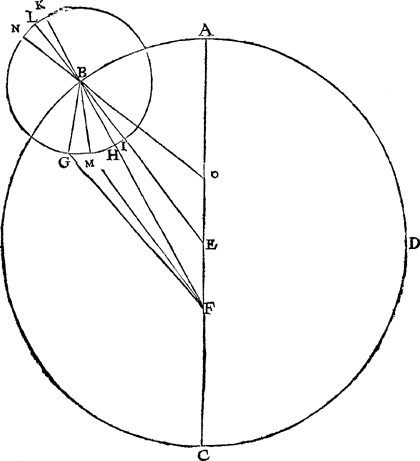ter handt quam, moest sijn an G, soo dat sijn inronts middellangde L G doet 150 tr. en sijn schijnbaer verheyt van t'verstepunt A ghesien uyt den Eertcloot F, soude hebben moeten sijn den houck A F G: Maer hy bevant sulckē houck metter daet cleender, als neem ick A F M, inder voughen dat den Dwaelder int inront wesentlick was an M, en niet volghens de rekening an G.

Hier uyt heeft hyaldus gedocht, nadien vanden Dwaelder tottet middelverstepunt moet wesen 150 tr. gelijck eerst gestelt wiert de booch L G, en dat den Dwaelder int inront soo veel voorder is dan G, als van G tot M, soo moet het middelverstepunt oock even soo veel voorder sijn van L, t'welck sy an N, en hier me is N M van 150 tr. ghelijck L G.

Nu dan N ghenomen sijnde als voor middelverstepunt, van daermen des Dwaelders middelloop begint te tellen, hy heeft van N deur B ghetrocken een rechte lini snyende de middellijn A C in O: Heeft daer na ghesocht hoe lanck de lini E O viel, en want alle noodige palen hem daer toe bekent waren, heeftse even bevonden met E F, en dat niet alleen in dit voorbeelt, maer in allen ande-

[p. 343]

ren tot wat plaets het inronts middelpunt in sijn wech, en den Dwaelder int inront wesen mochten: Sulcx dat hy hier af willende sijn spiegheling beschrijven, heeft O genoemt het^* onevenheyts punt, an t'welck genomen sijnde het oogh gestelt te wesen, men siet het inronts middelpunt B inden inrontswech A B C D, en den Dwaelder an G oirdentlick draeyen, waer uyt volght de voornomde twee punten B en M onoirdentlick te draeyen ghesien uyt des inrontwechs middelpunt E, of anders geseyt dattet inronts middelpunt B in sijn wech, en den Dwaelder M int inront, d'een tijt rasscher als d'ander moetē loopen, teghen de ghemeene natuerlicke oirden, en volghens sulcke stelling ghevonden wesende der Dwaelders voorofachtringen, en schijnbaer duysteraerlangde, soo bestaet hier in Ptolemeus voorschreven vondt en spiegeling die hy vermengt heeft by den loop hem van sijn voorgangers ter handt gecommen. T'beslvyt. Wy hebbē dan verclaert de somme van Ptolemeus bygevoughde spiegheling des langdeloops van Saturnus, Iupiter, Mars en Venus, na den eysch.

* Punctum inaequalitatis. Purbachius centrum aequantis.

7 Voorstel.

Te verclaren de somme van Ptolemeus byghevoughde spiegheling des langdeloops van Mercurius.

Alsoo Ptolemeus dickwils gaslouch Mercurius plaetsen, en daer benevens noch acht nam op de gaslaginghen sijnder voorganghers, heeft bevonden dat hy in elcken keer tweemael ten naesten by den Eertcloot quam (ghelijck de Maen, die in elck Maenschijn na sijn segghen tweemael ten naesten comt) het welcke t'elckens ghebeurde doen sijn inronts middelpunt schijnbaerlick was 120 tr. over weder sijden vant schijnbaer verstepunt, dat hy bevant in des duysteraers 190 tr. D'oirsaeck hier af stelde hy te wesen dattet inronts middelpunt totte twee voorschreven plaetsen altijt den Eertcloot ten naesten was. Dit int ghemeen gheseyt sijnde, wy sullen nu totte besonder verclaring van sijn meyning commen.

Laet in de volgende eerste form A B C D dē wech des inronts sijn, diēs middelpunt is E, verstepunt A, uytmiddelpunticheytpunt of den Eertcloot F, des inronts middelpunt A, waer op beschrevē is het inront G H I K, diens verstepunt G, naestepunt I, voort sy Mercurius ant verstepunt G, en dit alles ghenomen na den eenvoudigen loop soose Ptolemeus ter handt quam, en beschreven is int 2 bouck, met welcke ghestalt Ptolemeus gheen feyl en vandt, want hier me heeft hy int 8 Hooftstick sijns 9 boucx ghesocht de reden der uytmiddelpunticheytlijn, en des inronts halfmiddellijn tot des inrontwechs halfmiddellijn: Maer Mercurius buyten des inronts verstepunt of naestepunt wesende, of des inronts middelpunt buyten sijn wechs verstepunt of naestepunt, soo vielder verschil, t'welck Ptolemeus na verscheyden tastinghen en ondersouckinghen int 9 Hooftstick sijns 9 boucx verbeterde, en in form van spiegheling brocht als volght: Hy heeft opt middelpunt E des wechs in dese gestalt sijnde, beschreven een rondeken L M N, snyende A C in L en N, wesende des selfden rondekens halfmiddellijn E N den helft der uytmiddelpunticheytlijn E F, hier in heeft hy t'punt L anghesien als voor middelpunt des inrontwechs, hoe wel het in dees form eyghentlick E is, en t'selve middelpunt L gheseyt te draeyen int rondeken van L tegē het vervolgh der trappē na M, doende daer in

[p. 344]

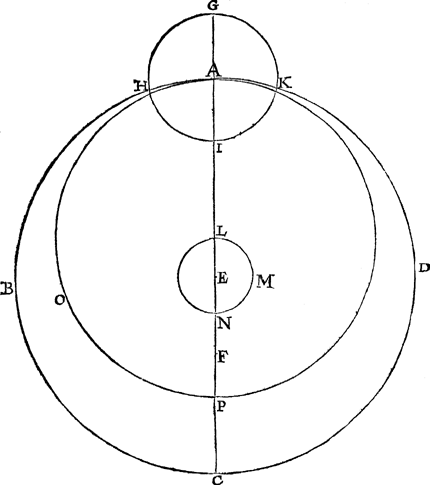een keer, op den selven tijt dattet inronts middelpunt in sijn wech een keer doet, op d'ander sijde na t'vervolgh der trappen, dats van A na B, en alsoo met hem draghende den heelen inrontwech.

Maer anghesien A L hier genomen is voor wechs halfmiddellijn deser bygevoughde spiegeling van Ptolemeus, soo moet des selven wechs omtreck cleender sijn dan A B C D na stelling des eenvoudighen loops soose Ptolemeus ter handt quam, daerom laet ons op L als middelpunt beschrijven den inrontwech der spiegheling van Ptolemeus A O P: En hoe wel die nu cleender is dan d'eerste, soo blijft hier nochtans de verheyt vandē Eertcloot F tot A de selve, en vervolghens soo blijft oock des inronts grijphouck de selve: En als des wechs middelpunt L ghecommen sal sijn van L over M tot N, soo sal volghens dit gestelde des inronts middelpunt A ghecommen sijn over d'ander sijde an C, en sal alsdan de verheyt vanden Eertcloot F, tot des inronts middelpunt, en vervolghens des inronts grijphouck oock de selve sijn als na de eenvoudige loop soose Ptolemeus ter handt quam: Sulcx dat dese spiegeling van Ptolemeus geen verandering en gheeft int voorschreven soucken der reden vande uytmiddelpunticheytlijn, en inronts halfmiddellijn, totte linitusschen den Eertcloot en t'verstepunt.

Dese ghedaente aldus verclaert sijnde, wesende des inronts middelpunt an

[p. 345]

t'punt A, verst vanden Eertcloot F, en oock an sijn teghenoverpunt C, soo sullen wy nu noch voorbeelt stellen wesende des inronts middelpunt tot een ander plaets, als neem ick 60 tr. middelloops vant verstepunt A, en Mercurius met 100 tr. inrontlangde. Laet tot dien eynde in dese tweede form de lini A B strecken deur t'verstepunt A (t'welck Ptolemeus vandt onder des duysteraers 190 tr.) en sijn teghenoverpunt sy B, den Eertcloot C, des rondekens middelpunt D, waer op beschreven is t'selve rondeken F G E H (in plaets vant rondeken



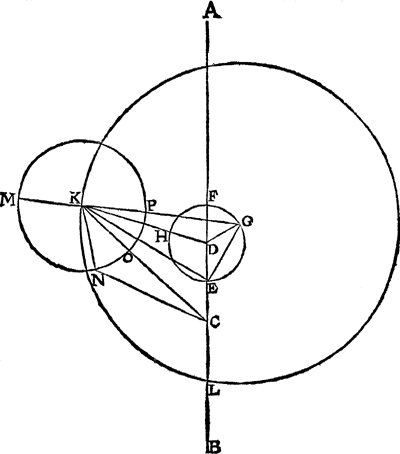L M N der eerste form) wesende des selfden verstepunt F, naestepunt E, en halfmiddellijn D E even met E C: Voort sy gheteyckent t'punt G, soo dat de booch van F tot G teghen t'vervolgh der trappen doe de ghegeven 60 tr. en op G als middelpunt sy beschreven den inrontwech I K L, daer na treck ick D K, soo dat den houck A D K, even is met F D G 60 tr. welverstaende dat van I tot K is na t'vervolgh der trappen, ghelijckt van F tot G daer tegen is, alles soo de boveschreven stelling vereyscht: Ick beschrijf daer na op K als middelpunt het inront M N O P, treck voort van G deur K de lini G K M, so dat M des inronts middelverstepunt beteyckent, ick neem daer na N te sijn Mercurius plaets, en de booch M N te doen de ghegheven 100 tr. en treck K N, N C, C K, snyende het inront in O, daer na E K, E G, D K, D G, en neem het inront van G K gesneen te worden in Pals middelnaestepunt.

Merckt nu noch dat Ptolemeus des inronts middelpunt K neemt oirdentlick te draeyen gesien uyt E, en daerom loopet onoirdentlick gesien uyt sijn wechs

[p. 346]

middelpunt G, dat is inde selve wech d'een tijt rasscher als d'a nder. Maer he oogh ghestelt an des wechs middelpunt G, soo neemt hy Mercurius van daer ghesien oirdentlick te loopen in sijn inront, en daerom loopt hy self int inront oock oirdentlick altijt even ras. En volgens sulcke stelling gevonden wesende Mercurius voorofachtring en schijnbaer duysteraerlangde, soo bestaet hier in Ptolemeus spiegheling. T'beslvyt. Wy hebben dan verclaert de somme van Ptolemeus byghevoughde spiegheling des langdeloops van Mercurius, na den eysch.

Tot hier toe is gheseyt van Ptolemeus byghevoughde spiegheling des langdeloops die hy vermengt heeft by den eenvoudighen loop hem van sijn voorgangers ter handt gecommen. Angaende sijn spiegheling des breedeloops, de somme daer af schijnt inde voorgaende breedeloop ghenouch verclaert.