Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift
(1608)–Simon Stevin–Nv van Copernicvs byghevoughde spiegheling der Dvvaelders met stelling eens roerenden Eertcloots.8 Voorstel.Te verclaren de somme van Copernicus byghevoughde spiegheling der Maen.
Nemende Copernicus dat Ptolemeus ervaringhen vande Manens gageslagen schijnbaer plaetsen recht waren, om daer op als vaste gront een spiegheling te stichten, en siende dat hy in sijn byghevoughde spiegheling haer loop int inront, en des inronts loop in sijn wech oneven stelde, d'een tijt rasscher als d'ander, ghelijck vooren geseyt is in deses Anhangs 2 voorstel, sulcx heeft hem ongheschickt ghedocht, alsoo oock dede het stellen van haer groote naerdering totten Eertcloot, strijdende teghen d'ervaring, deur welcke men bevint haer grijphouck de verandering niet te crijghen dieder uyt soude moeten volghen, inder vougen dat hy in die plaets een ander wijse beschreef: Om welcke te verclaren, soo is te weten dat hy lettende op de 5 tr. grootste voorofachtring der Maen in middelteghestant en middelsaming, maer van 7 tr. 40 ① in ettelicke middelvierdeschijnen door Ptolemeus gagheslaghen, als vooren gheseyt is, heeft ghenomen die reghel vast te gaen, en d'oirsaeck ghestelt dusdanich te wesen: Laet A B den inrontwech der Maen beteyckenen, diens middelpunt dats den Eertcloot C, en D E F het inront daer de Maen in loopt, volghens de eenvoudighe stelling soose Ptolemeus eerst ter handt quam, diens middelpunt A, en getrocken de rechte D A F C, oock E C gerakende het inront an E, soo doet den houck A C E de boveschreven 5 tr. daer na sy ghetrocken de lini C G, soo dat den houck A C G doe de 7 tr. 40 ① achtering, en op Hals middelpunt sy beschreven het rondeken E G, gherakende de linien C E, C G, daer na sy getrocken van A deur t'punt des boveschreven raecksels E de lini A E H G: En heeft de Maen in dit rondeken E G een loop dobbel ande middelmaenwinst, en des rondekens middelpunt H heeft sijn loop ghelijck mette loop die de Maen gheseyt wort te hebben int inront, volghens de eenvoudighe stelling ghelijckse | |||||||||||
[pagina 347]
| |||||||||||
 Ptolemeus ter handt quam. Hier uyt volght dat wesende de Maen in een middelsaming ant rondekens punt E naest A, soo moerse in de eerstvolgēde en alle navolgende middeltegestandē weerom sijn ant selve punt naest A (hoewel tot een ander plaets des inrondts DEF) want nadiē de Middelmaen vā middelsaming tot middeltegestant een halfront wint, op welcke tijt deur t'gestelde de Maē int rondekē tweemael soo veelloopt, dats een heel rondt, soo moetse ghelijck gheseyt is in middeltegestant weerom sijn an des rondekens punt naest A. Sghelijcx moetse in alle volghende middelsamingen an t'selve punt wesen, dat is oock altijt int inront D E F, waer deur de Manens grootste voorofachtringen in middelsaminghen en middelteghestanden, oock in Maenduysteringhen en Sonduysteringhen over de 5 tr. niet en can bevonden wordē. Voorts moetse volghens t'ghestelde, in middelvierdeschijn altijt wesen int rondekens punt verst van A, als G, want nadien de Middelmaen van middelsaming tot middelsaming een vierendeel ronts wint, op welcke tijt de Maen int rondeken tweemael soo veel loopt, dats een halfront, soo moet gelijck gheseyt is de Maen in middelvierdeschijn altijt sijn an des rondekens punt verst van A, als an G, waer deur haer grootste voorofachtring in middelvierdeschijn totte 7 tr. 40 ① can bevonden worden, gemerckt den houck der achtring A C G soo groot is. En deur t'gene tot hier toe geseyt is vande grootste achtring wesende het rondeken over die sijde des inronts D E F, wort oock derghelijcke verstaen vande grootste voordering wesende het rondekē over d'ander sijde des inronts: Maer wesende t'selve rondekens middelpunt ghecomen boven D als an I, en getrocken sijnde D I K, soo en valter dan in middelsaming noch middelteghestandt geen voorofachtring, om dat de Maen dan an D is, alsoot oock en doet in middelvierdeschijn om datse dan an K is: En sghelijcx en valter oock in middelsaming, middelteghestant noch middelvierdeschijn, geen voorofachtring als des rondekens middelpunt ghecommen is onder F. En deur sulcke stelling seght Copernicus de Maen tot haer behoorlicke plaets overal gevondē te sullē wordē. Angaende de reden der linien in dese stelling vallende, die is by Copernicus aldus berekent: De driehouck A E C heeft drie bekende palen, te weten den houck A C E 5 tr. de sijde A C 10000, en den houck A E C recht: Hier me | |||||||||||
[pagina 348]
| |||||||||||
Sulcx dat de meeste verheyt tot de minste in sulckē reden is als 11334, tot 8666, t'welck soo groot verschil der Manens grijphoucken niet en geeft als Ptolemeus palen int 3 voorstel deses Anhangs van 65 deelē 13 ① tot 34 deelen 9 ①, want segghende 34 deelen 9 ①, geven 65 deelen 13 ①, wat de Manens minste grijphouck 30 ①? Comt deur het 6 voorstel des 2 boucx de Manens meeste grijphouck na Ptolemeus byghevoughde spiegheling 57 ①, maer na Copernicus stelling alleenelick 39 ①, want segghende 8666, gheven 11334, wat de Manens minste grijphouck 30 ①? comt als vooren 39 ①: Doch ist 3 ① meer dan na de eenvoudighe stelling soose Ptolemeus eerst ter handt quam, welcke dede 36 ① (overeencommende soo men seght mette dadelicke ervaringhen) want als geseyt is inde Byeenvouging vant 13 voorstel des 3 boucx, de meeste verheyt doet 531, de minste 445, daerom seggende 445 gheeft 531, wat de Manens minste grijphouck 30 ①? comt als vooren 36 ①, sulcx dat Copernicus de sake daer in naerder ghecommen is dan Ptolemeus. Ten anderen soo en heeft Copernicus mettet rondeken gheen ongheregelde loop d'een mael rasscher als d'ander, ghelijck Ptolemeus stelling inhoudt. Angaende d'overeencomminghen mette dadelicke ervaringhen, Copernicus en Ptolemeus stellinghen gheven een selve besluyt in alle middelsaminghen en middeltegestanden, en oock in alle middelvierdeschijnen in welcke de Maen by des inronts middelverheden is, want alsdan de voorofachtring na d'een en d'ander wijse 7 tr. 40 ① doet, maer buyten die plaetsen valter tusschen d'een en d'ander stelling verschil. T'beslvyt. Wy hebben dan verclaert de somme van Copernicus byghevoughde spiegheling der Maen, na den eysch. | |||||||||||
9 Voorstel.Te verclaren de somme van Copernicus byghevoughde spiegeling des langdeloops van Saturnus, Iupiter en Mars.
Nemende Copernicus dat Ptolemeus ervaringhen van Saturnus, Iupiters en Mars gagheslaghen plaetsen recht waren, om daer op als vaste gront een spiegheling te stichten, en siende dat hy in sijn byghevoughde spieghelingen haer loop int inront, en des inronts loop in sijn wech oneven stelde, d'een tijt ras- | |||||||||||
[pagina 349]
| |||||||||||
scher als d'ander, ghelijck vooren gheseyt is in deses Anhangs 6 voorstel, sulcx heeft hem ongheschickt ghedocht, inder voughen dat hy in die plaets een ander wijse beschreef aldus toegaende: Laet A B C den inrontwech beteyckenen van een der drie bovenste Dwaelders, ick neem Saturnus, diens middelpunt D, den vasten Eertcloot E, deur welcke ghetrocken is de rechte lini A C, soo dat A t'verstepunt bediet, C t'naestepunt, D E de uytmiddelpunticheytlijn, doende na Ptolemeus rekening 3 deelen 25 ①, sulcke alsser D A 60 doet, daer na sy op A als middelpunt beschreven het inront F G, diens verstepunt F, naestepunt G, waer in den Dwaelder sy ant verstepunt F. Dit is tot hier toe de form der eenvoudighe stelling met een vasten Eertcloot, soose Ptolemeus eerst ter handt quam, waer op hy sijn boveschreven spiegheling veroirdende: Maer de selve an Copernicus als gheseyt is niet bevallende, heeft gedocht ofmen sijn versierde roersels niet bequamelicker en soude te wege brengen, met den Dwaelder te doen loopen in een rondeken beschreven int inront: En na verscheyden tastinghen quam tot dusdanich besluyt: Hy nam voor sich de lini tusschen den Eertcloot en het onevenheyts punt by Ptolemeus in sijn byghevoughde spiegeling int 5 Hooftstick sijns 11 boucx bevonden van 6 deelen 50 ①, sulcke alsser des inrontwechs halfmiddellijn 60 doet, waer voor Copernicus int 5 Hooftstick sijns 5 boucx ghebruyckt 1139 en 10000: Van dese 1139 der lini tusschen den Eertcloot en het onevenheytpunt, trock hy het vierēdeel doende 285,
en bleef 854, die heeft hy gheteyckent van D tot H, nemende t'selve punt H nu voor Eertcloot, die eerst deur E hadde, beteyckent geweest: Nam daer na het derdendeel van D H 854, dats E H doende 285, en teyckende die langde van F tot I, beschreef met F I als halfmiddellijn het rondeken I K, nemende den Dwaelder
 ten tijde van sijn saming mette middelson te wesen an het naestepunt I, hebbende eē loop mettet vervolgh der trappen van I na K, even metten loop des inrondts middelpunt A na B: Maer wesende den Dwaelder in dese middelsaming alsoo an het rondekens naestepunt I, t'is kennelick dat hy in alle middelsaminghen daer an moet wesen, in alle middelteghestant an het verstepunt K, en in alle middelvierdeschijn an een middelverheyt, en quamen hier me | |||||||||||
[pagina 350]
| |||||||||||
overeen Saturnus dadelicke langden na sijn meyning. Doch want sijn voornemen niet en was dese beschrijving aldus te doen met stelling eens vasten Eertcloots, maer met stelling eens roerenden, hy heeft die form verandert, beschrijvende op t'punt ghelijck H als middelpunt, een Eertclootwech even ant boveschreven inrondt, en opt verstepunt des Dwaelderwechs een rondeken even an t'ander, nemende den Dwaelder daer in te loopen. Laet tot opentlicker verclaring van dien A B C andermael het uytmiddelpuntichront beteyckenen,
 diens middelpunt D, en t'punt E sy hier in sulckē verheyt van D, alst in de eerste form van D was, daer na sy beschreven den Eertclootwech F G op t'punt H als middelpunt, wesende t'selve punt H in sulckē verheyt van D als t' punt H in d'eerste form vā D was, te weten 854 deelen, en des Eertclootwechs halfmiddellijn F G, doe soo veel als daer des inronts halfmiddellijn E G 1083, daer na sy mette halfmiddellijn evē an H E, beschreven op A als middelpunt het rondeken I K, even ant rondeken I K der eerste form, waer in Saturnus sy ant naestepunt I, met een loop als in d'eerste form vā I na K: Dese form met stelling eens roerenden Eertcloots, gheeft den Dwaelder al de selve schijnbaer duysteraerlangden die uyt d'eerste form met stelling eens vasten Eertcloots volgen, waer af ick eerst besonder bewijs gedaen hadde, maer denckende daer na de sake verstanelick ghenouch te connen sijn deur het ghene van dergelijcke vertoont is int 15 voorstel des 3 boucx, ten anderen lettende op de onsekerheyt des gronts daer dese stelling op gebout schijnt, ick heb dat bewijs cortheytshalven onbeschreven ghelaten. Merct noch hier vooren geseyt te wesen dat Copernicus het rondeken eerst verdocht int inront met stelling eens vasten Eertcloots, ende hoewel sulcx in sijn schriften niet en blijckt, ick hebt nochtans soo gheseyt om mijn meyning int corte beter te verclaren, en dattet metter daet soo schijnt toeghegaen te hebben. Deur dese voorgaende spiegheling seght Copernicus den Dwaelder altijt tot sijn behoirlicke plaets ghevonden te worden. Merckt noch int boveschreven te blijcken, dat Copernicus byghevoughde spiegeling een vermenging is van sijn vondt met wat uyt Ptolemeus byvouging ghetrocken, ghemerckt de lini daer hy de drievierendeel af neemt by Ptolemeus ghebruyckt wiert. Angaende het soucken van des Dwaelders schijn baer duysteraerlangde vol- | |||||||||||
[pagina 351]
| |||||||||||
gens dese spiegeling, t'is kennelick datmen inde tweede form sal vindē des rondekens middelpunts schijnbaer duysteraerlangde op de wijse ghelijck int 6 lidt vant 15 voorstel des 3 boucx ghevonden wiert des Dwaelders schijnbaer duysteraer langde, en daer noch by voughen de voorofachtring die den Dwaelder deur het rondeken crijcht, want datter uyt comt is t'begeerde. Deur t'ghene wy tot hier toe van Saturnus geseyt hebben, is derghelijcke te verstaen van Iupiter en Mars. T'beslvyt. Wy hebben dan verclaert de somme van Copernicus bygh evoughde spiegheling van Saturnus, Iupiter en Mars, na den eysch. | |||||||||||
10 Voorstel.Te verclaren de somme van Copernicus byghevoughde spiegheling des langdeloops van Venus. Angesien Venus met stelling eens roerenden Eertcloots alsoo loopt in haer wech die binnen den eertclootwech is, ghelijck de drie opperste Dwaelders in haer weghen loopen die boven den Eertclootwech sijn, soo soude mijns bedunckens Copernicus meyning uyt het voorgaende bekent sijn, alsmen het rondeken beschreef op Venuswech binnen den Eertclootwech: Doch te wijle hy achte de sake claerder te wesen, met Venuswechs middelpunt te doen draeyen in een rondeken even an t'ghene men anders op de wech als gheseyt is mocht beschrijven, soo sal ick dat verclaren. Laet A B C dē Eertclootwech sijn, diens 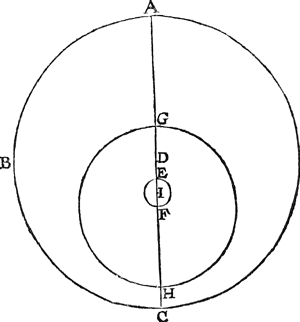 middelpunt D, halfmiddellijn D A doende 10000, en E is de plaets daer Venus wechs middelpunt bevonden wiert volghens de rekening gemaeckt op de eenvoudighe stelling soose Ptolemeus eerst ter handt quam, alwaer de uytmiddelpunticheytlijn D E dede 208: Maer na Copernicus spiegeling sy geteyckent het punt F, soo dat E F even is met E D, beduydende t'selve punt F Venuswechs middelpunt, waer op mette halfmiddellijn F G doende 7194, beschrevē is Venuswech G H in dese ghestalt: Daer na sy van E F ghenomen het middel I, en | |||||||||||
[pagina 352]
| |||||||||||
daer op als middelpunt beschreven het rondeken E F, daer deswechs G H middelpunt in draeyt, tweemael so ras als den Eertcloot, en oock na t'vervolgh der trappen, sulcx dat wanneer den Eertcloot is an t'verstepunt A of naestepunt C, soo is t'middelpunt des wechs G H altijt an E, maer den Eertcloot an een der middelverhedē sijnde, als B, soo is dat middelpunt altijt an F. En hier me seght Copernicus dat Venus altijt tot haer behoorlicke langde ghevonden wort. T'beslvyt. Wy hebben dan verclaert de somme van Copernicus byghevoughde spiegheling des langdeloops van Venus, na den eysch. | |||||||||||
Merckt.Alsoo Copernicus int 25 Hooftstick des 5 boucx, tot sijn spiegeling noodich verstont Mercurius te doen overentweer loopē in een rechte lini, en noch tans niet willende toelaten eenighe ongheschickte loop van ronden d'eenmael rasscherals d'ander, soo heeft hy int 4 Hooftstick sijns 3 boucx beschrevē een vertooch waer deur sulcx met even roersel van ronden te weghe can ghebrocht worden t'selve vertooch (daer oock af ghehandelt wort deur Proclus uytlegger der beginselen van Euclides) sal ick hier by setten als 11 voorstel, om te dienen tot bewijs des volghenden 12 voorstels. | |||||||||||
Vertooch. 11 Voorstel.Wesende opt middelpunt eens eerste ronts beschreven een tvveede, diens halfmiddellijn even is ande helft der halfmiddellijn van t'eerste, en op een puntindē omtreck vant tvveede beschrevē een derde, even ant tvveede, hebbende een loop dobbel anden loop vant tvveede, en op een ander sijde. Yder punt des omtrecx vant derde beschrijft een rechte halfmiddellijn vant eerste. 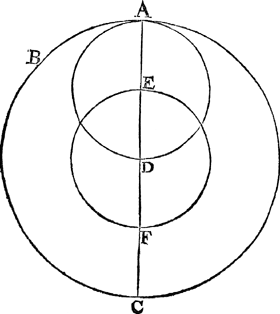 T'ghegeven. Laet in dees eerste form A B C het eerste rondt sijn, diens middelpunt D, halfmiddellijn A D, en op D sy beschreven een tweede rondt E F, diens halfmiddellijn D E even is anden helft vā A D des eersteronts A B C, daer na sy op een punt als Eindē omtreck vant tweede ront E F, beschreven een derde A D even ant tweede E F, en hebbende een loop van A na de rechter sijde, dobbel anden loop vant tweede rondt E F na de slijncker: Laet voort A | |||||||||||
[pagina 353]
| |||||||||||
eenich genomē punt sijn des omtrecx vant derde rondt A D. T'begeerde. Wy moeten hier me bewijsen dattet punt A des omtrecx A D vant derde ront, een rechte middellijn A C beschrijft des eersten rondts A B C. T'bereytsel. Latet punt E des tweede rondts E F inde eerste form gecommen sijn na de slijncker sijde tot G als in dees tweede geloopen hebbende dē booch E G, of houck A D B, sulcx dattet verstepunt A des derde ronts A D inde eerste form moet gecommē sijn vā A tot B in dees tweede: Hieren tusschē moettet genomen roerende punt in het derde rondt ghecommen sijn volgende t'gestelde van B na H, te weten na de rechter sijde, sulcx dat den booch B H dobbel is an E G, of den houck B G H, dobbel anden houck B D H, later sijn tot H. Om nu op dese derde form het begeerde noch opentlicker te verclaren, wy moeten bewijsen dat H valt inde lini A C. T'bewys. Angesien den houck B G H opt middelpunt G int rondt B H D dobbel is anden houck B D H opt punt des omtrecx D int selve ront B H D deur t'bereytsel, en ooc deur het 20 voorstel des 3 boucx van Euclides, so segh ick hierom t'punt H nootsakelick te vallen in A C, want by aldient daer buyten viel, ick neem an I, soo en soude dan den houck B G I niet het dobbel connen sijn des houcx E D G, het welck teghen t'gestelde waer. T'beslvyt. Wesende dan opt middelpunt eens rondts, beschreven &c. | |||||||||||
Vervolgh.De lini B H valt rechthouckich op A C om dese reden: Laet gheteyckent worden inden omtreck E F het punt K, soo dat de booch E K even is met E G, en daerom oock de booch B H met G K, daer na sy ghetrocken de lini D K en G K: Twelck soo wesende A D snijt de rechte G K in haer middel L, sulcx datse op malcander rechthouckich commen: Maer den driehouck B G H is even en ghelijck metten driehouck G D K, en de sijde B G light met G D in een rechte lini, waer deur B H evewijdeghe is met G K, en comt ghelijck de selve G K oock rechthouckich op A C. Dit soo sijnde ick segh aldus: Want op een gegeven tijt bekent is de booch A B, soo wort ghevonden de houckmaetpijl H A des houckmaets H B, of houcx A D B, in sulcke deelen alsmen A D toeschrijft deur het 14 voorstel vant Houtmaetmaecksel, maer mettet punt H wort Mercurius beteyckent, waer uyt blijckt sijn plaets inde middellijn A C bekent te worden. | |||||||||||
[pagina 354]
| |||||||||||
12 Voorstel.Te verclaren de somme van Copernicus byghevoughde spiegheling des langdeloops van Mercurius. Laet A B den Eertclootwech beteyckenen, diens middelpunt C, middellijn A B, uytmiddelpunticheytlijn D C, ghevonden na de wijse der eenvoudighe stelling soose Ptolemeus eerst ter handt quam van 947 deelen, sulcke alsser des Eertclootwechs halfmiddellijn A C 10000 doet, ende op D als middelpunt, en  mettet derdendeel van D C, t'welck sy D E, is beschreven een rondeken E F, sulcx dat F t'verstepunt beteyckent vā C, en E t'naestepunt, daer na op Fals middelpunt sy beschrevē den inrontwech G H, op wiens verstepunt H als middelpunt ick het inront I K teycken, en opt selve middelpunt H noch een cleender rondt L M, diens halfmiddellijn H M, even is an den helft der halfmiddellijn | |||||||||||
[pagina 355]
| |||||||||||
HI, en sniende A B in L en M, daer na op L als middelpunt het rondekē K H, diens halfmiddellijn L H de selve is des ronts beschreven op H L, in dit rondeken K H wort Mercurius ghedreghen. Dese form aldus voldaen sijnde, soo sullen wy haer beteyckening verclaren: F middelpunt des rondts H G doet des jaers twee keeren, d'een diet vanden Eertclootwech ontfangt, d'ander sijn eyghen, en beyde na t'vervolgh der trappen: T'middelpunt L des rondts K H, is vast inden omtreck des rondts L M, en wort daer in ghedreghen teghen het vervolgh der trappen doende des jaers een keer: Den loop van Mercurius int rondt K H, is na t'vervolgh der trappen, even anden boveschreven loop van F, te weten des jaers twee keeren, waer uyt volght dat Mercurius altijt overentweer loopt inde middellijn K I sonder daer uyt te commen, deur het 11 voorstel deses Anhangs. Wijder volght dat wesende den Eertcloot an A of B, soo moet het middelpunt des rondts H G dan altijt sijn an F, dats des rondts E F verstepunt van C: Maer den Eertcloot ande middelverheden sijnde, dats 90 tr. van A of B, soo moet het voorschreven middelpunt des rondts H G dan altijt sijn an E, dats des rondts E F naestepunt van C, het welck op verkeerde wijse toegaet van t'ghene met Venus ghebeurde. Wijder volght dat Mercurius de middellijn I K overentweer loopende soo gheseyt is, altijt het naestepunt an I sal sijn wesende den Eertcloot an A of B, maer an t'verstepunt K den Eertcloot ande middelverheden sijnde: Hier me ghebeuret dat het middelpunt van H G als F, int rondt E F, en Mercurius inde middellijn I K des jaers elck twee keeren doen: En hierentusschen is den eyghen loop des inrondts I K, of de lini F H int rondt H G eenvaerdelick ontrent de 88 daghen over een keer. En hier me segt Copernicus dat Mercurius tot sijn behoirlicke plaets ghevonden wort. T'beslvyt. Wy hebben dan verclaert de somme van Copernicus bygevoughde spiegheling des langdeloops van Mercurius, na den eysch. | |||||||||||
13 Voorstel.Verhael op der sterren onbekende loop: En des duysteraers onbekende afvvijcking vandenGa naar margenoot⋆ evenaer.
De vaste sterren worden gheseyt een onbekende loop te hebben d'een tijt rasscher als d'ander, want hoewelmense altijt eveverre van malcander bevint, nochtans heeft den heelen Hemelscloot een roersel van Westen int Oosten, sulcx dat haer duysteraerlangde die ande lentsne begint, gheduerlick grooter wort, en van Ptolemeus tijt tot nu toe over de 21 ① vermeerdert is: Maer volghens de ervaringhen sedert gheschiet, soo wort dit roersel seer onghereghelt gheacht, d'eenmael slapper als d'ander, ja soo eenighe meynen somwijlen ruggheling te loopen. Hier af sijn by ettelicke als Thebit, de Alfonsinen, Purbachius, Copernicus, Ioannes Venerus, verscheydenGa naar margenoot* spieghelinghen verdocht, elck na sijn goetduncken. Maer om van dit onbekent roersel mijn ghevoelen te segghen, het is te weten dat der sterrenGa naar margenoot* wanschaeuwing grooter bevonden wort in landen na denGa naar margenoot* aspunt dan na den evenaer, waer af wy seer merckelick voorbeelt hebben, deur de ervaring gheschiet op de vermaerde seylage van Willem Barentsen metten sijnen in Nova Zembla, wesende daer des aspunts verheffing van 76 tr. alwaer hemlien de Son eerst onder denGa naar margenoot* sichteinder ginck den vierden November 1596, diese op den eersten behoorden verlooren te hebben, sulcx datse hoogher scheen danse eyghentlick was, of wan- | |||||||||||
[pagina 356]
| |||||||||||
schaeuwing had ghelijck elck berekenen mach, van ontrent 1 tr. 9 ①: Maer 81 daghen daer na, te weten den 24 Ianuarius 1597, soo heeft den randt der Son haer weerom begonnen te openbaren, welcke sy sooder geen wanschaeuwing gheweest en had, op den 9 Februarius eerst behoorden gesien te hebben, inder voughen datse hoogher scheen danse eyghentlick was, of wanschaeuwing had by de 5 tr. welcke in dese laetste ervaring veel meerder bevonden wiert als in d'eerste, waer af d'oirsaeck bekent gheworden is an Philippus Lansbergius vlietichGa naar margenoot* Gaslagher en vermaert Wisconstenaer, die daer te vooren in sijn ervaringhen deur oneven wanschaeuwinghen langhe in twijffel gheweest had, want hoewel de Son tot lijckstandighe plaetsen vantGa naar margenoot* Winters keerpunt was, als neem ick 50 of 56 tr. daer voor, en 56 tr. daer na, soo en heeft hyse nochtans in d'een en d'ander niet met een selve hooghde boven den sichteinder bevonden, maer meerder inde laetste dan in d'eerste plaets, achtende nochtans alsdoen dit feyl van weghen wanschaeuwing niet te connen commen, om dat, als gheseyt is, de Son in d'een en d'ander ervaring eveverre van het winters keerpunt was: Maer het boveschreven voorbeelt van Nova Zembla t'sijnder kennis ghecommen sijnde, heeft d'oirsaeck besloten te wesen, en mijns bedunckens met goede reden, dat de coude wintersche vochticheden in Februarius dicker en waterachtigher sijn, dan inde warmer maent October eynde des voorganghen Somers. Nu dan de wanschaeuwing in Nova Zembla soo uytnemende groot wesende, en tot ander plaetsen daer de ervaringhen ghebeurt sijn, als Pruyssen, Duytslandt, Spaeigne, Italie, Egipten, soo groot als yders Noorderlickheyt mebrengt, boven dien tot een selve plaets op d'een tijt des jaers grooter als op d'ander, sonder nochtans by de Beschrijvers der voornoemde spieghelinghen daer op acht ghenomen te wesen, soo valt daer uyt te besluyten, dat de onevenheden by hemlien bevonden, niet nootsakelick en sijn van weghen onevenheyt des loops der sterren, want al waer die gantsch even, soo souder om de verscheydenheyt der wanschaeuwing moeten schijnen onevenheyt te wesen: Oft anders gheseyt, soo by hemlien volcommen evenheyt bevonden waer, t'soude teycken sijn van onevenheyt int wesen. Tot breeder bevesting van het voorseyde valt noch te anmercken, ten eersten dat uyt de ervaringhen in Egipten gheschiet, even loop bevonden wiert, te hondert Iaren van 1 tr. totten tijt van 432 Iaren toe: Ten anderen dat de onevenheyt met rasscher loop, gheoirdeelt wort uyt ervaringhen die daer na in verscheyden Noorderlicker landen gagheslaghen sijn, t'welck met reden vermoeden gheeft de onberekende wanschaeuwinghen daer af oirsaeck te meughen wesen, of volcommelick, of ten deele, maer welck van beyden men neemt, de voorschreven spieghelinghen vallen onghegront, en schijnt dat soo de Schrijvers van dien dese verscheyden grootheyden der wanschaeuwinghen ghenouch bedocht hadden, datse de selve spieghelinghen soo niet en souden veroirdent hebben, en daerom laet ick die onbeschreven, achtende datter voor al behooren te sijn ervaringhen van ghenouchsaem sekerheyt, eermen tottet veroirdenen en besluyten van sulcke spieghelinghen comt. Hier toe soudet connen voorderlick sijn, datmen tot Alexandrie in Egipten, daer de voorschreven eerste ervaringhen ghebeurden, dede gaslaen de Sonnens inganck der lentsne en erftsne, met haer meeste afwijcking vanden evenaer, en datmen daer na saghe hoe die overcommen met derghelijcke ons Noorderlicker ervaringhen op den selven tijt gheschiet. Tot hier toe is gheseyt vande onbekende roersels der vaste sterren: Angaende die der Dwaelders, van welcke in desen Anhang ghehandelt is, ick acht Pto- | |||||||||||
[pagina 357]
| |||||||||||
lemeus ervaringhen daerse op ghegront sijn oock voor onseker, want hoewel hy daer in groote looflicken aerbeyt ghedaen heeft, nochtans ghemerckt dat toeginck met een cleene cooperGa naar margenoot* Hemelloopstuych, van verscheyden ringhen ghemaeckt, elcke op haer as draeyende, sulcx datmen des tuychs duysteraer altijt evewijdich creech metten hemelschen: Voort dat hy de sterren deur sichtgaetkens der wijslijnen sach, met meerder plaets dan de grootheyt der sterre, onsekerder toegaende dan na het gebruyck van Tuycho Brahe, soo is hemlien die met sulcke reetschappen ommegaen, kennelick ghenouch de onsekerheden dieder in vallen, hoe sorchvuldich die oock ghemaeckt sijn, ghelijck Ptolemeus self daer af somwijlen vermaen doet. Maer der sterrenhoochden of verheden van malcander met groote reetschappen ghemeten, en de rest deur rekeninghen der platte en clootsche driehoucken ghewrocht, daer machmen vastelicker op te wercke gaen. Noch vielder in Ptolemeus ervaringhen eenige onsekerheyt van der Dwaelders schijnbaer duysteraerlangden, om dat de vaste sterren self daer de dadelicke meting op ghegront is, tot die tijt rouwelick beschreven waren met 10 ① voor cleenste maet, als in sijn tafelen blijckt. Voorts boven stelling van oneven onnatuerlicke loopen, soo betuyghen noch de dadelicke ghemeten grijphoucken der Dwaelders, voornamelick van Mars en de Maen, datse niet in sulcke verheyt en naerheyt des Eertcloots en commen als de spiegeling mebrengt, gelijck wy elders breeder verclaert hebben. Benevens t'ghene tot hier toe gheseyt is noch vervought t'ghetuychnis van verscheyden Gaslaghers, als onder anderen Regiomontanus, Bernhardus Waltheri, en Purbachius, in druck uytgaende, soo en worden der Dwaelders plaetsen niet bevonden t'overcommen mette spieghelinghen: Al t'welck anghemerckt, ten schijnt niet seker ghenouch ofter der Dwaelders onbekende roersels sijn, of wesende, dat wy van haer ghedaente gheen ghenouchsaem bescheyt en hebben, daerom meyn ick dat soo ymant voor hem naem een nieuwe spiegheling van dien te beschrijven, dattet oirboir waer sich voor al van soo veel ghewisse ervaringhen te voorsien, datse voor gront mochten verstrecken om op te bouwen. Doch hier mede mijn teghenwoordich ghevoelen verclaert sijnde, laet daerentusschen elck sijn goetduncken volghen. T'beslvyt. Wy hebben dan ghedaen een verhael op der sterren onbekende loop, en des duysteraers onbekende afwijcking vanden Evenaer, na den eysch.
Des derden Bovcx EYNDE.  |
|

