Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

(1608)–Simon Stevin– rechtenstatus

Byvovgh des breedeloops der vyf dwaelders Saturnus, Iupiter, Mars, Venus, en Mercurius, ghegront op stelling eens vasten Eertcloots.

Cortbegryp deses byvovghs.

INt 19 voorstel des 3 boucx is gheseyt, gherievigher te sijn rekeninghen vande langdeloop der Dvvaelders te maken op de oneyghen stelling eens vasten Eertcloots, dan op de eygen eens roerenden, en dien volghens soudemen om de selve reden meughen segghen derghelijcke met stelling eens vasten Eertcloots oockoirboirder te sijn vande breedeloop, en dat daerom de natuerlicke oirden soude vereysschen desen Byvough niet hier, maer int tvveede bouck met stelling eens vasten Eertcloots behooren vervought te vvesen, ghelijck mette Manens breedeloop daer ghedaen is. Om hier op te vvesen, soo is te vveten dat nadien grondelicke kennis deses handels ghetrocken vvort uyt de breedeloop met stelling eens roerenden Eertcloots, vvelcke alsdoen noch niet beschreven en vvas, noch volghens mijn voorghenomen oirden beschreven en moest vvesen, soo en conde dit daer niet bequamelick commen: Maer de selve breedeloop nu int derde bouck verclaert sijnde, soo connen vvy daer uyt trecken t'ghene de breedeloop met stelling eens vasten Eertcloots vereyscht, en daerom heb ick die hier beschreven.

De selve sal ses voorstellen hebben, vvesende d'eerste vierGa naar margenoot* vertooghen, de laetste tvveeGa naar margenoot* vverckstucken, te vveten:

Het 1 voorstel, dat de ronden der tvvee onderste Dvvaelders Venus en Mercurius die byde stelders eens vasten Eertcloots inront dragers genoemt vvordē, inrondē sijn, en t'gene sy inrondē heeten, inrontdragers te vvesen.

Het 2, dattet plat des inronts der vijf Dvvaelders Saturnus, Iupiter, Mars, Venus en Mercurius met stelling eens vasten Eertcloots, altijt evevvijdich is mettet plat des duysteraers.

Het 3, dat vvesende tvvee even en evevvijdege ronden, het een hooger alst ander, de lini tußchen het middelpunt vant leeghste, en een punt inden omtreck vant hooghste, even en evevvijdege te sijn mette lini tusschen sijn lijcstandich tegenoverpunt int leeghste, en het middelpunt vant hooghste.

Het 4, dat de Dvvaelders met stelling eens vasten Eertcloots deselve schijnbaer duyster aerbreede ontfangen, diese hebben met stelling eens roerenden Eertcloots.

Het 5, vvesende gegeven eens Dvvaelders meeste noordersche enzuydersche breede, te vindē sijn vvechs afvvijcking vanden duysteraer: Oock mede hoe verre de duysteraersne vanden Eertcloot valt, deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots.

Het 6, om te vindē eens Dvvaelders schijnbaer duysteraerbreede op een gegevētijt, deur vviscōstige vvercking gegrōt op stelling eēs vastē Eertcloots.

Vertooch. 1 Voorstel.

De ronden der tvvee onderste Dvvaelders Venus en Mercurius die by de stelders eens vasten Eertcloots ghenoemt vvordenGa naar margenoot⋆ inrontdragers, sijn inronden: En t'gene sy inronden heeten, sijn inrontdraghers.

T'is deur kennis der voorgaende stelling eens roerenden Eertcloots openbaer, dat de inronden der drie bovenste Dwaelders met stelling eens vasten Eertcloots niet int wesen en bestaen, dan versiert worden even te sijn anden Eertclootwech, maer t'gaet anders toe mette twee onderste, want t'ghene men Venus of Mercurius inront noemt, en is niet versiert noch even anden Eertclootwech, dan om eyghentlick te spreken het is hun wech self daer sy dadelick in loopen, en in stelling eens vasten Eertcloots, volghens d'oirden der drie bovenste, inrontwech behoort te heeten: En daerom alsmen de voorgaende regel der langdeloop vande bovenste met stelling eens vasten Eertcloots, soude willen ghemeen hebben over de twee onderste, men soude daer moeten op de selve wijse spreken, te weten inrontwech noemen het cleenste dat eyghentlick inrontwech is, en inront het grootste dat versiert wort even anden Eertclootwech, want daer me dan ghedaen als mette bovenste, de reghel sal ghemeen sijn. Maer om van sulcke stelling noch claerder te spreken ick segh aldus: Angesien yder Dwaelders inront even is anden Eertclootwech, soo moetense met malcander al evegroot sijn, waeruyt wijder volght, dat de weghen vande leegher Dwaelders teghen haer inronden verleken, minder sullen sijn dan de weghen vande hoogher Dwaelders.

Laet tot voorbeelt in dese eerste volghende form op A als middelpunt, beschrevē worden het rondt B C als Saturnus inrontswech, diens halfmiddellijn A B doet deur de Byeenvouging des 13 voorstels vant 3 bouck 92308, en op B als middelpunt, het inrondt diens halfmiddellijn D B even an den Eertclootwech diens halfmiddellijn doet 10000.

Ten tweeden sy op A als middelpunt, beschreven het rondt E F als Iupiters inrontswech, diens halfmiddellijn A E doet deur de Byeenvouging des 13 voorstels 52174, en op E als middelpunt het inront diens halfmiddellijn E G 10000.

Ten derden sy op A als middelpunt beschreven het rondt H I als Mars inrontswech, diens halfmiddellijn A H doet deur de Byeenvouging des 13 voorstels 15190, en op H als middelpunt het inront diēs halfmiddellijn H K 10000.

Ten vierden sy op L als middelpunt, beschreven het rondt M N als Venus inrontswech, diens halfmiddellijn M L doet deur de Byeenvouging des 13 voorstels 7194, en op M als middelpunt het inront, diens halfmiddellijn M O 10000, welck inront in hem heeft des inrontwechs middelpunt L, anders dan een der drie voorgaende formen: Doch is kennelick dat de reghel des langdeloops vooralle vier ghemeen moet sijn.

Ten vijfden sy op P als middelpunt beschreven het rondt Q R als Mercurius inrontswech, diens halfmiddellijn P Q doet deur de Byeenvouging des 13 voorstels 3572, en op Q als middelpunt het inront, diens halfmiddellijn Q S 10000, welck inront in hem heeft den heelen inrontwech Q R, anders dan in een der vier voorgaende formen, doch is kennelick dat de reghel des langdeloops

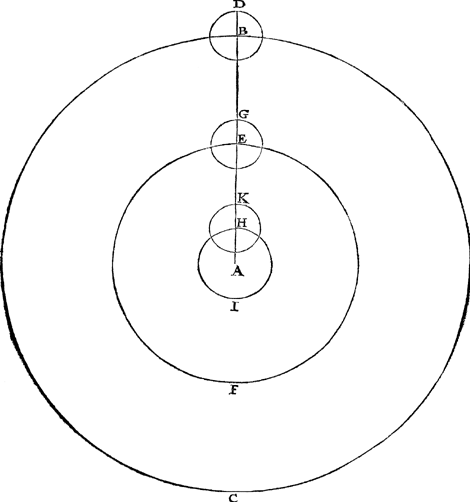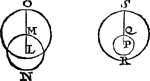voor alle vijf gemeen moet sijn, sonder de verkeerde hafpeling te vallen diemen ontmoet anders doende. Dit oude misbruyck heeft sijn bekende oirsaeck, want tewijle d'eerste ondersouckers des Hemelloops gheen kennis en hadden vande ghedaente des roerenden Eertcloots, soo en conden sy niet beter schrijven dan van t'ghene voor hemlien uyterlick scheen te wesen. Noch is oock te anmercken dat de regel des breedeloops (soo wel als des langdeloops) met stelling eens vasten Eertcloots, hier deur over allen ghemeen is ghelijck

int volghende blijcken sal. T'beslvyt. De ronden dan der twee onderste Dwaelders Venus en Mercurius die by de stelders eens vasten Eertcloots ghenoemt worden inrontdragers, sijn inronden: En t'ghene sy inronden heeten, sijn inrontdraghers, t'welck wy bewijsen moesten.

Vertooch. 2 Voorstel.

Het plat des inronts der vijf Dvvaelders Saturnus, Iupiter, Mars, Venus en Mercurius, is met stelling eens vasten Eertcloots altijt evevvijdich mettet plat des duysteraers.

Voor al anghesien het inront versiert is evegroot metten Eertclootwech, en dat den Dwaelder daer in ghenomen wort een langdeloop te hebben even en ghelijck mette langdeloop des Eertcloots in haer wech, soo volght daer ghenouchsaem uyt deser twee ronden evewijdicheyt behooren toegelaten te worden, ghemerckt datter anders gheen volcommen ghelijcke langdeloop sijn en soude, nochtans anghesien de selve evewijdicheyt uyt het voorgaende can bewesen worden, soo sal ick die beschrijven als volght: Ick verkies hier toe de form des 15 voorstels vant 3 bouck, waer me ick aldus segh: Ten eersten soo is deur de ghemeene reghel beschreven int 22 voorstel des 3 boucx, bekent hoe groot dat moet sijn de breede van Mars ter plaets des punts N ghesien uyt den roerenden Eertcloot O, maer soo groot die daer wesen moet, even soo groot moet Mars breede oock sijn ter plaets van I met stelling eens vasten Eertcloots, dats ghesien uyt A: Ende want A I even is met O N, soo volght daer uyt dat de lini van I rechthouckich opt plat des duysteraers even moet sijn ande lini van N rechthouckich opt plat des duysteraers. Ten tweedē segh ick, dat soo lanck als is de lini van N tot opt plat des duysteraers gesien uyt den roerenden Eertcloot an P, soo lanck moet oock sijn de lini van F tot opt plat des duysteraers ghesien uyt den vasten Eertcloot A, om dat A F even is met P N.

Maer elck der twee linien van F en N rechthouckich opt plat des duysteraers, aldus even sijnde ande lini van N tot opt plat des duysteraers, soo moeten die selve twee linien van F en N rechthouckich op t'plat des duysteraers met malcander even sijn, en vervolgens soo is des inronts heele halfmiddellijn I F evewijdich mettet plat des duysteraers. Ende op de selve voet ist openbaer te connen bethoont worden de middellijn deur H rechthouckich op F I soose ghetrocken waer, oock evewijdich te wesen mettet plat des duysteraers, want soo men deur t'punt K treckt een middellijn rechthouckich op O P, en datmen naem den roerenden Eertcloot te wesen ande uytersten van dien (het welck cortheytshalven ghelaten wort) t'bewijs soude daer me sijn als vooren: Nu dan de middellijn F I, met d'ander middellijn deur H, soose als gheseyt is getrocken waer, beyde evewijdich sijnde metten duysteraer, soo volghter uyt het heel plat des inronts F I evewijdich te wesen mettet plat des duysteraers. Ende sulcx als dit bewijs is wesende het inront met sijn middelpunt an H, alsoo sal derghelijcke bewesen worden tot alle plaetsen. Voort gelijck dit bewijs is geweest mette form des 15 voorstels, dienende voor de drie opperste Dwaelders, alsoo salt oock sijn mette form des 16 voorstels dienende voor de onderste.

T'beslvyt. Het plat dan des inronts der vijf Dwaelders Saturnus, Iupiter, Mars, Venus en Mercurius, is met stelling eens vasten Eertcloots altijt evewijdich mettet plat des duysteraers, t'welck wy bewijsen moesten.

Vertooch. 3 Voorstel.

Wesende tvvee even en evevvijdeghe ronden het een hoogher als t'ander, de lini tusschen het middelpunt vant leeghste, en een punt inden omtreck vant hoochste, is even en evevvijdege mette lini tusschen sijn lijckstandich teghenoverpunt int leeghste, en het middelpunt van het hoochste.

T'ghegheven. Laet A B het hoochste rondt sijn overcant ghesien diens middelpunt C, opperste punt A, onderste punt B, en D E sy het leeghste

illustratie

rondt, even en evewijdich met A B, diens middelpunt F, opperste punt D, onderste punt E, en F B sy de lini tusschē het middelpunt F vant leeghste rondt, en eenich punt inden omtreck vant hooghste rondt, daer ick hier toe neem het onderste punt B: Sghelijcx sy D C de lini tusschen sijn lijckstandich tegenoverpunt int leeghste, dat is het opperste punt D, en het middelpunt C vant hooghste rondt. Ende is te weten dat ick D ghenoemt hebbe lijckstandich tegenoverpunt van B, uyt oirsaeck dat E een lijckstandich punt van B is (als wesende in sijn rondt soo het onderste ghelijck D int sijne) en D teghenoverpunt van E.

T'begheerde. Wy moeten bewijsen dat F B even en evewijdeghe is met D C. T'bewys. Anghesien C B en D F even en evewijdeghe halfmiddellijnen sijn deur t'ghegheven, soo sijn F B en D C twee linien tusschen de uytersten van twee even en evewijdeghe, en daerom sijnse oock self even en evewijdeghe: En sulcx als hier bewesen is mettet lijckstandich tegenoverpunt vant onderste punt B, alsoo is derghelijcke openbaer mettet lijckstandich teghenoverpunt van alle voorghestelt punt des omtrecx.

T'beslvyt. Wesende dan twee even en evewijdeghe ronden het een hoogher als t'ander, de lini tusschen het middelpunt vant leeghste, en een punt inden omtreck vant hooghste is even en evewijdeghe mette lini tusschen sijn lijckstandich teghenoverpunt int leeghste, en het middelpunt vant hooghste, t'welck wy bewijsen moesten.

Vertooch. 4 Voorstel.

De Dvvaelders ontfanghen met stelling eens vasten Eertcloots de selve schijnbaer duysteraerbreede, diese hebben met stelling eens roerenden Eertcloots.

Anghesien de Son of Eertcloot nummermeer breede en hebben, soo en valter niet af te segghen. Angaende de breede der Maen, het is int voorgaen-

de ghebleken die in d'een en d'ander stelling een selve te wesen, sulcx datter alleenelick vande vijf ander verclaring behouft.

T'ghegheven. Laet A B den duysteraer bedien overcant ghesien ghelijck al d'ander ronden, C D sy den Eertclootwech, diens middelpunt E, waer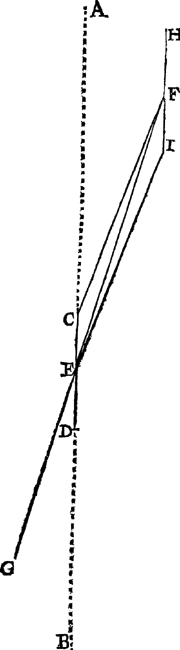

illustratie

1 FORM.

2 FORM.

deur als inde eerste form dienēde voor de drie bovēste Dwaelders, of waer buytē als inde 2 form we sende Mercurius teyckening dienende voor de twee onderste, getrockē den Dwaelderwech F G, in welcke ick neem den Dwaelder te wesen ant opperste punt F, en den Eertcloot an haer wechs opperste pūt C. Tot hier toe de teyckening gedaē sijnde vande stelling eēs roerendē Eertcloots, ick sal nu die eens vasten beginnen, tot welckē eynde ick des Eertclootwechs middelpūt E voor vasten Eertcloot neem, want dat in die stelling daer tegen sulcke beteyckening heeft deur het 15 voorstel des 3 boucx, en F G die eerst was Dwaelderwech, neem ick nu voor inrontwech: Voort anghesien den Dwaelder ghenomen is te wesen an des wechs opperste punt F, soo moet het inrondt t'welck H I sy, met sijn middelpunt wesen an F, oock even en evewijdich mettē Eertclootwech C D deur het 2 voorstel deses Byvoughs. Voort want den roerenden Eertcloot ghenomen wiert an C, soo moet den Dwaelder ghenomen sijn an I als lijckstandich tegenoverpunt van C, waer af de reden blijckt int 15 voorstel des 3 boucx. T'begheerde. Wy moeten bewijsen dat den Dwaelder an I, met stelling des vasten Eertcloots an E, de selve schijnbaer duysteraerbreede ontfangt, die hy heeft an F met stelling des roerenden Eertcloots an C.

T'bereytsel. Laet getrockē wordē de twee linien EI, CF. T'bewys. Anghesien C D even en evewijdeghe is met H I, soo sijn haer helften E C, F I oock even en evewijdeghe, en de twee linien daer tusschen E I, C F moeten oock evewijdege sijn, en daerom oock den houck A E I, wesende des Dwael-

ders schijnbaer duysteraerbreede ghesien uyt den vasten Eertcloot E, is even anden houck A C F wesende des Dwaelders schijnbaer duysteraerbreede ghesien uyt den roerenden Eertcloot C: Maer sulcx als hier bethoont is wesende den roerenden Eertcloot en den Dwaelder tot dier rondē hooghste en leeghste punt, sal oock alsoo blijcken tot alle plaetsen, om dat ghelijck in dese twee evewijdege ronden C D, H I, de lini E I tusschen het middelpunt E vant leeghste rondt, en het punt I inden omtreck vant hooghste, even en evewijdeghe is mette lini C F, tusschen sijn lijckstandich teghenoverpunt C int leeghste, en het middelpunt F vant hooghste, soo sijn alle sulcke linien overal evewijdeghe deur het 3 voorstel deses Byvoughs. T'beslvyt. De Dwaelders dan ontfanghen met stelling eens vasten Eertcloots de selve schijnbaer duysteraerbreede diese hebben met stelling eens roerenden Eertcloots, t'welck wy bewijsen moesten.

5 Voorstel.

Wesende ghegheven eens Dvvaelders meeste noordersche en zuydersche breede, te vinden sijn vvechs afvvijcking vanden duysteraer: Oock mede hoe verre de duysteraersne vanden Eertcloot valt, deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots.

Angesien den inrontwech der drie bovenste Dwaelders deur den Eertcloot streckt, of ghenomen wort voor na ghenouch daer deur te strecken, maer vande twee onderste daer buyten, soo sal ick daer af twee voorbeelden beschrijven.

1 Voorbeelt vande drie bovenste Dvvaelders.

T'ghegheven. Laet A B den duysteraer beteyckenen overcant ghesien, diens middelpunt dats den vasten eertcloot C, waer deur ghetrocken is Saturnus inrontswech D E, streckende C D na de noortsijde, C E na de zuytsijde, sulcx dat de twee houcken A C D, B C E, des inrontwechs afwijcking bedien, en by sijn uyterste punt D na t'Noorden als middelpunt is beschreven het inront F G, evewijdich metten duysteraer A B, diens verstepunt F, naestepunt G, van t'welck getrocken sy de lini G C, en den houck A C G, doet als bevonden wiert inde ervaring des 20 voorstels des 3 boucx 3 tr. 2 ①: Sghelijcx is opt uyterste punt E na het Zuyden als middelpunt, beschreven het inront H I, evewijdich metten duysteraer A B, diens verstepunt I, naestepunt H, van t'welck getrocken sy de lini H C, en den houck B C H doet als bevonden wiert inde ervaring des voorschreven 20 voorstels 3 tr 5 ①. T'begheerde. Wy moeten vinden des inrontwechs D E afwijcking vanden duysteraer, dats den houck A C D.

t'Werck.

De driehouck C D G heeft drie bekende palen, te weten D G 10000 deur t'gestelde, C G soo veel als ten tijde der ervaring dede de lini vanden Eertcloot tottet inronts naestepunt, t'welck deur t'vervolgh van het 13 voorstel des 3 boucx int ghemeen bekent wort, en besonderlick bevonden is int 21 voorstel des 3 boucx van 88718, of anders om gherieviger wercking machmen nemen

de lini C D, doende na ghenouch 10000 meer, dats 98718, en den houck D G C 176 tr. 58 ①, als even sijnde metten houck G C B, die halfrontschil is der bekende grootste breede A C G 3 tr. 2 ①: Hier me gesocht den houck C D G, wort bevonden deur het 5 voorstel der platte driehoucken van 2 tr. 43 ①, twelck oock is voor den houck A C D begheerde afwijcking des wechs vanden duysteraer, overeencommende mette 2 tr. 43 ① die int 22 voorstel des 3 boucx ghevonden wierden. Ick doe daer na derghelijcke wercking over d'ander sijde, souckende den houck B C E, tot dien eynde aldus segghende: De driehouck C H E heeft drie bekende palen, te weten E H 10000 deur t'ghestelde, C H 75210 deur t'vervolgh van het 13 voorstel des 3 boucx, en den houck C H E 176 tr. 55 ①, als even sijnde mettē houck A C H, die halfrontschil is vande bekende grootste breede 3 tr. 5 ①: Hier me ghesocht den houck H E C, wort bevonden deur het 6 voorstel der platte driehouckē van 2 tr. 43 ①, t'welck oock is voor den houck B C E, even vallende mettē boveschreven houck A C D oock van 2 tr. 43 ①, sulcx dat volghens dese rekening G H deur den vasten Eertcloot C streckt. Maer by aldien soodanighe evenheyt niet ghecommen en waer, ghelijckt mette twee onderste Dwaelders ghebeurt, men soude dan volghen de wijse des nabeschreven 2 voorbeelts.

1 Merck

Noch is te weten dat Saturnus inrontwechs afwijcking vanden duysteraermet stelling eens vasten Eertcloots can gevonden worden opeen ander wijse, welcke alsoose noch opentlicker verclaert de ghemeenschap der twee stellinghen eens vasten en roerenden Eertcloots, soo sal ick die met een beschrijven. Laet als by manier van bereytsel ghetrocken worden D K, even en evewijdeghe met G C: Sghelijcx E L, even en evewijdeghe met H C, t'welck soo sijnde de cruysvierhouck K D E L, is even en ghelijck metten cruysvierhouck A D E B des 22 voorstels vant 3 bouck, daerom hier me ghesocht des inrontwechs C D afwijcking vanden duysteraer na de manier des selven 22 voorstels, t'ghene daer uyt comt is t'begeerde, en moet nootsakelick even sijn mettet besluyt vande voorgaende eerste wercking. En blijckt hier me sichtbaerlick hoe de form der stelling eens roerenden Eertcloots, te weten den cruysvierhouck K D E L, metten Eertclootwech K L, een selve besluyt voortbrengt als de form der stelling eens vastē Eertcloots C, en haer inront ter eender sijde G D F, ter ander H E I, want den driehouck C D G is even en gelijck metten driehouck D C K, alsoo oock is C E H met E C L, waer uyt volght dat alsulcken afwijcking als van C D bevonden wort deur de bekende palen des driehoucx D C K, soodanighe moeter oock bevonden worden deur de bekende palen des driehoucx C D G. Oock is

sghelijcx te verstaen met d'ander twee driehoucken. En sulcx als hier gheweest is het voorbeelt met Saturnus, also ist kennelick te sullen sijn met d'ander twee bovenste Iupiter en Mars.

2 Voorbeelt vande tvvee onderste Dvvaelders.

Hoewel al de letters inde form deses 2 voorbeelts van sulcke beteyckening sijn als die des eersten voorbeelts, en dat yemant achten mocht de meyning van dit deur t'eerste genouch bekent te wesen, nochtans insiende de verscheydenheyt der uyterlicke form, te weten dat hier den inrontwech veel cleender is dan het inront, daer int 1 voorbeelt de wech veel grooter was, en dat bovē dien dese wech niet deur dē Eertcloot en strect, so beschrijf ick noch dit 2 voorbeelt.

T'gegeven. Laet de deelen der volgende form A B C D E F G H I K L

illustratie

sijn van Mercurius, met sulcke beteyckening als de deelen der form des eersten voorbeelts van Saturnus, doch daer in verschillende, dat desen inrontswech D E die ghevonden sy gheweest na de manier vant werck beschreven int 1 voorbeelt, niet en strecke deur den Eertcloot C, maer sniende den duysteraer int punt M: Ten anderen daer het inront van Saturnus veel cleender viel dan sijn wech, in die plaets ist ist hier veel grooter, te weten F G in sulckē reden tot D E, als inde form des 1 voorstels deses Byvoughs de lini P Q tot Q R, voort doet den houck B C G 1 tr. 45 ①, en A C H 4 tr. 5 ① als bevondē wiert inde ervaring van Mercurius breede achter het 25 voorstel des 3 boucx. T'begheerde. Wy moeten vinden des inrontwechs D E afwijcking vanden duysteraer, dats den houck A M D.

t'Werck.

Deur des driehoucx D C G drie bekende palen, wort als op de wijse des 1 voorbeelts ghevonden den houck	C D G.
En den houck	D C G.
Daer toe den ghegheven houck	B C G.
Comt den houck	B C D.
Die ghetrocken van 180 tr. blijft den houck	D C K.
Daer toe vergaert den ghegheven houck	K C H.
Comt den houck	D C H.
Deur des driehoucx E C H drie bekende palen wort als op de wijse des 1 voorbeelts, ghevonden den houck	H C E.
Die vergaert tot D C H sevende in d'oirdē, comt den houck	D C E.
De driehouck D C E heeft drie bekende palen, te weten dien houck D C E neghende in d'oirden, en de twee linien C D, C E, vanden Eertcloot tot des inronts middelpunt, die bekent worden

deur t'vervolgh van het 13 voorstel des 3 boucx: Hier me wort ghevonden den houck	C D E.
Daer toe vergaert dē houck C D G eerste in d'oirden, comt dē houck E D G, dats oock dē houck M D G, welcke evē sijnde met A M D, om dat M D is tusschen de twee evewijdege K M, D G, soo is daer bekent de begheerde afwijcking	A M D.
T'is oock kennelick hoe ghevonden sal worden de langde der lini M C, dat is soo verre de duysteraersne vanden Eertcloot valt, want den driehouck D C M heeft drie bekende palē, te weten dē houck C D M, als wesende den houck C D E achtste in d'oirden, voort den houck M C D, als even sijnde metten houck C D G eerste in d'oirden, om dat C D is tusschen de twee evewijdeghe K C, D G, ten derden de sijde C D, met welcke drie palen als gheseyt is bekent wort de lini	M C.

Noch is te weten dat Mercurius inrontwechs afwijcking vanden duysteraer met stelling eens vasten Eertcloots can gevonden worden op een ander wijse, welcke alsoose noch opentlicker verclaert de gemeenschap der twee stellinghen eens vasten en roerenden Eertcloots, soo sal ick die met een beschtijven. Laet als by manier van bereytsel ghetrocken worden D K, even en evewijdeghe met G C: Sghelijcx E L even en evewijdeghe met H C, t'welck soo sijnde, de cruysvierhouck K D E L, is even en ghelijck metten cruysvierhouck L O M P int 3 lidt van Mercurius breede achter het 25 voorstel des 3 boucx, daerom hier me ghesocht des inrontwechs M D afwijcking vanden duysteraer na de manier des selven 3 lidts, t'ghene daer uyt comt is t'begheerde, en moet nootsakelick even sijn mettet besluyt vande voorgaende eerste wercking. En blijckt hier me sichtbaerlick hoe de form der stelling eens roerenden Eertcloots, een selve besluyt voortbrengt als de form der stelling eens vastē Eertcloots, also van dergelijcke wat breeder geseyt is achter het 1 voorbeelt.

En sulcx als hier gheweest is het voorbeelt met Mercurius, alsoo ist kennelick te sullen sijn met dander onderste Dwaelster Venus. T'beslvyt. Wesende dan ghegheven eens Dwaelders meeste noordersche en zuydersche breede, wy hebben gevonden sijn wechs afwijcking vanden duysteraer: Oock mede hoe verre de duysteraersne vanden Eertcloot valt, deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

6 Voorstel.

Tevinden eens Dvvaelders schijnbaer duysteraerbreede op een ghegheven tijt, deur vvisconstige vvercking gegront op stelling eens vasten Eertcloots.

Om t'begheerde te crijghen, wy sullen eerst vinden de lini vanden Dwaelder int inront rechthouckich op den duysteraer. Als by gelijckenis inde form des 5 voorstels deses Byvoughs, de verdochte lini van F rechthouckich opt plat des duysteraers A B: Maer sulcke lini is tot allen plaetsen des inronts, even ande lini van des inronts middelpunt als D, rechthouckich op A B, deur diē D F evewijdeghe is met A B, en daerom salmen dese altijt vinden in plaets van die, t'welck doende soo en sal de manier van t'vinden der selve geen verschil hebben, mette vinding van derghelijcke lini in stelling eens roerenden Eertcloots

beschreven int 24 voorstel des 3 boucx: De oirsaeck deser ghelijckheyt is daer deur noch kennelicker, dat den Dwaelder met stelling eens roerenden Eertcloots, comt ter plaets van des inronts middelpunt met stelling eens vasten Eertcloots. Nu dan sulcke lini alsoo bekent wordende, en daer benevens deur t'vervolgh vant 13 voorstel des 3 boucx de lini vanden vasten Eertcloot totten Dwaelder, soo heeft den rechthouckighen driehouck begrepen onder de selve twee linien, en de derdeGa naar margenoot* schoensche drie bekende palen, waer me opnbaerlick ghevonden wort de begheerde breede als int 25 voorstel des 3 boucx met stelling eens roerenden Eertcloots, sulcx dat my onnoodich ghedocht heeft het selve hier andermael int langhe te beschrijven. T'beslvyt. Wy hebben dan ghevonden eens Dwaelders schijnbaer duysteraerbreede op een ghegheven tijt, deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

Saming

Van ettelicke overeencommingen en verschillen tusschen de beschrijving des breedeloops deses Byvoughs, mette breedeloop van Ptolemeus.

Alsoo my inde voorgaende beschrijving deser stof des breedeloops, somwijlen voorvielen eenighe verscheydenheden tusschen de selve en de breedeloop by Ptolemeus beschreven, soo heeft my bequamer ghedocht die hier by den anderen te versamen, dan inde voorgaende leering te vermenghen, sulcx dat ick daer af stellen sal de volghende leden.

1 Lidt.

Anghesien d'oirsaeck des breedeloops der Dwaelders ghetrocken wort uyt stelling eens roerenden Eertcloots die tot Ptolemeus tijt onbekent scheen, soo heeft hy nochtans int veroirdenen der spiegheling vande drie bovenste, de sake al seer na ghecommen, stellende het inront te wijle het loopt altijt bycans evewijdichvanden duysteraer te blijven, want soo hy dat gelijck de sake vereyscht, en int 2 voorstel des Byvoughs bewesen is te moeten sijn, voor heel evewijdich ghenomen hadde (t'schilde als blijckt int 3 Hooftstick sijns 13 boucx in Saturnusloop alleenelick 2 tr. 4 ①, dat den houck gemaeckt vant inront mette wech, ten alderhoochsten grooter was dan den houck gemaeckt vande wech metten duysteraer: In Iupiter was sulck verschil alleenelick van 1 tr. 6 ①, in Mars van 1 tr. 15 ①, ja het inront anden duysteraer sijnde, t'wasser volgens sijn stelling teenemael in sonder snyen, ghelijck na de volcommen spiegheling sijn moet) soo en waer de tastende onseker wercking int soucken vande afwijcking der inrontswegen beschreven int selve 3 Hooftstick niet noodich gheweest, en souden d'ander rekeninghen van der Dwaelders breeden, dan deurgaens overeenghecommen hebben met dese, sonder daer af inde rest soo te verschillen als int volghende 2 lidt gheseyt sal worden.

2 Lidt.

Ptolemeus tafel van Saturnus breedeloop int 5 voorstel sijns 13 boucx, en schijnt geen genouchsaem overeencomming te hebben met sijn spiegheling. Om van t'welck breeder verclaring te doen, soo is te weten dat hy int 4 voorstel

vant selfde 13 bouck, des inrontwechs afwijcking vanden duysteraer, die inde eerste form vant 5 voorstel deses Byvoughs beteyckent sy metten houck A C D neemt op	2 tr. 26 ①.
Den houck C D G op	4 tr. 30 ①.
Het halfrontschil van dien doet voor den houck C D F	175 tr. 30 ①.
By aldien nu vanden Eertcloot C, tot des inronts verstepunt F, wesende mettet middelpunt an sijn wechs verstepunt D, getrocken waer de lini C F, sy soude doen deur de Byeenvouging des 13 voorstels vant 3 bouck	108718.
Waer me sulcke driehouck C D F drie bekende palen soude hebbē, te weten dē houck C D F 175 tr. 30, derde in d'oirden, D F 10000, en C F 108718 vierde in d'oirden: Hier me ghesocht den houck D C F, wort bevondē deur het 5 voorstel der platte driehouckē vā	25 ①.
Die ghetrocken vanden houck A C D 2 tr. 26 ① eerste in d'oirden, blijft voor den houck A C F	2 tr. 1 ①.

En soo veel moet volghens Ptolemeus spiegeling wesen Saturnus breede als hy is an des inronts verstepunt F, met des inronts middelpunt an sijn wechs verstepunt D. Maer volgens t'gebruyck der boveschrevē tafels, so is hy dan sonder breede, waer deur die tafels soo veel van haer spiegheling verschillen.

En doēde dergelijcke op d'ander sijde als Saturnus is ant inrōts verstepunt I, men sal sijn breede bevinden van 1 tr. 58 ①, in welcker plaets hy volghens de tafels sonder breede bevonden wort. Inder vougen dat, volghens t'ghene ick voorgenomen hadde te verclarē, Ptolemeus tasel van Saturnus breedeloop geē genouchsaem overeencomming en schijnt te hebbē met sijn spiegelingen. En̄ dergelijcke is oock te verstaen vande tafels en spiegelingē der Dwaelders Iupiter en Mars. Maer hoe groot soodanighe breeden vallen met stelling eens roerenden Eertcloots, dats openbaer deur het 25 voorsteldes 3 boucx.

3 Lidt.

Int 1 lidt is geseyt dat Ptolemeus niet verre vande rechte spiegheling en was, stellende de inronden vande drie bovenste Dwaelders altijt bycans evewijdich vanden duysteraer te blijven, maer sulcx en is mette twee onderste soo na niet geluckt, waer af hy uyt sijn gageslagen ervaringen niet sulcken wijse van spiegeling trecken en conde, als hy uyt de drie bovenste gedaen hadde: De voornamelicste oorsaeck die hem verhinderde schijnt tweederley, d'eerste dusdanich: T'gene hy Mercurius inront noemde en daer voor gebruycte en wast niet deur het 1 voorstel deses Byvoughs, maer veel cleender dan na t'behooren, sulcx dat als hy t'selve al prouvende annam voor altijt bycans evewijdich vanden duysteraer te blijven, gelijck hy mette inronden der drie bovenste dede, dat en hadde mette ervaringen geen gemeenschap, want het was t'ander groot ront datmen daer toe nemen moest. D'ander oirsaeck te weten die hem de waggeling des inrontwechs dede besluyten, en de duysteraersne op een verkeerde sijde nemen, schijnt dat dusdanich was: Hy heeft sich in gebeelt alle gemeene sneen der inrontwegen en des duysteraers deur den Eertcloot te strecken: Als by voorbeelt dē inrontwech D E, die inde form des 5 voorstels deses Byvoughs dē duysteraer eygentlick in M deursnijt, heeft hy ghemeent te strecken deur den vasten Eertcloot C, waer op hy sijn rekeningē makende, soo isser uyt gevolght dat doen hy meende het inronts middelpunt gecommē te wesen van D tot C, en alsdan behoiren inden duysteraer A B te wesen sonder breede, soo bevant hijt metter

daet daer buyten an N (welverstaende dat D N even geteyckent is an D C) met soo veel breede als veroirsaeckt wort deur de verheyt van C tot N, welcke misgrijping hem heeft doē des inrontwechs waggeling versieren, die beschreven is int 2 lidt van Mercurius breede achter het 25 voorstel des 3 boucx.

4 Lidt.

Maer angesien Ptolemeus de voorschreven waggeling des Dwaelders van C tot N, seyde deur ervaring in Mercurius bevondē te hebben van 45 ①, soo sullē wy nu ondersouckē hoe sulcx hier me overeencomt: Tot dien einde segh ick dat de verheyt van C tot N, anghewesen wort mette lini N R inde form des 3 lidts van Mercurius loop achter het 25 voorstel des 3 boucx, diens langde ick aldus vinde: De driehouck Q N R heeft drie bekende palē, te weten dē houck N Q R 5 tr. 32 ①, als even sijnde met O Q L 5 tr. 32 ① deur des voorschrevē 3 lidts vierde in d'oirden, Q N 1364 deur des selfden lidts vijfde in d'oirden, en den houck Q N R recht: Hier me ghesocht de lini N R, wort bevonden deur het 4 voorstel der platte driehoucken van 132.

By aldien my Ptolemeus verclaert hadde, tot wat plaets de Son was ten tijde van sijn dadelicke ervaringē doen hy de afweging van 45 ① vandt, waer deur ons met stelling eens roerenden Eertcloots bekent soude sijn des selven Eertcloots plaets, soo mochten wy na die overeencommingen met meerder sekerheyt trachten, maer dat niet gheschiet sijnde, wy sullen de twee uyterste afwijckinghen soucken om te sien ofter de 45 ① oock tusschen vallen, als volght:

Doende de lini N R als vooren 132, en datmen daer an vervought na de manier des 25 voorstels int 3 bouck de meeste verheyt van Mercurius totten Eertcloot, doende deur de Byeenvouging des 13 voorstels vant 3 bouck 14519, soo wort deur de gemeene regel des selfden 25 voorstels Mercurius breede daer me bevonden van 31 ①: Maer van 1 tr. 21 ① op de minste verheyt 5481, tusschen welcke 1 tr. 21 ① en 31 ①, de boveschreven 45 ① der ervaring sijn. Soo nu bekent waer de lini vanden Eertcloot tot Mercurius ten tijde der ervaring, mē soude als geseyt is van dese overeencomming noch eygentlicker connē sprekē.

Angaende Venus afweging welcke Ptolemeus stelt op 10 ①, die soude na de voorgaende wijse van Mercurius ten cleensten bevonden worden van 20 ①: Watter eyghentlick af is, daer soudemen deur nieuwe dadelicke gaslaginghen nauwer af connen oordeelen.

Beslvyt des breedeloops.

Tot hier toe is vande breedeloop der vijf Dwaelders Saturnus, Iupiter, Mars, Venus en Mercurius, beschreven t'ghene ick voor my ghenomen hadde, waer me ick oock meyne de selve niet meer voor soo een onbekent roersel behooren ghenomen te worden ghelijckmen ghedaen heeft, als blijckende deur des Eertcloots loop sulcke verscheydenheden nootsakelick te moeten vallen, en elck Dwaelders hemel eenvoudelick te draeyen op haer as, sonder datmen behouft eenich onnatuerlick roersel daer by te versieren, en datmen al die voorgaende tijtslijtighe haspeling sal moghen verlaten, oock met oirsakelicker kennis sich voortaen daer in oeffenen.

margenoot*: Theoremata.

margenoot*: Problemata.

margenoot⋆: Deferens epiryclorum.

margenoot*: Hypothenusae

Vorige Volgende