Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift
(1608)–Simon Stevin–1 Lidt.Want mijn gevoelen is datter by de menschen eertijts een grondelicker ervarentheyt gheweest heeft, vande Dwaelders langdeloop met stelling eens roerenden Eertcloots, soo vermoede ick daer uyt by hemlien oock kennis geweest | |||||||||||||||||||
[pagina 298]
| |||||||||||||||||||
te sijne van der selve breedeloop, om datse, alsmender wat op let ghenouchsaem heur selven daer in openbaert, sulcx dat ick meen Ptolemeus gagheslaghen ervaringhen van dies niet d'eerste te wesen, maer datmender voor hem al dapperlick op ghelet, en spiegheling daer af gheformt heeft, doch de selve ter handt van hem noch niemant anders gecommen sijnde, datmen weet, soo sullen wy danckbaerlick annemen den vlietighen arbeyt by hem hier in ghedaen, sonder welcke het nu swaerlick soude by commen tot bescheyt deses handels te geraken, ghemerckt men te weynich gaslaghers vindt. Om dan totte sake te commen ick segh aldus: Ghelijckmen tottet soucken der ghedaente vande Sonnens schijnbaer evenaerbreede, en vande Manens schijnbaer duysteraerbreede, ten eersten tracht dadelick te vinden haer meeste afwijckinghen na het Zuyden en Noorden, om daer deur te commen tot kennis der plaets vande duysteraersne, en de rest dies angaende, alsoo heeft Ptolemeus int dadelick ondersoucken der ghedaente van Saturnus schijnbaer duysteraerbreede, ten eersten ghetracht na sijn meeste afwijckingen, en die bevonden op de Noortsijde van 3 tr. 2 ① (soo staetse in sijn tafel) ghebeurende altijts als sijn inronts middelpunt schijnbaerlick was 50 tr. voor sijn wechs verstepunt, te wetē onder des duysteraers 183 tr. en Saturnus an des inronts naestepunt: Maer buyten het naestepunt wesende, soo was sijn Noordersche afwijcking voor datmael cleender, ende ten minsten doen hy alsoo ant verstepunt was, want hoewel hy dat dadelick niet sien en conde, deur dien Saturnus doen by de Son was, soo merckte hijt nochtans by gissing deur de daghelicksche minderinghen die hy in sijn uyterste verschijninghen gade slouch. | |||||||||||||||||||
2 Lidt.Op de Zuytsijde bevant hy de meeste afwijcking van 3 tr. 5 ①, ghebeurende altijt als sijn inronts middelpunt was onder het teghenoverpunt des boveschreven 183 tr. dats onder des duysteraers 3 tr. en Saturnus an sijn inronts naestepunt: Maer buyten het naestepunt wesende, soo was sijn Zuydersche afwijcking voor datmael cleender, en ten minsten doe men hem alsoo an het verstepunt vandt. | |||||||||||||||||||
3 Lidt.Tot hier toe is gheseyt van Saturnus eyghenschappen wesende het inronts middelpunt an sijn wechs grootste afwijckingen, maer wesende tusschen beyden in een der duysteraersneen twee uytersten, soo bevant hy Saturnus altijt int plat des duysteraers sonder breede, tot wat plaets des inronts hy oock mocht wesen. | |||||||||||||||||||
4 Lidt.Het schijnbaerlickste dat Ptolemeus bedencken conde van d'oirsaeck deses seltsaem roersels, om daer op een spiegheling te gronden, deur welcke men Saturnus breede op alle toecommende tijden berekenen en van te vooren weten mocht, heeft hy beschreven int 3 hooftstick sijns 13 boucx, waer af den sin dusdanich is. Laet A B t'plat des duysteraers beteyckenen overcant ghesien, diens middelpunt dats den vasten Eertcloot C, waer deur ghetrocken is de wech D E, en streckende C D op de Noortsijde na des duysteraers 183 tr. als int 1 lidt, sulcx | |||||||||||||||||||
[pagina 299]
| |||||||||||||||||||
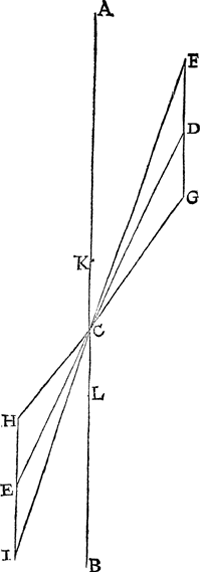 dat de twee houckē A C D, B C E des wechs afwijcking bediē, en op sijn uyterste punt D na het Noordē als middelpunt is beschrevē tinront F G bycans evewijdich mettē duysteraer A B, diēs naestepunt G, verstepunt F, vā welcke getrockē sijn de twee liniē G C, E C. Ick heb hier geseyt bycans evewijdich, deur dien t'verschil seer cleē is, alleenelick vā 2 tr. 4 ①, want dē houck A C D berekēde hy op 2 tr. 26 ①, en C D G op 4 tr. 30 ①, welcke twee houckē om volcommē evewijdicheyt te hebben evegroot soudē moetē sijn. Dese boveschrevē rondē wordē altemael gelijck vanden duysteraer geseyt is verstaē overcant gesiē te sijn. Voort wesende Saturnusant inronts naestepunt G, so wiert sijn schijnbaer afwijcking vandē duysteraer, dats dē houck A C G, ten grootstē bevonden van 3. tr. 2 ① daer afgheseyt is int 1 lidt. Maer buyten het naestepūt sijnde, als neem ick voor D, of an F, so was sijn Noordersche afwijcking voor datmael cleender, en ten minsten ant verstepunt F wesende, want cleender is dē houck A C F dā A C D. Maer om dergelijcke verclaring oock te doen op de Zuytsijde, so laet op des wechs uyterste punt Eals middelpūt. beschreven sijn het inront H I, oock bycans evewijdich mettē duysteraer A B, diens naestepunt H, verstepunt I, van welcke getrockē sijn de twee liniē H C, I C. Voort wesende Saturnus ant inronts naestepunt H, so wiert sijn afwijcking vanden duysteraer, dats den houck B C H, tē grootstē bevonden vā 3 tr. 5 ①, daer af geseyt is int 2 lidt, maer buyten het naestepunt sijnde, als neem ick voor E of in I, soo was sijn Zuydersche afwijcking voor datmael cleender, en tē minsten ant verstepunt wesende, want cleender is den houck B C I dan B C E. Dese twee eyghenschappen der afwijcking als het inront is ande uytersten D E aldus beschreven sijnde, wy sullen nu commen totte verclaring van d'oirsaeck der eyghenschappen verhaelt int 3 lidt, te weten alst tusschen beyden is. Ptolemeus ghevoelt dat commende het inront van D na de duysteraersne, het blijft daerentussch en altijt bycans evewijdich metten duysteraer, te weten soo gematicht, dat wesende het inront F G voor C, sijn plat is dan altijt teenemael int plat des duysteraers, als ter plaets van K L, en alsdan soo moetmē gelijck int 3 lidt gheseyt is, Saturnus altijt bevinden inden duysteraer sonder breede, tot wat plaets des inronts hy oock wesen mocht: Ende op sulcke spiegheling heeft Ptolemeus sijn voorstellen, tafelen en rekeninghen ghemaeckt, welcke ick na mijn stijl beschreven hadde, op dattet anderen tot hulp mochte strecken die na beter spiegheling trachten wilden, maer daer na ghevonden hebbende t'gene ick meen uyt kennis der oirsaken te commen, ghelijck ick dat int volgende beschrijven sal, heb sulcx onghedruckt ghelaten, ghenouch achtende de eyghen- | |||||||||||||||||||
[pagina 300]
| |||||||||||||||||||
schappen der eerste ervaringhen deur Ptolemeus met seltsaem yver en neersticheyt gagheslagen, int gemeen aldus verclaert te wesen, en daer me te commen totte voorghenomen spiegheling ghegront op stelling eens roerenden Eertcloots. T'beslvyt. Wy hebben dan beschreven Ptolemeus dadelicke ervaringhen van Saturnus schijnbaer duysteraerbreeden, dienende om daer uyt gemeene reghel te trecken van sijn breedeloops eyghenschappen, na den eysch. | |||||||||||||||||||
21 Voorstel.Te vinden de vvechlangden der tvvee punten van Saturnusvvechs schijnbaer grootste afvvijckingen vanden duysteraer, metsgaders de cortste verheden vanden Eertclootvvech totte selve tvvee punten. Oock me de langde der heele lini vant een punt dier grootste afvvijcking tottet ander, in sulcke deelē alsser des Eertclootvvechs halfmiddellijn 10000 doet, deur vvisconstighe vvercking gegront op stelling eens roerenden Eertcloots. T'ghegheven. Laet A B C D Saturnuswech beteyckenen, diens middelpunt E, des eertclootwechs middelpunt F, waer op beschreven is den Eert- 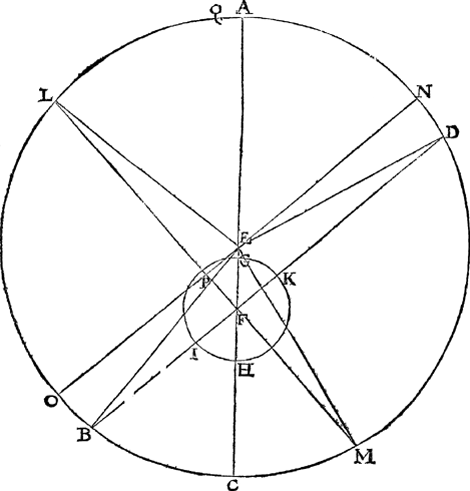 | |||||||||||||||||||
[pagina 301]
| |||||||||||||||||||
clootwech G H, en ghetrocken deur de twee punten F E Saturnuswechs middellijn A C, soo is A t'verstepunt, wesende onder des duysteraers 233 tr. deur het 13 voorstel deses 3 boucx, ende want deur het 1 lidt des 20 voorstels, Saturnus grootste Noordersche afwijcking gebeurde als hy schijnbaerlick was 50 tr. voor des duysteraers 233 tr. soo treck ick deur t'punt F de lini B F D, sniende den Eertclootwech in I en K, soo dat den houck A F D doe de selve 50 tr. en sullen daer me D en B sijn de twee punten van Saturnuswech daer hy schijnbaerlick in sijn grootste afwijckinghen vanden duysteraer can gesien worden, en dat uyt de punten K en I. T'begheerde. Wy moeten vinden de wechlangde der twee punten B en D, dat sijn de twee boghen A B en A B D, voort de cortste twee verheden K D, I B, vanden Eertclootwech totte selve twee punten, oock me de langde der heele lini vant een punt dier grootste afwijcking tottet ander, in sulcke deelen alsser des Eertclootwechs halfiniddellijn 10000 doet. T'bereytsel. Laet ghetrocken sijn E B, E D. | |||||||||||||||||||
t'Werck.
Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wy hebben dan ghevonden de wechlangden der twee punten van Saturnuswechs schijnbaer grootste afwijckingen vandē duysteraer, metsgaders de cortste verhedē vanden Eertclootwech totte selve twee punten, oock me de langde der heele lini vant | |||||||||||||||||||
[pagina 302]
| |||||||||||||||||||
een punt dier grootste afwijcking tottet ander, in sulcke deelen alsser des Eertclootwechs halfmiddellijn 10000 doet, deur wisconstighe wercking ghegront op stelling eens roerenden Eertcloots, na den eysch. | |||||||||||||||||||
22 Voorstel.Te vinden Saturnusvvechs afvvijcking vandē duysteraer. Metsgaders hoe verre de duysteraersne van des Eertclootvvechs middelpunt valt, in sulcke deelen alsser des Eertclootvvechs halfmiddellijn 10000 doet, deur vvisconstighe vvercking ghegront op stelling eens roerenden Eertcloots. T'ghegheven. Laet de lini A B den Eertclootwech bedien overcant ghesien, die ick even teycken an des Eertclootwechs middellijn I K inde form 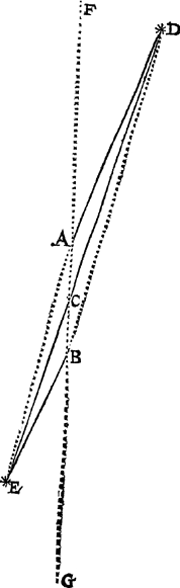 des 21 voorstels, C sy t'middelpunt, daer na treck ick dese D E, even met die D B inde selve form des 21 voorstels, doēde 1844959, en dese C D evē met die F D, dese C E even met die F B, en sniende dese twee linien malcander in of ontrent C, sulcx dat dē houck der afwijcking dier twee platten is A C D, en A D sy de lini vanden Eertcloot an A, tot Saturnuswechs uyterste noortsche punt der awijcking doēde deur het 21 voorstel 85610, wesende daer de lini K D: Sgelijcx sy B E de lini vanden Eertcloot an B, tot Saturnuswechs uyterste zuytsche punt der afwijcking E, doende deur het selve 21 voorstel 78849, welcke daer beteyckent is met F B, daer na A B an weder sijden verlangt wesende tot Fen G, soo sijn A F en B G int plat des duysteraers, en Saturnus meeste noordersche breede sy dē houck F A D, doende deur het 5 lidt des 20 voorstels 3 tr. 2 ①, maer sijn meeste zuydersche breede dē houck G B E, doende deur het 2 lidt des 20 voorstels 3 tr. 5 ①. T'begeerde. Wy moeten vinden Saturnuswechs afwijcking vanden duysteraer, dats dē houck A C D, metsgaders hoe verre de duysteraer sne van des Eertclootwechs A B middelpunt C valt. | |||||||||||||||||||
t'Werck.De cruysvierhouck A B D E heeft vijfbekende palen, te weten de sijde A B middellijn des Eertclootwechs 20000 deur t'ghestelde: Boven dien soo doet deur t'ghegheven A D 85610, B E 78849, den houck D A B 176 tr.58 ①, want soo veel blijfter alsmen treckt F A D 3 tr. 2 ①, vant halfront, en den houck E B A 176 tr. 55 ①, want soo veel | |||||||||||||||||||
[pagina 303]
| |||||||||||||||||||
blijfter alsmen treckt G B E 3 tr. 5 ① vant halfront: Merct noch dat benevens de boveschreven vijf bekende palen, tot meerder gerief bekent sijn drie ander, te weten D E lini tusschen de twee punten der uyterste breeden van Saturnus, doende deur het 21 voorstel deses 3 boucx 1844959, de lini A E 98849, als evē ghenouch sijnde met A B 20000, en B E 78849 t'samen: Voort de lini B D 105610, als even genouch sijnde met A B 20000, en A D 85610 t'samen: Hier me ghesocht den houck A C D, wort bevonden deur het 6 voorstel inde Byvough der platte veelhoucken voor Saturnuswechs begeerde afwijcking vanden duysteraer 2 tr. 43 ①, waer voor Ptolemeus int 3 Hooftstick sijns 13 boucx al tastende vandt 2 tr. 26 ①. Angaende de verheyt der duysteraersne van des Eertclootwechs middelpunt C, sy wort ghenouchsaem bevonden daer in te vallen, want onder verscheyden neminghen der palen daer t'werck deur gedaen can worden, soo viel my deur de ghene die ick nam den houck A D C van 19 ①, waer me des driehoucx D A C drie bekende palen, te weten de twee houcken A D C, D C A, en de sijde A D my uytbrochten de lini A C van 10294, t'welck te veel is 294, want om volcommen te wesen soudet sijn 10000, maer t'schilt soo weynich dat nemende voor den houck A D C 18 ①, in plaets van 19 ① als vooren, soo comt dan voor A C 9732, t'welck 268 weynigher is dan de volcommenheyt vereyscht, sulcx datment daer voor houden mach de duysteraersne te vallen deur des Eertclootwechs middelpunt C, overeencommende mette rekening die Ptolemeus op sijn spiegheling ghemaeckt heeft, aldaer vallende deur den vasten Eertcloot, want de selve in die stelling sulcx wat is als des Eertclootwechs middelpunt inde hare, ghelijck ick int 18 voorstel deses 3 boucx daer af wat verclaring ghedaen heb. Merckt noch dat ander manier van wercking dan de voorgaende mach gedaen worden, met eerst te vinden de lini C D (dat is van des Eertclootwechs middelpunt tot Saturnus ter ghegheven plaets sijns wechs) deur het 6 lidt des 15 voorstels deses 3 boucx, want die bekent sijnde, soo heeft den driehouck A D C drie bekende palen, te weten benevens die C D noch de lini A D, en dē houck A C D, waer me d'ander onbekende palen ghevonden worden. T'beslvyt. Wy hebben dan gevonden Saturnuswechs afwijcking vanden duysteraer: Metsgaders hoe verre de duysteraersne van des Eertclootwechs middelpunt valt, in sulcke deelen alsser des Eertclootwechs halfmiddellijn 10000 doet, deur wisconstighe wercking ghegront op stelling eens roerenden Eertcloots, na den eysch. | |||||||||||||||||||
Merck inhovdende verclaring dat Saturnus breedeloop seker ghetuychnis gheeft vant roersel des Eertcloots.Alsmen met stelling eens vasten Eertcloots seght Saturnus inronts middelpunt te wesen ande duysteraersne, soo bevintmen hem metter daet altijt int plat des duysteraers sonder breede, tot wat plaets hy oock int inront sijn mocht deur het 3 lidt des 20 voorstels, t'welck voor een wonder gehouden sijnde, soo heeft Ptolemeus daer toe verdocht sulcke spiegheling als beschreven is int selve 20 voorstel, maer met dese stelling eens roerendē Eertcloots sietmē alles nootsakelick te moeten volghen uyt de eenvoudighe draeying van Saturnus hemel op haer as, sonder yet nieus of vreemts daer by te moeten versieren, en datmen sich met reden verwonderen mocht, sooment anders bevonde, want commen- | |||||||||||||||||||
[pagina 304]
| |||||||||||||||||||
de by voorbeelt gheseyt, Saturnus van E tot dat hy is ande duysteraersne voor C, soo is hy dan int plat des duysteraers, en wantter den Eertcloot nummermeer buyten en loopt, soo volght daer uyt dat tot wat plaets haers wechs den selven Eertcloot dan is, soo en can Saturnus van daer niet dan inden duysteraer ghesien worden: En is onder anderen hier me het roersel des Eertcloots soo openbaer, dat ment by de ghene diet ontkennen, voorghebreck van ervarentheyt houden mach. | |||||||||||||||||||
23 Voorstel.Te vinden de vvechlangde der tvvee uyterste punten vande duysteraersne, en vande tvvee uyterste punten der afvvijcking in Saturnusvvech, oock der lini die vā Saturnusvvechs middelpunt op de duysteraersne rechthouckich valt in sulcke deelen alsser des Eertclootvvechs halfmiddellijn 10000 doet, deur vvisconstige vvercking ghegront op stelling eens roerenden Eertcloots.
T'ghegheven. Anghesien ick om mijn voornemen wel te verclaren hier soude moeten verteyckenen de form des 21 voorstels, om daer noch by te vervougē t'gene in dit voorstel vereyscht is, soo sal ick de voorschrevē form des 21 voorstels self daer toe gebruyckē, tot welcken einde ick aldus segh: Nadien de duysteraersne deur des Eertclootwechs middelpunt streckt, volgens t'inhout des 22 voorstels, soo treck ick inde form vant 21 voorstel deur des Eertclootwechs middelpunt F de lini L M, als duysteraersne rechthouckich op D B, van wiens twee uyterste punten L, M, ick treck de twee linien L E en M E: Treck daer na deur t'punt E Saturnuswechs middellijn N O evewijdeghe met D B, en sniende L M in P. T'begheerde. Wy moeten vinden de wechlangden van L', M, wesende de twee uyterste punten vande duysteraersne L M; Sghelijcx de wechlangde van N O, wesende de uyterste punten der afwijcking in Saturnuswech, ende E P langde der lini die van Saturnuswechs middelpunt E op de duysteraersne L M rechthouckich comt. | |||||||||||||||||||
t'Werck.
| |||||||||||||||||||
[pagina 305]
| |||||||||||||||||||
Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wy hebben dan ghevonden de wechlangde der twee uyterste punten vande duysteraersne, en vande twee uyterste punten der afwijcking in Saturnuswech, oock der lini die vā Saturnuswechs middelpunt op de duysteraersne rechthouckich valt, in sulcke deelen alsser des Eertclootwechs halfmiddellijn 10000 doet, deur wisconstighe wercking ghegront op stelling eens roerenden Eertcloots, na den eysch. | |||||||||||||||||||
Vervolgh.T'is kennelick dat Saturnus in sijn wech vanden 42 tr. 6 ① derde in d'oirden, dats inde form des 21 voorstels van L over B tot M, altijt Zuyderlick moet wesen, maer vanden 217 tr. 54 ① vierde in d'oirden, totten 42 tr. 6 ①, dats van M over A tot L altijt Noorderlick: Om t'welck noch opentlicker te verclaren, merckt dat de voorschreven booch van L over B tot M doende 217 tr. 54 ①, inde form des 22 voorstels anghewesen is deur de lini C F, waer me t'selve rontsdeel L B M beteyckent wort overcant ghesien te wesen: T'welck soo sijnde, Saturnus en can in C E der form des 22 voorstels tot sulcken plaets niet wesen, dat hy ghesien uyt den Eertcloot tot wat plaets die oock in haer wech A B mocht wesen, anders verschijne dan op de Zuytsijde des duysteraers F G: En sghelijcx en can hy int deel C D der form des 22 voorstels (beteyckenende het boveschreven rontsdeel M A L der form des 21 voorstels) tot sulckē plaets niet wesen, dat hy ghesien uyt den Eertcloot, tot wat plaets die oock in haer wech A B mocht wesen, anders verschijne dan op de Noortsijde des duysteraers F G. | |||||||||||||||||||
24 Voorstel.Te vinden de langde der lini die van een gegeven punt in Saturnusvvech rechthouckich valt opt plat des duy- | |||||||||||||||||||
[pagina 306]
| |||||||||||||||||||
steraers, in sulcke deelen alsser des Eertclootvvechs halfmiddellijn 10000 doet, deur vvisconstighe vvercking gegront op stelling eens roerenden Eertcloots. T'ghegheven. Laet A B C D Saturnus hemel sijn, diens middelpunt E, waer deur ghetrocken is de rechte B E D (van gedaente als N E O inde form des 21 voorstels) beteyckenende Saturnuswech overcant gesien, daer in t'punt 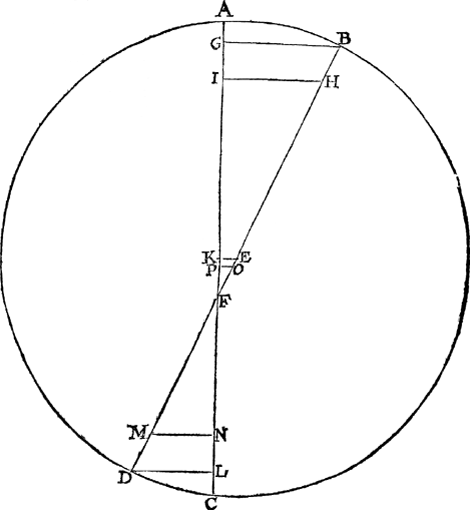 F sy de duysteraersne oock overcant ghesien, soo dat E F (even an E P int 21 voorstel) is de lini die van Saturnuswechs middelpunt op de duysteraersne rechthouckich comt, doende deur het 23 voorstel 3378, daer na ghetrocken deur t'punt F de rechte A F C, bediende t'plat des duysteraers overcant ghesien, ende den houck B F A, wesende de afwijcking des wechs van t'plat des duysteraers doet deur het 22 voorstel deses 3 boucx 2 tr. 43 ①. T'WERCK. | |||||||||||||||||||
1 Voorbeelt.Ghenomen ten eersten dat hier in ghevonden moet sijn de langde der lini B G, die van des wechs meeste afwijcking B, rechthouckich valt opt plat des duysteraers A C. Om daer toe te commen ick segh des wechs halfmiddellijn E B te doen 92308 deur het Byeenvoughsel vant 13 voorstel deses 3 boucx, en F E 3378 deur t'ghegheven, welcke vergaert maken t'samen 95686 voor de lini F B, waer me de driehouck B F G drie bekende palen heeft, te weten de sijde | |||||||||||||||||||
[pagina 307]
| |||||||||||||||||||
F B 95686, den houck B F G 2 tr. 43 ①, en den houck B G F recht deur t'ghegheven: Hier me ghesocht de sijde B G, wort bevonden deur het 4 voorstel der platte driehoucken voor t'begheerde van 4535. | |||||||||||||||||||
2 Voorbeelt.Ghenomen ten tweeden dat gevonden moet sijn de lini H I, commende uyt des wechs 30 trap, van t'punt der uyterste afwijcking B ghetelt, maer want die lini even is ande lini dieder valt uyt des wechs halfmiddellijn E B, van t'punt H als uyterste des houckmaet pijls B H, van 30 tr. soo laet ons E B ansien voor wechs halfmiddellijn, waer in E H sal sijn houckmaet van 60 tr, dats van t'vierendeelrontschil der ghegeven 30 tr. doende die houckmaet 8660. Dit soo sijnde ick segh aldus: Doende de halfmiddellijn EB 10000, soo doet E H 8660, wat sal E H doen wesende E B ghestelt op 92308? comt alsdan voor E H 79939, daer toe vergaert E F doende deur t'ghegeven 3378, comt voor F H 83317, waer me de driehouck H F I drie bekende palen heeft, te weten de sijde F H 83317, den houck H F I 2 tr. 43 ①, en den houck H I F recht: Hier me ghesocht de sijde H I, wort bevonden deur het 4 voorstel der platte driehoucken voor het begheerde van 3949. En̄ is kennelick H I te commen uyt Saturnuswechs 340 tr. want dese B wort inde form des 21 voorstels beteyckent met N, wesende in des wechs 310 tr. deur het 23 voorstel, waer toe de 30 tr. comt als vooren 340 tr. Merckt nu dat sulcx als hier gheweest is de manier van t'vinden der lini H I tusschen E en B, ofte int halfront E B, alsoo salse oock sijn tot allen plaetsen int selve halfront. | |||||||||||||||||||
3 Voorbeelt.Ghenomen ten derden dat gevonden moet sijn de lini E K, commende uyt des wechs 90 tr. van t'punt der uyterste afwijcking D ghetelt. Om daer toe te commen, ick segh dat anghesien E F doet 3378 deur t'ghegeven, soo heeft den driehouck E F K drie bekende palen, te weten F E 3378, den houck E F K 2 tr. 43 ①, en den houck E K F recht: Hier me ghesocht de sijde E K wort bevonden deur het 4 voorstel der platte driehoucken voor t'begheerde van 160. Dusdanich dan gheweest hebbende den voortganck int halfront E B, wy sullen nu derghelijcke doen int ander halfront E D. | |||||||||||||||||||
4 Voorbeelt.Ghenomen ten 4 dat ghevonden moet sijn de langde der lini D L, die van des wechs meeste Zuydersche afwijcking D, rechthouckich valt opt plat des duysteraers A C: Om daer toe te commen, ick segh des wechs halfmiddellijn E D te doen 92308 deur het Byeenvougsel vant 13 voorstel deses 3 boucx, en FE 3378 deur t'ghegheven, welcke ghetrocken vande 92308, blijft 88930, voor de lini F D, waer me de driehouck D F L drie bekende palen heeft, te weten de sijde F D 88930, den houck D F L 2 tr. 43 ①, en den houck D L F recht deur t'ghegheven: Hier me ghesocht de sijde D L, wort bevonden deur het 4 voorstel der platte driehoucken voor t'begheerde van 4215. | |||||||||||||||||||
5 Voorbeelt.Ghenomen ten vijfden dat ghevonden moet sijn de lini M N, commende uyt des wechs 30 trap van t'punt der uyterste afwijcking D ghetelt, maer want | |||||||||||||||||||
[pagina 308]
| |||||||||||||||||||
die lini even is ande lini dieder valt uyt des wechs halfmiddellijn, van t'punt M als uyterste des houckmaetpijls D M van 30 tr. soo laet ons E D ansien voor wechs halfmiddellijn, waer in E M sal sijn houckmaet van 60 tr. dats van t'vierendeelrontschil der ghegeven 30 tr. doende die houckmaet 8660: Dit soo sijnde ick segh aldus: Doende de halfmiddellijn E D 10000, soo doet E M 8660, wat sal E M doen wesende E D ghestelt op 92308? comt alsdan voor E M 79939, daer af ghetrocken E F doende deur t'ghegheven 3378, blijft voor F M 76561, waer me de driehouck M F N drie bekende palen heeft, te weten de sijde F M 76561, den houck M F N 2 tr. 43 ①, en den houck M N F recht: Hier me ghesocht de sijde M N, wort bevonden deur het 4 voorstel der platte driehoucken voor t'begheerde van 3629. Merckt nu dat sulcx als hier gheweest heeft de manier van t'vinden der lini M N tusschen F en D, alsoo salse oock sijn tot allen plaetsen tusschen F en D. | |||||||||||||||||||
6 Voorbeelt.Ghenomen ten sesten dat ghevonden moet sijn de lini O P, commende uyt des wechs 89 tr. van t'punt der uyterste afwijcking D ghetelt: Maer want die lini even is ande lini dieder valt uyt des wechs halfmiddellijn E D van t'punt O als uyterste des houckmaetpijls D O van 89 tr. soo laet ons E D ansien voor wechs halfmiddellijn, waer in E O sal sijn houckmaet van 1 tr. dats van t'vierendeelrontschil der ghegeven 89 tr. wesende die houckmaet van 175. Dit soo sijnde ick segh doende de halfmiddellijn E D 10000, soo doet E O 175, wat sal E O doen wesende E D ghestelt op 92308? comt alsdan voor E O 1615, die getrocken van E F doende deur t'ghegheven 3378, blijft voor O F 1763, waer me de driehouck O P F drie bekende palen heeft, te weten de sijde F O 1763, den houck O F P 2 tr. 43 ①, en den houck O P F recht: Hier me ghesocht de sijde O P wort bevonden deur het 4 voorstel der platte driehoucken voor t'begeerde van 84. Merckt noch dat sulcx als hier gheweest is de manier van t'vinden der lini O P tusschen E en F, alsoo salse oock sijn tot allen plaetsen tusschen E en F. T'beslvyt. Wy hebben dan gevonden de langde der lini die van een gegevē punt in Saturnuswech rechthouckich valt opt plat des duysteraers, in sulcke deelen alsser des Eertclootwechs halfmiddellijn 10000 doet, deur wisconstighe wercking ghegront op stelling eens roerenden Eertcloots, na den eysch. | |||||||||||||||||||
Vervolgh.T'is kennelick hoe datmen om de begheerde lini van Saturnuswech rechthouckich opt plat des duysteraers met lichticheyt te vinden, sal meughen maken een tafel dier linien van trap tot trap, vant verstepunt beginnende, als by voorbeelt om te hebbē de lini vallende alsoo van Saturnuswechs eersten trap, ick neem voor my de form des 21 voorstels, daer in teyckenende t'punt Q, alsoo dat van des wechs verstepunt A tot Q 1 tr. beteyckent, waer uyt volght N Q te doē 51 tr. (want de wechlangde van N doet deur het 23 voorstel 310 tr. wiens rontschil voor NA 50 tr. daer toe A Q 1 tr. comt als boven voor N Q 51 tr.) daerom alsmen deur dit 24 voorstel vindt de hanghende vanden 51 tr. van B afghetelt (ghelijck vooren mette hangende H I van 30 tr. gedaen wiert) men heeft t'begheerde, om dat die lini vallen sal uyt Saturnuswechs 1 tr. en alsoo met alle ander. Merckt noch dat wanneer dese dinghen niet aldus voorbeeltsche wijse ghedaen en wordē, maer met ernst om op een toecommende tijt dadelick de bree- | |||||||||||||||||||
[pagina 309]
| |||||||||||||||||||
de te vinden, dattet noodich soude sijn deur dadelicke ervaring eerst te vinden waer nu des wechs verstepunts schijnbaer duysteraerlangde is: Ten anderē hoe de duysteraersne verloopen mach sijn sichtent Ptolemeus tijt (diens ervaringen ick voorbeeltsche wijse ghenomen hebbe om de redenen t'haerder plaets verclaert) want de Beschrijvers der dachtafels nemen al of den loop van Saturnus duysteraersne, even waer met des wechs verstepuntsloop altijt 50 tr. van malcander blijvende, maer daer soude nieuwe dadelicke gagheslaghen ervaring af behooren te wesen, want by aldien den loop des verstepunts en des duysteraersnees van Saturnus verscheyden sijn, ghelijck vande Maen ghebeurt, soo mocht sulcx oirsaeck wesen waer deur sijn breeden niet dadelick soo bevonden en wierden, ghelijck rekeninghen der dachtafels mebrenghen. | |||||||||||||||||||
25 Voorstel.Te vinden Saturnus schijnbaer duysteraerbreede op een ghegeven tijt, deur vvisconstighe vvercking gegront op stelling eens roerenden Eertcloots. T'ghegheven. Laet Saturnus op den ghegheven tijt wesen in sijn wechs 340 tr. alwaer de lini van hem rechthouckich opt plat des duysteraers  doē sal 3949 deur het 2 voorbeelt des 24 voorstels deses 3 boucx: En de verheyt van hem totten Eertcloot die gevonden wort na de manier verclaert int 6 lidt des 15 voor stels deses 3 boucx, wesende daer de lini X V, sy neem ick, van 80000. T'Begheerde. Wy moeten hier me vinden Saturnus schijnbaer duysteraerbreede. T'bereytsel. Ick teycken de rechthouckige driehouck A B C recht an B, doende de sijde A B de ghegheven 3949, en A C 80000. | |||||||||||||||||||
t'Werck.De driehouck A B C heeft drie bekende palen, te weten de sijde A B 3949, de sijde A C 80000, en den houck B recht: Hier me ghesocht den houck A C B, wort bevonden deur het 5 voorstel der platte driehoucken voor de begheerde breede van 2 tr. 50 ①. Maer om nu te weten of die Zuydelick of Noordelick is, dat wijst sijn wechlangde, want deur t'vervolgh des 23 voorstels blijckt, dat die wesende tusschen den 44 tr. 12 ①, ende den 215 tr. 48 ①, sy is Zuydelick, maer inde rest des wechs (daer desen 340 tr. in valt) Noordelick. Waer af t'bewijs openbaer is. T'beslvyt. Wy hebben dan gevonden Saturnus schijnbaer duysteraerbreede op een ghegheven tijt, deur wisconstighe wercking ghegront op stelling eens roerenden Eertcloots, na den eysch. | |||||||||||||||||||
Merckt.Anghesien de reghel der ses voorstellen tot hier toe van Saturnus breede beschreven, gemeen is over de breeden van d'ander vier Dwaelders Iupiter, Mars, Venus en Mercurius, soo en sal ick daer op gheen gheformde voorstellen maken, ghelijck oock verhaelt is int Cortbegrijp deses 5 Onderscheyts, maer be- | |||||||||||||||||||
[pagina 310]
| |||||||||||||||||||
schrijven alleenelick by manier van vermaen t'gene breeder verclaring schijnt te vereysschen, beginnende met Iupiter als volght. |
|

