Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

[p. 5]

Bepalinghen.

ANghesien in des driehouckhandels 4 bouck, beschreven sijn de bepalinghen der Hemelsche ronden boghen en punten die wy daer behoufden, soo houden wy de selve hier voor bekent: Sulcx dat nu ghestelt sullen worden de resterende bepalinghen int volghende noodich.

1 Bepaling.

Den tijt van dat de Sonnens middelpunt uyt het middachront gaet, tot dattet vveder daer in comt, is een^⋆ natuerlicken dach. En die natuerlicke dagen vvorden ooc⁺ oneven gheseyt. En sulcke tijt int ghemeen^⋆ oneven tijt.

Dese tijt eens natuerlicken dachs is van een keer des^* evenaers, met noch sulcken boochsken des selfden, alsser deurlijdt te wijle de Son met haer eygen loop daerentusschen te rugh ghegaen is. Nu by aldien al die boochskens evegroot waren, soo souden de natuerlicke daghen al evelanck sijn; t'welck niet en ghebeurt. De reden van dier boochskens onevenheyt is tweederhande: Ten eersten deur dien de Sonwechboochskens op dien tijt vande Son beschreven niet evegroot en sijn, om de^* uytmiddelpunticheyts wille. Ten anderen al warense evegroot, nochtans soo en gaense met gheen even boochskens des evenaers deur^* t'middachront, om de scheef heyt of afwijcking des Duysteraers. En hoe wel dit verschil op een dach ongevoelelick is, nochtans op veel daghen t'samen cant merckelick sijn.

⋆ Dies naturalis.

+ Dies inaequales.

⋆ Tempus inaequale.

* Aequatoris.

* Excentricitatem.

* Meridianū. Zodiaci.

2 Bepaling.

^⋆ Natuerlick jaer is dē tijt der Sonnens omloop, vviens begin en einde een ghenomen punt is dat altijts evevvijt vande lentsne blijft, gheduerende 365 daghen 5 uyren, met noch een onseker ghedeelte.

Ptolemeus heesr dat onseker ghedeelte boven de 5 uyren, ghestelt op 55 ① 12 ②: Albategni op 46 ① 24 ②. Ander hebben ander uytcomst bevonden.

⋆ Annus naturalis.

3 Bepaling.

Egips jaer is dat 365 daghen begrijpt.

Dese Egipsche jaren verleken by de natuerlicke verloopen alle vier jaren bycans een dach.

[p. 6]

4 Bepaling.

Iuliaensche jaren sijn vvelcker drie 365 dagen vervanghen, het vierde 366, hebbende dan de maent Februarius 29 daghen, daerse anders maer 28 en heeft.

Om t'verloop der Egipsche jaren weerom te innen, en t'natuerlickjaer naerder te commen, soo heeft Iulius Cesar den voorschreven dach alle vier jaren in Februario veroirdent, welck gedaente van jaren Iuliaensche genaemt werden.

5 Bepaling.

Soo men neemt het natuerlick jaer te hebben soo veel even dagen en even uyren met haer gedeelte, alser oneven dagen en oneven uyren met haer gedeelte in sijn: Sy vvorden^⋆ evedaghen oock middeldagen ghenoemt. En sulcken tijt int ghemeen^⋆ eventijt ende middeltijt.

Doirsaeck des naems middeldaghen, is van weghen datse middelmatich sijn tusschen de langher en corter natuerlicke daghen der 1 bepaling.

⋆ Dies aequales & dies medy.

⋆ Tempus aequale Tempus medium.

6 Bepaling.

^⋆ Dvvaelders sijn seven vveereltlichten, die int uyterlick ansien schijnen sonder regel te loopen al ofse dvvaelden, met naem Saturnus, Iupiter, Mars, Son, Venus, Mercurius, Maen.

Hoewel den Eertcloot eyghentlick me een Dwaelder is, nochtans anghesien wy om de redenen vooren int Cortbegrijp verhaelt, die nemen vast te staen, soo en wortse hier onder de Dwaelders niet ghetelt.

⋆ Planetae.

7 Bepaling.

^⋆ Uytmiddelpuntichront noemtmen diens middelpunt buyten den Eertcloot staet. Maer^⋆ middelpuntichront diens middelpunt oock des Eertcloots middelpunt is.

⋆ Excentricus circulus.

⋆ Concentricus.

[p. 7]

Laet A B C een rondt sijn diens middelpunt D, en E den Eertcloot: Dit soo wesende, A B C heet uytmiddelpuntichront. Maer soo men naem het punt D den Eertcloot te sijn, t'soude dan middelpuntich heeten.

8 Bepaling.

De lini van des uytmiddelpuntich ronts middelpunt totten Eertcloots middelpunt heet^⋆ uytmiddelpunticheytlijn.

Als indeform der 7 bepaling de lini D E.

⋆ Lineaexeentricitatis.

9 Bepaling.

Uytmiddelpuntichronts^⋆ verstepunt noemtmen dat verst vanden Eertcloot is: En^⋆ naestepunt dat den Eertcloot naest staet.

Laet inde form der 7 bepaling de uytmiddelpunticheyt D F op beyden sijden voortghetrocken worden tot in den omtreck an A, en C, Twelck soo sijnde, want het punt A, inden omtreck A B C alderverst vanden Fertcloot E is, en C aldernaest, soo wert A des uytmiddelpuntichronts A B C verstepunt genoemt, en Chet naestepunt.

⋆ Apogeum,

⋆ Perigeum.

10 Bepaling.

Dvvaeldervvech is een uytmiddelpuntichront daer in⁺ een Dvvaelder loopt.

+ Deferensvel Via Planetae.

11 Bepaling.

Wesende op een punt als middelpunt, inden omtreck

[p. 8]

eens uytmiddelpuntichronts, beschreven een cleen ront, daer in men neemt een Dvvaelder te loopen: Dat cleender heet^⋆ inront, en t'grooter^* inrontvvech.

Laet inde form der 7 bepaling op eenich punt als A des uytmiddelpuntichronts A B C beschreven worden het cleender rondt F G H daer in men neemt een Dwaelder te loopen, t'selve cleender heet inront, en t'grooter A B C inrontwech.

⋆ Epiryclus.

* Deferens eptryclum.

12 Bepaling.

Inronts verstepunt noemtmen dat verst vanden Eertcloot is: En^* naestepunt dat die naest is: Maer^* inronts middelverstepunt, dat verst van sijn vvechs middelpunt is: En^* middelnaeste punt dat die naest is.

Laet inde form der 7 bepaling de middellijn C A voortghetrocken worden tot F inden omtreck des inronts: Tselve punt F boven alle punten des inronts ten versten vanden Fertcloot E sijnde, men noemet inronts verstepunt, en H naest wesende heet naestepunt. Maer om nu te verclarē de gedaente vant middelverstepunt, en middelnaeste punt, soo laet het inront ghecommen sijn tot een ander plaets sijns wechs, ick neem met sijn middelpunt an B, daer na sy getrocken de rechte D B K, sniende den omtreck ten naesten an I, en ten versten an K: Sghelijcx de rechte E L B M, sniende den omtreck ten naesten an L, en ten versten an M: Dit soo wesende, M is om de voorgaende redenen verste punt, en L naestepunt: Maer K verst van D is middelverstepunt, en I naest D middel naestepunt: Sulcx dat dese twee verstepunten M, K, het inront daer wesende, verscheyden plaetsen hebben: Maer als het inronts middelpunt an des wechs verstepunt A, of naestepunt C is, dan sijn verstepunt en middelverstepunt een selve, alsoo oock sijn naestepunt en middelnaestepunt. D'oirsaeck des naems van middelverstepunt en middelnaestepunt is dese: Want Keen verstepunt is, t'welck uyt D ghesien altijt eenvaerdelick everas voortgaet, maer M alsnu rasscher dan tragher, tusschen welck de loop van K als middelmatich sijnde, wort middelverstepunt gheheeten.

* Apogeum epirycli vel aux vera.

* Perigeum vel oppositū augis verae, Aux epirycli media.

* Oppositum augis mediae.

13 Bepaling.

Des inronts boochsken tusschen de tvvee verstepunten noem ick^* verstepuntensbooch: T'ander tusschen de tvvee naeste punten, naestepuntensbooch.

Als t'boochsken K M inde form der 7 bepaling tusschen t'verslepunt M, en het middelverstepunt K heet verstepuntensbooch, maer I L naestepuntensbooch.

* Aequatio centri in epiryclo.

[p. 9]

14 Bepaling.

Wechs eerste halfront noem ick de booch vant verstepunt tottet naestepunt, na 'tvervolgh der trappen, dats van t'begin totten 180, d'ander booch tvveede halfront.

15 Bepaling.

Schijnbaer Dvvaelder is een punt daer hy schijnt te vvesen, doch eygentlick niet en is: En Schijnbaerloop een booch die hy schijnt te loopen, doch eyghentlick niet en loopt.

Laet A B C den Dwaelderwech beteyckenē, diens middelpunt D, en E den Eertcloot, op welcke als middelpunt beschrevē sy den Duysteraer F G H. Voort sy ghetrocken deur E D des duysteraers middellini F I, sniende den Dwaelderwech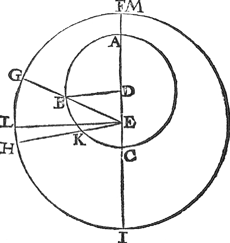



in A als verstepunt, en in C als naestepunt: En den Dwaelder sy inde wech ant punt B, deur t'welck uyt E getrocken is de rechte lini E B G. Dit soo wesende, den Dwaelder eyghentlick an B sijnde, sal uyt den Eertcloot E gesien, inden duysteraer schijnen te wesen tusschen de vaste sterren an G, en daerom heetet selve punt G schijnbaer Dwaelder. Maer so hy van B voortloopt, ick neem tot K, en deur K ghetrocken de rechte lini E K H, den Dwaelder die eyghentlick gheloopen heeft den booch B K, sal uyt den Eertcloot E ghesien schijnen gheloopen te hebben den booch G H, die metten eyghen loop B K onghelijck is: En daerom heet de selve booch G H (daermen anders oock wel voor neemt den houck B E K of G E H) des Dwaelders schijnbaerloop.

Vervolgh.

Deur dit voorbeelt van schijnbaer Dwaelder en sijn schijnbaer loop met stelling eens uytmiddelpuntighe wechs, is oock derghelijcke openbaer met stelling eens inronts.

Voort, deur t'ghene hier gheseyt is van schijnbaer Dwaelder en schijnbaer loop, is kennelick genouch watmen verstaen sal met schijnbaer booch, schijnbaer verstepunt als F, schijnbaer naestepunt als I, en dierghelijcke, welcke hier na alst de sake vereyscht ghenoemt sullen worden.

[p. 10]

16 Bepaling.

Middeldvvaelder is een verdocht punt inden duysteraer eenvaerdelick voortgaende, en altijt ant schijnbaer verstepunt vvesende, als den vvaren Dvvaelder gheen inront hebbende an sijn vvechs verstepunt is: Maer een inront hebbende, als des selfden inronts middelpunt ant verstepunt is: En sijn loop heet middelloop.

Als by voorbeelt wanneer den Dwaelder inde form der 15 bepaling is ant verstepunt A, soo isser een verdocht punt ant schijnbaer verstepunt Faltijt eenvaerdelick voortgaende, sulcx dat wanneer den waren Dwaelder weerom ghecommen is ant verstepunt A, ghedaen hebbende een volcommen keer, soo sal dat punt commen sijn an t'schijnbaer verstepunt, oock ghedaen hebbende een volcommen keer, met soo veel meer als daerentusschen het schijnbaer verstepunt geloopē heeft: Sulck punt heet Middeldwaelder, en sijn loop middelloop: De selve hier verclaert sijnde op den tijt eens volcommen keers des waren Dwaelders, wy sullen om alles noch breeder uyt te legghen, voorder verclaring doen op deel eens keers, tot welcken einde ick aldus segh: Den waren Dwaelder ghecommen sijnde ick neem van A tot B, soo sal den middeldwaelder volghende t'ghestelde daerentusschen gheloopen hebben een booch ghelijck met A B, welcke sy F L (te weten L soo ghestelt, dat E L evewijdeghe sy met D B) en noch soo veel meer als daerentusschen den loop des schijnbaer verstepunts bedraecht, t'welck sy van M tot F: Inder voughen dat M L is den middelloop overcommende in tijt met des waren Dwaelders wechloop A B, en heet middelloop, uyt oirsaeck dat soodanighe even loopen middelmatich sijn tusschen de schijnbaer rasscher en tragher.

Deur dit voorbeelt van Middeldwaelder en middelloop met stelling eens dwaelderwechs, is oock derghelijcke openbaer met stelling eens inronts, want nemende des inronts middelpunt als voor Dwaelder, soo sal al t'ghene vooren gheseyt is daer op overcommen.

17 Bepaling.

Voordering is t'ghene den vvaren Dvvaelder in den⁺ duysteraer schijnbaerlick voorder is dan den Middeldvvaelder: En^* achtering t'gene hy schijnbaerlick meer achtervvaert is. En deser tvvee ghemeene naem vvort^* voorofachteringh gheseyt.

Als by voorbeelt den waren Dwaelder inde form der 15 bepaling geloopen hebbende van A tot B, en schijnbaerlick sijnde an G, soo sal daerentusschen den Middeldvvaelder geloopen hebbē de booch F L gelijck met A B: Twelck soo wesende, dē Dwaelder is in dē duysteraer an G schijnbaerlick meer achterwaert dan den Middeldwaelder L, soo veel als de booch G L, en daerom heet de selve booch G L achtering, welcke achtering overal int eerste halfront des

+ Additio.

* Diminutio.

* Prosta phaeresis.

[p. 11]

wechs ghebeurt. Maer als sulcx met voordering valt, t'welck overal int tweede halfrondt gheschiet, men noemet voordering, en soodanighe twee int gheghemeen voorofachtering.

Merckt noch datmen soo wel den houck D B E, als de booch G L, achtering des Dwaelders noemt, om dat de ghetalen haerder tr. even sijn, uyt oirsaeck dat G L booch is des houcx G E L, even sijnde met D B E.

Tot hier toe is voorbeelt beschreven van een Dwaelder in een wech loopende, maer bovē dien een inrondt hebbende, hy heeft tweederley voorofachtering, d'eene van wegen sijn inrondts middelpunt, t'welck een voorofachtering ontfangt van ghedaente ghelijck de boveschreven des Dwaelders in sijn wech, d'ander van wegen sijn loop int inrondt, en de voorofachtering veroirsaeckt deur dese twee voorofachteringen t'samen, wort int gemeen des Dwaelders voorofachtering gheseyt.

Laet tot breeder verclaring inde form der 7 bepaling den Dwaelder int inrondt sijn an N, alwaer hy benevens de achtering die hy van weghen sijn inrondts middelpunt ontfangt, voordering crijcht des houcx B E N, welck by d'ander D B E vervought (te weten vergaert alsse beyde eennamich sijn maer van malcander ghetrocken verscheennamich wesende als hier) datter uyt comt is des Dwaelders voorofachtering

Merckt noch t'ghetal der trappen des verstepuntensbooch als hier M K, of des naestepuntensbooch als I L, altijt t'overcommen met het getal der voorofachtering vant middelpunt des inrondts als D B E, om dat I L beschreven is opt middelpunt B.

18 Bepaling.

Eerste voorofachtering is die des middelpunts vant inrondt. Tvveede voorofachtering die des Dvvaeldersint inrondt. Gheeffende voorofachtering die veroirsaeckt vvort deur t'vermenghen van d'eerste en tvveede.

Den Dwaelder sonder inrondt maer een voorofachtering hebbende, te weten die hy door de middeluytpunticheyt sijns wechs crijcht, en behouft gheen onderscheyden namen van eerste tweede noch gheeffende voorofachtering deser bepaling, welcke alleen de Dwaelders toecommen in inronden loopende, wiens eerste en tweede beyde voordering sijnde, haer somme is gheeffende voordering, ende beyde achtering wesende, haer somme is gheeffende achtering, maer d'een voordering d'ander achtering sijnde, soo is haer verschil mette naem van t'grootste ghetal der twee de gheeffende voorofachtering.

19 Bepaling.

Tghene d'een Dvvaelder op een ghestelde tijt voorder loopt als d'ander, of daer op vvint, vvort^⋆ Dvvaeldervvinst gheheeten.

Desen tijt wort dickwils verstaen te beghinnen op de saming tweer Dwaelders, sulcx dat mette schijnbaerbooch na t'vervolgh der trappen vandē traech-

⋆ Motus distantiae.

[p. 12]

sten Dwaelder totten snelsten, int ghemeen Dwaelderwinst beteyckent wort, welcke men soo wel berekent met middeldwaelders als ware.

20 Bepaling.

Tvvee vveereltlichten een selve schijnbaer duysteraerlangde hebbende vvorden in^⋆ saming gheseyt. Maer een schijnbaer half rondt verschillende, in^⋆ teghestant.

⋆ Conjunctione.

⋆ Oppositione.

21 Bepaling.

Der Middeldvvaelders saminghen en teghestanden vvorden haer^⋆ middelsaminghen ende middeltegestanden gheseyt.

⋆ Conjunctiones & oppositiones mediae.

22 Bepaling.

Ervarings dachtafels der Dvvaelders sijn vvaer in oirdentlick van dach tot dach beschreven staen de plaetsen der Dvvaelders soomense deur^⋆ vvisconstuygen daer toe bequaem dadelick bevonden heeft, met tijt haerder saminghen, soo mette vaste sterren als onder malcander, voort haer anclevende als duysteringhen, grootheyt des verduystert deels, over vvelcke sijde verduystert, vvanneer beginnende, vvanneer eindende, en dierghelijcke.

⋆ Instrumenta machematica.

23 Bepaling.

Berekende dachtafels der dvvaelders, sijn die deur kennis^* des Hemelloops berekent vvordē, vvaer in oirdentlick van dach tot dach beschreven staen, der Dvvaelders plaetsen, soo men meynt datse in toecommende tijden sijn sullen: Voort duy steringhen van Son en Maen, met haer anclevende.

Sulcke berekende dachtafels gaen nu veel in druck uyt, als van Ioannes Stofflerus, Erasmus Rheinoldus, Leovitius, Stadius, Maginus, Martinus Everarti, en dierghelijcke.

* Ephemerides.

24 Bepaling.

Keertijt eens Dvvaelders noemtmen, in vvelcke deur^* een groote menichte der gagheslaghen keeren van sijn

* Tempus periodicum.

[p. 13]

ronden, ghevonden vvort de rasheyt van yder rondts loop op bekende tijt.

Merckt.

Den duysteraer sal hier ghelijck den evenaer en meer ander ronden, ghedeelt worden in 360 trappen, sonder twaelf teyckens te ghebruycken elck van 30 tr. of namen van dien na d'oude ghewoonte, waer af ick de reden inden Anhang deses Hemelloops verclaren sal.