Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

[p. 187]

t'Eerste onderscheyt van vertooghen: Dienende als ghemeene grondt der voorstellen daer na volghende.

1 Vertooch. 1 Voorstel.

Soo t'een grootste rondt door t'ander grootste rondts^⋆ aspunt streckt, sy sijn op malcander rechthouckich.

Tghegheven. Laet A B C D een cloot wesen diens middelpunt E is, ende A wort ghenomen voor aspunt, opt welck beschreven is een grootste rondt B F D G.

Tbegheerde. Wy moeten bewijsen



dat de twee ronden op malcander rechthouckich sijn. Tbereytsel. Laet ghetrocken worden den halven as A E.

⋆ Polum.

Tbewys.

Anghesien den halven as A E rechthouckich is opt plat des rondts B F D G door t'gestelde, ende dat den selven as A E int plat des rondts A B C D is, soo moettet plat des selven rondts opt rondt B F D G oock rechthouckich wesen.

Tbeslvyt. Soo dan t'een grootsterondt door t'ander grootste rondts aspunt streckt, sy sijn op malcander rechthouckich, t'welck wy bewijsen moesten.

Merckt.

Want ettelicke vertooghen deser stof soo kennelick sijn datse gheen besonder voorstellen en schijnen te vereysschen, soo sullen wy die cortheyts halven mette nabeschreven vervolghen verclaren.

1 Vervolgh.

Tis kennelick dat A B een vierendeelrondts doet, deur wiens uyterste B ghetrocken is de booch of t'rondt B F D G rechthouckich op A B, ende dat daerom A aspunt is des selven rondts B F D G: Vyt het welckmen als by ghemeene reghel dit besluyt:

T'een uyterste des vierendeelrondts, is aspunt des boochs rechthouckich ghetrocken deur t'ander uyterste.

2 Vervolgh.

Sooder vant punt A ghetrocken wort een grootsterondts booch tot datse t'rondt B F D G gheraeckt, als A H, t'is kennelick datse ghelijck A B oock een

[p. 188]

vieren deelrondts moet doen, ende opt selve rondt B F D G rechthouckich sijn, Vythet welcke men als by ghemene reghel dit besluyt:

VVanneer vant uyterste eens vierendeelrondts eē booch ghetrocken vvort, tot datse den booch gheraeckt daer t'selve vierendeelronts rechthouckich op is, die ghetrocken booch doet oock een vierendeelrondts, ende is op de booch daerse op ghetrocken vvert oock rechthouckich.

Laet tot noch opentlicker verclaring I K in dees



besonder form een vierendeel rondts sijn, rechthouckich op den booch K L, ende vant uyterste punt I, sy ghetrocken een booch tot datse K L gheraeckt, als I M: T'welck soo sijnde, de selve I M is een vierendeel rondts, ende den houck I M K, oock I M L is recht.

3 Vervolgh.

Tis kennelick dat de twee booghen A B C, A H C, elck een halfrondt doen, malcander doorsniende in twee plaetsen A en C, sulcx dat de twee houcken diese maken, als B C H, B A H, met malcander even sijn, want de booch B H is grootheyt van d'een en d'ander deur de 2 bepaling: Waer uyt men dit besluyt.

Tvvee grootste rondts boghen op beyden eynden voortgetrocken sijnde tot datse malcander snijen, doen elck een halfrondt, vervanghende t'samen an beyden eynden even houcken.

4 Vervolgh.

Sooder uyt eenich punt als H des omtrecx B F D G, een grootste rondts booch verre ghenouch getrocken wort rechthouckich op den selven omtreck B F D G, t'is kennelick datse den booch B A D erghens deursnijen moet als in A, sulcx dat A D en A H elck een vierendeel rondts doen, ende dat haer ghemeene sne A, aspunt is des rondts B F D H: Vyt het welcke men als by ghemeene reghel dit besluyt:

VVanneer op een eerste booch, ghetrocken vvert een tvveede rechthouckich op d'eerste tot datse een derde ontmoet die op d'eerste oock rechthouckich is: De tvveede en derde snijen van malcander een vierendeel rondts, ende haer ghemeene sne is aspunt van d'eerste.

[p. 189]

Laet tot noch opentlicker verclaring N O in dees besonder



form een booch sijn, waer op een ander booch N P rechthouckich staet. Voort sy van eenich punt in O N als Q, getrocken een booch rechthouckich op O N, tot datse de booch N P gheraeckt, t'welck gheschiet neem ick in R: Dit soo sijnde, Q R ende R N doen elck een vierendeelrondts, ende R is aspunt van O N.

5 Vervolgh.

Sooder vant punt E tot H ghetrocken wort de rechte lini E H, t'is kennelick⁺ dat de twee houcken H E B, H E D, even sijn met twee rechtlinighe rechthoucken: Maer den plathouck H E B, ende den cloothouck H A B sijn even groot, ofte haer grootheyt wort met een selve booch B H anghewesen deur de 2 bepaling: S'ghelijcx is oock evegroot den cloothouck H A D, metten plathouck H E D, daerom de twee cloothoucken H A B, H A D (veroirsaeckt deur d'een booch H A op d'ander B A D ghetrocken) sijn even met twee rechthoucken, ende hebben even houckmaten deur de 2 bepaling vant houckmaetmaecksel: Vyt het welcke men als by ghemeene reghel dit besluyt:

D'een booch maeckt op d'ander tvvee houcken, t'samen even met tvvee rechthoucken, ende hebben die tvvee houcken even houckmaten, raecklijnen, en snylijnen.

Laet tot noch opentlicker verclaring S T in dees besonder form een booch sijn, ende daer op eenighe ander V X, t'welck soo wesende,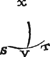



de twee houcken S V X, T V X sijn t'samen even met twee rechthoucken: Daerom d'een scherp sijnded'ander is plomp, d'een recht sijnde d'ander is oock recht, ende d'een bekent sijnde d'ander wort oock bekent. By voorbeelt doende den houck T V X 50 tr. ick treck die van twee rechthoucken dats van 180 tr. blijft voor den houck S V X 130 tr. Ende hebben 50 tr. en̄ 130 tr. even houckmaten, te weten elck 7660445 deur de 2 bepaling vant houckmaetmaecksel.

+ 13 v. des 1 boucx Euc.

6 Vervolgh.

Soo de booch A H voortghetrocken wort tot C, tis kennelick dat de booch A C, snyende de booch B H D in H, vier houcken maeckt, te weten A H D, D H C, C H B, B H A, diens tegenoverhoucken even sijn, als A H D met C H B, ende D H C met B H A, want de twee houcken B H A, A H D sijn even met twee rechthoucken, alsoo oock sijn de twee houcken A H D, D H C door het 5 veryolgh, daerom de twee houcken B H A, A H D, sijn t'samen even mette twee houcken A H D, D H C: Nu ghetrocken van elck haer ghemeene houck A H D, soo blijft den houck B H A, even met haer teghenoverhouck D H C: Ende s'ghelijcx sal oock be hoont worden den houck A H D even te wesen met haer teghenoverhouck C H B, uyt het welcke men als by ghemeene reghel dit besluyt:

Tvvee grootste rondts boghen malcander doorsnijende, hebben haer teghenoverhoucken even.

[p. 190]

7 Vervolgh.

Sooder opt punt A als aspunt, beschreven wort een kleender rondt Y Z, t'is kennelick dattet^* evewijdich moet sijn mettet rondt B F D H, t'welck door t'ghegheven opt selve aspunt oock beschreven is, voort want het grootste rondt A B C D, rechthouckich is opt grootste rondt B F D H, soo moet sijn vlack opt vlack vant rondt Y Z oock rechthouckich wesen: Vyt het welcke men als by ghemeene reghel dit besluyt:

Eens cloots grootste rondt streckende door het aspunt van een kleender rondt, heeft sijn vlack opt selve rechthouckich.

* Parallelus.

8 Vervolgh.

Want de sijde A H des rechthouckighen driehoucx A H B, den rechthouck an H gheraeckt, soo ist kennelick dat den houck, A B H teghenover de sijde A H, recht is: Vyt het welcke men als by ghemeene reghel dit besluyt:

Soo de sijde die eens driehoucx rechthouck raeckt, een vierendeelrondts is, haer tegenoverhouck sal recht sijn.

9 Vervolgh.

Want d'een sijde A H des rechthouckighen driehoucx A H B een vierendeelrondts doet, soo ist kennelick dat des rechthoucx H teghenoversijde A B, oock een vierendeelrondts doet: Vyt het welcke men als by ghemeene reghel dit besluyt:

Soo d'eene der tvvee rechthoucksijden een vierendeelrondts is, de^⋆ schoensche sal oock een vierendeelrondts vvesen.

⋆ Hipotenusa.

10 Vervolgh.

Want inden rechthouckighen driehouck A H B, des rechthoucx H teghen. oversijde A B een vierendeelrondts doet, soo ist kennelick d'eene der twee ander sijden die den rechthouck raken, als A H, oock een vierendeelrondts te wesen: Vyt het welcke men als by ghemeene reghel dit besluyt:

Soo inden clootschen rechthouckighen driehouck, des rechthoucx teghenoversijde een vierendeelrondts is, d'eene der tvve sijden die den rechthouck raeckt moet oock een vierendeelrondts vvesen.

11 Vervolgh.

Want inden driehouck A H B, den houck B die de teghenoversijde A B des rechthoucx H raeckt, een rechthouck is, soo ist openbaer de selve teghenoversijde A B een vierendeelrondts te wesen: Vyt het welcke men als by ghemeene reghel dit besluyt:

[p. 191]

Soo inden clootschen rechthouckighen driehouck, d'een der tvvee houcken die de teghenoversijde des rechthoucx raeckt, oock een rechthouck vvaer, de selve teghenoversijde sal een vierendeelrondts doen.

12 Vervolgh.

Want inden driehouck A H B, de teghenoversijde A B des rechthoucx H, een vierendeelrondts doet, soo ist kennelick d'een der twee houckē diese raeckt, als den houck B recht te wesen: Vyt het welcke men als by ghemeene reghel dit besluyt:

Soo in den clootschen rechthouckighen driehouck, de teghenoversijde des rechthoucx een vierendeelrondts vvaer: D'een der tvvee houcken diese raeckt moet recht sijn.

13 Vervolgh.

Tis kennelick dat A B, A H twee vierendeelenrondts sijn, ghetrocken van een selve aspunt A, op een derde booch B H, ende dat daerom de twee houcken A B H, A H B recht sijn: Vyt het welcke men als by ghemeene reghel dit besluyt:

Tvvee vierendeelenrondts van een selve^⋆ aspunt op een derde booch ghetrocken, sijn daer op rechthouckich.

⋆ Pole.

2 Vertooch. 2 Voorstel.

VVesende een clootsche rechthouckighe driehouck, vviens een rechthoucksijde kleender is dan een vierendeelrondts: Haer teghenoverhouck is scherp: maer isse grooter haer teghenoverhouck sal plomp sijn.

T'ghegheven vant 1 deel. Laet A B C een clootsche rechthouckighe driehouck sijn wiens rechthouck B is, ende een rechthoucksijde als A B sy kleender dan een vierendeelrondts. Tbegheerde. Wy moeten bewijsen dat haer teghenoverhouck A C B scherp is.

Tbereytsel. Laet B A voortghetrocken worden tot



D, sulcx dat B D een vierendeelrondts doe, daer na sy ghetrocken de booch D C.

Tbewys.

Anghesien de sijde B D een vierendeelrondts doet, soo sal t' punt D (deur dien de selve D B rechthouckich op B C is) aspunt vanden booch B C sijn deur het 1 vervolgh des 1 voorstels, van welck aspunt D ghetrocken wesende de booch tot C, sy sal rechthouckich op B C sijn, ende den houck D C B recht hebben deur het 2 vervolgh des 1 voorstels, ende vervolghens den houck A C B scherp, als kleender wesende dan den rechthouck D C B.

[p. 192]

T'ghegheven vant tvveede deel. Laet B D doende een vierendeelrondts alsboven, voortghetrocken worden tot E, daer na de grootste rondts booch E C.

Tbewys.

Nadien den houck D C B teghenover t'vierendeelrondts D B recht is, deur t'eerste deel, soo moet den houck E C B noch grooter sijnde plomp wesen, daerom de sijde E B grooter wesende dan een vierendeelrondts, haer tegenoverhouck E C B is plomp. Tbeslvyt. Wesende dan een clootsche rechthouckige driehouck, wiens een rechthoucksijde kleender is dan een vierendeelrondts, haer tegenoverhouck is scherp: Maer isse grooter, haer teghenoverhouck sal plomp sijn, t'welck wy bewijsen moesten.

Vervolgh.

Anghesien de sijde A B kleender dan een vierendeelrondts sijnde, haer teghenoverhouck A C B scherp heeft, soo moet weerom verkeert de scherphouck A C B haer teghenoversijde A B kleender hebben dan een vierendeelrondts: Ende om dierghelijcke redenen moet den plomphouck E C B haer teghenoversijde E B grooter hebben, waer uyt besloten wort t'verkeerde des voorstels aldus:

VVesende een clootsche rechthouckige driehouck vviens een scheefhouck scherp is: Haer teghenoversijde is kleender dan een vierendeelrondts: Maer isse plomp, haer teghenoversijde sal grooter sijn.

3 Vertooch. 3 Voorstel.

VVesende een clootsche rechthouckighe driehouck met tvve rechthoucksijden elck kleynder of elck grooter dan een vierendeelrondts: De^⋆ schoensche sal kleender sijn: Maer is d'eene kleender d'ander grooter, de schoensche sal grooter vvesen.

T'ghegheven vant 1 deel. Laet A B C een clootsche rechthouckige driehouck sijn, wiens rechthouck B is, ende haer twee sijden als A B, C B, sijn elck kleender dan een vierendeelrondts.

Tbegheerde. Wy moeten bewijsen dat



de schoensche A C kleender dan een vierendeelrondts is. Tbereytsel. Laet B A voortghetrocken worden tot D, ende C B tot E, sulcx dat B D en C E elck een vierendeelrondts doen: Daer na sy getrocken de grootste rondts booch D E, ende C A sy voortghetrocken tot datse D E in F ontmoet.

⋆ Hipotenusa.

Tbewys.

Want den houc A B C recht is, en̄ B D een vierendeelronts, so moet D^* aspunt des ronts C E wesen deur het 1 vervolgh des 1 voorstels, en̄ daerō dē houc D E C

* Polus.

[p. 193]

recht deur het 1 voorstel. Voort want den houck D E C recht is, ende C E een vierendeelrondts, soo moet, deur t'boveschreven 1 vervolgh, C aspunt des rondts D E wesen, ende daerom is C F oock een viereendeelrondts, deur het 2 vervolgh des 1 voorstels, wiens deel C A nootsakelick kleender is.

T'ghegheven des 2 deels. Laet het vierendeelrondts B D voortghetrocken worden tot G, ende het deel B C verlangt tot H, sulcx dat C H een vierendeelrondts doe, daer na sy ghetrocken de booch H G: Twelck soo sijnde, des driehoucx G B H houck G B H is recht, ende de twee sijden die hem gheraken als G B, en H B, sijn elck grooter dan een vierendeelrondts.

Tbegheerde. Wy moeten bewijsen dat des rechthoucx B teghenoversijde G H, kleender dan een vierendeelrondts is. Tbereytsel. Ick treck vant punt C deur t'punt D een grootste rondts booch, ontmoetende de voortghetrocken H G in I.

Tbewys.

Anghesien den houck D B H recht is, ende B D een vierendeelrondts, soo is D aspunt des boochs B H, deur het 1 vervolgh des 1 voorstels, ende den houck D C B recht deur het 2 vervolgh. Voort alsoo den booch C H een vierendeelrondts is, soo moet deur de voorgaende redenen, H aspunt sijn des boochs I C, waerom oock den booch H I een vierendeelrondts doet, vant welck G H een deel sijnde, soo moet de selve G H kleender wesen.

T'ghegheven vant 3 deel. Laet tusschen H en C een punt ghestelt worden als K, ende van t'selve ghetrocken sijn een grootste rondts booch deur t'punt D, tot datse t'voortghetrocken vierendeelrondts H I ontmoet in L. Nu anghesien D aspunt is des rondts E H, als int voorgaende blijckt, soo moet D K een vierendeelrondts doen, ende K L grooter daen een vierendeelrondts sijn, ende H K (deel des vierendeelrondts H C) kleender dan een vierendeelrondts, ende den houck D K H recht, diens teghenoversijde H L. Sulcx dat wy hier hebben na luyt vant derde deel deses voorstels een driehouck L K H, wiens twee sijden die den rechthouck L K H raken, als L K, H K, d'een kleender is dan een vierendeelrondts als H K, d'ander grooter als L K.

Tbegheerde. Wy moeten bewijsen dat des rechthoucx L K H teghenoversijde H L, grooter is dan een vierendeelrondts.

Tbewys.

Doende H I een vierendeelrondts deur t'bewijs des tweeden deels, ende een stuck sijnde van H L, soo moet H L grooter wesen. Tbeslvyt. Wesende dan een clootsche rechthouckighe driehouck met twee sijden, etc.

Vervolgh.

T'blijckt door t'eerste deel, dat des rechthouckighen driehoucx A B C twee sijden A B, B C, die den rechthouck A B C gheraecken, elck kleender dan een vierendeelrondts wesende, dat alsdan A C teghenoversijde des rechthoucx A B C, kleender is dan een vierendeelrondts. T'blijckt oock door het tweede deel, dat des rechthouckighen driehoucx G B H twee sijden G B, H B, die den rechthouck G B H gheraecken, elck grooter dan een vierendeelrondts wesende, dat alsdan G H teghenoversijde des rechthoucx G B A, kleender is dan een vierendeelrondts.

T'blijckt oock deur het 3 deel, dat des rechthouckighen driehoucx L K H sijde H K, die den rechthouck L K H gheraeckt, kleender sijnde dan een vieren-

[p. 194]

deelrondts, ende L K grooter, dat alsdan L H teghenoversijde des rechthoucx L K H, grooter is dan een vierendeelrondts. Deur t'verkeerde van t'welcke (als opentlick inde boveschreven form te sien is) oock t'verkeerde des voorstels volght, aldus:

VVesende een clootsche rechthouckige driehouck, vviens^⋆ schoensche kleender dan een vierendeelrondts is: De tvvee sijden die den rechthouck raken sijn elck kleynder dan een vierendeelrondts of elck grooter: Maer des rechthoucx teghenoversijde grooter vvesende, soo sal d'eene der tvvee die den rechthouck raeckt, kleender vvesen dan een vierendeelrondts, d'ander grooter.

⋆ Hypotenusa.

4 Vertooch. 4 Voorstel.

Soo de^⋆ schoensche ende d'een rechthoucksijde eens clootschen rechthouckighen driehoucx elck grooter sijn dan een vierendeelrondts: De derde moet kleender vvesen.

Tghegheven. Laet A B C des 1 voorbeelts een clootsche rechthouckighen driehouck sijn, diens houck B recht is, en̄ de schoensche A C metterechthoucksijde B C, sijn elck grooter dan een vierendeelrondts.

Tbegheerde. Wy moeten bewijsen dat de derde sijde A B kleender dan een vierendeelrondts is. Tbereytsel. Ick trecke C A, C B voorwaert, tot datse malcander ontmoeten, t'welck sy in D.

⋆ Hypotenusa.

Tbewys.

De twee boghen C A D en C B D doen elck een



halfrondt deur het 3 vervolgh des 1 voorstels, daer af ghetrocken C A, C B, die elck grooter sijnde dan een vierendeelrondts, soo blijven A D, B D elck kleender: Voort nadien den houck A B C recht is door t'ghegeven, soo moet den houck A B D oock recht sijn, door het 3 vervolgh des 1 voorstels. A B D dan is een rechthouckich driehouck, met een kleender schoensche A D, waer deur de twee rechthoucksijden A B, B D beyde kleynder of beyde grooter sijn dan een vierendeelrondts deur t'verkeerde van het 3 voorstel: Maer B D is kleender, A B dan moet oock kleender sijn.

Tbeslvyt. Soo dan de schoensche ende d'een rechthoucksijde eens clootschen rechthouckighen driehoucx grooter sijn dan een vierendeelrondts: De derde moet kleender wesen, t'welck wy bewijsen moesten.

5 Vertooch. 5 Voorstel.

VVesende een clootsche rechthouckige driehouck, vviens tvvee scheefhoucken beyde scherp of beyde plomp sijn: De schoensche sal kleender dan een vierendeelrondts

[p. 195]

vvesen. Maer is d'een plomp d'ander scherp, die schoensche sal grooter sijn.

T'ghegheven vant 1 deel. Laet A B C een clootsche rechthouckige driehouck sijn, wiens rechthouck B is, ende de twee scheefhoucken A, C, sijn beyde scherp, of beyde plomp. Tbegheerde. Wy moeten bewijsen



dat A C kleender dan een vierendeelrondts sal wesen.

Tbewys.

Anghesien de twee houcken A, C, beyde scherp of beyde plomp sijn, soo moeten de twee sijden A B, en B C elck kleender of elck grooter dan een vierendeelrondts wesen deur het 2 voorstel: Ende vervolghens soo moet dan deur het 3 voorstel A C corter sijn.

T'ghegheven vant 2 deel. Laet nu d'een der twee houcken A, C, scherp sijn, d'ander plomp. Tbegheerde. Wy moeten bewijsen dat de schoensche A C grooter dan een vierendeelrondts is.

Tbewys.

Anghesien dat d'een der twee houcken A, C, scherp, d'ander plomp is, soo moet d'een der twee sijden A B, B C kleender sijn dan een vierendeelrondts, d'ander grooter deur het vervolgh des 2 voorstels, ende daerom de schoensche A C grooter deur het 3 deel des 3 voorstels. Tbeslvyt. Wesende dan een clootsche rechthouckighe driehouck wiens twee scheefhoucken beyde scherp of beyde plomp sijn, de schoensche sal kleender dan een vierendeelrondts wesen. Maer is d'een plomp d'ander scherp, de schoensche sal grooter sijn, t'welck wy bewijsen moesten.

Vervolgh.

Deur t'verkeerde van dit voorstel (soomen opentlick inde boveschrevē form sien mach) is dit openbaer:

VVesende een clootsche rechthouckige driehouck, vviens schoensche kleender dan een vierendeelrondts is: De tvvee scheefhoucken sijn beyde scherp, of beyde plomp: Maer isse grooter dan een vierendeelrondts, d'een dier tvvee houcken sal scherp, d'ander plomp sijn.

6 Vertooch. 6 Voorstel.

Soo een clootsche driehouck tvvee scherphoucken of tvvee plomphoucken heeft: De^⋆ hanghende ghetrocken vanden derden houck na heur tegenoversijde valt binnen den driehouck: Maer soo d'een der tvvee scherp d'ander plomp is, sy valter buyten.

T'ghegheven des 1 deels. Laet A B C een clootsche driehouck wesen, diens twee houcken A B C, A C B scherp sijn.

⋆ Perpendicularis.

[p. 196]

Tbegheerde. Wy moeten bewijsen dat de hanghende vanden derden houck A, ghetrocken na heur teghenoversijde B C, binnen den driehouck valt.

Tbereytsel. Laet D^* aspunt sijn des rondts C B ende ghetrocken worden de twee vierendeelenrondts D B, D C.

* Polus.

Tbewys.

Anghesien de booch D B comt vant aspunt D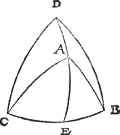



op haer rondt C B, soo moet den houck D B C recht sijn, deur het 1 voorstel: Maer den houck A B C is kleender, te weten scherp, daerom t'punt A valt op de slinckerhandt van D B. En̄ s'gelijcx sal bethoont worden t'selve punt A op de rechterhandt van D C te vallen, daerom oock vallet nootsakelick binnen den driehouck D B C: Alsoo oock doet de booch D A: Ende de selve D A voortghetrocken tot E, soo moet A E binnen den driehouck A B C vallen, want sooser buyten viel, t'vierendeelrondts D A E soude an A een houck moeten hebben kleender dan D A B, t'welck ongheschickt waer: Daerom A E en valt niet buyten den driehouck A B C na de rechterhandt: Ende s'ghelijcx sal oock bethoont worden datser niet buyten en valt na de slinckerhandt, sy valter dan nootsaeckelick binnen: T'selve sal oock alsoo bethoont worden wanneermen de twee houcken als C, B, stelt plomp te wesen.

T'ghegheven vant 2 deel. Laet A B C een clootsche driehouck wesen, diens houck C scherp is, B plomp. Tbegheerde. Wy moeten bewijsen dat de hanghende vanden derden houck A, op haer teghenoversijde (welverstaende ghenouch voortghetrocken) buyten den driehouck sal vallen.

Tbewys.

Sooser niet buyten en viel, sy sal in een der sijden A B, A C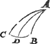



vallen, of binnen den driehouck: Angaende van in A B of A C te vallen, en can niet wesen, want alsdan soude den houck B of C recht sijn, teghen t'ghestelde. By aldiense binnen den driehouck viel, als, neem ick, van A tot D, soo souden de twee houcken A D B, A D C, moeten recht sijn, t'welck niet en is om dese redenen: Laet de houcken A D B, A D C, soot meughelick waer, recht wesen, sulcx dat wy hebben twee rechthouckighe driehoucken A D B, A D C, diens ghemeene sijde A D is. De selveals tegenoversijde des scherphoucx C sal moeten kleender sijn dan een vierendeelrondts deur t'vervolgh des 2 voorstels: Ende als teghenoversijde des plomphoucx B sal grooter sijn deur t'selve vervolgh: Maer kleender en grooter is onmeughelick, daerom de hanghende vanden houck C A B op haer teghenoversijde, en valt niet binnen den driehouck maer daer buyten. Tbeslvyt. Soo dan een clootsche driehouck twee scherphoucken of twee plomphoucken heeft, de hanghende ghetrocken vanden derden houck na haer teghenoversijde valt binnen den driehouck: Maer soo d'een der twee scherp d'ander plomp waer, sy valter buyten: T'welck wy bewijsen moesten.

[p. 197]

7 Vertooch. 7 Voorstel.

Hebbende een clootsche driehouck drie scherphoucken: Elcke sijde is kleender dan een vierendeelrondts.

Tghegheven. Laet A B C een clootsche driehouck sijn met drie scherphoucken. Tbegheerde. Wy moeten bewijsen dat elcke sijde kleender dan een vierendeelrondts is.

Tbereytsel. Laet ghetrocken worden een booch



van A rechthouckich op C B, als A D, welcke deur het 6 voorstel nootsakelick binnen den driehouck valt, om dat de houcken C, B beyde scherp sijn.

Tbewys.

Anghesien de twee houcken A D C, A D B, deur tbereytsel recht sijn, soo moeten de twee driehoucken A D C, A D B rechthouckich wesen, daerom na dien D A B en B twee scherphoucken sijn, soo sal A B kleender dan een vierendeelrondts wesen, deur het 5 voorstel. Desghelicx salmen bewijsen van A C: Oock van C B, midts datmen A B voor grondt neemt soo C B boven ghenomen is. Tbeslvyt. Hebbende dan een clootsche driehouck drie scherphoucken, elcke sijde is kleender dan een vierendeelrondts, t'welck wy bewijsen moesten.

8 Vertooch. 8 Voorstel.

Hebbende een clootsche driehouck tvvee even scherphoucken: De teghenoversijden der selve sijn kleender dan een vierendeelrondts.

Tghegheven. Laet A B C een clootsche driehouck sijn met twee scherphoucken B, C. Tbegheerde. Wy moeten bewijsen dat haer teghenoversijde A B, A C kleender dan een vierendeelrondts sijn.

Tbereytsel. Laet uyt het punt D, middel van C B, ghetrocken worden de booch A D, ende de selve verlangt van A tot E, alsoo dat D E een vierendeelrondts doe: Daer na de twee boghen E C, E B.

Tbewys.

Angesien den houck A B C even is aen den houck A C B



deur t'ghestelde, soo moet A B even sijn met A C, ende vervolghens A D opt middelste punt van C B commende, moet rechthouckich wesen op de selve C B, alsoo oock moet het vierendeelrondts E D, daerom E is aspunt des boochs C B deur het 1 voorbeelt des 1 voorstels, ende E C, E B oock rechthouckich op de selve C B commende, doen elck een vierendeelrondts deur het 2 vervolgh des selfden 1 voorstels. Nu dan den houck A B C scherp sijnde, ende E B C recht, soo moetet punt A onder E commen, ende A D corter sijn dan t'vierendeelrondts. Voort is D B oock kleender, om dattet den helft is des boochs C B, die deur de 2 bepaling kleender is dan een halfrondt. Wy hebben dan een rechthouckighen driehouck A D B, met twee sijden A D, D B, den rechthouck rakende, elck kleender dan een vierendeelrondts, waerom de derde A B oock kleender moet sijn deur het 3 voorstel.

[p. 198]

S'ghelijcx sal oock bethoont worden van A C kleender te wesen.

Tbeslvyt. Hebbende dan een clootsche driehouck twee even scherphoucken, de teghenoversijden der selve sijn kleender dan een vierendeelrondts, t'welck wy bewijsen moesten.

9 Vertooch. 9 Voorstel.

He bbende een clootsche driehouck tvvee oneven scherphoucken, ende een plomphouck: De teghenoversijde des scherpsten is kleender dan een vierendeelrondts, maer d'ander tvvee sijden connen vvesen van een vierendeelrondts, kleender of grooter.

Tghegheven. Laet A B C een clootsche driehouck sijn met twee oneven scherphoucken A B C, A C B, welcker scherpste sy A B C, ende den houck C A B sy plomp.

Tbegheerde. Wy moeten bewijsen



dat A C teghenoversijde des scherpsten houcx A B C kleender is dan een vierendeelrondts, maer dat de teghenoversijden van d'ander twee houcken, connen wesen of van een vierendeelrondts, of kleender of grooter.

T'bereytsel van t'eerste deel. Laet van t'punt A ghetrocken worden den booch A D rechthouckich op B C: De selve A D sal binnen den driehouck vallen deur het 6 voorstel, om dat de twee houcken A B C, A C B scherp sijn, ende sal de selve A D den houck A C B naerder sijn dan den houck A B C, om dat A B C scherper is dan A C B, daerom can in D B geteyckent worden t'punt E, also dat D E even sy met D C; t'welck ghedaen wesende, soo sy daer na ghetrocken de booch A E.

T'be vvijs van t'eerste deel. Wy hebben een evebeenighe driehouck A C E, met twee scherphoucken C, E, wiens sijde A C kleender is dan een vierendeelrondts, deur het 8 voorstel.

T'bereytsel vant 2 deel. Laet A B en A C beyde voortghetrocken worden tot datse malcander ontmoeten in F, laet oock int halfrondt A B F gheteyckent worden t'punt G, en̄ in A C F t'punt H, sulcx dat A G, A H elck een vierendeelrondts doen, voort sy ghetrocken de booch G H, ende daer in gheteyckent t'punt I, alsoo dat H I oock een vierendeelrondts doet, daer na sy ghetrocken de booch C I. Dit soo sijnde, de booch C B is of een vierendeelrondts, of kleender, of grooter: Maer ghenomen datse van een vierendeelrondts is, soo laet geteyckent worden t'punt K, tusschen A, B, doch alsoo dat A K grooter sy dan A C, want C K daer op ghetrocken sijnde, soo sal, als blijckt uyt het bewijs des eersten deels, den houck A K C, scherper sijn dan den houck A C K. Voort sy gheteyckent t'punt L, tusschen B en G, ende ghetrocken de booch G L.

T'be wijs vant 2 deel. Anghesien C B ghestelt is voor een vierendeelrondts,

[p. 199]

soo can ten eersten de teghenoversijde des plomphoucx C A B een vierendeelrondts doen. Voort is C K kleender dan t'vierendeelrondts C B, maer C K is teghenoversijde des ghegheven plomphoucx, in een driehouck A C K, vande ghedaente deses voorstels, door t'bereytsel des 2 deels, daerom de teghenoversijde des plomphoucx can oock kleender sijn dan een vierendeelrondts. Voort soo is C L grooter dan t'vierendeelrondts C B, maer C L is teghenoversijde des ghegheven plomphoucx C A B, ende dat in een driehouck vande ghedaente deses voorstels (want den houck C A L is den ghegheven plomphouck, ende A L C is noch scherper dan den houck A B C, ende A C L onscherper dan den houck A C B, nochtans den selven houck A C L niet plomp sijnde, gemerckt sy kleender is dan den rechthouck A C I, sulcx dat A L C scherper is dan A C L) daerom de teghenoversijde des plomphoucx can oock grooter sijn dan een vierendeelrondts.

Om nu te commen totte teghenoversijde des onscherpsten A C B, ick segh aldus: De booch A B is of een vierendeelrondts, of kleender, of grooter: Ghenomen dan datse van een vierendeelrondts is, soo can de teghenoversijde des onscherpsten houcx een vierendeelrondts doen: S'ghelijcx A K kleender wesende dan t'vierendeelrondts A B, ende A L grooter, welcke A K, A L, yder in haer driehouck des onscherpsten houcx teghenoversijde is deur t'voorgaende, soo is daer mede de rest des voorstels bewesen. Tbeslvyt. Hebbende dan een clootsche driehouck twee oneven scherphoucken ende een plomphouck, de teghenoversijde des scherpsten is kleender dan een vierendeelrondts, maer d'ander twee sijden connē wesen van een vierendeelrondts, kleender, of grooter, t'welck wy bewijsen moesten.

10 Vertooch. 10 Voorstel.

Hebbende een clootsche driehouck drie sijden elck kleender dan een vierendeelrondts: De teghenoverhoucken vande tvvee kleenste sijn scherp, maer de teghenoverhouc der grootste sijde can scherp, recht, of plomp vvesen.

Want de teghenoverhouck der grootste sijde scherp recht of plomp can wesen, soo sullen wy t'bewijs in drien deelen.

T'eerste deel is deur het 7 voorstel openbaer, te weten inden driehouck met drie scherphoucken, wiens sijden elck kleender dan een vierendeelrondts wesende, soo sijn de teghenoverhoucken vande twee cleenste sijden scherp, ende de teghenoverhouck der grootste sijde oock scherp.

Het tweede deel is openbaer inden rechthouckighen



driehouck met drie sijden elcke kleender dan een vierendeelrondts, als A B C, waer in de teghenoverhoucken A, C, vande twee kleenste sijden A B, B C, die den rechthouck B vervanghen scherp sijn deur het 2 voorstel, maer den teghenoverhouck B vande derde grootste sijde A C, is recht.

Het derde deel wort aldus verclaert: Laet de booch C A voortghetrocken worden tot D, daer na sy ghetrocken de booch B D, doch soo dat C D noch kleender sy dan een vierendeelrondts, ende B D kleender dan C A: T'welck soo wesende, beneven den scherphouck C, soo is den houck D noch scherper dan

[p. 200]

den scherphouck C A B, daerom D is oock scherp. Belanghende den houck D B C teghenover de grootste sijde D C, die moet plomp sijn, ghemerckt datse grooter is dan den rechthouck A B C. Tbeslvyt. Hebbende dan een clootsche driehouck drie sijden elck kleender dan een vierendeelrondts: De teghenoverhoucken vande twee kleenste sijn scherp, maer de teghenoverhouck der grootste sijde, can scherp, recht, of plomp wesen, t'welck wy bewijsen moesten.

11 Vertooch. 11 Voorstel.

VVesende tvvee sijden eens clootschen driehoucx elck kleender dan een vierendeelrondts, de derde grooter dan een van dien: De hanghende vanden houck der tvvee cortste, valt binnen den driehouck.

Tghegheven. Laet A B C een clootsche driehouck wesen, diens twee sijden A B, A C, elck kleender sijn dan een vierendeelrondts ende de derde B C grooter dan A B of A C, ende A D sy de hanghende vanden houck C A B tot op de grootste sijde B C. Tbegheerde. Wy moeten bewijsen dat A D binnen den driehouck A B C valt.

Tbewys.

De derde grootste sijde als B C, is of kleender dan



een vierendeelrondts, of van een vierendeelrondts, of grooter. Laetse ten eersten kleender sijn, t'welck soo ghenomen, A B C is een driehouck wiens drie sijden elck kleender dan een vierendeelrondts wesende, soo sijn de twee teghenoverhoucken der kleenste sijden, als den houck C, en A B C, scherp, deur het 7 voorstel, ende A D valt tusschen beyden binnen den driehouck deur het 6 voorstel. Laet ten tweeden de derde grootste sijde van een vierendeelrondts wesen, als neem ick de voortghetrocken C B tot E, des driehoucx A E C, wesende A E oock kleender dan een vierendeelrondts, ende kleender dan C E: T'welck soo sijnde, A D teghenoversijde des scherphoucx C, indenrechthouckighen driehouck A D C, is kleender dan een vierendeelrondts deur het 2 voorstel, ende haer teghenoverhouck A E D des rechthouckighen driehoucx A D E, is deur t'selve voorstel oock scherp, ende de hanghende A D valt tusschen beyden binnen den driehouck deur het 6 voorstel. S'ghelijcx sal oock t'bewijs sijn van een derde grootste sijde grooter dan een vierendeelrondts: Als neem ick de voortghetrocken C E tot F, des driehoucx A F C, wesende A F kleender dan een vierendeelrondts, ende kleender dan C F. Tbeslvyt. Wesende dan twee sijden eens clootschen driehoucx elck kleender dan een vierendeelrondts, de derde grooter dan een van dien: De hanghende vanden houck der twee cortste valt binnen den driehouck, t'welck wy bewijsen moesten.

12 Vertooch. 12 Voorstel.

Hebbende een clootsche driehouck tvvee sijden elck kleender dan een vierendeelrondts, de derde niet kleender: De tvvee teghenoverhoucken vande kleenste sijden sijn

[p. 201]

scherp: Maer de teghenoverhouck vande grootste sijde is plomp.

Want de sijde niet kleender dan een vierendeelrondts, sijn can grooter dan een vierendeelrondts, of van een vierendeelrondts, soo sullen wy daer aftwee voorbeelden beschrijven.

1 Voorbeelt

Tghegheven. Laet A B C een clootsche driehouck sijn, diens twee sijden A B, A C, elck kleender sijn dan een vierendeelrondts, de derde B C grooter.

Tbegheerde. Wy moeten bewijsen dat de twee cleenste sijdens teghenoverhoucken A B C, A C B scherp sijn, maer de grootste sijdens C B teghenoverhouck C A B plomp. Tbereytsel. Laet A B, A C, voortghetrocken worden tot D en E, sulcx dat A D, A E, elck een vierendeelrondts doen, daer na sy op A als aspunt, beschreven de booch E D, ende A F rechthouckich op C B, welcke A F binnen den driehouck A B C valt, deur het 14 voorstel, want A B, A C sijn elck kleender dan een vierendeelrondts, ende C B is grooter dan een van dien: De selve A F sy voortghetrocken tot G, in E D.

Tbewys.

Anghesien E D beschreven is op A als



aspunt, soo moet den houck A E D recht sijn, ende A G vallende op E D, moet ghelijck A E oock een vierendeelrondts doen, deur het 2 vervolgh des 1 voorstels. Maer A F is deel van A G, daerom A F is kleender dan een vierendeelrondts: Sy is oock teghenoversijde des houcx A C F, ende dat inden rechthouckighen driehouck A F C, daerom den houck A C F, of A C B, is scherp, deur het 2 voorstel: S'ghelijcx sal oock bethoont worden den houck A B C scherp te wesen. Maer den houck C A B plomp te sijn, wort aldus bethoont: By aldien E D maer een vierendeelrondts en dede, soo soude den driehouck A D E evesijdich ende evenhouckich sijn, te weten drie sijden elck van een vierendeelrondts, ende met drie rechthoucken, sulcx dat de grootste booch daer in ghetrocken, maer en soude connèn wesen van een vierendeelrondts: Maer C B is grooter deur t'ghegheven, ende E D noch grooter: Maer E D wijst ons an de grootheyt des houcx E A D, deur de 2 bepaling, daerom E A D, of, dattet selve is, C A B, is grooter dan een rechthouck, het is dan een plomphouck.

2 Voorbeelt.

Laet ten tweeden C B een vierendeelrondts doen, blijvende de rest alsboven: T'welck soo wesende, dat de twee houcken A C B, A B C scherp moeten sijn, is deur t'bewijs des 1 voorbeelts openbaer. Maer den houck C A B plomp te sijn, wort aldus bethoont: By aldien E D maer een vierendeelrondts en dede, soo soude den driehouck A D E evesijdich ende evenhouckich sijn, te weten drie sijden elck van een vierendeelrondts, ende met drie rechthoucken, sulcx dat de grootste boghen daer in ghetrocken, te weten uyt een houck tot haer teghenoversijde, maer en soude connen wesen van een vierendeelrondts, ende alle ander boghen niet commende uyt een houck, als de booch C B, souden moeten kleender wesen, maer C B en is niet kleender, want sy doet een vierendeelrondts

[p. 202]

deur t'ghestelde, E D dan moet grooter wesen: Maer E D wijst ons an de grootheyt des houcx E A D, deur de 2 bepaling, daerom E A D, of dattet selve is C A B, is grooter dan een rechthouck, het is dan een plomphouck.

Tbeslvyt. Hebbende dan een clootsche driehouck twee sijden elck kleender dan een vierendeelrondts, de derde niet kleender: De twee teghenoverhoucken vande kleenste sijden sijn scherp: Maerde teghenoverhouck vande grootste sijde is plomp, t'welck wy bewijsen moesten.

13 Vertooch. 13 Voorstel.

Hebbende een clootsche driehouck een sijde van een vierendeelrondts, d'ander kleender, de derde grooter: De tvvee teghenoverhoucken vande kleenste sijden sijn scherp, maer de teghenoverhouck vande grootste sijde is plomp.

Tghegheven. Laet A B C een clootsche driehouck wesen, diens sijde A B sy van een vierendeelrondts, A C kleender, ende B C grooter.

Tbegheerde. Wy moeten bewijsen dat de twee kleenste sijdens teghenoverhoucken A B C, A C B scherp sijn: Maer de grootste sijdens C B tegenoverhouck C A B plomp. Tbereytsel. Laet A C voortghetrocken worden tot D, sulcx dat A D een vierendeelrondts doe: Daer na sy op A als aspunt, beschreven de booch B D ende ghetrocken A E rechthouckich op C B.

Tbewys.

Dat de twee houckē A C B, A B C scherp



moeten sijn, blijckt aldus: Anghesien A B een vierendeelrondts doet, ende den houck A E B recht is, soo moet E B een vierendeelrondts doen, door het 10 vervolgh des 1 voorstels, ende E C moet kleender sijn, om dat de heele booch C B kleender is dan een halfrondt deur de 1 bepaling: Voort moet A E oock kleender sijn door t'vervolgh des 3 voorstels, want des rechthoucx A E C teghenoversijde A C kleender sijnde, soo moeten d'ander twee A E, C E elck kleender of elck grooter wesen, maer C E is kleender, A E dan moet oock kleender sijn, daerom oock is haer teghenoverhouck C scherp deur het 2 voorstel. Ende de selve kleender A E, de grootheyt anwijsende des houcx A B E, door de 2 bepaling, soo moet den houck A B E, ofte A B C scherp sijn.

Maer den houck C A B plomp te sijn, wort aldus bethoont: By aldien D B maer een vierendeelrondts en dede, soo soude den driehouck A D B evesijdich ende evenhouckich sijn, te weten drie sijden elck van een vierendeelrondts, met drie rechthoucken, sulcx dat de grootste booch daer in ghetrocken maer en soude connen wesen van een vierendeelrondts: Maer C B is grooter door t'ghegheven, ende D B noch grooter, welcke ons anwijst de grootheyt des houcx D A B deur de 2 bepaling, daerom D A B, of dattet selve is C A B, is grooter dan een rechthouck: Het is dan een plomphouck. Tbeslvyt. Hebbende dan eē clootsche driehouck een sijde van een vierendeelrondts, d'ander kleender, de derde grooter: De twee teghenoverhoucken vande kleenste sijden sijn scherp, maer de teghenoverhouck vande grootste sijde is plomp, t'welck wy bewijsen moesten.

[p. 203]

14 Vertooch. 14 Voorstel.

Des clootschen driehoucx driehoucken sijn t'samen grooter dan tvvee rechthoucken.

Tghegheven. Laet A B C een clootsche driehouck sijn, diens drie houcken sijn A, B, C. Tbegheerde. Wy moeten bewijsen de selve drie houcken t'samen grooter te sijn dan twee rechthoucken. Tbereytsel. Laet eenighe twee boghen als A B, A C, voortghetrocken worden tot datse malcander ontmoeten in D, daer na (alsoo A B D, A C D elck een halfrondt doen deur het 3 vervolgh des 1 voorstels) den as A D, ende der drie boghen A B, B C, C A drie pezen A B, B C, C A: Laet oock in de peez A B ergens geteyckent sijn t'punt E, ende van daer ghetrocken worden de rechte lini E F, rechthouckich op den as A D, daer na van F G, inde peez A C, de rechte lini F G, rechthouckich op den as A D, ende ten laetsten de rechte lini G E.

Tbewys.

Anghesien G F rechthouckich is op A F, soo is G A



langher dan G F, want het viercant van G A, is even an de twee viercanten van G F, F A: S'ghelijcx sal oock bethoont worden E A langher te sijn dan E F, daerom is den houck G F E, grooter dan den houck G A E: Maer den houck G F E is oock de grootheyt des cloothoucx C A B deur de 2 bepaling (want G F E is oock den houck der platten vande twee grootste ronden daer A B, A C, boghen af sijn) daerom den cloothouck C A B, is grooter dan den plathouck C A B. Ende s'ghelijcx sal oock bewesen worden den cloothouck A B C grooter te sijn dan den plathouck A B C, ende den cloothouck B C A grooter dan den plathouck B C A. Ende vervolghens de drie cloothoucken sijn t'samen grooter dan de drie plathoucken, maer de drie plathoucken sijn t'samen even an twee rechthoucken, daerom de drie cloothoucken des driehoucx A B C, sijn t'samen grooter dan twee rechthoucken. Tbeslvyt. Des clootschen driehoucx drie houcken dan, sijn t'samen grooter dan twee rechthoucken, t'welck wy bewijsen moesten.

Vervolgh.

Tis uyt het voorgaende openbaer, dat wesende eens driehoucx twee houcken t'samen niet grooter dan een vierendeeltondts, de derde moet grooter sijn.

15 Vertooch. 15 Voorstel.

Des clootschen driehoucx grootsten houck comt teghenover de grootste sijde.

Tghegheven. Laet A B C des 14 voorstels een clootsche driehouck wesen, diens sijde A C de grootste sy, A B kleender, B C de minste.

Tbegheerde. Wy moeten bewijsen dat den houck A B C, teghenover de grootste sijde A C, grooter is als een van d'ander.

Tbewys.

De grootste boghen hebben de

[p. 204]

grootste pezen, daerom is de peez A C de grootste van drien: Voort, de pezen die den grootsten plathouck maken, haer boghen maken de grootste cloothoucken, blijckende int selve 14 voorstel: Maer de twee kleender pezen A B, B C, maken den grootsten plathouck, daerom de kleender bogen A B, B C, maken den grootsten cloothouck, ende dat teghenover de grootste sijde A C. S'ghelijcx sal oock bethoont worden den houck A C B, teghenover de sijde A B, grooter te wesen dan den houck C A B, teghenover de sijde B C, om dat A B deur t'ghestelde grooter is dan B C. Tbeslvyt. Des clootschen driehoucx grootsten houck dan, comt teghenover de grootste sijde; t'welck wy bewijsen moesten.

16 Vertooch. 16 Voorstel.

VVesende een clootsche rechthouckighe driehouck, diens een scheefhouck scherp is: De booch ghetrocken van d'ander scheefhouck tot haer teghenoversijde, sal kleender sijn dan de schoensche, ende grooter dan de teghenoversijde van den scherphouck. Maer d'een scheefhouck plomp vvesende, de booch ghetrocken van d'ander scheefhouck tot haer teghenoversijde, sal grooter sijn dan de schoensche, ende kleender dan de teghenoversijde van den scherphouck.

1 Voorbeelt met d'een scheefhouck scherp.

Tghegheven. Laet A B C een clootsche driehouck sijn, diens houck B recht is, C scherp, ende A D sy de booch van d'ander scheefhouck A, tot haer teghenoversijde B C. Tbegheerde. Wy moeten bewijsen dat A D kleender is dan de schoensche A C, maer grooter dan A B, teghenoversijde des scherphoucx C.

Tbewys.

Anghesien den houck C, des rechthouckighen driehoucx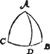



A B C, scherp is, haer teghenoversijde A B is kleender dan een vierendeelrondts deur t'vervolgh des 2 voorstels: Maer A B kleender wesende, haer teghenoverhouck A D B, des rechthouckigen driehoucx A B D, is scherp, deur het 2 voorstel, ende daerom den houck A D C plomp, deur het vervolgh des 1 voorstels: Sulcx dat A D C een driehouck is, diens scherphouck C kleender is dan haer plomphouck A D C, daerom deur het 15 voorstel, A D tegenoversijde vanden kleenderē houck C, is kleender dan A C teghenoversijde vanden grooteren houck A D C. Wederom A B teghenoversijde des scherphoucx C, kleender sijnde dan een vierendeelrondts, haer teghenoverhouck A D B des rechthouckighen driehoucx A D B, is scherp, deur het 2 voorstel. Sulcx dat A D B een rechthouckich driehouck is, diens rechthouck B grooter is dan den scherphouck A D B, daerom deur het 15 voorstel, A D teghenoversijde vanden grootsten houck B, is grooter dan A B teghenoversijde vanden kleensten houck A D B.

[p. 205]

2 Voorbeelt met d'een scheefhouck plomp.

Tghegheven. Laet nu d'een houck C plomp sijn, de rest alsboven.

Tbegheerde. Wy moeten bewijsen dat A D grooter is dan de schoensche A C, maer kleender dan A B teghenoversijde des plomphoucx C.

Tbewys.

Anghesien den houck C, des rechthouckighen driehoucx A B C, plomp is, haer teghenoversijde A B is grooter dan een vierendeelrondts, deur t'vervolgh des 2 voorstels: Maer A B grooter wesende, haer teghenoverhouck A D B des rechthouckighen driehoucx A B D is plomp, deur het 2 voorstel, ende daerom den houck A D C scherp, deur het vervolgh des 1 voorstels: Sulcx dat A D C een driehouck is, diens plomphouck C grooter is dan haer scherphouck A D C, daerom deur het 15 voorstel A D teghenoversijde vanden grooten houck C, is grooter dan A C, teghenoversijde vanden kleenderen houck A D C. Wederom, A B teghenoversijde des plomphoucx C, grooter sijnde dan een vierendeelrondts, haer teghenoverhouck A D B, des rechthouckighen driehoucx A D B, is plomp, deur het 2 voorstel: Sulcx dat A D B een rechthouckich driehouck is, diens rechthouck B kleender is dan den plomphouck A D B, daerom deur het 15 voorstel, A D tegenoversijde vanden kleensten houck B, is kleender dan A B teghenoversijde vanden grootsten houck A D B. Tbeslvyt. Wesende dan een clootsche rechthouckighe driehouck, diens een scheefhouck, &c.

17 Vertooch. 17 Voorstel.

Des clootschen driehoucx tvvee sijden sijn alsins grooter dan de derde.

Soo den driehouck drie even sijden heeft, of dat de twee grootste even waren, de saeck en behouft gheen bewijs, dacrom sullen wy alleenelick segghen vanden driehouck met een grootste sijde van drien.

Tghegheven. Laet A B C een clootsche driehouck sijn, diens grootste sijde B C is. Tbegheerde. Wy moeten bewijsen dat haer twee sijden alsins grooter sijn dan de derde. Tbereytsel. Angesien B C grooter is dan A B, so laet ons van B C snijen B D even an A B, ende trecken de booch A D: Laet daer na voortgetrocken worden B A, B D, tot datse malcander ontmoeten in E.

Tbewys.

Anghesien de sijde B C de grootste



van drien is, soo moet de selve met een van d'ander twee nootsakelick grooter sijn dan de derde, sulcx dat wy daer af gheen bewijs behouvende, sullen alleenlick bethoonē A C met A B, grooter te sijn dan B C, tot desen eynde segh ick aldus: B A E ende B D E doen elckeen halfrondt deur het 3 vervolgh des 1 voorstels, waer af E A even sijnde met E D (deur dien A B even is met B D) soo moet den houck E A D, even sijn metten houck E D A: Ende ghetrocken den houck E A C, vanden houck E A D, blijft den houck C A D, kleender dan den houck E A D, ende vervolghens kleender dan den houck E D A, of C D A, ende daerom is A C tegenoversijde vanden grooter houck C D A, grooter dan C D teghenoversijde vanden kleender houck C A D deur het 15 voor-

[p. 206]

stel: Ende soo veel A C grooter is dan C D, soo veel sijn de twee sijden C A, C B t'samen, openbaerlick grooter dan C B. Tbeslvyt. Des clootschen driehoucx twee sijden dan, sijn alsins grooter dan de derde, t'welck wy bewijsen moesten.

Vervolgh.

Tis uyt het voorgaende openbaer dat wesende twee sijden eens driehoucx t'samen niet grooter dan een vierendeelrondts, de derde moet kleender sijn. Maer wesende haer verschil niet kleender dan een vierendeelrondts de derde moet grooter sijn.

18 Vertooch. 18 Voorstel.

Des clootschen driehoucx drie sijden sijn t'samen kleender dan een rondt.

Tghegheven. Laet A B C een clootsche driehouck sijn.

Tbegheerde. Wy moeten bewijsen dat haer drie sijden t'samen kleender sijn dan een rondt. Tbereytsel. Laet eenighe twee sijden voortghetrocken worden, ick neem A B, A C, tot datse malcander ontmoeten, t'welck sy in D.

Tbewys.

De twee boghen A B D, A C D, doen deur het 3 vervolgh



des 1 voorstels, elck een halfrondt, dats t'samen een rondt: Ende de twee boghen A B, A C, doen t'samen een rondt, min de twee bogen B D, C D: Daerom so C B even waer an B D met C D, de drie sijden des driehoucx A B C, souden t'samen even sijn an een rondt: Maer C B des driehoucx C B D, is kleender als d'ander twee B D, C D, deur het 16 voorstel, daerom de drie sijden des driehoucx A B C, sijn t'samen kleender dan een rondt.

Tbeslvyt. Des clootschen driehoucx drie sijden dan, sijn t'samen kleender dan een rondt, t'welck wy bewijsen moesten.

Vervolgh.

Tis uyt het voorgaende openbaer, dat wesende twee sijden eens driehoucx t'samen niet kleender dan drie vierendeelrondts, de derde moet kleender sijn.

19 Vertooch. 19 Voorstel.

Rechthovcx houckmaet is^⋆ Media proportionalis. middeleveredenighe tusschen des ghesteldens boochs raecklijn, ende de raecklijn van haer schilbooch.

Tghegheven. Laet A B C een halfrondt sijn,



diens middelpunt D is, en̄ B C een vierendeelrondts, waer in C E een ghestelde booch is, diens raecklijn C F, ende B E haer schilbooch, diens raecklijn B G, ende C D rechthoucx houckmaet.

Tbegheerde. Wy moeten bewijsen dat D C middeleveredenighe is tusschen C F en B G.

⋆

Tbewys.

De twee driehoucken C F D, B D G sijn recht an C

[p. 207]

en B, ende den houck F D C, is even anden houck D G B, daerom de selve twee driehoucken sijn ghelijck, ende haer lijckstandighe sijden everedenich, dat is:

Ghelijck C F tot C D, alsoo D B tot B G:

Maer C D is even an D B, daerom

Ghelijck C F tot C D, alsoo C D tot B G.

Sulcx dat C D middeleveredenighe is tusschen C F ende B G.

Tbeslvyt. Rechthoucx houckmaet dan, is middeleveredenighe tusschen des ghesteldens boochs raecklijn, ende de raecklijn van haer schilbooch, t'welck wy bewijsen moesten.

20 Vertooch. 20 Voorstel.

Tvveer boghen raecklijnen sijn overhandt everedenich mette raecklijnen van haer schilboghen.

Tghegheven. Laet inde form des 19 voorstels, ghetrocken worden de rechte lini van D tot H inde lini C F, sniende de booch B C in I: Laet oock B G voortghetrocken worden tot K inde lini D H: T'welck soo sijnde, wy hebben twee boghen C I, C E, diens raecklijnen C H, C F, ende haer schilbogens I B, E B raecklijnen, sijn B K, B G. Tbegheerde. Wy moeten bewijsen dat der twee boghen C I, C E, raecklijnen C H, C F, overhandt everedenich sijn met haer schilbogens raecklijnen B G, B K dat is, ghelijck C H tot B G: Alsoo C F tot B K.

Tbewys.

D C is deur het 18 voorstel middeleveredenighe tusschen C F en B G: Ende deur t'selve voorstel is D C oock middeleveredenighe tusschen C H en B K, sulcx dattet viercant van D C even is anden rechthouck begrepen onder C F en B G: Oock is t'selve viercant even anden rechthouck begrepen onder C H B K, daerom die twee rechthoucken sijn even, ende haer sijden overhandt everedenich, dat is: Ghelijck C H tot C F, alsoo B G tot B K. Tbeslvyt. Tweer boghen raecklijnen dan, sijn overhandt everedenich mette raecklijnen van haer schilboghen, t'welck wy bewijsen moesten.

21 Vertooch. 21 Voorstel.

Rechthovcx houckmaet is middeleveredenighe tusschen de ghestelde boochs houckmaet, ende de snylijn van haer schilbooch.

Tghegheven. Laet A B C een halfrondt



sijn, diens middelpunt D is, ende B C een vierendeelrondts, waer in B E een booch is, diens houckmaet F E. Voort is C E haer schilbooch, diens snylijn D G, ende C D rechthoucx houckmaet.

Tbegheerde. Wy moeten bewijsen dat C D middeleveredenighe is tusschen F E houckmaet van B E, en D G snylijn van haer schilbooch E C.

Tbewys.

De driehouck en G D C, D E F, sijn recht an C en F, en̄ den houck G D C, is even anden houck D E F, daerom die selve twee driehoucken sijn ghelijck, ende lijckstandighe sijden everedenich, dat is:

[p. 208]

Ghelijck F E tot E D, alsoo D C tot D G:

Maer D C is even an E D, daerom

Ghelijck F E tot D C, alsoo D C tot D G.

Sulcx dat D C middeleveredenighe is tusschen F E ende D G.

Tbeslvyt. Rechthoucx houckmaet dan, is middeleveredenighe tusschen de ghestelde boochs houckmaet, ende de snylijn van haer schilbooch, t'welck wy bewijsen moesten.

Vervolgh.

Tis openbaer dat rechthoucx houckmaet, oock middeleveredenighe is tusschen schilboochs houckmaet, ende de snylijn van haer gestelde: Want nemende C E voor ghestelde diens schilbooch B E, wy segghen dat de voorschreven rechthoucx houckmaet D C, middeleveredenighe is tusschen F E schilboochs houckmaet van B E, en D G snylijn van haer ghestelde E C.

22 Vertooch. 22 Voorstel.

Tvveer boghen houckmaten, sijn overhandt everedenich mette snylijnen van haer schilboghen.

Tghegheven. Laet inde form des 21 voorstels, ghetrocken worden de rechte lini van D tot H inde lini C G, sniende de booch B C in I: Laet oock ghetrocken worden I K rechthouckich op D B: T'welck soo sijnde, wy hebben twee boghen B I, B E, diens houckmaten sijn K I, F E, ende haer verschilbogens I C, E C, snylijnen D G, D H. Tbegheerde. Wy moeten bewijsen dat dier twee boghen B I, B E, houckmaten K I, F E, overhandt everedenich sijn met haer schilbogens snylijnen, dat is, ghelijck K I, tot D G, alsoo F E tot D H.

Tbewys.

D C is deur het 21 voorstel middeleveredenighe tusschen E F, en D G: Ende deur t'selve voorstel is D C oock middeleveredenige tusschen K I en D H, sulcx dattet viercant van D C, even is anden rechthouck begrepen onder E F en D G, oock is t'selve viercant even anden rechthouck begrepen onder K I en D H, daerom die twee rechthoucken sijn even, ende haer sijden overhandt everedenich: Dat is, ghelijck K I tot D G, alsoo F E tot D H.

Tbeslvyt. Tweer boghen houckmaten dan, sijn overhandt everedenich mette snylijnen van haer schilboghen.

Vervolgh.

Tis openbaer dat twee schilboghens houckmaeten, oock overhandt everedenich sijn mette snylijnen van haer ghestelde, want nemende K I, F E voor schilboochs houckmaten van I C, E C, wy segghen dat de selve overhandt everedenich sijn met haer ghesteldens B I, B E, snylijnen D H, D G: Dat is ghelijck K I tot D G, Alsoo F E tot D H, t'welck boven bewesen is.