De Thiende

(1965)–Simon Stevin– rechtenstatus



[pagina 13]
Het ander deel der Thiende vande Werckinche.
I. Voorstel vande Vergaderinghe. Wesende ghegeven Thiendetalen te vergaderen: hare Somme te vinden. T'Ghegheven. Het sijn drie oirdens van Thiendetalen, welcker eerste 27 ⓞ 8 ① 4 ② 7 ③, de tweede, 37 ⓞ 6 ① 7 ② 5 ③, de derde, 875 ⓞ 7 ① 8 ② 2 ③, T'begheerde. Wy moeten haer Somme vinden. Wercking. Men sal de ghegheven ghetalen in oirden stellen als hier neven, die vergaderende naer de ghemeene manie re der vergaderinghe van heelegetalen aldus: Comt in Somme (door het 1. probleme onser Franscher Arith.) 9 4 1 3 0 4 dat sijn (t'welck de teeckenen boven de ghetalen staende, anwijsen) 9 4 1 ⓞ 3 ① 0 ② 4 ③. Ick segghe de selve te wesen de ware begheerde Somme. Bewys. De ghegeven 27 ⓞ 8 ① 4 ② 7 ③, doen (door de 3^e. bepaling) 27 8/10, 4/100, 7/1000, maeckē t'samen 27 847/1000. Ende door de selve reden sullen de 37 ⓞ 6 ① 7 ② 5 ③ weerdich sijn 37 675/1000; Ende de 875 ⓞ 7 ①
[pagina 14]
8 ② 2 ③ sullen doen 875 782/1000 welcke drie ghetalen als 27 847/1000 37 675/1000 875 782/1000, maecken t'samen (door het 10. probleme onser Franscher Arith.) 941 304/1000. Maer soo veel is oock weerdich de somme 941 ⓞ 3 ① 0 ② 4 ③, het is dan de ware somme, t'welck wy bewijsen moesten. Beslvyt. Wesende dan ghegheven Thiendetalen te vergaderen, wy hebben haer somme ghevonden soo wy voorghenom en hadden te doen.
Merckt. SOo inde ghegheven Thiendetalen eenich der natuerlicke oirden ghebraecke, men sal sijn plaetse vollen met dat ghebreeckende. Laet by exempel de gegheven Thiendetalen sijn 8 ⓞ 5 ① 6 ②, ende 5 ⓞ 7 ②, in welck laetste ghebreect het Thiendetal der oirden ①, men sal in sijn plaetse stellen 0 ①, nemende dan als voor ghegeven Thiendetal 5 ⓞ 0 ① 7 ② die vergaderende als vooren, in deser voughen: Dit vermaen sal oock dienē tot de drie volgende voorstellē, alwaermē altijt d'oirden der gebreeck ender Thiendetalen vervullen moet, gelijck in dit exempel gedaen is.
II. Voorstel vande Aftreckinghe. Wesende ghegheven thiendetal daermen aftrect, ende Thiendetal af te trecken: De Reste te vinden.
[pagina 15]
T'Ghegheven. Het sy Thiendetal daermen aftrect 2 3 7 ⓞ 5 ① 7 ② 8 ③, ende Thiendetal af te trecken 5 9 ⓞ 7 ① 4 ② 9 ③. T'begheerde. Wy moetē haer Reste vinden. Wercking. Men sal de ghegheven Thiendetalen in oirden stellen als hier neven, aftreckende naer de ghemeene maniere der Aftreckinge van heele ghetalen aldus: Rest (door het 2. Probleme onser Franscher Arith.) 1 7 7 8 2 9, dat sijn (twelck de teeckenen boven de ghetalen staende anwijsen) 1 7 7 ⓞ 8 ① 2 ② 9 ③. Ick segghe de selve te wesen de begheerde Reste. Bewys. De ghegheven 2 3 7 ⓞ 5 ① 7 ② 8 ③ doen (doer de 3^e. Bepalinge) 2 3 7 5/10 7/100 8/1000, maecken t'samen 237 578/1000; Ende door de selve reden sullen de 59 ⓞ 7 ① 4 ② 9 ③ weerdich sijn 59 749/1000, welcke ghetrocken van 237 578/1000, rest (door het 11^e. Probleme onser Franscher Arith.) 177 829/1000: Maer so veel is oock weerdich de voornoemde reste 177 ⓞ 8 ① 2 ② 9 ③, het is dan de ware Reste, twelck wy bewijsen moesten. Beslvyt. Wesende dan ghegheven Thiendetal daermen aftrect, ende Thiendetal af te trecken, wy hebben haer Reste ghevonden, als voorghenomen was ghedaen te worden.

[pagina 16]
III. Voorstel vande Menichvvldighinghe. Wesende ghegheven Thiendetal te Menichvuldighen, ende Thiendet al Menichvulder: haer Uytbreng te vinden. TGhegheven. Het sy Thiendetal te Menichvuldighen 32 ⓞ 5 ① 7 ②, ende het Thiendetal Menichvulder 89ⓞ4①6②. Tbegheerde. Wy moeten haer Vytbreng vinden. Wercking. Men sal de gegevē getalē in oirden stellen als hier nevē, Menichvuldigende naer de gemeene maniere van Menichvuldighen met heele ghetalen aldus: Gheeft Vytbreng (door het 3^e. Prob. onser Fran. Arith.) 29137122: Nu om te weten wat dit sijn, men sal vergaderen beyde de laetste gegeven teeckenen, welcker een is ②, ende her ander oock ②, maecken tsamen ④, waer uyt men besluyten sal, dat de laetste cijffer des Vytbrengs is ④, welcke bekent wesende soo sijn oock (om haer volghende oirden) openbaer alle dander, Inder voughen dat 2913ⓞ7①1②2③2④, sijn het begheerde Vytbreng. Bewys, Het ghegheven Thiendetal te menichvuldighen 32 ⓞ 5 ① 7 ②, doet (als
[pagina 17]
blijct door de derde Bepaling) 3 5/100 7/100, maecken tsamen 32 17/100; Ende door de selve reden blijct den Menichvulder 89 ⓞ 4 ① 6 ②, weerdich te sijne 89 46/100, met de selve vermenichvuldicht de voornoemde 32 57/100, gheeft Vytbreng (door het 12^e. probleme onser Franscher Arith.) 2913 7122/10000; Maer soo veel is oock weerdich den voornoemden Vytbreng 2913ⓞ7①1②2③2④, het is dan den waren Vytbreng; Twelck wy bewijsen moesten. Maer om nu te bethoonen de reden waerom ② vermenichvuldicht door ②, gheeft Vytbreng (welck de somme der ghetalen is) ④. Waerom ④ met ⑤, geeft Vytbreng ⑨, ende waerom ⓞ met ③ gheeft ③, etc. soo laet ons nemen 2/10 ende 3/100 (welcke door de derde Bepalinghe sijn 2 ① 3 ② hare Vytbreng is 6/1000, welcke door de voornoemde derde Bepalinge sijn 6 ③. Vermenichvuldighende dan ① met ②, den Vytbreng sijn ③. Beslyt. Wesende dan gegeven Thiendetal te Menichvuldighen, ende Thiendetal Menichvulder, wy hebben haren Vytbreng ghevonden; als voorghenomen was gedaen te worden.
Merckt. SOo het laetste teecken des Thiendetals te Menichvuldigē ende Menichvulders ongelijck waren, als by exempel deen 3 ④ 7 ⑤ 8 ⑥, dander 5 ① 4 ②; Men sal doen als vooren, ende de ghesteltheyt der letteren vande Werckinghe sal soonadich sijn.

[pagina 18]
IIII. Voorstel vande Deelinghe. Wesende ghegeven Thiendetal te Deelen, ende Thiendetal Deeler: Haren Soomenichmael te vinden. TGhegheven. Het sy Thiendetal te deelen 3 ⓞ 4 ① 4 ② 3 ③ 5 ④ 2 ⑤, ende deeler 9 ① 6 ②. Tbegheerde. Wy moeten haer Soomenichmael vinden. Wercking. Men salde gegevē Thiendetalen deelen (achterlatende haer teeckenen) naer de ghemeene maniere van deelen met heele getalen aldus: 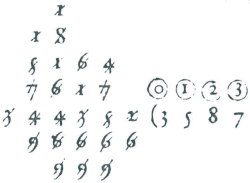Geeft Somenichmael (door het vierde Probleme onser Franscher Arith.) 3 5 8 7: Nu om te weten wat dit sijn, men sal af trecken het laetste teecken des Deelders, welck is ②, van t'laetste teecken des Thiendetals te deelen ⑤, rest ③, voor het teecken der laetster cijfferletter des Soomenichmaels, welcke bekent wesende, soo sijn oock (om haer volghende oirden) openbaer alle dander, inder voughen dat; ⓞ 5 ① 8 ② 7 ③ sijn den begheerden Soomenichmael. Bewys, Het ghegeven Thiendetal 3 ⓞ 4 ① 4 ② 3 ③ 5 ④, 2 ⑤ doet (als blijct door de 3^e Bepaling) 3 4/10 4/100 3/1000 5/10000 2/100000 maecken tsamen 3 44352/100000;
[pagina 19]
Ende door de selve reden blijct den Deelder 9 ① 6 ② weerdich te sijne 96/100, door twelcke gedeelt de voornoemde 3 44352/100000, gheeft Soomenichmael (door het 13. Probleme onser Franscher Arith.) 3 587/1000. Maer so veel is oock weerdich den voornomden Soomenichmael 3 ⓞ 5 ① 8 ② 7 ③, het is dan den waren Soomenichmael, Twelck wy bewijsen moeften. Beslvyt. Wesende dan gegheven Thiendetal te Deelen, ende Thiendetal Deeler, wy hebben haren Soomenichmael gevonden, als wy voorghenomen hadden te doen.
I. Merckt. SOo de teeckenen des Deelders hoogher waren dan des Thiendetals te Deelen, men sal by het Thiendetal te deelen soo veel 0 stellen, alsmen wil, ofte alst noodich valt. By exempel 7 ② sijn te deelen door 4 ⑤, ick stelle neven de 7 ettelicke 0 aldus 7000, die deelende als voorengedaen is in deser vougē: Geeft Soomenichmael 1 7 5 0 ⓞ. Het ghebuert oock altemet dat den Soomenichmael met gheen heele ghetalen en can uytghesproken worden, als 4 ① ghedeelt door 3 ② in deser manieren: Alwaer blijct datter oneyndelicke drien uyt commen souden, sonder eenichmael even uyt te gheraecken: In sulcken ghevalle machmen soo naer commen als de saecke dat voordert, ende het overschot verloren laten. Wel is waer
[pagina 20]
dat 13 ⓞ 3 ① 3 1/3 ②, ofte 13 ⓞ 3 ① 3 ② 3 1/3 ③, etc. souden het volcommen begheerde sijn, maer ons voornemen is in dese Thiende te wercken met louter heele ghetalen, want wy opsicht hebben naer t'ghene in sMenschen handel plaets houdt, alwaermen het duysenste deel van een Mijte, van een Aes, van een Graen ende dierghelijcke, verloren laet; So tselfde oock byden voornaemsten Meters ende Telders dickmael onderhouden wort, in vele rekeninghen van grooten belanghe: Als Ptolemeus ende Ian van Ga naar margenoot+Kuenincxberghe, en hebben hare Boogpees Tafelen met de uyterste volmaectheyt niet beschreven, hoe wel het door Veelnamighe Ghetalen doenlick was, Reden dat dese onvolmaectheyt (ansiende dier dinghen Eynde) nutter is dan soodanighe volmaectheydt.
II. Merct. DE Vyttreckinghen aller specien der Wortelen mueghen hier in oock gheschien. By exempel om te vinden den viercanten Wortel van 5 ② 2 ③ 9 ④ (dienende tot het maecken der Boogpeez Tafelen naer Ptolomeus maniere) men sal wercken naer de ghemeene ghebruyck aldus: Ende den wortel sal sijn 2 ① 3 ②, want den helft van het laetste teecken des gheghevens is altijt het laetste teecken des wortels: Daerom soo het laetste ghegheven teecken oneffen ghetal ware,
[pagina 21]
men salder noch een naestvolghende teecken toedoen, ende wercken dan als boven. Insghelijcx oock int Vyttrecken des Teerlincxwortel, daer sal het laetste teecken des wortels, altijt het derdendeel sijn van het laetste ghegheven teecken, ende alsoo voort in allen anderen specien der wortelen. Eynde der Thiende	margenoot+ Tabulas Arcuum & Chordarum. Multinomios numeren.