De natuurkunde van 't vrije veld. Deel I
(1937)–Marcel Minnaert–Licht en kleur in het landschap
[pagina 134]
| |
Het beoordelen van vorm en beweging.99. Gezichtsbedrog omtrent stand en richting.Stel ons gezichtsveld bestaat uit twee groepen voorwerpen; binnen elke groep zijn die voorwerpen evenwijdig of haaks op elkaar, maar de twee groepen hellen ten opzichte van elkaar: dan zijn we geneigd de ‘overheersende’ groep als werkelijk Fig. 95. Schijnbare richtingsverandering van de zwaartekracht bij het remmen van een trein.
vertikaal en werkelijk horizontaal te beschouwen. Als een trein toevallig in de bocht stilstaat of langzaam rijdt, en de treincoupé dus in de dwarsrichting helt, zie ik alle palen, huizen, torens daarbuiten in de andere zin overhellen. Blijkbaar geef ik er mij wel enigszins rekenschap van dat mijn coupé helt, maar lang niet in voldoende mate. In de gangen van een schip dat helt (bv. als de wind dwars op het schip blaast), lijken mij alle mensen scheef te staan ten opzichte van de loodlijn. Iets dergelijks speelt ook een rol bij het beoordelen van geringe hellingen, althans voor een fietser.Ga naar voetnoot1) Het terrein waarop ik rijd zie ik altijd ‘te horizontaal’; als ik fietsende van een steile helling afdaal, schijnt het water in een reservoir langs de weg niet horizontaal te staan, maar mij tegemoet te hellen. Bevind ik mij op een zacht dalend stuk, dan lijkt de weg verderop te stijgen - terwijl | |
[pagina 135]
| |
hij feitelijk vlak is; ik zie de stijging in de verte te sterk en de daling te zwak. Mijn ogen leren mij vooral hoe de helling vóór mij verandert; dikwijls zijn hun indrukken tegengesteld aan wat ik uit de tegenstand bij het trappen zou besluiten. Een eigenaardige begoocheling kunnen we waarnemen als we ons bevinden in een trein die remt. Vestig de aandacht op schoorstenen, huizen, randen van treinraampjes en andere vertikale voorwerpen: op het ogenblik dat de trein sterk vertraagt krijgt u de indruk dat al deze lijnen enigszins voorover hellen, het duidelijkst als de trein net stilstaat; onmiddellijk daarna staan ze ineens weer rechtop. Zelfs de horizontale vlakte van een weiland scheen mee te hellen en is nu weer waterpas geworden. - De verklaring is, dat we ons bij het remmen naar voren voelen gaan, alsof de richting van de zwaartekracht gewijzigd was. Ten opzichte van wat onze spieren nu voelen als ‘de vertikaal’ hellen de werkelijke voorwerpen voorover (fig. 95). | |
100. Het zien van bewegingen.Ga naar voetnoot1)Meestal stelt men zich voor dat bewegingen waargenomen worden, doordat men een voorwerp ten opzichte van vaste merkpunten eerst in een bepaalde stand, daarna in een gewijzigde stand ziet. Dit is echter niet altijd het geval; een snelheid kan als een enkelvoudige indruk waargenomen worden, evengoed als een lengte of een tijd. Als u naar de beweging der wolken kijkt, krijgt u onmiddellijk een indruk van hun richting en van hun snelheid. Men heeft gevonden, dat wij snelheden kunnen waarnemen die niet groter zijn dan 1' of 2' per sekunde; dit is het geval, wanneer we vaste punten in het gezichtsveld hebben (ook al vergelijken we daar niet bewust mee). Zonder vaste punten wordt de waarneming der snelheid ongeveer 10 maal onzekerder; het onbewegelijke vergelijkingsstelsel is in dergelijke gevallen uw eigen oog, waarvan u door uw spieren voelt dat het in rust is, en waarin u met de gezichtszin de beelden over het netvlies voelt schuiven. Bekijk de voorbijtrekkende wolken, en tracht hun trekrichting bij het eerste rustige kijken ineens te bepalen. Varieer de omstandigheden: lage wolken, hoge wolken; weinig wind, veel wind; met maan, zonder maan. - Een snelheid van 2' per sekunde betekent dat de wolk in 15 sec. over de maanschijf trekt. | |
[pagina 136]
| |
Een net met brede mazen is uitgehangen om te drogen. Men ziet duidelijk elke windstoot over het net lopen; maar bekijkt men één der mazen, dan is er nauwelijks beweging te zien. Het oog schijnt erg gevoelig voor kleine bewegingen die in onderling verband geschieden. | |
101. De bewegende sterren.Ga naar voetnoot1)Omstreeks 1850 is men groot belang gaan stellen in een geheimzinnig verschijnsel, daarin bestaande, dat een ster die men scherp aankeek soms heen en weer scheen te zwaaien en van plaats te veranderen. Het effekt zou in de schemering optreden, en alleen aan sterren in de buurt van de gezichteinder, minder dan 10o hoog. Men zag de sterk fonkelende ster met rukjes bewegen, evenwijdig aan de horizon, dan 5 tot 6 sekunden blijven staan, evenzo weer achteruit bewegen, enz. Het verschijnsel was voor veel waarnemers zó duidelijk, dat zij het als objektief beschouwden en door slieren warme lucht beproefden te verklaren.Ga naar voetnoot2) Er kan echter geen sprake zijn van een natuurkundig verschijnsel. Een beweging van ½o per sekunde voor het ongewapend oog zou overeenkomen met 100o of meer voor een kijker met matige vergroting: de sterren zouden heen en weer zwiepen en door het veld schieten als meteoren. Ieder waarnemer weet dat daar geen sprake van is. Zelfs bij de allerslechtste luchttoestand zijn de plaatsveranderingen tengevolge der scintillatie beneden de grens van wat het oog kan waarnemen. Psychologisch behoudt het verschijnsel echter zijn volle belang. Misschien ontstaat het, als er geen vergelijkingsobjekt is ten opzichte waarvan we de stand van de ster goed kunnen waarnemen; wij zijn er ons niet van bewust, dat ons oog voortdurend kleine onwillekeurige bewegingen uitvoert, en moeten dus de verplaatsingen van het beeld over het netvlies wel aan verschuiving van de lichtbron toeschrijven. Iemand heeft mij eens gevraagd hoe het komt dat een ver verwijderd vliegtuig zich steeds met kleine rukjes vooruitbeweegt, als men het aandachtig bekijkt, Blijkbaar was hier een zelfde psychologische oorzaak in 't spel als bij het ‘bewegen’ der sterren. | |
[pagina 137]
| |
De uitdrukking ‘ver verwijderd’ schijnt er op te wijzen, dat ook dit verschijnsel vooral nabij de gezichteinder optreedt. Wat moet men ervan denken, dat drie personen, onverwachts en gelijktijdig, de maan op en neer zien dansen gedurende ongeveer 30 minuten?!Ga naar voetnoot1) | |
102. Begoochelingen omtrent rust en beweging.Een zeer bekende begoocheling ontstaat, als men in een stilstaande trein zit en de trein daarnaast in beweging ziet komen Je meent dan dat het je eigen trein is die heel zachtjes vertrekt. Of we kijken langs een toren of hoge radiomast naar de voorbijtrekkende wolken: weldra lijkt het, alsof de wolken stilstonden maar alsof de toren bewoog. Evenzo zien sommige mensen de maan voorbijsnellen door het stilstaande wolkenzwerk. Als men op een plank over een beek loopt, moet men oppassen niet naar het stromende water te kijken, op straffe van duizeligheid: het oordeel over rust en beweging komt in de war, omdat een zo groot gedeelte van het gezichtsveld beweegt.Ga naar voetnoot2) - Degene die voor het eerst op zee vaart, ziet de hangende voorwerpen in zijn hut heen en weer schommelen, terwijl de hut zelf stilstaat. In al deze gevallen is de begoocheling nauw verwant met die van § 99. Volgende algemene regel schijnt te gelden: als we de voorwerpen in ons gezichtsveld verdeeld zien in twee groepen, de ene bewegend, de andere in rust, dan hebben we neiging om de grootste groep als in rust te beschouwen. Merk op dat die begoocheling tenslotte neerkomt op een vergissing betreffende de beweging der spieren van ons oog.
Ik zit bij het raampje van de trein en kijk dromend naar de voorbijvliegende grond. De trein stopt; en terwijl ik zeker weet dat hij stilstaat, heb ik toch bij het naar buiten kijken de onweerstaanbare indruk dat hij langzaam achteruit glijdt. Het is niet zó dat het gehele gezichtsveld even snel verschuift: dicht bij mij is de beweging sneller, op grotere afstand langzamer; zij is ook langzamer op enige afstand rechts en links van het punt naar hetwelk ik tuur. Het is, alsof het gehele landschap langzaam om dit punt draaide, en daarbij uit een lederachtig rekbare stof bestond, die zich vervormt; de draaiingsrichting is de tegengestel- | |
[pagina 138]
| |
de van die welke gold toen de trein bewoog (§ 107). Het zou aardig zijn, op het ogenblik dat de trein stopt fluks aan het andere raampje te gaan zitten: de beweging zou dan in de oorspronkelijke zin moeten doorgaan. Men kan zich voorstellen dat onze oogspieren de gewoonte hebben aangenomen, de voorbijvliegende voorwerpen onbewust min of meer te volgen; staat de trein stil, dan gaan we voort met die onwillekeurige oogbewegingen, en blijven nog een tijd lang als 't ware een constante ‘compensatiesnelheid’ bij de werkelijke optellen. De wijze echter waarop de snelheid verandert naar de randen van het gezichtsveld toe, kan nooit door één enkele oogbeweging verklaard worden. Men heeft zelfs proeven genomen, waarbij lange tijd getuurd werd naar voorwerpjes die voortdurend van een middenpunt uit naar buiten bewogen werden, de ene naar boven, de andere naar beneden, naar rechts en naar links: bij stop zetten van de beweging zag de waarnemer de lichtpunten van alle kanten naar het centrum terugstromen, hetgeen toch onmogelijk door een oogbeweging te verklaren is! Het is dus veeleer ‘onze geest’, die in elk deel van het gezichtsveld een deel van de snelheid heeft leren wegredeneren, en daarmee nog doorgaat na het ophouden der beweging. De waarneming welke wij beschreven hebben treedt ook op, wanneer we een stipje op de ruit van de treincoupé fixeren, en dus de oogbeweging uitschakelen; mits de beweging niet zò snel is, dat de voorwerpen buiten tot strepen ineenvloeien.Ga naar voetnoot1) Daartegenover staat nu weer een reeds oude waarneming van Brewster, die wel degelijk op onwillekeurige oogbewegingen wijst.Ga naar voetnoot2) Als we uit het treinraampje kijken, lijken de steentjes en keitjes tot streepjes uitgerekt; kijk nu snel naar de grond op een iets groter afstand: een heel kort ogenblik ziet u dan even de steentjes in rust, als werden ze verlicht door een electrische vonk. Dit bewijst toch dat ons oog inderdaad de bewegende voorwerpen volgt, maar niet met de volle snelheid. Brewster deed nog een andere waarneming (t.a.p.), toen hij naar de voorbijvliegende steentjes keek door een spleet in een blad papier. Draaide hij opeens de ogen opzij, zodat hij de steentjes in het indirekte gezichtsveld zag (steeds door de spleet kijkend), dan was het gehele tafereel een kort ogenblik scherp. Verklaring?? | |
[pagina 139]
| |
Ik loop langs een speelterrein voor kinderen, aan mijn rechterhand, afgezet door een zeer lang hek. Al lopende kijk ik naar de kinderen, daarbij voortdurend het hoofd naar rechts gekeerd houdend. Na 1 tot 2 minuten kijk ik weer voor mij uit, en zie nu de straatkeien en andere voorwerpen vóór me van rechts naar links schuiven. Tracht ik de proef te herhalen, maar fixeer ik het hek in plaats van de kinderen, dan is het verschijnsel veel minder opvallend. - Bij dergelijke waarnemingen vindt men, dat men niet altijd de snel bewegende voorwerpen zelf met het oog moet volgen, maar dat het gunstig is naar een voorwerp met weinig struktuur te turen, terwijl beelden met sterke tegenstellingen van licht en donker over het netvlies schuiven.Ga naar voetnoot1) Ik kijk aandachtig naar vallende sneeuwvlokken, volg één ervan in zijn val, richt dan snel de blik omhoog en zoek een nieuwe uit; en zo gedurende enige minuten. Werp ik nu mijn ogen op de besneeuwde grond, dan zie ik hem letterlijk oprijzen terwijlik mezelf voel dalen. Kijk een tijdje naar het water van een snelstromende rivier, of naar de ijsgang der drijvende schotsen, en fixeer hier bij de punt van een ducdalf, of een detail op een eilandje. Als u nu de blik weer op de vaste grond richt, ziet u een ‘antistroombeweging’. Na het bewonderen van een waterval, schijnen de oevers opwaarts te bewegen. Purkinje keek geruime tijd van uit zijn raam naar een optocht van ruiters; daarna had hij de indruk, alsof de huizenrij aan de overkant in tegengestelde richting bewoog. Als u langs een smal paadje tussen het koren loopt, en naar de maan in de verte tuurt, zijn de omstandigheden alweer gunstig voor het optreden der begoocheling. Die omstandigheden zijn, kort samengevat: de beweging moet tenminste 1 minuut duren; ze mag niet te snel zijn; het oog moet turen, hetzij naar een bewegend, hetzij naar een rustend voorwerp, maar altijd zo dat de beelden die over het netvlies trekken enige tegenstellingen en een duidelijke struktuur vertonen. | |
103. De slingerende dubbelsterren.Ga naar voetnoot2)Dit is een verschijnsel, reeds door den groten Herschel waargenomen. Kijk met een eenvoudig toneelkijkertje naar de voor- | |
[pagina 140]
| |
laatste ster van de Grote Beer. U ziet heel duidelijk dat er naast de heldere ster nog een zwakke zit (fig. 61, 78). Doe nu de proef liefst als die twee sterren min of meer
 Fig. 96. Schijnbare slingering van dubbelsterren, door een heen-en-weer bewegend toneelkijkertje waargenomen.
vertikaal onder elkaar zitten (- het gaat anders toch ook -). U beweegt uw kijkertje zachtjes een klein eindje naar links, net zo snel dat u de beide sterren nog als puntjes blijft zien; dan weer naar rechts; dan weer terug naar links, enz. Daarbij schijnt het nu alsof de zwakkere ster telkens iets achterbleef bij de heldere, het lijkt wel alsof ze aan een touwtje hing en een slingerbeweging uitvoerde (fig. 96)! Het verschijnsel is te verklaren, doordat het licht een zekere tijd nodig heeft om een indruk op ons netvlies te maken. Die tijd is des te korter naarmate de ster helderder is; tegen dat de zwakste gezien wordt is de heldere al een eindje verder. Ditzelfde verschijnsel is in de laatste jaren door Pulfrich gebruikt om een nieuw type van fotometer te bouwen. | |
104. Gezichtsbedrog bij het beoordelen van de draaiingszin.Een windmolen draait in de avondschemering. We kijken van uit een richting, schuin op het vlak der wieken, en zien in de verte hun donker silhouet (fig. 97a). U kunt u voorstellen dat de wieken rechtsom draaien, maar evengoed dat ze linksom gaan (fig. 97b). Het overgaan van de éne voorstelling op de andere vereist een ogenblik concentratie van de aandacht; meestal is het ook voldoende, rustig te blijven kijken, dan slaat het beeld ‘vanzelf’ om. - Meteorologische stations hebben meestal een windmeter van Robinson: het is een molentje, dat om een vertikale as draait, en gebruikt wordt om de windsterkte te meten. Als ik het van op afstand rustig blijf aankijken, schijnt de draaiingszin telkens na ongeveer 25 of 30 sekunden om te slaan, zonder dat mijn wil daar bewust aan meewerkt. Ook een windvaan die heen en weer zwaait kan ons aan het twijfelen brengen, vooral indien hij niet te hoog geplaatst is (fig. 97c). In al deze gevallen hangt ons oordeel over de draaiingszin ervan af, welke delen van de baan we dichter bij ons, en welke we verder van ons af achten. Die waarop toevallig onze aandacht | |
[pagina 141]
| |
het meest gevestigd is, lijken ons in 't algemeen dichterbij. Het omslaan van de schijnbare draaiingszin is dus aan een verspringen van de aandacht toe te schrijven.  Fig. 97. Het silhouet van de molen in de avond:
a. wat de waarnemer ziet; b. welke voorstelling hij ermee verbinden kan. c. Andere bedriegelijke silhouetten. | |
105. Stereoskopische verschijnselen.Met slechte treinruitjes, zoals men ze hier en daar wel nog aantreft, kan men een grappig optisch verschijnsel waarnemen. Wacht tot de trein stopt, en kijk aandachtig door de ruit naar de keien van de grond. Ogen dicht bij het glas, hoofd rustig houden, en u vrijmaken van de vooropgezette gedachte dat de grond vlak is! U bemerkt nu ineens dat hij lijkt te golven, zelfs heel sterk te golven! Verplaatst men langzaam het hoofd, dan lopen de golvingen in tegengestelde zin over de grond; verwijdert men zich een weinig van de ruit, dan schijnen ze ongeveer even hoog te blijven maar wijder te worden. Verklaring. Het glas van de ruit is niet vlak, het vertoont heel zwakke hobbels, meestal evenwijdig aan een bepaalde richting, want ze zijn ontstaan door het uitrollen van het gloeiend-vloei- | |
[pagina 142]
| |
bare glas onder stalen rollen. Zulk een hobbel werkt als een prisma van geringe brekende hoek en doet de lichtstralen een weinig afwijken. In fig. 98 is aangenomen dat de ogen L, R die naar het punt A van de grond kijken, de invloed van de hobbels in het glas nog niet merken. Bij het waarnemen
 Fig. 98. Als men door een hobbelige ruit kijkt, lijkt de grond te golven.
van het punt B echter wordt de lichtstraal BR gebroken en volgt hij de weg BCR. Het gevolg is, dat de ogen gericht zijn alsof zij het punt B' bekeken, dat dichter bij ons ligt dan B. In een ander deel van de ruit wijken de stralen weer anders af, zodat het voorwerp verder van ons af schijnt te liggen. Zo begrijpt men, dat de zwakke hobbeligheid van het glas een sterke schijnbare golving van de voorwerpen buiten zal veroorzaken, al is natuurlijk de samenwerking der invloeden op rechter en linker oog soms vrij ingewikkeld. Als het linkeroog bv. door een effen gedeelte van de ruit kijkt, het rechteroog door de hobbels, kan men gemakkelijk het ontstaan der stereoskopische werking in bijzonderheden nagaan. Sluit het linker oog en schommel met het hoofd een weinig heen en weer: waar de ruit een hol gedeelte (M) heeft (fig. 98), schommelen de bijzonderheden van de grond in dezelfde zin; waar de ruit bol is (O), tegengesteld (Waarom?). Open nu beide ogen: de gebieden M en O komen nu overeen met plaatsen van de grond die we op normale afstand zien; door N kijkend met het rechter oog zien we een berg en door P een dal. Overtuig u van dit alles door de waarneming en geef u rekenschap van de opgemerkte bijzonderheden!
Een verschijnsel dat hier nauw mee verwant is neemt men waar als men vlak bij een wateroppervlak staat met zeer zwakke golfjes. De ogen trachten zich te richten naar het spiegelbeeld | |
[pagina 143]
| |
van een boomtak bijvoorbeeld; maar doordat elk oog op een verschillend golfoppervlak kijkt, worden de twee beelden onophoudelijk op andere hoekafstanden van elkaar gebracht, en is het onmogelijk er de oogassen rustig op in te stellen. Dit geeft een zeer bijzonder en moeilijk te beschrijven gevoel. Zodra we één oog sluiten zien we het wateroppervlak zelf nauwelijks meer; we kunnen ons voorstellen dat we niet een spiegelbeeld zien, maar de boom zelf, door de wind bewogen. Kijken we met twee ogen, dan krijgen we ineens het bewustzijn van het gerimpeld wateroppervlak zelf, maar dit oppervlak glanst: dit is het typisch verschijnsel dat ontstaat, als de twee ogen zeer verschillende beelden geven, het ene licht en het andere donker. | |
106. Het mannetje in de maan.Ga naar voetnoot1)‘Het mannetje in de maan’ is een uitstekend voorbeeld om ons te leren voorzichtig zijn bij het waarnemen. De donkere en lichte vlekken op de maan zijn eigenlijk de vlakten en de bergen, en het is duidelijk dat hun verdeling een zeer grillige is. Onbewust nu zoeken we in die grillige lichtverdeling naar bekende vormen: we vestigen de aandacht op bepaalde bijzonderheden, en daardoor schijnen die duidelijker en opvallender te worden; terwijl de vormen waar we niet op letten minder duidelijk worden. Zo kan men in de volle maan tenminste drie vormen van menselijk gelaat zien: van opzij, drie kwart, en van voren. Men kan er een vrouwefiguur in zien, een oud vrouwtje met een takkebos, een haas, een kreeft, enz. Dergelijke begoochelingen hebben aan de beste waarnemers parten gespeeld, onder andere in het beroemde geval van de ‘kanalen’ op Mars. Bij menige fantastische beschrijving van een luchtspiegeling of fata morgana is het goed hieraan te denken. | |
107. Het draaiende landschap en de meelopende maan.Let op twee bomen of twee huizen die ongelijk ver van ons verwijderd zijn: zodra wij bewegen, zien we hoe het verste van de twee met ons meegaat, en het dichtstbij gelegen achterblijft. Het | |
[pagina 144]
| |
is een eenvoudig verschijnsel van verschilzicht (= ‘parallax’), een verschijnsel van meetkundige aard, zonder bijzondere natuurkundige achtergrond.
Het landschap in de omlijsting van de raampjes
Snelt met een wilde vaart, en hele vlakten
Met plassen, velden, bomen, en wat hemel,
Zij storten zich in 't wentlen van de draaikolk ...
P. Verlaine, La bonne Chanson.
Een van de eerste dingen die mij als kind troffen als ik in de trein zat, is de merkwaardige draaiende beweging die het landschap schijnt uit te voeren. Stel ik kijk aan de rechterzijde van de trein: dan zie ik al de dichtbijgelegen dingen naar rechts wegvluchten, terwijl de ver afgelegen partijen met mij mee naar links bewegen. Het is alsof het gehele landschap draait om een denkbeeldig punt: het punt waar ik toevallig de blik op richt. Of ik in de verte tuur of meer dichtbij, altijd lijkt mij het punt dat ik bekijk op zijn plaats te blijven, terwijl de verdere punten meelopen, de dichterbij gelegen punten achterblijven. Neem de proef! Het is duidelijk dat deze gezichtsindrukken volgen uit het verschilzicht; het nieuwe wat erbij komt, is dat we alles betrekken op het punt waarheen onze blik gericht is, en dit in rust zien: dit is een psychologische eigenaardigheid van onze gezichtswaarnemingen. Als we 's avonds wandelen, fietsen, sporen, zien we de maan aan de verre gezichteinder getrouw ‘met ons meegaan’. Ook de zon, ook de sterren - maar daar letten we niet zo op. Dit bewijst dat we onze aandacht vestigen op het landschap, en dus bepaalde partijen daarvan in rust zien; de verder gelegen hemellichamen schijnen dan door verschilzicht mee te bewegen. | |
108. Het zoeklichtverschijnsel.Ga naar voetnoot1) De wolkenbanden.Een zoeklicht werpt horizontaal een slanke, ijle lichtbundel over het nachtelijke heidelandschap. Ik weet dat de bundel zuiver rechtlijnig loopt; maar ik kan mij niet onttrekken aan de begoocheling dat hij gebogen is, in het midden het hoogst, aan beide kanten naderend tot de grond. Alleen door een stokje vóór mijn oog te houden overtuig ik er mij van dat de bundel werkelijk over zijn gehele lengte recht is. Wat is de oorsprong van die begoocheling? Ik ben geneigd, | |
[pagina 145]
| |
de baan als een boog te zien, omdat ik haar aan de ene zijde naar links zie dalen, aan de andere zijde naar rechts. Alsof een simpele horizontale, rechtlijnige telegraafdraad niet net hetzelfde vertoonde! Bij de lichtbundels in de avond heb ik echter geen aanknopingspunten om de afstanden te schatten met behulp van het geheel der omringende voorwerpen, en weet ik a priori niets over de vorm van de bundel. Een dergelijk verschijnsel zien we 's avonds, aan een rij hoog opgehangen straatlantarens, vooral wanneer er geen evenwijdig lopende huizenrijen zijn, of indien bomen die aan 't gezicht onttrekken. Men ziet dan de rij der lichten gekromd, juist zoals een zoeklichtenbundel.Ga naar voetnoot1) Onmiddellijk hieraan verwant is de waarneming, dat de verbindingslijn der horens van de Maan, tussen eerste kwartier en volle Maan bijvoorbeeld, volstrekt niet loodrecht schijnt op de richting Zon-Maan; klaarblijkelijk denken we ons deze richting als een gekromde lijn. De wolkenrijen die schijnen uit te stralen van een punt van de gezichteinder, en zich aan de andere zijde van het uitspansel weer verenigen, zijn in werkelijkheid volgens evenwijdige rechte lijnen gerangschikt. Zie ook § 191. Het is bijzonder indrukwekkend om zich 's nachts dichtbij een sterke vuurtoren te bevinden. De grote bundels zwaaien over het landschap, convergeren aan de andere zijde naar het tegenpunt en wentelen daar omheen. | |
109. De schijnbare afplatting van het hemelgewelf.Ga naar voetnoot2)Wanneer we buiten in het vrije veld staan, en naar de hemel kijken, hebben we in 't algemeen niet de indruk van een grenzeloze ruimte boven ons; ook niet de indruk van een halve bol die over ons en de aarde gestulpt is. Veeleer lijkt het een gewelf, waarvan de hoogte boven ons hoofd veel geringer is dan de afstand van ons tot aan de gezichteinder (fig. 99). Het is een indruk, meer niet, maar voor de meeste mensen een zeer overtuigende, de verklaring zal dus een psychologische moeten zijn, niet een natuurkundige. | |
[pagina 146]
| |
Iets van die schijnbare afplatting te meten is natuurlijk onmogelijk, maar we kunnen schattingen maken. a. We vragen ons af hoe groot de verhouding wel schijnt; volgens de waarnemers en de omstandigheden krijgt men antwoorden die meestal tussen 2 en 4 liggen. b. We schatten zo goed mogelijk de richting waarin zich het midden van de boog zenith-gezichteinder schijnt te bevinden. Bij nameting (§ 235) blijkt dit midden niet op 45o hoogte te liggen, maar veel lager, meestal op 20o-30o; veel zeldzamer vindt men waarden zo laag als 12o of zo hoog als 45o. Het komt  Fig. 99. Over het landschap schijnt zich de hemel als een soort kap te welven.
er op aan, onbevooroordeelde waarnemers te vinden, en hun duidelijk te maken dat ze niet de hoek, maar de boog in twee moeten delen. Ook is het zeer belangrijk, de plaats van het zenith goed te schatten: liefst door zich eerst naar de éne, dan naar de tegenovergestelde windstreek te keren, en te kijken of de twee aldus gemaakte schattingen overeenstemmen. Voor elk der kenmerkende getallen a en b neme men het gemiddelde van een 10-tal schattingen. De schijnbare afplatting van het hemelgewelf hangt van allerlei omstandigheden af. Ze neemt sterk toe als de hemel bewolkt is en bij schemering, ze neemt af bij donkere sterrelucht. Gemiddeld is de ‘halveringshoek’ 22o bij dag, 30o bij nacht. Merk op dat waarnemingen op zee hieromtrent van grote waarde zijn, aangezien daarbij het uitzicht geheel vrij is en geen nevenomstandigheden de schatting storen. Door een stuk rood glas gezien - zó groot dat men niet afge- | |
[pagina 147]
| |
leid wordt door de begrenzingen ervan - lijkt de hemel vlakker; door een stuk blauw glas hoger en dichter bij de halve bolvorm.Ga naar voetnoot1) Uitvoeriger schattingen kunnen ons nog nauwkeuriger inlichten over de welving die we onbewust aan de hemelkap toeschrijven. Het blijkt dat veel waarnemers er een soort helmvorm in zien. | |
110. Overschatting van de hoogte. (fig. 100)Met de afplatting van het schijnbare hemelgewelf schijnt samen te hangen, dat wij de hoogten boven de gezichteinder meestal te groot schatten. Blijkbaar verwarren wij onbewust steeds de meting van de boog met de meting van de hoek; het punt M, zo gekozen dat HM = MZ, Fig. 100. De schijnbare boog van zenith tot horizon in twee verdelen.
ligt veel lager dan 45o boven de horizon, en lijkt ons toch halfweg. De zon in de winter, op middagtijd, schijnt vrij hoog te staan, en is in onze gewesten toch slechts 15o boven de kim. 's Zomers lijkt ze ‘bijna in het zenith’, terwijl ze feitelijk nooit hoger komt dan 61o. Evenzo overschatten we de hoogte van heuvels en de steilheid van een voor ons opstijgende helling. Zelfs komt het voor, dat waarnemers de kleine kring om de zon of de maan (§ 134) als hoger dan breed beschrijven. Men vermijdt deze gezichtsbegoochelingen grotendeels, als men het landschap met half dichte ogen bekijkt: dan werken alleen licht- en schaduwpartijen als grote massa's. | |
111. De schijnbare vergroting van zon en maan aan de gezichteinder.Dit is een van de sterkste en meest algemeen bekende gezichtsbegoochelingen. Schrikwekkend groot kan de maan koperkleurig oprijzen, maar nietig klein is ze als ze hoog in de lucht zit! En de zon:
't wordt watergroene, omhooge;
omleege, brandt en broeit
de groote zonne nog,
die zinkt en grooter groeit.
G. Gezelle, Rijmsnoer, X (Avondrood).
| |
[pagina 148]
| |
De groote, tomaatroode zon ....
De zon wierd grooter en grooter, en rood.
Timmermans, Pallieter, blz. 3 en blz. 30.
 Fig. 101a. Het ontwerpen van een zonnebeeldje met een brilleglas van lange brandpuntsafstand.
stuk papier op, en zie, daar tekent zich een keurig scherp beeldje van de zon af! Is het niet helemaal rond, dan ligt dit daaraan, dat het brilleglas niet goed loodrecht op de invallende zonnestralen stond: draai het een weinig heen en weer, laat het iets meer of iets minder hellen. Zoek de plaats waar u het papier moet houden om het zonnebeeldje zo scherp mogelijk te krijgen, teken met twee potloodstreepjes de grootte van de middellijn aan, en meet die met een meetlatje, op 0,5 mm nauwkeurig. Neem liefst de horizontale diameter, omdat de vertikale door de aardse straalbreking iets verkleind wordt. Herhaal deze meting een paar maal en neem het gemiddelde. Nu dezelfde proef bij hoge zon! De opstelling is iets moeilijker; | |
[pagina 149]
| |
bevestig de kurk met een spijker hoog tegen een paal: door de juiste zijde van de paal te kiezen, en de kurk om de spijker te laten draaien, kan men het brilleglas goed loodrecht op de lichtstralen instellen (fig. 101b). Meet het zonnebeeldje: het is (binnen de waarnemingsfouten) bij hoge zon precies even groot als bij lage zon! Zelfs de nauwkeurigste metingen met de
 Fig. 101b.
sterkste kijkers vertonen niet het minste verschil. De vergroting van zon en maan nabij de gezichteinder is dus een psychologisch verschijnsel. Maar ook dat gehoorzaamt aan vaste wetten, ook dat kan in getalmaat geschat worden. Verschaf u een witkartonnen schijf van 30 cm middellijn, en verwijder er u zover van, dat de schijf even groot lijkt als de maan. Natuurlijk is een werkelijke vergelijking niet toegelaten, anders vindt u evenals bij een ware meting dat de grootte altijd dezelfde is. Keer u dus eerst naar het hemellichaam, prent u goed in hoe groot het lijkt, draai u om en vergelijk het herinneringsbeeld met de schijnbare grootte van de schijf. 't Gaat nog mooier als u een reeks witte schijven van toenemende grootte op een zwarte achtergrond plakt, en u altijd op dezelfde afstand er vandaan plaatst. Voer dergelijke schattingen zowel bij hoogstaande als bij laagstaande maan uit. - Ook met de zon zijn zulke schattingen mogelijk; vermijd verblinding door gebruik van een donker glaasje, bv. een sterk gesluierde fotografische plaat, en kijk daarna met onbeschermd oog naar de witte schijven. De waarnemingen zijn moeilijk, omdat het psychologische verschijnsel de invloed ondergaat van allerlei subtiele faktoren, schommelingen van de aandacht, enz. Merk op hoeveel beter het na enige oefening gaat! De aldus verkregen getallen leren ons, dat de zon of de maan nabij de gezichteinder wel 2,5 tot 3,5 maal zo groot lijken als hoog aan de hemel! Het verschil tussen het natuurkundig en het psychologisch verschijnsel is dus wel zeer opvallend. Het effekt neemt nog toe bij bewolkte lucht en in de schemering. De schijnbare vergroting der ondergaande zon is veel opvallender in de vlakte dan wanneer ze achter hoge bergen ondergaat; op zee nochtans is de vergroting gering.Ga naar voetnoot1) | |
[pagina 150]
| |
112. Het verband tussen de schijnbare vergroting der hemellichamen nabij de gezichteinder en de vorm van het hemelgewelf. (fig. 102)Men heeft getracht, dit verschijnsel te herleiden tot dat van de schijnbare afplatting van het hemelgewelf. De opvatting is, dat wij ons de zon en de maan even ver denken als dit hemelgewelf, de lage zon dus verscheiden malen verder verwijderd dan de hoge zon; dat wij ze toch onder dezelfde gezichtshoek waarnemen, schrijven wij (onbewust) daaraan toe, dat ze verscheiden malen groter is: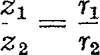 . Om de juistheid van deze samenhang te toetsen, heeft men de schijnbare grootte van zon en maan op verschillende hoogten  Fig. 102. Waar het hemelgewelf ver verwijderd lijkt, schijnt de zonneschijf groter.
boven de kim geschat (vgl. § 111). Deze proeven zijn moeilijk. Zowel bij dag en blauwe lucht als 's nachts bij onbewolkte sterrenhemel bewijzen de uitkomsten, dat de grootte van zon of maan inderdaad ongeveer evenredig met de afstand van het hemelgewelf schijnt te veranderen. - De laagstaande zon lijkt door de nabijheid van wolken vergroot (niet door voorwerpen op aarde die zich tegen de kim aftekenen); dit komt, omdat het bewolkte hemelgewelf zoveel afgeplatter is dan het onbewolkte, dus zoveel verder van ons verwijderd aan de kim, en wij de zon even ver terugschuiven, om haar althans niet vóór de wolken te denken. - Evenzo wordt de laagstaande maan, bij dag, door de nabijheid van wolkenmassa's groter geschat. Bij heldere lucht is bijzonder opmerkelijk, dat zij in de schemering veel groter lijkt dan bij dag of bij nacht: dat komt overeen met de grotere afplatting van het hemelgewelf bij de schemering. Als het 's nachts nevelig is, zodat de maan de naburige hemel sterk verlicht, wordt voor ons gevoel de weinig afgeplatte hemelvorm van de nacht weer vervangen door de platte schemeringsvorm, en de maan lijkt weer groter. Aan wie zou denken dat de schijnbaar grotere afmetingen van de maan nabij de kim of bij nevel samenhangen met de lichtverzwakking welke zij dan ondergaat, kan door twee waarnemingen geantwoord worden: a. de maansikkel lijkt niet groter bij nevel; | |
[pagina 151]
| |
voor ons is dit begrijpelijk, omdat de sikkel de omgevende lucht slechts weinig verlicht; b. bij maansverduisteringen lijkt de hoogstaande maan niet vergroot. Uit al het vorige blijkt wel, dat het aankomt op de hemelachtergrond, en dat die bepaalt hoe groot we zon en maan schatten. - Toch moeten wij toegeven, dat er ook bezwaren zijn tegen het leggen van een zo nauw verband tussen beide verschijnselen: vele mensen zien de zon of de maan aan de horizon juist ‘dichterbij’, of zijn helemaal niet in staat iets over de schijnbare afstand te zeggen, terwijl ze toch sterk de indruk van de vergfoting hebben. Beslissend behoeft zulk een tegenwerping mijns inziens niet te zijn; want het is mogelijk dat we, bij het rechtstreeks stellen van de vraag omtrent de afstand, andere psychologische motieven in werking brengen dan die welke bij de onbewuste beoordeling de doorslag geven. | |
113. De holle aarde.Ga naar voetnoot1)Dit is een mooie tegenhanger van de gezichtsindruk die het hemelgewelf op ons maakt: van uit een luchtballon ziet men bij heldere lucht hoe de aarde zich in de verte opwaarts schijnt te welven, zodat ze een holle schaal lijkt boven dewelke wij zweven. Het horizontale vlak door ons oog schijnt ons altijd vlak te blijven; andere horizontale vlakken daarboven of daaronder schijnen zich in de verte altijd naar dit vaste horizontale vlak toe te buigen. Als de ballon zich op een paar kilometer boven wolkenbanden bevindt, zien wij die gekromd, met de bolle zijde naar beneden en de holle zijde naar ons toe. Is er een wolkenlaag beneden en een andere boven ons, dan schijnen wij te zweven tussen twee reusachtige horlogeglazen. Dezelfde begoochelingen zullen allicht ook in een vliegtuig waar te nemen zijn. | |
114. De onderschattingstheorie.Op geniale wijze is von Sterneck er in geslaagd, een wiskundige formulering te geven van het schijnbaar zo onbepaalde psychologische verschijnsel van ‘het hemelgewelf’. Het moge waar zijn dat hij het niet afdoende verklaart, hij brengt het in elk geval terug tot een grote groep waarnemingen, waar we door dagelijkse ervaring vertrouwd mee zijn. | |
[pagina 152]
| |
Hoe verder de voorwerpen, hoe moeilijker het is om hun afstanden te onderscheiden. Straatlantarens verder dan 150 m lijken 's nachts alle even ver. - De bergen aan de gezichteinder, de hemellichamen lijken de een niet verder verwijderd dan de andere. De normale, ‘naieve’ waarnemer onderschat al de verre afstanden: een brand bij nacht; inslaande bliksem; de lichten van een haven, gezien van uit de volle zee. Die onderschatting van de afstanden is gering voor de nabije voorwerpen, en wordt sterker naarmate zij verder verwijderd zijn; tenslotte nadert de schijnbare afstand tot een grens. Rechthoekige velden, gezien van uit de trein, maken de indruk van trapezia: want de hoek waaronder ik de zijde a zie past bij haar ware afstand, maar is te klein voor haar (geringere) schijnbare afstand. - Als de trein een tunnel nadert, en u kijkt uit het raampje naar de gemetselde muur van de tunnelingang, ziet u de stenen zienderogen zwellen en groter wordenGa naar voetnoot1); verklaring: als de ware afstand tweemaal kleiner wordt, zien we de stenen onder een tweemaal grotere hoek, maar de schijnbare afstand lijkt ons slechts anderhalf maal kleiner (bijvoorbeeld) en dus is het alsof de stenen zelf waren gegroeid. Von Sterneck beproefde het volgende eenvoudig verband te leggen tussen de schijnbare afstand d' en de ware afstand d:  . Hierin is c een constante voor elk bijzonder geval: de grootste afstand die we onder de gegeven omstandigheden van belichting enz. nog kunnen schatten; c variëert van 200 meter tot 20 km. Wij zien hoe met deze formule d' praktisch gelijk is aan d, zolang d klein is ten opzichte van c; wordt d vergelijkbaar met c, dan treedt toenemende onderschatting op; voor grote d nadert de schijnbare afstand tot een grens. De formule beschrijft dus de ervaring qualitatief goed, en uitvoeriger waarnemingen gaven ook verrassend goede quantitatieve overeenstemming. De onderschattingstheorie verklaart de overschatting der berghellingen door den waarnemer W die beneden staat, en die de afstand WB schat alsof het WB' was, dus AB als AB' ziet. En zij eist als logisch gevolg een onderschatting der hellingen door den waarnemer die zich op de hoogte bevindt (fig. 103). We zullen thans zien hoe zij ook de schijnbare vorm van het | |
[pagina 153]
| |
hemelgewelf tracht te verklaren, en daardoor dus ook de schijnbare vergroting der hemellichamen bij de kim. Stellen wij ons bijvoorbeeld een wolkenlaag voor, op een hoogte van 2,5 km boven ons hoofd. We zouden die moeten zien als een uiterst vlakke schaal, want door de kromming der aarde is ons oog 178 km van het wolkendek bij de gezichteinder verwijderd, 2,5 km van het wolkendek in 't zenith. Zo zien we echter stellig de bewolkte hemel niet! De korte afstand wordt een weinig, de lange wordt zeer onderschat. Stel dat we de verhouding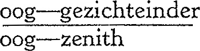 als ongeveer 5 schatten; dan betekent dit, dat in deze omstandigheden c = 10,6 km bedraagt: de onderschattingsformule  Fig. 103. De waarnemer W overschat de stijging en onderschat de daling.
levert dan de goede waarden (beproef dit!). Hieruit volgt, dat we de bewolkte lucht als een soort gewelf, een ‘omwentelingshyperboloïde’ moeten zien, wat inderdaad met de algemene indruk overeenkomt die wij ervan krijgen. - Merk op, dat we dus eigenlijk het hemelgewelf niet afgeplat zien, maar juist relatief hoger dan het is! Hoe wordt het nu echter voor de blauwe lucht, voor de sterrenhemel? Von Sterneck neemt telkens maar een andere waarde van c, en het blijkt dat zijn formule dan in elk bepaald geval de waarnemingen verrassend goed beschrijft. Het wordt echter wel moeilijk te begrijpen hoe wij in deze gevallen kunnen spreken van een bepaalde ‘afstand’, die onderschat wordt. - En zo komen wij tot de algemener vragen: hoe krijgen wij enige indruk van afstand bij zulke onbepaalde voorwerpen als wolken? En bij de blauwe lucht? Bij de onbewolkte nachthemel? De onderschattingstheorie moge waar zijn voor aardse voorwerpen, over wier afmetingen en afstanden we door allerlei ervaringen ingelicht zijn, - het lijkt zeer twijfelachtig of zij op het uitspansel toegepast mag worden. Daarenboven is de oorsprong der onderschatting nog onopgehelderd. | |
[pagina 154]
| |
115. De blikrichtingstheorie van Gauss.Er zijn nu een reeks waarnemingen, die aantonen dat de vorm van het hemelgewelf en de schijnbare vergroting der hemellichamen nabij de kim in hoofdzaak samenhangen met de blikrichting ten opzichte van ons lichaam. Door de ervaring van vele geslachten zijn we beter ingesteld op het waarnemen vóór ons uit dan in de hoogte, en dit heeft blijkbaar invloed op de schatting van afstanden en afmetingen. Als de volle maan hoog aan de hemel staat, zetten wij ons in een schommelstoel; of op de grond, met de rug tegen een hellend voorwerp. Terwijl we aldus in sterk achteruit hellende houding waarnemen, maar het hoofd in zijn gewone stand ten opzichte van het overige van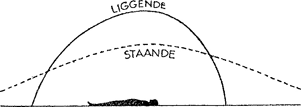 Fig. 104. De vorm van het hemelgewelf van een staande en voor een liggende waarnemer.
het lichaam houden, schijnt de maan ons merkbaar groter. Komen we gauw overeind, zodat onze blik nu naar boven gericht moet worden, dan lijkt ze weer kleiner. Omgekeerd lijkt de volle maan nabij de gezichteinder veel kleiner als we ons naar voren buigen. Beide verschijnselen kan men afwisselend zien als de zon 30o tot 40o hoog zit, en haar licht door mist getemperd is. Buig u achteruit en vooruit: de schijf lijkt afwisselend groter en kleiner. Leg u met de rug plat op de grond: het hemelgewelf lijkt samengedrukt aan de zijde naar dewelke nu onze schedel gekeerd is; terwijl het aan de tegenovergestelde zijde zuiver bolvormig lijkt (fig. 104). Wij zien hier duidelijk, dat de (t.o.v. ons lichaam) naar beneden gerichte en de vooruit gerichte blik ongeveer gelijkwaardig zijn, terwijl de naar boven gerichte blik de voorwerpen samengedrukt doet lijken. Hang u met de knieën aan een rekstok en kijk met het hoofd naar beneden rond: u ziet het hemelgewelf als een halve bol.Ga naar voetnoot1) Al deze waarnemingen bevestigen elkaar. Hier komt nog bij, dat sterrebeelden, gezien door een kijker, dus onttrokken aan de invloed van het landschap, insgelijks groter schijnen wanneer | |
[pagina 155]
| |
ze zich laag boven de kim bevinden; het enige dat hier invloed kan hebben is de blikrichting.Ga naar voetnoot1) Beproef nu niet, een verdere controle te verkrijgen door de schijnbare grootte van zon of maan in een spiegel te beoordelen, en aldus bv. de hoogstaande maan met horizontale blikrichting te bekijken. Zodra de waarnemer iets merkt van de aanwezigheid van een spiegel, is de begoocheling al ten dele verdwenen. Deze soort proef is daarom zeer moeilijk goed uit te voeren.
Verschillende andere theorieën omtrent de hier besproken gezichtsindrukken zijn gemakkelijk te weerleggen. Zo heeft men wel beweerd, een ‘physische theorie’ van de vorm van het hemelgewelf te kunnen geven, welke theorie dan blijkt neer te komen op het zeer onbegrijpelijke beginsel, dat we de hemel des te verder verwijderd zien naarmate zijn helderheid groter is, en wel evenredig met de wortel uit de helderheid.Ga naar voetnoot2) De blauwe hemel is donkerder in 't zenith dan aan de horizon, en zou daardoor gedrukt schijnen. Deze theorie wordt echter afdoende weerlegd, door dat de gelijkmatig bewolkte hemel gebleken is helderder te zijn in het zenith dan aan de kimGa naar voetnoot3), terwijl we hem toch ook gedrukt zien. Bij bewolkte lucht schijnt trouwens de plaats waar de zon zit, en die helderder lijkt, altijd dichter bij ons dan de omringende delen van het uitspansel. | |
116. Invloed van de aardse voorwerpen op de schatting van de afstand tot het hemelgewelf.Ga naar voetnoot4)Plaats u voor een lange rij huizen en kijk naar de middenste daarvan: de hemel daarboven is veel dichter bij u, boven de uiteinden van de rij is hij veel verder verwijderd. - Evenzo lijkt de hemel boven het bos veel dichter bij ons, over 't vrije veld veel verder weg. Blijkbaar schatten we dus de afstand van het hemelgewelf op 50 of 60 meter bv.! Maar het is voldoende dat we voorwerpen zien waarvan we de verre afstand kennen, opdat hun hemelachter- | |
[pagina 156]
| |
grond ons onmiddellijk veel verder verwijderd zou schijnen. De aardse voorwerpen nemen in zekere mate elk hun hemelachtergrond met zich mee. - Men ziet hoe zuiver psychologisch al deze verschijnselen bepaald zijn, en hoe onmogelijk het is, te spreken van een ideaal ‘referentie-oppervlak’ dat voor ons het hemelgewelf zou zijn! Kijk langs een lange spoorweglijn of een grote weg met bomen, die ons duidelijk de grote afstand tot bewustzijn brengen: de hemel lijkt in die Fig. 105. De schijnbare vorm van het hemelgewelf boven radiomasten.
richting veel verder verwijderd dan in andere windstreken. Bedek echter het landschap tot aan de gezichteinder metbehulp van een stuk papier: de gezichteinder komt ineens dichterbij. Bij wijze van tegenproef kunnen we op een dergelijke wijze aan de blik een geleiding geven in vertikale richting: de hemel lijkt daar dan hoger geworden. Buitengewoon treffend is dit verschijnsel aan de voet van een hoge toren, of nog beter bij de hoge ranke masten van een groot radiostation. Het hemelgewelf daarboven schijnt een soort koepelvormige opwelving te vertonen; tussen drie masten lijkt de gehele hemel opwaarts gedrukt. Verschillende waarnemers tekenen onafhankelijk van elkaar de schijnbare vorm op dezelfde wijze (fig. 105). Kijkend naar zulk een mast vindt u een veel groter halveringshoek (§ 109) dan wanneer u op enige afstand een nieuwe bepaling doet met de rug naar de mast gekeerd. Bedek de horizon terwijl u naar de mast kijkt: er komen nu zelfs halveringshoeken van meer dan 45o, tot 56o toe! Het hemelgewelf wordt dus nu hoger dan een halve bol gezien! | |
[pagina 157]
| |
Hoe overtuigend deze waarnemingen ook zijn, - toch bedenke men dat zij, opzichzelf beschouwd, nooit de vorm van het hemelgewelf of de schijnbare vergroting aan de kim kunnen verklaren. Ook als men door een zeer donker glaasje waarneemt, ziet men nog altijd de hoge zon klein, de lage zon groot, terwijl er dan van het landschap niets meer te bemerken is. | |
117. De schijnbare grootte van zon en maan, gemeten in centimeters. De methode der nabeelden.Ga naar voetnoot1)We weten dat de ‘grootte’ van zon en maan niet in lengtemaat door ons waargenomen kunnen worden; we kunnen alleen de hoek aangegeven waaronder wij ze zien. En toch is het merkwaardig, dat een groot aantal mensen volhouden dat ze die hemellichamen zien ‘als een ‘soepbord’; daarnaast is er een minderheid, die afmetingen opgeeft van de orde van een geldstuk. Wie daarover glimlacht, bedenke wel, dat ook een wetenschappelijk geschoold man het als een volstrekte onmogelijkheid voelt, de grootte der maan op te geven als 1 mm of als 10 meter; terwijl hij toch weet, dat 1 mm op 10 cm afstand, of 10 meter op 1 kilometer de maanschijf precies zouden bedekken. De psychologische faktoren die hier een rol spelen zijn nog zeer weinig bekend. Iedereen weet, dat men nabeeldjes van de zon krijgt als men heel vluchtig in het felle hemellichaam kijkt en knipoogt (§ 88). Zulk een nabeeldje projekteert zich nu op elk voorwerp waar men naar tuurt; op een dichtbije muur maakt het de indruk van een erg klein, nietig ding; op verder verwijderde voorwerpen gezien, lijkt het groter. (Let wel: we schatten niet de gezichtshoek, maar de grootte van ‘het ding zelf’). Dit effekt is volkomen begrijpelijk, want wil een voorwerp op afstand onder dezelfde hoek gezien worden als een voorwerp dichtbij ons, dan moet het in lengtemaat groter zijn. - Vrage: wanneer lijkt het nabeeld even ‘groot’ als de zon zelf? Verschillende waarnemers oordeelden, dat dit het geval was, wanneer de muur 50 tot 60 m verwijderd was, en wel geldt dit even goed bij dag als bij nacht: ziedaar dus de afstand waarop wij de maan en de zon van ons verwijderd voelen. Aangezien de gezichtshoek 1/108 is, zou dit overeenkomen met een middellijn van 45 tot 55 cm. Op dezelfde wijze kon aangetoond worden, dat het nabeeld | |
[pagina 158]
| |
op een muur die verder verwijderd is dan 60 m, nog altijd even groot lijkt als dat op de hemel vlak erboven (dus aan de kim). Terwijl het nabeeld, hoog in de lucht geprojecteerd, bepaald kleiner leek dan dat op een muur van 60 m afstand. Hier blijkt dus nog eens, dat wij inderdaad de afstand tot aan het hemelgewelf boven ons hoofd kleiner zien dan de afstand tot de kim, en dat 60 m al enigszins de grensafstand is van de onderschattingstheorie (vgl. § 114).
Door een nameting van zijn vroegere schetsen, heeft Vaughan Cornish getracht een belangwekkende grootheid te bepalen: de omvang (in hoekmaat) van het veld dat de mens als een eenheid ziet, het tafereel. De algemene indruk van een landschap hangt daar nauw mee samen.Ga naar voetnoot1) |
|

