Zichtbare en onzichtbare bewegingen
(1901)–H.A. Lorentz–
[pagina 102]
| |
V. Molekulaire bewegingen.De lichtverschijnselen hebben ons tot het denkbeeld geleid dat in elke ruimte die geen vast, vloeibaar of gasvormig lichaam bevat, toch nog altijd de middenstof aanwezig is, die men met den naam van aether bestempelt. Deze blijft over, wanneer wij den hoogsten graad van luchtverdunning bereikt hebben, die de tegenwoordige hulpmiddelen mogelijk maken, en heeft dan, voor zoover wij weten, altijd gelijke eigenschappen, dezelfde als de aether van de wereldruimte. Zoo vertoont dit medium eene eenvormigheid, waardoor het ten eenenmale verschilt van de ‘gewone’, d.w.z. onmiddellijk voor onze zintuigen waarneembare lichamen in hunne bonte verscheidenheid; het moet wel iets van geheel anderen aard zijn. Om het onderscheid uit te drukken kunnen wij die gewone lichamen alle met den naam van ‘materie’ aanduiden, dien wij dan niet op den aether toepassen, of van ‘weegbare stof’ spreken, in tegenstelling met den ‘onweegbaren’ aether. Een spraakgebruik, dat wel gewettigd is, daar wij geen grond hebben om aan te nemen dat de aether aan de algemeene aantrekkingskracht onderworpen zou zijn, en dus ‘gewicht’ zou hebben. In vroeger tijden namen de natuurkundigen het bestaan van nog andere onweegbare stoffen, of imponderabilia aan. Oude leerboeken der chemie beginnen met een hoofdstuk over de | |
[pagina 103]
| |
‘warmtestof’; deze zou in elk voorwerp aanwezig zijn, des te meer naarmate de temperatuur hooger is. Hare deeltjes zouden elkander afstooten, en zoo zou zij de welbekende uitzetting bij verwarming teweegbrengen. Veel was er ongetwijfeld dat op deze wijze begrepen kon worden, zooals b.v. de overgang van warmte bij de aanraking van een verhit en een koud lichaam, of de warmtegeleiding tusschen het in het vuur geplaatste en het daaruit stekende deel eener metalen staaf. Maar andere verschijnselen, die wij dagelijks waarnemen, leverden groote moeilijkheden op, die bij nader onderzoek onoverkomelijk bleken, en zoo heeft de warmtestof met algemeene instemming het veld moeten ruimen voor eene andere opvatting. Ieder weet hoe men twee voorwerpen warm kan maken door ze tegen elkander te wrijven of te laten stooten, hoe de assen van een spoorwegrijtuig warm kunnen loopen, een zaag of een hamer bij het gebruik verhit worden, en niemand zou kunnen zeggen, waar in dergelijke gevallen de meerdere warmtestof, die in de verhitte voorwerpen aanwezig zou moeten zijn, van daan moest komen. Daarentegen zult gij het aanstonds begrijpelijk vinden, wanneer de hedendaagsche natuurkunde U verklaart dat men hier te doen heeft met eene omzetting van eene zichtbare beweging, die de lichamen in hun geheel hebben, in eene onzichtbare beweging, over zeer geringe afstanden, van de kleine deeltjes, de molekulen, waaruit de materie is opgebouwd. Het kost U geene moeite, U voor te stellen dat bij de wrijving door tal van kleine stootjes de molekulen in beweging gebracht worden, en gij vindt dit denkbeeld des te natuurlijker, nu wij weten dat een warm lichaam trillingen in den aether opwekt, wat het zeker niet zou kunnen doen, als het niet zelf de zetel eener beweging was. Zoo komen wij op het uitgestrekte gebied der molekulaire bewegingen waaruit ik dezen avond eenige grepen zal doen; ik | |
[pagina 104]
| |
zal daarbij alleen over gasvormige lichamen spreken, daar deze de eenvoudigste eigenschappen hebben en wij dientengevolge met hunne molekulaire theorie het verst zijn gevorderd. De meest in het oog vallende eigenschap van een gas is het onbegrensde uitzettingsvermogen. Wij kunnen, als wij in een cilinder onder een verplaatsbaren zuiger eene hoeveelheid lucht hebben afgesloten, die eerst dezelfde dichtheid heeft als de dampkringslucht, den zuiger zoover opheffen, dat het volume vertienvoudigd of verhonderdvoudigd wordt, en aanstonds zal het gas zich over de geheele ruimte die wij het aanbieden verspreiden. Houden wij den zuiger vast, dan tracht nog altijd, als ik dat woord gebruiken mag, de lucht zich uit te zetten; zij oefent daardoor naar alle zijden een druk uit. Ook de lucht hier in deze kamer drukt tegen elk oppervlak aan, waarmede zij in aanraking is. Zij perst dit blok hout een weinig ineen, drukt, in welke richting ik het ook houd, aan weerskanten tegen dit blad papier, en stuwt in eene buis die in een bakje met water staat de vloeistof omhoog, zoodra ik, door aan het boveneinde te zuigen, de lucht daaruit voor een deel wegneem. En daar aan het uitzettingsvermogen nooit een eind komt, houdt, hoe groot ik het volume ook maak, de druk nooit op; al had ik den zuiger in onzen cilinder van zooeven tot eene hoogte opgeheven, millioen maal zoo groot als de oorspronkelijke, eenige druk, hoe klein dan ook, zou er nog altijd zijn. De tegenwoordige physica verklaart dit alles uit eene beweging der luchtmolekulen. Zij laat deze in alle richtingen heen en weer vliegen, met eene snelheid die des te grooter is naarmate het gas eene hoogere temperatuur heeft; zij laat daarbij de deeltjes herhaaldelijk tegen elkander en ook tegen de wanden van een vat of andere begrenzende voorwerpen botsen, en in het bombardement tegen deze laatste ziet zij de oorzaak van den door 't gas uitgeoefenden druk. Wat den aard der beweging betreft, maakt zij de meest eenvoudige onderstellingen. De | |
[pagina 105]
| |
gasmolekulen zijn zoo klein dat zij misschien slechts het duizendste deel der ruimte werkelijk vullen, en oefenen alleen bij de aanraking of even te voren merkbare krachten op elkaar uit. Tusschen twee botsingen in zal dus een molekuul aan geene kracht onderworpen zijn - wanneer wij van de zwaartekracht, die bij niet al te groote gasmassa's eene ondergeschikte rol speelt, afzien -; het zal derhalve in eene rechte lijn voortgaan. Bij elke botsing zal intusschen de bewegingsrichting veranderen, en zoo heeft elk deeltje eene onregelmatige zigzag-beweging. Om niet bij deze algemeenheden te blijven staan, Fig. 30
zullen wij berekenen, hoe snel zich de luchtmolekulen moeten bewegen om den waargenomen druk uit te oefenen; wij zullen aannemen dat dit de gewone druk van den dampkring is en vragen vooreerst naar de grootte daarvan. De bekende barometer wijst ons die aan. In een bakje met kwik M (Fig. 30) staat eene verticale van boven gesloten buis A B, die geene lucht bevat, zooals wij kunnen zien door de buis genoegzaam te doen hellen. Het kwik vult haar dan tot aan den top, om dien weer te verlaten als wij de buis rechtop zetten. Ter loops willen wij hierbij opmerken dat dan in de ruimte boven het kwik aether moet zijn, daar het licht er anders niet doorheen kon schijnen, en dat die aether daar niet had kunnen komen, wanneer hij niet door het glas of het kwik kon heendringen. Maar wij behoeven ons nu verder met den aether niet bezig te houden; die blijft van avond buiten spel. Het is er nu om te doen, in te zien, hoe de druk der buitenlucht op den kwikspiegel C de vloeistof in de buis omhoog drijft, maar niet verder dan tot op eene bepaalde hoogte D, zoodat, wanneer de buis maar lang genoeg is, zij niet geheel met kwik gevuld is, maar boven de vloeistof eene luchtledige ruimte bevat. | |
[pagina 106]
| |
Hoe nu het hoogteverschil der twee kwikspiegels in de buis en in den bak ons eene maat voor den luchtdruk oplevert, is duidelijk. Wanneer de dampkring er niet was, zou het kwik in de buis tot dezelfde hoogte kunnen worden opgedreven, als wij de vloeistof in den bak op hetzelfde niveau als D konden brengen. Daaruit besluiten wij dat de kwikspiegel in den bak even sterk door de lucht naar beneden gedrukt wordt, als hij dat zou worden door eene kwikmassa van de hoogte die door het punt D wordt aangegeven. Die hoogte is niet altijd dezelfde. Wij zullen intusschen, om de gedachten te bepalen, stellen dat zij 76 cM. is, en wel in een barometer gevuld met kwik van 0o C. Elke cM.3 daarvan weegt 13,60 gram. En nu kunnen wij den barometer wel verlaten en ons voorstellen dat boven het horizontale blad dezer tafel eene 76 cM. hooge kwiklaag stond. Boven een vierkanten centimeter van het oppervlak zouden dan 76 cM.3 kwik staan, en het gewicht daarvan, d.i. het gewicht van76 × 13,60 = 1030 gramzou dat deel der tafel te dragen hebben. Wij moeten dit eindelijk nog in onze krachtseenheid, de dyne, uitdrukken; daar deze het 981ste deel van het gewicht van een gram is, wordt de uitkomst 1030 × 981 = 1010000 dynes. 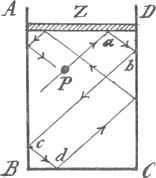 Fig. 31.
Zoo groot is nu niet alleen de druk tegen een cM.2 van het tafelblad, maar tegen elk oppervlak van die grootte, en zoo groot zal ook de druk per cM.2 zijn, die de molekulen tegen den zuiger Z van een cilinder A B C D (Fig. 31) uitoefenen, wanneer wij dezen met lucht van de onderstelde dichtheid vullen. Daar wij de snelheid voor eene bepaalde tempe- | |
[pagina 107]
| |
ratuur willen berekenen, zullen wij aannemen dat deze 0o C. is. Om nu de becijfering uit te voeren zullen wij ons een paar vrijheden moeten veroorloven, die voor een geoefend wiskundige overbodig zouden zijn. Vooreerst zien wij kort en goed van alle onderlinge botsingen der molekulen af. Eene dieper gaande beschouwing leert werkelijk dat, als de deeltjes maar klein genoeg zijn, deze ontmoetingen geen invloed op den druk tegen de wanden zullen hebben, en gij kunt dat ook wel zonder berekening inzien. In de figuur is b.v. een molekuul P voorgesteld, dat naar den zuiger toe vliegt, en dezen na eenigen tijd zal bereiken, en dan iets tot den druk tegen den zuiger zal bijdragen. Nu kan het evenwel gebeuren dat dit deeltje, vóór het tegen Z komt, door een ander molekuul wordt onderschept en teruggeworpen. Daar het dan niet tegen den zuiger vliegt, schijnt het een oogenblik dat de druk hierdoor kleiner zal uitvallen. Bedenkt men evenwel dat het deeltje dat, van boven naar beneden gaande, P heeft tegengehouden, nu zelf tegen den zuiger is teruggekaatst, terwijl het anders naar den bodem van het vat zou zijn doorgegaan, dan gevoelt men wel dat hierdoor de vermindering van druk weer kan worden gecompenseerd. Onze tweede vereenvoudiging zoeken wij in de gedaante van het vat; wij kiezen daarvoor een kubus, waarvan de bodem B C het grondvlak en de zuiger Z het bovenvlak uitmaakt. Eigenlijk vliegt nu elk molekuul volgens eene lijn, zooals P a b c d, in de ruimte heen en weer, maar wij zullen aannemen - ook dit wordt door meer aandachtige beschouwing gewettigd - dat de zaak op hetzelfde neerkomt, alsof een derde gedeelte der molekulen in verticale richting tusschen B C en Z heen en weer ging, het tweede derde gedeelte zich loodrecht op de zijwanden A B en C D bewoog, en het laatste derde gedeelte door eene beweging van voren naar achteren en weer terug den druk tegen voor- en achtervlak had uit te oefenen. | |
[pagina 108]
| |
Wij kennen nu eindelijk aan onzen kubus eene ribbe van een centimeter toe, wat wij wel mogen doen, daar wij een vat van willekeurige grootte met lucht van de onderstelde dichtheid kunnen vullen. Wij hebben dan, zooals uit de weging der lucht gebleken is, in 't geheel 0,001293 gram, en de massa der molekulen, die naar onze voorstelling voor den druk tegen den zuiger zorgen bedraagt 1/3 daarvan, d.i. 0,000431 gram. Wij zullen kortheidshalve in plaats van deze getallen m en 1/3 m schrijven. Stelt nu dat de snelheid der molekulen v cM. per sec. bedraagt; dit is onze onbekende grootheid. Een molekuul moet tusschen twee botsingen tegen den zuiger een weg van 2 cM. afleggen, nl. 1 cM. naar beneden, en dan weer 1 cM. naar boven; zoo menigmaal als deze weg in den per seconde afgelegden weg van v cM. begrepen is, zoo dikwijls zal het deeltje in de seconde tegen den zuiger stooten. Derhalve komt elk molekuul v/2 maal in de seconde tegen den zuiger. Nu moet nog nader beschouwd worden wat er bij eene botsing gebeurt, en daarbij zullen wij ons voorstellen dat de wand werkelijk door elk klein stootje eene snelheid krijgt; wij zullen uitrekenen hoe zich deze uitwerkingen gedurende eene seconde opeenhoopen, en dan uit de snelheid die de zuiger in eene tijdseenheid ontvangt besluiten tot de grootte der kracht die hij ondervindt. Nu hangt natuurlijk de beweging die aan den zuiger wordt gegeven van zijne massa af; wij zullen, om een bepaald geval te hebben, aannemen dat die massa duizend maal zoo groot is als de massa van het derde gedeelte van het in den kubus aanwezige gas, d.w.z., het gedeelte waarmede wij nu te doen hebben. De molekulen zullen elk 1/2 v maal tegen den zuiger botsen, | |
[pagina 109]
| |
en dit is voor alle hetzelfde getal, wanneer de snelheden gelijk zijn. Wij kunnen ons nu voorstellen dat alle deeltjes juist op hetzelfde oogenblik tegen den wand komen; dan zal dus telkens de geheele massa van 1/3 m gram dat doen. Bij de botsing moeten wij twee perioden onderscheiden. In de eerste wordt door de kracht die de zuiger op de deeltjes uitoefent de snelheid vernietigd. Eene kracht die dit kan doen zou, wanneer zij even lang in de richting der beweging werkte, eene snelheid v aan de molekulen geven. Verder weten wij dat de kracht waarmede de molekulen op den zuiger werken juist gelijk en tegengesteld is aan de werking van dezen op de molekulen. Zoo zien wij dat gedurende het eerste deel der botsing op den zuiger eene kracht werkt, die aan eene massa 1/3 m eene snelheid v kan geven. Aan de 1000 maal zoo groote massa van den zuiger geeft zij dus eene duizend maal kleinere snelheid, d.w.z. eene snelheid 0,001 v. Gedurende de tweede helft der botsing krijgt elk molekuul eene snelheid v van den wand af; daaruit volgt door toepassing van hetzelfde beginsel als zoo even dat ook nu weder aan den zuiger eene snelheid 0,001 v wordt gegeven. Door ééne botsing krijgt hij dus, alles samengenomen, eene snelheid 0,002 v, en daar er 1/2 v van die botsingen zijn, wordt de snelheid die het gas in eene seconde aan den zuiger geeft, in cM. per sec. voorgesteld door het getal 0,002 v × 1/2 v = 0,001 v2. Dit getal moeten wij nu met het aantal grammen dat de massa van den zuiger bedraagt vermenigvuldigen om de kracht in dynes te vinden. Daar het aantal grammen 1000 × 1/3 m is, vinden wij voor die kracht | |
[pagina 110]
| |
p = 1000 × 1/3 m × 0,001 v2,of p = 1/3 m v2 dynes. Wij willen nu hierbij opmerken dat dezelfde uitkomst verkregen zou zijn, wanneer wij de massa van den zuiger 10000 of een millioen maal zoo groot als die van het derde deel van het gas hadden ondersteld; een der factoren in onze berekening was dan wat kleiner, maar een andere in dezelfde verhouding grooter geworden. In het algemeen stelt het gevonden getal den druk op een cM2 (daar dit het oppervlak van den zuiger is) voor. Maar die druk is 1010000 dynes; dus 1/3 m v2 = 1010000,en, daar 1/3 m = 0,000431 is, v2 = 1010000/0,000431 = 2340000000. De snelheid zelf wordt dus voorgesteld door het getal dat met zich zelf vermenigvuldigd deze waarde oplevert; dit geeft ons v = 48000 cM. per sec.Wij zien hieruit dat wij niet overdrijven, wanneer wij zeggen dat de molekulen snel heen en weer vliegen. Bij de formule p = 1/3 m v2willen wij nu nog opmerken, dat zij ons niet alleen doet zien hoe bij gelijke dichtheid van het gas de druk des te grooter is, naarmate de temperatuur stijgt (immers, dan wordt v grooter), maar ook dat de druk des te meer bedraagt, naarmate een zelfde ruimtedeel meer gas bevat. Men moet nl. onder m de massa van het gas in een cM3 verstaan. | |
[pagina 111]
| |
Ik heb hier in een diepen kwikbak eene lange van boven gesloten buis geplaatst, op dezelfde wijze als de buis A B van den barometer (Fig. 30) in het bakje M. Maar deze buis bevat boven het kwik nog eene hoeveelheid lacht, en dientengevolge staat het kwik lager dan in de barometerbuis. Het zijn de luchtmolekulen die, onvermoeid tegen den kwikspiegel stootende, de vloeistof naar beneden houden. Ik kan nu de buis dieper in den kwikbak drukken; daardoor pers ik natuurlijk de afgesloten luchthoeveelheid in een kleiner volume samen. Nu zullen dezelfde luchtmolekulen als zooeven in denzelfden tijd een grooter aantal malen tegen het kwik stooten; deeltjes b.v. die de geheele lengte der luchtkolom hadden te doorloopen zullen, nu deze korter is gemaakt, met kleinere tusschenpoozen tegen de vloeistof komen. Werkelijk ziet gij, wanneer ik de buis naar beneden beweeg, den kwikspiegel medegaan, zij het dan ook over kleineren afstand. Hoe het nu komt dat, bij het opheffen der buis, de luchtdruk daarin kleiner wordt en dus het kwik stijgt, behoef ik niet meer te zeggen. Terwijl ik de buis op dezelfde hoogte laat staan kan ik het kwik doen dalen door, zooals ik thans doe, de lucht te verwarmen. De snelle beweging der deeltjes in de vlam, die het gevolg is van de bij het verbranden van het lichtgas plaats hebbende scheikundige verbinding, wordt medegedeeld aan de molekulen der buitenste laag van den glaswand. Dan geleidt het glas de warmte naar binnen, d.w.z. de buitenste deeltjes deelen hunne sterker geworden molekulaire beweging aan de binnenste mede. Eindelijk neemt ook de bewegingssnelheid van de luchtmolekulen toe en de kwikspiegel ondervindt daarvan de gevolgen. Het denkbeeld van zoo snelle molekulaire beweging als wij zoo even uit de theorie hebben afgeleid heeft zeker op het eerste gezicht iets vreemds, maar de theorie heeft alle bedenkingen die men heeft aangevoerd glansrijk overwonnen. Bij het bezwaar | |
[pagina 112]
| |
dat men die beweging niet ziet en niet voelt behoef ik nauwelijks stil te staan. Zij is onzichtbaar omdat de molekulen elk afzonderlijk niet waarneembaar zijn. En wat het voelen betreft, ja wij kunnen de molekulaire beweging eigenlijk even goed voelen als den wind. Ook dezen nemen wij waar door den druk dien hij tegen ons uitoefent en de twee gevallen zijn dus werkelijk niet zoo geheel verschillend. Er is echter dit onderscheid dat de molekulen van niet voortstroomende lucht een naar alle zijden gelijken druk teweegbrengen. Bovendien bestaat in alle vloeistoffen en gassen die ons lichaam bevat dezelfde druk als in de buitenlucht. Voor wij verder gaan, willen wij nog opmerken dat in eene stroomende luchtmassa tweeerlei beweging bestaat, nl. de onzichtbare, naar alle zijden gerichte molekulaire beweging, en de beweging van het gas in zijn geheel. Men kan het ook zoo uitdrukken dat, terwijl in een stilstaand gas de molekulen gelijkelijk naar alle kanten gaan, in een stroomend gas eene bepaalde bewegingsrichting de overhand heeft. Eene bedenking die ernstig kan schijnen is de volgende. Wanneer de gasmolekulen zich met snelheden van honderden meters in de seconde bewegen, zouden zij in zeer korten tijd dit vertrek kunnen doorvliegen; men zou kunnen verwachten dat er dus eene onophoudelijke zeer snelle vermenging der verschillende luchtlagen zou plaats hebben. In werkelijkheid bestaat zulk eene vermenging wel, maar gebeurt zij vrij langzaam. Wanneer de lucht in deze zaal niet door de temperatuurverschillen in te sterke circulatie wordt gebracht, kan het vrij lang duren, eer men aan de eene zijde een aan zijn reuk kenbaar gas waarneemt, dat aan den anderen kant wordt ontwikkeld. Hoe is dat te rijmen met eene snelle molekulaire beweging, en hoe is het te begrijpen dat een zwaar gas, zooals het koolzuur, merkbaren tijd in een open glas kan blijven staan of nabij den bodem eener grot kan opgehoopt blijven, terwijl de | |
[pagina 113]
| |
molekulen snelheden hebben, waarmede zij, tegen de zwaartekracht in, duizenden meters zouden kunnen opstijgen? De theorie weerlegt deze bedenkingen door de onderlinge botsingen der deeltjes te hulp te roepen. Gij moet U de zaak zoo voorstellen dat in alle gewone gevallen een molekuul wel eene groote snelheid heeft, maar daarmede niet ver komt. Telkens en telkens weer stoot het tegen een ander molekuul aan, en doorloopt eene zigzaglijn met zeer korte zijden. Wanneer het in het geheel een kilometer heeft afgelegd, is het misschien nog geen millimeter van het punt van uitgang verwijderd. Men is er in geslaagd ook deze ingewikkelde bewegingsverschijnselen wiskundig te behandelen, en heeft aldus, juist uit de snelheid waarmede twee gassen zich vermengen, de lengte van den weg kunnen afleiden, dien een molekuul tusschen twee botsingen doorloopt. Bij lucht van de temperatuur en de dichtheid die hier in dit vertrek zijn bedraagt de lengte van dien weg gemiddeld 0,00001 cM. Dat er hier slechts van bepaling van eene gemiddelde lengte sprake kan zijn, is duidelijk. De bewegingen der tallooze molekulen zijn zeer onregelmatig, en het een zal allicht, wat het doordringen te midden zijner buren betreft, onder gunstiger omstandigheden verkeeren dan het ander; het zal langer ongestoord kunnen voortgaan. Trouwens, met zulke gemiddelden hebben wij in de theorie der gassen altijd te rekenen; ook het getal dat wij voor de snelheid hebben gevonden moet gij niet zoo opvatten, dat nu alle molekulen juist die snelheid zouden hebben. Zoodra twee deeltjes tegen elkander vliegen, en als veerkrachtige bollen teruggekaatst worden, zal meestal een verschil in snelheid ontstaan, al was dat er eerst nog niet, en het is zeer goed mogelijk dat sommige onder de deeltjes door eene opeenvolging van gunstige ontmoetingen eene snelheid hebben gekregen, die het dubbel of zelfs het tienvoud is van het gemiddelde dat wij berekend hebben. Maar natuurlijk is het maar | |
[pagina 114]
| |
een klein gedeelte van het geheel, dat zoo bevoorrecht is. Wanneer ik U nu nog zeg dat men, op grond van verschijnselen die ik hier moet laten rusten, naar eene redelijk nauwkeurige schatting, het aantal molekulen in een mM3 van de ons omringende lucht kan voorstellen door een getal van 17 cijfers, dan hebt gij een vrij goed beeld van de werkelijkheid verkregen. Gij ziet nu ook dat wij, wanneer wij b.v. de voortplanting van het geluid met zijne verdichtingen en verdunningen beschouwen, zeer goed de hoeveelheid lucht die in een dergelijken mM3 aanwezig is in het oog kunnen vatten, en de trillingen die zij uitvoert, evenals de dichtheidsveranderingen die zij ondergaat van oogenblik tot oogenblik kunnen volgen. Wij behoeven niet te vreezen dat die kleine hoeveelheid, waarop wij onze aandacht vestigen, ons onder de handen ontsnapt, en in een oogwenk naar wijd en zijd verstrooid is. Er dringen wel deeltjes van buiten in door, maar, zooals ons bleek, slechts over een afstand van 0,00001 cM.; de meeste dier deeltjes worden dan weder teruggekaatst. Eveneens zullen ook verreweg de meeste die uit den kubieken millimeter trachten te ontsnappen daarin niet slagen, maar weldra teruggeworpen worden. Gedurende geruimen tijd blijven dus, juist tengevolge van de onderlinge botsingen, de deeltjes bij elkander, en behoudt de kleine hoeveelheid lucht hare individualiteit. Zij neemt van buiten zoo goed als geene nieuwe bestanddeelen in zich op, zij kan, terwijl hare deeltjes snel heen en weer vliegen zich bovendien in haar geheel een weinig heen en weer bewegen, en daarbij, nu eens meer dan eens minder door het bombardement van de deeltjes uit hare omgeving samengedrukt, van dichtheid veranderen. Op dergelijke nog uit onnoemelijk vele molekulen bestaande kleine luchtmassa's, en niet op de afzonderlijke molekulen, hadden wij het oog, toen wij over de voortplanting van het geluid handelden. | |
[pagina 115]
| |
Ik zal U nu met een drietal verschijnselen bekend maken, die bijzonder geschikt zijn om U nog nader van de juistheid der theorie die ik U heb voorgedragen te overtuigen. Om het eerste op te helderen heb ik hier naast elkander een grooten en een kleinen ivoren bal, aan draden opgehangen; de bedoeling is dat de kleine een gasmolekuul en de groote een zuiger waartegen dat botst zal voorstellen. Houd ik den grooten kogel vast, dan keert de kleine, als hij er met zekere snelheid tegen valt, met diezelfde snelheid terug, en dat is ook nog nagenoeg het geval wanneer de groote kogel, zonder nu juist vastgehouden te worden, eerst stil hangt. De zaak wordt anders wanneer op het oogenblik der botsing de groote bol eene zekere snelheid heeft, waarmede hij den anderen te gemoet komt; gij ziet hoe deze dan tot grootere hoogte terugspringt dan waarvan ik hem liet vallen. Wijkt daarentegen vóór de botsing de groote bol terug, dan zal de snelheid van den kleinen na den stoot kleiner zijn dan daarvoor. Wij passen een en ander op den vroeger beschouwden met een gas gevulden en door een zuiger afgesloten cilinder toe. Stelt, ik drijf den zuiger naar binnen. Elk molekuul dat er tegen stoot keert dan met iets grootere snelheid terug, en het kan niet missen, of de gemiddelde snelheid der gasdeeltjes moet daardoor toenemen. Immers, wanneer een zeker aantal molekulen meerdere beweging verkregen hebben, gaat die bij de onderlinge botsingen niet verloren; zij wordt daarbij alleen over het geheele aantal verdeeld. Eene grootere snelheid der molekulaire beweging beteekent echter een hoogeren warmtegraad; wij voorspellen dus eene stijging der temperatuur bij samendrukking van het gas. Eene redeneering van denzelfden aard leert ons dat eene uitzetting van het gas van eene afkoeling vergezeld moet gaan. Deze temperatuurveranderingen zijn inderdaad sedert lang bekend, en kunnen gemakkelijk worden waargenomen, als wij | |
[pagina 116]
| |
maar zorgen dat in het eene geval de meerdere molekulaire beweging niet voor een te groot deel aan de wanden van het vat en aan de verdere omringende voorwerpen wordt medegedeeld, en dat in het andere geval niet door aanvoer van molekulaire beweging van buiten de vermindering wordt vergoed. Het eenvoudigste middel om ons daarvoor te vrijwaren is, dat wij de volumeveranderingen snel doen plaats hebben; dan is er geen tijd voor eene merkbare wisseling van warmte met de wanden. Dat de bewegelijke wand juist een zuiger in een cilinder is, is niet noodig. Als ik het kwik in de buis die ons straks gediend heeft snel liet dalen, zou evengoed de temperatuur van de lucht daarboven verlaagd worden. Evenmin blijven deze verschijnselen uit, wanneer ergens in eene uitgestrekte luchtmassa eene plaatselijke verdichting of verdunning ontstaat. Wij hebben reeds besproken hoe, dank zij den korten weg tusschen twee botsingen, de eene luchtmassa de molekulen eener daar naast liggende kan terugkaatsen, en dus dezelfde rol kan spelen als de zuiger in onzen cilinder. Het volume van een gedeelte eener luchtmassa kan nu alleen kleiner worden als de naburige luchtlagen naar elkander toeschuiven, en dan zullen de molekulen van dat gedeelte bij de terugkaatsing door die lagen grootere snelheid krijgen. De temperatuurverhooging bij samendrukking kan men vertoonen met de zoogenaamde ‘vuurpomp’, eene stevige glazen buis, aan het eene einde gesloten, en waarin een zuiger plotseling naar binnen wordt geduwd. Men neemt de verwarming waar door de ontbranding van eenigen zwavelkoolstofdamp dien men in de lucht gebracht heeft. Om den tegenhanger van dit verschijnsel te laten zien, heb ik deze glazen klok met vochtige lucht gevuld; men merkt nu, zoodra ik de klok met eene met verdunde lucht gevulde ruimte in gemeenschap stel, een nevel op, en deze is het bewijs voor de afkoeling. Men kan dit alles alweder berekenen en | |
[pagina 117]
| |
vindt dan b.v. dat, wanneer lucht van 15o C. plotseling tot het vijfde deel van het oorspronkelijke volume wordt samengeperst, de temperatuur tot 280o C. stijgt. Geen wonder, dat een verschijnsel dat in zoodanige mate plaats heeft, in de praktijk en in de natuur eene belangrijke rol kan spelen. Wij moeten er b.v. rekening mede houden, wanneer wij de temperatuurverdeeling in den dampkring willen beschouwen. In dezen is voortdurend eene sterker of zwakker luchtstrooming, niet alleen in horizontale, maar ook hier en daar in stijgende of dalende richting. Wilde men nu daaruit afleiden dat de temperatuur wel, evenals in eene watermassa die dooreengeroerd wordt, overal dezelfde zal worden, dan zou men zich zeer vergissen. Eene opstijgende luchtmassa komt onder lageren druk; zij zet zich dus uit en moet afkoelen, terwijl eene dalende hoeveelheid wordt samengeperst en bij gevolg verwarmd. Wanneer echter het dooreenroeren zoo gebeurt, dat de stof niet kan neerdalen zonder warmer en niet kan opstijgen zonder kouder te worden, moet het resultaat zijn dat de temperatuur, wel verre van overal gelijk te zijn, juist in eene bepaalde mate van beneden naar boven daalt. Het bekende verschil in temperatuur tusschen de verschillende lagen van den dampkring is werkelijk ten naaste bij zoo groot als aan deze beschouwing beantwoordt. Ons tweede verschijnsel is de zoogenaamde inwendige wrijving van een gas. Wij weten dat een houten blok dat ik over de tafel voortschuif, daarvan eene wrijvingskracht ondervindt, die zich tegen de beweging verzet, en dat het zelf de tafel met gelijke kracht tracht mede te sleepen. Iets dergelijks heeft plaats telkens wanneer twee lagen van eene vloeistof of een gas zich evenwijdig aan het vlak dat hen scheidt met ongelijke snelheid bewegen. Er is dan eene werking tusschen beide, die er toe strekt, het snelheidsverschil te vereffenen, d.w.z., de beweging der snelst gaande laag te vertragen, en die der langzaamst voortgaande te versnellen. | |
[pagina 118]
| |
Bij gasvormige lichamen verklaren wij dat op eene zeer eigenaardige wijze. Wij behoeven nl. in het geheel niet eene werkelijke kracht tusschen de twee deelen van het gas te onderstellen, maar kunnen volstaan met de molekulaire beweging in aanmerking te nemen. Er heeft eene voortdurende uitwisseling van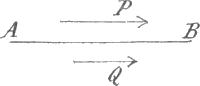 Fig. 32.
deeltjes door het vlak A B (Fig. 32) heen plaats, en in de laag Q zullen dus molekulen die in de kleine snelheid dier laag deelden vervangen worden door andere, die, uit P komende, eene grootere snelheid naar rechts hebben. Natuurlijk zal daarbij de snelheid die Q in zijn geheel naar rechts vertoont, en die wij rechtstreeks waarnemen, moeten toenemen. Wat er plaats heeft, kunnen wij in 't kort beschrijven als eene vermenging der lagen van ongelijke snelheid, en al gaat deze om de straks vermelde reden tamelijk langzaam, bij berekening blijkt zij toch voldoende te zijn om van de waarnemingen rekenschap te geven. Die waarnemingen kunnen op velerlei wijze gedaan worden; ik wil alleen vermelden dat door de inwendige wrijving der lucht eene uit een vaste stof bestaande plaat, die in haar eigen vlak wordt voortgeschoven, eene andere, in evenwijdigen stand maar op zekeren afstand opgestelde kan medesleepen. De plaat neemt nl. eerst de lucht in hare onmiddellijke nabijheid mede; deze laag draagt dan, door de uitwisseling van molekulen, de beweging op eene volgende over, deze op eene derde, en zoo vervolgens, tot ten slotte de tweede plaat door de lucht daarnaast wordt medegevoerd. Ik kan het verschijnsel laten zien met behulp van twee horizontale ronde micaplaatjes, die op dezelfde wijze als kompasnaalden op stiften hangen, en in hun eigen vlak kunnen draaien. Zij bevinden zich hier onder deze glazen klok, met de middelpunten boven elkander, en ik kan met behulp van een mag- | |
[pagina 119]
| |
neet het onderste schijfje, waaraan een paar gemagnetiseerde stalen naalden bevestigd zijn, ronddraaien. De bovenste wordt dan medegevoerd, zooals men aan het beeld op het scherm kan zien. De vraag is nu, wat hieraan zal veranderen wanneer de lucht onder de klok verdund wordt, welken invloed dit dus op de inwendige wrijving heeft. Natuurlijk wordt het aantal deeltjes, die in een bepaalden tijd door een vlak zooals A B in Fig. 32 heen gaan, daarbij kleiner, wat er toe leiden zou, de overbrenging van beweging te verminderen. Doch daar staat iets anders tegenover. Bij de proef met onze schijven verandert natuurlijk de snelheid der horizontale luchtlagen geleidelijk van beneden naar boven, en zoo iets kunnen wij ons ook in Fig. 32 denken. Het overbrengen van beweging door het vlak heen zal nu klaarblijkelijk niet alleen van het aantal deeltjes afhangen, die daaraan mededoen; het komt er ook op aan, uit welke lagen boven en beneden A B deze afkomstig zijn. Naarmate b.v. de naar beneden gaande molekulen uit eene hooger boven A B liggende laag komen, zullen zij meer naar de rechterzijde gerichte beweging naar beneden overbrengen. De deeltjes hebben nu gedeeld in de stroomende beweging van de laag waar zij hunne laatste botsing ondergaan hebben, en deze laag ligt gemiddeld des te verder van A B, naarmate het gas meer verdund is; dan heeft een molekuul natuurlijk meer kans om ver te midden der andere door te dringen. Deze tweede invloed der verdunning weegt nu, zooals eene grondige berekening leert, juist tegen de vermindering van het aantal door het vlak gaande deeltjes op, en de inwendige wrijving blijft dezelfde, al verkleint men ook de dichtheid. Die is thans, met behulp der luchtpomp, tot ongeveer een vijfde van het oorspronkelijke bedrag verminderd, en toch kan ik de eene schijf nog even goed door de andere laten medesleepenGa naar voetnoot1). | |
[pagina 120]
| |
Ik heb hierbij stilgestaan, omdat deze onafhankelijkheid der inwendige wrijving van de dichtheid, voor zoover ik zie, op geene andere wijze dan met behulp der molekulaire bewegingen verklaard kan worden. Zij is ook opmerkenswaardig als iets dat uit de theorie voorspeld is, nog voor men het had waargenomen. Het derde verschijnsel kan ik U niet laten zien, daar het eerst bij fijne onderzoekingen over de spectraallijnen van lichtgevende gassen is te voorschijn gekomen. Zulk eene lijn heeft altijd eene zekere breedte, die ten deele aan de wijdte der spleet en aan zekere onvolkomenheden van den spectroscoop moet worden geweten, ten deele ook aan de lichtbron eigen is; vergrooting van de dichtheid van het lichtgevende gas maakt b.v. om redenen die hier achterwege moeten blijven de lijnen breeder. Michelson heeft nu met behulp van eene vernuftige indirecte methode, op de bestudeering van interferentieverschijnselen berustende, weten te onderzoeken, in hoeverre de verbreeding der lijnen op rekening der verschillende oorzaken kan worden gesteld. Het bleek hem toen dat een zeer verdund gas, waarvan het spectrum met een volkomen instrument onderzocht wordt, nog altijd lijnen van eene zekere zeer geringe breedte zou geven, en dit verklaart hij uit de beweging der molekulen. Zulk een deeltje straalt wegens zijne trillingen licht uit, en vliegt, terwijl het dat doet, voort. Dit laatste doen de deeltjes in alle richtingen; sommige zullen dus naar den waarnemer toe, en andere van hem af gaan. En als wij nu de beschouwing toepassen, waarmede wij de vorige week eindigden, zien wij in dat, terwijl de deeltjes die bij hunne beweging niet naar ons toe of van ons af gaan, de lijnen op hunne ware plaats geven, de strepen die door andere worden voortgebracht een weinig naar rechts of links verschoven zijn; daar nu die verschuiving, wegens het verschil | |
[pagina 121]
| |
der snelheden, allerlei grootte kan hebben, moet het resultaat eene streep zijn van zekere breedte. Het bedrag daarvan vond Michelson in overeenstemming met wat wij van de snelheid der molekulen weten, en het komt mij dan ook voor dat aan zijne verklaring redelijkerwijze niet kan worden getwijfeld. Vergis ik mij hierin niet, dan heeft Michelson ons voor de beweging der gasmolekulen een rechtstreeksch bewijs geleverd, dat, merkwaardig genoeg, van denzelfden aard is als het bewijs dat de sterrespectra ons van de beweging der hemellichamen geven.
Wat wij nu besproken hebben is uit den aard der zaak slechts een zeer klein gedeelte der molekulaire theorieën. Liet de tijd het toe, dan zou ik gaarne Uwe aandacht gevraagd hebben voor het verschil der snelheden in het eene en het andere gas en voor den vaak ingewikkelden bouw der molekulen, die bijna altijd uit een grooter of kleiner aantal atomen, de kleinste deeltjes der scheikundige grondstoffen, zijn samengesteld. Ik had U dan duidelijk kunnen maken, hoe een molekuul, terwijl het in zijn geheel voortvliegt, eene inwendige beweging der samenstellende atomen ten opzichte van elkander kan hebben, als ware het een planetenstelsel in het klein, trouwens zonder één centraal lichaam dat met de zon zou kunnen worden vergeleken. Wij moeten dit alles echter laten rusten, en werpen ook slechts van verre een blik op den inwendigen toestand der vloeistoffen, het gebied waar Prof. van der Waals de natuurkundigen onzer dagen den weg heeft gewezen. Ik zal er alleen van zeggen dat hier de aantrekking die de molekulen op zeer kleine afstanden van elkander ondervinden in hooge mate op den voorgrond treedt. Zij is het, die de deeltjes, ondanks de beweging die zij nog altijd hebben, bij elkander houdt, in eene ruimte die niet meer, zooals bij de gassen, veel grooter is dan het gezamenlijk volume der molekulen zelve; | |
[pagina 122]
| |
de tusschenruimten zijn du vergelijkbaar met de afmetingen. Met vaste lichamen eindelijk is het wederom geheel anders gesteld. Wij dienen ons ook hier de deeltjes nog wel voor te stellen als geheel van elkander gescheiden, maar de molekulaire krachten zijn hechte banden geworden; aantrekkingen en allicht ook afstootingen wijzen elk deeltje een bepaalden evenwichtsstand aan, om welken het bij verhitting al sterker en sterker heen- en weertrilt, en waaruit wij het door uitwendige krachten die 't lichaam vervormen een weinig verplaatsen. Misschien blijken eenmaal alle molekulaire werkingen wel het gevolg te zijn van den toestand van den aether in de kleine tusschenruimten; als dat zoo is, wordt een over eene brug rijdende spoortrein bij slot van rekening gedragen door spanningen in den aether, waardoor de deeltjes van het ijzer, als liepen er veerkrachtige banden tusschen, aan elkander zijn gehecht. |
|

