Zichtbare en onzichtbare bewegingen
(1901)–H.A. Lorentz–
[pagina 76]
| |
IV. Lichttrillingen.Wij zullen ditmaal beginnen met de bespreking der voortplantingssnelheid van het licht; vervolgens zal ik U het bewijs leveren dat het zeer snelle trillingen zijn, die van een lichtgevend voorwerp uitgaan en, tot ons netvlies doorgedrongen, eene gezichtsgewaarwording teweegbrengen. De theorie waaraan Christiaan Huygens zijn naam heeft verbonden zal ons het wezen onthullen van veel dat wij elken dag waarnemen, en tevens van verschijnselen die men alleen door eene tot hooge volkomenheid ontwikkelde waarnemingskunst op het spoor is gekomen. De groote moeilijkheid bij het meten der voortplantingssnelheid is dat die zoo verbazend groot is. Dat het geluid een tijd noodig heeft om tot ons te komen, kunt gij waarnemen, telkens wanneer gij op een voldoenden afstand een heiblok ziet vallen, of met een hamer ziet slaan, maar in dergelijke gevallen en bij al onze gewone waarnemingen plant het licht zich zoo goed als oogenblikkelijk voort, wat gij begrijpelijk zult vinden als ik U, op de uitkomst vooruitloopend, zeg dat het in eene seconde meer dan 7 maal den omtrek der aarde kan afleggen. Het zijn dan ook astronomische verschijnselen geweest, waarbij zeer groote afstanden in het spel zijn, die het eerst eene oplossing van het vraagstuk mogelijk hebben gemaakt. Later hebben intusschen de Fransche natuurkundigen Fizeau en Foucault | |
[pagina 77]
| |
den tijd gemeten, die voor de voortplanting over een afstand op de aarde vereischt wordt; ik kan U met behulp van Fig. 26 het beginsel van eene der daarbij gevolgde methoden leeren kennen. L is hier een lichtgevend punt, en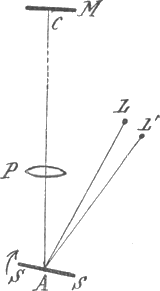 Fig. 26.
S S een vlakke spiegel die om eene door A gaande en loodrecht op het vlak der figuur staande as zeer snel in de richting der pijl wordt rondgedraaid. De van L uitgaande stralen vallen op den spiegel, en worden, als deze een stand heeft, zooals in de figuur is geteekend, volgens A C - en andere weinig daarvan verschillende lijnen - teruggekaatst. Zij moeten thans een grooten afstand in die richting doorloopen, en dan terugkeeren; de bedoeling is nl., den tijd te meten, die voor het tweemaal doorloopen van dien afstand noodig is. Daartoe staat aan het einde van den langen weg een spiegel M, en bij P eene bolle lens, die de stralen op hun verren tocht bijeen moet houden. Zoo gaan zij dan naar M, worden daar gereflecteerd, bereiken op nieuw den spiegel S, en zouden nu, wanneer deze nog denzelfden stand had, als toen hij de stralen den eersten keer terugkaatste, juist in het punt van uitgang L samenkomen. Maar - en hierop berust juist de methode - terwijl het licht van S S naar M heen en weerliep, is de spiegel een weinig gedraaid, en daar elke richtingsverandering van een spiegel aanleiding geeft tot eene verandering in den loop der teruggekaatste stralen, zal het licht op zijn terugtocht niet meer in het punt L, maar in een op eenigen afstand daarvan gelegen punt L′ komen. Men meet den grooten afstand van A tot C, den afstand A L en de kleine verplaatsing L L′ van het beeld; kent men bovendien | |
[pagina 78]
| |
de snelheid van wenteling van den spiegel, dan heeft men alle noodige gegevens. Ziethier eenige getallen, aan de proeven van den Amerikaansche natuurkundige Michelson ontleend. De afstand L L′ was, als de spiegel 257,9 omwentelingen in de seconde maakte, 13,77 cM.; dus, zooals gij ziet, zeer goed meetbaar. Hieruit, in verband met de lengte van A L, die ongeveer 10 meter bedroeg, berekende Michelson dat de spiegel in het 240.000ste deel eener seconde de kleine wenteling had volbracht, die noodig is om een teruggekaatsten straal uit de richting A L in de richting A L′ over te brengen. Dien kleinen tijd heeft het licht gebruikt om over den afstand van A tot C, die 62450 cM. bedroeg, heen en weer te gaan. De einduitkomst van Michelson was dat de snelheid van voortplanting 2998 × 107 cM. per seconde bedraagt; wij zullen gemakshalve dit getal afronden tot 3000 × 107 of 3 × 1010 cM. per sec. Het is in goede overeenstemming met hetgeen de astronomen hadden gevonden. Hoe komen wij nu tot de wetenschap dat het trillingen zijn, die zich met deze snelheid voortspoeden, en b.v. den afstand van de zon tot de aarde in ongeveer 8 minuten afleggen? Waarom zijn het niet, zooals men wel gemeend heeft, kleine projectielen die de zon naar alle zijden uitzendt? Wij zullen dit laatste niet verwerpen omdat wij het vreemd zouden vinden; wie voor het eerst verneemt van trillingen met eene voortplantingssnelheid als de genoemde krijgt even goed den indruk van iets ongewoons. Zulke indrukken mogen ten slotte geen invloed hebben op ons oordeel; wij moeten het antwoord in de waarnemingen zoeken. En, zoo wij nu ten slotte het licht voor een trillingsverschijnsel verklaren, dan is het omdat bij lichtstralen verschijnselen bestaan, die alleen bij trillende bewegingen voorkomen, en alleen als men zich zulke bewegingen voorstelt, begrepen kunnen worden. | |
[pagina 79]
| |
Over overeenkomstige verschijnselen bij watergolven en geluidstrillingen spraken wij reeds in het kort en het is goed daar thans nog eens op terug te komen. Ik bedoel, om nu maar bij het geluid te blijven, het gelijktijdig bestaan in de lucht der trillingen die van verschillende geluidsbronnen afkomstig zijn. Wij zagen in gedachten de verdichte en verdunde lagen in de lucht, en stelden ons voor, hoe deze elkander doorkruisen, zonder in hunne voortplanting gestoord te worden. Wij kregen zoo een beeld van de geheele luchtruimte waarin de bewegingen plaats hadden. Maar laten wij nu, om de gedachten te bepalen, eens een enkel punt in het oog houden, en op eene kleine hoeveelheid lucht die zich daar bevindt, en die wij maar een ‘luchtdeeltje’ zullen noemen, letten. Dat deeltje zal zich, als er in 't geheel geen geluid wordt voortgebracht, op eene bepaalde plaats A (Fig. 27) bevinden. Wordt het nu door de trillingen die van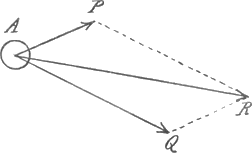 Fig. 27.
eene geluidsbron uitgaan getroffen - denkt U voor een oogenblik nog maar ééne geluidsbron - dan verlaat het dien stand, en is op zeker oogenblik b.v. in het punt P. Op dezelfde wijze zou ook eene tweede geluidsbron, als die alleen trilde, het deeltje uit zijn evenwichtsstand verplaatsen; stelt dat zij het op hetzelfde oogenblik in Q zou brengen. De regel voor het ‘samenstellen van trillingen’ is nu zeer eenvoudig; hij zal U aan het parallelogram van krachten herinneren. Wij vereenigen A met P en met Q, en beschrijven op de lijnen A P en A Q als zijden een parallelogram. Het vierde hoekpunt daarvan is dan de plaats, die het deeltje onder den gelijktijdigen invloed der twee bewegingsoorzaken zal innemen; de diagonaal A R wijst ons aan naar | |
[pagina 80]
| |
welke zijde van den evenwichtsstand het dan verschoven is, en hoe ver het daarvan is verwijderd. Natuurlijk hadden wij een veel kleiner figuurtje moeten teekenen, wanneer wij de verplaatsingen in hunne ware grootte hadden willen voorstellen. Ook geldt de teekening maar voor één oogenblik, en valt zij, als wij haar herhalen, telkens weer anders uit. Eindelijk zou voor ieder luchtdeeltje eene afzonderlijke figuur geteekend kunnen worden, maar wij zullen ons in dit alles niet verdiepen. Het gezegde zal voldoende zijn om U van het beginsel waarnaar trillingen met elkander samengesteld worden, een denkbeeld te geven. Wij hebben nu ook verder geene moeite om te begrijpen wat er gebeurt, als niet twee, maar drie of meer geluidsbronnen, of zoo veel als gij maar wilt, met elkander samenwerken, want niets belet ons, om, altijd op dezelfde wijze, de beweging die door de samenstelling van twee trillingen verkregen is, met eene derde trilling te vereenigen, wat wij dan vinden weder met eene vierde, en zoo vervolgens. Ook behoeft het geen betoog dat deze uiteenzettingen voor alle trillende stelsels gelden. Wij weten nu in het algemeen hoe trillingen tegelijk kunnen bestaan, en wij hebben ook het middel om sommige merkwaardige verschijnselen die zich daarbij voordoen, en die men gewoonlijk interferentieverschijnselen noemt, te begrijpen. Gelukkig is daarbij de zaak niet altijd zoo ingewikkeld, als ik het zooeven heb voorgesteld. Dikwijls wordt een punt getroffen door twee trillingen die het beide langs dezelfde rechte lijn doen heen en weergaan, en dan gaat het samenstellen gemakkelijker; er is niet eens meer een parallelogram voor noodig. Twee verplaatsingen naar denzelfden kant zullen te zamen eene verplaatsing opleveren, die gelijk is aan hunne som. Daarentegen zal een punt dat door twee oorzaken in tegengestelde richting uit zijn evenwichtsstand wordt gebracht, in werkelijkheid eene verplaatsing verkrijgen naar den kant van de grootste van de twee, en gelijk aan hun verschil; d.w.z., | |
[pagina 81]
| |
wanneer de eene oorzaak het b.v. 5 lengte-eenheden naar rechts, en de andere 2 lengte-eenheden naar links verplaatst, zullen wij eene verplaatsing van 3 lengte-eenheden naar rechts hebben. Men zegt dat twee trillingen dezelfde phase hebben, wanneer zij een punt naar dezelfde zijde doen uitwijken, en spreekt van tegengestelde phasen als de uitwijkingen naar verschillende zijden zijn. Het zal nu duidelijk zijn geworden, dat twee trillingen van dezelfde phase elkander versterken, maar dat twee bewegingen van tegengestelde phasen elkaar verzwakken. Zijn, in dit laatste geval, de twee verplaatsingen die wij hebben samen te stellen even groot, dan blijft het bewegelijke punt in den evenwichtsstand. De twee trillingen heffen elkander dan op. Dat zoo twee trillingen naar gelang van omstandigheden elkander kunnen versterken of verzwakken, is het karakteristieke bij de interferentieverschijnselen. Natuurlijk zal men het 't gemakkelijkst opmerken, wanneer men de versterkingen of verzwakkingen met elkander kan vergelijken, zoodat de tegenstelling tusschen beide onze aandacht trekt, en ik zal U daarom eerst een geluidsverschijnsel laten hooren, waarbij de waargenomen intensiteit achtereenvolgens, bij afwisseling, groot en klein is. Deze beide stemvorken geven bijna denzelfden toon, zoodat gij, wanneer ik ze elk afzonderlijk doe trillen, geen onderscheid zult bemerken. Maar er is toch eenig verschil, en dit heeft ten gevolge dat men, wanneer ik beide heb aangestreken, het geluid beurtelings sterker en zwakker hoort worden. De verklaring daarvan ligt nu voor de hand, en zal het duidelijkst zijn als ik van de trillingsgetallen gebruik maak; voor de eene stemvork bedraagt dit 256 en voor de andere b.v. 252 per sec. Let nu eens op Uw trommelvlies en bedenkt dat dit, als de eene stemvork alleen trilt, 256 maal in de seconde, en als de andere er alleen is, 252 maal in de seconde naar binnen gedrukt wordt. Laten wij verder aannemen dat op zeker oogenblik de twee geluidsbronnen beide het trommelvlies naar binnen doen gaan; dan | |
[pagina 82]
| |
is er versterking, en dat zal gedurende de eerstvolgende trillingen zoo blijven. Maar weldra wordt de zaak anders. Immers, 1/8 sec. na dat eerste oogenblik zal de eerste oorzaak het vlies weder naar binnen doen gaan, omdat in dat achtste deel eener seconde juist 256/8 = 32 volle trillingen van den eersten toon komen, maar van de trillingen die de tweede stemvork opwekt hebben wij er in denzelfden tijd 252/8 = 31½; waren deze trillingen er alleen, dan zou dus het trommelvlies op dat latere oogenblik naar buiten gaan. Zoo hebben wij dus, 1/8 sec. na het eerstbeschouwde oogenblik, tegenstelde phasen, en eene verzwakking van het waargenomen geluid. Weder een achtste sec. later zijn er, van 't begin af, 64 en 63 volle trillingen geweest, en hebben wij dus, evenals in het begin, gelijke phasen, wat eene versterking ten gevolge heeft, en ik behoef met de redeneering wel niet door te gaan, om U de regelmatige afwisseling van sterk en zwak geluid begrijpelijk te maken. Dit zijn de zwevingen, die altijd worden waargenomen als twee tonen met een klein verschil in trillingsgetal tegelijk worden voortgebracht, en die, wat de snelheid der intermittentie betreft, aan een eenvoudigen regel voldoen. In ons voorbeeld komt telkens na 1/4 sec. weder eene versterking, zoodat het aantal zwevingen in de seconde 4 bedraagt, juist even veel als het verschil der trillingsgetallen, iets dat in het algemeen doorgaat. Schuif ik op de beenen der stemvork met den laagsten toon een paar kleine caoutchouc-ringetjes, en doe ik haar dus - wegens de vermeerdering der massa - langzamer trillen en meer van de andere stemvork verschillen, dan hoort gij de aanzwellingen der geluidsterkte sneller op elkander volgen. Tegenge- | |
[pagina 83]
| |
stelden invloed heeft eene vergrooting van de massa der andere stemvork. De graphische voorstelling van eene trillende beweging met zwevingen liet ik U reeds den vorigen keer zien; gij zult U de golflijn herinneren, waarvan de golven afwisselend eene groote en eene kleine amplitudo hadden. Zij was werkelijk verkregen door twee, een weinig van elkander verschillende tonen op een vlies dat met eene schrijfstift verbonden was, te laten werken. Met het oog op eene later te maken toepassing willen wij hierbij nu nog opmerken dat de beweging van dat vlies - of van het trommelvlies dat de zwevingen waarneemt - op twee geheel verschillende wijzen kan beschreven worden. Ik kan zeggen dat het eene trilling uitvoert, waarvan de amplitudo aan periodieke verandering onderhevig is. Maar ook dat het te gelijkertijd twee trillende bewegingen van ietwat verschillend trillingsgetal en ieder op zich zelf van standvastige amplitudo heeft. Het een komt op hetzelfde neer als het ander. Het lijdt b.v. geen twijfel dat een trillend lichaam, waarvan de amplitudo in grootte wisselt, in zijne omgeving dezelfde verschijnselen zal teweegbrengen als of men met een dubbel stel van trillingen te doen had. Ik heb bij de zwevingen wat lang stil gestaan, omdat zij op zich zelf de aandacht verdienen, en uitstekend geschikt zijn als eerste voorbeeld van een interferentieverschijnsel. Wat wij zoo aanstonds bij het licht zullen waarnemen is evenwel van iets anderen aard; de lichtstralen die elkander versterken en verzwakken zullen daarbij nl. volkomen hetzelfde trillingsgetal hebben. Dan is er geen sprake van, dat op eene bepaalde plaats de twee trillingen bij afwisseling dezelfde en de tegengestelde phase hebben. Ook bij ons trommelvlies zou dat niet mogelijk zijn, als het door twee geluidsbewegingen van dezelfde toonhoogte werd getroffen. Was dan eenmaal de phase der twee bewegingen dezelfde, dan zou die nooit tegengesteld wor- | |
[pagina 84]
| |
den, evenmin als twee slingers van gelijken schommeltijd, die eerst tegelijk naar rechts uitwijken, ooit tegengestelde uitslagen zullen vertoonen. Om bij gelijke hoogte van twee tonen eene afwisseling van groote en kleine geluidsterkte te vinden, zou men van het eene punt der ruimte naar het andere moeten gaan; inderdaad kunnen twee trillingen van hetzelfde trillingsgetal, die van verschillende punten uitgaan, elkander zeer goed op de eene plaats versterken en op de andere verzwakken. De proef die wij nu zullen nemen is in het begin der vorige eeuw door Fresnel bedacht. AO en OB (Fig. 28) zijn twee verticaal geplaatste spiegels (met de vlakken loodrecht op het vlak der teekening) die bijna, maar niet geheel, in elkanders verlengde vallen. L is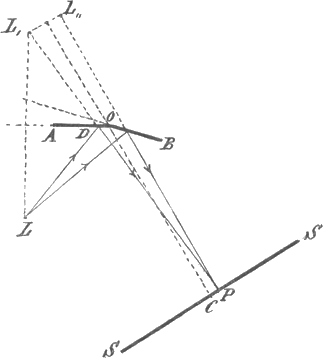 Fig. 28.
een lichtpunt of eigenlijk eene verlichte verticale spleet, en de stralen daarvan worden na de terugkaatsing op een scherm SS opgevangen. In een of ander punt van dit laatste komen nu twee stralen te zamen, waarvan de een door den spiegel AO en de ander door den spiegel OB teruggekaatst is; het is ons juist om de interferentie der trillingen van deze stralen te doen. Vooreerst gaan wij hun loop na en maken daarbij gebruik van de ‘beelden’ L͵ en L〟, die de twee spiegels van het lichtpunt geven. Hebben wij die in de figuur | |
[pagina 85]
| |
aangegeven, en willen wij nu weten, welke stralen in een of ander punt P van het scherm komen, dan vereenigen wij dit met L͵ en L〟, en trekken van de punten, waar de eerste verbindingslijn den spiegel A O, en de tweede den spiegel O B snijdt, lijnen naar het lichtpunt. Zoo ziet men in de figuur den weg, eerst van L naar D, en dan van D naar P, waarlangs het licht, door A O teruggekaatst, het punt P bereikt; daar L D = L͵ D is, heeft deze weg dezelfde lengte als de rechte lijn L͵ P. Evenzoo is de weg dien het licht volgt, als het eerst den tweeden spiegel aandoet, even lang als de rechte lijn L〟P. Wij spreken over de lengte dezer wegen, omdat, wanneer het licht uit trillingen bestaat - zooals wij bij wijze van hypothese op den voorgrond zullen stellen - die lengte beslist over hetgeen op het scherm wordt waargenomen. Om nu een bepaald eenvoudig geval voor oogen te hebben, nemen wij aan dat van L slechts ééne soort van enkelvoudig licht uitgaat, en dat dit een bepaald trillingsgetal per seconde, stelt N, heeft. De trillingstijd is dan 1/N sec. Wij zullen verder onderstellen dat de lichttrillingen, wat hunne richting betreft, op de trillingen van een gespannen koord gelijken, d.w.z. dat zij loodrecht op de richting der lichtstralen staan. Laat een lichtgevend deeltje van L loodrecht op het vlak der teekening, dus in verticale richting, heen en weer gaan; dan zijn het afwisselend naar boven en naar beneden gerichte evenwichtsverstoringen, die zich langs de stralen voortplanten. Bij die voortplanting is er eene bepaalde ‘golflengte’, die wij l zullen noemen, en die, als men het trillingsgetal N en de voortplantingssnelheid v kende, door de formule l = v/Nzou bepaald worden. Zooals deze vergelijking ons nog weder herinnert, is l de weg over welken het licht zich voortplant in | |
[pagina 86]
| |
1/N seconde, d.w.z. in den tijd gedurende welken ééne trilling volbracht wordt. Op elken lichtstraal die van L uitgaat vindt men op afstanden gelijk aan de golflengte evenwichtsverstoringen van dezelfde richting, die achtereenvolgens, met tusschenpoozen van een trillingstijd, van het lichtpunt zijn vertrokken. In twee punten daarentegen, die eene halve golflengte uiteenliggen, bestaan op hetzelfde oogenblik tegengestelde verplaatsingen; deze zijn een halven trillingstijd na elkander uitgezonden. Wij beschouwen nu een punt C van het scherm (op de lijn SS is er slechts één dergelijk punt) dat even ver van L͵ en L〟 ligt. De twee wegen die van L naar dit punt loopen zijn even lang en worden in gelijke tijden afgelegd. In C komen derhalve verplaatsingen te zamen, die op hetzelfde oogenblik van L zijn vertrokken, en dus beide naar boven, of beide naar beneden gericht zijn. Deze evenwichtsverstoringen moeten elkander versterken. Anders is het rechts en links van C. Gaan wij naar rechts, dan komen wij verder van L͵ dan van L〟 en wij kunnen een punt P zoo kiezen, dat het verschil der afstanden juist eene halve golflengte bedraagt. Dan vereischt de voortplanting langs den eenen weg een halven trillingstijd meer dan die langs den anderen weg; evenwichtsverstoringen die op hetzelfde oogenblik in P zullen samentreffen moeten van L vertrekken op oogenblikken, die een halven trillingstijd uiteen liggen, en dus noodzakelijk tegengesteld gericht zijn, de eene naar boven en de andere naar beneden. Van daar, dat wij in dit punt verzwakking en daar onder de omstandigheden van de proef de amplitudines even groot zijn, duisternis moeten krijgen. Nog wat meer naar rechts moeten wij weer licht vinden, omdat, als wij het beschouwde punt verder naar die zijde verplaatsen, het verschil der twee wegen grooter wordt dan in P, dus grooter dan eene halve golflengte. Een punt dat op zeer weinig na tweemaal zoo ver van C ligt als het punt P, ligt eene golflengte verder van L͵ | |
[pagina 87]
| |
dan van L〟; daar komen dus evenwichtsverstoringen te zamen, die met een interval van een vollen trillingstijd door L zijn uitgezonden. Deze hebben dezelfde richting en versterken elkaar. Hoe nu deze beschouwing verder kan worden voortgezet en ook op punten links van C kan worden toegepast, ligt voor de hand. Wij kunnen verwachten dat in eene reeks van punten langs SS afwisselend licht en donker zal worden waargenomen. Dit is werkelijk het geval, en daar het op geene andere wijze te verklaren is, geeft het ons een onomstootelijk bewijs voor het bestaan der lichttrillingen. Ik stip slechts aan dat het verschijnsel hetzelfde zal blijven wanneer de trillingen eene andere richting hebben dan wij ondersteldenGa naar voetnoot1) en dat wij bij het gebruik eener verticale spleet, en van verticaal geplaatste spiegels, op het scherm eveneens verticale, bij afwisseling lichte en donkere banden, interferentiestrepen, te zien krijgen. Natuurlijk heeft men de proef met verschillende soorten van enkelvoudig licht, stelt eerst met rood en dan met blauw licht, genomen. Het bleek toen dat in ieder geval lichte en donkere banden ontstaan, maar dat de afstand waarop deze van elkander liggen met de gebezigde lichtsoort verandert. In het punt C is, zooals de theorie verlangt, altijd licht, maar de eerste donkere band P is dichter bij C, wanneer men met blauw, dan wanneer men met rood licht werkt. Wij besluiten daaruit dat de golflengte van het blauwe licht kleiner is dan die van de roode stralen; immers, bij elke der beide proeven wordt de halve golflengte gegeven door het verschil der afstanden P L͵ en P L〟, en dat verschil is bij het blauwe licht het kleinst, omdat daarbij P dichter bij C valt, dan wanneer wij met rood licht experimenteeren. | |
[pagina 88]
| |
Tevens kunnen wij nu voorspellen wat wij te zien krijgen, als wij wit licht, dus samengesteld licht, gebruiken. Wij moeten ons voorstellen dat elke kleur haar eigen interferentiebeeld geeft, en dat deze beelden op elkander geplaatst worden. In C krijgen wij nu alle kleuren bijeen, dus te zamen weder wit. Maar rechts en links van C zullen de strepen van de eene kleur niet met die der andere samenvallen. Waar b.v. het blauw door interferentie is uitgedoofd, zullen de andere kleuren nog aanwezig zijn, en dan is de totaal-indruk niet meer die van wit, maar van gekleurd licht. Zoo kan het U niet verwonderen, dat zich aan weerskanten van een witten lichten band een aantal gekleurde banden vertoonen. Ik moet U nu verzoeken, elk afzonderlijk deze te komen zien. Dat de inrichting der proef een weinig afwijkt van de gegeven uiteenzetting, is van ondergeschikt belang. Ik zal daarover niet uitweiden en wij zullen ons ook niet ophouden met de waarneming in licht van eene bepaalde kleur; houdt men een rood of blauw gekleurd glas op den weg der stralen, dan valt het in 't oog dat in het eene geval de strepen verder van elkander staan dan in het andere. Voor de moeite die wij aan de bespreking en de waarneming van het interferentieverschijnsel besteed hebben worden wij beloond door een zeer bevredigend inzicht in het wezen der lichtverschijnselen. Niet alleen is alle twijfel aan het bestaan der trillingen weggenomen, maar wij hebben ook geleerd, wat het onderscheid tusschen de verschillende bestanddeelen van het witte licht is. Dit zien wij thans in de golflengte, die voor de minst breekbare, d.i. de roode stralen, het grootst is, en van daar naar de violette stralen toe, gestadig afneemt. Met dit onderscheid gaat een verschil in de snelheid van trilling gepaard. Wij kunnen de voortplantingssnelheid in de lucht voor alle kleuren even groot stellen, en zien dan aan de formule van p. 67 dat aan eene kleine golflengte eene groote waarde van N beantwoordt. Naar het violet toe neemt dus het trillings- | |
[pagina 89]
| |
getal of de frequentie steeds toe, en tusschen de kleuren van het licht bestaat hetzelfde onderscheid als tusschen de tonen van verschillende hoogte bij het geluid. Wij behoeven niet bij deze algemeene beschouwingen te blijven staan, maar kunnen het eigenaardige der verschillende kleuren door bepaalde getallen uitdrukken. Men kan bij de proef van Fresnel den onderlingen stand van de spleet, de spiegels en het scherm S S, alsmede de ligging der punten C en P door meting bepalen. Daaruit vindt men de lengte van L͵ P en L〟 P, en het dubbele verschil dezer lijnen geeft ons de golflengte. Dergelijke metingen, die naar andere op hetzelfde beginsel berustende methoden nauwkeuriger kunnen worden verricht, leeren ons dat de golflengte, vergeleken met die van het geluid en met alle afstanden, waarmede wij gewoonlijk te doen hebben, zeer klein is. Zij is voor het uiterste rood dat in het zonlicht voorkomt, ongeveer 0,00008 en voor het uiterste violet 0,00004 cM. Nu hebben wij nog onze formule N = v/l;die gebruiken wij om de frequentie der onzichtbare trillingen te berekenen. Wegens het groote bedrag der voortplantingssnelheid en de kleine golflengte wordt het aantal trillingen per seconde zeer groot. Het is voor het roode licht dat zoo even beschouwd werd 375 billioen en voor het blauwe licht 750 biljoen.
De vraag is al wel reeds bij U gerezen, in welke stof zich deze trillingen voortplanten. Zij komen van de verst verwijderde hemellichamen tot ons, en er moet dus in de wereldruimte, ook buiten de dampkringen der planeten, een medium aanwezig zijn, dat de lichtbeweging naar ons overbrengt. Dit medium, door zijne eigenschappen nog altijd een der groote raadselen der natuurkunde - al staan wij er niet geheel machteloos | |
[pagina 90]
| |
tegenover - is de alles doordringende aether. Ik zeg ‘alles doordringend’, want men moet zich voorstellen dat de aether in gassen, vloeistoffen en vaste lichamen aanwezig is, kortom dat hij in geene enkele stof ontbreekt. Ik hoop dat gij dit wel op gezag zult willen aannemen, en met eene enkele toelichting, die op de lucht betrekking heeft, genoegen zult nemen. Zooals reeds vermeld werd, is de voortplantingssnelheid zoowel door astronomische waarnemingen als door metingen op het oppervlak der aarde bepaald; daarbij is dezelfde uitkomst gevonden, of, juister gezegd, deze metingen waren niet nauwkeurig genoeg, om het kleine verschil aan den dag te brengen. Nu is natuurlijk de door de sterrenkundigen bepaalde snelheid die in de hemelruimte, en de overeenstemming der twee resultaten zou volkomen onbegrijpelijk zijn, wanneer de lucht geen aether bevatte, en wij dus met eene voortplanting in twee geheel verschillende stoffen te doen hadden. Wij dienen wel aan te nemen dat, bij den voortgang van een lichtstraal in de lucht, hoofdzakelijk de aether in het spel is, en dat alleen eene kleine wijziging der snelheid van voortplanting, die men niet uit rechtstreeksche metingen, maar langs indirecten weg heeft afgeleid, op rekening van de luchtdeeltjes moet worden gesteld.
Boden reeds de geluidsverschijnselen ons eene groote verscheidenheid aan, rijker en grootscher is nog de wereld die zich ons thans ontsluit. Wij behoeven niet eens te spreken van de onmetelijke hemelruimte, doorstraald door het licht van tallooze zonnen, wier trillingen vele jaren noodig hebben om ons te bereiken. Ook hier, in onze naaste omgeving, vinden wij millioenen en millioenen lichtgolven, die in alle richtingen door elkander loopen, en zoo fijn bewerktuigd zijn, dat b.v. in de golven die door deze zaal van de linker naar de rechterzijde gaan, alle bijzonderheden liggen opgesloten, die de linkerzijde van het vertrek ons te zien geeft. | |
[pagina 91]
| |
Soms blijven de verschillende bestanddeelen der witte stralen, elk met zijne eigen periode trillende, bij de voortplanting bij elkander, en blijft het licht dus wit, maar in andere gevallen worden zij van elkander gescheiden en ontstaan allerhande kleurverschijnselen. Soms door de ongelijke breking van de verschillende stralen, zooals in een glazen prima of in de regendruppels die tot het voortbrengen van een regenboog medewerken. Een ander maal wordt bij den doorgang door een niet volkomen doorschijnend lichaam de eene kleur meer dan de andere opgeslorpt, geabsorbeerd, een verschijnsel, dat wij ons zoo zullen voorstellen, dat de lichttrillingen in beweging van anderen aard worden omgezet, en dus voor de lichtwaarneming verloren gaan. Laat op deze wijze eene glasplaat de roode stralen meer door dan andere, dan is het geen wonder dat wij alles door die ruit heen roodgekleurd zien. De kleuren, zooals die van dit groene tafelkleed, die wij bij opvallend licht zien, zijn eveneens aan absorptie te wijten. De proef van Fresnel bewees ons reeds hoe kleuren ontstaan kunnen wanneer sommige lichtsoorten door interferentie worden uitgedoofd. Aan eene dergelijke werking moet gij ook de bekende schitterende tinten der zeepbellen toeschrijven. Het dunne bolvormige vlies kaatst de opvallende stralen zoowel met zijn binnen- als met zijn buitenoppervlak terug, en in een punt van ons netvlies kunnen dientengevolge twee bewegingen samenkomen, waarvan de eene een zeker eind weegs, nl. zoo iets als de dubbele dikte van het vlies, meer heeft afgelegd dan de andere. Vandaar eene interferentie, die, wegens het verschil in golflengte, bij de eene lichtsoort tot versterking en bij de andere tot verzwakking leidt, en aanleiding geeft tot eene met de dikte van het vlies en met den invalshoek wisselende resulteerende kleur. Andere dunne doorschijnende laagjes, zooals een op water drijvend vliesje olie, vertoonen dezelfde verschijnselen, en de theorie der lichttrillingen kan van dit | |
[pagina 92]
| |
alles en nog van veel meer dat ik niet kan vermelden volkomen rekenschap geven. Misschien heeft het U reeds verwonderd, dat wij niet nog veel meer interferentieverschijnselen zonder bijzondere hulpmiddelen waarnemen. Ook dit kan de theorie verklaren. Het is te wijten, eensdeels aan de uitgebreidheid onzer lichtbronnen, die uit onnoemelijk vele lichtgevende deeltjes zijn samengesteld, ten tweede aan de samengesteldheid der stralen die zij uitzenden, en dan ook hieraan, dat de meeste lichamen waarmede wij de lichtstralen opvangen afmetingen hebben, die in vergelijking met de kleine lichtgolven zeer groot zijn.
Wij zullen nu nog eens terugkeeren tot de ontleding van het samengestelde licht met behulp van een prisma. Te werk gaande naar het beginsel dat in Fig. 25 is aangegeven, ontwerp ik nu op het scherm het kleurenband, of het spectrum, zooals men het noemt, van het kalklicht dat ik op eene spleet laat vallen. Het strekt zich onafgebroken van het rood tot het violet uit, en het licht blijkt dus alle verschillende trillingsgetallen en golflengten tusschen de reeds genoemde grenzen te bevatten. Eenvoudiger verschijnsel zien wij, wanneer wij als lichtbron een gasvormig lichaam gebruiken; het spectrum bestaat dan uit een kleiner of grooter aantal afzonderlijke lichte lijnen, beantwoordende aan even zoo vele soorten van enkelvoudig licht, die door het lichtgevende gas worden uitgestraald. Met de twee zeer dicht bij elkaar gelegen lijnen, die het spectrum der met kenkenzout gekleurde vlam uitmaken, hebben wij reeds kennis gemaakt. Evenmin als dat kan ik U, met de hulpmiddelen die ik hier heb, andere lijnenspectra in voldoende lichtsterkte op een scherm vertoonen. Trouwens, de gewone wijze van waarnemen is die, welke wij de vorige week bezigden; men beziet de spectra in een kijker, waarin de stralen worden opgevangen, die door eene nauwe spleet zijn gegaan, | |
[pagina 93]
| |
en vervolgens een of meer prisma's doorloopen hebben. Het geheele instrument, de spectroscoop, is een gewichtig hulpmiddel der nieuwere natuurwetenschap geworden. Hier staan een paar kleine spectroscopen van het gewone model. Voor de spleet van den eenen bevindt zich eene zoogenaamde Geissler'sche buis met waterstofgas van geringe dichtheid gevuld; dat gas wordt tot lichtgeven gebracht, wanneer ik er electrische ontladingen door heen laat gaan. De andere spectroscoop is op een klein electrisch vonkje gericht, dat ik tusschen twee ijzerdraden laat overspringen. Gij zult nu in het eene instrument het drietal lichte lijnen zien, die het waterstofspectrum uitmaken, en in het andere de lichtsoorten waarnemen, die aan het door de hitte der vonk vervluchtigde ijzer eigen zijn. In Fig. 29 heb ik aangegeven welken stand de drie waterstoflijnen H1, H2, H3 ten opzichte van het doorloopende van rood tot violet gaande spectrum van het witte licht hebben.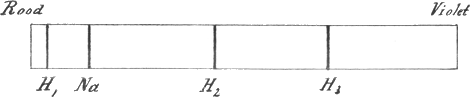 Fig. 29.
Bovendien is er de lijn Na in opgenomen - en wel, wegens de kleine schaal der teekening, als eene enkele, en niet als eene dubbele - die wij met het keukenzout kregen. Deze stof is eene verbinding van het metaal natrium met chloor, en hetzelfde gele licht dat wij hebben waargenomen krijgen wij ook, wanneer wij eene andere verbinding van dat metaal in de vlam brengen, of wanneer wij een stukje van het metaal verbranden. Wij onderstellen daarom dat het keukenzout in de vlam ontleed is, en dat het de atomen van het vrije natrium zijn geweest, die het licht uitstraalden. | |
[pagina 94]
| |
Wat gij in deze kleine spectroscopen waarneemt geeft U slechts een flauw denkbeeld van den rijkdom van verschijnselen, dien het onderzoek der spectra, tot een afzonderlijken tak der natuurkunde opgegroeid, aan het licht heeft gebracht. Grootere hulpmiddelen doen ons fijne lijntjes waarnemen, die ons bij deze instrumenten ontsnappen, en splitsen lijnen die wij eerst voor enkel hielden in tweeën of drieën. Bovendien photographeert men de spectra en kan men aldus het onderzoek uitstrekken tot stralen die ons oog niet meer waarneemt - evenals het oor ongevoelig is voor al te snelle luchttrillingen - en die, meer gebroken wordende dan de violette stralen, buiten het violet in het spectrum vallen. Ook ‘ultraroode’ stralen zijn er, minder breekbaar dan de roode; daartoe behooren de warmtestralen die door verhitte, maar niet lichtgevende voorwerpen worden uitgezonden. Zoo is het veld van onderzoek naar weerszijden uitgebreid, en in welke mate dat het geval is kan hieruit blijken, dat, terwijl de golflengten der zichtbare stralen tusschen 0,00008 en 0,00004 cM. liggen, de uiterste ultraroode en ultraviolette stralen golflengten van ongeveer 0,003 en 0,00001 cM. hebben. Vooral in het ultraviolet worden de spectra rijk aan lijnen; het gedeelte eener photographie van het ijzerspectrum, waarvan nu een beeld op het scherm staat, geeft U daarvan een denkbeeld. Over de groote beteekenis van dit alles behoef ik niet veel te zeggen. Men begrijpt welk een onschatbaar hulpmiddel men in de spectra heeft om de eene stof van de andere te onderscheiden, en menige nieuwe scheikundige grondstof is men dan ook op het spoor gekomen door dat men in een spectrum eene lijn waarnam, die niet aan bekende elementen kon worden toegeschreven. De hoogste theoretische beteekenis is echter hierin gelegen, dat elke spectraallijn eene bepaalde soort van enkelvoudig licht, met een bepaald trillingsgetal, en dus vergelijkbaar met een enkelvoudigen toon, vertegenwoordigt. | |
[pagina 95]
| |
Twee spectraallijnen die op een afstand van elkander liggen hebben altijd een verschil in golflengte, en deze is, wanneer wij het spectrum teekenen, zooals in Fig. 29, altijd het kleinst voor de lijn die het meest naar rechts ligt. Hierbij mag ik wel opmerken dat juist voor deze scherp bepaalde lichtsoorten de golflengte met eene hooge mate van nauwkeurigheid gemeten is. Zij is voor de twee natriumlijnen 0,00005895 en 0,00005889 cM., voor de drie waterstoflijnen in Fig. 29 0,0000656; 0,0000486 en 0,0000434 cM. Dat nu de atomen der elementen juist trillingen kunnen volbrengen met de frequentie die wij in de ligging hunner spectraallijnen zien afgespiegeld, moet natuurlijk van den bouw, de eigenschappen en de afmetingen dier kleine deeltjes afhangen, en het is een groot vraagstuk voor de toekomst, voorstellingen omtrent de structuur der atomen te ontwikkelen, die van de ligging der spectraallijnen rekenschap zullen geven. Zijn wij vooralsnog daarvan ver verwijderd, wij kunnen toch reeds met zeer eenvoudige beschouwingen belangrijke uitkomsten bereiken. Daarvan mogen U een tweetal verschijnselen overtuigen, die wij thans nog in het kort zullen behandelen. Het eerste is het medetrillen van het eene voorwerp met het andere. Men kan een lichaam dat met een vasten trillingstijd - bepaald door de massa en de terugdrijvende kracht - heen en weer kan schommelen, in zoodanige beweging brengen door zeer kleine krachten, wanneer men deze maar intermitteerend laat werken, en wel zoo dat de tusschenpoozen juist gelijk zijn aan den schommeltijd van het lichaam. Ik geef b.v. aan den bol van een slinger een klein stootje naar rechts, wacht dan met een tweede stootje tot de slinger is uitgeweken, naar links is teruggekeerd en weer naar rechts gaat, en ga zoo voort, telkens eene kracht naar rechts uitoefenende als de bol naar die zijde gaat. Natuurlijk versterk ik dan voortdurend de reeds bestaande beweging en kan ik veel grooter amplitudo berei- | |
[pagina 96]
| |
ken dan wanneer ik de stootjes zonder eenige regelmaat, of met andere tusschentijden, op elkander liet volgen. In plaats van op den bol te werken, kan ik ook den draad in de hand houden en zoo het boveneinde met de geschikte frequentie een weinig heen en weer bewegen. Iets dergelijks gebeurt bij deze proef. Aan hetzelfde statief hangen twee slingers met denzelfden schommeltijd, een groote, uit een staaf met een gewicht bestaande, en een bol aan een draadje. Breng ik nu den grooten slinger in schommeling, dan ziet gij weldra ook den kleinen heen en weer gaan, een gevolg van de kleine rukken die de eerste slinger aan het statief geeft, en die op het ophangpunt van het draadje worden overgebracht. Hier zien wij dus het medetrillen van den eenen slinger met den anderen, en hetzelfde verschijnsel bestaat nu bij twee geluidgevende lichamen, mits zij gelijk gestemd zijn. Dan geven de trillingen van het eene, door de lucht of op andere wijze naar het andere overgebracht, daaraan stootjes, die juist met eene geschikte snelheid op elkander volgen, om een merkbare trilling van dat tweede lichaam teweeg te brengen. Gij hoort thans hoe van deze twee gelijke stemvorken de eene met de andere medeklinkt. Ieder zal wel reeds het besluit hebben getrokken dat deze beschouwingen ook voor de lichttrillingen gelden; wij zullen er eene toepassing van maken op de absorptieverschijnselen. Wanneer zullen de lichttrillingen sterk door een lichaam worden opgeslorpt? Wij mogen vermoeden dat dit het geval zal zijn, wanneer zij door kleine deeltjes in dat lichaam gemakkelijk kunnen worden opgenomen, en dat zal gebeuren, wanneer deze deeltjes kunnen trillen met eene periode, overeenkomende met die der invallende stralen. In een gas hebben wij nu, zooals ons bleek, een lichaam, waarvan de deeltjes in staat zijn, trillingen met een bepaalden trillingstijd uit te voe- | |
[pagina 97]
| |
ren en wij kunnen ons wel ter vereenvoudiging een gas denken, dat slechts één trillingstijd heeft, en dus maar ééne spectraallijn zou geven. Zijn onze overwegingen juist, dan zal zulk een gas juist licht, van dezelfde soort als de stralen die het kan uitzenden, absorbeeren. Wij gaan in onze bespiegelingen nog wat verder, en verwachten dat een gas dat twee of drie of meer lichtsoorten van bepaalde golflengten kan uitstralen, juist stralen van diezelfde golflengten zal opslorpen. Daargelaten, of bij deze beschouwingen misschien het een of ander over het hoofd is gezien, zij verdienen wel dat wij ze op de proef stellen; zij worden inderdaad door de waarneming bevestigd. De vorige week hebt gij de proef reeds gezien; immers, toen wij, een deel van het spectrum van het kalklicht beschouwende, eene natriumvlam tusschen de lichtbron en de spleet plaatsten, verschenen er twee donkere lijnen, juist op de plaats waar de natriumvlam zelf lichte lijnen gaf. Die donkere lijnen kunnen alleen uit eene absorptie verklaard worden, en wel uit eene absorptie die zoo sterk is, dat de lichtvermindering die zij op de twee plaatsen in het spectrum geeft meer bedraagt dan de intensiteitsvermeerdering die de vlam daar door hare eigen uitstraling teweegbrengt. Het was noodig, U op dit merkwaardige verband tusschen de uitstraling en de absorptie door gasvormige lichamen te wijzen, omdat gij daardoor de beteekenis leert kennen van spectra waarin donkere lijnen voorkomen. Zoodanig spectrum is b.v. dat van het zonlicht. Neemt men het met een kleinen spectroscoop waar, dan merkt men een zevental donkere lijnen op, maar met een instrument van grooter vermogen ziet men er vele honderden, zooals U kan blijken uit deze photographie van een deel van het spectrum. Deze lijnen komen alle met lichte lijnen in het spectrum van bepaalde elementen overeen, en hierin heeft men eene vingerwijzing omtrent hun ontstaan. Zij kunnen slechts zijn voortgebracht door de absorptie die het licht in dampen, die | |
[pagina 98]
| |
de bedoelde elementen bevatten, ondergaan heeft. Uit het feit dat in het zonnespectrum dezelfde donkere dubbele lijn gevonden wordt, die wij de vorige week met de natriumvlam verkregen, heeft men b.v. afgeleid dat in den dampkring der zon natriumdamp aanwezig is, die eene absorptie heeft uitgeoefend op het licht dat door diepere lagen van het hemellichaam werd uitgestraald. Het andere verschijnsel waarop ik straks doelde bestaat in den invloed dien eene beweging van de geluids- of de lichtbron ten opzichte van den waarnemer op het waargenomen aantal trillingen heeft. Ik merkte vroeger op dat, als een geluidgevend lichaam staat te trillen, elk punt der omringende luchtmassa, en ook het trommelvlies van een waarnemer, even dikwijls heen en weer gaat als de deeltjes der geluidsbron zelf. Maar daarbij werd stilzwijgend ondersteld dat deze voortdurend even ver van den waarnemer af blijft. Dan moeten twee gelijke evenwichtsverstoringen die het trillende lichaam met een tusschenpoos van één trillingstijd aan de lucht mededeelt, denzelfden weg doorloopen; zij zullen dus even veel na elkander het trommelvlies bereiken, als zij na elkander worden voortgebracht. Het is duidelijk dat dit anders zal worden, wanneer het trillende lichaam tusschen het uitzenden van de eerste en de tweede evenwichtsverstoring dichter bij den waarnemer is gekomen. Dan zal de tweede evenwichtsverstoring een kleineren weg hebben te doorloopen dan de eerste; zij zal daar minder tijd aan besteden, en het tijdsverloop tusschen de twee oogenblikken van aankomst zal zooveel kleiner worden als de aankomst van de tweede verstoring door de verkorting van den weg bespoedigd is. Hebben wij met een geluidsverschijnsel te doen, dan zal dus het trommelvlies bij nadering van het trillende lichaam meer keeren naar binnen gedrukt worden; de toon dien wij waarnemen zal hooger zijn. Om eene dergelijke reden zal de toon lager worden als de geluidsbron zich van ons verwijdert. | |
[pagina 99]
| |
Gij kunt deze veranderingen b.v. opmerken aan het geluid van de stoomfluit eener locomotief die langs U heenrijdt; terwijl hij U passeert, wordt de toon plotseling lager. Wij vervangen nu in gedachten het geluidgevende lichaam door een hemellichaam waarin een gasvormig bestanddeel eene bepaalde soort van enkelvoudig licht uitstraalt, en het waarnemende oor door een spectroscoop. Door eene redeneering als zoo even overtuigen wij ons er van, dat eene beweging van het hemellichaam naar de aarde toe het aantal trillingen die per seconde de spleet van het instrument bereiken zal vergrooten, en dat dit aantal verkleind zal worden, als het hemellichaam zich van ons af beweegt. In het eene geval zal in den spectroscoop hetzelfde gebeuren alsof de spleet door stralen van een stilstaand lichtpunt met een iets grooter trillingsgetal werd getroffen, en daar nu vergrooting van dat getal de spectraallijn naar den kant van het violet doet gaan, zullen wij eene verschuiving der streep naar die zijde verkrijgen. Natuurlijk moet de streep zich naar den anderen kant verplaatsen, wanneer de ster zich van ons verwijdert. Zoodra wij weten welke verhouding er is tusschen de snelheid der ster en de snelheid van het licht, kunnen wij berekenen hoeveel het aantal trillingen verandert en omgekeerd zou men, wanneer het gelukte deze laatste verandering uit eene verschuiving der spectraallijn af te leiden, daaruit de snelheid der beweging van het hemellichaam kunnen vindenGa naar voetnoot1). Dank zij de welwillendheid van Prof. Vogel te Potsdam kan ik U eene photographie projecteeren van het spectrum der ster α. Tauri. Gij ziet daarin een aantal donkere lijnen - dus | |
[pagina 100]
| |
absorptielijnen, maar op deze is de theorie even goed van toepassing als op lichte lijnen - en daarnaast ziet gij lijnen van een ijzerspectrum dat gelijktijdig met het sterrespectrum in hetzelfde instrument gephotographeerd werd. Het valt nu in het oog dat bij elke ijzerlijn eene lijn in het spectrum der ster behoort, maar dat die altijd iets verschoven is. Deze verschuiving is naar den kant der groote golflengten, en wijst op eene verwijdering van de ster van de aarde. Uit de meting der verschuiving leidt Prof. Vogel af dat de afstand van de ster tot de aarde met 75 kilometer per seconde toeneemt. Met dergelijke waarnemingen, die vooral daarom van belang zijn, omdat eene verplaatsing van een hemellichaam in de richting der gezichtslijn op geene andere wijze kan worden waargenomen, is men aan het Astrophysikalische Observatorium te Potsdam in 1887 begonnen en vier jaren later was reeds van 47 sterren de beweging gemeten. Naderhand is dit onderzoek, ook aan een aantal andere sterrenwachten, voortgezet en men mag thans, zooals Vogel het uitdrukt, verwachten dat, dank zij deze methode, in den loop der nieuwe eeuw onze kennis van de wereld der zoogenaamde vaste sterren op eene dergelijke wijze zal worden uitgebreid als in de vorige eeuw die van het zonnestelsel. Ik kan niet nalaten nog iets te zeggen van bijzonder merkwaardige uitkomsten, die men bij eenige sterren verkregen heeft. Bij de ster Algol bleken de lijnen voortdurend van plaats te veranderen, en wel zoo dat zij in eene periode van bijna 3 dagen heen- en weerschommelden. Dit is niet anders te verklaren, dan door aan te nemen dat de ster beurtelings naar ons toe en van ons af gaat, en dat is te begrijpen, wanneer men zich voorstelt dat zij in een cirkel rondloopt, dien wij op zijn kant zien. Dit aannemende kan men, daar men den omloopstijd kent, en de snelheid uit de verschuiving der strepen afleidt, berekenen hoe lang de omtrek, en dus ook hoe groot | |
[pagina 101]
| |
de straal van den cirkel is. Dat men nu ook met de beste kijkers niets van deze beweging ziet, is geen bezwaar; daartoe staat het lichaam veel te ver van ons af. Maar, zooals wij weten, geen lichaam kan in een cirkel rondloopen wanneer er niet eene kracht naar het middelpunt op werkt, en dus moet er een ander lichaam zijn, dat de rondloopende ster aantrekt. Dat lichaam moet donker zijn, daar het anders ook een spectrum zou geven, welks lijnen zich niet op dezelfde wijze als de waargenomene verschuiven. Werkelijk had men nu sedert lang bij Algol wisselingen der lichtsterkte met de genoemde periode waargenomen; men schrijft deze thans hieraan toe, dat het donkere lichaam telkens vóór de lichte ster komt te staan, en deze gedeeltelijk aan ons oog onttrekt. Op dergelijke wijze is nu reeds het bestaan van een aantal dubbelsterren waargenomen. Bij sommige is er niet alleen eene verschuiving, maar eene verdubbeling der strepen, in dier voege dat de verdubbeling tot een zeker bedrag toeneemt, dan weer verdwijnt, op nieuw ontstaat, enz. Ook hier ligt de verklaring voor de hand; twee sterren, beide lichtgevend, loopen om een zelfde middelpunt rond, zooals twee lichamen onder den invloed van elkanders wederkeerige aantrekking kunnen doen. Als het eene naar ons toegaat, verwijdert zich het andere, zoodat de strepen zich naar tegengestelden kant verplaatsen, en bij hun terugkeer over elkander heen gaan en dan gedurende korten tijd samenvallen. Eene verklaring, die hierdoor bevestigd wordt, dat somwijlen verschillende lijnen, sommige naar den eenen, en andere naar den tegengestelden kant gaan; de eene groep lijnen behoort dan bij het eerste, en de andere bij het tweede hemellichaam. |
|

