Zichtbare en onzichtbare bewegingen

[p. 24]

II. Beweging langs kromme lijnen.

Bij kromlijnige bewegingen, aan welker beschouwing wij dezen avond zullen wijden, hebben wij uit den aard der zaak met meer ingewikkelde verschijnselen te doen dan bij de rechtlijnige, waarmede wij ons de vorige week in hoofdzaak hebben bezig gehouden. De snelheid kan ook nu weder standvastig blijven of toe- of afnemen, maar bovendien verandert de beweging onophoudelijk van richting, en wij hebben daarom aan de bewegingswetten die wij reeds kennen nog eene nieuwe toe te voegen, die ons leert welk verband er tusschen die richtingsverandering en de op het lichaam werkende kracht bestaat. Wij zullen deze wet uit een eenvoudig verschijnsel afleiden, dat wij allen dikwijls hebben waargenomen.

Wij werpen een bal verticaal in de hoogte en vangen hem dan in de hand op. Wanneer men zich daarin wat heeft geoefend kan men ook hetzelfde doen, terwijl men met standvastige snelheid voortloopt. Werpt men weer den bal omhoog, met dezelfde handbeweging die men maakte toen men stilstond, dan vangt men hem eenigen tijd later op, ofschoon men een eind verder is gekomen; de bal is, terwijl hij steeg en daalde, juist even veel in horizontale richting voortgegaan als wij zelf, en wij hebben om dat teweeg brengen niets bijzonders behoeven te doen.

In plaats van voort te loopen, kunnen wij ons in een vaar-

[p. 25]

tuig begeven, dat met standvastige snelheid wordt bewogen. Stelt, wij zitten in de kajuit, met gesloten raampjes, zoodat wij niets van onze beweging zien. Dan zullen wij daarvan ook door de beweging van den bal niets bemerken. Wij kunnen hetzelfde met hem doen als wanneer het vaartuig stil ligt, en ook wanneer wij zijne beweging langs eene verticale lijn tusschen den vloer en den zolder der kajuit nauwkeurig gingen bestudeeren, wanneer wij onderzochten hoever hij in achtereenvolgende kleine tijdsdeelen komt, en daaruit afleidden hoe de snelheid van oogenblik tot oogenblik verandert, zouden wij niet den minsten invloed van de beweging van het vaartuig bespeuren. Intusschen neemt de verticale rechte lijn aan deze beweging deel, en wij komen derhalve tot het besluit:

Langs eene verticale lijn die in horizontale richting met onveranderlijke snelheid verschoven wordt, kan een lichaam op dezelfde wijze stijgen en dalen als langs eene stilstaande lijn.

Eene eenvoudige figuur zal ons nu doen zien hoe in een dergelijk geval de werkelijke beweging van het voorwerp is. Wij letten vooreerst op het dalen. Stelt dat

Fig. 4.

a e in Fig. 4 de verticale lijn is, in den stand dien zij heeft op het oogenblik dat de daling in het punt a begint. Stond de lijn stil, dan zou het lichaam in achtereenvolgende seconden, of andere even groote tijdsdeelen, de steeds grooter wordende afstanden a b, b c, c d, enz. doorloopen; daarbij zou, zooals uit eene vroeger afgeleide formule volgt, a c = 4 a b, a d = 9 a b, enz. zijn.

Wordt nu de verticale lijn verschoven, dan zal zij op de beschouwde oogenblikken de standen a′ e′, a″ e″, a‴ e‴, enz. hebben, en wel zoo, daar deze beweging gelijkmatig is, dat de horizontale stukken a a′, a′ a″, a″ a‴, enz. alle even lang zijn. Ondertusschen daalt het lichaam even ver als wanneer de hori-

[p. 26]

zontale beweging er niet was. Na één tijdsdeel is het op de hoogte van b gekomen, maar op de lijn a′ e′, dus in het punt b′, dat wij krijgen wanneer wij b b′ horizontaal trekken; evenzoo vinden wij dat het aan het einde van het tweede tijdsdeel in c″, na het derde tijdsdeel in d‴ gekomen is, en zoo vervolgens. Trekken wij nu door de punten a, b′, c″, d‴, en andere op dergelijke wijze bepaalde daar tusschen gelegen punten eene kromme lijn, dan krijgen wij de baan van het lichaam.

Evenzoo kannen wij den weg vinden, die bij het stijgen beschreven is; gij ziet dien links van a e, en men kan dit deel der lijn, dat zich in a met eene horizontale richting aan a b′ c″ d‴ aansluit, gemakkelijk krijgen, wanneer men dit laatste deel om a e omslaat.

De geheele lijn wordt eene parabool genoemd, en van zulk eene parabool kan naar gelang van omstandigheden een kleiner of grooter deel doorloopen worden. Wanneer iemand die zelf stilstaat den bal beschouwt, die door een voortloopenden of in een vaartuig geplaatsten waarnemer wordt opgeworpen en weer gevangen, zal hij hem zulk een weg zien beschrijven. Ook een steen dien wij, zonder voort te loopen, in schuine richting opwerpen heeft deze parabolische beweging, en deze is U ook uit de gedaante van den waterstraal eener fontein welbekend. Alle waterdeeltjes volgen, achter elkander, een dergelijken weg. Springt de straal niet naar boven, maar komt hij in horizontale richting uit eene opening, dan heeft men natuurlijk alleen met de eene helft a b′ c″ d‴ der kromme lijn te doen.

Hoe is het nu met de snelheid bij zulk eene parabolische beweging? Bij onderzoek blijkt dat zij gedurende het opstijgen tot in den top a afneemt, en bij het dalen weder toeneemt. In het eerste herkent gij gemakkelijk de vertraging bij het omhoog, en in het tweede de versnelling bij het omlaag gaan langs eene verticale lijn. Maar als het lichaam juist in den top der kromme lijn is, kunnen wij niet zeggen dat de

[p. 27]

snelheid af- of toeneemt; een oogenblik blijft zij van dezelfde grootte. In den top heeft de bal alleen de snelheid der verticale lijn; de bewegingsrichting is horizontaal, en dus loodrecht op de zwaartekracht. Wij zien hieruit dat eene kracht loodrecht op de beweging van een lichaam de snelheid niet vergroot of verkleint. Zij heeft alleen tengevolge dat de baan gekromd wordt. De zwaartekracht zorgt er voor dat de bal, van a af, niet, met de snelheid die hij daar heeft, in horizontale richting volgens a a′ a″ a‴ vérder gaat, maar van die richting afwijkt. Deze richtingsverandering is des te aanmerkelijker, naarmate de kracht grooter is; konden wij de zwaartekracht versterken, dan zou van a af eene parabool beschreven worden, die nog meer van de rechte lijn afwijkt, en in a sterker gekromd is dan de baan die wij eerst hadden.

Als men weet hoe groot de snelheid is, en aan welke kracht loodrecht daarop het lichaam is onderworpen, kan men de kromming der baan berekenen. Om U de daarvoor noodige formule te doen begrijpen, moet ik eene meetkundige definitie laten voorafgaan. Men kan bij elke kromme lijn een zeer klein gedeelte bij benadering als een cirkelboog beschouwen, en wel met des te minder fout, naarmate dat gedeelte kleiner wordt gekozen. De cirkel waartoe het bedoelde boogje behoort, heet de kromtecirkel der lijn in het beschouwde punt, zijn straal de kromtestraal der lijn; de lengte daarvan kan ons als eene maat voor de kromming dienen, onder dien verstande dat de kromming, de afwijking van eene rechte lijn, des te kleiner is, naarmate de kromtestraal eene grootere lengte heeft.

Om dit op te helderen heb ik bij de parabool A B C in Fig. 5 den kromtecirkel in den top B geteekend; M is het middelpunt daarvan. Deze cirkel sluit zich nauwer dan eenige andere die door het punt B gaat, aan de parabool aan. De kromtecirkels in andere punten der lijn hebben alle grootere stralen dan M B; die b.v. welke bij het punt C behoort, heeft zijn

[p. 28]

middelpunt ergens op het verlengde van de lijn C N, op een afstand van ongeveer 13 cM. van het punt C.

Fig. 5.

Wanneer nu de snelheid die het lichaam in den top der parabool heeft, v cM. per sec. bedraagt, de massa m gram, en de kracht waarmede de aarde het aantrekt K dynes, dan wordt de straal r van den kromtecirkel in den top gegeven door de formule

r = m v²/K.

Daar wij hiervan belangrijke toepassingen zullen maken, is het wel de moeite waard, de vergelijking even te bewijzen. Daartoe merken wij vooreerst op dat K dezelfde kracht is, die het lichaam bij den val langs eene verticale lijn eene versnelling van g (981) cM. per sec. zou geven, en dat dus volgens eene onzer fundamenteele formules (p. 14)

K = m g

is. Ten tweede beschouwen wij Fig. 6, waarin A B een zeer klein gedeelte der parabool, van den top A naar rechts loopende,

Fig. 6.

voorstelt, en waarin gij den kromtecirkel met het middelpunt in M, waarvan A B een deel is, geteekend ziet. De afstand A M is dus r cM.

Wij laten uit B eene loodlijn B C op de verticale middellijn A D van den cirkel neer.

Herinneren wij ons nu wat wij bij Fig. 4 hebben opgemerkt, dan zien wij dat A C kan worden opgevat als de afstand waarover het lichaam daalt, terwijl de verticale lijn

[p. 29]

waarlangs dit plaats heeft, zich in horizontale richting over den afstand C B verschuift. Is dus de tijd, aan het doorloopen van den boog A B besteed, t seconden - de bedoeling is dat t eene zeer kleine breuk is - dan is

C B = t v,

en volgens eene vroegere formule

A C = ½ t² g.

Verder passen wij eene meetkundige stelling toe. De lengte van de lijn C D wordt verkregen, wanneer wij het getal dat de lengte van B C voorstelt met zich zelf vermenigvuldigen, en de uitkomst deelen door het getal dat A C aangeeft. Vermenigvuldigen wij t v met zich zelf, dan krijgen wij t² v², en als wij dit door ½ t² g deelen, komt er na eenige vereenvoudiging

t² v²/½ t² g = v²/½ g = 2 v²/g.

Dit zou dus de lengte van C D zijn. Maar niet nauwkeurig. De boog A B van de parabool valt nl. niet, zooals wij ondersteld hebben, volkomen met een cirkelboog samen. Om de fout te verminderen, moeten wij de lengte van den boog al kleiner en kleiner maken. Het punt B kiezen wij dus al dichter en dichter bij A. Daarbij nadert C eveneens tot A. Daar nu de gevonden uitkomst met des te kleiner fout de waarde van C D voorstelt, naarmate deze lijn minder van de middellijn A D verschilt, moet die uitkomst juist de lengte van deze laatste lijn aangeven. Om den straal te vinden hebben wij verder nog door 2 te deelen; dus:

r = v²/g.

Vermenigvuldigen wij hier nu eindelijk teller en noemer met m, en bedenken wij dat m g = K is, dan komen wij tot de reeds aangevoerde formule

r = m v²/K.

[p. 30]

Wij zien daaruit dat, zooals reeds gezegd werd, r kleiner wordt, d.w.z. de kromming sterker, wanneer wij de kracht K vergrooten, en ook dat, wanneer wij de kracht hetzelfde laten, de kromming vermindert bij toenemende snelheid. Op een snel bewogen lichaam heeft eene kracht loodrecht op de bewegingsrichting, wat de verandering dier richting betreft, minder vat dan op een lichaam met eene kleine snelheid. Men vergelijke de beweging van een geweerkogel met die van een kaatsbal, of twee waterstralen die met verschillende snelheden in horizontale richting uit een vat spuiten.

Wij zijn tot de formule gekomen door de beschouwing van het bijzondere geval, dat de werkende kracht de zwaartekracht is, en dat het lichaam zich juist in den top der parabool bevindt. Maar de uitkomst is algemeen. Telkens wanneer op een in beweging verkeerend lichaam eene kracht werkt, loodrecht op de bewegingsrichting, verandert de grootte der snelheid niet, maar wordt de baan in zoodanige mate gekromd dat de kromtestraal door de formule bepaald wordt. Staat de kracht niet slechts, zooals bij de parabool, in één punt loodrecht op de bewegingsrichting, maar is dat aanhoudend het geval, dan zal de snelheid altijd door onveranderd blijven. Daarbij kan het

Fig. 7.

nu voorkomen dat de kracht van oogenblik tot oogenblik in grootte verandert; dan zal de kromming der baan ook telkens eene andere zijn, en zal zij dus soms zeer ingewikkelde vormen hebben. Is echter de kracht die loodrecht op de bewegingsrichting staat voortdurend dezelfde, dan moet r even groot blijven, en dat kan alleen als de baan een cirkel is. Zoo komen wij tot het belangrijke geval dat een lichaam A (Fig. 7) met de standvastige snelheid v in een

[p. 31]

cirkel rondloopt, terwijl er eene kracht K, naar het middelpunt M gericht, op werkt.

Met deze cirkelbeweging zullen wij ons van avond verder voornamelijk bezig houden. Wij zullen echter den draad onzer beschouwingen hier voor een oogenblik afbreken, om een punt uit de leer der krachten te bespreken, dat ons verder van dienst kan zijn.

Het gebeurt dikwijls dat op een lichaam niet ééne kracht, maar twee of meer krachten, die, zooals ik zal aannemen, verschillende richting hebben, te gelijk werken. Om in zulk een geval eene duidelijke voorstelling van die krachten te krijgen, gebruiken wij meetkundige figuren, waarin de richting en de grootte der krachten door de richting en de lengte van rechte lijnen worden aangegeven. In Fig. 8,

Fig. 8.

waar de pijl a c tweemaal zoo lang is als a b, is het de bedoeling dat in het eene geval eene kracht werkt, dubbel zoo groot als in het andere geval. Heeft men vastgesteld, hoe lang de lijn zal zijn, die eene kracht van 1 dyne voorstelt, dan zullen krachten van 3, 10, of 100 dynes enz. worden aangegeven door 3, 10 of 100-maal zoo groote lengten. Het hulpmiddel waarvan wij ons bedienen om de gezamenlijke werking van twee krachten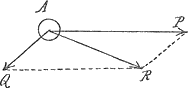

Fig. 9.

te bepalen, is de stelling van het parallelogram van krachten. Wanneer (fig. 9) de twee op het lichaam A werkende krachten door de lijnen A P en A Q worden voorgesteld, beschrijven wij op die lijnen als zijden een parallelogram, d.w.z. wij trekken Q R evenwijdig aan A P, en P R evenwijdig

[p. 32]

aan A Q. De lijn die het punt A met het tegenoverstaande hoekpunt vereenigt, de diagonaal van het parallelogram, stelt door hare richting en grootte eene bepaalde kracht voor, en de uitwerking die A P en A Q te zamen hebben is dezelfde als die, welke deze door A R voorgestelde kracht alleen heeft. Zoo kunnen wij twee krachten door eene enkele vervangen. Wanneer wij dat doen, zeggen wij dat wij ze met elkander hebben samengesteld; wij noemen de kracht A R de resultante van de twee gegeven krachten A P en A Q.

Vooral dient hierbij opgemerkt te worden dat de regel altijd

Fig. 10.

doorgaat, welken hoek de twee gegeven krachten ook met elkander maken, en welke grootte zij ook hebben. In Fig. 10 ziet gij nog eens een parallelogram van krachten van andere gedaante dan het vorige en gij kunt er zelf nog meerdere teekenen. Wanneer gij b.v.

Fig. 11.

twee krachten neemt, die even groot zijn en bijna in elkaars verlengde vallen, zult gij vinden dat zij elkander bijna opheffen; zij leveren eene kleine resultante op, die op weinig na loodrecht staat op de richtingen der krachten zelf.

De stelling is uit de ervaring afgeleid, en daarom mag ik U wel even eene proef laten zien, waardoor zij, al is het dan ook maar voor eene bepaalde klasse van krachten, wordt bewezen.

Over twee katrolschijven A en B (Fig. 11) is een koord geslagen, dat aan de uiteinden de gewichten P en Q draagt,

[p. 33]

terwijl aan het punt C van den draad een ander koord is vastgeknoopt, dat verticaal naar beneden hangt en door een gewicht R gespannen wordt. Ik kan nu het punt C, zooals gij ziet, naar rechts of links in beweging brengen, maar wanneer ik den toestel aan zich zelf overlaat, nemen het punt C en de koorden bepaalde standen aan. Dan is er evenwicht, en wij kunnen met behulp van een parallelogram van krachten vinden aan welke voorwaarde daarbij voldaan moet zijn. Wanneer nl. aan het eene einde van een koord dat over eene katrolschijf loopt met zekere kracht wordt getrokken, trekt het andere einde, door zijne spanning, met eene even groote kracht aan het voorwerp waaraan het bevestigd is. Op het punt C werken daarom twee krachten in de richtingen van C A en C B, die gelijk zijn aan de gewichten P en Q; wij zullen ze door de lijnen C D en C E voorstellen. Bovendien werkt op het punt C de spanning van het naar beneden hangende koord. Deze is gelijk aan het gewicht R en kan, op dezelfde schaal als de andere krachten, door eene lijn C F worden voorgesteld.

Om nu te vinden wanneer de drie krachten C D, C E en C F evenwicht met elkander zullen maken, beschrijven wij op C D en C E als zijden een parallelogram. De diagonaal C G daarvan stelt de kracht voor, waardoor C D en C E vervangen kunnen worden; deze kracht moet dus evenwicht maken met C F, wat klaarblijkelijk alleen dan het geval zal zijn, wanneer zij juist tegengesteld aan C F, dus verticaal naar boven, is gericht, en dezelfde grootte heeft als die kracht. Het toestelletje, waarin de figuur op een plankje achter de draden is geteekend, doet U zien dat dit werkelijk uitkomt, en daarmede is de stelling van het parallelogram van krachten bewezen.

Van die stelling kan nu gebruik gemaakt worden, niet alleen om twee krachten door eene enkele, maar even goed om eene gegeven kracht door twee andere te vervangen, wat in vele gevallen voor de beoordeeling harer uitwerking dienstig is. Stelt

[p. 34]

b.v. dat in Fig. 9 de kracht A R gegeven is. Wij kunnen dan de richtingen A P en A Q willekeurig kiezen, mits zoo dat die van A R er tusschen ligt, en door R Q evenwijdig aan P A en R P evenwijdig aan Q A te trekken, een parallelogram teekenen, waarvan A R de diagonaal is. De zijden A P en A Q van deze figuur stellen krachten voor, die wij, te zamen genomen, voor A R in de plaats kunnen stellen. Wat wij nu gedaan hebben wordt het ontbinden van eene kracht genoemd; de twee verkregen krachten A P en A Q heeten de componenten van A R. Natuurlijk kan dit ontbinden op allerlei wijzen worden gedaan, want gij kunt tal van parallelogrammen teekenen, die alle A R tot diagonaal hebben.

Ziet hier eene toepassing van dat ontbinden van krachten. Als de twee koorden, die in Fig. 11 schuin naar boven loopen, niet over katrolschijven geleid worden, maar aan het boveneinde zijn bevestigd, kunnen wij vinden hoe sterk zij door het gewicht R gespannen worden. Want de spanningen moeten te zamen dit gewicht dragen. Zij moeten dus eene resultante opleveren, die verticaal naar boven gericht en gelijk aan C F is. Laat C G deze kracht zijn. Dan krijgen wij de spanning der koorden, als wij C G met een parallelogram in C D en C E ontbinden.

Duidelijker wordt de zaak misschien wanneer men begint met het gewicht C F te ontbinden in twee krachten, waarvan de eene in het verlengde van A C en de andere in het verlengde van B C werkt. De eene van deze componenten spant het koord A C en de andere het koord B C.

Het is leerzaam, zulke figuren nog eens te teekenen, als het punt C hooger gekozen wordt, terwijl A en B op hunne plaats blijven. Men vindt dan dat de spanningen der in A en B komende koorden grooter worden, en eindelijk, als C nog maar weinig beneden de lijn A B ligt (op die lijn kan het punt nooit komen) veel grooter worden dan het gewicht R. Ieder weet hoe sterk

[p. 35]

men een horizontaal touw moet spannen om te maken dat een gewicht dat in het midden wordt opgehangen, niet veel doorzakt.

Hangt er geen gewicht in het midden, dan belet toch altijd het gewicht van het koord zelf het spannen tot eene rechte lijn, en ook nu gaat het door, dat de spanning in het koord des te grooter moet zijn, naarmate men het strakker wil hebben. De theorie van dit geval is wat moeilijker, maar berust op dezelfde beginselen. Is een telegraaf- of telefoondraad aan twee palen bevestigd, die 100 Meter van elkander staan, en zakt hij in het midden 0,5 M. door - gij kunt dat gemakkelijk zien wanneer gij er langs spoort - dan is de spanning aan de uiteinden, dus de kracht, waarmede de draad aan de palen trekt, 25-maal het gewicht van den draad. Wordt de draad op een winterdag zwaar met ijzel bedekt, dan komt daar nog het 25-voud van het gewicht ijzel bij; gij kent wel voorbeelden, dat de draad daardoor breekt.

Ik verzoek U nu nog eens naar Fig. 5 terug te keeren, en op het oogenblik te letten, waarop het lichaam dat de parabool beschrijft in C is. Laat C P de zwaartekracht voorstellen; deze ontbinden wij in de kracht C Q volgens de richting der beweging, en de kracht C R loodrecht daarop. Den invloed der zwaartekracht op de beweging kunnen wij nu beschrijven door te zeggen dat C Q de snelheid grooter maakt (en wel door eene snelheidsvermeerdering te geven, die van de grootte dezer component en van de massa van het lichaam afhangt) en dat de kromming der baan voor rekening van C R komt. De kromtestraal wordt door de formule van p. 28 bepaald, als men nu daarin voor K de grootte der kracht C R neemt, en natuurlijk voor v de snelheid die er in het punt C is.

Ik vrees bijna, met deze uiteenzettingen te veel van Uw geduld te hebben gevergd, maar wij hebben nu dan ook alle beginselen leeren kennen, door welke een mathematicus de beweging van lichamen onder de werking van gegeven krachten kan berekenen,

[p. 36]

of althans, want dikwijls wordt het te moeilijk, kan trachten te berekenen. De kracht kan altijd ontbonden worden in ééne component langs en ééne loodrecht op de baan, en steeds bepaalt de eene component de verandering van de grootte der snelheid en de andere de verandering van de richting der beweging.

Hoe ver men het in zulke berekeningen gebracht heeft, zal straks nog blijken; voor 't oogenblik kiezen wij eenvoudiger onderwerp.

Het bleek ons alreeds dat een lichaam (Fig. 7) een cirkel kan beschrijven, als er eene kracht op werkt, die steeds naar het middelpunt gericht is. Die kracht is ook werkelijk noodig en zij moet eene bepaalde grootte hebben, die wij uit de eerste formule van p. 28 kunnen afleiden. Vermenigvuldigen wij met K, dan komt er

K r = m v²;

dus:

K = m v²/r.

Zooveel dynes moet de kracht bedragen, als m de massa in grammen, r de straal in cM. en v de snelheid in cM. per seconde is. Was de kracht naar het middelpunt er in 't geheel niet, dan zou het

Fig. 12.

lichaam in eene rechte lijn voortgaan, langs de raaklijn aan den cirkel. Was de kracht kleiner dan zoo even werd opgegeven, dan zou de baan wel is waar van de rechte lijn afwijken, maar minder dan de cirkel dit doet; het lichaam zou nog wel wat verder van het middelpunt komen. Zoo daarentegen de kracht grooter was dan voor de beweging in den cirkel vereischt wordt, zou de baan binnen den cirkel vallen.

Wij kunnen nu een aantal verschijnselen begrijpen, die men gelegenheid heeft, bij draaiende bewegingen op te merken. Ik heb hier b.v. eene staaf A B (Fig. 12), die om haar middelpunt

[p. 37]

M in een horizontaal vlak snel kan worden rondgedraaid; over die staaf kan eene doorboorde kogel C zich verschuiven; men ziet nu dat door de wenteling de kogel zich van het middelpunt M verwijdert, en naar het uiteinde B der staaf vliegt. Dit is gemakkelijk te verklaren; wij hebben er eene bevestiging in te zien van de wet dat een lichaam, als er geene kracht is die dat belet, met eene eenmaal verkregen snelheid langs eene rechte lijn voortgaat. Als de staaf in beweging gebracht wordt, terwijl de kogel in C is, krijgt deze, in de wenteling deelende, eene snelheid in de richting van C E; langs die lijn gaat de bol dan voort, en is dus in het punt D gekomen, als de staaf den stand A′ B′ bereikt heeft. Het is duidelijk hoe de afstand tot het middelpunt grooter is geworden.

Stelt nu dat wij den kogel met een koord aan het midden M van A B hadden bevestigd. Dan zou hij ook weer beginnen met zich van M te verwijderen, maar daaraan zou weldra een eind komen. Het koord zou uitgerekt worden, wegens zijne elasticiteit zou het eene kracht, naar M toe, op den kogel uitoefenen, en deze kracht zou tegelijk met de uitrekking toenemen, totdat zij de door onze formule aangegeven grootte heeft. Dan zou zij juist voldoende zijn, om het lichaam te dwingen in een cirkel rond te loopen; de verwijdering van het middelpunt zou ophouden en het koord dan ook niet nog verder gespannen worden.

Op dezelfde wijze als in dit voorbeeld wordt ook een koord gespannen, waarvan wij het eene einde vasthouden, terwijl aan het andere een kogel is bevestigd, dien wij door eene bekende handbeweging in een cirkel in een verticaal vlak doen rondgaan. Laten wij op eene of andere wijze, zooals bij den bekenden werpslinger, den kogel glippen, dan vliegt hij volgens de raaklijn aan den tot op dat oogenblik beschreven cirkel weg, en beschrijft onder den invloed der zwaartekracht eene parabool.

Hoe sterk het koord moet zijn, om in zulk een geval niet te breken, kunnen wij door de formule uitrekenen. Ik wil b.v.

[p. 38]

aan een staaldraad van 1 M. lengte een lichaam van 1 kilogram met eene snelheid van 10 M. per seconde doen rondgaan. Dan is in onze C.G.S. eenheden m = 1000, v = 1000, r = 100, en de formule leert dat de kracht die naar het middelpunt toe moet werken 10 millioen dynes moet zijn. Zoo groot dient dus de spanning van den draad te worden. Rekenen wij nu dat een staaldraad van 1 mM² doorsnede een gewicht van hoogstens 80 K.G., gelijkstaande met ongeveer 80 millioen dynes, kan dragen, dan blijkt het dat de doorsnede minstens ⅛ mM² moet zijn, als de draad niet zal breken. Men zou evenzoo kunnen becijferen hoe snel de wenteling moet zijn om een draad van gegeven dikte te verscheuren, en naar hetzelfde beginsel, al gaat het wat minder gemakkelijk, kan berekend worden, bij welke snelheid een vliegwiel zou stuk vliegen, zooals wel eens gebeurd is.

Met het toestelletje dat ons straks gediend heeft, kan ik U nog een paar andere voorbeelden geven van het verschijnsel dat een lichaam of de deelen van een lichaam zich bij eene wenteling, ten gevolge van de snelheden die zij verkrijgen, van de as verwijderen. Plaats ik op de verticale draaiende as dit stel van twee geelkoperen hoepels C G D H en C E D F (Fig. 13),

Fig. 13.

13), die dus om de verticale middellijn A B in wenteling worden gebracht, dan zullen de deelen bij G, E, H en F de door de pijlen voorgestelde snelheden krijgen en zich daardoor van de as verwijderen. In horizontale richting zetten de hoepels zich uit, tot dat de veerkracht van het metaal er paal en perk aan stelt. Die uitzetting gaat gepaard met eene verkorting van de verticale middellijn, en zoo ziet gij een verschijnsel dat menigmaal vertoond wordt, om de afplatting der aarde op te helderen. Ongetwijfeld is ook deze, in

[p. 39]

een tijd toen de aarde nog niet vast was, door de aswenteling ontstaan, al zijn de krachten die bij de aarde eene verdere uitzetting aan den evenaar belet hebben van geheel anderen aard geweest dan de veerkracht van deze metaalreepen.

Hoe nu, wanneer ik een cilindrisch glas dat gedeeltelijk met water gevuld is, om de as doe omwentelen, de vloeistof tegen den rand gaat opstaan, zoodat het oppervlak een fraaien gebogen vorm aanneemt, behoef ik U nauwelijks te laten zien, en niet nader uit te leggen. Evenmin dat wanneer de lucht in eene dergelijke cilindrische, van boven gesloten ruimte in wenteling wordt gebracht, zij nabij de as wordt verdund, en aan den omtrek zal ontsnappen wanneer daar openingen

Fig. 14.

zijn, en zich zal ophoopen, wanneer de ruimte daar gesloten is. De verdunning in het centrale deel der ruimte kan men doen zien door dat deel te verbinden met het boveneinde eener verticale in een bakje met water geplaatste buis; het gevolg der wenteling is dan dat de vloeistof in die buis opstijgt.

Tot nog toe gaven wij aan de beschouwde lichamen eene bepaalde snelheid van wenteling; daardoor ontstond dan in het koord b.v. juist eene spanning die de door onze formule verlangde grootte heeft. Die kracht schikte zich dus naar de bewegingssnelheid.

Er zijn echter ook gevallen, waarin de kracht die het lichaam naar het middelpunt drijft door de omstandigheden bepaald is. Dan kan het lichaam alleen dan in een cirkel loopen, wanneer het juist eene bepaalde snelheid heeft. Die snelheid kan uit onze formule worden gevonden. Het blijkt uit de eerste vergelijking van p. 36 dat de tweede macht der snelheid gelijk moet zijn aan het

[p. 40]

getal dat men krijgt, als men K r door m deelt, wat wij uitdrukken door te schrijven



De snelheid moet dus des te grooter zijn naarmate de kracht grooter is.

Tot opheldering hiervan kan een slinger dienen zooals wij reeds de vorige week gebruikten. Wij lichten thans den bol A (Fig. 14) weder tot zekere hoogte op, maar geven hem nu, terwijl wij hem los laten, eene snelheid, loodrecht op het vlak waarin wij hem uit den evenwichtsstand hebben gebracht. Is die snelheid groot, dan beschrijft de bol eene langwerpige of elliptische baan, waarin hij zich verder dan het punt A van den evenwichtsstand verwijdert. Bij eene kleine snelheid is de baan eveneens elliptisch, maar zoo dat het lichaam meer dan in A tot den evenwichtsstand nadert. Door de snelheid behoorlijk af te passen kan ik den bol juist in een cirkel, met het middelpunt in M doen rondloopen.

Wij behoeven hier naar de kracht die het lichaam naar het middelpunt drijft, en zonder welke geene cirkelbeweging mogelijk is, niet ver te zoeken. Zij vloeit uit de aantrekking der aarde voort en hare grootte wordt door eene eenvoudige figuur opgeleverd. Wij ontbinden nl. het gewicht A P van den bol met behulp van het in de figuur geteekende parallelogram in eene component A R in het verlengde van het koord en eene component A Q, die naar het punt M gericht is. De eerste kracht spant het koord, maar heeft geen invloed op de beweging. De tweede is de kracht die het lichaam dwingt, in een cirkel rond te gaan, en door voor K in onze laatste formule de grootte van deze component te nemen, zouden wij de snelheid vinden, die wij aan het lichaam moeten geven om de cirkelbaan te krijgen.

Ik zal de berekening achterwege laten, niet omdat zij te

[p. 41]

moeilijk is, maar omdat zij te veel tijd zou kosten. De uitkomst hangt van den straal af, dien ik aan den cirkel wil geven. Bij elken straal behoort eene bepaalde snelheid en ook een bepaalde omloopstijd. Deze laatste blijkt des te kleiner te zijn, naarmate de straal grooter wordt gekozen, zooals gij gemakkelijk kunt zien, wanneer ik twee naast elkander opgehangen slingers cirkels doe beschrijven, maar den een een grooten en den ander een kleinen cirkel.

Ik vertrouw U met al het voorgaande ook wel duidelijk gemaakt te hebben, dat men, zoodra men heeft waargenomen, welke beweging een voorwerp heeft, daaruit kan afleiden, welke kracht er op werkt. Het merkwaardigste voorbeeld daarvan hebben ons de sterrenkundigen gegeven, die uit den waargenomen loop der hemellichamen tot de krachten waaraan zij onderworpen zijn hebben besloten. De omstandigheid dat vele hemellichamen in banen loopen, die weinig van cirkels afwijken, maakt het ons mogelijk, hen in deze onderzoekingen te volgen en met zeer bescheiden wiskundige hulpmiddelen tot uitkomsten te geraken, die voor onze kennis der natuur van het hoogste belang zijn.

Wij zullen beginnen met het hemellichaam dat ons het naast is, de maan. Zij beschrijft eene cirkelvormige loopbaan om de aarde, en moet dus aan eene kracht naar de aarde toe onderworpen zijn. Niemand zal er aan twijfelen dat deze kracht aan een invloed der aarde is toe te schrijven; wij kunnen haar daarom gerust eene aantrekking door de aarde noemen.

Maar nu rijst eene belangrijke vraag. Wij weten reeds dat alle lichamen nabij het oppervlak der aarde door onze planeet worden aangetrokken en wel in verticale richting, d.w.z. naar het middelpunt der aarde toe. Is nu deze aantrekking van denzelfden aard als die, welke op de maan werkt, is zij b.v. aan eene zelfde toestandsverandering in het medium dat de aarde omringt te wijten, of is zij iets geheel anders? Een oogenblik zou men kunnen meenen dat dit niet uit te maken

[p. 42]

is, zoo lang wij niet zoowel met het mechanisme waardoor een vallende steen naar de aarde wordt getrokken, als met de wijze waarop de aarde op de maan werkt bekend zijn, en daarvan zijn wij ongelukkigerwijze nog ver verwijderd. Maar bij nadere overweging vinden wij toch een middel om tot eene beslissing te komen. Eene werking der aarde die aan eene bepaalde grondoorzaak te wijten is, zal wel bij verwijdering van de aarde naar een of anderen vasten regel afnemen; zijn dus de krachten die op de maan en op een vallenden steen werken van denzelfden aard, dan mogen wij verwachten dat er een verband, misschien wel een eenvoudig verband, tusschen die krachten en de afstanden tot het middelpunt der aarde is. Daarentegen kunnen wij op zulk een verband niet rekenen, en wij zouden het, als het bestond, niet begrijpen, wanneer de krachten van geheel verschillenden oorsprong waren. Hiermede is de weg dien wij moeten inslaan aangewezen. Wij zullen bij wijze van onderstelling al vast aannemen dat er eene verwantschap tusschen de krachten bestaat, maar om die hypothese op de proef te stellen, zullen wij moeten onderzoeken of een verband, zooals ik het daareven bedoelde, werkelijk te vinden is. Daartoe moeten wij de grootte der kracht die op de maan werkt met behulp van de formule

K = m v²/r

bepalen.

Nu is de afstand der maan tot het middelpunt der aarde, d.w.z. de straal van hare loopbaan, 60,3 maal zoo groot als de straal der aarde, en dezen laatsten kennen wij, omdat wij weten dat de omtrek der aarde 40 millioen meters bedraagt. Wij vinden hieruit

r = 384 × 10⁸ cM.¹⁾.

Verder is waargenomen dat de maan haren loop in 27,3 dag

1) Dit beteekent 384, gevolgd door 8 nullen.

[p. 43]

volbrengt. Daar wij uit den straal den omtrek van den cirkel kunnen berekenen, is deze omloopstijd ons voldoende, om de snelheid der beweging te leeren kennen. De uitkomst is

v = 102300 cM. per sec.

Wij stuiten nu op het bezwaar dat gij de massa m der maan niet kent. Maar onze hypothese brengt mede dat de aarde op elk gram dat in de maan aanwezig is dezelfde kracht uitoefent, evenals hier aan de aardoppervlakte elk gram aan gelijke kracht onderhevig is. Wij berekenen daarom de kracht die niet op de geheele maan, maar op één gram van dat hemellichaam werkt en vergelijken die dan met de kracht op één gram in onze omgeving. Stellen wij nu m = 1, en nemen wij voor v en r de opgegeven getallen, dan vinden wij voor de kracht op dat ééne gram in de maan werkende

0,272 dynes,

d.i. 3610 maal minder dan de kracht op een gram aan het oppervlak der aarde, die, zooals wij weten, 981 dynes bedraagt. Nu is de verhouding der afstanden tot het middelpunt der aarde 60,3 en wanneer ik van dat getal de tweede macht neem, krijg ik 60,3 × 60,3 = 3640. Dit is bijna hetzelfde als wij zooeven voor de verhouding der aantrekkingen vonden. Wij zullen maar aannemen, dat het verschil te wijten is aan omstandigheden die wij bij de berekening over 't hoofd hebben gezien - ik zal U daarvan straks nog rekenschap geven - en dus, daar wij een zeer eenvoudig verband vinden, onze hypothese van de gelijksoortigheid der twee krachten als bevestigd beschouwen. Tevens komen wij dan tot het besluit dat de aantrekking der aarde omgekeerd evenredig met de tweede macht van den afstand tot het middelpunt verandert; nu wij gevonden hebben dat, op 60 maal grooteren afstand, de aantrekking 60² maal kleiner uitvalt, mogen wij wel verwachten dat in 't algemeen als men den afstand a maal grooter maakt, de aantrekking a² maal zwakker zal worden.

[p. 44]

Wij hebben hiermede den eersten stap gedaan in de beroemde door Newton gevestigde leer der algemeene aantrekkingskracht. Over de verdere ontwikkeling zijner theorie, over hare zorgvuldige vergelijking, gedurende meer dan twee eeuwen, met oude en nieuwe waarnemingen, zal ik kort zijn. Ik wijs er dus slechts met een enkel woord op dat wij, evenals wij de beweging der maan met die van een vallend lichaam vergeleken hebben, ook de beweging van twee of meer wachters, zooals de planeet Jupiter die heeft, met elkander kunnen vergelijken. Dit vraagstuk, dat eenige overeenkomst heeft met de vraag hoe de snelheid veranderen moet, wanneer wij den vroeger besproken slinger nu eens in een grooten en dan eens in een kleinen cirkel willen doen rondloopen, kan alweder met onze formules worden opgelost.

Men vindt dat, als de kracht omgekeerd evenredig met de tweede macht van den afstand verandert, zooals Newton leerde, de meest verwijderde wachter de kleinste snelheid moet hebben, en wel moet de tweede macht der snelheid omgekeerd evenredig met den straal der loopbaan zijn. De beweging der manen van Jupiter stemt hiermede werkelijk overeen; eene aanwijzing dus dat ook de door deze planeet op naburige lichamen uitgeoefende aantrekking aan de wet van Newton voldoet. Eene bevestiging op nog grooter schaal levert ons de beweging der planeten om de zon; de snelheden van de aarde en van Jupiter b.v. staan tot elkander als de getallen 2,28 en 1, en de afstanden tot de zon verhouden zich als 1 en 5,20. Werkelijk is 5,20 = 2,28 × 2,28 en zoo blijkt Newton's wet omtrent het verband tusschen de aantrekking en den afstand ook op de door de zon uitgeoefende werking toepasselijk te zijn. Moest ik mij niet beperken, dan zou ook de werkelijke gedaante der banen van de planeten dienen besproken te worden. Dat zij min of meer van cirkels afwijken is niet te verwonderen; op een bepaalden afstand van de zon is er slechts eene enkele snelheid waarmede eene cirkelbaan kan beschreven worden, en

[p. 45]

elke afwijking van die snelheid moet eene andere baan geven. Als ik een slinger in een cirkel wil doen loopen, maak ik allicht de snelheid wat te groot of te klein, en krijg dan niet eene cirkelvormige, maar eene elliptische baan. Evenzoo beschrijft eene planeet, die met eene kracht omgekeerd evenredig met de tweede macht van den afstand naar de zon wordt gedreven, eene ellips, zoodra hare snelheid van de voor een cirkel vereischte afwijkt; alleen bestaat er tusschen de twee gevallen dit onderscheid, dat bij den slinger de evenwichtsstand in het middelpunt der ellips valt, en dat de zon niet in het middelpunt der baan staat, maar op eenigen afstand daarvan verwijderd. Men kan uit de grondbeginselen der mechanica afleiden hoe het hiermede gesteld moet zijn, en ook hoe de snelheid bij de elliptische beweging van oogenblik tot oogenblik verandert. Al deze bijzonderheden vindt men bij de waarneming bevestigd, of liever, Keppler had die reeds uit de waarnemingen afgeleid, voor dat Newton den sleutel ter verklaring gaf.

In haar meest algemeenen vorm is de wet van Newton eene grootsche generalisatie. Zij zegt dat elk paar stofdeeltjes elkander met eene kracht omgekeerd evenredig met de tweede macht van den afstand aantrekken. Zij bepaalt zich dus niet meer tot de attractie die van een hemellichaam in zijn geheel uitgaat, maar, veel dieper doordringende, vat zij deze op als de resultante van tallooze krachten, die elk door één stofdeeltje van het lichaam worden uitgeoefend. Zij stelt aan de wiskunde het vraagstuk, de resultante van al deze elementaire werkingen te bepalen.

Het antwoord luidt dat de resulteerende aantrekking van een bol, over welks volume de massa gelijkelijk verdeeld is, naar het middelpunt is gericht en omgekeerd evenredig met de tweede macht van den afstand tot dit punt verandert. Zoo wordt het gerechtvaardigd dat wij, toen wij den steen en de maan beschouwden, altijd met de afstanden tot het middelpunt der aarde hebben gerekend.

[p. 46]

De wet van Newton gaat nog in een ander opzicht verder dan de beschouwingen die ik U mededeelde; zij beweert dat de twee lichamen elkander aantrekken. Inderdaad bestaat bij twee lichamen nooit eene eenzijdige, maar altijd eene wederkeerige werking. Oefent het eerste voorwerp op het tweede, op welke wijze dan ook, eene kracht van zekere richting en grootte uit, dan ondervindt het daarvan te gelijkertijd eene kracht van dezelfde grootte, maar van juist tegenovergestelde richting. Een regel, dien wij zonder uitzondering bevestigd vinden. Een gewicht dat op de tafel ligt drukt deze naar beneden, maar wordt met eene even groote kracht door het hout, dat ietwat vervormd is, naar boven gedrukt. De twee tegen elkander botsende bollen van vroeger drukken tegen elkander en een stuk ijzer

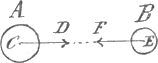Fig. 15.

trekt even goed eene magneetpool aan, als het zelf daardoor aangetrokken wordt. Stellen wij de kracht, waarmede een lichaam A een lichaam B aantrekt, door de pijl E F (Fig. 15) voor, dan moeten wij de werking op A door eene even lange pijl C D aangeven.

Wanneer deze figuur op de algemeene aantrekkingskracht of de zwaartekracht betrekking zal hebben, moet, zooals wij reeds van vallende lichamen weten, en zooals de astronomische verschijnselen het ons voor de hemellichamen bevestigen, de kracht E F verdubbeld worden wanneer wij de massa van B verdubbelen; de gelijkheid der twee krachten vereischt dat dan ook C D verdubbeld wordt. Maken wij vervolgens de massa van A b.v. 3 maal zoo groot, als zij eerst was, dan moeten de beide krachten weder 3 maal zoo groot worden, en dus het 6-voud van wat zij oorspronkelijk waren. Aldus vinden wij dat de wederkeerige aantrekking zoowel met de massa van het eene als met die van het andere lichaam evenredig is, m.a.w., dat zij evenredig is met het produkt der getallen die de twee massa's voorstellen.

[p. 47]

Deze bijvoeging was nog noodig om U de ontdekking van Newton in haar vollen omvang toe te lichten, en U het wapen te doen kennen, waarmede de sterrenkundigen het onderzoek der bewegingen die de hemel ons aanbiedt met het bekende gelukkige gevolg hebben ter hand genomen. Ik zou te ver gaan als ik beweerde dat zij alles hebben ontraadseld; er blijven b.v. in de beweging der planeet Mercurius kleine afwijkingen van de theorie over, waarvan men nog geene rekenschap heeft kunnen geven, maar het verschil tusschen de getallen 3610 en 3640, dat wij straks hebben verwaarloosd, kon toch geheel verklaard worden, toen men de ware beweging der maan en de juiste gedaante der aarde in aanmerking nam, en de kleine afwijkingen van de elliptische beweging, die door de wederkeerige aantrekking van alle lichamen van het zonnestelsel worden veroorzaakt, konden met steeds toenemende nauwkeurigheid uit de theorie worden afgeleid. Zoo is de theoretische sterrenkunde het schitterendste voorbeeld geworden van eene wetenschap die de verschijnselen weet te voorspellen, en zijn wij van de geldigheid der wetten van de algemeene aantrekkingskracht zoo vast overtuigd geworden, dat de gedachte zelfs niet opkomt, dat eene zonsverduistering, zooals die tot welker waarneming in Nederlandsch-Indië vaderlandsche geleerden zich thans uitrusten, eene minuut te vroeg of te laat zou kunnen komen.

Gij gevoelt dat de wensch ontstaan moest, om de bewering der gravitatietheorie dat twee willekeurig gekozen lichamen, twee stukken metaal b.v., elkander aantrekken, door rechtstreeksche waarneming te bevestigen. Daarin is men inderdaad geslaagd, ofschoon de waar te nemen krachten uiterst zwak zijn. Lang geleden mat Cavendish de attractie door een looden kogel van 150 kilogram uitgeoefend, en verscheidene natuurkundigen hebben deze proeven met de verfijnde hulpmiddelen van onzen tijd herhaald. Ik noem slechts het onderzoek dat Boys tusschen 1892 en 1895 verricht heeft. Een klein en licht

[p. 48]

horizontaal staafje, opgehangen op de in Fig. 1 (p. 4) aangegeven wijze, maar aan een zeer dun draadje van kwarts, droeg aan elk uiteinde een gouden bolletje van een paar gram. Op eenigen afstand van deze bolletjes bevonden zich looden kogels van ruim 7 kilogram, zoo geplaatst dat de uitwerking hunner aantrekking op de gouden bollen zoo groot mogelijk zou zijn, en nu gelukte het werkelijk, door die kracht eene geringe, maar toch goed meetbare standverandering te verkrijgen. Ik behoef U wel niet te zeggen hoeveel talent en volharding voor deze waarnemingen noodig zijn geweest, die door de minste trilling van den bodem of den zwaksten luchtstroom rondom het draaibare staafje onmogelijk werden gemaakt.

De einduitkomst van Boys is dat twee bolletjes, elk van 1 gram, en waarvan de middelpunten 1 cM. van elkâar verwijderd zijn, elkander met eene kracht van

6,66/10⁸ dynes

aantrekken.

Het is duidelijk dat men, dit wetende, de aantrekking tusschen twee massa's van gegeven grootte en op gegeven afstand van elkander gebracht, met behulp van de wet van Newton kan voorspellen, en dat men ook, als men de attractie, de grootte der eene massa en de betrekkelijke ligging kent, de grootte der andere massa kan uitrekenen. Zoo kan men te weten komen, welke massa de aarde moet hebben, ten einde een gram nabij haar oppervlak met eene kracht van 981 dynes aan te trekken. Voert men de berekening uit, en neemt men het bekende volume in aanmerking, dan vindt men dat de massa 5,53 maal zoo groot is als wanneer de aarde geheel uit water bestond.