Zichtbare en onzichtbare bewegingen

[p. 1]

I. Rechtlijnige bewegingen.

Toen ik van het Bestuur van het Nutsdepartement de uitnoodiging ontving, eenige voordrachten over natuurkundige onderwerpen voor U te houden, heb ik mij daartoe gaarne bereid verklaard, hopende dat het mij zou kunnen gelukken, U iets dat voor U de moeite loont te toonen van het tafereel dat de hedendaagsche physica ons aanbiedt. Mijne bedoeling kan niet zijn, U dat in zijn geheel te laten overzien; daartoe zouden wij ons op zoo grooten, afstand moeten plaatsen, dat schier elke bijzonderheid U zou ontsnappen, en eene dergelijke oppervlakkigheid zou U zeker niet welkom zijn. Ook wil ik niet tot elken prijs, en op het gevaar af van slechts half verstaanbaar te zijn, Uwe aandacht vestigen op wat het meest uitblinkt en in het oog valt, al is de verleiding ook sterk, om vooral nieuwe ontdekkingen en theorieën op den voorgrond te plaatsen, en uit te weiden over groote algemeene vragen of over de toepassingen, waarin onze tijd meer dan eenige vroegere zich kan verheugen. Zoo veel mag ik U niet beloven. Zult gij waarlijk een inzicht verkrijgen in den gang van natuurkundige beschouwingen, dan moet gij U geheel kunnen indenken in de vraagstukken die wij ter hand nemen. Eenvoudig moeten deze dus, met het oog op den beschikbaren tijd, zijn; evenwel vertrouw ik ze zoo te kunnen kiezen, dat gij ze Uwe aandacht waardig zult keuren.

Wij moeten naar dit werkplan met het begin beginnen, en

[p. 2]

dat is voor de natuurkunde de zoogenaamde mechanica, de leer der bewegingsverschijnselen. Eene wetenschap, op zich zelve reeds van grooten omvang, zoowel door de uitgebreidheid van haar onderwerp als door de veelzijdigheid van hare methoden. Zij omvat alle bewegingen die wij om ons heen zien, het vallen der lichamen, het stroomen van het water, de winden in den dampkring, en bij haar moeten wij te rade gaan, wanneer wij werktuigen willen bouwen, die ons tot groote krachtsontwikkeling of tot fijne bewerkingen in staat zullen stellen. Zij verheft zich ver boven de aarde en vindt als ‘mécanique céleste’ in de beweging der hemellichamen het arbeidsveld waarop zij hare krachten het meest geoefend en hare grootste lauweren geplukt heeft. En, aan den anderen kant, daalt zij tot het kleine en onzichtbare af, en stelt regelen voor de trillingen van het geluid en het licht en voor de verborgen bewegingen waarin wij het wezen van de warmte en van menig ander verschijnsel zien.

Hare methoden zijn wiskundige, want zij werkt steeds met maat en getal; om ons denkvermogen te hulp te komen bij de haast verbijsterende verwikkeling der verschijnselen, stelt zij alle hulpmiddelen der wiskunde in haren dienst, en, zoo zij iets betreurt, dan is het dit, dat de wiskunde niet bij machte is haar nog veel meer hulp te verleenen.

Maar zoo zou ik U bijna den indruk geven, dat gij goed geschoolde mathematici zoudt moeten zijn, om van dit alles iets te verstaan. Gelukkig is dat geenszins het geval. De beginselen zijn eenvoudig genoeg, en de grondleggers der mechanica, Galilei, Huygens, Newton hebben zich bij menig vraagstuk van berekeningen bediend, die ieder van U met eenig geduld gemakkelijk zou kunnen volgen. Bovendien, zoodra gij maar inziet dat het een of ander voor berekening vatbaar moet zijn, wilt gij de uitvoering daarvan wel aan een mathematicus overlaten en op zijne uitkomsten, zonder ze na te cijferen, vertrouwen, evenals gij wel wilt gelooven dat men uit de lengte

[p. 3]

der zijden van een driehoek de grootte der hoeken kan afleiden, al zijt gij zelf daartoe misschien niet in staat.

De verschijnselen waartoe wij ons dezen avond zullen bepalen zijn van den allereenvoudigsten aard; wij zullen niet veel anders bespreken dan bewegingen langs eene rechte lijn, en de omstandigheden onder welke deze plaats hebben. Voorbeelden daarvan hebt gij voor het grijpen, en de spreekwijze dat zulk eene beweging door eene gedurende eenigen tijd werkende kracht wordt teweeggebracht, is U niet vreemd. Wij duwen of trekken b.v. eene slede voort en oefenen dan, zooals het heet, eene kracht in de richting der beweging uit. In andere gevallen zeggen wij dat niet door ons zelf eene kracht op het in beweging gerakende lichaam wordt uitgeoefend, maar door een ander voorwerp. Trouwens, wanneer de slede met een touw wordt voortgetrokken, ondervindt zij rechtstreeks alleen eene werking van dit laatste; iets uitgerekt zijnde, tracht het zich weder samen te trekken en oefent op de slede eene kracht uit, die wij de spanning van het touw noemen. Ook duwen, drukken of stooten kan het eene lichaam tegen het andere; denkt slechts aan den waterdamp die den zuiger eener stoommachine voortdrijft, aan de werking van het water op de schoepen van een waterrad, aan een hamer waarmede een bal wordt voortgeslagen, enz. In andere gevallen zien wij een lichaam een ander medesleepen door eene kracht die niet loodrecht op, maar langs het aanrakingsvlak der twee voorwerpen werkt; als ik b.v. een blok dat op de tafel ligt in horizontale richting voorttrek, dan zal dat blok de tafel, als deze gemakkelijk in beweging kan gebracht worden, medesleepen. De kracht die ditmaal in het spel is noemen wij de wrijving.

Al deze voorbeelden zijn op het eerste gezicht eenvoudig genoeg, al stuit men ook, bij dieper nadenken erover, nog op menig raadsel. Maar er zijn andere verschijnselen, die ons aan-

[p. 4]

stonds als geheimzinnig en vreemd treffen. De magneet dien ik hier in de hand houd trekt dezen ijzeren kogel naar zich toe, zooals wij kunnen waarnemen, wanneer wij den kogel

Fig. 1.

P (Fig. 1) aan het einde eener staaf C D bevestigen, die in horizontalen stand met haar midden B aan een dunnen metaaldraad A B is opgehangen, en dus gemakkelijk in een horizontaal vlak kan draaien. Het is of er onzichtbare koorden tusschen den magneet en het ijzer loopen, en geen physicus twijfelt er dan ook aan, dat hier eene stof tusschen de twee lichamen, eene middenstof of een medium, zooals men zegt, in het spel is. Ook is het duidelijk dat die stof niet op het ijzer zou kunnen werken, zooals zij dat doet, wanneer haar toestand niet op eene of andere wijze door den invloed van den magneet veranderd was, maar men gevoelt hoeveel meer moeite het gekost moet hebben, van die veranderingen iets te weten te komen dan van de uitrekking van een koord met behulp waarvan een lichaam wordt voortgetrokken. Wij verdiepen ons in dit alles niet, en ontleenen er alleen het recht aan, ons de aantrekking van het ijzer door den magneet onder het beeld van het voorttrekken door een gespannen koord voor te stellen.

Aantrekkende, en ook afstootende krachten treffen wij in de natuur zeer vele aan. Ik kan b.v. de staaf C D in Fig. 1 door eene magneetstaaf vervangen en U dan doen zien hoe er tusschen de uiteinden of polen van die magneetstaaf en van een magneet dien ik in de hand houd aantrekkingen en afstootingen werkzaam zijn. Of ik kan op eene dergelijke wijze als C D eene willekeurige metaalstaaf ophangen en aantoonen dat deze door eene glazen staaf die ik met eene zijden lap gewreven, en daardoor, zooals men zegt, geelectriseerd heb, wordt aange-

[p. 5]

trokken. Ik kan deze proef, met hetzelfde gevolg, herhalen met eene met een wollen lap of een kattevel gewreven stang hars of lak, in plaats van de staaf glas. Eindelijk zou ik U kunnen aantoonen dat het glas en het lak, die bij deze waarnemingen gediend hebben, ofschoon zij beide geelectriseerd worden, toch niet in alle opzichten dezelfde werkingen uitoefenen. Immers, hang ik, in plaats van de metalen staaf, het gewreven glas zelf op, dan blijkt dit door een ander geelectriseerd stuk glas te worden afgestooten, maar door een geelectriseerd stuk lak te worden aangetrokken.

In al deze gevallen zouden wij dergelijke opmerkingen kunnen maken als bij de werking van den magneet op het ijzer, en wij zouden dat ook kunnen doen met betrekking tot de kracht die de lichamen doet vallen, de zwaartekracht of de aantrekkingskracht der aarde.

Nadat wij nu een zeker aantal krachten hebben leeren kennen, zal het noodig zijn, eenige algemeene stellingen of natuurwetten tot uitgangspunt voor onze verdere beschouwingen te kiezen. Vooreerst: wat zal er gebeuren als een lichaam aan geene enkele kracht onderworpen is? Natuurlijk zal het dan, als het eenmaal in rust is, in rust blijven. Heeft het echter reeds eene beweging, dan behoudt het die onveranderd, waarmede bedoeld wordt 1^o. dat het in eene rechte lijn voortgaat, en 2^o. dat het in gelijke tijden even groote afstanden aflegt. Doorloopt het b.v. in de eerste seconde een weg van 15 cM., dan zal het in elke volgende seconde even ver gaan; in elke halve seconde zal de weg 7,5 cM. bedragen, in elk tiende deel van eene seconde 1,5 cM., enz.

Wij moeten ons voorstellen dat deze wet uit de waarneming is afgeleid, ofschoon men nooit eene proef kan nemen, waarbij de onderstelling dat er geene kracht op een lichaam werkt volkomen vervuld is. Wij slaan b.v. een bal die op eene horizontale tafel ligt met een hamer voort. Natuurlijk werkt er

[p. 6]

dan gedurende de aanraking van den hamer met den bal eene kracht, en deze is de oorzaak der beweging, maar daarover willen wij voor 't oogenblik niet spreken. Wij willen alleen letten op de beweging, nadat de stoot is afgeloopen. Werkelijk zien wij nu den bal in eene rechte lijn voortgaan, en het eerste deel der wet komt dus uit, maar, wat de in achtereenvolgende seconden doorloopen wegen betreft, deze worden hoe langer hoe kleiner, en na eenigen tijd ligt de bal stil.

Ik behoef U nauwelijks te zeggen, hoe wij de zaak moeten opvatten. Ieder weet dat de beweging des te spoediger is uitgeput, naarmate de oppervlakken ruwer zijn, en ieder zal het dus natuurlijk vinden, dat wij de vertraging der beweging hieraan toeschrijven, dat het blad der tafel wegens die ruwheden eene kracht, tegen de bewegingsrichting in, uitoefent, en dat, zoo wij deze kracht, de wrijving, door de oppervlakken volkomen glad te maken, konden wegnemen, de beweging werkelijk nooit zou ophouden. Onze wet zou bevestigd bevonden worden, als wij de omstandigheden waarvan zij spreekt maar konden verwezenlijken.

Beter dan bij rechtlijnige bewegingen kunnen wij bij draaiende lichamen opmerken hoe lang de beweging kan voortduren, als de wrijving, of de weerstanden van anderen aard, die zich er tegen verzetten, maar klein genoeg zijn, Hoe lang kan een goede tol niet blijven draaien, en in de wenteling der aarde om hare as is nooit eenige vertraging bespeurd. Men kan uit astronomische waarnemingen afleiden dat de tijd dien de aarde aan eene wenteling besteedt, en die 24 uren bedraagt, zeker in eene eeuw niet met het honderdste deel van eene seconde toeneemt. En mocht ooit eene kleine toename worden vastgesteld, dan zou ons dat het bewijs zijn van een of anderen weerstand, dien men zou hebben op te sporen.

Om nu tot de rechtlijnige beweging terug te keeren, en wel tot die, waarbij in gelijke tijdsdeelen even lange wegen door-

[p. 7]

loopen worden, dus de beweging zonder kracht, moet ik U nog met een paar namen bekend maken. Men noemt zulk eene beweging gelijkmatig, en zegt dat zij des te sneller is, naarmate het lichaam in een bepaalden tijd verder komt. Als maat voor de snelheid zullen wij den weg nemen, die in de seconde wordt doorloopen; wij spreken dus in het straks genoemde voorbeeld van eene snelheid van 15 cM. per seconde.

De verdere bewegingswetten leeren ons iets over de grootte der snelheid die een lichaam onder deze of gene omstandigheden verkrijgt. Wij zullen deze wetten uit proeven afleiden, echter niet uit proeven die ik hier werkelijk voor U neem, maar uit denkbeeldige proeven, waarbij alle omstandigheden zoo gunstig mogelijk gedacht worden, en alle storende invloeden, die er bij elke werkelijke proef zijn, geheel worden weggedacht. Gij kunt echter verzekerd zijn dat, wanneer hetgeen ik nu ga zeggen niet waar was, ook bij de aandachtige bestudeering van werkelijk bestaande verschijnselen daarvan iets zou blijken.

Wij beginnen met de op een lichaam werkende kracht, die, zooals ieder aanstonds begrijpt, groot of klein kan zijn, te meten. Daartoe moet eene eenheid van kracht gekozen worden, evenals wij, om lengten of tijden te meten, eenheden van lengte en tijd noodig hebben. Hoe wij die keus doen, komt er voorloopig weinig op aan; het meest ligt wel voor de hand, als eenheid de kracht te kiezen, waarmede de aarde een bepaald voorwerp, b.v. een stuk messing van vastgestelde grootte, aantrekt, het gewicht dus van dat stuk metaal. Stelt U voor dat wij een aantal stukken messing, elk gelijk aan deze gewichtseenheid, hebben. Verder is er nog een meetwerktuig noodig. Daarvoor nemen wij een spiraalvormig opgewonden veerkrachtigen metaaldraad, d.w.z. een draad die de eigenschap heeft, na eene uitrekking, als wij hem weer aan zich zelf overlaten, tot de oorspronkelijke lengte terug te keeren.

Eene dergelijke veer, zooals die U uit briefwegers en uit

[p. 8]

sommige weegwerktuigen voor huishoudelijk gebruik welbekend is, ijken wij door er achtereenvolgens een, twee, drie enz. van onze gewichtseenheden aan op te hangen, en te zien hoe ver zij telkens wordt uitgerekt. Dit gedaan zijnde, kan ik ook, wanneer ik met de hand aan de veer trek, uit de mate van uitrekking tot de grootte der kracht die ik uitoefen besluiten. En dat niet alleen, als het andere uiteinde der veer aan een vast punt is bevestigd, maar eveneens als ik dat aan een of ander lichaam haak, dat ik aldus, in horizontale richting b.v., in beweging breng. Ook dan zie ik aan het bedrag der uitrekking op elk oogenblik de grootte der kracht. Er bestaan b.v. zoogenaamde dynamometers, op dit beginsel berustende - al heeft de veer daarbij een anderen vorm -, waarmede men de kracht kan meten, die een voor een wagen gespannen paard uitoefent.

Ziethier nu onze denkbeeldige proeven en de wetten die wij er uit afleiden.

I. Wij laten op eenzelfde lichaam altijd eene kracht van dezelfde, standvastig gehouden grootte werken, maar nu eens gedurende korteren, dan eens gedurende langeren tijd. Na afloop van dezen tijd, dus nadat de kracht opgehouden heeft te werken, heeft het lichaam eene gelijkmatige beweging; wij meten de snelheid dier beweging, dat is dus de snelheid die het lichaam door de werking der kracht verkregen heeft. Het blijkt dat deze snelheid evenredig is met den tijd gedurende welken de kracht heeft gewerkt. Geeft dus eene bepaalde kracht in ééne seconde eene snelheid van q cM. per seconde aan het lichaam, dan zal, als de kracht 3, of 5, of 8, 5 seconde werkt, eene snelheid van 3 q, 5 q of 8, 5 q cM. per seconde verkregen worden.

Wij hebben ons hierbij voorgesteld dat wij de snelheid meten, nadat de kracht heeft opgehouden te werken, en dan kunnen wij het rustig doen. Maar ook terwijl de kracht nog werkzaam is, is er op elk oogenblik eene snelheid van bepaalde grootte. Stelt b.v. dat de kracht gedurende twee seconden werkt, en dat

[p. 9]

dus het lichaam ten slotte eene snelheid 2 q verkrijgt. Dan heeft het, op het oogenblik waarop de kracht ééne seconde gewerkt heeft, reeds de snelheid q, die zou blijven bestaan, als op dat oogenblik de kracht ophield, en die wij dan gemakkelijk zouden kunnen meten. Blijft de kracht bestaan, dan kunnen wij de snelheid niet zoo gemakkelijk meten, daar zij, terwijl wij dat doen, al weder verandert. Maar wij kunnen 't ons toch wel verbeelden; wij kunnen ons voorstellen dat wij, midden in den loop der beweging, het lichaam gedurende een zeer korten tijd, een tiende, of een honderdste, of, als daarin de bewegingstoestand nog te veel mocht veranderen, een millioenste van eene seconde, in het oog houden, dat wij zien hoe ver het in dien korten tijd komt, en daaruit afleiden, hoe ver het, als het op dezelfde wijze doorging, in eene volle seconde zou komen. Zoo krijgen wij eene maat voor de snelheid op elk oogenblik bij eene niet gelijkmatige of veranderlijke beweging, en wij zien nu, hoe de snelheid, gedurende de werking eener standvastige kracht, geleidelijk, en wel juist evenredig met den tijd toeneemt. Met het oog op dit laatste spreken wij van eene eenparig versnelde beweging. Die moet altijd ontstaan, wanneer de kracht steeds dezelfde is. Wie dus voortdurend even sterk tegen eene slede drukte, zou, als er geen weeerstand was, ten slotte elke gewenschte snelheid kunnen bereiken. Maar hij zou daartoe natuurlijk zelf even hard moeten kunnen voortvliegen.

Het karakteristieke in de uitwerking eener kracht blijkt nu de snelheid te zijn, die zij in eene seconde aan het lichaam geeft, bij de snelheid die dit reeds had. Wij noemen die per seconde verkregen snelheid de versnelling.

II. Wij laten eene kracht, nu eens van deze, dan eens van gene grootte werken, maar altijd op hetzelfde lichaam en gedurende denzelfden tijd. Wij vinden dat de verkregen snelheid evenredig met de grootte der kracht is. Derhalve is ook de versnelling evenredig met de kracht.

[p. 10]

III. Wij onderzoeken eindelijk het geval dat eene zelfde kracht achtereenvolgens op verschillende voorwerpen wordt uitgeoefend. Voor deze laatste nemen wij, om meê te beginnen, lichamen die uit dezelfde zelfstandigheid, b.v. ijzer, bestaan, maar waarvan het volume, en dus de hoeveelheid stof die zij bevatten, verschillend zijn. Het eene lichaam is b.v. 3 maal zoo groot als het andere. Dan neemt men waar dat de versnelling die het verkrijgt het derde gedeelte is van de versnelling die aan het kleine voorwerp wordt medegedeeld. Evenzoo, wanneer de hoeveelheden stof zich verhouden als de getallen 4 en 7, zullen de versnellingen tot elkander staan als 7 en 4. In het algemeen zal de versnelling die door eene bepaalde kracht wordt te weeg gebracht, omgekeerd evenredig zijn met de hoeveelheid stof. Men zegt gewoonlijk: omgekeerd evenredig met de massa, omdat men overeengekomen is, de hoeveelheid stof door dit woord aan te duiden, wanneer men in het bijzonder de meerdere of mindere gemakkelijkheid waarmede de lichamen in beweging gebracht worden op het oog heeft.

Wij moeten nu ook nog verschillende zelfstandigheden met elkander vergelijken, en wij zullen daarbij partij trekken van de waarneming dat alle lichamen op dezelfde plaats der aarde, en als

Fig. 2.

van den weerstand der lucht mag worden afgezien, even snel vallen, iets waarvan wij ons gemakkelijk kunnen overtuigen door ons van een slinger te bedienen. In zijn eenvoudigsten vorm bestaat deze uit een bolletje C, zooals hier aan een draad opgehangen (Fig. 2). Hef ik den bol op, tot in B b.v., en laat hem dan los, dan valt hij langs den cirkelboog B C naar beneden, stijgt aan den anderen kant tot dezelfde hoogte op, die hij in B had, keert dan terug, en schommelt op deze wijze heen en weer, daarbij telkens aan de beweging van B naar C, van C naar D,

[p. 11]

van D naar C, enz. evenveel tijd bestedende. Het blijkt nu dat twee slingers van dezelfde lengte, waarbij de bollen uit verschillende zelfstandigheden bestaan, bij hunne schommelingen gelijken tred met elkaar houden. Hieruit zien wij dat verschillende lichamen met dezelfde snelheid langs den cirkelboog B C dalen en gij kunt verzekerd zijn dat dit ook geldt van den val langs eene rechte lijn, wanneer maar de weerstand der lucht niet te veel invloed heeft.

Stelt nu dat wij een stuk ijzer en een stuk lood hebben, van hetzelfde gewicht, waarvan wij ons door eene balans kunnen verzekeren. Vallen nu die lichamen, dan verkrijgen zij dezelfde versnelling, en het feit dat zij hetzelfde gewicht hebben, dus even sterk door de aarde worden aangetrokken, bewijst ons dat zij die even groote versnellingen door even groote krachten verkrijgen. Maar dan moeten ook andere krachten die aan elkander gelijk zijn, en die ik b.v. in horizontale richting met spiraalveeren zou kunnen uitoefenen, gelijke versnellingen aan de lichamen geven. Trok ik b.v. aan elk met eene kracht, gelijk aan het derde deel van zijn gewicht, dan zou bij het eene zoowel als bij het andere lichaam de versnelling het derde deel zijn van die, welke de zwaartekracht hun geeft. In het algemeen dus kunnen de twee lichamen van gelijk gewicht even gemakkelijk in beweging gebracht worden, en dit drukken wij uit, door hun gelijke massa's toe te schrijven. Het behoeft nu wel nauwelijks gezegd te worden dat, wanneer ik het stuk ijzer onveranderd laat, maar het stuk lood door een ander dat tweemaal zoo groot is vervang, dezelfde kracht aan dit nieuwe stuk lood eene versnelling zal geven, half zoo groot als die welke zij aan het ijzer mededeelt. Het ligt voor de hand, te zeggen dat dit stuk lood eene tweemaal zoo groote massa heeft als het ijzer, en bij vergelijking van deze twee verschillende zelfstandigheden, blijkt dus weder de versnelling omgekeerd evenredig met de massa te zijn. Zoo overtuigen wij ons van de

[p. 12]

algemeene geldigheid dezer wet. Tevens weten wij nu dat men de massa's van twee lichamen kan vergelijken door ze te wegen.

De invloed van de grootte der massa doet zich bij tal van verschijnselen gevoelen. Zij valt b.v. bij slingerende of schommelende bewegingen gemakkelijk in het oog. Kon ik aan den bol van den zooeven beschouwden slinger iets bevestigen, dat zelf niet aan de zwaartekracht onderworpen was, dan zou wegens de vergrooting der massa de beweging van B naar C langzamer geschieden, dus de tijd voor die beweging, en ook die voor eene geheele schommeling noodig, zou langer worden.

Eene stof die niet aan de zwaartekracht onderhevig is, is niet te vinden, en de bedoelde proef dus onmogelijk, maar ik kan toch wel eene proef nemen die op hetzelfde neerkomt. Ik bezig daartoe dezen slinger, die uit eene staaf met een gewicht aan het ondereinde, en draaibaar om een punt in 't midden der lengte, bestaat. Hij heeft een bepaalden schommeltijd en gij ziet hoe deze langer wordt, wanneer ik nu twee gelijke massa's, de eene boven het draaipunt, en de andere even ver daar beneden, aanbreng. De invloeden die de zwaartekracht op deze massa's heeft heffen elkander op, en de beweging wordt dus verlangzaamd, werkelijk omdat eene grootere hoeveelheid stof in beweging gebracht moet worden.

Zooals U bekend zal zijn, zijn de snaren eener piano, die de laagste tonen voortbrengen, met fijn metaaldraad omwikkeld. Men heeft daardoor de massa vergroot, en dus het aantal trillingen in de seconde verkleind, wat juist noodig is om een lageren toon te verkrijgen.

Een gevolg van den invloed der massa is het ook dat, bij een zelfden overdruk, lucht langzamer uit een vat stroomt dan lichtgas. Een zeker volume van dit laatste heeft nl. eene kleinere massa dan een even groot volume lucht, en zal dus door dezelfde kracht sneller in beweging gebracht worden.

Deze voorbeelden zouden nog met andere vermeerderd kunnen

[p. 13]

worden, maar liever dan daarover uit te weiden, zullen wij tot onze wetten terugkeeren en, om die gemakkelijk te kunnen toepassen, er den beknopten vorm aan geven, die door eene wiskundige formule wordt opgeleverd. Tevens zullen wij van nu af bepaalde eenheden invoeren, en ik mag hierbij terloops wel opmerken dat de keus van geschikte eenheden voor allerlei natuurkundige grootheden, eenheden die op eenvoudige wijze bij elkander passen en door alle physici gebruikt worden, voor den voortgang der wetenschap van het grootste nut is gebleken. Van daar dan ook, dat in de 19^de eeuw de vaststelling van zoodanige eenheden, met name voor de grootheden die bij de electrische en magnetische verschijnselen te pas komen, herhaaldelijk op internationale congressen en conferenties is besproken.

In wetenschappelijke onderzoekingen wordt tegenwoordig bijna uitsluitend het zoogenaamde centimeter-gram-seconde (C.G.S.) stelsel van eenheden gebezigd. Eenheid van lengte is daarbij de centimeter, eenheid van tijd de seconde, en daarbij voegen wij nu nog als eenheid van massa het gram, d.w.z. de massa van een cM³. water bij de temperatuur van 4^o C. De eenheid van kracht leiden wij daaruit af. Wij stellen ons te dien einde eene kracht voor, waarvan de grootte zoo geregeld wordt dat zij, op eene massa van een gram werkende, daaraan eene versnelling 1 geeft, d.w.z., dat zij daaraan in 1 seconde eene snelheid van 1 cM. per seconde mededeelt. Deze kracht zal de eenheid zijn; wij noemen haar eene dyne.

De formule die ik op 't oog had ligt nu voor de hand. Wij weten dat eene kracht van 1 dyne, op eene massa van 1 gram werkende, eene versnelling 1 geeft. Is nu de kracht niet 1 dyne, maar K dynes, maar blijft de massa nog 1 gram, dan moet de versnelling K maal zoo groot worden, en kan zij dus door het getal K worden voorgesteld. En vervangen wij nu de massa van 1 gram door eene massa van m gram, dan wordt dientengevolge de versnelling m maal kleiner, en wordt zij dus door het getal

[p. 14]

q = K/m

bepaald. In woorden: het getal dat de versnelling voorstelt wordt gevonden, als men het getal dat de kracht voorstelt deelt door het getal dat de massa aangeeft. Natuurlijk kan men uit de vergelijking ook afleiden

K = m q,

wat men eveneens gemakkelijk in woorden kan uitdrukken.

Ik heb deze formules neergeschreven omdat zij ons in staat stellen, zonder omhaal van woorden eenvoudige vraagstukken op te lossen. Neem b.v. het vallen der lichamen. De waarneming heeft geleerd dat dit, wanneer de weerstand der lucht niet in het spel is, eene eenparig versnelde beweging is, en wel is de versnelling in het C.G.S.-stelsel hier te Leiden door het getal 981 voor te stellen. Op andere plaatsen der aarde is zij wat grooter of kleiner. Passen wij dus onze laatste formule op een vallend lichaam toe, waarvan de massa 1 gram bedraagt, dan is m = 1, q = 981, en dus K = 981 dynes. Maar de kracht die nu de beweging veroorzaakt is wat wij het gewicht van het gram noemen. Dit is dus 981 dynes, of eene dyne is het 981^ste deel van het gewicht van een gram, iets meer dan het gewicht van een milligram.

Ik wil hier nog een paar opmerkingen aan toevoegen. Uit het feit dat de val eene eenparig versnelde beweging is, volgt dat gedurende het vallen de kracht dezelfde blijft. Dus, of het lichaam nog boven in het vertrek is, of reeds een eind gedaald, steeds trekt de aarde het met dezelfde kracht aan¹⁾. Verder kunnen wij nu gemakkelijk uitrekenen, welke snelheid het lichaam in zekeren tijd verkrijgt en hoever het in dien tijd komt. Wij zullen

1) Wij zien hier af van eene uiterst geringe toeneming der zwaartekracht als het lichaam dichter bij de aarde komt. De beweging is daardoor niet volkomen eenparig versneld, maar de afwijking is onmerkhaar.

[p. 15]

ter bekorting, zooals men gewoonlijk doet, voor het getal 981 de letter g schrijven. D.w.z., gedurende 1 seconde wordt bij het vallen eene snelheid van g cM. per sec. verkregen, en daar de snelheid evenredig met den tijd toeneemt, vinden wij dat zij, t seconden na het begin der beweging, t g cM. per sec. moet bedragen. Stellen wij dus de snelheid na t sec. door v voor, dan hebben wij de formule

v = t g.

Ook het aantal cM. die het lichaam in die t sec. doorloopen heeft, en dat wij door h (de valhoogte) zullen voorstellen, kan nu gemakkelijk berekend worden. De snelheid is gedurende de beweging van 0 tot v toegenomen. Nu kan men door eene wiskundige redeneering aantoonen dat bij eene eenparig versnelde beweging het lichaam even ver komt, alsof het gedurende het geheele beschouwde tijdsverloop eene snelheid had gehad, die juist het gemiddelde is van de begin- en de eindsnelheid, d.w.z. eene snelheid, die door de eindsnelheid evenveel overtroffen wordt, als zij zelf de beginsnelheid overtreft. Die gemiddelde snelheid is in ons geval ½ v, en de weg dien het lichaam met deze snelheid in t seconden zou afleggen, bedraagt t × ½ v. Derhalve, als wij de waarde van v in aanmerking nemen,

h = t × ½ t g = ½ t² g.

Is b.v. de tijd 6 seconden, dan wordt de afgelegde weg

h = ½ × 36 × 981

of ruim 17600 cM.

Het is ook niet moeilijk, ons rekenschap te geven van de beweging van een lichaam dat met eene zekere beginsnelheid verticaal omhoog wordt geworpen; terwijl bij het vallen de snelheid in elke seconde met het door g bepaalde bedrag toeneemt, neemt zij thans in elke seconde met hetzelfde bedrag af; de beweging is eenparig vertraagd. Wanneer de beginsnelheid v is, vindt men voor de hoogte waartoe 't lichaam opstijgt, v²/2 g.

[p. 16]

De snelheid waarmede het lichaam weder beneden komt is even groot als de beginsnelheid v.

De zwaartekracht verdient wel dat wij bij hare uitwerking wat uitvoerig hebben stilgestaan, omdat zij eene werkelijk universeele kracht is. Alle vaste, vloeibare en gasvormige lichamen die wij rondom ons waarnemen gehoorzamen haar. Ik heb aan den eenen arm dezer balans een glazen ballon opgehangen, waaruit vooraf de lucht grootendeels met behulp van eene luchtpomp is verwijderd; door gewichten aan de andere zijde is de balans in evenwicht gebracht. Laat ik nu door de geopende kraan de buitenlucht in den ballon toestroomen, dan wordt, zooals gij ziet, het evenwicht verbroken. De ballon is zwaarder geworden, nu er lucht in is gekomen. Zoo overtuigen wij ons er van dat de aarde de lucht aantrekt, eene werking, waaraan wij het te danken hebben dat de dampkring bij de aarde wordt gehouden.

Zeer merkwaardig is het, dat het gewicht van een lichaam steeds hetzelfde blijft, hoe wij den toestand ervan ook veranderen. Of ik eene hoeveelheid water verwarm, doe bevriezen, of in damp doe overgaan, het heeft alles niet den minsten invloed op de totale kracht waarmede zij door de aarde wordt aangetrokken. En wanneer ik dit stukje koper in salpeterzuur oplos tot eene groen gekleurde vloeistof, kunt gij verzekerd zijn, dat het gezamenlijke gewicht van het salpeterzuur en het koper vóór de proef juist even groot is als het gewicht der groene vloeistof, vermeerderd met dat van het gas dat in bellen ontsnapt is. Dit is de groote wet van het standvastig blijven van het gewicht, die door Lavoisier ruim eene eeuw geleden werd uitgesproken en die den toets der nauwkeurigste wegingen doorstaan heeft.

Verschijnselen als de genoemde geven veel te denken. Het is eene behoefte van onzen geest, te midden van de veelvuldige wisselingen in de wereld rondom ons, iets blijvends, on-

[p. 17]

veranderlijks te zien; aan deze behoefte hebben de zoogenaamde molekulaire en atomistische theorieën haar ontstaan te danken. Wijsgeeren der Oudheid hebben het reeds uitgesproken, en de nieuwere natuurwetenschap heeft de groote vruchtbaarheid van het denkbeeld meer en meer aan het licht gebracht, dat de lichamen die wij waarnemen slechts schijnbaar een deel der ruimte geheel vullen, maar in werkelijkheid uit een zeer groot aantal van elkander gescheiden uiterst kleine, en daarom onzichtbare deeltjes zijn opgebouwd, die nu eens op kleinere dan eens op grootere afstanden van elkander liggen, soms op eene of andere wijze vast aan elkander verbonden zijn, dan weder eene meerdere vrijheid van beweging ten opzichte van elkander hebben, maar, terwijl zij zoo op tal van wijzen gegroepeerd kunnen zijn, elk op zich zelf hunnen aard behouden. Volgens deze opvatting zien wij in het ijs, het water en den waterdamp steeds een stelsel van dezelfde kleine deeltjes voor ons; alleen is bij de smelting en nog meer bij de verdamping de band waardoor zij in het ijs aan elkander waren vastgelegd verbroken. En al is in onze groene vloeistof oogenschijnlijk geene enkele eigenschap van het vaste koper meer waarneembaar, wij schromen niet te beweren dat die vloeistof nog altijd de deeltjes bevat, die eerst het stuk metaal opbouwden, maar thans met kleine lichaampjes die het salpeterzuur uitmaakten op bepaalde wijze vereenigd. Wanneer nu deze kleine deeltjes molekulen en wanneer zij atomen genoemd worden, kunnen wij thans laten rusten; waar ik U op wilde wijzen is dit, dat het standvastig blijven van het gewicht begrijpelijk wordt, wanneer men aan elk klein deeltje zijn eigen onveranderlijk gewicht toeschrijft. Wij vinden het toch ook zeer natuurlijk dat het totale gewicht van een aantal kogels van verschillende soort, die wij in eene doos bijeen hebben, niet verandert, hoe wij ze ook door elkander mengen, of welke bijzondere standen wij er aan geven.

De allerkleinste deeltjes die de atomistische theorie zich voor-

[p. 18]

stelt zijn die van de verschillende scheikundige grondstoffen of elementen, waaruit alle lichamen die wij kennen zijn opgebouwd. Wij kunnen de eene dezer grondstoffen niet in de andere doen overgaan, het koper of een ander zoogenaamd onedel metaal b.v. niet in goud, zooals de droom der alchemisten was. Toch wijst het feit dat elk lichaam even snel valt er op, dat de atomen van het eene element en die van het andere niet ten eenenmale van elkander verschillend kunnen zijn, dat er eenige overeenkomst, al is die tot nog toe aan onze nasporing ontsnapt, bestaan moet.

Wij zullen hiermede voor het oogenblik van de zwaartekracht afscheid nemen. Op alle andere krachten zijn de formules die straks werden afgeleid evenzeer van toepassing. Ik schat b.v. de kracht waarmede een van de polen dezer magneetstaaf den ijzeren bol van Fig. 1 aantrekt, als de afstand 10 cM. bedraagt, op 35 dynes. De massa van den kogel is 150 gram. Daaruit kunnen wij afleiden dat de aantrekking van den magneet - gesteld dat de afstand voortdurend dezelfde blijft - den bol in eene seconde eene snelheid van 35/150 = 7/30 cM. per seconde kan geven. En eene dergelijke berekening zou ook in andere gevallen kunnen worden uitgevoerd.

Er is in onze regels omtrent de uitwerking van krachten nog iets, dat verdient opgemerkt te worden. De snelheid die eene gegeven kracht een bepaald lichaam doet aannemen hangt ook van den tijd af, gedurende welken zij werkt. Kom ik b.v. met de magneetpool slechts voor een oogenblik bij den ijzeren kogel aan het uiteinde der staaf CD in Fig. 1, dan verkrijgt de kogel nauwelijks eenige beweging; om eene goed zichtbare verplaatsing aan de staaf te geven, moet ik de aantrekkende kracht eenigen tijd gunnen.

Het zal nu duidelijk zijn dat men, als men al het overige kent, van de waargenomen uitwerking eener kracht wel eens partij zal kunnen trekken, om den tijd te meten, gedurende

[p. 19]

welken zij bestaan heeft. Om U daarvan een voorbeeld te geven, heb ik hier aan metaaldraden die in de punten A en C bevestigd zijn (Fig. 3) twee bollen van messing B en D opgehangen; als ik den eenen bol, b.v. tot in B, oplicht, en hem dan tegen den anderen laat vallen, stelt deze zich in beweging, zooals gij ziet, terwijl B vrij wel in rust komt. Het is de vraag, hoe lang bij deze botsing de aanraking der twee lichamen duurt.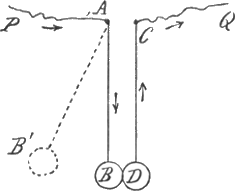

Fig. 3.

In A en C zijn de draden verbonden met koperdraden P en Q, die naar een galvanisch element loopen, d.i. een toestel waardoor wij in metaaldraden een electrischen stroom kunnen voortbrengen. Die stroom bestaat alleen wanneer de bollen elkander aanraken, en loopt dan, in het raakpunt van den eenen bol op den anderen overgaande, in de richting der pijltjes rond; het verschijnsel houdt op, zoodra de bollen weder van elkander zijn gescheiden. Om den stroom waar te nemen dient de galvanometer dien gij ginds op een afzonderlijk, aan den wand bevestigd tafeltje ziet staan. Daarin hangt aan een zeer fijn draadje een klein magneetstaafje, op dezelfde wijze als in Fig. 1 de staaf CD en als hier deze groote magneetstaaf aan een draad is opgehangen. Gij ziet aan den grooten magneet, en gij hebt het allen bij eene kompasnaald waargenomen, hoe hij een bepaalden evenwichtsstand aanneemt, en hoe hij, in beweging gebracht, om dien stand heen en weer schommelt. Dat deze schommelingen met die van een slinger vergeleken kunnen worden, ligt voor de hand; alleen zijn de krachten die het lichaam naar den evenwichtsstand drijven nu van geheel anderen aard. Bij den slinger is dat de zwaartekracht, bij de magneetstaaf zijn

[p. 20]

het krachten die op de polen werken, en waarvan wij ons eenig denkbeeld vormen, door de aarde als een grooten magneet te beschouwen. Natuurlijk zou het mij te ver leiden, over den aard dier krachten uit te weiden, maar dat is ook niet noodig; de vergelijking met den slinger is voor ons doel voldoende. Ik kan dezen laatsten uit zijn evenwichtsstand brengen, als ik op den bol ervan eene horizontale kracht doe werken, en evenzoo het magneetnaaldje in den galvanometer door geschikte krachten op de polen. Deze komen nu in werking - en hierop berust het gebruik dat wij van het instrument maken - zoodra onze electrische stroom door een koperdraad geleid wordt, die in den toestel, in de nabijheid van het magneetje, is aangebracht. Wij hebben bij onze proef alleen te doen met een stroom die zeer kort duurt, even kort nl. als de aanraking der bollen B en D in Fig. 3, zoo kort, dat het magneetje zich in dien tijd nog niet noemenswaard uit zijn evenwichtsstand kan verwijderen. Wij kunnen wel zeggen dat de stroom plotseling, terwijl het magneetje in dien stand is, eene snelheid daaraan geeft; met die snelheid wijkt het dan over een zekeren hoek uit, evenals een slinger dien wij, terwijl hij verticaal hangt, een stoot geven, voor een oogenblik over een zekeren hoek zal uitslaan.

Waar het nu op aan komt is dit, dat de snelheid die de door den electrischen stroom op den magneet uitgeoefende krachten teweegbrengen, des te kleiner zal zijn, naarmate die krachten gedurende korteren tijd werken. Te gelijk met die snelheid wordt ook de bereikte afwijkingshoek kleiner, en zoo zal het U duidelijk zijn, dat wij in dezen hoek eene maat hebben voor den tijd gedurende welken de bollen B en D in Fig. 3 met elkander in aanraking zijn.

Om de bewegingen van het magneetje in den galvanometer zichtbaar te maken, bezigen wij een hulpmiddel dat in vele dergelijke gevallen gebruikt wordt. Aan den magneet is nl. een klein spiegeltje bevestigd, waarop wij een bundel lichtstralen

[p. 21]

uit deze lantaarn laten vallen; het spiegeltje kaatst de stralen naar het scherm daarginds terug en doet daar een lichtbeeld ontstaan, dat zich in horizontale richting verplaatst, zoodra het magneetje, en daarmede het spiegeltje gedraaid wordt.

De plaats waar gij thans het lichtbeeld waarneemt beantwoordt aan den evenwichtsstand, en nu ziet gij hoe, nadat ik het magneetje in beweging heb gebracht, door mijn zakmes bij den galvanometer te houden, het lichtbeeld heen en weer schommelt. Wij wachten tot het weer in rust is gekomen, en nemen dan de proef, die hierin bestaat, dat wij den bol B opheffen en dan tegen D laten stooten, waarbij wij zorg dragen, dat wij de bollen na den stoot uit elkander houden. Wij letten dan telkens op de uitwijking die het lichtbeeldje voor een oogenblik uit zijn evenwichtsstand verkrijgt.

Nemen wij nu de proef twee maal, met dit verschil dat wij eerst B slechts weinig en de tweede maal aanmerkelijk hooger optillen, dan vinden wij dat de uitwijking van den galvanometer den tweeden keer kleiner is dan de eerste maal. Wij besluiten daaruit dat de botsing tusschen de twee bollen des te korter duurt, naarmate de een met grootere snelheid tegen den ander komt.

Wij hebben hier twee gevallen met elkander vergeleken, maar wanneer wij alles wat bij de proef te pas komt hadden gemeten, en wat meer mechanica en mathematische berekening konden gebruiken, dan ons thans ten dienste staat, hadden wij uit de uitkomst van elke proef op zich zelf kunnen afleiden, hoe lang bij die proef de botsing geduurd heeft. Wat wij daarbij zouden gevonden hebben, kan langs theoretischen weg uit de hoogte, van welke de bol B viel, de grootte van den bol en de eigenschappen van het metaal waaruit hij bestaat berekend worden. Een der grootste natuurkundigen die in onzen tijd geleefd hebben, Heinrich Hertz, heeft ons daartoe door een bewonderenswaardig onderzoek in staat gesteld. Uit de door hem opgestelde formule

[p. 22]

vind ik dat, toen ik den bol B tot eene hoogte van 12 cM. oplichtte, de aanraking 0,0002 sec. geduurd heeft.

Wij kunnen uit dit getal nog eene merkwaardige uitkomst afleiden. De bol B heeft, toen hij van de zooeven genoemde hoogte viel, eene snelheid van 150 cM. per seconde verkregen en hij heeft die vrij wel onveranderd op D overgedragen, natuurlijk door op dezen bol eene kracht uit te oefenen. Hoe groot is die kracht geweest? Zij heeft 0,0002 sec. gewerkt en heeft aan D in dien tijd eene snelheid van 150 cM. per sec. gegeven. Had zij eene volle seconde gewerkt, dan zou zij eene snelheid van 750000 cM. per seconde hebben doen ontstaan. Daar nu de bol eene massa van 800 gram heeft, is de kracht 800 × 750000 of 600 millioen dynes geweest, wat overeenkomt niet een gewicht van bijna 600 kilogram.

Intusschen moet dit niet zoo worden opgevat, alsof de kracht van het begin tot het einde der aanraking voortdurend deze grootte zou gehad hebben. Dat het eene lichaam tegen het andere drukt, hangt hiermede samen, dat het nabij de aanrakingsplaats wordt afgeplat, en dan zijn oorspronkelijken vorm weer tracht te hernemen. Deze indrukking bestaat natuurlijk op het oogenblik waarop de aanraking begint nog niet; zij neemt dan langzamerhand toe, en verdwijnt gedurende het laatste gedeelte der botsing. Derhalve zal ook de kracht eerst grooter en dan weder kleiner worden; het boven gevonden getal stelt hare gemiddelde grootte voor, waaruit natuurlijk volgt dat zij op het oogenblik der grootste indrukking nog aanzienlijker is geweest. De afplatting der bollen is op dat oogenblik dezelfde geweest als wanneer zij met die groote kracht aanhoudend tegen elkander waren gedrukt.

Tot besluit van dit eerste deel onzer beschouwingen, wil ik U nu nog wijzen op de groote beteekenis die de weerstanden, welke zich tegen de beweging verzetten, en van welke wij bij onze denkbeeldige proeven hebben afgezien, in

[p. 23]

werkelijkheid hebben. Door de wrijving tusschen vaste langs elkander schuivende of rollende lichamen, of tusschen twee langs elkaâr strijkende lagen van eene vloeistof of een gas, kan eene beweging na korter of langer tijd worden uitgeput; ook verhindert in menig geval een weerstand het ontstaan eener beweging, zooals wanneer men een voorwerp op een ruw hellend vlak plaatst. Ik behoef U er wel nauwelijks op te wijzen hoe de wereld er geheel anders zou uitzien, als er volstrekt geene weerstánden waren, als wij ons steeds op spiegelgladde oppervlakken moesten bewegen, als niets op eene tafel kon blijven liggen (omdat die nooit volkomen horizontaal is), als geen wervelwind werd tot staan gebracht, en als in elk vertrek een ondragelijk gegalm bestond, omdat de eenmaal voortgebrachte geluidstrillingen, onophoudelijk door de wanden weerkaatst, nooit zouden worden uitgedoofd.

Wegens de weerstanden kan een lichaam alleen dan in eene rechtlijnige beweging met standvastige snelheid gehouden worden, wanneer er voortdurend eene kracht in de bewegingsrichting op werkt, een geval, waaraan wij door de dagelijksche waarneming zoo gewoon zijn geraakt, dat het ons eerst eenige moeite kost, ons de denkbeeldige omstandigheden die bij de bewegingswetten ondersteld zijn, goed voor te stellen. Wij denken b.v. nog eens aan de slede waarmede wij begonnen. Zeker, in den beginne geven wij daaraan eene versnelde beweging. Maar wanneer eene zekere snelheid bereikt is, is de weerstand die uit de ruwheid der oppervlakken voortvloeit juist gelijk geworden aan de kracht die wij uitoefenen. Er zijn dan twee krachten van tegengestelde richting, die elkander opheffen, het is zoo goed alsof er in het geheel geene kracht werkte, en, alles wel beschouwd, is het verschijnsel in volkomen overeenstemming met de grondwet der mechanica dat, als er geene kracht is, eene eenmaal verkregen snelheid behouden blijft.