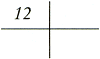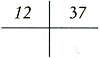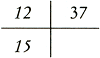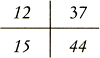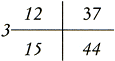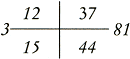Die conste vanden getale
(1999)–Marjolein Kool–Een studie over Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw, met een glossarium van rekenkundige termen
[pagina 198]
| |||||||
Hoofdstuk 5
| |||||||
5.1 Doelgroep en doelstellingVoor wie schrijven de auteurs hun rekenboeken? Veel rekenmeesters vermelden in hun voorrede welke doelgroep ze op het oog hebben. De meeste geven aan dat ze | |||||||
[pagina 199]
| |||||||
voor een jong publiek schrijven. Een enkeling blijkt zich ook tot ouderen te richten. Over het algemeen gaat men uit van een eenvoudig publiek. Uitzonderingen zijn Van Halle en Van der Schuere.Ga naar voetnoot4 Zij schrijven, naar eigen zeggen, ook voor ‘geleerde’ lezers. Wentsel meldt als enige dat ook meisjes met behulp van zijn boek rekenen kunnen leren.Ga naar voetnoot5 | |||||||
5.1.1 De leerlingen van de Franse schoolIn hoofdstuk 2 is gebleken dat een aantal Nederlandstalige rekenboeken gebruikt is op de Franse scholen.Ga naar voetnoot6 Deze scholen worden over het algemeen bezocht door jongens van 10 à 12 tot 15 jaar. Inderdaad richten sommige auteurs zich in de voorrede van hun rekenboek expliciet tot jonge leerlingen. Petri schrijft in zijn voorwoord: So hebbe ick hier van eenGa naar margenoot+ Stockmans richt zich in zijn inleiding: ... tot de joncheyt.Ga naar margenoot+Ga naar voetnoot8 Van der Schuere schrijft voor: ... const-lievende jeught.Ga naar margenoot+Ga naar voetnoot9 En Van den Dijcke begint met: ... goetwillighe jonghers.Ga naar margenoot+Ga naar voetnoot10 Op de Franse school worden de leerlingen opgeleid voor onder andere een toekomst in de handel. Van Varenbraken speelt daar met zijn werk op in en meldt in de proloog dat hij arithmetica naer der coopmanscepe wil onderwijzen.Ga naar voetnoot11 Ook Van den Hoecke heeft blijkbaar als doelgroep voor zijn rekenboek toekomstige kooplieden op het oog. Op de titelpagina van zijn rekenboek uit 1545 zijn twee kooplieden afgebeeld.Ga naar voetnoot12 Zie figuur 5.1. De één meet een lap stof af, de ander weegt het gewicht van een baal op een balans. Uit de vraagstukken die in de rekenboeken voorkomen blijkt, dat vrijwel alle auteurs toekomstige kooplieden als hun belangrijkste doelgroep beschouwen. | |||||||
[pagina 200]
| |||||||
Maar behalve voor het koopmanschap konden leerlingen die de Franse school doorlopen hadden, ook kiezen voor allerlei financiële en administratieve beroepen waarvoor kennis van de rekenkunde onontbeerlijk is. Van der Gucht schrijft zijn rekenboek voor coop-lieden, factueren,Ga naar margenoot+  Figuur 5.1. Twee kooplieden. Afbeelding van de titelpagina van D-Hoe-1545.
Van der Schuere noemt cooplieden, facteurs,Ga naar margenoot+ Van den Dijcke cooplieden, rentmeesters, Wentsel vermeldt in zijn voorrede dat hij zijn leerlingen voorbereidt op allerlei technische ambachten waarin de rekenkunde een rol speelt. Dat geldt voor metselaren, timmerlieden,... | |||||||
[pagina 201]
| |||||||
silversmeden, clockeghieters Het merendeel van de vraagstukken die Wentsel in zijn rekenboek behandelt, betreft echter het kopen en verkopen van goederen en het omgaan met allerlei muntsoorten. Ook bij hem vormen kennelijk kooplieden en beoefenaars van financiële en administratieve beroepen de belangrijkste doelgroep. Aan het rekenboek van RaetsGa naar voetnoot17 is een tractaat over wijnroeien toegevoegd. Ook Van den Hoecke behandelt dit onderwerp.Ga naar voetnoot18 Hieruit zou men kunnen afleiden dat sommige auteurs ook toekomstige wijnhandelaren tot hun doelgroep rekenen. Over het algemeen vormen vraagstukken die betrekking hebben op de handel en het geldwezen de hoofdmoot in de rekenboeken. Een veel kleiner deel heeft betrekking op technische en andere beroepen.Ga naar voetnoot19 In ieder geval staat de rekenkunde in de rekenboeken vrijwel volledig in dienst van de beroepspraktijk en daardoor vormen deze boeken ideaal lesmateriaal voor de leerlingen van de Franse school. | |||||||
5.1.2 VolwassenenSommige auteurs richten zich niet uitsluitend tot kinderen en jongeren. Peter Heyns bijvoorbeeld schrijft zijn rekenboek ook voor andere rekenaars: Notabele meesters, constigheGa naar margenoot+ Met die ander die trekenen useren moet Heyns wel volwassenen bedoelen. Ook Van der Gucht en Van Varenbraken laten blijken dat ze zowel voor jonge als voor oudere rekenaars schrijven. Van der Gucht schrijft: ... principalick om derGa naar margenoot+ Van der Gucht houdt inderdaad rekening met zijn brede doelgroep. Zo presenteert hij bijvoorbeeld de tafels van vermenigvuldiging op twee manieren. Eerst noteert hij ze in een vierkant schema en later behandelt hij ze speciaal voor kinderen | |||||||
[pagina 202]
| |||||||
kolomsgewijs, omdat deze uitvoerige vorm makkelijker uit het hoofd te leren zou zijn. Van der Gucht schrijft hierover: Om de kinderen het eerste Van Varenbraken behandelt speciaal voor kinderen en leerlingen een lange, uitvoerige oplosmethode. Aan het einde daarvan schrijft hij: Ende in deser voorscreven Vervolgens behandelt hij een kortere methode voor ‘volwassenen’. De auteurs richten zich, zoals hiervoor beschreven is, tot cooplieden, facteurs, cassiers, enz. Geen enkele auteur gebruikt daarbij het woord ‘toekomstige’. Ook dat doet een volwassen doelgroep vermoeden. Misschien hopen de auteurs die zich niet alleen tot jonge maar ook tot volwassen leerlingen richten op deze wijze de verkoop van hun boek te bevorderen. Resoort meldt dat ook zestiende-eeuwse schoolboekjes voor de andere vakken vaak niet zo nadrukkelijk als schoolboek gepresenteerd worden om ook lezers buiten de schoolmuren te bereiken.Ga naar voetnoot24 Volwassenen die een rekenboekje kopen, doen dat waarschijnlijk in de eerste plaats om ook rekenen te leren, vermoedelijk door middel van zelfstudie. Stockmans bevestigt deze veronderstelling. Op de titelpagina van zijn rekenboek schrijft hij: Een korte ende eenvuldigheGa naar margenoot+ Stockmans was Francoysche schoolmeester en zijn werk zal ongetwijfeld op zijn Franse school gebruikt zijn. Maar daarnaast, blijkt uit het citaat, rekent hij erop dat men zijn boek voor zelfstudie aanschaft. In zijn voorwoord schrijft hij dat zijn rekenboek bestemd is voor degenen: | |||||||
[pagina 203]
| |||||||
... die den middel, tijdt oftGa naar margenoot+ Ook is het mogelijk dat volwassenen die het rekenen al wel onder de knie hebben, een rekenboek kopen om het te gebruiken als naslagwerk: als een bepaalde rekenregel of oplosmethode vergeten is, kan deze opgezocht worden. Het idee om een rekenboek als naslagwerk te gebruiken komt uit Italië. Volgens Van Egmond fungeerden de Italiaanse abacusboeken in de eerste plaats als catalogi van verschillende probleemtypen en de bijbehorende oplossing.Ga naar voetnoot27 Grendler meldt dat de leerlingen van de Italiaanse abacusscholen allemaal hun eigen rekenkundige naslagwerk schreven.Ga naar voetnoot28 De leraar dicteerde de vraagstukken met hun oplossing. Als de leerling later als koopman, klerk of bankier, een vraagstuk tegenkwam dat hij niet kon oplossen, zocht hij in zijn dictaat het vraagstuk op dat er het meest op leek en gebruikte de oplosmethode die daarbij vermeld was. Hoe meer vraagstukken in allerlei variaties met hun bijbehorende oplosmethode in het naslagwerk waren opgenomen, hoe beter het was. Ook de Nederlandse koopman heeft vermoedelijk een rekenboek bij de hand gehad om in geval van nood een oplosmethode op te zoeken. De wijze waarop de vraagstukken en oplossingen in de boeken worden gepresenteerd en geordend, bevestigt dit vermoeden.Ga naar voetnoot29 Er valt bovendien nog meer informatie in de rekenboeken op te zoeken. Zo zijn er bijvoorbeeld tabellen en lijsten opgenomen met de waarde van munten, maten en gewichten uit verschillende landen en steden.Ga naar voetnoot30 Van der Gucht vermeldt in zijn rekenboek jaarmarkten en waterstanden.Ga naar voetnoot31 Van Halle geeft tabellen waarin lezers die niet kunnen rekenen, de prijs van een aantal goederen kunnen aflezen als de prijs per stuk bekend is. Van Halle schrijft hierover: Hier volghen tafelen van Overigens zijn deze tabellen ook bijzonder handig voor mensen die wel kunnen rekenen, bijvoorbeeld om hun berekeningen te controleren. Seer nut ende bequaeme voirGa naar margenoot+ | |||||||
[pagina 204]
| |||||||
geldt-rekeners al ist oockGa naar margenoot+ Dit soort praktische informatie is over het algemeen in speciale koopmansboekjes te vinden. Dat zijn almanakachtige boekjes, die de koopman bij zich draagt en die gevuld zijn met tabellen van prijzen, koersen, enz. Maar ook rekenboeken met vergelijkbare tabellen zouden heel goed als naslagwerk gebruikt kunnen zijn, zowel voor de praktische informatie als voor de rekenregels, of om de tafels van vermenigvuldiging bij de hand te hebben. Van der Gucht verwijst daarnaar. Hij legt uit dat complementair vermenigvuldigen heel handig is: ... als ghi de tafelen nietGa naar margenoot+ Vervolgens rijst de vraag of de Nederlandse leerlingen op school ook hun naslagwerk gedicteerd kregen, zoals dat in Italië gebeurde. Dat zou inhouden dat men op school de beschikking had over voldoende papier. In het zestiende-eeuwse onderwijs is papier echter een schaars artikel. De lei en het wastafeltje zijn nog steeds zeer gebruikelijk. Volgens Fortgens komt het voor dat leerlingen van de Latijnse school tijdens de Latijnse les aantekeningen maken op schrijftafeltjes, die na correctie op vellen papier worden overgeschreven, zodat de leerlingen op den duur over hun eigen grammatica kunnen beschikken.Ga naar voetnoot35 Zouden ze zo ook hun eigen rekenkundig naslagwerk hebben geschreven? Op de Latijnse scholen gebeurt dat zeker niet. Daar wordt in de zestiende eeuw nauwelijks rekenles gegeven. Misschien is een vergelijkbare aanpak op de Franse scholen gebruikelijk geweest, maar daar zijn geen bewijzen van. Er zijn enkele Nederlandstalige manuscripten overgeleverd die doen vermoeden dat ze voor persoonlijk gebruik geschreven zijn. Het zijn de rekentraktaten van Heyndrik Nouts, Josse Verniers en Cornelis Pijck.Ga naar voetnoot36 In deze manuscripten ontbreekt een inleiding waarin onderwijsdoel en doelgroep omschreven worden. De auteurs beginnen hun werk allemaal met de mededeling dat het manuscript hun persoonlijke eigendom is. Het rekenboek H-BSA-1584 begint bijvoorbeeld met Dese sijfverboeck behoort toe Cornelis Pijck. Dit zou erop kunnen wijzen dat de aantekeningen voor persoonlijk gebruik gemaakt zijn. Dat hoeft niet per se op | |||||||
[pagina 205]
| |||||||
school te zijn gebeurd. Heyndrik Nouts schreef zijn rekenboek in de periode van 1562 tot 1582. Hij heeft beslist niet twintig jaar op school gezeten. Zijn rekenboek lijkt niet voor onderwijsdoeleinden geschreven. Na een korte inleiding over de hoofdbewerkingen volgen vele tientallen vraagstukken met hun gecijferde oplossing. Bij die oplossingen ontbreekt elk woord, elke toelichting. Dat zou erop kunnen wijzen dat Nouts deze vraagstukken voor zichzelf verzameld heeft. Hoe het ook zij, het lijkt gebruikelijk voor zestiende-eeuwse kooplieden om een rekenboek in bezit te hebben. Misschien was het een boekje dat ze zelf volgeschreven hadden, maar anders was het gewoon gekocht en waarschijnlijk gedrukt. Het voordeel van de gedrukte boekjes is het handzame formaat. De meeste zijn octavo en passen in elke jaszak.Ga naar voetnoot37 Een enkeling zal zijn rekenboek gebruikt hebben voor zelfstudie, om zonder leermeester de rekenkunde te leren. De meeste volwassenen gebruiken het rekenboek waarschijnlijk als naslagwerk om een oplosmethode terug te zoeken of om informatie over prijzen, koersen, enz. te verkrijgen. | |||||||
5.1.3 Een enkele ‘geleerde’Jong of oud, het publiek dat de auteurs voor ogen hebben is eenvoudig geschoold. De rekenboeken behandelen de elementaire rekenkunde. Ze hebben een praktische, geen wetenschappelijke doelstelling. Van den Dijcke schrijft in zijn voorwoord: T'is al voor die simplen dieGa naar margenoot+ Stockmans schrijft: Dit en is den gheleerden nietGa naar margenoot+ Uitzonderingen bevestigen de regel. Sommige auteurs behandelen naast de bekende basisstof enkele onderwerpen die speciaal voor ‘geleerden’ dat wil zeggen geschoolde, goed opgeleide personen, opgenomen zijn.Ga naar voetnoot40 Van den Hoecke, Petri en Van Halle geven uitleg over algebra. Van den Hoecke past dit onderwerp toe in een paar astronomische berekeningen. Hij leidt het als volgt in: Om het selve te wercken inGa naar margenoot+ | |||||||
[pagina 206]
| |||||||
meesters die wat ghestileert Van Halle behandelt ook nog de traditionele getallenleer, waarin hij allerlei getallen en getalsverhoudingen classificeert. Tevens beschrijft hij een methode om samengestelde interest te berekenen. Hij doet dit naar eigen zeggen: om wat voir die gheleerde te Van der Schuere bespreekt voor de ‘geleerde’ het worteltrekken tot de negende macht.Ga naar voetnoot43 Voorgaande voorbeelden zijn uitzonderingen, maar ze tonen aan dat sommige rekenboekauteurs waarschijnlijk ook enige contacten in ‘geleerde’ kringen hebben.Ga naar voetnoot44 | |||||||
5.1.4 Jongens en misschien enkele meisjesOver het algemeen zullen de leerlingen die rekenles krijgen uit de rekenboeken van het mannelijk geslacht zijn. Maar in de zestiende eeuw komt het ook voor dat meisjes rekenen leren.Ga naar voetnoot45 In de rekenboeken zijn daar geen directe aanwijzingen voor te vinden. Vraagstukken die speciaal voor vrouwelijke leerlingen bestemd zijn, ontbreken. De rekenende dame op de titelpagina van het rekenboek van Van de Gucht, zie figuur 5.2, is de personificatie van arithmetica.Ga naar voetnoot46 Traditiegetrouw is dit een vrouw en die afbeelding is dus niet bedoeld als extra aansporing voor meisjes om de rekenkunde te gaan leren. Wentsel is de enige auteur die expliciet een vrouwelijke doelgroep in zijn voorwoord vermeldt. Hij adviseert ouders om ook hun dochters rekenkunde te laten leren:  Figuur 5.2. Arithmetica. Afbeelding van de titelpagina van D-Guc-1569.
| |||||||
[pagina 207]
| |||||||
Dierhalven soo doen die Wentsel schrijft zijn rekenboek in 1599. Mogelijk beginnen tegen die tijd de opvattingen over rekenonderwijs aan vrouwen wat te veranderen. Zijn eerdere collega's maken in hun rekenboeken in ieder geval geen melding van een vrouwelijke doelgroep. | |||||||
SamenvattendDe rekenboeken zijn in de eerste plaats geschreven voor een jong, mannelijk, eenvoudig opgeleid publiek. Een aantal van de rekenboeken is gebruikt op de Franse school om de leerlingen praktisch rekenonderwijs te geven. Ze bevatten veel materiaal om hen te laten oefenen met oplosmethodes voor vraagstukken uit de handel en allerlei financiële, administratieve en technische beroepen. Daarnaast bezitten soms ook volwassenen een rekenboekje. Een deel van hen gebruikt dit om zich de rekenkunde door middel van zelfstudie eigen te maken. Anderen gebruiken hun rekenboek vermoedelijk als naslagwerk om oplosmethodes op te zoeken en informatieve tabellen te raadplegen. Waarschijnlijk hebben ‘geleerden’ en meisjes niet of nauwelijks van de rekenboeken gebruik gemaakt. | |||||||
5.2 De leerstofNu duidelijk is geworden welke doelgroepen gebruikmaken van de rekenboeken, rijst de vraag of de leerstof in de rekenboeken aansluit bij de behoeftes van die doelgroepen. Zijn de behandelde onderwerpen, rekenregels, voorbeelden en vraagstukken inderdaad van nut voor de (toekomstige) kooplieden en beoefenaars van financiële, administratieve en technische beroepen? Sluit het rekenkundige niveau van de rekenboeken aan bij de voorkennis van de leerlingen die er gebruik van maken? | |||||||
5.2.1 Elementaire leerstofHoewel de auteurs van de rekenboeken elementaire rekenkunde behandelen, beginnen ze niet helemaal op het nulniveau. Uit de leerstof blijkt dat ze enige rekenkundige voorkennis bij hun leerlingen veronderstellen. Alle rekenboeken beginnen met de uitleg van de Hindoe-Arabische cijfers en het decimale positiesysteem. De leerling leert hoe hij getallen moet lezen en noteren. Vervolgens leert hij met deze getallen schriftelijk rekenen, wat tegenwoordig ‘cijferen’ genoemd wordt. Voordat een leerling kan leren cijferen moet hij al be- | |||||||
[pagina 208]
| |||||||
paalde rekenkundige basiskennis bezitten. Hij moet de cijfers van 0 tot en met 9 kunnen optellen, aftrekken en vermenigvuldigen. Wie deze elementaire berekeningen niet paraat heeft, is nog niet toe aan het cijferen. Het is opvallend dat in alle rekenboeken het uit-het-hoofd-leren van de tafels van vermenigvuldiging ruim aandacht krijgt, terwijl optel- en aftrektabellen nergens voorkomen.Ga naar voetnoot48 In een enkel buitenlands rekenboek komen wel optel- en aftrektabellen voor. Leonardo van Pisa verbindt in zijn Liber Abaci (1202) een opteltabel met een vermenigvuldigtabel. Hij geeft de optellingen van 0 + 0 tot en met 9 + 9 en vervolgens 10 + 10, 20 + 20 ... 90 + 90. Tartaglia geeft in zijn rekenboek een kleine optel- en een kleine aftrektabel die uit het hoofd geleerd moeten worden.Ga naar voetnoot49 Zij zijn uitzonderingen. In de overige buitenlandse en in de Nederlandse rekenboeken komen geen optel- en aftrektabellen voor. Alle Nederlandse auteurs gaan er kennelijk vanuit dat hun leerlingen de elementaire optellingen en aftrekkingen al uit hun hoofd kennen. De vraag is alleen: waar hebben ze die kennis opgedaan? In de zestiende-eeuwse Nederlanden komen verschillende vormen van basisonderwijs voor. Ze bestaan zelfstandig of ze zijn als onderbouw verbonden aan een grote of Franse school.Ga naar voetnoot50 Op deze kleine scholen speelt het rekenonderwijs echter slechts een marginale rol. De leerlingen leren eerst lezen, daarna schrijven en pas daarna eventueel rekenen. Als de leerlingen al aan rekenonderwijs toekomen, leren ze waarschijnlijk niet het rekenen met Hindoe-Arabische cijfers, want dat wordt in alle rekenboeken volledig vanaf de basis uitgelegd. Misschien leren leerlingen van de kleine school optellen en aftrekken met penningen. Dat zou verklaren waarom de optellingen en aftrekkingen in de rekenboeken niet meer gememoriseerd hoeven te worden en het zou ook verklaren waarom Van Halle en Van der Gucht in hun rekenboeken wel het vermenigvuldigen en delen met penningen behandelen, maar optellen en aftrekken met penningen bekend veronderstellen.Ga naar voetnoot51 Van Halle schrijft aan het begin van zijn uitleg over penningrekenen: Te addeeren ende subtraheerenGa naar margenoot+ Wie bij het penningrekenen de elementaire optellingen en aftrekkingen al gememoriseerd heeft, hoeft dat bij het rekenen met Hindoe-Arabische cijfers natuurlijk niet nog eens opnieuw te doen. Dat zou verklaren waarom de auteurs van de rekenboeken deze elementaire berekeningen niet aan de orde stellen. | |||||||
[pagina 209]
| |||||||
5.2.2 Praktische en realistische voorbeelden en vraagstukkenIn paragraaf 5.1.1 is beschreven dat leerlingen van de Franse scholen de rekenkunde leren om daarmee vraagstukken op te lossen die ze in hun latere beroep kunnen tegenkomen. Ook degenen die het rekenboek als naslagwerk of zelfstudiemateriaal gebruiken is het om de praktische toepassingen van de rekenkunde te doen. Beide groepen komen uitvoerig aan hun trekken, want de rekenboeken zijn voor het grootste gedeelte gevuld met vraagstukken voor de (toekomstige) kooplieden en beoefenaars van financiële, administratieve en technische beroepen. Er zijn vooral veel vraagstukken uit de handel, over kopen, verkopen en ruilen van goederen, geld wisselen, rente berekenen, enz. Van der Gucht behandelt bijvoorbeeld het volgende vraagstuk: Drie coop-lieden maken een Voor de ambachtsman is het aanbod iets minder groot, maar toch zijn er verschillende vraagstukken over de samenstelling van metaallegeringen, het aantal leien op een dak, tegels op een vloer, enz. Van Halle stelt bijvoorbeeld het volgende vraagstuk aan de orde: Om eenen kelder te pavayenGa naar margenoot+ Zo zijn er vele voorbeelden van praktische vraagstukken te geven. Praktische vraagstukken komen niet alleen voor als verwerking en toepassing van de geleerde rekenstof, ze fungeren ook vaak als voorbeeld tijdens de uitleg van de hoofdbewerkingen. Stockmans begint bijvoorbeeld zijn uitleg over aftrekken met het volgende vraagstuk: | |||||||
[pagina 210]
| |||||||
In de rekenboeken is rekenkunde synoniem met het kunnen oplossen van vraagstukken. De rekenkunde is geen doel, maar een middel. Je kunt pas rekenen als je de rekenkunde kunt toepassen. Een enkele keer worden rekenkundige begrippen zelfs genoemd naar de praktische situatie waarin ze veelvuldig worden toegepast. Verschillende auteurs noemen het aftrektal en de aftrekker respectievelijk schult en betalinge, omdat de bewerking aftrekken vrijwel steeds wordt toegepast in situaties waarin een schuld wordt afgelost. Helmduyn schrijft bijvoorbeeld: Die derde specie is teGa naar margenoot+ Ook rekenregels worden vaak genoemd naar de praktische situatie waarin ze worden toegepast: regel van mangelinge, regel van wisselinge, regel van geselschap, enz.Ga naar voetnoot57
De praktische voorbeelden en vraagstukken die in de rekenboeken voorkomen, lijken vaak zeer realistisch, alsof ze zo uit het leven gegrepen zijn. In veel gevallen is dat ook zo en daarmee vormen de rekenboeken een informatiebron voor nader onderzoek naar de zestiende-eeuwse samenleving. Prijzen, salarissen, handelsgebruiken, producten die gekocht of verkocht worden, de rekenboeken staan er vol mee. Toch blijft hier voorzichtigheid geboden. De rekenboeken zijn in de eerste plaats schoolboeken. De vraagstukken en de gebruikte getallen kunnen aangepast zijn aan het leerdoel en niet met de werkelijkheid overeenkomen.Ga naar voetnoot58 Auteurs die vraagstukken uit oudere of buitenlandse rekenboeken overnemen, zullen ook niet steeds de bedragen en producten aanpassen aan de eigen tijd en regio. Smeur heeft als tweede stelling bij zijn dissertatie: ‘De opgaven in de zestiende-eeuwse rekenboeken bevatten tal van gegevens, van belang voor onze kennis van het maatschappelijk leven van die tijd.’Ga naar voetnoot59 Dat is juist, maar men kan deze gegevens pas onderscheiden van de fictieve of anachronistische gegevens die eveneens op | |||||||
[pagina 211]
| |||||||
grote schaal in de rekenboeken voorkomen, na zorgvuldig vergelijken met andere informatiebronnen over de zestiende-eeuwse economie en het geldwezen. Hoe bedrieglijk echt de leerstof in de rekenboeken kan zijn, blijkt uit het rekenboek van Peter Heyns. Dit boek bevat vele bladzijden die zo uit een kasboek lijken te komen. Bovenaan elke bladzijde staan opschriften als: Adam Bernaerds moet hebbenGa naar margenoot+ Slechts de alfabetische volgorde van de namen en de rekenkundige regelmaat van de data verraden dat het hier om fictieve situaties gaat. Fictief of niet, in de rekenboeken wemelt het van de praktische vraagstukken, niet alleen in het tweede gedeelte, dat van de rekenregels en praktische toepassingen, maar ook in het eerste deel, waar de hoofdbewerkingen worden uitgelegd. | |||||||
5.2.3 Onpraktische en onrealistische voorbeelden en vraagstukkenPraktische oefeningen, realistische vraagstukken, tabellen waarin munten, maten en gewichten omgerekend zijn, .... wie een rekenboek openslaat, ziet nuttig, realistisch rekenmateriaal dat de zestiende-eeuwse kooplieden en beoefenaars van financiële, administratieve en technische beroepen goed van pas komt in hun beroepspraktijk. Maar hier en daar wordt het oog getroffen door zaken die niet nuttig en realistisch zijn. De belangrijkste functie van de rekenboeken is weliswaar de leerling te laten oefenen voor en voor te bereiden op de praktijk, maar soms wordt die praktische doelstelling even ingeruild voor een andere. Verschillende auteurs behandelen speciale berekeningen die in een bijzondere vorm zijn weergegeven. Van Halle maakt bijvoorbeeld optellingen in de vorm van geometrische figuren.Ga naar voetnoot61 Zie figuur 5.3.
Ook in het rekenboek van Wentsel komen berekeningen met een opvallend uiterlijk voor.Ga naar voetnoot62 Zie figuur 5.4. Van der Gucht beschrijft een recept voor het maken van een deling in een bijzondere vorm.Ga naar voetnoot63 Dit soort rekensierkunst heeft weinig praktisch nut. Een ander opvallend aspect betreft de getallen die in de vraagstukken gebruikt worden. Over het algemeen lijken ze ‘uit het leven gegrepen’, maar een enkele keer kiezen de auteurs voor bijzondere getallen, die bijvoorbeeld bestaan uit een op- of aflopende cijferreeks. Kennelijk vindt men in deze situaties een ‘mooi’ ge- | |||||||
[pagina 212]
| |||||||
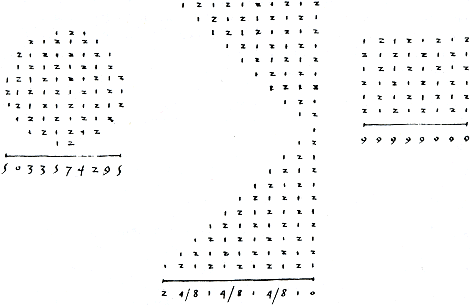 Figuur 5.3. Optellingen in de vorm van geometrische figuren.
tal beter op zijn plaats dan een realistisch getal of een getal waarmee handig gerekend kan worden. Pijck berekent bijvoorbeeld de vermenigvuldiging 12 × 34567.Ga naar voetnoot64 Van der Gucht berekent hoeveel guldens 4321 stuivers waard zijn en het product van 654321 × 123456.Ga naar voetnoot65 Van Halle vermenigvuldigt het getal 6751 achtereenvolgens mer 234, 456, 678 en 890.Ga naar voetnoot66  Figuur 5.4. Delingen in bijzondere vormen.
| |||||||
[pagina 213]
| |||||||
Ook in het hoofdstuk over het lezen en schrijven van Hindoe-Arabische cijfers zijn de getallen opvallend. De leerlingen krijgen soms enorme getallen voorgeschoteld. Van Halle legt bijvoorbeeld uit hoe men een getal van 19 cijfers moet lezen. Pijck behandelt zelfs een getal van 30 cijfers.Ga naar voetnoot67 De leerling krijgt zo weliswaar overtuigend te zien dat het systeem van de Hindoe-Arabische cijfers in principe eindeloos uitbreidbaar is zonder dat er nieuwe symbolen nodig zijn, zoals dat bij de Romeinse cijfers wél het geval is, maar in het dagelijkse leven komen dergelijke grote getallen niet voor.Ga naar voetnoot68 Van Halle is de enige auteur die daar een opmerking over maakt: Aldus machmen voorts van alle Naast de onrealistische getallen die in sommige vraagstukken gebruikt worden, komt het ook voor dat de context van vraagstukken zeer onwaarschijnlijk en onpraktisch is. Van der Gucht behandelt bijvoorbeeld het volgende vraagstuk: Een man gaende alle daghe 11 Het lijkt niet erg waarschijnlijk dat een zestiende-eeuwse reiziger tijdens zijn reizen elke nacht een stuk terug zou lopen. Het blijkt hier om een eeuwenoud vraagstuk te gaan. Volgens Tropfke komen varianten van dit bewegingsvraagstuk al in de negende eeuw in India voor. Er staat eveneens een variant in het Arabische werk van al-Karagi (eind 10de-begin 11de eeuw). Ook komt het in verschillende Europese rekenboeken voor, onder andere in het Liber abaci van Leonardo van Pisa (1202).Ga naar voetnoot71 De andere fantasievolle vraagstukken die in de rekenboeken voor- | |||||||
[pagina 214]
| |||||||
komen, zijn eveneens vaak zeer oud en men vindt ze terug in allerlei verschillende, historische rekenteksten. Men kan zich afvragen waarom in de praktische rekenboeken, die geschreven zijn voor (aankomende) koop- en ambachtslieden en beoefenaars van financiële en administratieve beroepen, onpraktische zaken staan als berekeningen in geometrische vormen, vraagstukken met onrealistische getallen en vraagstukken die een onwaarschijnlijke situatie beschrijven. De fantasievolle vraagstukken zijn kennelijk uit traditie opgenomen. Vraagstukken die al eeuwenlang zijn overgeleverd en in allerlei landen en culturen voorkomen, hebben hun waarde bewezen en verdienen een plaatsje in het rekenboek. Het zijn steeds dezelfde eeuwenoude vraagstukken die, al dan niet met een kleine variatie, in de verschillende rekenboeken terugkeren. Bovendien hebben de onrealistische vraagstukken een recreatieve functie. Ze zijn vaak verpakt in vermakelijke verhaaltjes. Tropfke noemt ze: ‘Probleme der Unterhaltungsmathematik’.Ga naar voetnoot72 Van Egmond, die dergelijke vraagstukken aantrof in de Italiaanse abacusboeken, is eveneens van mening dat ze dienen om variatie aan te brengen, om de lezer wat ontspanning te bieden en om de sleur van de eindeloze rijen realistische handelsvraagstukken te doorbreken.Ga naar voetnoot73 Soms is bij het oplossen van dit soort vraagstukken maar weinig rekenkunde nodig. Dan zijn het meer een soort raadsels, waarvan de oplossing door scherpzinnig redeneren gevonden kan worden. Zoals bijvoorbeeld het vraagstuk uit het rekenboek van Van Varenbraken over de man die 8 stopen bier in twee gelijke hoeveelheden wil verdelen en daarbij uitsluitend een 8-stoopkan, een 5-stoopkan en een 3-stoopkan tot zijn beschikking heeft.Ga naar voetnoot74 Benoit noemt deze vraagstukken ‘jeux’.Ga naar voetnoot75 Van Varenbraken geeft sommige vraagstukken het opschrift mee: Een questie uut ghenouchten. Eén van de vraagstukken die hij expliciet voor het plezier heeft ingevoegd is het volgende: Een questie uut ghenouchten.Ga naar margenoot+ Ook Van den Dijcke probeert het nuttige met het aangename te verenigen. Aan het eind van zijn rekenboek leidt hij een verzameling vraagstukken als volgt in: | |||||||
[pagina 215]
| |||||||
Hier na volghen vele Van der Gucht meldt: Hier naer volghen zommigheGa naar margenoot+ Ook Peter van Halle houdt wel van een grapje. In zijn rekenboek verklaart hij het raadsel van de 12 pelgrims die op weg naar Rome langs een perenboom kwamen waaraan 12 peren hingen... Ende elck track een af endeGa naar margenoot+ Stockmans plaatst de vermakelijke vraagstukken aan het eind van zijn rekenboek: Volgen sommige exempelen endeGa naar margenoot+ Naast recreatieve vraagstukken hebben sommige rekenboeken ook illustraties met een diverterende functie. Het Italiaanse handschrift van Filippo CalandriGa naar voetnoot81 heeft schitterende miniaturen en randversieringen in kleuren en bladgoud. Elke bladzijde is een lust voor het oog. Maar ook de houtsneden uit de Duitse rekenboeken van Ries en Widman verhogen het rekengenot.Ga naar voetnoot82 Zie bijvoorbeeld in figuur 5.5 de illustratie bij een erfenisvraagstuk in het rekenboek van Widman. In de Nederlandse rekenboeken komen afgezien van de titelpagina nauwelijks illustraties voor. Van Halle heeft één plaatje en plaatst sommige rijmpjes in een | |||||||
[pagina 216]
| |||||||
omlijsting van krullen en grotesken.Ga naar voetnoot83 In het werk van Van VarenbrakenGa naar voetnoot84 en in H-GeU-1584 komen een paar randversieringen voor, maar in de gedrukte boeken ontbreekt elke illustratie. Mogelijk hebben financiële of technische aspecten hierbij een rol gespeeld. Het opnemen van een afbeelding in een rekenboek vereist de medewerking van een kunstenaar of vakman die bijvoorbeeld een houtsnede maakt, terwijl het opnemen van een recreatief vraagstuk technisch geen extra problemen oplevert.  Figuur 5.5. Verdeling van een erfenis. Afbeelding uit Widman 1489, fol. 97v.
Er is nog een derde verklaring voor het optreden in de rekenboeken van berekeningen in mooie vormen, met bijzondere en grote getallen en fantasievolle vraagstukken. Mogelijk zijn ze opgenomen om de leerling te imponeren, te overtuigen van de kwaliteit en de schoonheid van de rekenkunde. Swetz beschouwt ze als showstukjes, bedoeld om de vaardigheid van de rekenaar en de grote mogelijkheden van de rekenkunde te demonstreren.Ga naar voetnoot85 De auteur laat ermee zien dat je met de rekenregels niet alleen alledaagse vraagstukken kunt oplossen, maar ook fraaie staaltjes rekenkunst kunt afleveren. Deze opvatting sluit aan bij de wijze waarop de meeste auteurs in hun voorwoord de rekenkunde ophemelen. Zij beschouwen arithmetica als de belangrijkste van de kunsten van het quadrivium. Zonder de rekenkunde kunnen de andere drie ‘exacte’ kunsten niet bestaan.Ga naar voetnoot86 De auteurs van de rekenboeken tonen in hun werk in ieder geval een groot enthousiasme voor hun onderwerp. In de eerste plaats willen ze hun leerlingen nuttige rekenkunde leren. Daar hebben ze het grootste deel van hun rekenboek voor gereserveerd. Daarnaast willen ze uit traditie, of uit ontzag voor de kracht en schoonheid van hun vak of uit puur plezier hun leerlingen een enkele keer laten zien welke mooie, wonderlijke, indrukwekkende zaken er ook met de rekenkunde te beleven zijn. | |||||||
[pagina 217]
| |||||||
5.3 De didactiekHoe wordt in de rekenboeken de leerstof gepresenteerd en geoefend? Welke didactische opvattingen hanteren de auteurs, bewust of onbewust, om hun dubbele doelstelling te bereiken? Wat is de stijl en de structuur van een boek dat enerzijds gebruikt kan worden als leerboek voor jonge leerlingen en anderzijds als zelfstudieboek of naslagwerk voor volwassenen kan fungeren? De auteurs doen zelf geen uitspraken over hun aanpak, maar uit hun werk zijn verschillende didactische principes af te leiden. | |||||||
5.3.1 Een opbouw van makkelijk naar moeilijkDe volgorde van de onderwerpen in de rekenboeken is niet willekeurig. De auteurs zijn er zich terdege van bewust dat ze een leerboek schrijven en dus is - zoals men kan verwachten - in hun werk duidelijk een opbouw van makkelijk naar moeilijk waar te nemen. Dat geldt met name voor het eerste deel van de rekenboeken, waarin de hoofdbewerkingen worden behandeld en de basis van de rekenkunde wordt gelegd. Eerst twee getallen optellen, daarna meer getallen. Eerst een even getal halveren, daarna een oneven getal. Eerst een aftrekking zonder lenen uitvoeren, dan een met lenen. Eerst ‘kale’ getallen optellen, dan benoemde getallen, dat wil zeggen munten, maten en gewichten. Eerst leren rekenen met ‘gehele’ getallen, daarna met breuken. Eerst vermenigvuldigen met factoren die uit één cijfer bestaan, daarna met factoren die uit twee, drie of meer cijfers bestaan. Nieuwe rekenkundige kennis wordt steeds op de voorgaande gestapeld. Bij elk nieuw onderwerp wordt verondersteld dat men het voorgaande beheerst. De leerling moet het eerste deel van het rekenboek van voor naar achter doorwerken. Wie in het midden begint, loopt onherroepelijk vast. De lijn die opklimt in moeilijkheidsgraad moet gevolgd worden. Van Varenbraken schrijft hierover: Voort beghere ic aen alle dieGa naar margenoot+ De opbouw van het eerste deel is in alle rekenboeken vrijwel gelijk. In het tweede deel van de rekenboeken, waar de rekenkunde wordt toegepast en de auteur allerlei rekenregels behandelt waarmee vraagstukken opgelost kunnen worden, ligt de volgorde minder vast. Alle auteurs beginnen uiteraard met de regel van drieën, dat is immers de basis van de toegepaste rekenkunde, maar de re- | |||||||
[pagina 218]
| |||||||
gels die daarna volgen, kunnen in principe in willekeurige volgorde aangeleerd worden. Dat betekent niet dat het tweede deel van de rekenboeken lukraak in elkaar is gezet. Wentsel schrijft over het probleem van de juiste volgorde: Sommighe schoolmeesters Het is niet bekend welke schoolmeesters de Italiaanse praktijk en de algebra vóór de regel van drieën behandelen. In geen van de Nederlandse rekenboeken komt de door Wentsel geschetste volgorde voor.
Hoe zorgvuldig de auteurs in het eerste deel van hun rekenboek ook het principe hanteren dat ze geen kennis en vaardigheden mogen gebruiken die nog niet behandeld zijn, een enkele keer wijken ze daar toch van af. Zo komen in een aantal rekenboeken bij halveren en delen al breuken voor terwijl de uitleg daarvan pas later volgt. Van der Gucht behandelt bij het optellen van ‘gehele’ getallen het volgende voorbeeld met breuken:Ga naar voetnoot89 8 balen wulle weghen als hier onder:Ga naar margenoot+ De breuken worden pas vele bladzijden later behandeld. Van Halle en Van den Hoecke gebruiken al voortijdig breuken bij delen.Ga naar voetnoot90 Bij het optellen en aftrekken van benoemde getallen moeten eenheden vaak in grotere of kleinere eenheden omgerekend worden. Van de leerling wordt dan verwacht dat hij kan vermenigvuldigen en delen terwijl dat pas later behandeld wordt. Ook bij het uitvoeren van de zevenproef gaat men er stilzwijgend van uit dat de leerling al kan delen. Slechts Van Halle geeft als voorbereiding op de zevenproef een tabel met resten die ontstaan na delen door 7.Ga naar voetnoot91 | |||||||
[pagina 219]
| |||||||
In de meeste rekenboeken worden eerst alle bewerkingen voor ‘gehele’ getallen uitgelegd en daarna pas voor breuken. Van Varenbraken wijkt hiervan af.Ga naar voetnoot92 Na het optellen van ‘gehele’ getallen behandelt hij meteen het optellen van breuken. Dat brengt hem al snel in de didactische problemen. Het optellen van ongelijknamige breuken is immers niet mogelijk als je nog niet kunt vermenigvuldigen en delen. Aanvankelijk stelt Van Varenbraken zaken als het vereenvoudigen van breuken nog even uit: Ende wanneer tghebroken es Maar op den duur ontkomt hij er niet aan rekenhandelingen te gebruiken die pas later uitgelegd worden.Ga naar voetnoot94 De voortijdige breuken, delingen en vermenigvuldigingen komen echter maar incidenteel voor. Over het algemeen wordt - zoals hiervoor beschreven is - de rekenkunde zeer zorgvuldig vanaf de basis opgebouwd, opklimmend in moeilijkheidsgraad. Op één aspect wijken echter alle rekenboeken van die regel af. De hoofdbewerkingen voor breuken worden in alle rekenboeken in dezelfde volgorde behandeld als bij de natuurlijke getallen. Dus: optellen, aftrekken, vermenigvuldigen en delen. De volgorde van makkelijk naar moeilijk zou echter bij breuken zijn: vermenigvuldigen, delen, optellen en aftrekken. Bij de eerste twee hoofdbewerkingen hoeft men immers niet eerst de breuken gelijknamig te maken. Geen enkele auteur heeft voor deze volgorde gekozen. Hieruit blijkt hoe krachtig de traditie kan zijn. De volgorde: optellen, aftrekken, vermenigvuldigen en delen voor ‘gehele’ getallen komt al in het rekenboek van al-Khwarizmi voor. Ook Sacrobosco houdt zich aan deze volgorde.Ga naar voetnoot95 In beide werken wordt het rekenen met breuken niet behandeld, maar op het moment dat de breuken wél hun intrede in de rekenboeken doen, is de traditionele volgorde van de hoofdbewerkingen al zo diepgeworteld, dat men kennelijk niet meer op het idee komt om daarvan af te wijken. Van den Hoecke is bij het penningrekenen wel van de gebruikelijke volgorde afgeweken. Hij behandelt eerst optellen en vermenigvuldigen en daarna pas aftrekken en delen. Deze volgorde klimt inderdaad op van makkelijk naar moeilijk, maar wordt door niemand nagevolgd. Tot slot volgt hier nog één ander volgorde-aspect. In de meeste rekenboeken, ook die in het buitenland, wordt het penningrekenen na het rekenen met Hindoe-Arabische cijfers behandeld. Adam Ries draait in zijn rekenboek deze volgorde | |||||||
[pagina 220]
| |||||||
om.Ga naar voetnoot96 Hij doet dat bewust, omdat hij vindt dat rekenen met penningen een goede voorbereiding is op het rekenen met Hindoe-Arabische getallen. Inderdaad is het rekenen met penningen concreter en daardoor eenvoudiger dan het rekenen met abstracte cijfers. Petri is de enige Nederlandse auteur die dezelfde volgorde heeft als Ries.Ga naar voetnoot97 Van der Gucht, Van Varenbraken en Van den Hoecke handhaven de traditionele, minder logische volgorde.Ga naar voetnoot98
Samenvattend kan men stellen dat over het algemeen de stof in de rekenboeken logisch gepresenteerd is; zoals men van een leerboek kan verwachten zijn de onderwerpen van makkelijk naar moeilijk geordend. Er zijn enkele uitzonderingen op deze regel. Voor een deel zijn die veroorzaakt door vasthouden aan de traditie. | |||||||
5.3.2 RekenreceptenDe auteurs beschrijven rekenrecepten; series rekenkundige handelingen die stap-voor-stap, in een vaste volgorde uitgevoerd moeten worden en die dan, mits toegepast in de juiste situatie, gegarandeerd de goede oplossing opleveren. Bewijzen van of argumenten voor een bepaalde aanpak of oploswijze ontbreken.Ga naar voetnoot99 De leerling wil vraagstukken leren oplossen. De auteur kent de recepten waarmee dat mogelijk is. Niemand is geïnteresseerd in het waarom van die recepten. Het belangrijkste is dat ze werken en een goede uitkomst opleveren. Wie een cake wil bakken, doet een ei in het deeg en vraagt niet naar een bewijs van de noodzaak. Wie wil optellen, krijgt het advies om het grootste getal bovenaan te zetten en hoeft niet te weten waarom hij dat moet doen.Ga naar voetnoot100 Overigens moet men zich realiseren dat het bewijzen van de juistheid van bepaalde rekenkundige algoritmes, zoals bijvoorbeeld staartdelen en worteltrekken, behoorlijk moeilijk kan zijn. Bewijzen ontbreken, maar er wordt wel veel aandacht besteed aan de zogenoemde proeven, controles van de gemaakte berekeningen. Een koopman moet uiteraard foutloos kunnen rekenen. Het eerste rekenrecept wordt meestal meteen al aan het begin van de uitleg van iedere hoofdbewerking gegeven. Het lijkt een soort ‘definitie’, maar vaak is het een korte samenvatting van de te volgen procedure. Petri begint zijn uitleg van de hoofdbewerking aftrekken bijvoorbeeld als volgt: Substractio leeret omme af teGa naar margenoot+ | |||||||
[pagina 221]
| |||||||
Vaak gelden deze ‘definities’ alleen voor het gebied van de natuurlijke getallen. Dat is bijvoorbeeld het geval met de ‘definitie’ waarmee Van Varenbraken zijn uitleg over vermenigvuldigen begint: Multiplicatie en es andersGa naar margenoot+ Zodra er echter met breuken kleiner dan 1 vermenigvuldigd wordt, wordt het product niet groter dan de factoren en gaat het bovenstaande niet meer op. Van den Hoecke en Wentsel zijn de enige auteurs die daar een opmerking over maken.Ga naar voetnoot103 Kortom, definities ontbreken of schieten tekort, maar voor het bereiken van de doelstelling van de rekenboeken is dat van ondergeschikt belang. De leerling wil geen wiskunde leren, maar oplosmethodes voor praktische vraagstukken. Het gaat erom dat hij de juiste rekenhandelingen in de juiste volgorde kan uitvoeren. Onthouden is belangrijker dan begrijpen. Slechts een enkele keer probeert een auteur iets uit te leggen en zo kennelijk toch wat inzicht bij te brengen. Dat is bijvoorbeeld het geval bij rekenen met breuken. De meeste auteurs delen alleen maar mee dat een breuk bestaat uit twee getallen met een streepje ertussen. Een enkeling laat het daar niet bij. Pijck probeert het begrip van breuken bij zijn leerlingen te verdiepen. Hij doet dat als volgt: ¼ betekent een vierendeel.Ga naar margenoot+ Van den Hoecke geeft de volgende toelichting bij het optellen van breuken: Om te verstane wat is de | |||||||
[pagina 222]
| |||||||
So neemt eenen nommer oft Inzicht in een breuk van een breukGa naar voetnoot106 brengt Van den Hoecke als volgt bij: Om te verstane wat is Pijck heeft vrijwel hetzelfde verhaal.Ga naar voetnoot108 Dit soort pogingen om begrip bij te brengen zijn over het algemeen een zeldzaamheid. De lezer die op zoek is naar een rekenrecept, heeft vermoedelijk weinig behoefte aan een dergelijk betekenisvol verhaaltje.Ga naar voetnoot109 Enkele auteurs gebruiken incidenteel een visueel model om hun uitleg te ondersteunen. Van der Gucht en de auteur van H-TSB-1578 gebruiken bij hun uitleg van progressio tekeningen waarmee de som van de reeksen in principe natelbaar is geworden.Ga naar voetnoot110 Van Halle verklaart met een tekening het begrip breuk van een breuk. In figuur 5.6 is te zien wat men zich kan voorstellen bij ¾ van ⅔ van 6/7 = 3/7. 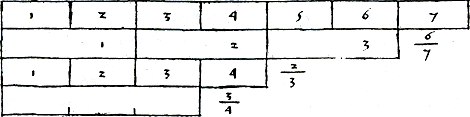 Figuur 5.6. ¾ van ⅔ van 6/7 = 3/7.Ga naar voetnoot111
| |||||||
[pagina 223]
| |||||||
Ook op andere momenten probeert Van Halle zijn uitleg met een visueel model inzichtelijk te maken: Daer is een viercant tichelen Een rechthoek van 33 bij 43 hokjes maakt de berekening van 33 maal 43 voorstelbaar en natelbaar. In de andere rekenboeken komen dergelijke tekeningen niet voor. Er is geen behoefte aan of misschien veroorzaakt het vervaardigen van de houtsneden te veel extra werk of onkosten. Wentsel wijst het gebruik van tekeningen in zijn rekenboek om principiële redenen expliciet af. In zijn voorreden schrijft hij: Men ghebruyckt wel somtijts Wentsel gebruikt geen tekeningen. Het is niet helemaal duidelijk wat hij met arithmetische demonstrationen bedoelt. Misschien slaat het op de schematische voorstellingen waarmee hij de oplossingen van zijn vraagstukken probeert weer te geven.Ga naar voetnoot114 Wentsels rekenboek onderscheidt zich niet van het werk van zijn collega's. Het bevat rekenrecepten zonder bewijzen of verklaringen. In zijn werk en dat van de andere auteurs gaat het erom dat de oplosmethodes helder beschreven, goed na te volgen en makkelijk uit het hoofd te leren zijn. Het stellen van de ‘waarom’-vraag is overbodig. | |||||||
[pagina 224]
| |||||||
5.3.3 Representatieve voorbeeldenAls Van Varenbraken uit wil leggen hoe de bewerking halveren uitgevoerd moet worden, kiest hij niet voor een algemene omschrijving, maar behandelt hij een voorbeeld. Hij begint zijn onderwerp als volgt: Mediatie en es anders nietGa naar margenoot+ Met ‘etcetera’ drukt Van Varenbraken uit dat alle vergelijkbare halveringen op overeenkomstige wijze uitgevoerd moeten worden. Vervolgens legt hij uit hoe het getal 3579 gehalveerd moet worden.Ga naar voetnoot116 Omdat in dit getal oneven cijfers voorkomen, behandelt Van Varenbraken het alsof het een volkomen nieuw probleem is. De overeenkomsten met het vorige voorbeeld vermeldt hij niet. Evenmin wordt de aanpak in algemene bewoordingen samengevat. Ook bij de overige auteurs worden rekenrecepten in de vorm van representatieve voorbeelden aangeleerd. De auteur van D-Man-1508 behandelt bijvoorbeeld het vermenigvuldigen van twee ongelijknamige breuken als volgt: Wildi adderen broken die | |||||||
[pagina 225]
| |||||||
8. Die addeert tot 9, wort De getallen in de vraagstelling van het voorbeeld hebben hier als het ware de functie van een variabele. De rekenaar mag elk getal door een willekeurig ander getal vervangen. De aanpak blijft dezelfde. De meeste auteurs behandelen elk type vraagstuk met behulp van minstens een representatief voorbeeld. Het aantal typen dat onderscheiden wordt, is groot en het aantal voorbeelden is dus minimaal net zo groot. Er is minstens een voorbeeldvraagstuk voor het vermenigvuldigen van twee breuken en minstens een ander voor het vermenigvuldigen van een breuk met een geheel getal, enz. Stockmans onderscheidt voor het optellen van breuken acht verschillende somtypen.Ga naar voetnoot118 De overeenkomsten tussen de oplosmethodes worden niet besproken. Men heeft geen behoefte aan verdere generalisaties. Ook op deze regel zijn weer uitzonderingen te vinden. Van den Hoecke, Van der Gucht en Pijck onderscheiden net als hun collega's allerlei afzonderlijke situaties bij het optellen en aftrekken van breuken, maar bij de hoofdbewerkingen vermenigvuldigen en delen doen ze dat niet. Daar behandelen ze al de situaties in één keer met een algemene regel. Van der Gucht vat het vermenigvuldigen van breuken, breuken van breuken en gemengde getallen als volgt samen: Reghel generael, om alleGa naar margenoot+ Verschillende rekenkundige situaties onder één regel vangen, zoals in het voorgaande citaat gebeurt, is een uniek verschijnsel in de Nederlandse rekenboeken. Meestal lijkt de auteur er juist naar te streven zoveel mogelijk verschillende situaties te onderscheiden en voor elke situatie een aparte regel of een aparte oplosmethode te beschrijven. Die oplossing volgt ook altijd onmiddellijk na het gegeven | |||||||
[pagina 226]
| |||||||
voorbeeld. De antwoorden achter in het boek zetten of geheel weglaten, zoals in moderne rekenboeken het geval is, zou de functie van het rekenboek als naslagwerk in de weg staan. Soms worden vraagstuktypen door middel van een opschrift van elkaar gescheiden. In sommige gevallen beschrijft dat opschrift het kenmerk waardoor dit vraagstuk afwijkt van zijn voorganger. Van Varenbraken onderscheidt bijvoorbeeld allerlei aparte situaties voor het geval dat er in de regel van drieën een of meer breuken voorkomen: Deerste questie behelstGa naar margenoot+ Soms is het opschrift de naam van een rekenregel. Vaak is dat een naam waaruit de leerling kan afleiden in welke situatie de regel toepasbaar is. Bijvoorbeeld: regel van geselschap, regel van gout en silver, regel van wisselinge, enz. Het grootste deel van deze regels is rekenkundig gezien gelijk, het gaat steeds om de regel van drieën, toegepast in een andere situatie. Helmduyn noemt zijn vraagstukken naar het product dat erin verhandeld wordt. Bijvoorbeeld: haringh, hoppe, Haerlems laken, Hollandtsche butter, ossen, enz. De opschriften zijn vaak in een grotere letter midden boven het vraagstuk of boven aan de bladzijde afgedrukt of geschreven. Dat brengt structuur aan en vergroot het opzoekgemak. De opschriften zijn vaak in de inhoudsopgave opgenomen. Een lezer die het rekenboek wil raadplegen om de oplossing van een bepaald praktisch vraagstuk te vinden, zoekt in de inhoudsopgave naar een opschrift dat in aanmerking komt en vergelijkt vervolgens de voorbeelden die onder dat opschrift gegeven worden met zijn eigen vraagstuk. Ziet hij een voorbeeld dat vergelijkbaar is, dan vult hij zijn eigen getallen in en vindt het antwoord op zijn vraag. | |||||||
5.3.4 Rekenen en het geheugenIn alle rekenboeken wordt van de leerling geëist dat hij de tafels van vermenigvuldiging grondig uit het hoofd leert. Van Varenbraken vermeldt naast zijn tafels: Dese tafel moet men leerenGa naar margenoot+ Van Varenbraken laat zijn leerlingen de tafels van vermenigvuldiging tot 12 × 12 uit het hoofd leren. Sommige auteurs vinden dat niet genoeg. In H-GeU-1592 is | |||||||
[pagina 227]
| |||||||
een schema opgenomen met de tafels van vermenigvuldiging tot 17 × 27 en ook daar krijgt de leerling de opdracht dat geheel uit zijn hoofd te leren.Ga naar voetnoot122 Van der Gucht geeft na een vierkant schema de tafels nogmaals weer, maar dan in kolomvorm, omdat naar zijn zeggen kinderen ze zo beter van buiten kunnen leren.Ga naar voetnoot123 Misschien verwijst hij hier impliciet naar het klassikaal opdreunen, want bij de tafels in kolomvorm staan de vermenigvuldigingen volledig genoteerd. In de buitenlandse rekenboeken is het al niet anders. Tartaglia adviseert zijn leerlingen de tafels van vermenigvuldiging tot en met 40 (!) uit het hoofd te leren. Hij beveelt vooral de tafels aan van getallen die in de praktijk veel voorkomen. Dat zijn bijvoorbeeld de waarden van munten, maten en gewichten.Ga naar voetnoot124 De vermenigvuldigsommen die gememoriseerd moeten worden, worden in de rekenboeken allemaal tegelijkertijd, dat wil zeggen in een overzicht gepresenteerd. Ze moeten samen met hun uitkomst als losse rekenfeiten in het geheugen geprent worden. Verbanden tussen sommen worden niet aangegeven en strategieën om een vermenigvuldiging uit een reeds bekend product af te leiden worden niet behandeld. De lezer wordt er bijvoorbeeld niet op geattendeerd dat 4 × 7 het dubbele is van 2 × 7. Later, in de Welsche of Italiaanse praktijk, blijkt, dat hij dit soort eigenschappen wel moet kennen en gebruiken. Toch is er één vermenigvuldigstrategie die de meeste auteurs al eerder gebruiken, ook al maken ze er niet expliciet melding van. Dat is de commutatieve eigenschap.Ga naar voetnoot125 Veel auteurs geven de tafels in kolomvorm weer. In deze kolommen worden vermenigvuldigingen die een omkering zijn van een al eerder genoemde berekening, niet nogmaals genoteerd. Ook Van Halle blijkt de commutatieve eigenschap te kennen. Hij geeft de tafels van vermenigvuldiging niet in een vierkante, maar in een driehoekige tabel weer.Ga naar voetnoot126 Er is echter geen enkele auteur die zijn leerlingen verklaart waarom hij bijna de helft van de vermenigvuldigingen heeft weggelaten en dat je het antwoord van bijvoorbeeld 6 × 3 kunt vinden door bij 3 × 6 te kijken. Verbanden en structuren zijn niet belangrijk. Het gaat erom dat de leerling voldoende rekenfeiten uit het hoofd leert. Die rekenfeiten blijven niet beperkt tot de tafels van vermenigvuldiging. Raets geeft het advies om de eerste negen kwadraatgetallen uit het hoofd te leren. Pijck voegt daar nog de eerste negen derdemachtsgetallen aan toe.Ga naar voetnoot127 In H-TSB-1578 krijgt de leerling de opdracht een complete tabel uit het hoofd te leren waarin gebroken ponden zijn omgerekend in schellingen en penningen.Ga naar voetnoot128 Zie figuur 5.7. | |||||||
[pagina 228]
| |||||||
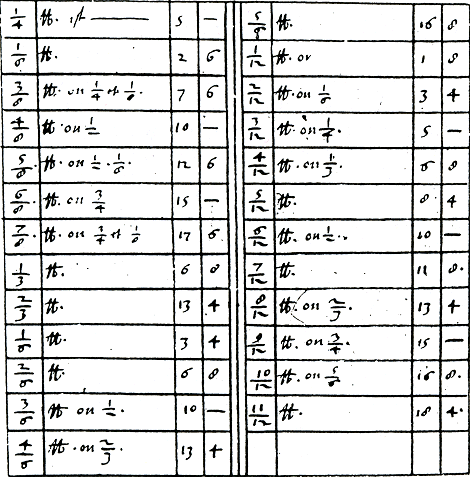 Figuur 5.7. Tabel waarin gebroken ponden zijn omgerekend in schellingen en penningen.Ga naar voetnoot129
Behalve feiten moet de leerling ook oplosmethodes uit het hoofd leren. Want ook al worden sommige rekenboeken in de beroepspraktijk als naslagwerk gebruikt,Ga naar voetnoot130 het is niet erg handig als de koopman voor ieder vraagstuk naar zijn boek moet grijpen. De leerlingen moeten in ieder geval de rekenrecepten voor de hoofdbewerkingen en de meest voorkomende rekenregels uit het hoofd kennen. De rekenles bestaat voor het grootste gedeelte uit memoriseren. Nu is het uit-het-hoofd-leren niet alleen aan het vak rekenen voorbehouden. Het speelt een belangrijke rol in het gehele Middeleeuwse onderwijs. In hoofdstuk 2 is vermeld dat dat een dubbele reden heeft. Enerzijds is men op memoriseren aangewezen omdat boeken schaars zijn en papier duur is. Anderzijds is men ervan overtuigd dat het memoriseren een goede vorm van onderwijs is.Ga naar voetnoot131 Hoe wordt er gememoriseerd? Het klassikaal opdreunen is een oude methode. Kerkvader Augustinus maakt er al melding van: Unum et unum duo, duo et duo Het is niet bekend of er in de zestiende-eeuwse scholen veel klassikaal gedreund is. Op de Grote school zitten vaak leerlingen van verschillende klassen bij elkaar in | |||||||
[pagina 229]
| |||||||
één lokaal. De stof die gememoriseerd moet worden, is nooit voor de hele groep gelijk. Volgens De Planque leren de leerlingen in groepjes. Gevorderde leerlingen helpen de minder gevorderden met het overhoren en instuderen van hun lessen.Ga naar voetnoot133 Mogelijk is deze werkvorm ook op de Franse scholen gebruikelijk geweest. Veel schoolboeken zijn in dialoogvorm geschreven. Deze vraag- en antwoordstijl is een handig hulpmiddel bij het overhoren en het ondersteunt het uit-het-hoofd-leren.Ga naar voetnoot134 Een zeer populair schoolboek in dialoogvorm is de Donaat, waarmee de leerlingen van de Grote school de basis van hun Latijn leren. Dit boek is een middeleeuwse bewerking van Ars minor van Aelius Donatus, rond 350 geschreven voor de Romeinse jeugd. Het boek bestaat uit vragen die direct door een antwoord gevolgd worden.Ga naar voetnoot135 Een ander schoolboek in dialoogvorm is t'samen-sprekinghen, waarin allerlei schoolvakken vragenderwijs aan de orde komen.Ga naar voetnoot136 Een enkele keer komt de dialoogvorm ook in rekenboeken voor, zoals in The ground of Artes (ca. 1541) van Robert Recorde. Dit Engelse rekenboek is een samenspraak tussen een leraar en een leerling. De leraar vertelt of stelt vragen en de leerling reageert daar op. Het is de bedoeling dat de lezer zich kan identificeren met de leerling. Door middel van handig vragen en suggereren worden nieuwe ideeën ontvouwd. Later volgen nog enkele andere Engelse rekenboeken in dialoogvorm. Elcius Mellema gebruikt deze stijl in zijn twee Franse rekenboeken,Ga naar voetnoot137 maar afgezien van deze voorbeelden komt de dialoogvorm in de rekenboeken niet voor. In de Nederlandstalige rekenboeken wordt deze stijl geen enkele keer aangetroffen. Toch moest er uit het hoofd geleerd worden. Om dat te bereiken gebruikte men in het onderwijs dikwijls het rijm als mnemotechnisch hulpmiddel. Valcooch verklaart in de voor-rede van zijn Regel der Duytsche School-meesters (1597) waarom hij zijn werk berijmd heeft: So heb ick dan dit boecxken Een berijmde tekst laat zich makkelijker in het geheugen prenten dan een prozatekst. Dat moet ook Alexander de Villa Dei gedacht hebben toen hij rond 1225 | |||||||
[pagina 230]
| |||||||
zijn berijmde rekentekst, Carmen de Algorismo, schreef. Verder zijn er geen rekenboeken bekend die volledig in verzen zijn geschreven. Wel komen er in sommige Nederlandse rekenboeken korte rekenkundige rijmpjes voor. Dat is met name het geval bij Van Halle en Van der Schuere. Van Halle begint elk nieuw onderwerp met een rijmpje. Bijvoorbeeld: Regel de tri, hoe gheGa naar margenoot+ Bij het rekenen met goud en zilver moet de rekenaar specifieke kleine gewichts-eenheden kennen. Van der Schuere rijmt: Tot het rauw gout ghewichte Soms worden ook bepaalde rekenhandelingen en oplosmethodes op rijm gezet. Van Halle noteert als inleiding op het aftrekken: Trecket affe die betalinghe Van der Schuere vermeldt bij de regel van gezelschap: Ter slinckerhandt den In de overige Nederlandse rekenboeken komt geen rijm voor. | |||||||
[pagina 231]
| |||||||
Geen dialoog, weinig rijm; de traditionele mnemotechnische hulpmiddelen ontbreken in de rekenboeken. Misschien voldoen ze niet helemaal in de praktische rekenkunde. In tegenstelling tot andere vakken moeten er in de rekenkunde zowel feiten als oplosmethodes gememoriseerd worden. Dat is informatie die de rekenaar in andere situaties moet kunnen toepassen. Hier is wellicht een andere manier van uit-het-hoofd-leren meer geschikt. De auteurs kiezen voor eindeloze herhaling en oefening van vraagstukken die onderling slechts in de gebruikte getallen verschillen. Na ieder vraagstuk volgt de volledig uitgewerkte oplossing.Ga naar voetnoot143 De leerling moet ‘eindeloos’ nadoen wat de meester heeft voorgedaan tot hij de methode zelf zonder hulp op een ‘nieuw’ vergelijkbaar vraagstuk kan toepassen. Naarmate de boekdrukkunst zich verder ontwikkelt en papierkosten dalen, neemt de hoeveelheid oefenmateriaal in de rekenboeken toe. In D-Man-1508 beslaat de rekenkunde inclusief de toepassingen 96 pagina's. Maar dat aantal stijgt snel in latere boeken. Aan het eind van de eeuw gebruiken Stockmans en Van der Schuere voor hun werk respectievelijk 416 en 408 pagina's.Ga naar voetnoot144 Volgens Swetz bestaat rond 1525 ongeveer eenderdedeel van de rekenboeken uit vraagstukken.Ga naar voetnoot145 Halverwege de zestiende eeuw nemen in de Nederlandse rekenboeken de vraagstukken zeker tweederdedeel van het geheel in beslag. Het is niet bekend of werkelijk al die vraagstukken met hun bijbehorende oplosmethode uit het hoofd geleerd moeten worden. In ieder geval ontwikkelt men in de loop van de zestiende eeuw wel een manier om oplossingen korter en schematischer weer te geven. Dit vergemakkelijkt het memoriseren.Ga naar voetnoot146 Het geheugen van de zestiende-eeuwse leerling wordt tijdens de rekenles nog in een ander opzicht zwaar belast. Niet alleen moeten oplosmethodes en de inhoud van tabellen in het geheugen geprent worden, de auteurs stimuleren hun leerlingen bovendien om bepaalde berekeningen uit het hoofd te doen. Dat wil zeggen, dat zij hun leerlingen adviseren om schriftelijk cijferwerk waar mogelijk, in gedachten, zonder papier, lei of wastafel uit te voeren. Pijck leert bijvoorbeeld zijn leerlingen vermenigvuldigen zonder de tussenproducten te noteren: Multiplicatie sonder additien.Ga naar margenoot+Ga naar voetnoot147 Hij gaat er hier blijkbaar vanuit dat de rekenaar de tafel van 12 uit het hoofd kent. Van der Gucht behandelt moeilijkere voorbeelden. Hij laat zijn leerlingen, in gedachten cijferend, het product berekenen van: 25 × 34, 3104 × 5461 en zelfs | |||||||
[pagina 232]
| |||||||
654321 × 123456.Ga naar voetnoot148 Hij legt niet uit hoe er hier uit het hoofd gerekend moet worden. Het lijkt niet aannemelijk dat men de tafel van bijvoorbeeld 5461 uit het hoofd kende. Bij het uit-het-hoofd uitvoeren van staartdelingen geeft hij wel enkele aanwijzingen, maar die berusten op de tafels die men gememoriseerd heeft: Als men wil divideren bij In figuur 5.8 is te zien welke voorbeelden hij behandelt. 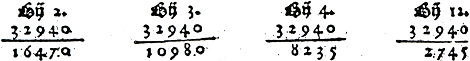 Figuur 5.8. Delingen die uit-het-hoofd zijn uitgevoerd.
Mogelijk hebben de vingers bij dit hoofdrekenwerk een rol gespeeld. In sommige abacusboeken, onder andere dat van Pacioli, legt men uit hoe getallen met de vingers weergegeven kunnen worden. Voor de eenheden worden vingers opgestoken en voor de tientallen worden vingerkootjes aangewezen.Ga naar voetnoot150 Er is niet zo zeer sprake van rekenen op de vingers maar meer van getallen uitbeelden. Volgens Tropfke werden de vingers op deze manier als geheugensteun bij het rekenen ingezet.Ga naar voetnoot151 In de Nederlandse rekenboeken komt alleen bij Van Halle een afbeelding van twee paar handen voor, maar elke verdere toelichting ontbreekt daar.Ga naar voetnoot152 Hoe er in het hoofd gecijferd wordt, is dus niet duidelijk, maar het wordt in ieder geval door verschillende auteurs van harte aanbevolen. De Italiaanse wiskundige Dionigi Gori (1510-ca. 1586) legt uit wat de voordelen van het cijferen-in-gedachten zijn: | |||||||
[pagina 233]
| |||||||
Sempre l'omo non à la penno Wie geen schrijfmateriaal bij zich heeft, zou nog kunnen rekenen met penningen, maar degene die uit zijn hoofd kan rekenen, zonder pen of penningen, heeft een voorsprong op collega's die dat niet kunnen. Voor moeilijke berekeningen met grote getallen is hoofdcijferen niet mogelijk, maar daar waar het kan, biedt het praktische voordelen. | |||||||
5.3.5 Het schriftelijk weergeven van berekeningen en oplosmethodesHet eerste wat een moderne lezer opvalt als hij een zestiende-eeuws rekenboek openslaat, zijn de grote stukken tekst. Vooral de boeken uit de vijftiende en het begin van de zestiende eeuw doen bij de eerste aanblik niet aan een rekenboek denken. De oplossingen worden uitvoerig, bijna in verhaalvorm, beschreven en ook voor berekeningen gebruikt men hele volzinnen. De taal is familiair, meestal wordt de eerste of tweede persoon gebruikt, en doet denken aan de wijze waarop recepten in kookboeken beschreven worden. Zie bijvoorbeeld het volgende fragment uit H-GeU-1532: 15 stuvers gheven my 1 elleGa naar margenoot+ Het oog vindt weinig houvast op een volgeschreven bladzijde. Om toch enige structuur in hun tekst aan te brengen, gebruiken de auteurs verschillende middelen. In paragraaf 5.3.3 is al vermeld dat opschriften boven een vraagstuk of bovenaan een bladzijde de zoekende lezer steun kunnen bieden. Kapitalen aan het begin van een nieuw onderwerp vervullen dezelfde functie. Daarnaast structureren de auteurs hun tekst door regelmatig gebruik van vaste woorden en uitdrukkingen. Exempel staat vaak aan het begin van een vraagstuk en item als er een vraagstuk van dezelfde soort volgt. Proeve kondigt een controle | |||||||
[pagina 234]
| |||||||
aan, nota waarschuwt dat er iets belangrijks komt en facit vestigt de aandacht op de uit uitkomst van de berekening. Om aan te kondigen dat een berekening is voltooid, gebruikt men uitdrukkingen als ende is ghedaen of dus doet van alle deser ghelijcke. Deze aanduidingen, vaak wat groter of apart afgedrukt, vereenvoudigen het opzoeken van een bepaald vraagstuk of een bepaalde berekening.Ga naar voetnoot155 Stockmans probeert dat te bereiken door het begin van elk vraagstuk met een wijzend handje te markeren. Bovendien scheidt hij vraagstukken van elkaar door middel van een horizontale lijn over de volle breedte van de bladzijde.Ga naar voetnoot156 Al deze hulpmiddelen maken de bladspiegel overzichtelijker. Tevens zoeken vrijwel alle auteurs naar mogelijkheden tot verkorting van de volledig in volzinnen uitgeschreven berekeningen en vraagstukken. Zo noteert bijvoorbeeld Van der Gucht niet iedere keer opnieuw de volledige berekening van de regel van drieën, maar schrijft hij werck naerden reghel. Hopelijk weet de lezer wat hem te doen staat.Ga naar voetnoot157 Heyns en Van den Dijcke gebruiken accolades om eindeloze herhaling van dezelfde tekst te vermijden. Zie figuur 5.9.  Figuur 5.9. Verkorte notatie van tien vermenigvuldigingen.Ga naar voetnoot158
Berekeningen kan men in woorden beschrijven, maar men kan ze ook in onder of naast elkaar geschreven getallen weergeven, een gecijferde weergave. Zie bijvoorbeeld de aftrekking in figuur 5.10.Ga naar voetnoot159 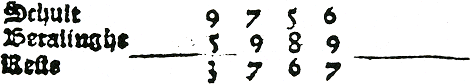 Figuur 5.10. Een aftrekking ‘gecijferd’ weergegeven.
| |||||||
[pagina 235]
| |||||||
In de edities van Die Maniere komen niet zoveel gecijferde voorbeelden voor, ongeveer een à twee per hoofdbewerking. Ze gaan vergezeld van een uitvoerige uitleg in woorden. In de overige rekenboeken staan veel meer berekeningen in de vorm van een cijferschema. Stockmans geeft bijvoorbeeld bij de hoofdbewerking optellen maar liefst 43 gecijferde voorbeelden; daarvan worden er zes ook nog volledig in woorden uitgelegd.Ga naar voetnoot160 Sommige auteurs werken van hun gecijferde voorbeelden er slechts een in volzinnen uit. Hier kunnen didactische motieven een rol gespeeld hebben. Gecijferde berekeningen geven de rekenboeken een rekenkundig aanzien. Maar ook in de boeken waarin veel cijferschema's voorkomen, spelen woorden en volzinnen nog steeds een grote rol. Dat komt omdat de auteurs vrijwel geen gebruik maken van rekenkundige symbolen.Ga naar voetnoot161 Men is op woorden aangewezen. Sommige rekenwoorden krijgen een soort symboolfunctie en dragen bij aan verkorting. Dat geldt bijvoorbeeld voor woorden als mael, ende, van, enz. Ze krijgen een vaste rekenkundige betekenis. Van Halle schrijft bijvoorbeeld: Hoe dat men weeten sal oft Op basis van dergelijke afspraken is het mogelijk rekenhandelingen verkort weer te geven. Stockmans schrijft bijvoorbeeld: 6⅓ van 3¼ tot 4⅚ van ⅞ komt 24 23/36.Ga naar voetnoot163 Dit regelmatige gebruik van ‘verkortende’ woorden heeft op den duur wél sommige rekenkundige symbolen opgeleverd, onder andere het teken =. De Engelsman Robert Recorde is de eerste die dit symbool gebruikt. Hij schrijft in zijn The whetstone of witte (1557) dat hij eindeloze herhaling van de woorden is equalle to wil vermijden. In plaats daarvan noteert hij twee horizontale strepen bicause noe 2. thynges, can be moare equalle.Ga naar voetnoot164 Met name in het tweede deel van hun rekenboek, bij het toepassen van rekenregels en het oplossen van vraagstukken, gebruiken vrijwel alle auteurs grafische middelen om hun oplosbeschrijvingen te schematiseren en te verkorten.Ga naar voetnoot165 Getallen worden via lijnen, kaders en steekwoorden met elkaar verbonden en overzich- | |||||||
[pagina 236]
| |||||||
telijk ruimtelijk neergezet, zodat het mogelijk wordt de oplossing in één oogopslag te overzien. In figuur 5.11 is te zien hoe Wentsel een optelling van twee ongelijknamige breuken noteert:Ga naar voetnoot166 addeert ⅕ met 1⅔.Ga naar margenoot+ 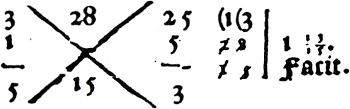 Figuur 5.11. ⅕ + 1⅔ = 1 13/15.
En een vermenigvuldiging van een geheel getal met een breuk ziet er bij Van Wentsel uit zoals in figuur 5.12 is te zien: Een sale is 20 voeten lanc 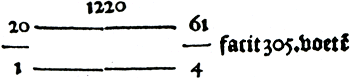 Figuur 5.12. 20 × 15¼ = 305
In de uitwerking van het volgende vraagstuk uit H-TSB-1578 wordt geen enkel woord gebruikt.Ga naar voetnoot168 Zie figuur 5.13. Addeert ¾ van ⅚ tot ⅔ van ¼, facit 19/24. 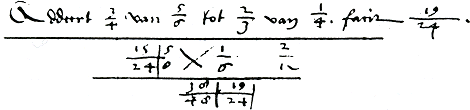 Figuur 5.13. ¾ × ⅚ + ⅔ × ¼ = 19/24.
Hoe groot het verschil is tussen deze schematische weergave en de beschrijving in volzinnen laat zich het best demonstreren aan de hand van een vergelijkbaar vraagstuk in D-Man-1510 en in D-Wen-1599. In D-Man-1510 staat: 165 pont was costen 2 ponden | |||||||
[pagina 237]
| |||||||
miten. Wat sullen costen 22?Ga naar margenoot+ Bij Wentsel wordt een vergelijkbaar vraagstuk als volgt gepresenteerd: | |||||||
[pagina 238]
| |||||||
Item een elle tafta voorGa naar margenoot+ 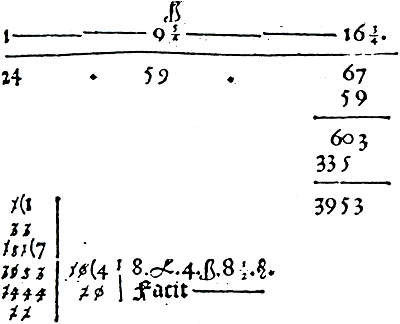 Figuur 5.14. Berekening met de regel van drieën schematisch weergegeven.
De oplosmethode die in Die Maniere vele regels tekst in beslag neemt, wordt door Wentsel in enkele lijnen en getallen weergegeven. Het gebruik van schema's maakt de weergave van de oplossing overzichtelijker. Daardoor wordt het eenvoudiger om de oplosmethode uit het hoofd te leren. Bovendien wordt de kans op fouten kleiner. Als het schema juist is ingevuld, kan er met de berekening bijna niets meer mis gaan. De functie van de rekenkundige schema's is vergelijkbaar met de cirkelfiguren die in de werken over tijdrekenkunde voorkomen, zoals bijvoorbeeld dat van meester Jacobus. Ook daar ondersteunen de schema's het geheugen en verkleinen ze de kans op fouten.Ga naar voetnoot171 Een duidelijk voorbeeld uit de rekenboeken van een schema dat de rekenaar moet invullen om het juiste antwoord te vinden, geeft Van Varenbraken:Ga naar voetnoot172 Een coopman heeft eenen sack | |||||||
[pagina 239]
| |||||||
| |||||||
[pagina 240]
| |||||||
Vergelijkbare schema's worden vaak ingevuld bij het controleren van een berekening met de zeven- of negenproef.Ga naar voetnoot174 Waarom het klopt is voor de leerling niet belangrijk, maar als hij zijn schema volledig en correct invult, vindt hij het juiste antwoord en daar gaat het om. Samenvattend kan men zeggen dat in de vijftiende-eeuwse rekenboeken en de edities van Die Maniere de rekenkunde vooral in woorden en volzinnen weergegeven wordt, terwijl in de overige rekenboeken naast deze verhalende manier van uitleggen een aanzienlijk aantal berekeningen met behulp van cijfers en andere grafische middelen is weergegeven. Deze verkortende weergaven van berekeningen en oplosmethodes bevorderen het uit-het-hoofd leren en het foutloos rekenen. Tevens vormen ze een belangrijke stap in de richting van de symbolische stijl van de moderne wiskunde. | |||||||
5.3.6 Algemene en alternatieve oplosmethodesIn vrijwel alle rekenboeken leert de leerling ‘blindelings’ rekenen. Hij moet het vraagstuk herkennen en vervolgens de juiste bijbehorende oploswijze toepassen. Over het algemeen leert de leerling voor elk soort probleem slechts een oplosmanier. Dat is de methode die in alle gevallen - van dezelfde soort - toepasbaar is. Helmduyn behandelt bijvoorbeeld de volgende methode om te bepalen welke van twee breuken de grootste is: Om te weten welcke broke van 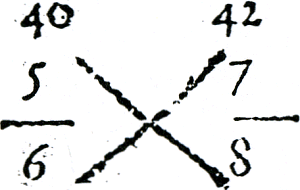 Figuur 5.15. Welke breuk is groter: ⅚ of ⅞?
De noemers worden gelijknamig gemaakt door ze met elkaar te vermenigvuldigen en vervolgens worden de tellers met elkaar vergeleken. Het is een methode die altijd opgaat. De auteur vermeldt niet dat dit specifieke voorbeeld eventueel ook op een andere manier opgelost had kunnen worden. Hij had de noemers ook tot 24 kunnen herleiden. Het is zelfs mogelijk om in één oogopslag te zien dat ⅞ de groot- | |||||||
[pagina 241]
| |||||||
ste breuk is, omdat het verschil van 1 en ⅞ slechts ⅛ is, terwijl het verschil van 1 en ⅚ meer, namelijk ⅙ is. Deze alternatieve oplosmogelijkheden gelden alleen voor deze speciale getallen en daarom behandelt Helmduyn ze niet. Het gaat de auteurs van de rekenboeken namelijk om regels die voor alle vraagstukken van dezelfde soort bruikbaar zijn, ook al wordt het rekenwerk er soms omslachtig door. Het voordeel van deze aanpak is dat hij de rekenaar houvast biedt. Bij elk probleem hoort één vaste regel en als je die toepast vind je hoe dan ook het goede antwoord. Natuurlijk zijn er ook op deze regel weer uitzonderingen te vinden. Van den Hoecke behandelt twee manieren om 2⅔ + ⅘ te berekenen.Ga naar voetnoot176 Pijck beschrijft twee manieren om een breuk te verdubbelen en ook nog een alternatieve manier om twee breuken gelijknamig te maken.Ga naar voetnoot177 Maar afgezien van deze voorbeelden geven de auteurs van de rekenboeken bij ieder vraagstuktype slechts een oplosmethode en dat is de methode die voor dat type vraagstuk ‘altijd’ opgaat. Toch wordt in een aantal rekenboeken tamelijk plotseling van deze didactische opvatting afgeweken. Dat gebeurt in het hoofdstuk over de Welsche of Italiaanse praktijk.Ga naar voetnoot178 Opeens worden er naast de voorgeschreven standaard procedures alternatieve rekenregels behandeld, handige oplosmethodes die het rekenwerk kunnen versnellen en vereenvoudigen. Het zijn regels die niet universeel bruikbaar zijn, maar die alleen in speciale gevallen met geschikte getallen, bij bepaalde gewichten, munten of maten rekengemak opleveren. Hierbij is dus geen sprake van een algemene oplosprocedure die de leerling ‘blindelings’ kan volgen. Integendeel, de rekenaar moet bij het toepassen van de Welsche of Italiaanse praktijk inzicht hebben in de eigenschappen van getallen, handige maten kennen en kennis van rekenstrategieën bezitten. Alleen dan kan hij zelf voor een vraagstuk de geschiktste oploswijze kiezen. De Welsche of Italiaanse praktijk is een ‘creatieve’ manier van rekenen. De methode wordt slechts in enkele rekenboeken behandeld en krijgt daar vaak slechts een bescheiden plaats toebedeeld. Het lijkt erg onwaarschijnlijk dat leerlingen die met behulp van de rekenboeken hebben leren rekenen en opgevoed zijn met het blindelings uitvoeren van voorgeschreven rekenrecepten, tot dit inzichtelijke rekenwerk in staat zijn. De kloof tussen beide rekenmanieren is daarvoor te diep. Dit doet vermoeden dat het leerproces nog niet is afgelopen als de rekencursus uit het boek ten einde is. Het werkelijke koopmansrekenen met gebruikmaking van handige rekenregeltjes die tijdwinst en rekengemak op kunnen leveren, wordt waarschijnlijk pas in de praktijk goed geleerd. Volgens Benoit en Swetz gaan in Italië toekomstige kooplieden, nadat ze op school koopmansrekenen hebben geleerd, als leerling bij een koopman in dienst om hun opleiding te voltooien.Ga naar voetnoot179 Mogelijk gebeurt dat in de Nederlanden ook. Uit de rekenboeken blijkt in ieder geval dat de leerling nog veel moet bijleren voordat hij werkelijk flexibel, efficiënt en | |||||||
[pagina 242]
| |||||||
met inzicht kan rekenen. Het is noodzakelijk dat hij dat niveau op den duur bereikt, want de praktijk stelt hoge eisen aan de rekenvaardigheid van de koopman. Simon Stevin doet in De Thiende een poging om het ingewikkelde praktische rekenwerk te vereenvoudigen.Ga naar voetnoot180 Hij blijkt goed op de hoogte te zijn van de re kenkundige problemen uit de dagelijkse praktijk van koop- en ambachtsman. Hij kent ... de verdrietighe Daarom schrijft hij De Thiende want Sy leert ... alle rekeninghenGa naar margenoot+ Dit moet menigeen als muziek in de oren geklonken hebben, want het decimale systeem van munten, maten en gewichten waar Stevin in zijn Aenhangsel voor pleit maakt de Welsche of Italiaanse praktijk vrijwel overbodig. Hij richt zijn werk tot ... den sterrekyckers, Hij legt uit hoe ze de hoofdbewerkingen met decimale breuken moeten uitvoeren, waarbij hij ervan uitgaat dat ze de basis van het rekenen al onder de knie hebben. De Thiende is geen schoolboek. Het is evenmin als naslagwerk te gebruiken want er staan geen tabellen, rekenregels en praktische vraagstukken in. De doelgroep die Stevin noemt, heeft het boekje waarschijnlijk nauwelijks in handen gekregen. De zestiende-eeuwse kooplieden maakten geen kennis met zijn decimale breuken. Dat was misschien jammer, maar het zou hun voorlopig erg weinig rekengemak hebben opgeleverd. Hun dagelijkse praktijk was er nog niet op ingesteld. Nog eeuwenlang moeten kooplieden blijven werken met allerlei niet ge- | |||||||
[pagina 243]
| |||||||
standardiseerde munten, maten en gewichten en blijven worstelen met het ingewikkelde rekenwerk dat daaruit voortkomt. Pas in de negentiende eeuw wordt er in Nederland een decimaal matensysteem bij wet ingevoerd. In de rekenboeken leren kooplieden de basis van de rekenkunde, maar de werkelijke rekenvaardigheid wordt opgedaan in de praktijk. | |||||||
Ten slotteIn dit hoofdstuk is gebleken dat de auteurs van de Nederlandse rekenboeken publiekgericht schrijven. Ze hebben twee doelgroepen op het oog:
Beide groepen zijn geïnteresseerd in rekenrecepten waarmee ze vraagstukken uit hun (toekomstige) praktijk kunnen oplossen. De rekenboeken voorzien in deze behoefte. Grote aantallen realistische vraagstukken worden stap-voor-stap voorgerekend. Oplosmethodes worden gepresenteerd als rekenrecepten. In sommige gevallen zijn de recepten wel wat omslachtig, maar wie ze toepast op vraagstukken die vergelijkbaar zijn met het voorgerekende, representatieve voorbeeld, vindt altijd het goede antwoord. Bewijzen en definities ontbreken over het algemeen. Waarom het rekenrecept werkt, is niet belangrijk. De doelstelling van de rekenboeken is praktisch en niet wiskundig. De leerling wil weten wat hij moet doen en niet waarom hij het zo moet doen. Door middel van voorbeelden met hun oplossing worden de rekenrecepten in het geheugen geprent. In de vijftiende-eeuwse rekenboeken en in de edities van Die Maniere volstaat men met een à twee voorbeelden per onderwerp, waarvan de berekening volledig in volzinnen uitgelegd wordt. In de latere rekenboeken neemt het aantal vraagstukken toe en verschijnen soms tientallen voorbeelden bij een onderwerp. Een ander opvallend verschijnsel in de latere rekenboeken is het feit dat de uitvoerige uitleg in woorden en volzinnen in steeds meer gevallen vervangen is door een gecijferde, schematische weergave van de oplosmethode. Zo'n cijferschema heeft als voordeel dat de oplosmethode overzichtelijk is en minder ruimte in beslag neemt. Bovendien is de oplosmethode makkelijker uit het hoofd te leren en wordt de kans op het maken van fouten verkleind. In deze verkortende, schematische weergave kan men een voorbode van de latere symbolische wiskundenotatie zien. In veel rekenboeken treft men grootgedrukte opschriften, suggestieve namen voor rekenregels en een inhoudsopgave aan. Zo is het mogelijk oplosmethodes snel terug te vinden en het rekenboek als naslagwerk te gebruiken. Hoewel de rekenboeken in de eerste plaats een praktische doelstelling hebben en voornamelijk realistische vraagstukken bevatten, komen er toch altijd wel enkele niet-realistische berekeningen en vraagstukken in voor. Deze zijn waarschijnlijk toegevoegd om hun traditionele, esthetische of recreatieve waarde. In de rekenboeken wordt over het algemeen voor ieder vraagstuk slechts een | |||||||
[pagina 244]
| |||||||
oplosmethode behandeld. Alleen in het hoofdstuk van de Welsche of Italiaanse praktijk komen alternatieve - meestal efficiëntere - oplosmanieren aan de orde. Dit hoofdstuk komt in slechts enkele rekenboeken voor. Wie standaardrecepten wil leren of opzoeken, kan met de rekenboeken een heel eind komen. Wie een vlotte, flexibele rekenaar wil worden, die met begrip en inzicht in alle omstandigheden de handigste en efficiëntste oplosmethode weet te kiezen, moet eerst nog flink oefenen in de praktijk. |
|


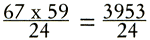 = 8 ponden 4 schellingen 8½ penningen.
= 8 ponden 4 schellingen 8½ penningen.